Cable-Driven Parallel Robot Actuators: State of the Art and Novel Servo-Winch Concept

Abstract

Cable-Driven Parallel Robots (CDPRs) use cables arranged in a parallel fashion to manipulate an end-effector (EE). They are functionally similar to several cranes that automatically collaborate in handling a shared payload. Thus, CDPRs share several types of equipment with cranes, such as winches, hoists, and pulleys. On the other hand, since CDPRs rely on model-based automatic controllers for their operations, standard crane equipment may severely limit their performance. In particular, to achieve reasonably accurate feedback control of the EE pose during the process, the length of the cable inside the workspace of the robot should be known. Cable length is usually inferred by measuring winch angular displacement, but this operation is simple and accurate only if the winch transmission ratio is constant. This problem called for the design of novel actuation schemes for CDPRs; in this paper, we analyze the existing architectures of so-called servo-winches (i.e., servo-actuators which employ a rotational motor and have a constant transmission ratio), and we propose a novel servo-winch concept and compare the state-of-the-art architectures with our design in terms of pros and cons, design requirements, and applications.

1. Introduction

Large-scale handling of bulky loads is a widespread necessity throughout the world. Manufacturing plant logistics, infrastructure construction and maintenance are just two of the most prominent examples where anyone can observe several overhead cranes, truck-mounted and fixed-installation cranes, working independently, and entirely manually operated. Conversely, Cable-Driven Parallel Robots (CDPRs in short) work like fully-automated collaborative cranes. They are parallel robotic manipulators where rigid links are replaced by extendable cables. The latter are wound and unwound by linear or rotational actuation units (called winches in the following) and routed using guidance devices toward a shared end-effector (EE in short), on which they are attached in a parallel fashion [1].

CDPRs potentially have a large and reconfigurable workspace. First, because very long cables can be coiled on rotary winches. Furthermore, cables operate in a structurally efficient manner, being subject only to tensile loads. In addition, if properly designed, actuation units and guidance systems can be rearranged discretely [2] and continuously [3], allowing for rapid changes in workspace size and shape. However, since multiple cables act in parallel on the same load, part of the work they exert is spent keeping each other in tension [4]. Nevertheless, they may be more efficient than industrial robots, as the latter have to carry their weight around [5]. Additionally, if the task and worksite characteristics are specified, cables can also be balanced with counterweights [6].

Despite their advantages, the use of CDPRs in the industry is still limited due to their design, control, and safety challenges. Controllability and safety, on the one hand, can be enhanced by employing more cables than the EE degrees of freedom (DoFs in short). However, this can cause cables to collide with each other and their surrounding environment, limiting the robot’s workspace or forcing the use of rigorous design techniques to avoid it [7]. In this case, workspace accessibility may be improved by suspending the EE, using a redundant number of cables [8,9]. Regardless, the likelihood of cable-to-cable interference could increase [10]. Therefore, in order to simplify the design and rationalize the cost of the robot, simpler suspended CDPR have been proposed, with fewer cables than EE’s DoFs, which, on the other hand, require dedicated control schemes for their effective use since the EE is unconstrained [11,12].

The earliest example of a CDPR is the famous Skycam® [13], which is still used as a camera motion device for overhead sport event shooting. However, research interest in the possible applications of this technology only began a few years later, when Higuchi et al. [14] highlighted the numerous advantages of cranes’ automatic cooperation. Only in the nineties the RoboCrane® was introduced [15]: this equipment was the first to allow both position and orientation of its EE to be automatically controlled with six cables. Since then, numerous applications have been proposed and successfully implemented by researchers: large-scale additive manufacturing [16], laser-based manufacturing [1], contour crafting [17], marine handling systems [18], warehouse retrieval systems [6], large-scale handling systems [19,20], facade cleaning [21] and installation [7] systems, motion simulators [22], large-aperture telescopes [23], measurement devices [24,25,26,27], rehabilitation devices [28], and haptic interfaces [29].

Different cable-driven applications usually have highly different requirements: even though the principal mean of transmission is a cable, its actuation unit and guidance system are engineered according to other principles. Ref. [30] reports a comprehensive study of cranes, winches, and hoists to be used in civil engineering applications. On the opposite spectrum than civil applications, there are cable-driven hands and fingers, where cables are used to actuate joints remotely, so that most of the actuation weight is as distant as possible to where the force application is needed [31,32]. Miniaturization, force capability, and motion accuracy is instead required in so-called tendon-driven continuum robots, where a remote cable actuation is needed to control the deformation of slender links [33,34], and in tensegrity-based robots [35]. Lastly, the growing interest in mobile robot applications has motivated researchers to develop lightweight and small winches with high-force capabilities [36,37].

For industrial applications, guidance systems are usually a combination of fixed and swiveling pulleys [1], whose geometry and installation configuration are dictated by geometric and loading conditions of the operation (many research prototypes have even simpler guidance systems, such as eyelets where cables may slide through [38]). Conversely, the design of the actuation unit is driven by application requirements in terms of rated power, cable tension, and speed, but also by the requirements of the control system. The most common one is the ability to feedback control the EE pose. To succeed in such a task, one may rely on exteroceptive measurement devices directly providing EE pose information [39,40], state estimators [41,42], or forward kinematics based on cable length estimation. The latter approach is widely used thanks to well-established techniques in the solution to the forward kinematic problem and thanks to the fact that no sensors other than the ones embedded in the actuators for their low-level feedback control need to be added to the robot (additional sensors can be added to speed-up computation, improve accuracy [43,44], or if embedded sensors are not sufficient [45]). However, accurate pose information is achievable through forward kinematics if and only if (i) a cable model suitable to the application requirement is used [46,47,48], and (ii) there is a clear correlation between actuator displacement $\mathsf{\Delta }\theta$ and cable displacement $\mathsf{\Delta }l$, namely the actuation unit transmission ratio $K=\mathsf{\Delta }l/\mathsf{\Delta }\theta$. If the latter condition is not satisfied, it is unlikely that the use of a suitable cable model would work without additional sensors. This fact motivated researchers to characterize existing types of cable actuation systems or develop new ones suitable for robotic purposes [49].

Concerning actuation, the most straightforward way to wind a cable is using a smooth drum connected to a motor [50,51]. Unfortunately, it is not trivial to determine how the cable is wound over the drum, as the axial a and radial r winding distances are not a function of the motor angle (Figure 1a). As an alternative, cables can be overlapped (i) on very short drums [52] (Figure 1b), (ii) on smooth or grooved drums by a self-reversing screw (Figure 1c), or even (iii) on variable-radius drums [53,54]; all these choices allow for a correlation between cable and motor displacement. Unfortunately, the transmission ratio K is a function of the absolute motor angle, which may not be known at start-up time, and, furthermore, a varying r implies varying tension-speed limits for a given motor-rated power. The possibly simpler and commercially available solution for a constant and known K is to use a hoist (Figure 1d), and a linear actuator for its control [55]. However, if long cables need to be used, the installation space, transmission ratio, and cable wear increase alongside the number of pulleys in the hoist [49].

To the best of the authors’ knowledge, the first example of a servo-winch, namely a rotary winch characterized by a constant and known transmission ratio, was proposed in [56]. Since then, many other solutions have been proposed in the literature, mainly to compensate for the lack of existing commercial devices. Generally speaking, to build a CDPR prototype for research or industrial purposes, a dedicated winch must be designed in-house. A comparison of existing architectures of servo-winches is not available in the literature, and thus, one can choose between different designs, based solely on experience, if any. The reason for choosing one servo-winch is, to say the least, unclear and not shared among the cable-robotic community. Thus, this paper aims to (i) provide a comprehensive description of the state-of-the-art solutions for servo-winch design, (ii) propose a novel servo-winch design, and, lastly, (iii) provide guidelines for the selection of optimal servo-winch architecture based on the benefits and drawbacks of the existing solutions. The remainder of the paper is structured as follows: Section 2 analyzes the state of the art in the servo-winch design, while Section 3 describes a novel design, called Spline Winch; design comparison and architecture selection guidelines are discussed in Section 4. Finally, conclusions are drawn.

2. Servo-Winch State of the Art

As introduced above, to have accurate information on the EE pose, servo-controlled winches should have a constant transmission ratio K. For this purpose, two aspects must be considered:

• Cable overlapping on the drum surface should be avoided, which can be done, for example, by grooving the drum to accommodate the cable (this is also desirable for reducing cable wear [57]);
• The cable should exit the drum in a fixed, known direction.

There are several solutions in the literature to achieve such desired design requirements, which can be organized into three classes: (i) the rototranslating-drum winch, (ii) the spooling-helper winch, and (iii) the translating-motor winch.

2.1. The Rototranslating-Drum Design

By rototranslating the drum [24,38,56], the cable exit point, and consequently, its direction, is fixed with respect to (w.r.t. in short) the winch frame, while the cable is coiled and uncoiled (Figure 2a). A scheme of the winch is shown in Figure 2b: a screw/nut system (helicoidal pair, H) is employed to convert the rotational motion of the motor (M) into rotational and translational motion of the drum (D). The screw shaft is fixed to the winch frame, and the drum slides on passive prismatic joints (P) along two rods parallel to the drum axis but mounted with a radial offset w.r.t. the drum. The motor can be coupled to the drum using a transmission, such as a synchronous belt, as in Figure 2a. As an alternative, other mechanisms can be employed for this purpose, such as a crank mechanism [58]. By simply considering that the drum rotates and translates, and for each motor turn, a complete helix is wound or unwound, the transmission ratio K can be evaluated as:

$$K=\sqrt{K_S^2+r_D^2}[\mathrm{m}/\mathrm{rad}],K_S=\frac{h}{2\pi }[\mathrm{m}/\mathrm{rad}]$$

(1)

where h is the helix pitch, $r_D$ is the drum grooving radius, and $K_S$ is the screw/nut transmission ratio.

2.2. The Spooling-Helper Design

In [59], an auxiliary cable guiding device equipped with a pulley, called spooling helper, is employed. Similar to the concept of the self-reversing screw, but only using a traditional screw/nut system, the spooling helper continuously follows the variable cable exit point on the rotating drum by translating parallel to the drum axis so as to ensure that the cable direction connecting the drum and the spooling helper is constant (Figure 3a). According to Figure 3b, the rotation of the motor/drum system (M and D) is transmitted to the spooling helper (S) using a synchronous belt (B). Thanks to a helical pair (H), the spooling helper slides onto two fixed rods (prismatic joints, P). Due to the presence of the spooling helper, the transmission ratio of this design differs from the one of the rototranslating drums:

$$K=\sqrt{K_S^2+r_D^2}-K_S[\mathrm{m}/\mathrm{rad}]$$

(2)

2.3. The Translating-Motor Design

A different solution, less common to the author’s knowledge [1,60], consists of translating the entire motor/drum system on a linear guide (Figure 4a). As shown in Figure 4b, motor (M) and drum (D) are directly connected and mounted on a carriage (C). The motor is fixed w.r.t. the carriage, whereas the drum can rotate supported by two bearings (R). The rotational motion of the drum is transformed into the translation of the carriage along two prismatic pairs (P) thanks to a helical pair (H). The latter is usually realized using a screw/nut system, where the nut is fixed to the drum. This solution has the same kinematic behavior as the rototranslating design, and its transmission ratio is hereby reported for completeness:

$$K=\sqrt{K_S^2+r_D^2}[\mathrm{m}/\mathrm{rad}]$$

(3)

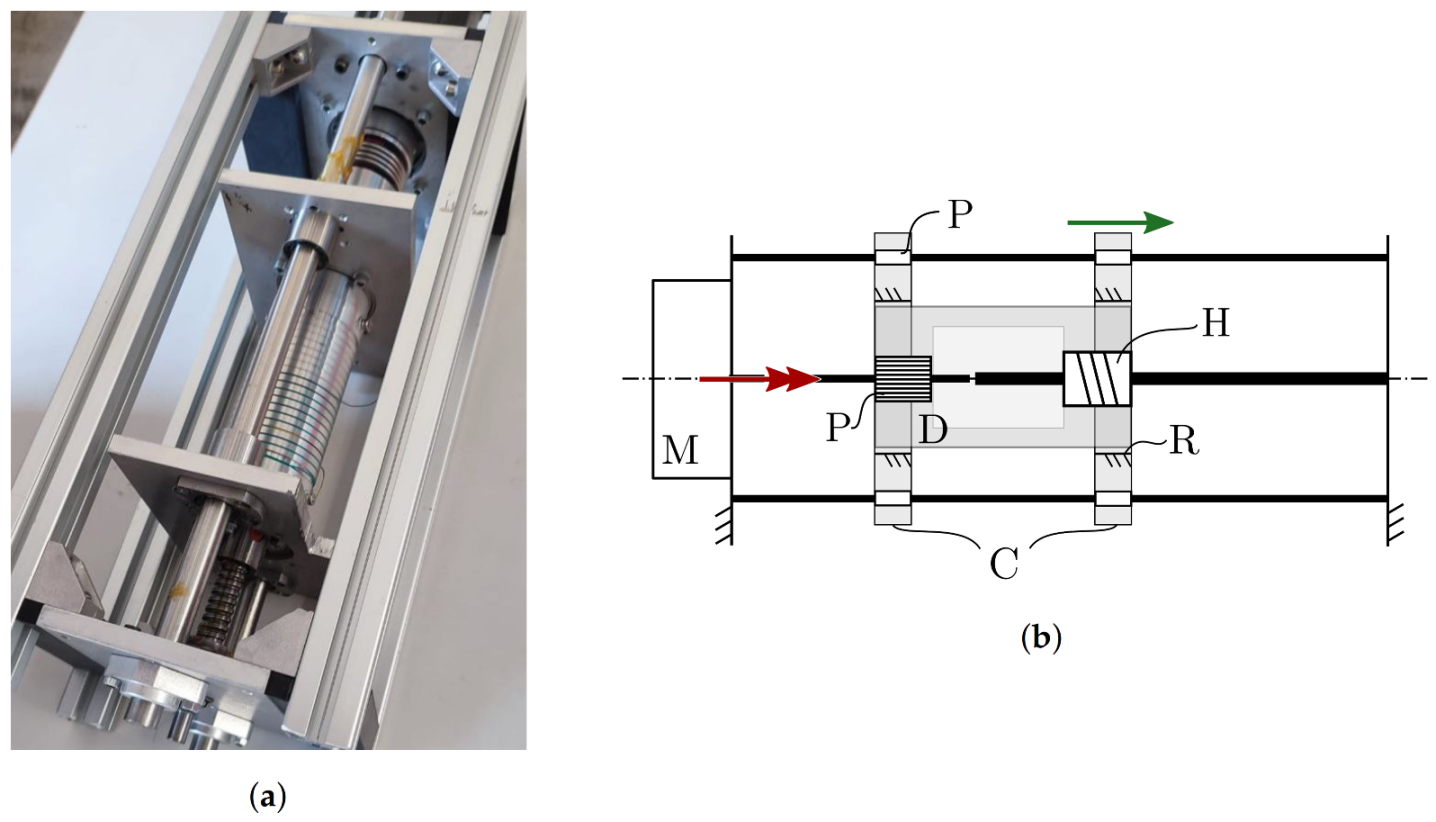
3. The Spline Winch

The winch design proposed in this paper, called Spline Winch, is shown in Figure 5. The proposed design concept aims to merge the benefits of the rotrotranslational-drum design with the ones of the translating-motor system, as detailed in Section 4.

3.1. Kinematics

The motor (M) is fixed to the winch frame, while the drum (D) can (see Figure 5):

• Rotate since a spline shaft is rigidly attached to the motor axis, and a spline nut is attached to the drum; the spline shaft/nut pair is effectively a prismatic joint (P), designed so as to transmit torque while allowing axial translation;
• Translate since a screw shaft is rigidly attached to the winch frame, and a screw nut is attached to the drum; this is the classical helical pair (H) used in all winch designs.

The drum is supported via two plates (or carriages, C): a revolute joint (R) and two prismatic joints (P) are embedded into each plate, so that the drum can freely rotate w.r.t. the plates, and the drum-plates assembly can translate w.r.t. the winch frame.

Since the drum rototranslates, the overall transmission ratio K of the spline winch is the same as the rototranslating-drum one, namely:

$$K=\sqrt{K_S^2+r_D^2}[\mathrm{m}/\mathrm{rad}]$$

(4)

3.2. Mechanical Design

The proposed Spline Winch was designed and built at IRMA L@B (Figure 6). Its mechanical design is detailed hereafter and shown in Figure 6b. Its frame consists of two aluminum plates (1), connected by extruded aluminum profiles (see Figure 6a). Two floating plates (2) are connected with four ball bushings (3), that allows the translation w.r.t. to two rods (4); the latter are connected to the frame through rigid couplings (5). The motor is coupled to the ball spline shaft (6) through a bellow coupling (torsionally stiff but flexurally compliant, see Figure 6a since motor and coupling are not represented in the cross section). Instead of a regular spline shaft, a ball spline shaft is chosen due to its zero-backlash and low friction properties; this component is widespread and cost-effective due to its frequent use in machining equipment tool-change systems. A ball screw shaft (8) is also attached to the winch frame, on the opposite side w.r.t. the ball spline shaft.

The ball spline (7) and ball screw (9) nuts are rigidly attached to two drum covers (10), which are free to rotate w.r.t. the floating plates (2) thanks to radial bearings (11), and are rigidly attached to a tube drum (12). The choice of decomposing the drum in two covers allows to (i) critically reduce weight, (ii) save machining waste (for a single component drum of the same weight, most of the raw material would only be waste), modify the winch transmission ratio by only machining a new tube—the last feature is particularly interesting for research prototypes, whose performance requirements may vary over time.

At last, the ball spline and ball screw shaft are aligned with a coupling (14), which embeds a bushing (13) to allow the rotational motion of the spline w.r.t. the screw.

The winch is structurally optimal, since the shafts (4) resist the external load imposed by the cable, and the overall moving mass and inertia are inherently reduced w.r.t. to rototranslating-drum and translating-motor winches. With $r_d=29\mathrm{mm}$ and $h=5\mathrm{mm}$, the winch has a transmission ratio $K=29.01\mathrm{mm}/\mathrm{rad}$. Thanks to the $P_{m,r}=750\mathrm{W}$ of rated power, and $T_{m,r}=2.39\mathrm{Nm}$ of rated torque, the winch can nominally balance a tension of $\tau =82.38\mathrm{N}$, while displacing the cable at $9.103\mathrm{m}/\mathrm{s}$. The applications intended for this winch are highly dynamic ones.

4. Design Comparison and Application Guidelines

After briefly revising existing servo-winch architectures, and introducing the Spline Winch, a critical comparison of each winch’s pros and cons is in order. By the end of this section, we aim to provide some winch architecture selection guidelines, depending on application requirements. In the following, friction in the components is neglected. This choice was deemed necessary not because friction is, in fact, negligible but because we want to highlight several important factors which are fundamental regardless of friction. The reader is referred to Chapter 8.6.2 [61] for details about single component selection for optimizing winch frictional behavior. Additionally, the effect of the gravitational force on the winch dynamics is not explicitly accounted for, because it varies depending on the winch installation configuration. This effect will only be evaluated qualitatively in the following.

We start by observing that all winch architectures share some components, such as a drum, some rods w.r.t. whom the drum can slide, a translating component (whether the drum or the spooling helper), and a screw/nut system for transforming rotational motion in a linear one. We can then divide the architectures into two groups, namely one group characterized by the rototranslation of the drum (rototranslating-drum, translating-motor, and Spline Winch design), and one group represented by the decoupling of rotation and translation for achieving constant cable direction exiting the drum, namely the spooling-helper design.

For each winch, the overall dynamics is:

$$T_M=J^{🟉}\ddot{\theta }+K\tau$$

(5)

where $T_M$ is the motor torque, K is the winch transmission ratio, and $J^{🟉}$ the overall transmission inertia reduced to the motor axis. From a dynamic point of view, the first group of winches shares similar load distributions when transforming the motor torque into cable tension. The rototranslating drum is selected to provide a schematic representation (see Figure 7a). The drum rotational dynamics is given by (see Figure 7b):

$$J\ddot{\theta }+T_s+r_D{\tau }_{CS}=r_{S}F$$

(6)

where J is the inertia of all the rotating components, $T_s$ is the screw reaction torque, ${\tau }_{CS}$ is the tension component projected onto the drum cross-section, $r_{S}F=T_M$ is the product between the shaft radius and the shaft reaction force, which equals the torque exerted by the motor. If we consider the relationship between the axial force Q and the torque $T_S$ exchanged in the screw/nut pair to be:

$$T_S=K_{S}Q,K_S=\frac{h}{2\pi }\mathrm{m}/\mathrm{rad}$$

(7)

The translational dynamics of the drum are (Figure 7c):

$$Q={\tau }_{AX}+M{K}_S\ddot{\theta }$$

(8)

where M is the mass of all translating components, and ${\tau }_{AX}$ is the component of $\tau$ directed as the winch axis.

If we now remember helix geometrical properties, we have:

$$\tau =\sqrt{{\tau }_{AX}^2+{\tau }_{CS}^2},\frac{{\tau }_{AX}}{h}=\frac{{\tau }_{CS}}{2\pi r_D}$$

(9)

and substitute Equations (7) and (8) in (6), after some algebraic manipulation we finally get:

$$T_m=r_{S}F=\left(J+K_S^{2}M\right)\ddot{\theta }+\left(\sqrt{K_S^2+r_d^2}\right)\tau$$

(10)

which compared with Equation (5) gives:

$$J^{🟉}=J+K_S^{2}M,K=\sqrt{K_S^2+r_d^2}$$

(11)

According to the provided analysis, it is possible to compare some of the winches’ performances:

• The rototranslating-drum design, though conceptually simple, suffers from three main drawbacks:

  -

  To transmit torque to the drum, the shafts that pass through the winches are subject to a radial force which may be critically higher than the cable tension by design since $r_d>r_S$; this means that these shafts need to be bulky enough, which in turns means that the drum radius (and thus the transmission ratio) cannot vary freely.

  -

  If an open-end design of the shafts is employed, such as the one proposed in Figure 2a, the torsional load of the winch may deform the rods without actually transmitting force to the drum.

  -

  The manufacturing tolerance of the shaft, the drum, and the bushing inside the drum, need to be very high in order to avoid the winch stalling [38]; this, in turn, highlights that the mechanical design should be everything but simple.

  Its primary advantage is the possibility to freely install the winch in any configuration since its dynamics is only affected by the drum weight, which can be very low.
• The translating motor winch has three significant advantages, namely:

  -

  It can be easily miniaturized since it has no components passing through the drum other than the screw;

  -

  It is mechanically straightforward (most of the components for its manufacturing are commercially available), and thus also cheap;

  -

  It is structurally efficient since the rods withstanding the external load (but possibly also the motor weight) can be placed in a convenient position, and be as sturdy as needed since $r_R>r_d$.

  On the other hand, its main characteristic is also its main drawback: the motor (and gearbox, if used) mass needs to be translated with the drum, which means that:

  -

  According to Equation (11), the overall transmission inertia may be critically high since M includes both the drum and the winch mass, thus severely limiting winch dynamics;

  -

  If the winch is installed with its axis vertical, the weight of both the motor and the drum has to be compensated by the motor torque, which is not very efficient.

• As previously mentioned, the Spline Winch attempts to summarize the rototranslating-drum and translating-motor winches’ advantages, while not suffering from the drawbacks:

  -

  As the rototranslating-drum design, it can be freely installed because it does not have to carry the motor weight around, even though it needs to compensate for the two additional translating plates (and bearings) as a trade-off;

  -

  As the translating-motor design, it can be miniaturized (small screw and spline shaft are commercially available). The additional mechanical complexities are the spline shaft and the motor-shaft-spline-shaft coupling, which is commercially available and structurally efficient.

  It does not suffer from any rototranslating-drum and translating-motor design drawbacks, but it strictly requires two more components: the spline shaft and the motor-shaft-spline-shaft coupling. This means that it may not be as cheap and small as the translating-motor design.

The dynamic of the spooling-helper winch is slightly different, due to the decoupled nature of rotating and translating components (see Figure 8a). The drum rotational dynamics are given by (see Figure 8b):

$$J\ddot{\theta }+T_{SB}+r_D{\tau }_{CS}=T_M$$

(12)

where $T_{SB}=T_S$ is the torque transmitted through the synchronous belt to the screw, which are equal if we neglect friction and elasticity. The translational dynamics of the spooling helper are instead (Figure 8c):

$$Q=\tau -{\tau }_{AX}+M{K}_S\ddot{\theta }$$

(13)

If we substitute Equations (7), (9), and (13) in (12), after some algebraic manipulation we finally get:

$$T_m=\left(J+K_S^{2}M\right)\ddot{\theta }+\left(\sqrt{K_S^2+r_d^2}-K_S\right)\tau$$

(14)

which compared with Equation (5) gives:

$$J^{🟉}=J+K_S^{2}M,K=\sqrt{K_S^2+r_d^2}-K_S$$

(15)

The inertia of the rotating components includes the motor, the drum, the synchronous pulleys, and the screw, while the only translating part is the spooling helper. This winch is the only one optimizing the cable-to-footprint ratio quantity since the drum does not translate and can occupy all the winch length. One minor disadvantage is the necessity to use one more pulley than other designs since the spooling helper necessitates one to deflect the cable from the drum to a direction parallel to the helper translation. One possibly major disadvantage, if cable tension is measured on the spooling helper (as it is usually done in these winches), is that the dynamic bandwidth of the winch is severely limited due to loadcell translational motion with the helper. A summary of the discussed pros and cons can be found in

Table 1. Summary of the various design pros and cons. Scale: (++) very positive, (+) positive, (o) neutral, (-) negative, (–) very negative.

	Rototranslating Drum	Translating Motor	Spooling Helper	Spline Winch
Mechanical simplicity	–	++	-	+
Free configuration installation	+	–	++	o
No limits on transmission ratio	–	+	++	+
Dynamic capabilities	o	–	++	++
Built-in sensor capabilities	o	o	–	o
Cost	-	–	+	+

.

5. Conclusions

This paper presented the state of the art in servo-winch design for cable-driven robots. A novel design concept was introduced and critically compared to the existing and proposed architectures from an application point of view. It was shown that the rototranslating-drum concept presents no significant advantages, even though it was the first one historically developed. The translating-motor concept is an optimal choice for low-cost, not-highly dynamical applications, where installation orientation requirements are not strict. At the same time, the novel Spline Winch is the go-to choice for vertical-winch axis installations and high-dynamic applications. The spooling helper solution optimizes the quantity of stored cable w.r.t. winch footprint. However, highly dynamical operations should be avoided if a load cell is embedded in the helper for measuring cable tension.