Design, Micro-Fabrication, and Characterization of a 3-DoF Micro-Conveyor Based on Digital Actuators
Abstract
:1. Introduction
2. Principle
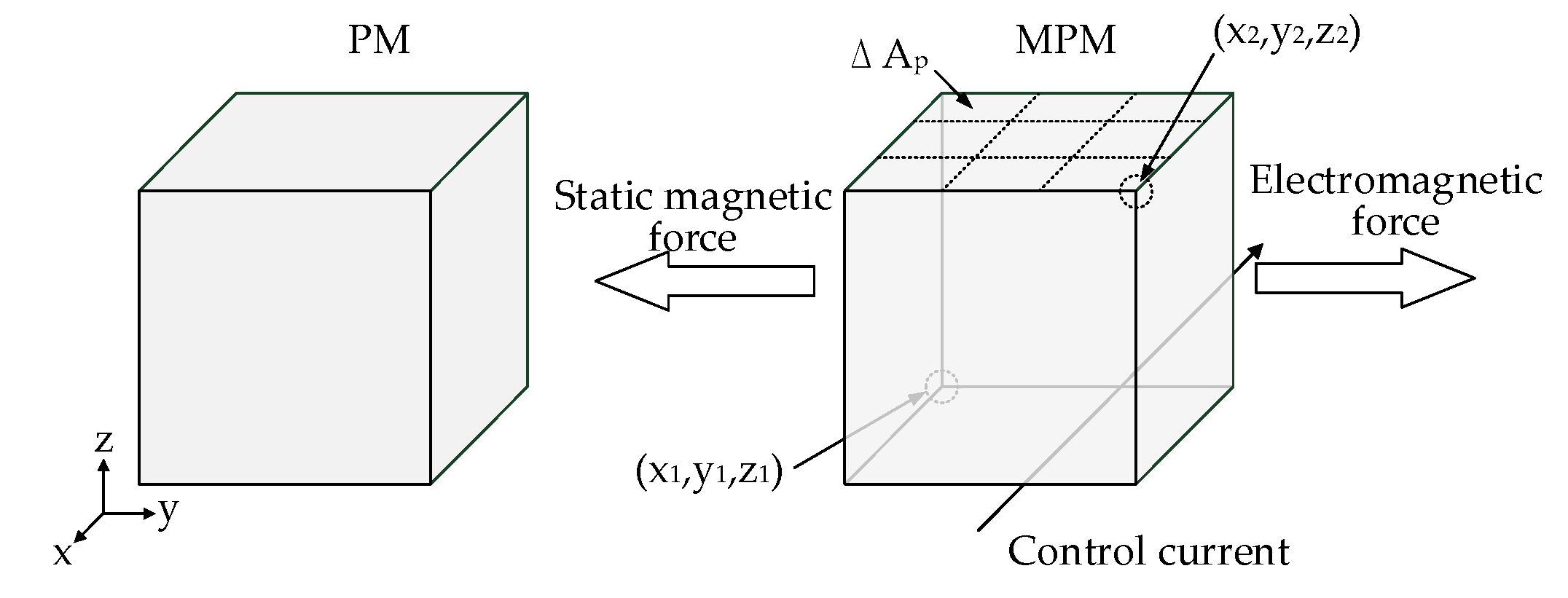
2.1. Principle of the Elementary Electromagnetic Digital Actuator
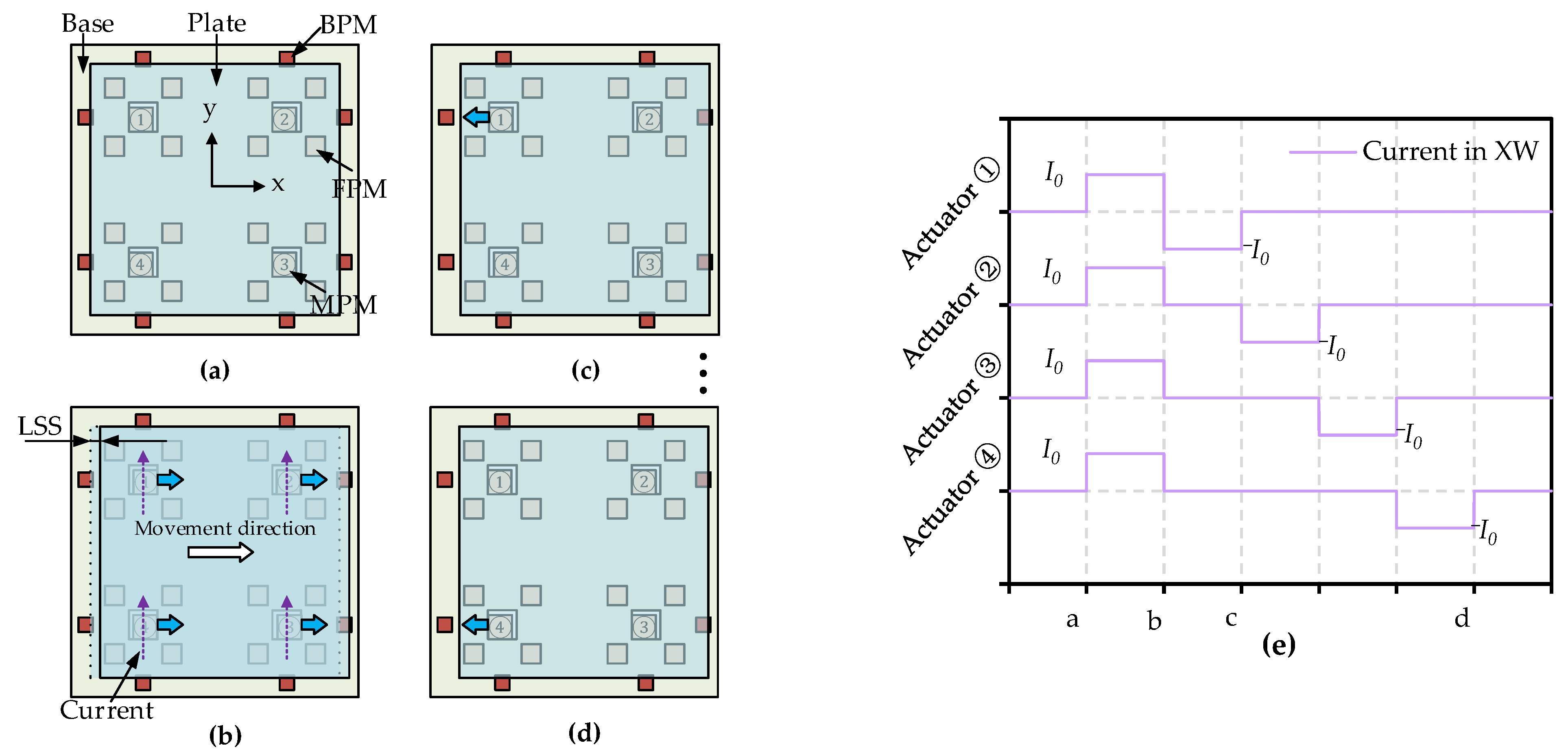
2.2. Principle of the Micro-Conveyor
2.2.1. Linear Conveyance (X-, Y-Axis Direction Movement)
2.2.2. Planar Rotation (Z-Axis Rotation)
3. Modeling and Design Analysis
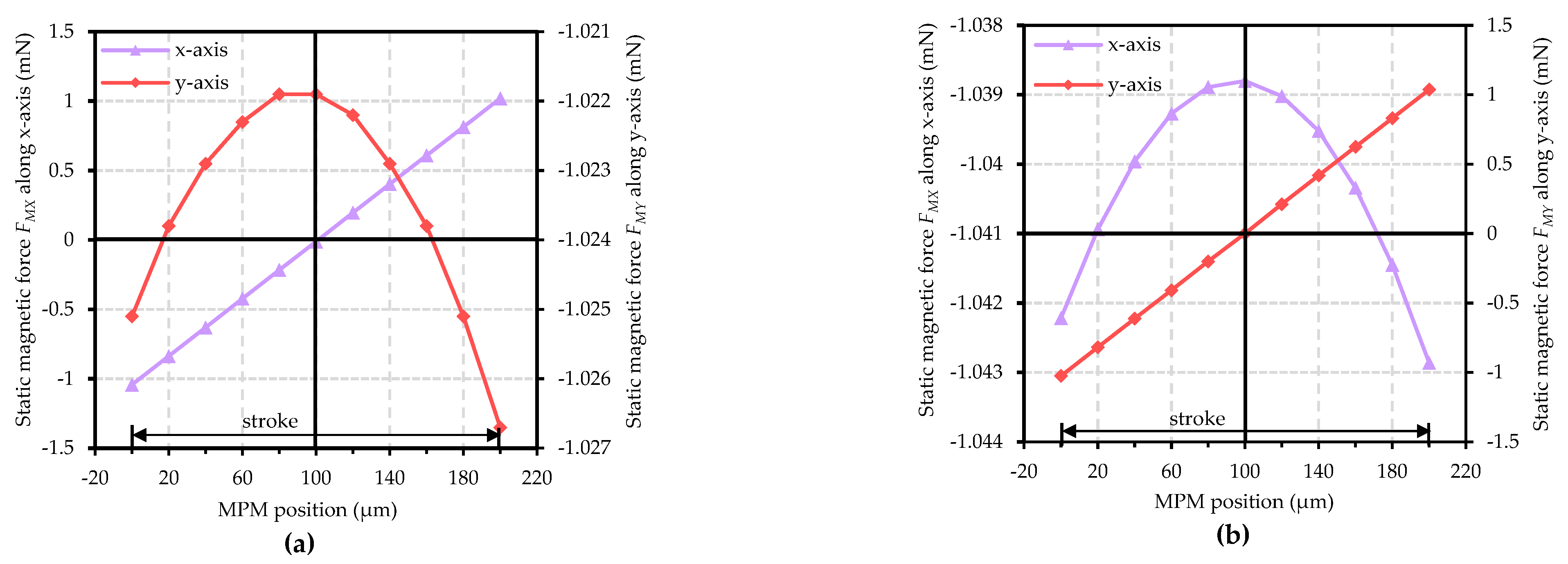
3.1. MATLAB Static Model
3.2. ADAMS Dynamic Model
4. Experiments and Analysis
4.1. Experimental Setup
4.1.1. Description of the Prototype
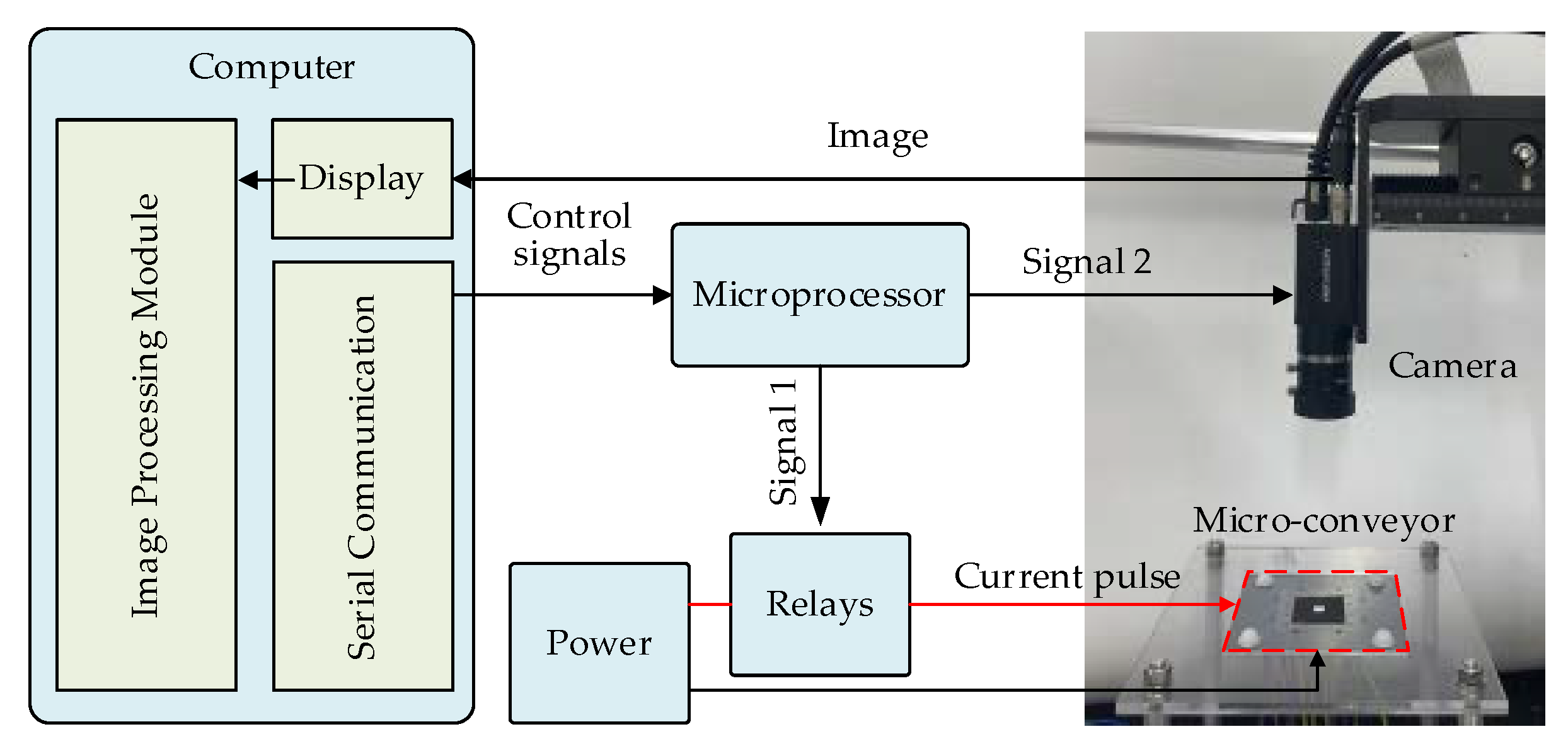
4.1.2. Control System
4.2. Experimental Results and Analysis
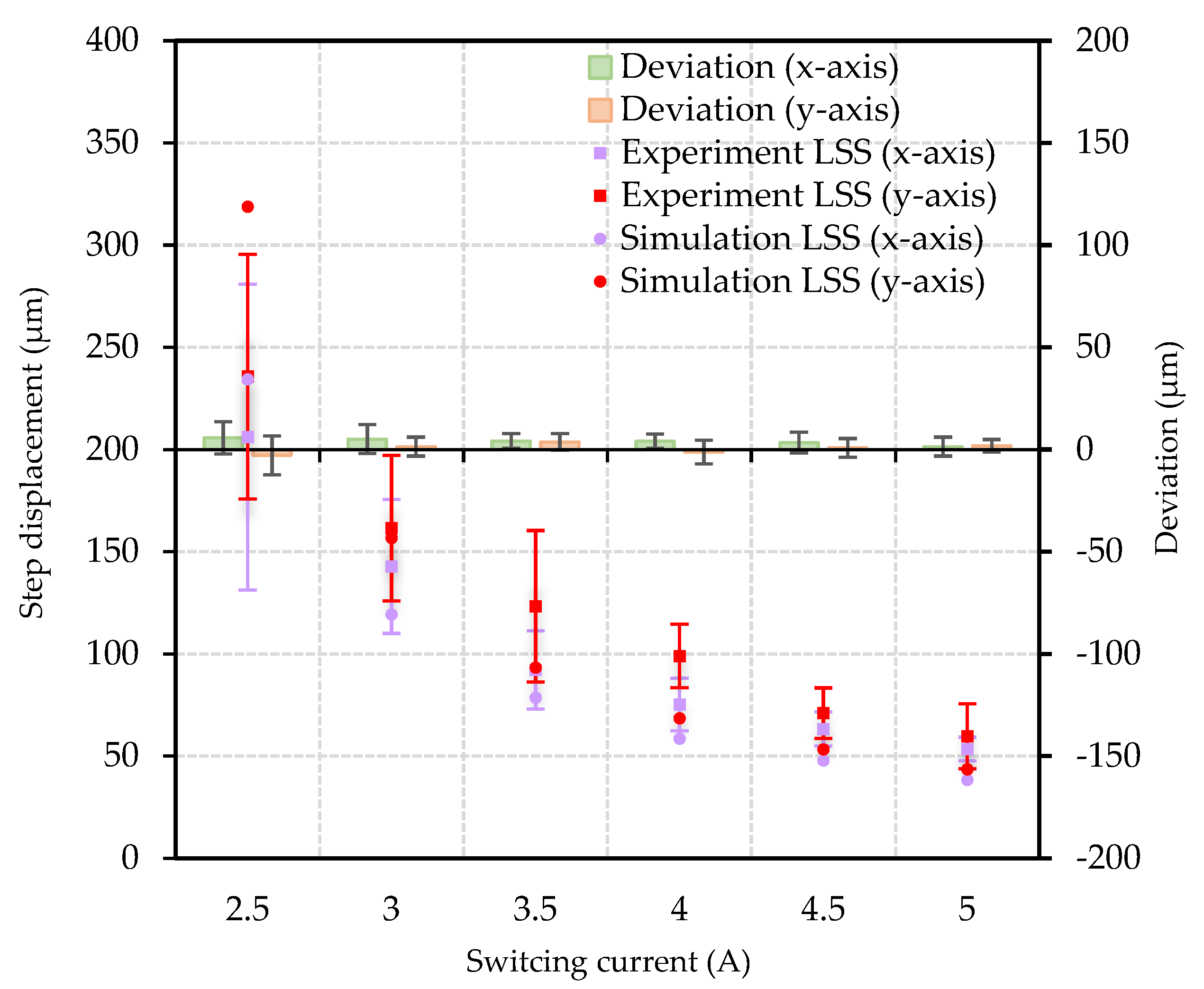
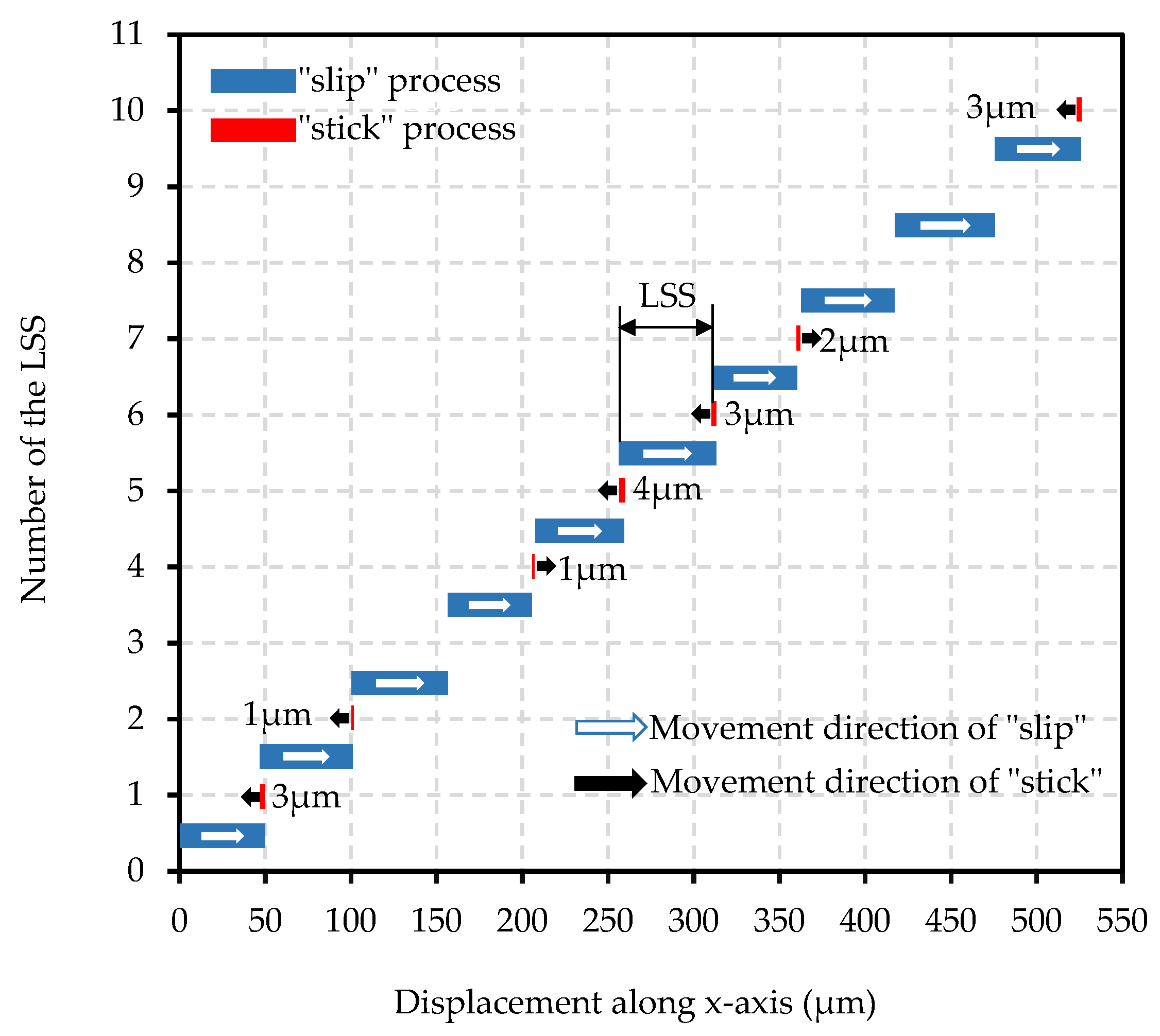
4.2.1. Influence of Switching Current Value on LSS
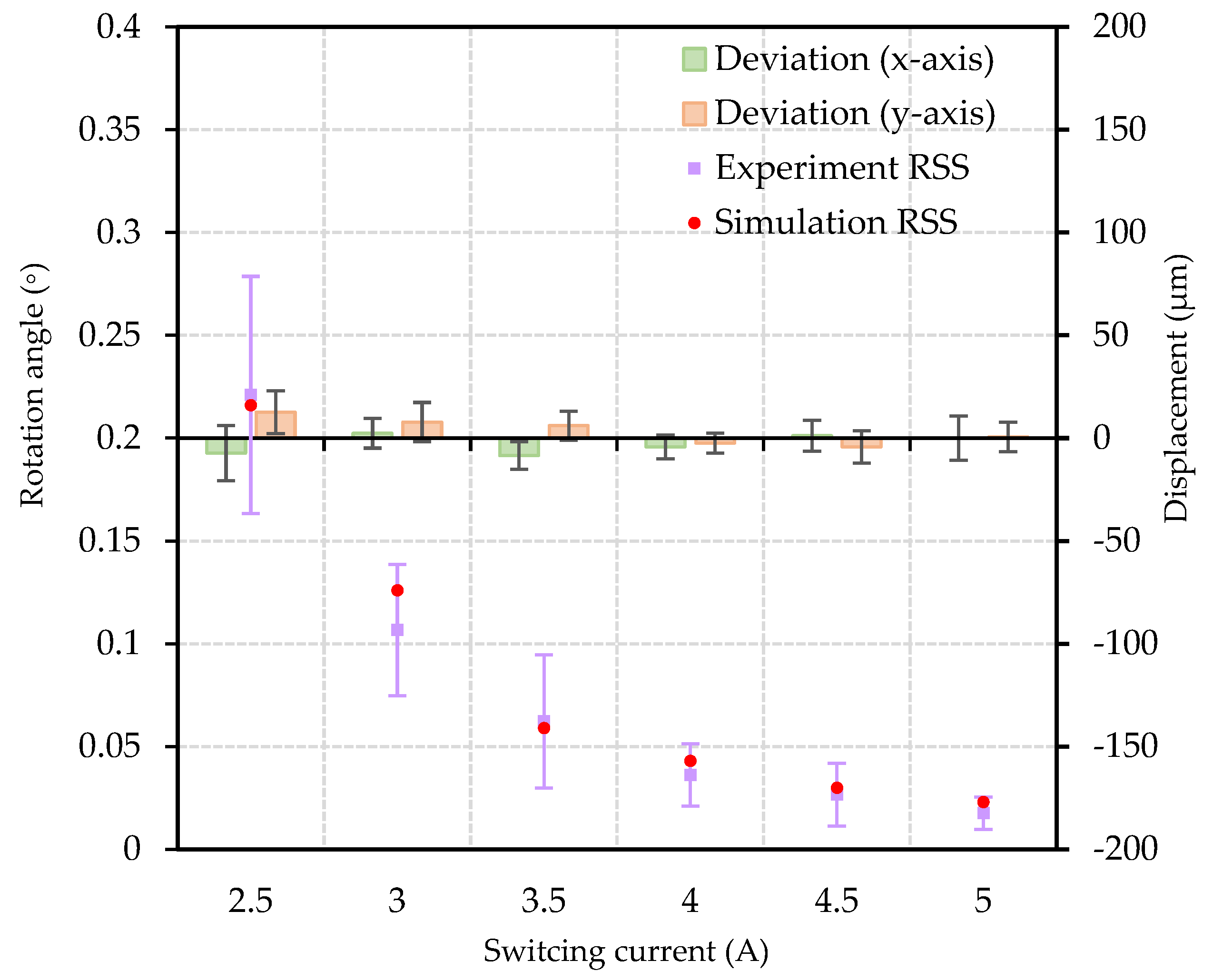
4.2.2. Influence of Switching Current Value on RSS
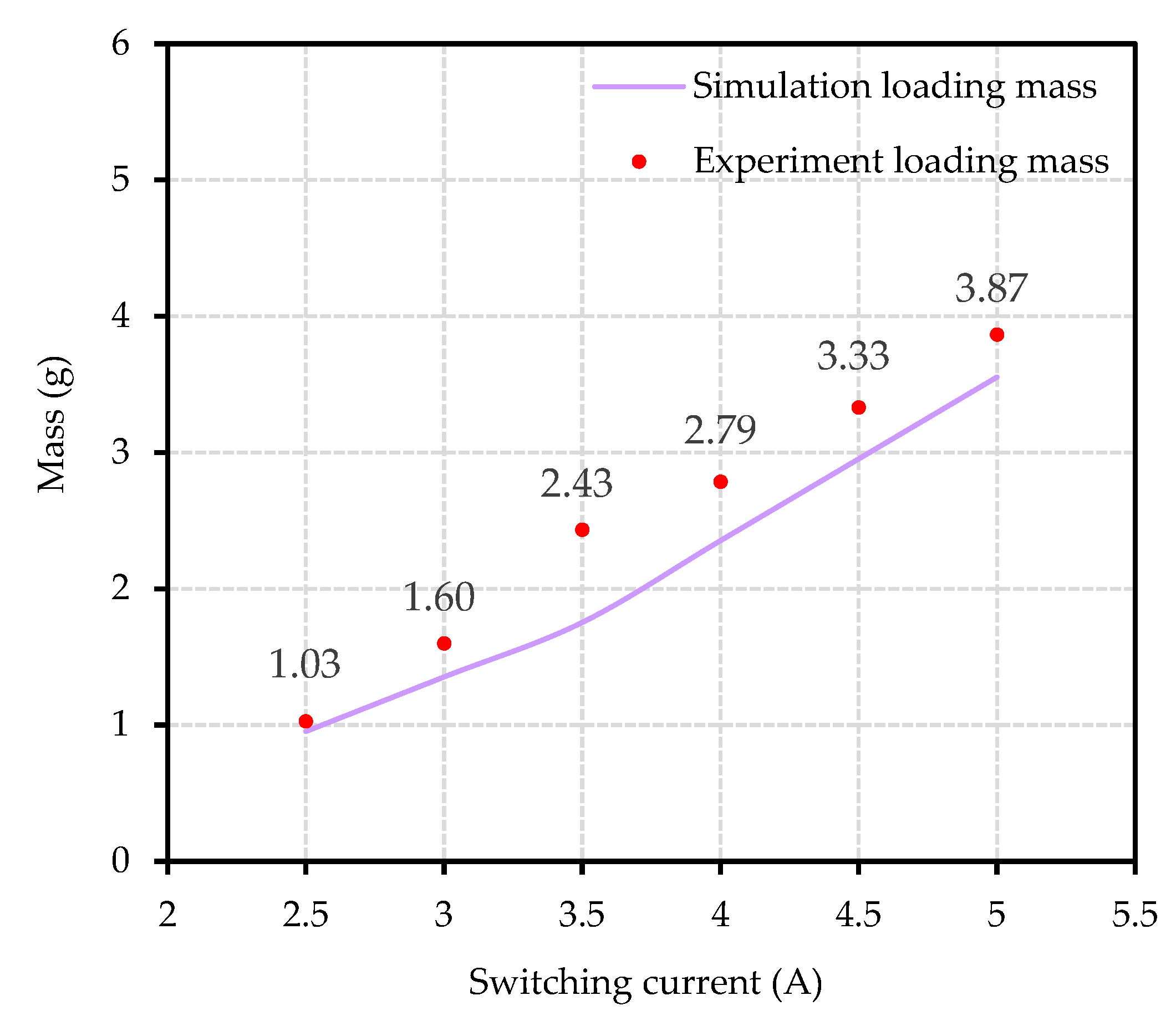
4.2.3. Loading Capacity Test
4.2.4. Influence of the “Backward Motion”
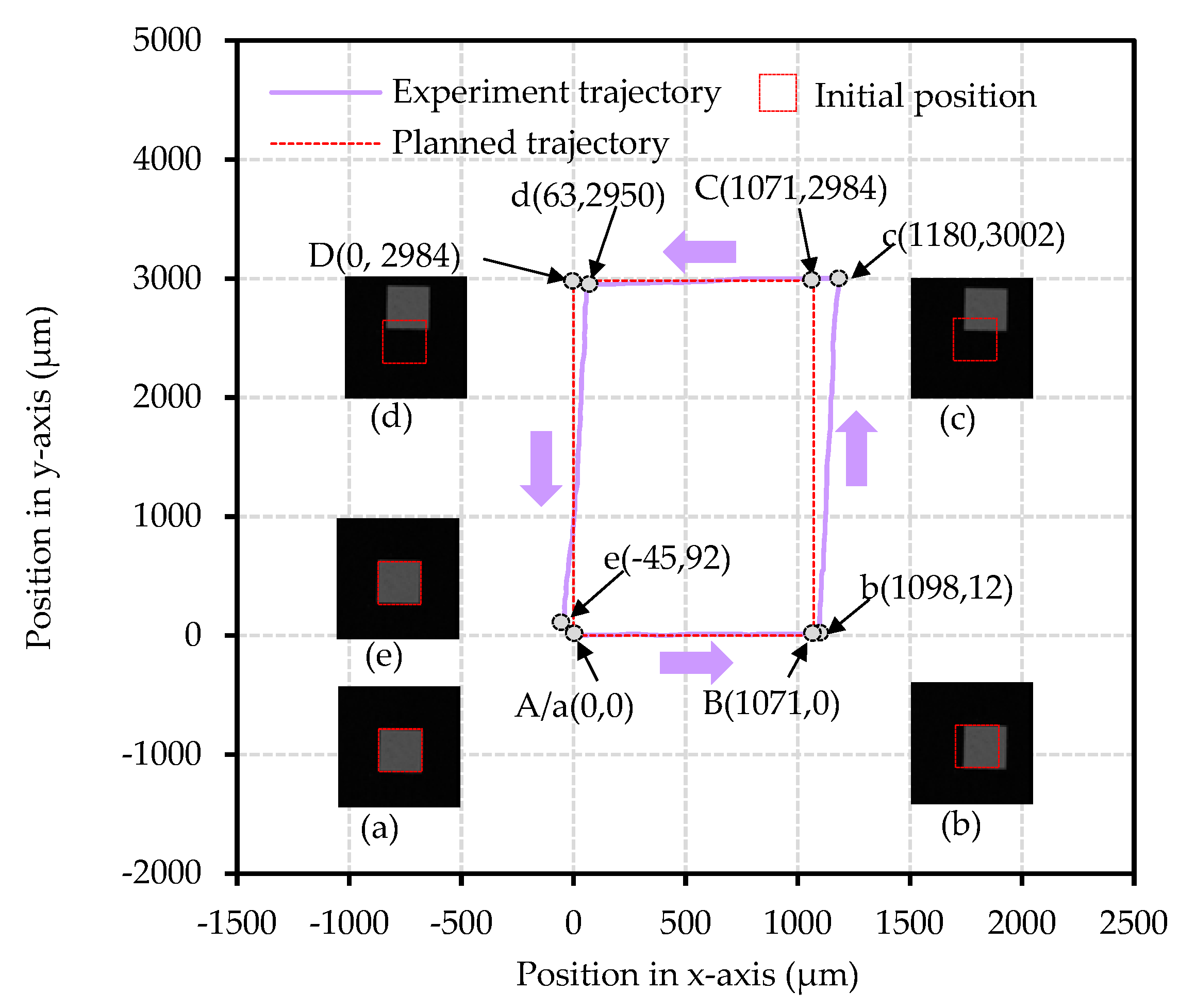
4.2.5. Long-Range Conveyance Test
4.3. Comparison among This Work and Other Researches
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Quiñones, B.; Zhu, H.; Solovev, A.; Mei, Y.; Gracias, D. Origami Biosystems: 3D Assembly Methods for Biomedical Applications. Adv. Biosys. 2018, 2, 1800230. [Google Scholar] [CrossRef]
- Garcia-Gradilla, V.; Orozco, J.; Sattayasamitsathit, S.; Soto, F.; Kuralay, F.; Pourazary, A.; Katzenberg, A.; Gao, W.; Shen, Y.; Wang, J. Functionalized ultrasound-propelled magnetically guided nanomotors: Toward practical biomedical applications. ACS Nano 2013, 7, 9232–9240. [Google Scholar] [CrossRef]
- Li, J.; Alfares, A.; Zheng, Y. Optical manipulation and assembly of micro/nanoscale objects on solid substrates. Iscience 2022, 25, 104035. [Google Scholar] [CrossRef]
- Malak, S.; Hajjar, H.; Dupont, E.; Khan, M.; Prelle, C.; Lamarque, F. Optical Localization and Tracking Method of a Mobile Micro-Conveyor over a Smart Surface. IEEE Sens. J. 2021, 21, 10618–10627. [Google Scholar] [CrossRef]
- Tellers, M.; Pulskamp, J.; Bedair, S.; Rudy, R.; Kierzewski, I.; Polcawich, R.; Bergbreiter, S. Characterization of a piezoelectric MEMS actuator surface toward motion-enabled reconfigurable RF circuits. J. Micromech. Microeng. 2018, 28, 035001. [Google Scholar] [CrossRef]
- Gendreau, D.; Gauthier, M.; Hériban, D.; Lutz, P. Modular architecture of the microfactories for automatic micro-assembly. Robot. Comput.-Integr. Manuf. 2010, 26, 354–360. [Google Scholar] [CrossRef] [Green Version]
- Zhakypov, Z.; Uzunovic, T.; Nergiz, A.; Baran, E.; Golubovic, E.; Sabanovic, A. Modular and reconfigurable desktop micro-factory for high precision manufacturing. Int. J. Adv. Manuf. Technol. 2017, 90, 3749–3759. [Google Scholar] [CrossRef]
- Hosobata, T.; Yamamoto, A.; Higuchi, T. Transparent synchronous electrostatic actuator for long-stroke planar motion. IEEE/ASME Trans. Mechatron. 2014, 20, 1765–1776. [Google Scholar] [CrossRef]
- Dao, D.; Pham, P.; Sugiyama, S. Multimodule micro transportation system based on electrostatic comb-drive actuator and ratchet mechanism. J. Microelectromech. Syst. 2010, 20, 140–149. [Google Scholar] [CrossRef]
- Yahiaoui, R.; Zeggari, R.; Malapert, J.; Manceau, J. A MEMS-based pneumatic micro-conveyor for planar micromanipulation. Mechatronics 2012, 22, 515–521. [Google Scholar] [CrossRef]
- Robertson, M.; Murakami, M.; Felt, W.; Paik, J. A compact modular soft surface with reconfigurable shape and stiffness. IEEE/ASME Trans. Mechatron. 2018, 24, 16–24. [Google Scholar] [CrossRef]
- Ruiz-Díez, V.; Ababneh, A.; Seidel, H.; Sánchez-Rojas, J. Design and Characterization of a Planar Micro-Conveyor Device Based on Cooperative Legged Piezoelectric MEMS Resonators. Micromachines 2022, 13, 1202. [Google Scholar] [CrossRef]
- Iizuka, T.; Sakai, N.; Fujita, H. Position feedback control using magneto impedance sensors on conveyor with superconducting magnetic levitation. Sens. Actuators A Phys. 2009, 150, 110–115. [Google Scholar] [CrossRef]
- Deshmukh, A.; Petit, L.; Khan, M.; Lamarque, F.; Prelle, C. Planar Micro-Positioning Device Based on a 3D Digital Electromagnetic Actuator. Actuators 2021, 10, 310. [Google Scholar] [CrossRef]
- Piranda, B.; Laurent, G.; Bourgeois, J.; Clévy, C.; Möbes, S.; Le Fort-Piat, N. A new concept of planar self-reconfigurable modular robot for conveying microparts. Mechatronics 2013, 23, 906–915. [Google Scholar] [CrossRef]
- Morkvenaite-Vilkonciene, I.; Bucinskas, V.; Subaciute-Zemaitiene, J.; Sutinys, E.; Virzonis, D.; Dzedzickis, A. Development of electrostatic microactuators: 5-year progress in modeling, design, and applications. Micromachines 2022, 13, 1256. [Google Scholar] [CrossRef]
- Cai, T.; Fang, Y.; Fang, Y.; Li, R.; Yu, Y.; Huang, M. Electrostatic pull-in application in flexible devices: A review. Beilstein J. Nanotechnol. 2022, 13, 390–403. [Google Scholar] [CrossRef] [PubMed]
- Mabed, H.; Dedu, E. Short and long term optimization for micro-object conveying with air-jet modular distributed system. J. Parallel Distrib. Comput. 2020, 144, 98–108. [Google Scholar] [CrossRef]
- Fukuta, Y.; Chapuis, Y.; Mita, Y.; Fujita, H. Design, fabrication, and control of MEMS-based actuator arrays for air-flow distributed micromanipulation. J. Microelectromech. Syst. 2006, 15, 912–926. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, Y.; Huang, C. Nano-scale positioning design with piezoelectric materials. Micromachines 2017, 8, 360. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.; Zhang, B.; Li, X.; Xu, Z.; Wang, J.; Liu, C.; Cao, Y. A stick-slip piezoelectric actuator with suppressed backward motion achieved using an active locking mechanism (ALM). Smart Mater. Struct. 2021, 30, 095015. [Google Scholar] [CrossRef]
- Meessen, K.; Paulides, J.; Lomonova, E. Analysis of a novel magnetization pattern for 2-DoF rotary-linear actuators. IEEE Trans. Magn. 2012, 48, 3867–3870. [Google Scholar] [CrossRef]
- Jansen, J.; Van-Lierop, C.; Lomonova, E.; Vandenput, A. Magnetically levitated planar actuator with moving magnets. IEEE Trans. Ind. Appl. 2008, 44, 1108–1115. [Google Scholar] [CrossRef] [Green Version]
- Huyan, P.; Huang, Y.; Li, P.; Cui, X.; Petit, L.; Prelle, C. Experimental Characterization of a Stick-Slip Driving Micro Conveyance Device Consisting of Digital Actuators. Actuators 2022, 4, 112. [Google Scholar] [CrossRef]
- Furlani, E.P. Permanent Magnet and Electromechanical Devices; Furlani, E.P., Ed.; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Hu, X.; Zhen, Z.; Sun, G.; Wang, Q.; Huang, Q. Improvement on the uniformity of deep reactive ion etch for electrically isolated silicon-based substrates. J. Micromech. Microeng. 2022, 32, 045005. [Google Scholar] [CrossRef]
- Jin, Y.; Wei, W. Image edge enhancement detection method of human-computer interaction interface based on machine vision technology. Mob. Netw. Appl. 2022, 27, 775–783. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, Z.; Li, X.; Sun, W.; Huang, H. A high-performance stick-slip piezoelectric actuator achieved by using the double-stator cooperative motion mode (DCMM). Mech. Syst. Signal Process. 2022, 172, 108999. [Google Scholar] [CrossRef]
- Qin, F.; Tian, L.; Huang, H.; Wang, J.; Liang, T.; Zu, X.; Zhao, H. Actively controlling the contact force of a stick-slip piezoelectric linear actuator by a composite flexible hinge. Sens. Actuators A Phys. 2019, 299, 111606. [Google Scholar] [CrossRef]


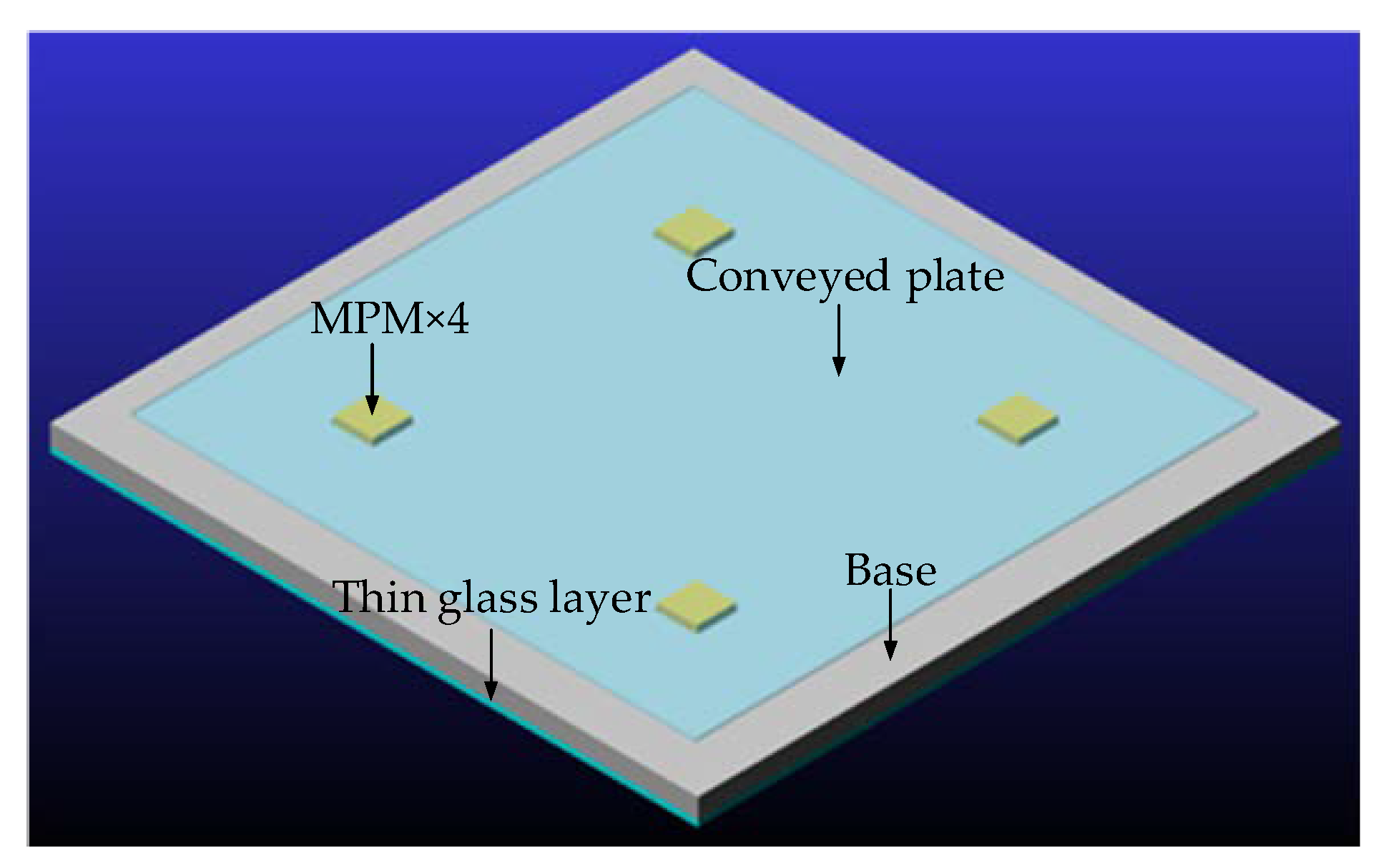


| Element | Dimensions (mm) | Mass (g) | Material | Mag (T) |
| MPM | 2.45 × 2.45 × 1.55 | 0.072 | NdFeB | 1.4 |
| FPM | 2.45 × 2.45 × 0.95 | 0.040 | NdFeB | 1.4 |
| BPM | 1.85 × 1.85 × 0.95 | 0.023 | NdFeB | 1.4 |
| Base | 80.00 × 80.00 × 1.25 | 10.025 | Silicon | - |
| Conveyed plate | 40.00 × 40.00 × 0.16 | 0.657 | Silica | - |
| Thin glass layer | 80.00 × 80.00 × 0.16 | 2.628 | Silica | - |
| PCB | 80.00 × 80.00 × 0.10 | 2.761 | Polyethylene terephthalate | - |
| Parameter | Distance between | Value (mm) | ||
| D1 | Cavity and FPM | 10.00 | ||
| D2 | Elementary actuator | 20.00 | ||
| D3 | Cavity and BPM | 11.72 | ||
| d1 | XW and MPM | 0.18 | ||
| d2 | YW and MPM | 0.24 | ||
| Stroke | - | 0.20 | ||
| Static Magnetic Force | ||||||||
| Aspect 1 | ||||||||
| Comparison | Previous design | Present design | ||||||
| Average static magnetic force (mN) | 0.624 ± 0.059 (9.46%) | 1.031 ± 0.007 (0.68%) | ||||||
| Aspect 2 | ||||||||
| Comparison | Previous design | Present design | ||||||
| Stable position | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 |
| Static magnetic force (mN) | 0.628 | 0.571 | 0.605 | 0.694 | 1.034 | 1.027 | 1.028 | 1.036 |
| Maximum Variation (mN) | 0.123 | 0.009 | ||||||
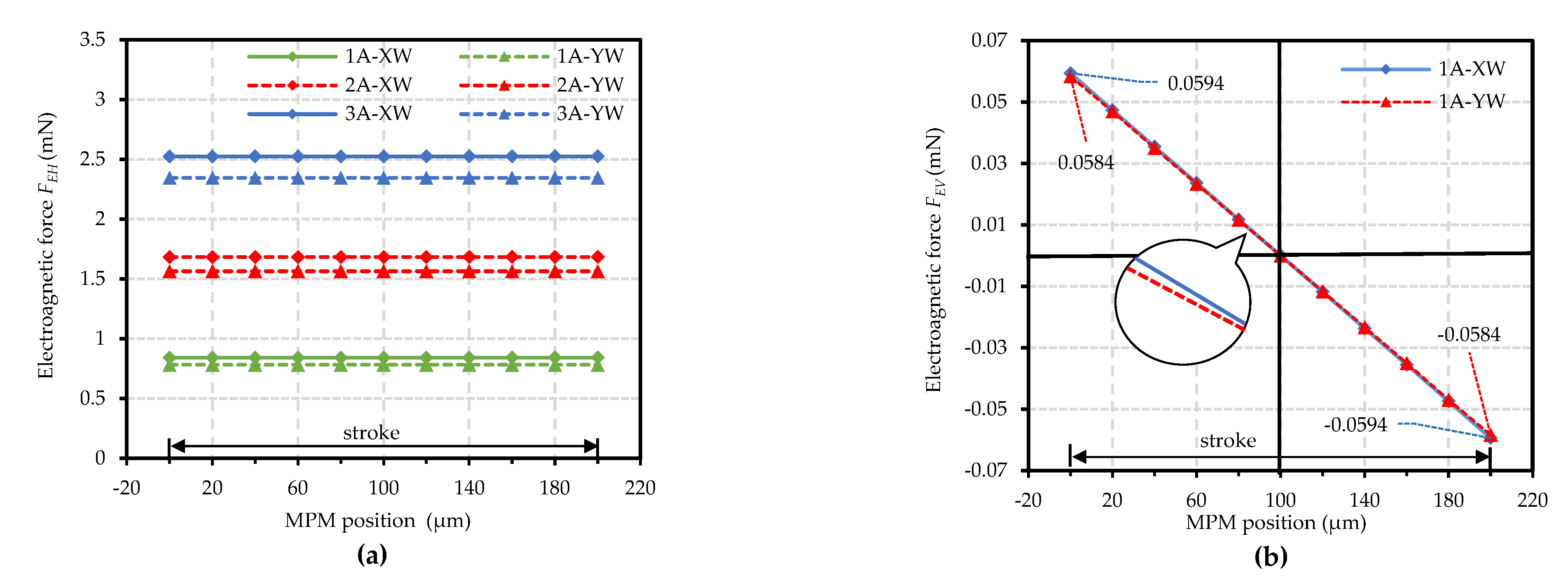
| Electromagnetic force | ||||||||
| Comparison | Previous design | Present design | ||||||
| Electromagnetic force for 1 A (mN) | 0.97 mN (XW)/0.73 mN (YW) | 0.84 mN (XW)/0.78 mN (YW) | ||||||
| Difference between XW and YW (mN) | 0.24 mN | 0.06 mN | ||||||
| Element | Constraint | Elastic Modulus | Poisson’s Ratio |
| MPM | Mobile pair | 160 GPa | 0.24 |
| Base | Fixed pair | 190 GPa | 0.27 |
| Conveyed plate | Contact | 55 GPa | 0.25 |
| Thin glass layer | Fixed pair | 55 GPa | 0.25 |
| Coulomb friction elements | Friction coefficient | ||
| MPM and Base | = 0.40, = 0.32 | ||
| MPM and Conveyed plate | = 0.35, = 0.28 | ||
| MPM and Thin glass layer | = 0.35, = 0.28 | ||
| Contact parameters | Value | ||
| Stiffness | 1.6 × 105 N/mm | ||
| Exponent | 1.4 | ||
| Previous Design | Present Design | |
|---|---|---|
| Manufacturing method | Conventional fabrication | Micro-fabrication |
| Manufacturing Error (µm) | +9 to +50 | −4.52 to +8.03 |
| Static magnetic force variation (mN) | +0.028 to +0.158 | −0.029 to +0.041 |
| Relative variation | +4.48% to +25.28% | −2.81% to +3.98% |
| Current Value (A) | Displacement (µm) |
|---|---|
| 2.5 | −1.40 ± 1.35 |
| 3 | 0.40 ± 1.43 |
| 3.5 | −0.60 ± 1.17 |
| 4 | −1.30 ± 0.67 |
| 4.5 | 0.62 ± 1.43 |
| 5 | −1.10 ± 2.02 |
| Trajectory | A→B | a→b | B→C | b→c | C→D | c→d | D→A | d→e |
|---|---|---|---|---|---|---|---|---|
| Displacement along x-axis (µm) | 1071 | 1098 | 0 | 82 | 1071 | 1117 | 0 | 108 |
| Displacement along y-axis (µm) | 0 | 12 | 2984 | 3066 | 0 | −34 | 2984 | 2858 |
| Average Positioning error (x-/y-axis) (µm) | 27/12 | 109/18 | −63/−34 | −45/92 | ||||
| Average Linearity | - | 97.8% | - | 97.3% | - | 97.0% | - | 96.2% |
| Comparison | DoF | LSS (5 A Current) | The Linearity of Long-Range Conveyance |
|---|---|---|---|
| Previous | 2 | 40.88 ± 19.03 µm | 84.8% |
| Present | 3 | 53.53 ± 5.73 µm | 96.2% |
| DoF | Active Area | Actuator | Scalability | Range | Load | Resolution | |
|---|---|---|---|---|---|---|---|
| [8] | 2 | 132 × 132 mm2 | electrostatic | No | - | 18 g | 400 µm |
| [9] | 1 | 10 × 10 mm2 | electrostatic | No | <10 mm | - | 10 µm |
| [10] | 2 | 9 × 9 mm2 | pneumatic | No | <9 mm | 2 mg | 1.2 mm |
| [11] | 2 | 93 × 110 mm2 | pneumatic | No | - | 739 g | 26 mm |
| [5] | 2 | 2 × 5 mm2 | piezoelectric | Yes | <5 mm 2π rad | 2 mg | - |
| [12] | 2 | 5 × 1 mm2 | piezoelectric | No | 3 mm | 100 mg | 0.1 μm |
| [13] | 2 | 12 mm × 12 mm | electromagnetic | No | 12 mm | 0.38 g | 1.2 mm |
| Present | 3 | 45 × 45 mm2 | electromagnetic | Yes | 42.45 mm 2π rad | 3.87 g | 53.53 µm 50 μrad |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huyan, P.; Li, P.; Huang, Y.; Cui, X. Design, Micro-Fabrication, and Characterization of a 3-DoF Micro-Conveyor Based on Digital Actuators. Actuators 2022, 11, 294. https://doi.org/10.3390/act11100294
Huyan P, Li P, Huang Y, Cui X. Design, Micro-Fabrication, and Characterization of a 3-DoF Micro-Conveyor Based on Digital Actuators. Actuators. 2022; 11(10):294. https://doi.org/10.3390/act11100294
Chicago/Turabian StyleHuyan, Pengfei, Pengchao Li, Yulin Huang, and Ximing Cui. 2022. "Design, Micro-Fabrication, and Characterization of a 3-DoF Micro-Conveyor Based on Digital Actuators" Actuators 11, no. 10: 294. https://doi.org/10.3390/act11100294
APA StyleHuyan, P., Li, P., Huang, Y., & Cui, X. (2022). Design, Micro-Fabrication, and Characterization of a 3-DoF Micro-Conveyor Based on Digital Actuators. Actuators, 11(10), 294. https://doi.org/10.3390/act11100294






