Research on Optimal Oil Filling Control Strategy of Wet Clutch in Agricultural Machinery

Abstract

To improve the wet clutch engagement quality, which is widely used in agricultural machinery, the oil filling control strategy of a wet clutch is studied based on the method of simulation and experiment in detail in this paper. Firstly, this paper carries out the dynamic analysis of the wet clutch engagement process, establishes the mathematical model of the mechanical domain and the hydraulic domain of the hydraulic execution system, and designs the backstepping oil pressure controller. The controllability of the output oil pressure of the clutch hydraulic actuator is verified on the joint simulation platform of Matlab/Simulink (Version R2017b, MathWorks, Natick, MA, USA) and AMESim (Version 2019.1, Simcenter Amesim, Siemens Digital Industries Softwares, Berlin&Munuch, Germany). Then, this paper analyzes the clutch engagement process, extracts five factors affecting the oil filling process, and selects four clutch engagement quality evaluation indexes. An amount of 50 groups of experiments are carried out on the wet clutch oil filling test simulation platform built by SimulationX (Version 3.8, ESI ITI GmbH, Dresden, Germany). The response surface method (RSM) and stepwise regression analysis method are used to explore the mathematical models of the quality evaluation index and influencing factors of the oil filling process. Through 15 groups of random tests, the prediction accuracy of the stepwise regression model and the RSM model of each index is compared, and the models with high accuracy are selected to establish the comprehensive prediction mathematical model of clutch engagement quality, combined with the variance weight method. Finally, according to the working condition of the 3 MPa oil filling pressure studied in this paper, the optimal oil filling control strategy is obtained by the proposed clutch engagement quality prediction model. Under the target condition, when the oil filling rate of stage 1 is the highest and the proportion of phase 1’s duration to the total oil filling time is 69.65%, the oil filling rate of stage 2 is the lowest and the proportion of phase 2’s duration to the total oil filling time is 21.85%, and the proportion of phase 3’s duration to the total oil filling time is 8.51%, the engagement quality of wet clutch is the best. The research method of wet clutch optimal oil filling control strategy proposed in this paper provides a reliable method for the ride comfort research of agricultural machinery and clutch control.

1. Introduction

The wet clutch consists of friction disks (driving parts) and separate disks (driven parts). During the engagement process, the wet clutch transmits the torque by the friction between disks [1,2,3]. The wet clutch is widely used in agricultural equipment because of its smooth engagement and large torque transmission. The PST (power shift gearbox) relies on the sliding friction of a wet clutch to achieve the shift process without interruption, effectively improving the efficiency of agricultural machinery operations [4,5]. To realize tractor commutation without power interruption by switching forward and backward wet clutch, reducing the complexity of the drivers’ operation is required [6]. In HMCVT (hydraulic mechanical continuously variable transmission), the impact is reduced and the shift quality is improved by reasonably controlling multiple wet clutches [7]. As a key component, the dynamic engagement characteristics of the wet clutch will directly affect the performance of agricultural equipment. The wet clutch relies on hydraulic oil to combine. It is of great significance to study the oil-filling characteristics of the wet clutch to improve the clutch engagement quality.

The engagement pressure and engagement speed of the wet clutch are controlled by the hydraulic system of the clutch, so the oil pressure characteristics of the clutch have an important influence on the engagement quality. Li et al. [8] studied the relationship between clutch oil filling flow and clutch boost characteristics and proposed a clutch pre-oil filling control method. Wu et al. [9] established the mathematical model of a wet clutch hydraulic system, analyzed the influence of the control signal on the oil filling characteristics, and obtained that the selection of time area with a slowly rising duty ratio directly determined the action time and effect of buffer. Meng et al. [10] established a clutch electro-hydraulic control model and proposed a feedforward–feedback control strategy, and the control parameters were optimized according to the oil temperature and engine load. Kong et al. [11] designed an adaptive sliding mode controller to control the piston position of the wet clutch. Compared with the boundary layer sliding mode controller, the adaptive sliding mode controller had smaller fluctuation and faster convergence speed. Xue et al. [12] obtained the optimal curve of clutch engagement pressure by establishing a quadratic comprehensive performance index function in the wet clutch engagement process. Zeng et al. [13] built a simulation model of wet clutch hydraulic execution system, proposed a feedforward and PID feedback control algorithm based on the model, and verified that its control effect was better than the PID control algorithm. Fu et al. [14] constructed a complete nonlinear dynamic model of a wet clutch actuator and designed a wet clutch pressure controller based on MFAPC with the aim of investigating clutch cylinder pressure. In summary, the current research mostly focuses on the design of the wet clutch hydraulic control system to achieve accurate control of the clutch piston oil pressure, but there are few studies on the oil filling process, and there is a lack of research on the oil filling control strategy of the wet clutch from the perspective of improving the clutch engagement quality.

Because of the above problems, this paper mainly studies the following four points: (1) the hydraulic control system of the wet clutch is established based on AMESim and Simulink software; (2) the controllability of wet clutch piston pressure is verified by PID and backstepping controllers; (3) five factors influencing the oil-filling control process of the wet clutch are extracted, and the mathematical model between clutch engagement quality evaluation index and control factors is established by the RSM test; (4) the optimal oil-filling control strategy is obtained with stepwise regression analysis. This paper’s research provides a reliable method for improving the smoothness of agricultural machinery and the control of the wet clutch.

2. Materials and Methods

2.1. Modeling of Wet Clutch Engagement Process

With the increase in oil pressure, the wet clutch will exist in three states:

(1)

When the wet clutch is sliding, the dynamic equation of the clutch is:

$$T_e-T_{fc}=J_e\frac{d{\omega }_e}{dt}, T_{fc}-T_f=J_c\frac{d{\omega }_c}{dt}$$

(1)

In the formula, $T_e$ is the input torque of the wet clutch; $T_{fc}$ is the friction torque of the wet clutch; $T_f$ is the resistance torque of the clutch driven shaft; $J_e$ is the rotational inertia of the clutch input shaft; $J_c$ is the rotational inertia of the clutch driven shaft; ${\omega }_e$ is the rotational speed of the clutch input shaft; ${\omega }_c$ is the rotational speed of the clutch driven shaft.

The calculation formula of wet clutch transmission torque is:

$$T_{fc}=\frac{2}{3}\mu A_{p}z\frac{R_1^3-R_2^3}{R_1^2-R_2^2}\left[P_c-\frac{k_p\left(x_0+x_p\right)}{\pi \left(R_3^2-R_4^2\right)}\right]$$

(2)

In the formula, $\mu$ is sliding friction coefficient, and its value is related to the rotational speed difference; $z$ is the number of friction plates; $R_1$ is the outer diameter of the friction plates; $R_2$ is the inner diameter of the friction plates; $R_3$ is the outer diameter of the piston; $R_4$ is the inner diameter of the piston, $A_p$ is the effective force area of the piston, $k_p$ is the stiffness of the return spring, $x_p$ is the displacement of the piston, and $x_0$ is the initial compression of return spring.

(2)

When the wet clutch is fully engaged, the speed of the input end and the output end is equal, and the dynamic equation is:

$$T_e-T_f=\left(J_e+J_c\right)\frac{d{\omega }_c}{dt}$$

(3)

(3)

When the wet clutch is completely separated (assuming that the friction force can be neglected in this state), the dynamic equation is:

$$T_{fc}=0$$

(4)

2.2. Establishment of Wet Clutch Hydraulic Control Platform

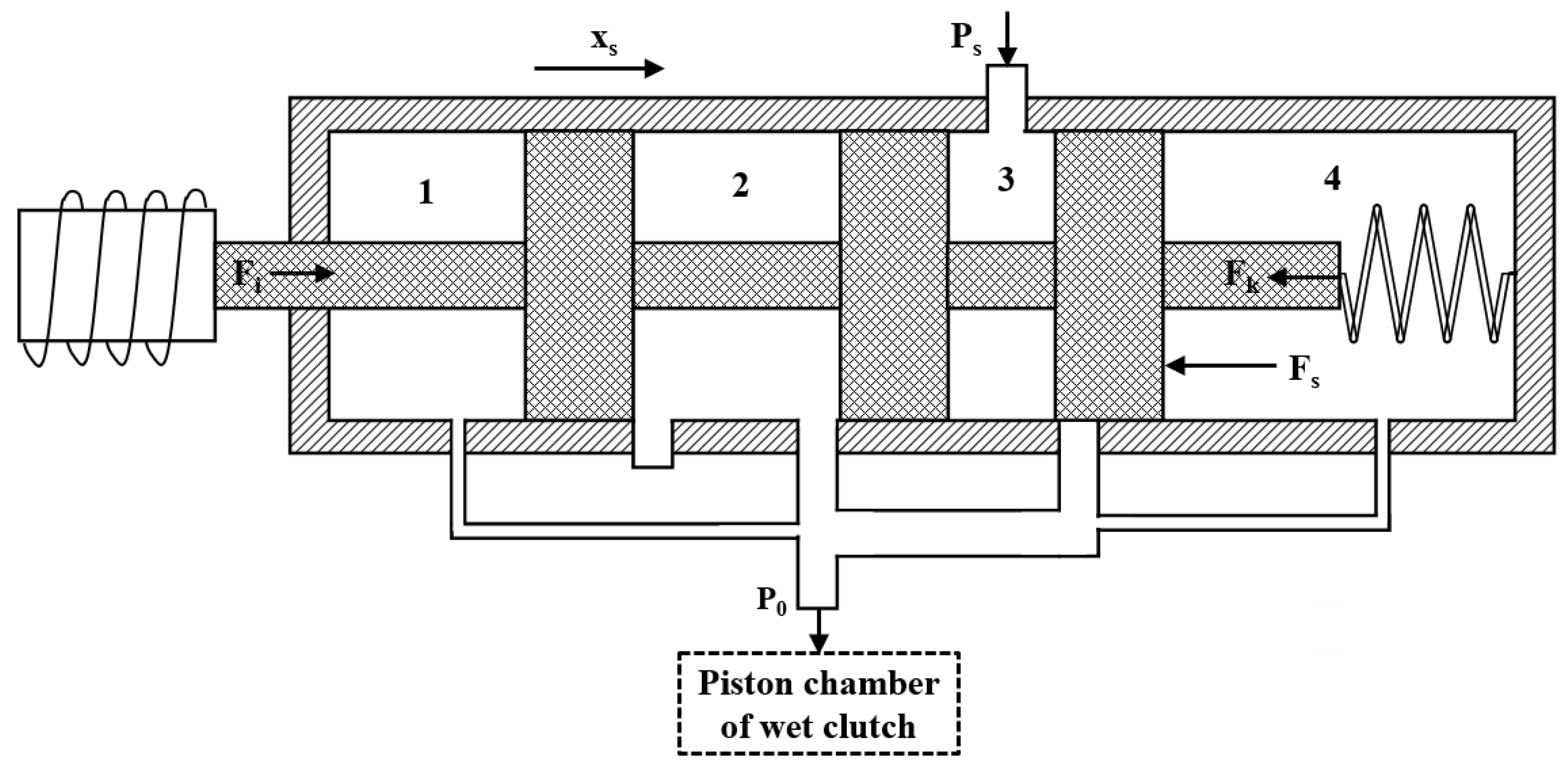
The hydraulic control system of the wet clutch consists of three parts: the power source, the oil pressure regulator, and the clutch hydraulic chamber. Figure 1 is the structure diagram of the pressure proportional solenoid valve and the clutch hydraulic chamber. Its main components are the proportional solenoid, valve spool, valve body, return spring, channel, oil drain hole, oil inlet, and oil outlet. The valve spool divides the valve body into four hydraulic chambers. Chambers 1 and 4 are decompressing cavities, which are connected with pressure-regulating chamber 2 through channels 1 and 2. Chamber 3 is the pressure supply chamber connected with a constant pressure source. When the solenoid valve coil is not powered, the valve spool is in the leftmost position because of the return spring. The oil inlet is closed, and chamber 2 is connected to the oil drain hole. The oil outlet’s pressure is 0 MPa, and the wet clutch is not combined. When the solenoid valve coil is powered, the valve spool compresses the return spring and moves to the right, and the oil inlet is gradually opened. The oil flows into chamber 2 through an oil outlet, which makes the pressure of chamber 2 and the output pressure of the solenoid valve increase gradually. Therefore, the oil pressure in the wet clutch’s piston chamber increases, and the engagement of the wet clutch is promoted. As the solenoid valve’s output pressure increases gradually, the pressure in chamber 1 and chamber 4 also increases gradually. Due to the different areas of the two decompressing cavities, the forces acting on the pressure feedback cavities are also different. Finally, the electromagnetic force, the return spring force, and the force of the pressure feedback chamber on both sides are balanced, and the solenoid valve’s output pressure is stable.

For the pressure-proportional solenoid valve that has strong nonlinear properties, in order to simplify the system modeling, this paper makes three simplifications: ① to ignore the influence of oil leakage during valve movement; ② the pressure of chamber 1 and chamber 4 is approximately equal to the output pressure proportional solenoid valve; and ③ to ignore the volume of chamber 1 and chamber 4 and the flow of hydraulic oil [15,16].

The kinematic equations of pressure proportional solenoid valve spool are shown in Formula (5).

$$\begin{array}{l}{F}_i-F_s=m_s\frac{d^2{x}_s}{d{t}^2}+c_0\frac{d{x}_s}{dt}+k_s{x}_s\\ F_i=k_{i}i\\ F_s=p_0\left(A_l-A_r\right)\end{array}\}$$

(5)

In which $F_i$ is the electromagnetic force caused by the powered solenoid valve coil (N), $i$ is the excitation current flowing through the solenoid valve coil (N/A), $F_s$ is the resultant force acting on chamber 1 and chamber 4 (N), $k_i$ is the proportion coefficient of electromagnetic force and the current of the solenoid valve coil (N/A), $P_0$ is the output pressure of the solenoid valve (pa), $A_l$ and $A_r$ are the force areas of the solenoid valve’s left and right sides (m²), $m_s$ is the mass of the valve spool (kg), $x_s$ is the displacement of the valve spool (m), $c_0$ is the damping coefficient of the valve spool (Ns/m), and $k_s$ is the stiffness of the return spring (N/m).

The flow balance equations of the pressure-proportional solenoid valve are:

$$\begin{array}{l}{Q}_{in}-Q_0-Q_{out}=\frac{Vt}{\beta e}\stackrel{•}{p_0}\\ Q_{in}=C_q\pi d{x}_s\sqrt{\frac{2\left|p_s-p_0\right|}{\rho }}\\ Q_{out}=C_q\pi d(x_u-x_s)\sqrt{\frac{2\left|p_0-p_{out}\right|}{\rho }}\end{array}\}$$

(6)

In which $Q_{in}$ is the flow rate of the solenoid valve’s oil inlet (L/min), $Q_{out}$ is the flow rate of the solenoid valve’s oil drain hole (L/min), $Q_0$ is the flow rate flowing from the solenoid valve into the wet clutch’s piston chamber (L/min), $Vt$ is the volume of the solenoid valve chamber (m³), $\beta e$ is the bulk modulus of oil (indicating the ability of oil to resist compression), $C_q$ is the flow coefficient of the solenoid valve, $d$ is the diameter of the valve spool (m), $\rho$ is the density of the hydraulic oil (kg/m³), $p_s$ is the oil pressure of the solenoid valve’s stabilized supply source (pa), $p_{out}$ is the oil pressure of the tank which is connected to the oil drain hole (pa), $x_u$ is the length of the solenoid valve’s oil drain hole (m), and $P_0$ is the output pressure of the solenoid valve (pa).

The mathematical model of the pressure-proportional solenoid valve, obtained from formula (5) and (6), is as formula (7):

$$\begin{array}{l}\stackrel{••}{x_s}=-\frac{c_0}{m_s}\stackrel{•}{x_s}-\frac{k_s}{m_s}{x}_s+\frac{k_i}{m_s}i-\frac{p_0\left(A_l-A_r\right)}{m_s}\\ \stackrel{•}{p_0}=-\frac{{\beta }_e}{v_t}{Q}_0-\frac{x_u{x}_s{\beta }_e{C}_q\pi d}{v_t}\sqrt{\frac{2\left|p_s-p_0\right|}{\rho }}+\frac{x_s{\beta }_e{C}_q\pi d}{v_t}\sqrt{\frac{2\left|p_0-p_{out}\right|}{\rho }}\end{array}\}$$

(7)

When a certain amount of hydraulic oil flows into the clutch piston chamber, the volume flow and dynamic oil pressure in the piston chamber can be expressed as:

$$Q_0=A_p\frac{d{x}_p}{dt}+\frac{V_0+A_p{x}_p}{{\beta }_e}\frac{d{p}_0}{dt}$$

(8)

$A_p$ is the effective force area of the piston, $x_p$ is the displacement of the piston, $\beta e$ is the bulk modulus of oil (indicating the ability of oil to resist compression), $P_0$ is the output pressure of the solenoid valve (pa), and $V_0$ is the initial volume of the clutch piston chamber (m³).

Additionally, the dynamic model of the piston during clutch engagement is:

$$p_0{A}_p-k_p{x}_p-F_{cl}=C_p\frac{d{x}_p}{dt}+m_p\frac{d^2{x}_p}{d{t}^2}$$

(9)

In the formula, $F_{cl}$ is the reaction force of the piston under contact pressure, $C_p$ is the damping coefficient of the piston, and $m_p$ is the mass of the piston.

According to formulas (5) to (9), the hydraulic control simulation platform of the wet clutch is established based on AMESim software (Version 2019.1, Simcenter Amesim, Siemens Digital Industries Softwares, Berlin&Munuch, Germany), as shown in Figure 2.

2.3. Design of Wet Clutch Oil Filling Controller Based on Backstepping Algorithm

Based on the mathematical model of the pressure-proportional solenoid valve, this paper adopts the backstepping algorithm [17,18,19] to design the oil pressure following the controller of the wet clutch. The principle of backstepping is to split the research system into multiple subsystems with lower orders, and to design virtual controllers for each subsystem from the subsystem where the control variable is located to the end of the input subsystem, so that the subsystem is stable in the Lyapunov sense [20]. The obtained system control input is obtained by backstepping and recursion.

By dividing formula (8) into three subsystems, and by selecting three state variables, ($x_1$, $x_2$, $x_3$), let the state variable $x=\left[x_1,x_2,x_3\right]$=$\left[p_0,x_s,\stackrel{•}{x_s}\right]$, where $x_3$ is the velocity of the valve spool. The system control input is $u$, and the state equation of the wet clutch hydraulic control system is as follows:

$$\begin{array}{l}\stackrel{•}{x_1}=f_1(x_1)x_2\\ \stackrel{•}{x_2}=x_3\\ \stackrel{•}{x_3}=f_2(x_1,x_2,x_3)+a_{1}u\end{array}\}$$

(10)

$$\begin{array}{l}{f}_1(x_1)=-\frac{{\beta }_e}{v_t}{Q}_0+\frac{{\beta }_e{C}_q\pi d}{v_t}\left(\sqrt{\frac{2\left|p_s-x_1\right|}{\rho }}-\sqrt{\frac{2\left|x_1-p_{out}\right|}{\rho }}\right)\\ f_2(x_1,x_2,x_3)=-\frac{\left(A_l-A_r\right)}{m_s}{x}_1-\frac{k_s}{m_s}{x}_2-\frac{c_0}{m_s}{x}_3+\frac{k_i}{m_s}i\\ a_1=\frac{k_i}{m_s}\end{array}\}$$

(11)

The design of the backstepping controller is divided into three steps. First, to realize oil pressure following control, which is to make the solenoid valve’s output pressure $p_0$ follow the ideal control curve, then $x_1\to x_{1d}$, $x_{1d}$ is the excepted value of $x_1$. Let error1 be $e=x_{1d}-x_1$. At this time, the control target is converted into $e\to 0$. When taking the Lyapunov function $v_e=\frac{1}{2}{e}^2$, then

$$\stackrel{•}{v_e}=e\left(\stackrel{•}{x_{1d}}-x_1\right)$$

(12)

According to Lyapunov stability theory, the system is stable when $x_2$ takes the virtual control value $x_{2d}=\frac{\stackrel{•}{x_{1d}}+k_{1}e}{f_1(x_1)}$, $\stackrel{•}{v_e}=-k_1{e}^2$, $k_1>0$, and then $e\to 0$.

To make $x_2\to x_{2d}$, let error2 be $\delta =x_{2d}-x_2$, and take the Lyapunov function as $v(e,\delta )=\frac{1}{2}{e}^2+\frac{1}{2}{\delta }^2$. Thus:

$$\stackrel{•}{v}(e,\delta )=-k_1{e}^2+\delta \left[f_1(x_1)e+\stackrel{•}{\delta }\right]$$

(13)

According to the Lyapunov stability theory, the system is stable when $x_3$ takes the virtual control value $x_{3d}=f_1(x_1)e+\stackrel{•}{x_{2d}}+k_2\delta$, $\stackrel{•}{v}(e,\delta )=-k_1{e}^2-k_2{\delta }^2$ and $k_1>0$, $k_2>0$ (then $\delta \to 0$).

To make $x_3\to x_{3d}$, let error3 be $\theta =x_{3d}-x_3$, and take the Lyapunov function as $v(e,\delta ,\theta )=\frac{1}{2}{e}_1{}^2+\frac{1}{2}{\delta }^2+\frac{1}{2}{\theta }^2$. Thus:

$$\stackrel{•}{v}(e,\delta ,\theta )=-k_1{e}^2-k_2{\delta }^2+\theta (\delta +\stackrel{•}{\theta })$$

(14)

According to the Lyapunov stability theory, the system is stable when the system control input satisfies formula (12): $\stackrel{•}{v}(e,\delta ,\theta )=-k_1{e}^2-k_2{\delta }^2-k_3{\theta }^2$ and $k_1>0$, $k_2>0$, $k_3>0$ (then $\delta \to 0$). Formula (14) is the control law of the system control input.

$$u=\frac{\left(x_{2d}-x_2\right)}{a_1}+\frac{\stackrel{•}{x_{3d}}}{a_1}-\frac{f_2(x_1,x_2,x_3)}{a_1}+\frac{k_3}{a_1}(x_{3d}-x_3)$$

(15)

The co-simulation of Matlab/Simulink and AMESim is used to verify the control effect of the system input control law of formula (14) on the piston oil pressure. The controller in Figure 3 is the oil pressure controller obtained by formula (15).

2.4. Wet Clutch Oil Filling Characteristics Influence Factor Divisions and Smoothness Evaluation Indexes

The wet clutch oil-filling process is generally divided into four stages [21,22,23]:

• Phase 1: after the solenoid valve coil of the wet clutch is electrified, the pressure in the piston cavity begins to build, and the gap between the friction plate and the steel plate is eliminated.
• Phase 2: with the increase in piston oil pressure, the friction plates and steel plates are further pressed. At this time, the clutch relies on rough friction torque and viscous torque to transmit torque.
• Phase 3: the piston oil pressure rises to the set value to ensure that the wet clutch has a certain reserve torque. At this time, there is no relative speed between friction plates and steel plates.
• Phase 4: the piston oil pressure remains constant until the controller issues new instructions.

Through analysis, this study selected five factors that affect the oil-filling characteristics curve—the oil-filling rate of phase 1, the proportion of phase 1’s duration to the total oil filling time, the oil-filling rate of phase 2, the proportion of phase 2’s duration to the total oil filling time, and the proportion of phase 3’s duration to the total oil filling time—to explore the influence of different oil-filling control strategies on the engagement quality of the wet clutch. In this paper, dynamic load, sliding friction work, impact degree, and engagement time are selected to evaluate the engagement quality of the wet clutch, and the comprehensive evaluation index of engagement quality of the wet clutch is established [24,25,26].

Dynamic load refers to the ratio of the maximum transmission torque to the stable transmission torque, indicating the fluctuation degree of the torque transmitted by the wet clutch.

$$y_1=\frac{T_{\max }}{T_0}$$

(16)

In the formula, $y_1$ is dynamic load, $T_{\max }$ is the maximum transmission torque during the wet clutch engagement process (Nm), and $T_0$ is the stable transmission torque during the wet clutch engagement process (Nm).

Sliding friction work is the work generated by the friction torque of the wet clutch when sliding, and sliding means there is a relative speed between friction plates and steel plates of the wet clutch. The friction work will accelerate the wear of clutch friction plates and reduce the service life of the clutch.

$$y_2={\displaystyle {\int }_{t_1}^{t_2}{T}_{cl}({\omega }_1-{\omega }_0)\mathrm{dt}}$$

(17)

In the formula, $y_2$ is the sliding friction work (J), $T_{cl}$ is the friction torque of the wet clutch (Nm), ${\omega }_1$ is the rotation speed of the friction plates (rad/s), ${\omega }_0$ is the rotation speed of the steel plates (rad/s), $t_1$ is the sliding start time (s), and $t_2$ is the sliding end time (s).

Impact degree refers to the change rate of the tractor’s longitudinal acceleration; the greater the impact, the lower the smoothness and the driving comfort of the tractor.

$$y_3=\frac{d^2{v}_t}{d{t}^2}$$

(18)

In the formula, $y_3$ is the impact degree (m/s³) and $v_t$ is the speed of tractor (m/s).

The engagement time refers to the time when the wet clutch receives the engagement instruction until there is no rotational speed difference between the friction plates and the steel plates.

$$y_4=t_0-t_{stable}$$

(19)

In the formula, $y_4$ is the full engagement time (s), $t_0$ is the time when the wet clutch actuator receives the combined instruction (s), and $t_{stable}$ is the time when there does not exist a speed difference(s) between the friction plate and the steel plate.

2.5. Simulation Test Platform for Oil Filling Control Strategy of Wet Clutch

Due to the noise interference in a bench test, this paper studies the oil filling control strategy of the wet clutch based on SimulationX software (Version 3.8, ESI ITI GmbH, Dresden, Germany), taking one stage of a stepped gearbox as an example. The specific parameters of the wet clutch in the oil-filled test platform are shown in

Table 1. Simulation Parameters of wet clutch oil filling test platform.

Parameter	Value	Parameter	Value
Sticking friction coefficient	0.12	Slipping friction coefficient	0.08
Outer diameter of clutch friction plates (mm)	135	Number of clutch friction pairs	8
External diameter of clutch friction plates (mm)	164	The thickness of clutch friction plates	3

, and the simulation test platform is shown in Figure 4. The working condition of the test is that a certain type of tractor (8.5 t) runs on flat ground without hanging agricultural machinery, and the engine speed is 1070 r/min. To validate the simulation model, this paper conducts simulation tests and bench tests of eight operating conditions (clutch oil pressure is 0.5, 1, 1.7, 2.4, 3.1, 3.8, 4.3, and 4.8 MPa, respectively) and compares the results (

Table 2. Results comparison.

Number	Bench Test Results (r/min)	Simulation Test Results (r/min)	Relative Error (%)	Average Relative Error (%)
1	291	282.01	3.04	5.3
2	299.25	283.21	5.3
3	306.25	284.17	7.2
4	302.75	285.66	5.6
5	303.25	286.64	5.5
6	304.75	287.22	5.8
7	304.25	287.78	5.4
8	303.75	288.12	5.1

). One should adjust the simulation platform to match the engine speed (1070 r/min) and load (85.17 Nm) of the bench (Figure 5) and record the speed fluctuation of the gearbox output shaft. The comparison results are shown in Table 1.

For these 8 conditions, the relative error between the simulation results and the test results of the maximum output speed of the gearbox is 5.3%, which verifies the correctness of the simulation model.

2.6. Experimental Design Based on RSM

In this paper, the central composite design (CCD) in response surface methodology (RSM) is selected to design the simulation test of clutch engagement quality [27,28], and the number of the test groups is 50 in total (

Table 3. Factors and levels of RSM test.

Factors	Levels
A	15° (−2)	30° (−1)	45° (0)	60° (1)	75° (2)
B	10% (−2)	15% (−1)	20% (0)	25% (1)	30% (2)
C	15° (−2)	30° (−1)	45° (0)	60° (1)	75° (2)
D	10% (−2)	15% (−1)	20% (0)	25% (1)	30% (2)
E	10% (−2)	15% (−1)	20% (0)	25% (1)	30% (2)

Note: The code value in brackets corresponding to each level of each factor in RSM tests.

and

Table 4. RSM test design and results of different oil filling curves on the wet clutch engagement quality.

Test Number	The Code Value of Factors					Evaluation Index of Wet Clutch Engagement Quality
	A	B	C	D	E	y1	y2 (J)	y3 (m/s3)	y4 (S)
1	−1	1	1	−1	1	3.3891	608.7464	18.0604	0.4475
2	−1	1	1	−1	−1	3.3891	608.7464	18.2110	0.4475
3	0	0	0	0	0	3.0969	486.8665	16.2769	0.3275
4	0	−2	0	0	0	3.1004	486.5006	16.7344	0.3222
5	0	2	0	0	0	3.0950	486.3843	18.1973	0.3289
6	1	1	−1	1	1	3.7551	396.2355	25.9036	0.2277
7	−1	1	−1	−1	1	2.5997	620.9123	12.2579	0.4658
8	0	0	2	0	0	3.6988	486.1870	20.4988	0.3183
9	1	−1	1	1	1	3.7539	396.2330	22.0172	0.2263
10	0	0	0	0	0	3.0969	486.8635	16.2769	0.3261
11	1	−1	1	−1	1	3.7539	396.2330	22.4485	0.2263
12	1	−1	−1	−1	−1	3.7539	396.2330	22.0376	0.2263
13	0	0	−2	0	0	2.9059	487.0966	15.5220	0.3246
14	−2	0	0	0	0	3.0984	609.4035	17.1849	0.5345
15	0	0	0	0	0	3.0969	486.8484	16.4291	0.3227
16	1	−1	−1	1	−1	3.7539	396.2330	21.6240	0.2263
17	−1	−1	−1	−1	1	3.0752	620.4315	14.9747	0.4699
18	1	−1	1	1	−1	3.7539	396.2330	22.2299	0.2263
19	1	−1	−1	−1	1	3.7539	396.2330	21.8362	0.2263
20	−1	−1	−1	1	−1	3.7336	534.9278	20.7967	0.3808
21	−1	−1	1	1	1	4.3965	507.8907	29.7387	0.3555
22	1	−1	1	−1	−1	3.7539	396.2330	22.4491	0.2263
23	0	0	0	0	0	3.0969	486.8665	16.2769	0.3275
24	0	0	0	0	2	3.0969	486.8665	16.1278	0.3275
25	−1	−1	−1	1	1	2.6025	620.5252	13.2391	0.4654
26	−1	1	−1	1	−1	2.5997	620.9123	12.1363	0.4658
27	1	1	1	1	−1	3.7551	396.2325	27.1737	0.2264
28	1	1	−1	1	−1	3.7551	396.2325	26.6489	0.2264
29	0	0	0	0	0	3.0969	486.8433	16.4291	0.3202
30	0	0	0	0	0	3.0969	486.8665	16.4291	0.3275
31	−1	1	1	1	1	3.3891	608.7451	17.5980	0.4462
32	−1	−1	1	1	−1	3.7336	534.9278	20.4164	0.3808
33	1	1	−1	−1	−1	3.7551	396.2325	25.8938	0.2264
34	1	1	−1	−1	1	3.7551	396.2325	26.1471	0.2264
35	0	0	0	−2	0	3.0969	486.8433	16.2723	0.3202
36	−1	1	−1	−1	−1	2.5997	620.9123	12.3657	0.4658
37	−1	1	1	1	−1	3.3891	608.7272	17.7497	0.4414
38	0	0	0	2	0	3.0969	486.8433	15.9782	0.3202
39	1	1	1	−1	1	3.7551	396.2235	28.5734	0.2244
40	−1	−1	−1	−1	−1	3.3482	620.3871	17.3163	0.4652
41	−1	1	−1	1	1	2.5997	620.9123	12.9101	0.4658
42	1	1	1	1	1	3.7551	396.2325	28.8718	0.2264
43	0	0	0	0	0	3.0969	486.8433	16.9029	0.3202
44	0	0	0	0	0	3.0969	486.8665	16.9029	0.3275
45	2	0	0	0	0	5.0108	314.6145	29.2979	0.1461
46	−1	−1	1	−1	1	3.7336	534.9278	21.4024	0.3808
47	1	−1	−1	1	1	3.7539	396.2330	22.7041	0.2263
48	1	1	1	−1	−1	3.7551	396.2325	27.9957	0.2264
49	−1	−1	1	−1	−1	3.7336	534.9278	20.9810	0.3808
50	0	0	0	0	−2	3.0969	486.8433	16.5790	0.3202

). CCD has the advantages of flexible design and fewer test times, which are widely used in scientific experiments.

The RSM is based on the least squares regression method to fit the statistical model, to approximate the real functional relationship, and to describe the relationship between input and response scientifically. The model can optimize and predict the response.

The code value and the actual value of each factor can be selected when modeling. The items in the model established by the two methods are the same, but each parameter is different. The relationship between the factors ($A$, $B$, $C$, $D$, and $E$) and the response values ($y_1$, $y_2$, $y_3$, $y_4$, and $y_5$) is shown in formula (19) [29,30].

$$y=f(A, B, C, D, E)+\epsilon$$

(20)

In the formula, $A$ is the oil filling rate of phase 1, $B$ is the proportion of phase 1’s duration to the total oil filling time, $C$ is the oil filling rate of phase 2, $D$ is the proportion of phase 2’s duration to the total oil filling time, $E$ is the proportion of phase 3’s duration to the total oil filling time, and $\epsilon$ is the variation from other sources that the model cannot explain.

The first-order or second-order Taylor expansion is used to approximate the function form of the model in a relatively small region. The second-order model is:

$$y={\beta }_0+{\displaystyle \sum _{i=1}^k{\beta }_i}{x}_i+{\displaystyle \sum _{i=1}^k{\beta }_{ii}}{x}_i{}^2+{\displaystyle \sum _{i<j}{\displaystyle \sum _{j=2}^k{\beta }_{ij}}}{x}_i{x}_j+\epsilon$$

(21)

3. Results and Discussion

3.1. Verification of Wet Clutch Piston Oil Pressure Control Effect

To verify the control effect of the controller designed in Chapter 2.3 on the clutch piston oil pressure under different system inputs, this paper studies the square wave signal and sine signal as the oil pressure control target for verification. As shown in Figure 6 and Figure 7, the oil pressure on the clutch piston can be effectively tracked according to the target curve.

When the target value changes with a square wave signal (Figure 6a), the total simulation test time is 3 s. In the first stage, the target oil pressure is 2.165 MPa, and the time required for the controller to stabilize to the target value is 0.05 s. The maximum oil pressure overshoot in this process is 0.923 MPa. In the second stage, the target oil pressure is 1.627 MPa, and the time required for the controller to stabilize to the target value is 0.106 s. In this process, the maximum oil pressure overshoot is 0.091 MPa. In the third stage, the target oil pressure is 1.075 MPa, and the time required for the controller to stabilize to the target value is 0.144 s. In this process, the maximum oil pressure overshoot is 0.102 MPa. Figure 6b is the error between the actual oil pressure and the target value in the process of oil pressure following control. The maximum following error of the first stage is 2.165 MPa, the maximum following error of the second stage is 0.538 MPa, and the maximum following error of the third stage is 0.552 MPa. When the target value of the wet clutch’s oil filling pressure changes with the sine signal (Figure 7), the total simulation test time is 3 s, the controller response time is 0.1 s, the following error is less than 0.01 MPa, and the maximum overshoot oil pressure is 0.026 MPa in the process of oil pressure following.

The simulation results show that the piston oil pressure controller, based on the backstepping algorithm, can achieve a better tracking effect to control the wet clutch with different oil filling characteristics curves.

At the same time, in order to further verify the control effect of the oil pressure controller designed in this paper, taking the square as an example, the backstepping controller is compared with the PID controller, which is commonly used in engineering. As shown in Figure 8, the final stable value of the square wave signal is 1.165 MPa. The PID controller oscillates violently within 0–0.099 s, and the overshoot of the backstepping controller is reduced by 78% compared with that of the PID controller. The backstepping controller is slower to stabilize to the expected value, but both controllers can quickly change to the expected value, and the required times are 0.099 s and 0.189 s, respectively.

The overshoot of the backstepping controller is relatively small, and the fluctuation of oil filling pressure is small. In the process of the wet clutch engagement, the fluctuation degree of oil filling pressure will directly affect the value of the wet clutch’s sliding friction work, which will aggravate the wear of the wet clutch in the long term and affect the service life and engagement quality.

3.2. Analysis of RSM Test Results

3.2.1. Analysis of Dynamic Load RSM Modeling Results

According to simulation test results of wet clutch engagement quality in Table 4, a quadratic regression polynomial model with dynamic load $y_1$ as a response value is established:

$$\begin{array}{l}{y}_1=7.547-0.087A-15.489B-0.007C-2.084D-10.973E+0.184AB-0.0008AC\\ -0.024AD+0.031AE+0.013BC-7.195BD+9.265BE+0.031CD+0.086CE-2.44DE\\ +0.001A^2+10.009B^2+0.0004C^2+9.929D^2+9.929E^2\end{array}$$

(22)

In the formula, $A$ is the oil filling rate of phase 1, $B$ is the proportion of phase 1’s duration to the total oil filling time, $C$ is the oil filling rate of phase 2, $D$ is the proportion of phase 2’s duration to the total oil filling time, $E$ is the proportion of phase 3’s duration to the total oil filling time, and $y_1$ is the dynamic load. Variance analysis of each model’s item is carried out to test the significance, and the results are shown in

Table 5. Significance test of the dynamic load regression model.

Source	Sum of Squares	df	Mean Square	F-Value	Prob > F	Result
Model	9.72	20	0.49	10.55	<0.0001	significant
A	9.72	20	0.49	10.55	<0.0001
B	0.22	1	0.22	4.79	0.0369
C	0.016	1	0.016	0.35	0.5589
D	0.10	1	0.10	2.25	0.1446
E	3.494 × 10−3	1	3.494 × 10−3	0.076	0.7849
AB	0.024	1	0.024	0.51	0.4789
AC	0.61	1	0.61	13.21	0.0011
AD	1.12	1	1.12	24.39	<0.0001
AE	0.010	1	0.010	0.22	0.6389
BC	0.017	1	0.017	0.37	0.5462
BD	3.196 × 10−3	1	3.196 × 10−3	0.069	0.7941
BE	0.010	1	0.010	0.22	0.6389
CD	0.017	1	0.017	0.37	0.5462
CE	0.018	1	0.018	0.38	0.5414
DE	0.13	1	0.13	2.90	0.0993
A2	1.191 × 10−3	1	1.191 × 10−3	0.026	0.8734
B2	2.23	1	2.23	48.53	<0.0001
C2	0.020	1	0.020	0.44	0.5147
D2	0.19	1	0.19	4.03	0.0540
E2	0.020	1	0.020	0.43	0.5180

.

It can be seen from Table 5 that the p-value of the dynamic load regression model is less than 0.0001, indicating that the regression model is highly significant. Therefore, the model fitting accuracy is high and can be used to describe the sample. The fitting coefficient of the dynamic load regression model is 0.8792, the coefficient of adjustment is 0.7959, and the coefficient of variation is 6.29%. In summary, the regression model has high fitting accuracy, which can reflect the relationship between the five influencing factors and the dynamic load and can analyze and predict the dynamic load accurately.

In the variance analysis of the model, the influence of one-degree items A and B are significant (p < 0.05), and the significant degree of the five factors from high to low is A > B > D > C > E. B² is the signature item in the second-order items (p < 0.05), indicating that the influence of factor B on dynamic load is nonlinear. In the cross items, AC and AD are significant (p < 0.05), indicating that there is a significant interaction between factor A and factor C, as well as factor A and factor D.

Figure 9 shows a curved surface, indicating that the influence of the interaction between factors A and C on the dynamic load is nonlinear. With the increase of the oil filling rate of phase 1 and the oil filling rate of phase 2, the dynamic load value increases gradually.

3.2.2. Analysis of Sliding Friction Work RSM Modeling Results

According to simulation test results of wet clutch engagement quality in Table 4, a quadratic regression polynomial model with sliding friction work $y_2$ as a response value is established:

$$\begin{array}{l}{y}_2=838.768-5.24A+397.917B-4.138C-803.71D+350.639E-17.069AB+0.046AC\\ +4.685AD-2.443AE+9.788BC+1404.928BD-732.41BE+2.43CD-4.695CE+731.823DE\end{array}$$

(23)

It can be found from

Table 6. Significance test of the sliding friction work regression model.

Source	Sum of Squares	df	Mean Square	F-Value	Prob > F	Result
Model	3.575 × 105	15	23,833.52	63.58	<0.0001	significant
A	1374.87	1	1374.87	3.67	0.0639
B	46.63	1	46.63	0.12	0.7265
C	337.00	1	337.00	0.90	0.3497
D	455.36	1	455.36	1.21	0.2781
E	7.990 × 10−5	1	7.990 × 10−5	2.132 × 10−5	0.9996
AB	5244.89	1	5244.89	13.99	0.0007
AC	3450.10	1	3450.10	9.20	0.0046
AD	395.05	1	395.05	1.05	0.3119
AE	107.42	1	107.42	0.29	0.5959
BC	1724.33	1	1724.33	4.60	0.0392
BD	394.76	1	394.76	1.05	0.3120
BE	107.28	1	107.28	0.29	0.5961
CD	106.27	1	106.27	0.28	0.5979
CE	396.73	1	396.73	1.06	0.3109
DE	107.11	1	107.11	0.29	0.5964

that the p-value of the sliding friction work regression model is less than 0.0001, indicating that the regression model is highly significant. Therefore, the model fitting accuracy is high, and can be used to describe the sample. The fitting coefficient of the model is 0.9656, the coefficient of adjustment is 0.9504, and the coefficient of variation is 3.95%. In summary, the model has high fitting accuracy, which can reflect the relationship between the five influencing factors and the sliding friction work and can analyze and predict the sliding friction work accurately.

In the variance analysis of the sliding friction work regression model, the influence of the cross items AB, AC, and BC are significant (p < 0.05), indicating that there is a significant interaction between factor A and factor B, factor A and factor C, and factor B and factor C.

Figure 10 is almost a plane, indicating that the interaction between factors A and B has a linear effect on the sliding friction work. When the oil filling rate of phase 1 is constant, the value of the sliding friction work decreases with the increase in the proportion of phase 1’s duration to the total oil filling time.

3.2.3. Analysis of Impact Degree RSM Modeling Results

According to simulation test results of wet clutch engagement quality in Table 4, a quadratic regression polynomial model with impact degree $y_3$ as a response value is established. Variance analysis of each model’s item is carried out to test the significance. The results are shown in

Table 7. Significance test of the impact degree regression model.

Source	Sum of Squares	df	Mean Square	F-Value	Prob > F	Result
Model	1053.59	20	52.68	13.77	<0.0001	significant
A	52.12	1	52.12	13.62	0.0009
B	7.62	1	7.62	1.99	0.1688
C	6.96	1	6.96	1.82	0.1879
D	2.28	1	2.28	0.60	0.4464
E	6.76	1	6.76	1.77	0.1941
AB	187.39	1	187.39	48.98	<0.0001
AC	48.01	1	48.01	12.55	0.0014
AD	2.66	1	2.66	0.69	0.4113
AE	0.16	1	0.16	0.041	0.8409
BC	0.25	1	0.25	0.065	0.8009
BD	3.02	1	3.02	0.79	0.3815
BE	0.084	1	0.084	0.022	0.8834
CD	0.20	1	0.20	0.053	0.8200
CE	12.94	1	12.94	3.38	0.0761
DE	1.04	1	1.04	0.27	0.6068
A2	150.60	1	150.60	39.36	<0.0001
B2	16.84	1	16.84	4.40	0.0447
C2	23.76	1	23.76	6.21	0.0187
D2	4.88	1	4.88	1.27	0.2682
E2	6.40	1	6.40	1.67	0.2059

.

$$\begin{array}{l}{y}_3=75.266-0.979A-243.458B-0.202C-35.621D-131.546E+3.227AB-0.005AC\\ -0.384AD+0.093AE+0.117BC-122.915BD+20.47BE+0.106CD+0.848CE\\ +71.958DE+0.01A^2+290.194B^2+0.004C^2+156.134D^2+178.949E^2\end{array}$$

(24)

It can be seen from Table 7 that the p-value of the impact degree regression model is less than 0.0001, indicating that the regression model is highly significant. Therefore, the model fitting accuracy is high, and can be used to describe the sample. The fitting coefficient of the dynamic load regression model is 0.9047, the coefficient of adjustment is 0.8390, and the coefficient of variation is 9.89%. In summary, the regression model has high fitting accuracy, which can reflect the relationship between the five influencing factors and the impact degree and can analyze and predict the impact degree accurately.

In the variance analysis of the model, the influence of one-degree item A is significant (p < 0.05). In the second order items, A², B², and C² are significant, indicating that the influence of factors A, B, and C on dynamic load is nonlinear. In the cross items, AB and AC are significant (p < 0.05), indicating that there is a significant interaction between factor A and factor B, as well as factor A and factor C.

The response surface in Figure 11 has a certain degree of bending. It indicates that the interaction between the oil filling rate of phase 1 and the proportion of phase 1’s duration to the total oil filling time has a linear effect on impact degree. When the oil filling rate of phase 1 is small and the proportion of phase 1’s duration to the total oil filling time is large, the impact degree is small.

3.2.4. Analysis of Engagement Time RSM Modeling Results

According to simulation test results of wet clutch engagement quality in Table 4, a quadratic regression polynomial model with full engagement time $y_4$ as a response value is established. Variance analysis of each model’s item is carried out to test the significance. The results are shown in

Table 8. Significance test of the full engagement time regression model.

Source	Sum of Squares	df	Mean Square	F-Value	Prob > F	Result
Model	1.062 × 10−3	1	1.062 × 10−3	4.86	0.0343	significant
A	4.081 × 10−5	1	4.081 × 10−5	0.19	0.6682
B	2.115 × 10−4	1	2.115 × 10−4	0.97	0.3320
C	4.656 × 10−4	1	4.656 × 10−4	2.13	0.1534
D	1.286 × 10−7	1	1.286 × 10−7	5.891 × 10−4	0.9808
E	4.198 × 10−3	1	4.198 × 10−3	19.23	0.0001
AB	4.073 × 10−3	1	4.073 × 10−3	18.65	0.0001
AC	4.879 × 10−4	1	4.879 × 10−4	2.23	0.1442
AD	1.509 × 10−4	1	1.509 × 10−4	0.69	0.4116
AE	1.240 × 10−3	1	1.240 × 10−3	5.68	0.0229
BC	3.799 × 10−4	1	3.799 × 10−4	1.74	0.1960
BD	1.122 × 10−4	1	1.122 × 10−4	0.51	0.4784
BE	1.019 × 10−4	1	1.019 × 10−4	0.47	0.4991
CD	3.994 × 10−4	1	3.994 × 10−4	1.83	0.1851
CE	1.225 × 10−4	1	1.225 × 10−4	0.56	0.4589
DE	1.062 × 10−3	1	1.062 × 10−3	4.86	0.0343

.

$$\begin{array}{l}{y}_4=0.723-0.006A+0.378B-0.004C-0.833D+0.377E-0.015AB+0.00005AC\\ +0.005AD-0.003AE+0.008BC+1.378BD-0.749BE+0.002CD-0.005CE+0.783DE\end{array}$$

(25)

It can be found from Table 8 that the p-value of the impact degree regression model is less than 0.05, indicating that the regression model is highly significant. Therefore, the model fitting accuracy is high, and can be used to describe the sample. The fitting coefficient of the dynamic load regression model is 0.9832, the coefficient of adjustment is 0.9758, and the coefficient of variation is 4.50%. In summary, the regression model has high fitting accuracy, which can reflect the relationship between the five influencing factors and the full engagement time and can analyze and predict the full engagement time accurately.

In the variance analysis of the model, the influence of one degree item E is significant (p < 0.05). In the cross items, AB, AE, and DE are significant (p < 0.05), indicating that there is a significant interaction between factor A and factor B, factor A and factor E, and factor D and factor E.

Figure 12 is almost a plane. It indicates that the interaction between the oil filling rate of phase 1 and the proportion of phase 1’s duration to the total oil filling time has a linear effect on full engagement time. When the proportion of phase 1’s duration to the total oil filling time is constant, the value of full engagement time gradually decreases with the increase of the oil filling rate of phase 1.

3.3. Comparison of Two Modelling Method

To improve the model accuracy and simplify the model, this paper uses the stepwise regression method [31,32] to model the simulation test data in Table 4 and compares the prediction accuracy of the two methods. The regression models of the four evaluation indexes established by the stepwise regression method are shown in formulas 26–29:

$${\eta }_1=-0.09A-10.472B+0.184AB-0.0007AC+0.0012A^2+0.0005C^2+5.677$$

(26)

$${\eta }_2=-4.792A+532.42B-4.591C-17.07AB+0.046AC+9.788BC+777.426$$

(27)

$$\begin{array}{l}{\eta }_3=-0.979A-243.458B-0.202C-35.621D-131.546E+3.227AB-0.005AC\\ -0.384AD+0.093AE+0.117BC-122.915BD+20.47BE+0.106CD+0.848CE\\ +71.958DE+0.01A^2+290.194B^2+0.004C^2+156.134D^2+178.949E^2+75.266\end{array}$$

(28)

$${\eta }_4=-0.006A+0.504B-0.005C-0.015AB+0.00005AC+0.008BC+0.664$$

(29)

The fitting coefficient of the dynamic load’s stepwise regression model is 0.847, and the coefficient of adjustment is 0.826. The fitting coefficient of the sliding friction work’s stepwise regression model is 0.960, and the coefficient of adjustment is 0.955. The fitting coefficient of the impact degree’s stepwise regression model is 0.877, and the coefficient of adjustment is 0.859. The fitting coefficient of the full engagement time’s stepwise regression model is 0.978, and the coefficient of adjustment is 0.975.

At the same time, 15 trials are randomly carried out to compare the prediction accuracy of RSM and stepwise regression model. The results are shown in

Table 9. Comparison of prediction accuracy between the RSM models and the stepwise models.

Evaluation Index	Prediction Accuracy (%)
	RSM	Stepwise Regression Method
Dynamic load Sliding friction work (J)	90.90	91.23
	94.25	96.29
Impact degree (m/s3)	76.73	38.63
Full engagement time (s)	92.16	94.72

.

By comparing the prediction accuracy of the stepwise regression model, it is shown that dynamic load, sliding friction work, impact degree, and full engagement time are higher than that of the RSM model. The prediction accuracy of the RSM model for impact degree is higher than the stepwise regression model. Therefore, the stepwise regression model is used to predict the dynamic load, sliding friction work, and full engagement time of the wet clutch during oil filling. The RSM model is used to predict the impact degree.

3.4. Optimal Oil Filling Control Strategy

To obtain the optimal oil-filling control strategy, this paper selects the variance weight method [33] to establish the comprehensive evaluation index of the wet clutch (Table 1) oil-filling process. After calculation, the weight of the dynamic load (w₁) is 0.1516, the weight of the sliding friction work (w₂) is 0.3146, the weight of the impact degree (w₃) is 0.2997, and the weight of the full engagement time (w₄) is 0.2341. By combining (26), (27), (28), and (29), the mathematical model of the comprehensive evaluation index of the wet clutch oil filling process is shown to be:

$$\begin{array}{l}Y=268.151-1.816A+93.065B-1.506C-10.676D-39.424E-4.379AB+0.013AC\\ -0.115AD+0.028AE+3.116BC-36.838BD+6.135BE+0.032CD+0.254CE\\ +21.566DE+0.003A^2+86.97B^2+0.001C^2+46.793D^2+53.63E^2\end{array}$$

(30)

For the wet clutch in Table 1, when the oil filling pressure is 3 MPa, the optimal oil filling control strategy is determined according to the mathematical model of the comprehensive evaluation index of the oil filling process, as shown in Figure 13 (A = 75°, B = 69.65%, C = 15°, D = 21.85%, and E = 8.51%). Compared with the 50 groups of control strategies in Table 4, the clutch engagement quality of the oil-filling control strategy in Figure 13 is the best, and the comprehensive evaluation value is $Y_{\min }=108.1288$.

4. Conclusions

In this paper, the wet clutch, which is widely used in agricultural machinery, is taken as the research object. From the aspect of improving the engagement quality of the wet clutch, the oil-filling control strategy of the clutch is studied.

(1) The clutch oil pressure controller is established by the dynamic model of the wet clutch engagement process, and the controllability of the output oil pressure of the clutch hydraulic actuator is verified. Comparing the control effect of the backstepping oil pressure controller and the PID oil pressure controller, the overshoot generated in the control process of the former is smaller.

(2) For the wet clutch in Table 1, the stepwise regression model and RSM model between the four engagement quality evaluation indexes and the oil filling control strategy are compared. After comparison, it was found that the model prediction accuracy of dynamic load, sliding friction work, and engagement time using the stepwise regression method is higher, which corresponds to values of 91.23%, 96.29%, and 94.72%, respectively. The RSM model of impact degree has higher prediction accuracy. Through the variance weight analysis method, it was determined that, in the comprehensive evaluation index of engagement quality, the weight of the dynamic load is 0.1516, the weight of sliding friction work is 0.3146, the weight of impact degree is 0.2997, and the weight of engagement time is 0.2341.

(3) In this paper, the oil filling pressure of 3 MPa is taken as the research condition, and the optimal oil filling control strategy is obtained by the proposed clutch engagement quality prediction model. Under the target condition, when the oil filling rate of phase 1 is the highest and the proportion of phase 1’s duration to the total oil filling time is 69.65%, the oil filling rate of phase 2 is the lowest and the proportion of phase 2’s duration to the total oil filling time is 21.85%, and the proportion of phase 3’s duration to the total oil filling time is 8.51%, the wet clutch engagement quality is the best. The research method of wet clutch optimal oil filling control strategy proposed in this paper can provide a reliable method for the ride comfort research of agricultural machinery and the clutch control.