Before the optimal design of the dual-insulated electroadhesion pad, it is necessary to confirm and verify the pad characteristics for the variables affecting the electroadhesion force. Therefore, this section aims to confirm the characteristics of each parameter of the pad and to confirm the accuracy between the proposed modeling and the finite element analysis data.
3.1. Analytical Modeling of Electroadhesion Pad
In
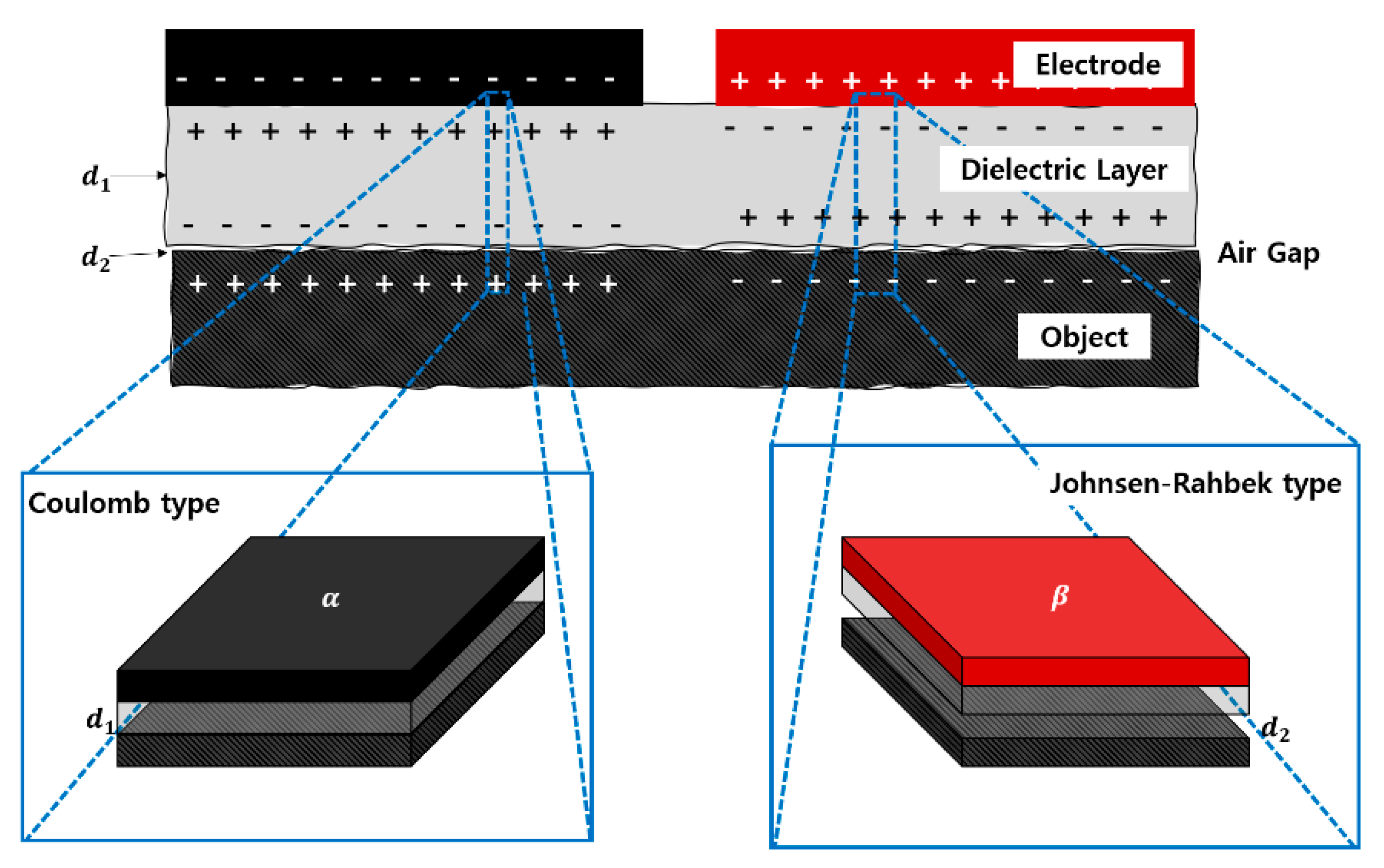
Section 2, the electroadhesion force could be derived as shown in Equation (1) by Coulomb’s law and the law of energy conservation. Contrary to the previous assumption, since the pad and the attachment surface cannot be in an ideal close contact in the real environment, it can be modeled separately by the Coulomb force and the Johnsen–Rahbek force [
13,
14], as shown in
Figure 4, considering the formed air layer.
denotes the thickness of the dielectric between the electrode and the wall surface of the pad, and
denotes the thickness of the air layer formed between the pad and the wall surface.
and
represent the areas of the Coulomb force and the Johnson–Rahbek force, respectively. Therefore, Equation (2) below expresses the modeling of the single-insulating electroadhesion pad:
The modeling of the double-insulated electroadhesion pad is the same as that of the single-insulated structure.
Figure 5 and Equation (3) illustrate how the model is modeled, while
Figure 5a,c shows the presence or absence of an air gap in the dual-insulated structure, and
Figure 5b,d shows the presence or absence of an air gap in the single-insulated structure.
is the area where a single dielectric layer is present, and ideal adhesion is achieved.
is the area where the dielectric layer and insulating layer exist, and, thereby, ideal adhesion is achieved.
is the area where a single dielectric layer is present, and an air layer is present.
is the area where the dielectric layer and the insulating layer are present, and, thereby, the air layer is present.
Figure 5 shows that
to
refer to the thickness of the dielectric layer, insulating layer, and the air layer, respectively.
When the electroadhesion force according to each variable in
Table 2 is confirmed through the Ansys Maxwell, each characteristic and influence can be considered and applied to the optimal design.
The design and finite element analysis to confirm the characteristics of the electrostatic adsorption pad were conducted in the Ansys Maxwell. The solution type was set to Electrostatic. Meshing was set to a highly robust volumetric meshing (TAU), provided by the Ansys Maxwell, and the bonding target is made of 0.6 mm thick silicon material. To consider the air layer of the proposed modeling equation, the thickness was set to 5 μm to confirm the electrostatic field and the applied force.
Figure 6 shows the designs of single- and dual-insulated electroadhesion pads composed of two electrodes in the Ansys Maxwell. In this study, for a fast simulation process, the simplified pad shape was used, as shown in
Figure 7.
As a result, it was confirmed that when the electrode area was set to increase the electrode length, the larger the area was, the larger the electroadhesion became for the area. It is confirmed that as the electrode width increases, the electroadhesion per area decreases, and the applied voltage increases in the form of a quadratic curve. The change was insignificant compared to the difference in the range of variation in electrode thickness, and as the distance between the electrodes increased, the electroadhesion decreased. Likewise, as the thickness of the dielectric increased, the electroadhesion decreased, and as the dielectric constant increased, the electroadhesion increased. These are predictable results through the formula derived above. However, when the influence on the change in the adsorption force is confirmed with this, key parameters, such as applied voltage, electrode area, dielectric thickness, and permittivity, are selected as key parameters for the pad optimization, and then modeling verification and optimal design are performed.
Each parameter was selected according to the pad structure and formula and can be confirmed, as illustrated in
Figure 7. Each parameter was selected as the applied voltage
, the electrode area
, the electrode width
w, the electrode thickness
, the dielectric thickness
, the inter-electrode distance
, and the dielectric constant
.
Figure 7 shows the design of the reference pad with an applied voltage of 2
, an electrode area of 9600
, an electrode width of 48
, an electrode thickness of 16
, a dielectric thickness of 100
, an inter-electrode distance of 5
, a dielectric constant of 3.5
, and an aluminum electrode.
Table 2 represents the range for experiments in future studies for each parameter, and 4–5 samples were used.
Analysis data for each parameter are compared by measuring the force acting between the pad electrode and the attachment target.
Figure 8 and
Figure 9 show the simulation results for meshing, applied voltage, electric field, and surface force density to which the reference setting of the pad, according to each structure, is applied. In
Figure 8a and
Figure 9a, fine meshing is made on the edge portions of the electrode where the electric field is applied.
Figure 8b and
Figure 9b show that the potential difference of the applied voltage is set to be 2 kV.
Figure 8c,d and
Figure 9c,d show that a uniform force acts from the electrode to the suction pad for single insulation and that the force generated at one electrode is relatively reduced by the added insulation layer for dual insulation.