Establishment and Experimental Verification of a Nonlinear Position Servo System Model for a Magnetically Coupled Rodless Cylinder
Abstract
:1. Introduction
2. Experimental Set-Up
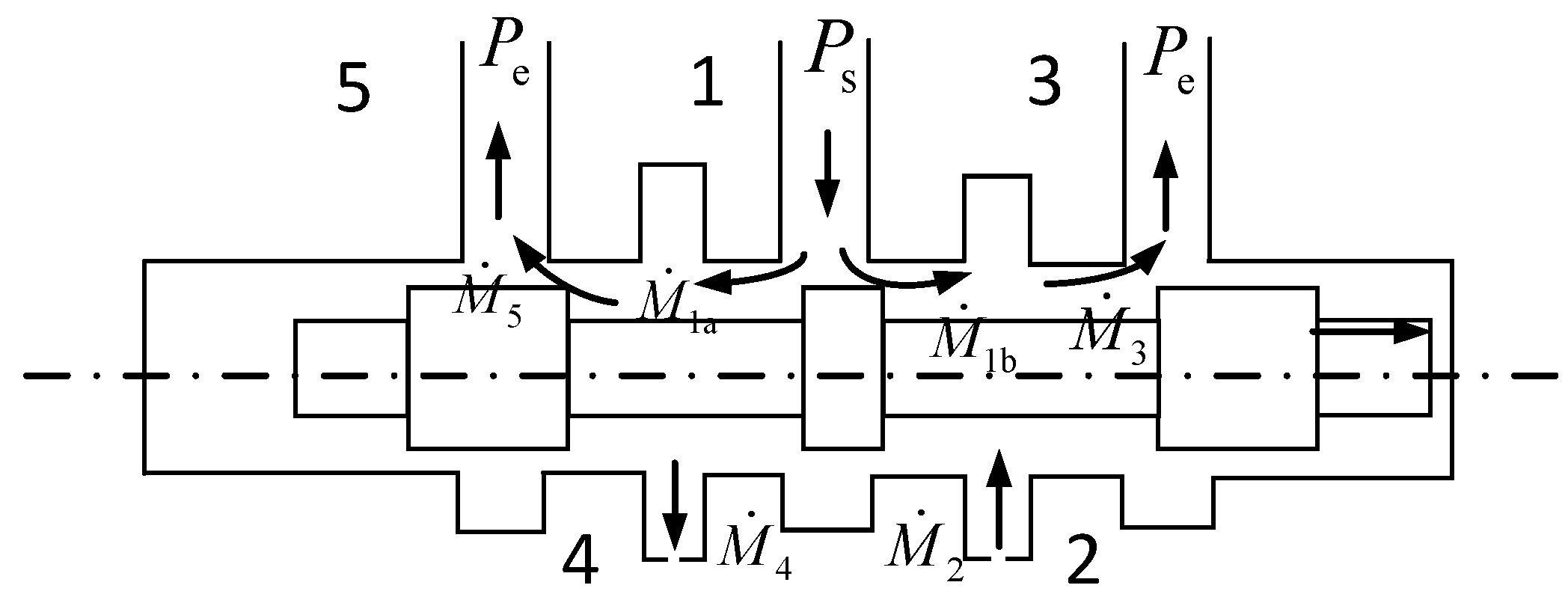
3. Establishment of the Mass Flow Equation for Proportional Directional Control Valves
- (1)
- The air used in the system is an ideal gas;
- (2)
- When the gas flows through the proportional directional control valve and cylinder, it is regarded as an isentropic insulation state;
- (3)
- The gas pressure and temperature in the same chamber are equal everywhere;
- (4)
- During the left-and-right round-trip movement of the piston in the cylinder, the heat exchange between the gas inside the two chambers and the outside world does not occur as an insulation process;
- (5)
- The pressure and temperature of the gas supply are not affected by the external surrounding environment and remain constant.
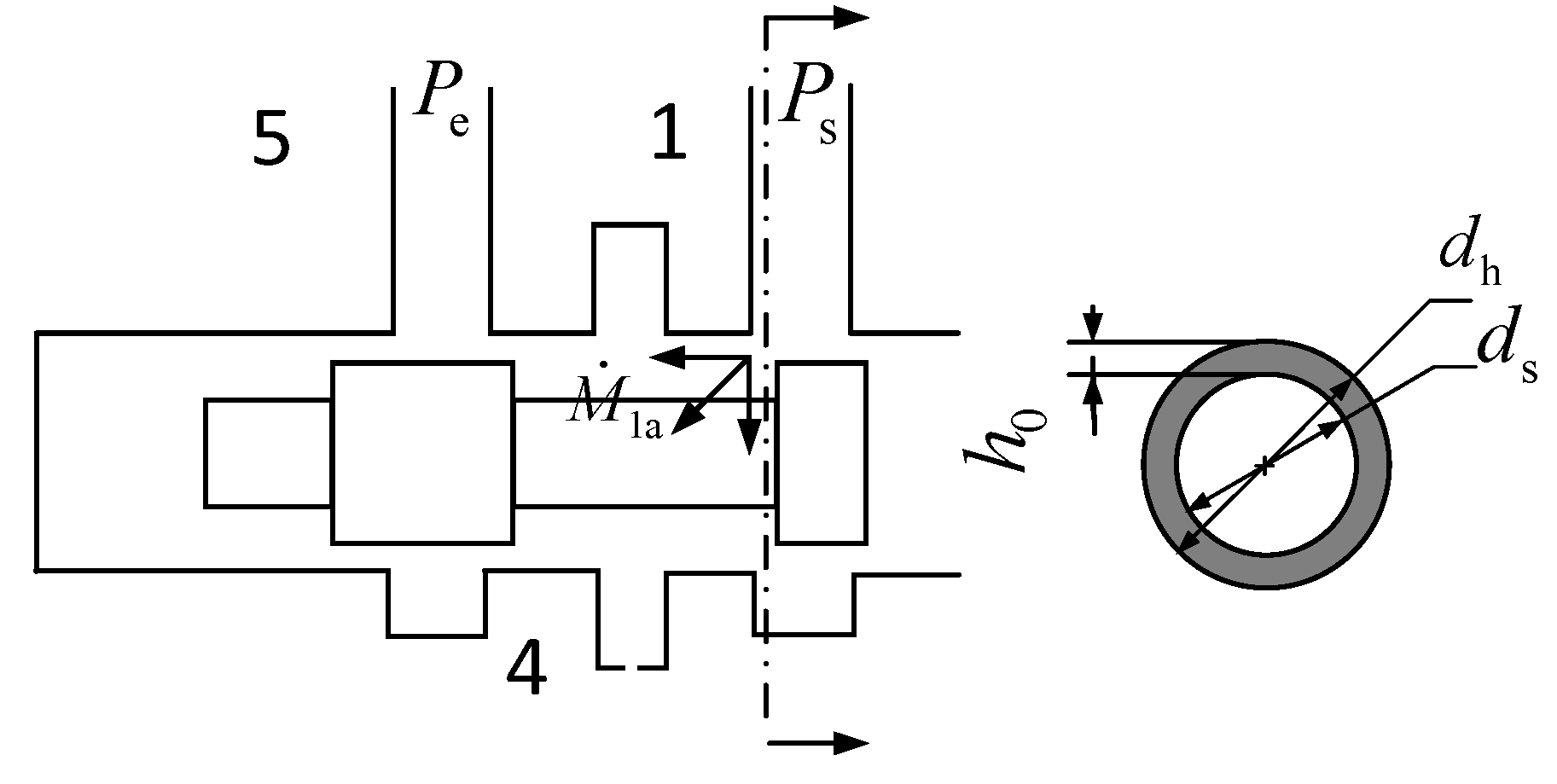
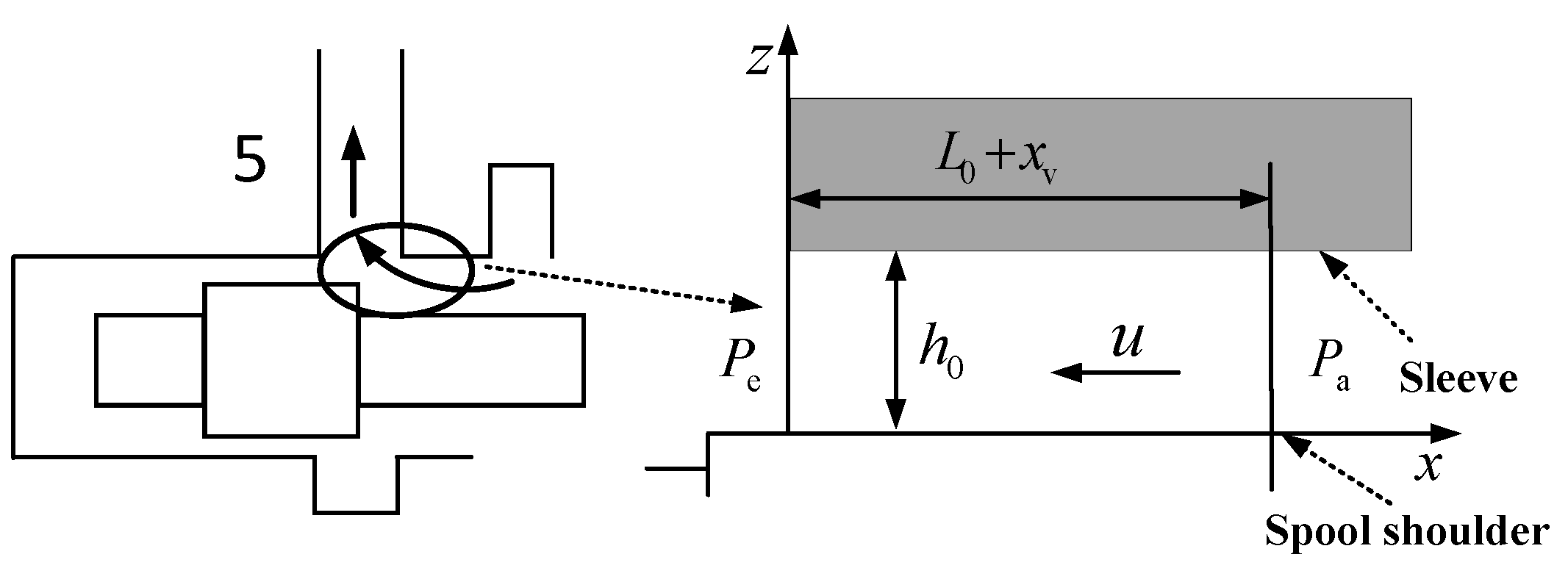
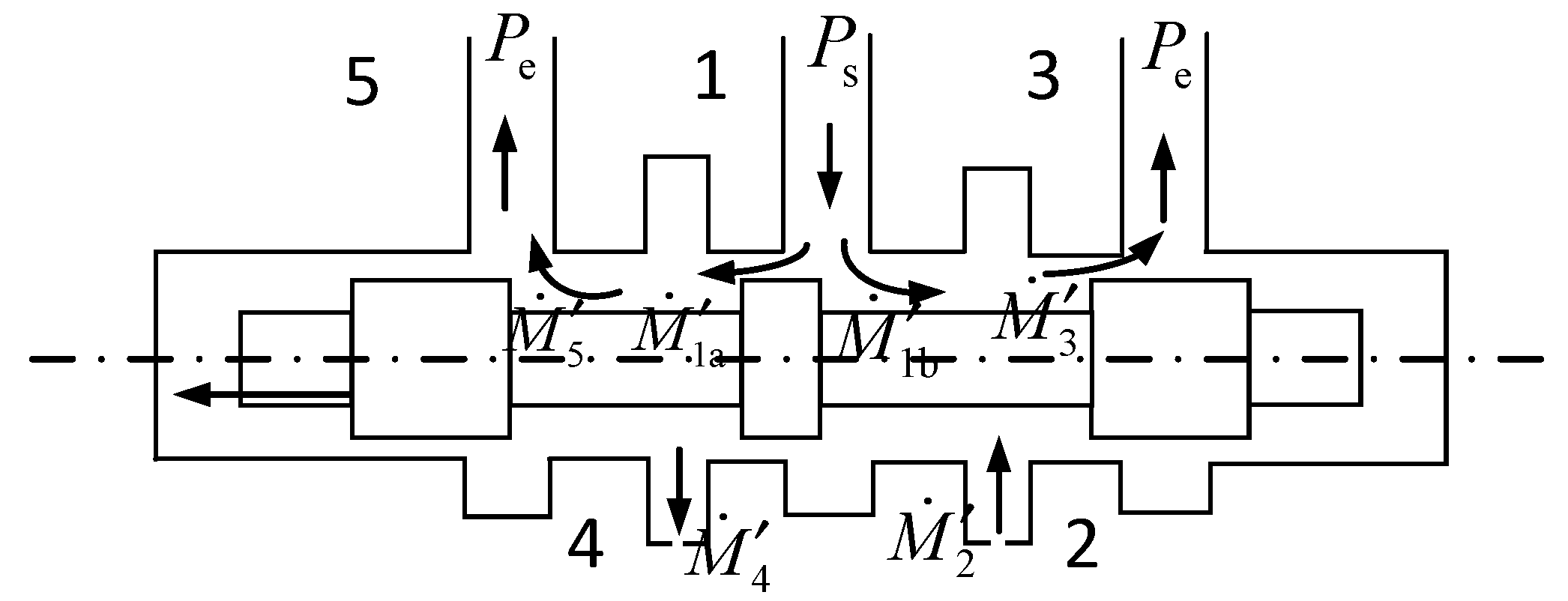
3.1. Establishment of Mass Flow Equation When the Spool Is Moving Forward
3.2. Establishment of the Mass Flow Equation for Gases at the Orifice
3.3. Establishment of the Mass Flow Equation for Gases at Gaps
3.4. Establishment of the Mass Flow Equation When the Spool Moves in Reverse
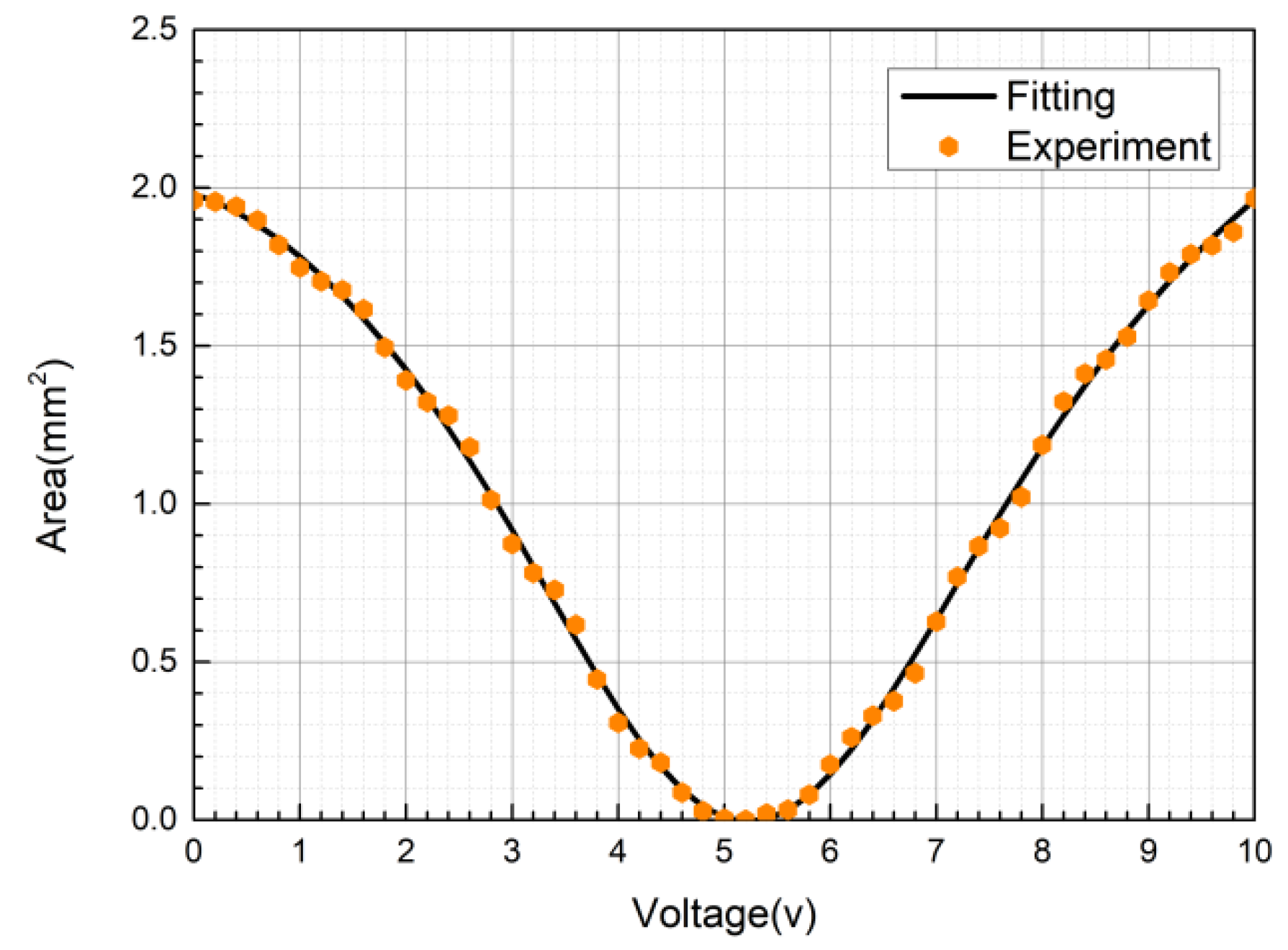
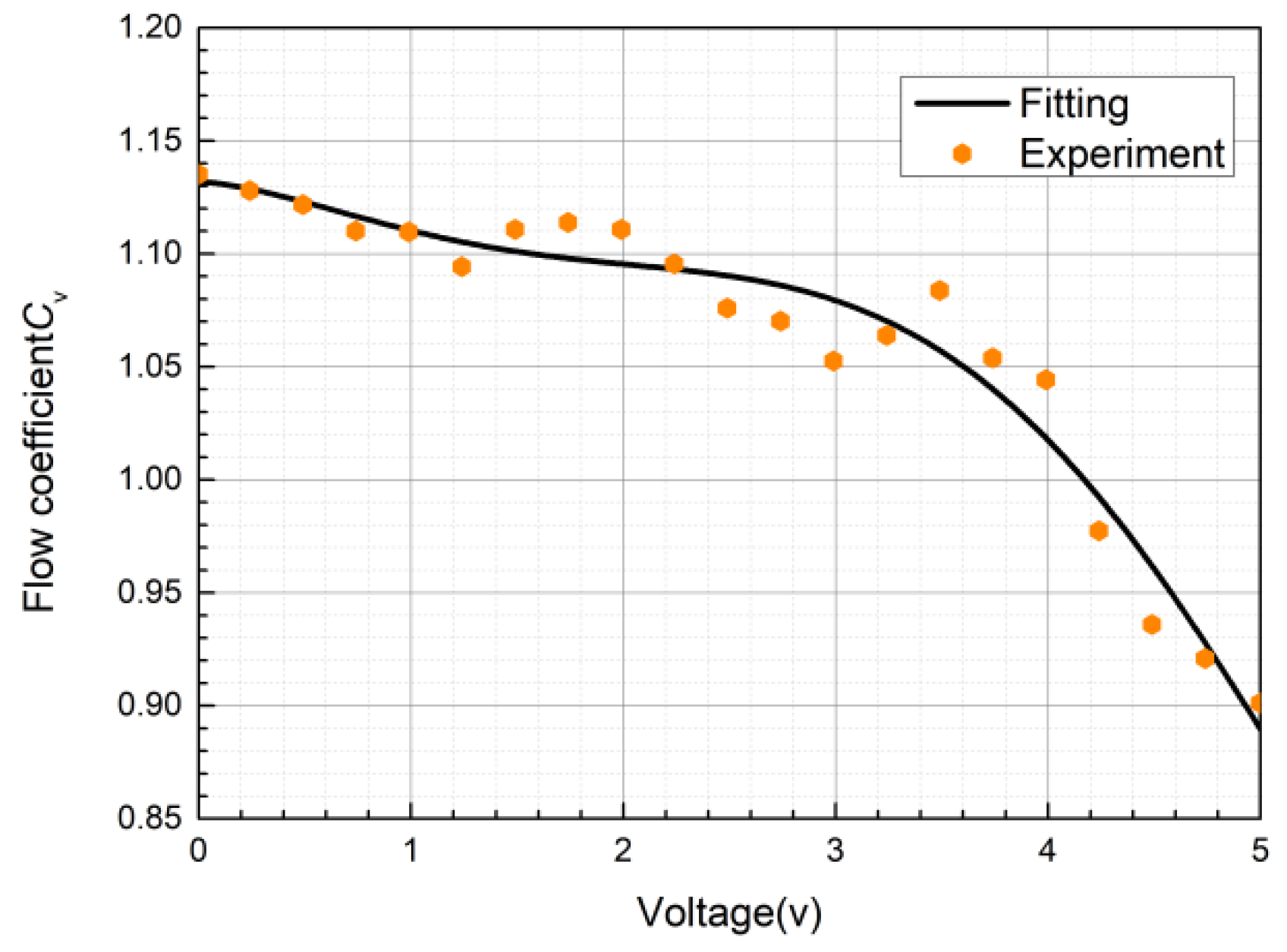
3.5. Measurement of Flow Coefficient of Proportional Directional Valve
4. Establishment of Differential Pressure Equations
5. Establishment of Kinetic Equations
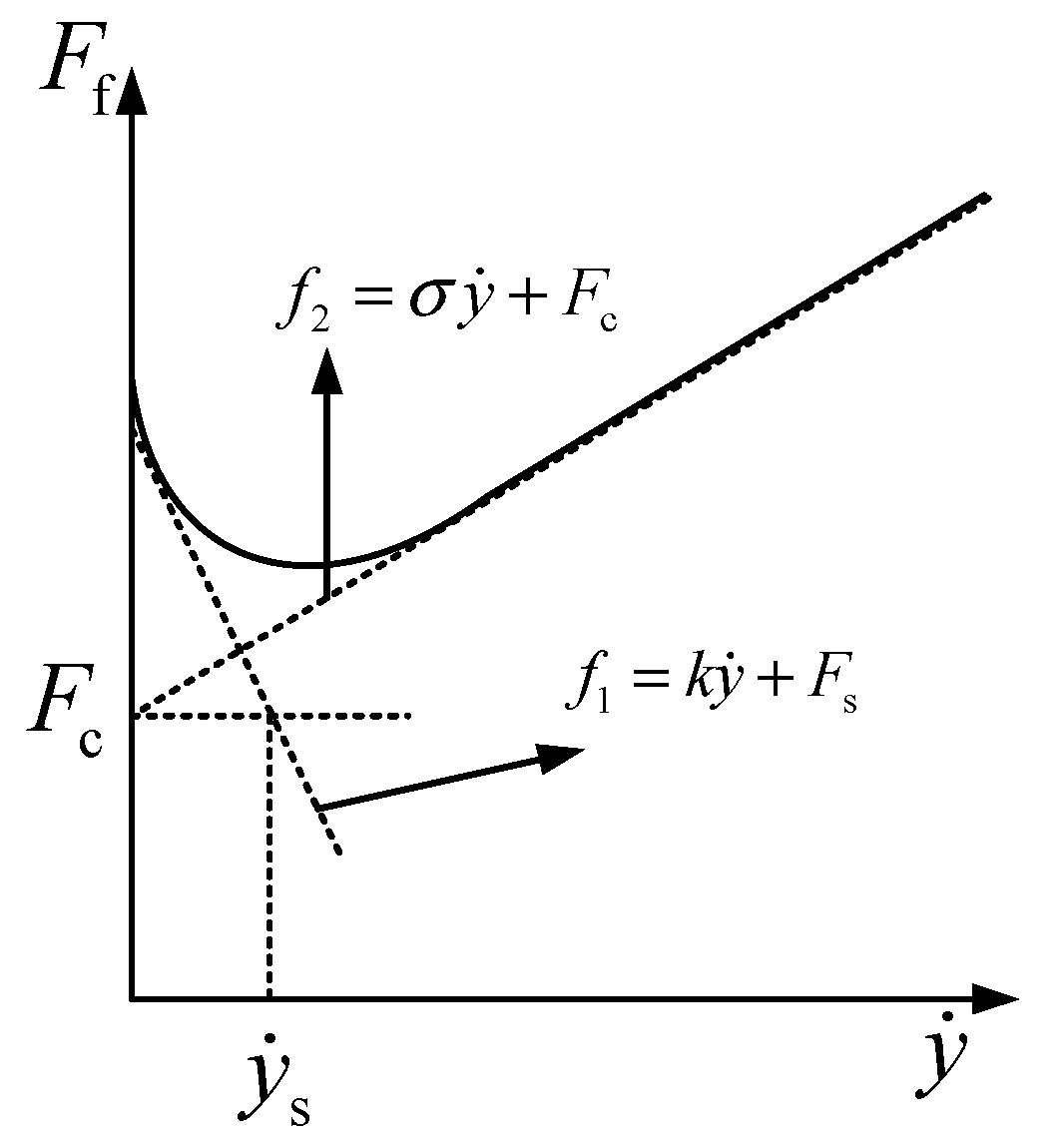
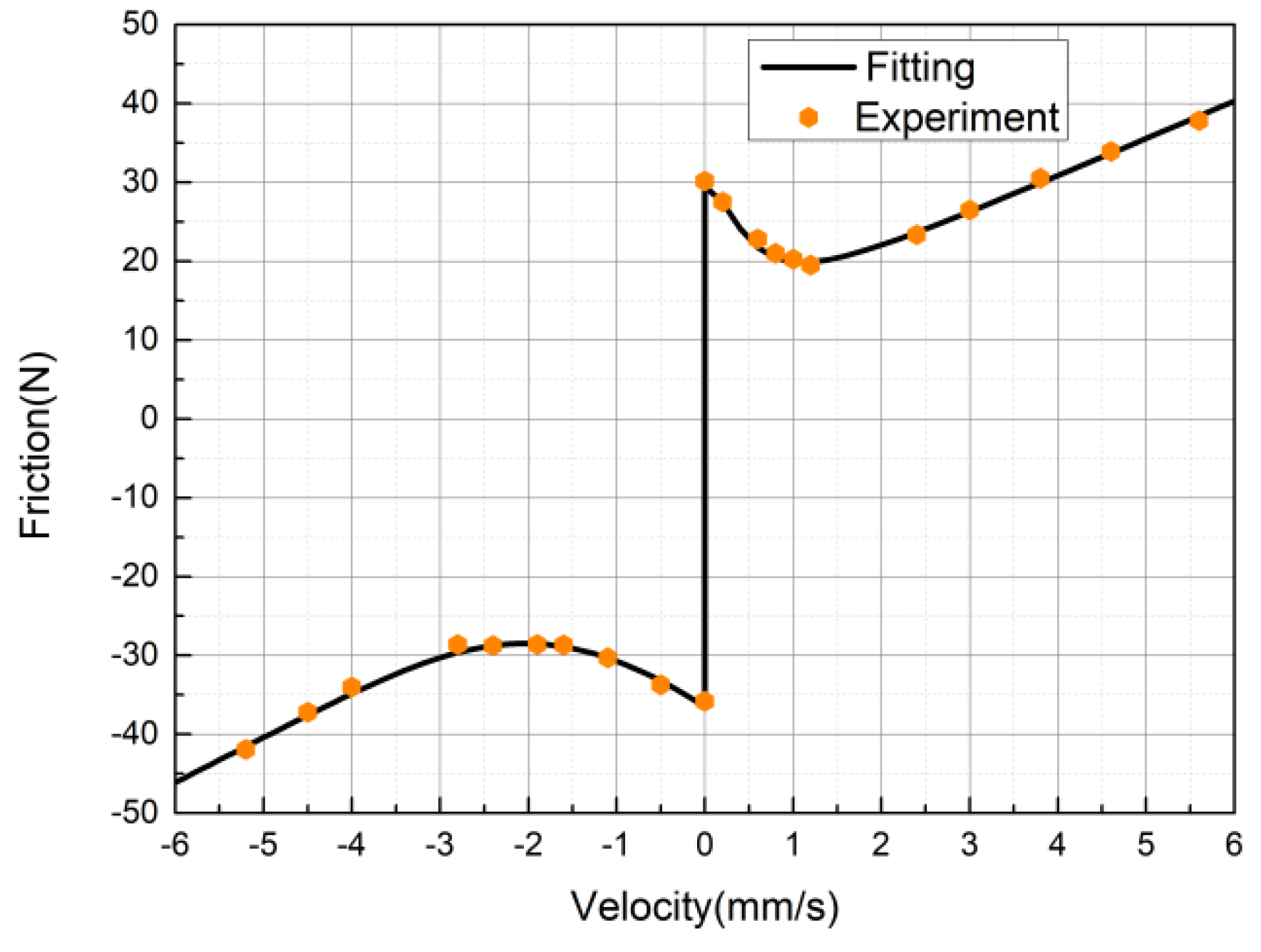
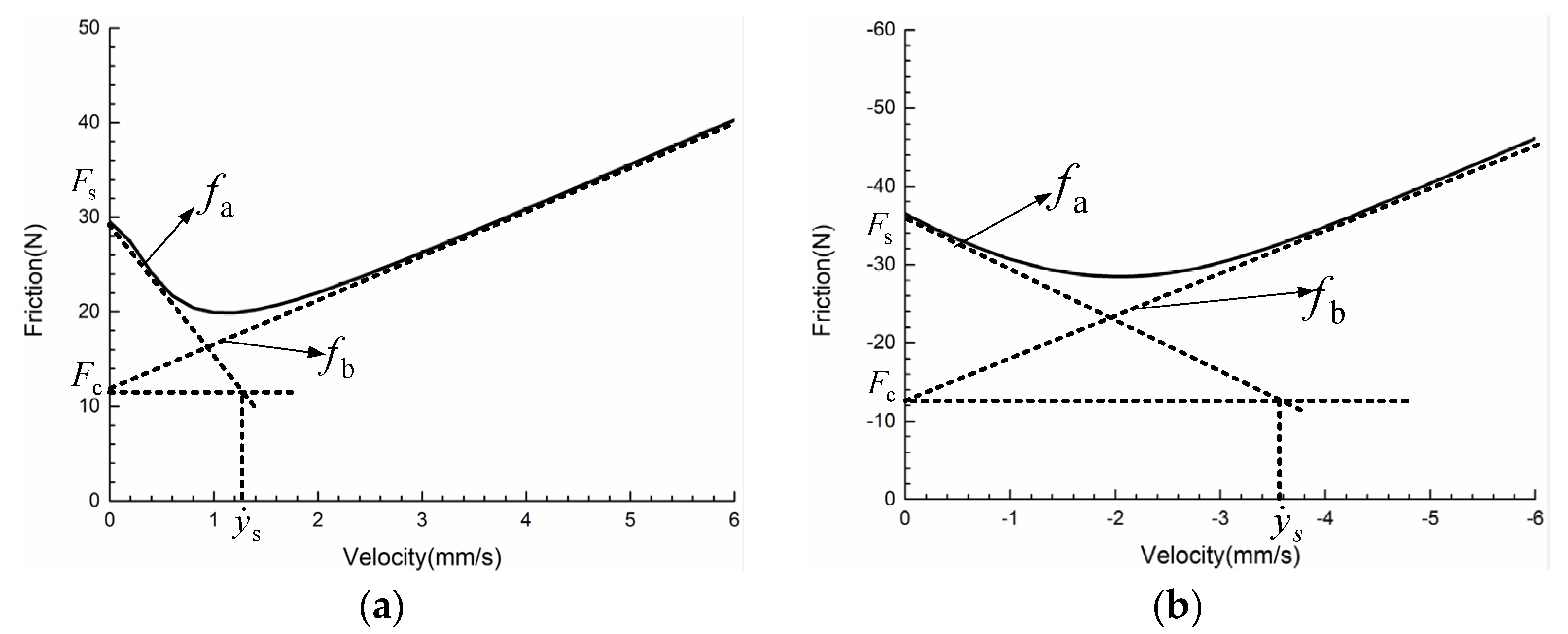
5.1. Measurement of Stribeck Friction Model Parameters
5.2. Establishment of Kinetic Equations
6. Validation of Nonlinear Models of the System
6.1. Validation of Inflation and Deflation of Fixed Chambers
- (1)
- With the increase in the supply pressure, when the pressure of the gas in the chamber reaches a stable value, the error between the experiment and the simulation will gradually increase. This is due to the fact that the greater the supply pressure, the leakage of the gas will gradually increase, meaning the experiment cannot be changed according to the ideal situation.
- (2)
- As the supply pressure increases, the initial pressure of the gas will gradually increase. This is because when the spool is located in the middle of the valve body, there is a gap between the spool and the valve sleeve, and the gas will enter the two chambers of the cylinder through the gap.
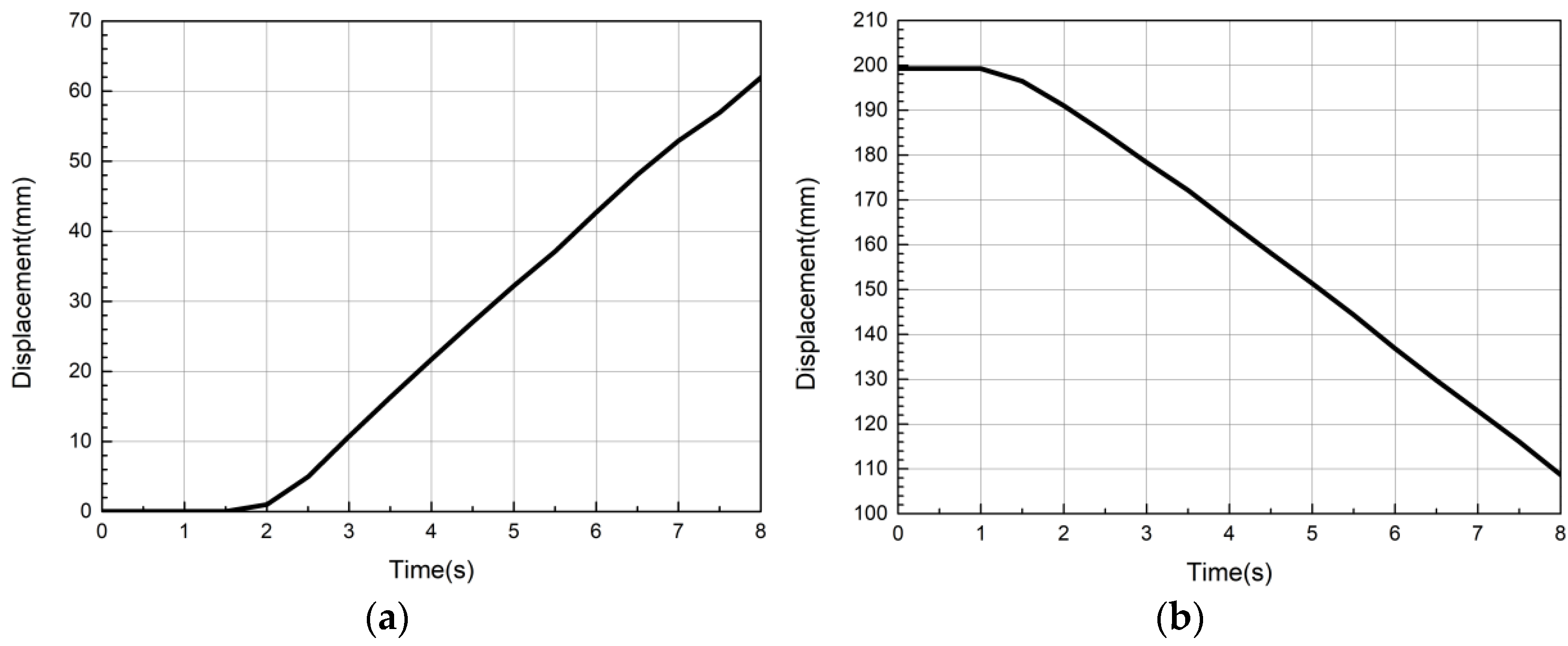
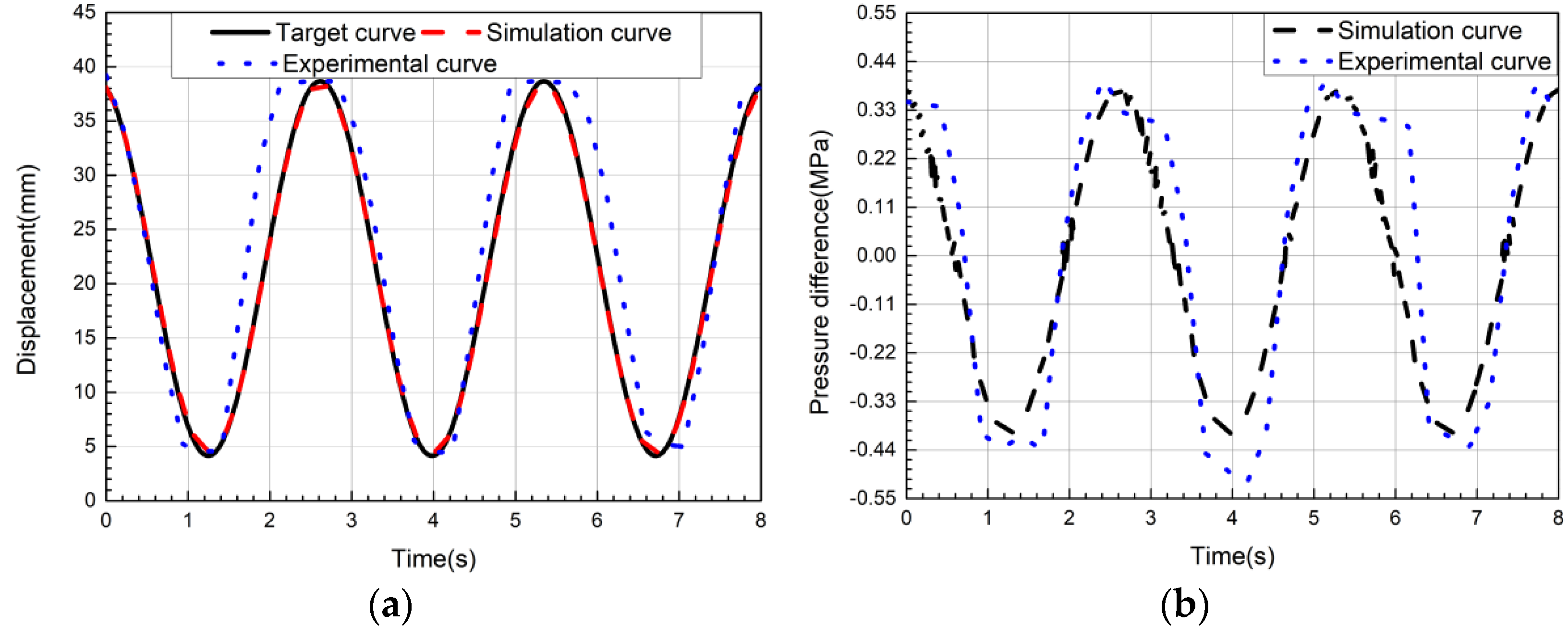
6.2. Positioning Experiment Verification of Nonlinear Model Systems
6.3. Trajectory Tracking Experimental Verification of Nonlinear Model Systems
- (1)
- The friction coefficient is variable during the experiment, and the fixed friction coefficient is considered when modeling and simulation, which will also produce a certain error;
- (2)
- There is a certain gas leakage in the gas circuit system and the cylinder;
- (3)
- The sensitivity of the sensor element is too small;
- (4)
- The instability of the gas supply pressure of the gas source.
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Mass flow rate of the gas in Chamber A or B (kg/s) | |
| Pressure of cylinder Chamber A or B (MPa) | |
| Temperature of cylinder Chamber A or B (K) | |
| Mass of the load (kg) | |
| Displacement of the cylinder (mm) | |
| Atmospheric pressure (MPa) | |
| Supply pressure (MPa) | |
| Mass flow rate of the gas flowing from Port 1 to Chamber A or B (kg/s) | |
| Mass flow rate of the gas flowing through Port 4 or 5 (kg/s) | |
| Mass flow rate of the gas flowing through Port 2 or 3 (kg/s) | |
| Length of the clearance (m) | |
| Inner diameter of the sleeve (m) | |
| Diameter of the spool shoulder (m) | |
| Effective area of the valve opening (mm2) | |
| Absolute pressure upstream of the valve body (MPa) | |
| Temperature upstream of the valve body (K) | |
| Volume flow through the valve port (L/min) | |
| Gas constant (J/(kg·K)) | |
| Critical pressure ratio | |
| Isentropic index | |
| Flow coefficient | |
| Initial length of the clearance (m) | |
| Spool displacement (m) | |
| Velocity of the gas micelles in the horizontal direction (m/s) | |
| Atmospheric density (kg/ m3) | |
| Viscosity coefficient of the gas (Pa·s) | |
| Mass flow rate of gas when the spool moves in the opposite direction (kg/s) | |
| Temperature under standard conditions (K) | |
| Control voltage (V) | |
| Initial volume of Chamber A or B (m3) | |
| Time (s) | |
| Thermodynamic energy change in a chamber (J) | |
| Velocity of the gas micelles in the horizontal direction (m/s) | |
| Initial volume of Chamber A or B (m3) | |
| Effective area of the actuator piston (m2) | |
| Coulomb friction force, friction and the maximum static friction force (N) | |
| Stribeck speed (mm/s) | |
| Viscous friction coefficient (N·s/mm) | |
| Speed of cylinder (mm/s) | |
| Positive constant |
References
- Wu, X. Modern Pneumatic Components and System; Chemical Industry Press: Beijing, China, 2015; Volume 1. [Google Scholar]
- Xie, Y.; Hao, C. Hydraulic and Pneumatic Technology; Fudan University Press: Shanghai, China, 2011; pp. 22–36. [Google Scholar]
- Wu, D. Greater development of pneumatic technology is expected. Hydraul. Pneum. Seals 2013, 9, 104–105. [Google Scholar]
- Yan, J.; Shi, P.; Zhang, X.B. Review of biomimetic mechanism, actuation, modeling and control in soft manipulators. J. Mech. Eng. 2018, 54, 1–14. [Google Scholar] [CrossRef]
- Li, X. The development for pneumatic drive. Mach. Build. Autom. 2003, 2, 5–7. [Google Scholar]
- Chen, Q. Thinking about the present and future development of china pneumatic industry suggestions to the 12th five-year development plan for pneumatic field. Hydraul. Pneum. Seals 2012, 32, 16–22. [Google Scholar]
- Luo, W.; Zhang, Q.; Huang, R.; Wang, S. Model of calculus of variation used for determination of sliding surface. J. Yangtze River Sci. Res. Inst. 2000, 3, 35–37. [Google Scholar]
- Liu, S.; Bobrow, J.E. An Analysis of a pneumatic servo system and its application to a computer-controlled robot. J. Dyn. Syst. Meas. Control 1988, 110, 228–235. [Google Scholar] [CrossRef]
- Rao, Z.; Bone, G.M. Non-linear Modeling and Control of Servo Pneumatic Actuators. IEEE Trans. Control. Syst. Technol. 2008, 16, 562–569. [Google Scholar]
- Lee, L.-W.; Li, I.-H. Wavelet-based adaptive sliding-mode control with H∞ tracking performance for pneumatic servo system position tracking control. IET Control. Theory Appl. 2012, 6, 1699–1714. [Google Scholar] [CrossRef]
- Blackburn, J.F.; Reethof, G.; Shearer, J.L. Fluid Power Control; Technology Press of M.I.T: Boston, MA, USA, 1966. [Google Scholar]
- Scavarda, S.; Kellal, A.; Richard, E. Linearised models for an electropneumatic cylinder servo valve system. In Proceedings of the Science and Engineering Education Lecture, Tokyo, Japan, 29 August 2013; pp. 306–307. [Google Scholar]
- Valdiero, A.C.; Ritter, C.S.; Rios, C.F.; Rafikov, M. Nonlinear mathematical modeling in pneumatic servo position applications. Math. Probl. Eng. 2011, 2011, 472903. [Google Scholar] [CrossRef]
- Bai, Y.; Li, X. Establishment of simulation model of pneumatic position servo system. Mach. Tool Hydraul. 2008, 7, 87–89, 128. [Google Scholar]
- Tao, G.; Mao, W.; W, X. Experimental study on mechanism modeling of pneumatic servo system. Hydraul. Pneum. Seals 1999, 5, 26–31. [Google Scholar]
- Wang, X. Modeling study of the PCM pneumatic servo system. Mach. Tool Hydraul. 1997, 4, 20–22. [Google Scholar]
- Bai, Y. Research on Pneumatic Rotation Position Servo Control Technology; Nanjing University of Science & Technology: Nanjing, China, 2006. [Google Scholar]
- Zhang, Y.; Li, K.; Wang, G.; Liu, J.; Cai, M. Nonlinear model establishment and experimental verification of a pneumatic rotary actuator position servo system. Energies 2019, 12, 1096. [Google Scholar] [CrossRef] [Green Version]
- Sanville, F.E. A new method of specifying the flow capacity of pneumatic fluid power valves. Hydraul. Pneum. Power 1971, 17, 120–126. [Google Scholar]
- Daugherty, R.L.; Ingersoll, A.C. Fluid Mechanics; McGraw Hill: New York, NY, USA, 1954. [Google Scholar]
- Wang, Y. Research Trajectory on Three-Axis Pneumatic Servo Space Control System; Harbin Institute of Technology: Harbin, China, 2008. [Google Scholar]
- Cai, M. Theory and Practice of Modern Pneumatic Technology Lecture 5: Characteristics of Cylinder Drive System. Hydraul. Pneum. Seals 2007, 6, 55–58. [Google Scholar]
- Yuan, D.; Liu, L.; Liu, H.; Wu, Z.; Wang, Z. Progress of Pre-sliding Friction Model. J. Syst. Simul. 2009, 4, 1142–1147. [Google Scholar]
- Zhang, Y.; Li, K.; Xu, M.; Liu, J.; Yue, H. Medical Grabbing Servo System with Friction Compensation Based on the Differential Evolution Algorithm. Chin. J. Mech. Eng. 2021, 34, 107. [Google Scholar] [CrossRef]


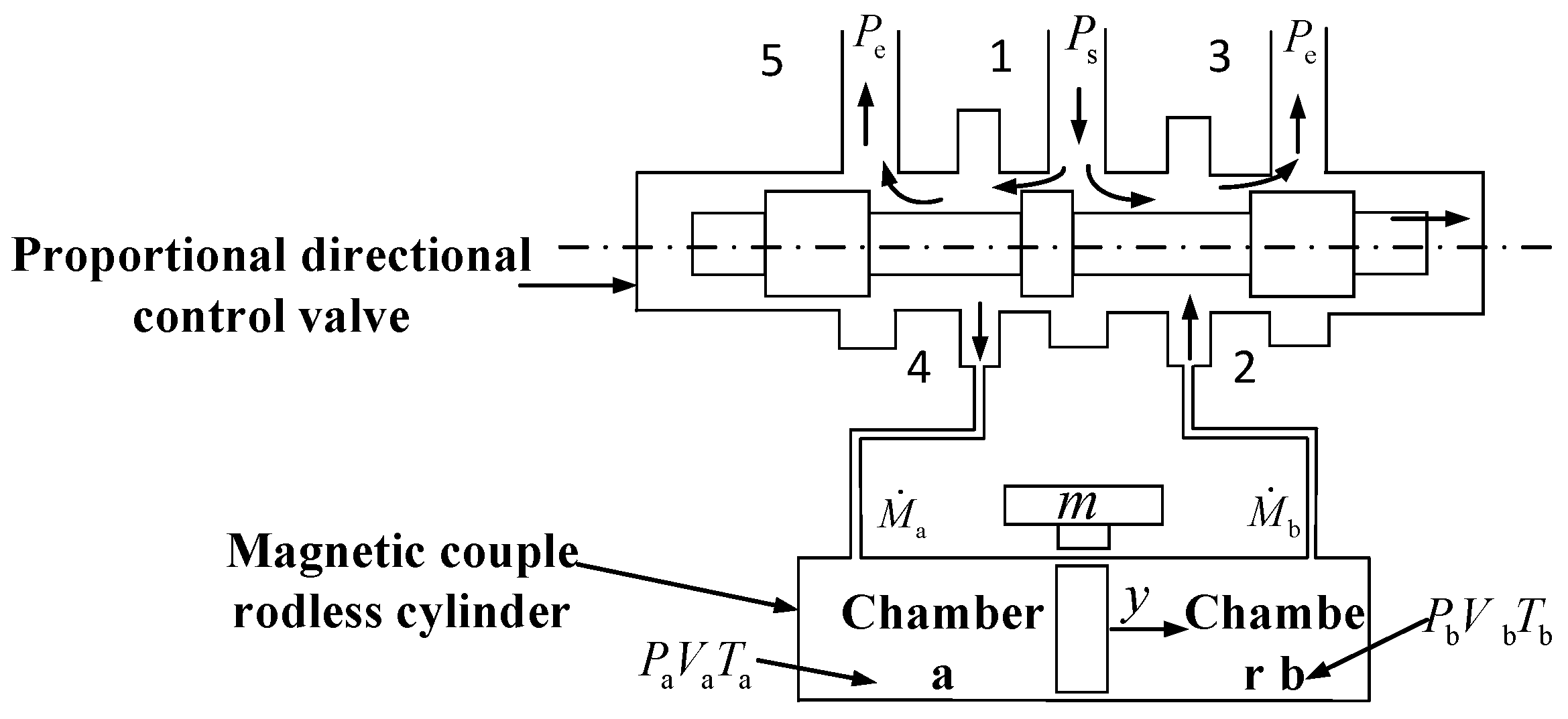

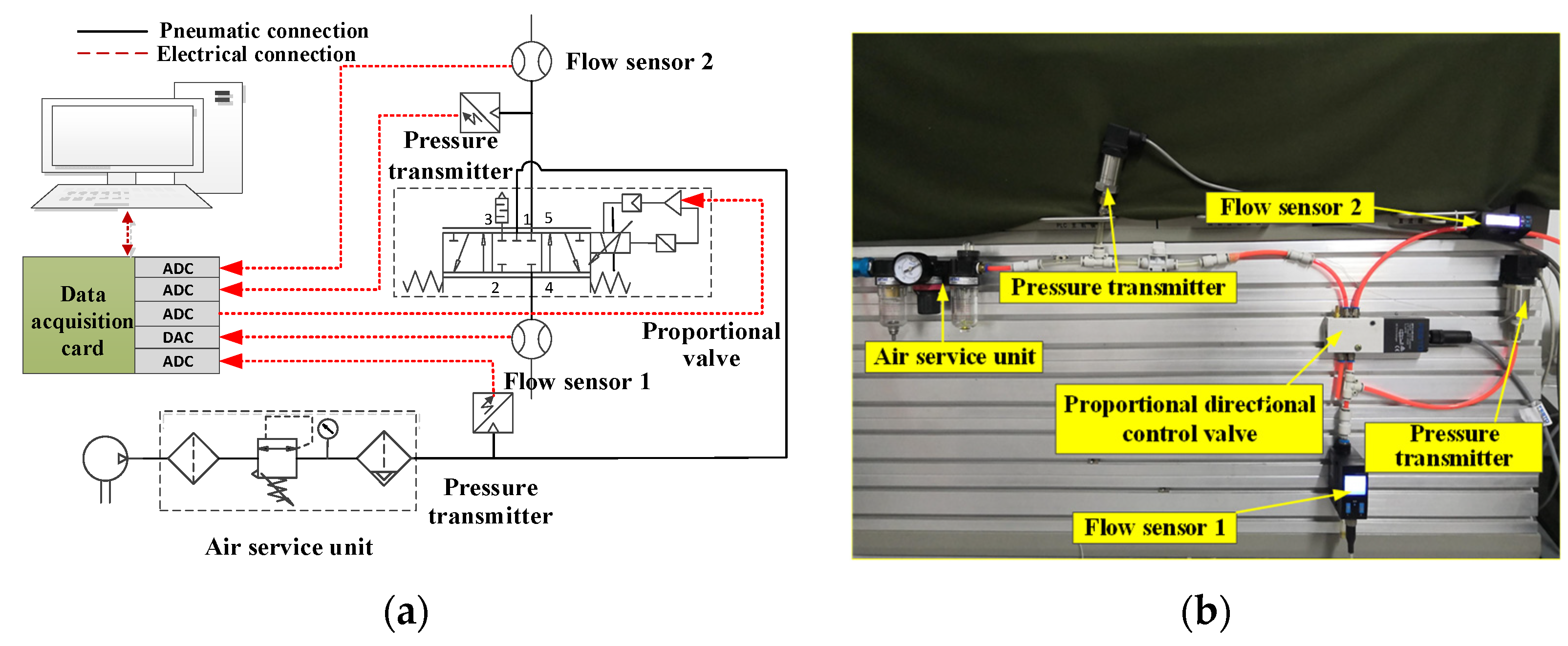

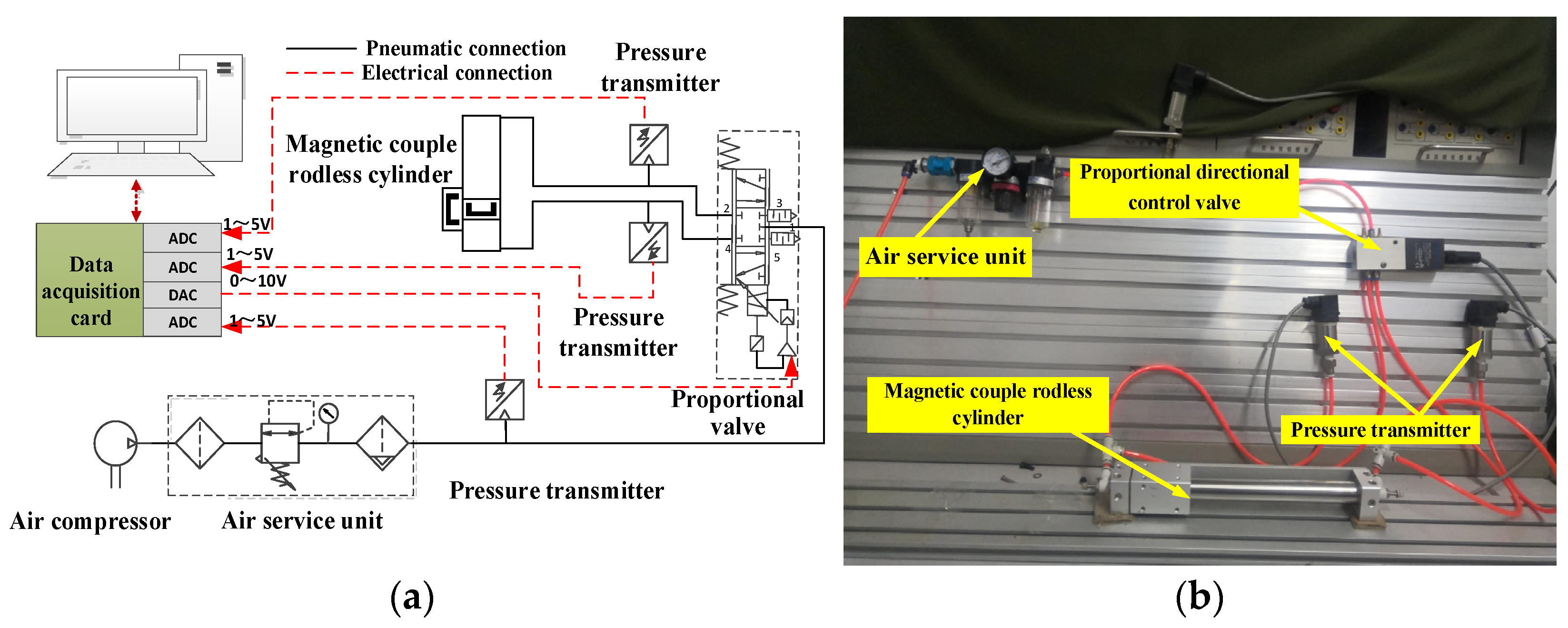


| No. | Component | Model | Parameter |
|---|---|---|---|
| 1 | Air compressor | PANDA 750-30L | Maximum supply pressure: 0.8 MPa |
| 2 | Air service unit | AC3000-03 | Maximum working pressure: 1.0 MPa |
| 3 | Pressure transmitter | MIK-P300 | Range: 0–1 MPa; accuracy: 0.5% F.S. |
| 4 | Proportional directional control valve | FESTO MPYE-5-M5-010-B | Range: 0–100 MPa; rated flow rate: 100 L/min |
| 5 | Pull-rod displacement sensor | KTC-V1-200 | Linear: ±0.05; repeatability accuracy: 0.01 mm |
| 6 | Magnetically coupled rodless cylinder | SMC CY3R25-200 | Maximum working pressure: 1.0 MPa |
| 7 | Data acquisition card | NI PCI-6353 | 32-channel analog input; 4-channel analog output; 32-bit counter |
| IPC | IPC-610H | 32-bit processor, standard configuration |
| Forward Movement | Value | Negative Movement | Value |
|---|---|---|---|
| 29 (N) | −36 (N) | ||
| 12 (N) | −12.5 (N) | ||
| 1.3 (mm/s) | −3.6 (mm/s) | ||
| 4.5 (N·S/mm) | 4.8 (N·S/mm) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Li, K.; Cai, M.; Wei, F.; Gong, S.; Li, S.; Lv, B. Establishment and Experimental Verification of a Nonlinear Position Servo System Model for a Magnetically Coupled Rodless Cylinder. Actuators 2022, 11, 50. https://doi.org/10.3390/act11020050
Zhang Y, Li K, Cai M, Wei F, Gong S, Li S, Lv B. Establishment and Experimental Verification of a Nonlinear Position Servo System Model for a Magnetically Coupled Rodless Cylinder. Actuators. 2022; 11(2):50. https://doi.org/10.3390/act11020050
Chicago/Turabian StyleZhang, Yeming, Kaimin Li, Maolin Cai, Feng Wei, Sanpeng Gong, Shuping Li, and Baozhan Lv. 2022. "Establishment and Experimental Verification of a Nonlinear Position Servo System Model for a Magnetically Coupled Rodless Cylinder" Actuators 11, no. 2: 50. https://doi.org/10.3390/act11020050
APA StyleZhang, Y., Li, K., Cai, M., Wei, F., Gong, S., Li, S., & Lv, B. (2022). Establishment and Experimental Verification of a Nonlinear Position Servo System Model for a Magnetically Coupled Rodless Cylinder. Actuators, 11(2), 50. https://doi.org/10.3390/act11020050






