High-Precision Anti-Interference Control of Direct Drive Components
Abstract
:1. Introduction
2. System Modelling and Problem Statement
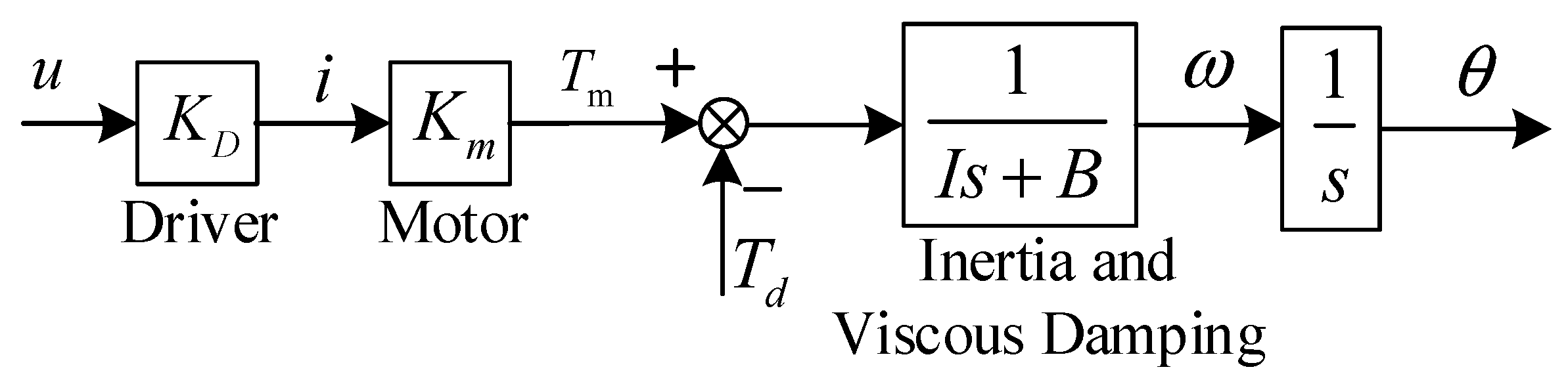
2.1. Modelling of DDCs
2.2. Problem Statement
3. Controller Design and Analysis
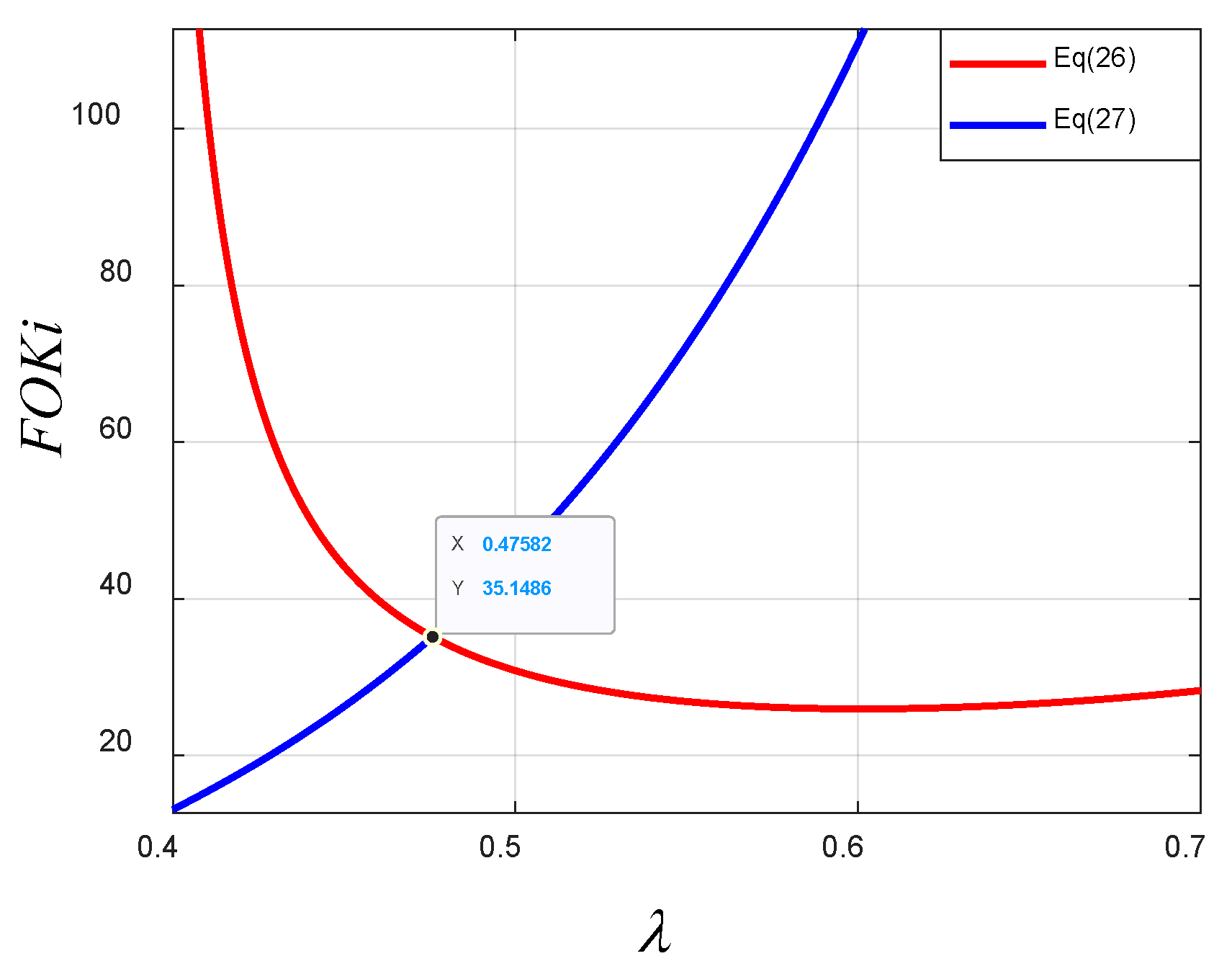
3.1. Design of FOPI Controller
- A.
- Phase margin specification:
- B.
- Robustness to variation in the gain of the plant:
- C.
- Gain crossover frequency specification:
- where, , , .
- where the frequency range to be fit is defined as (, ), is the order of the filter.
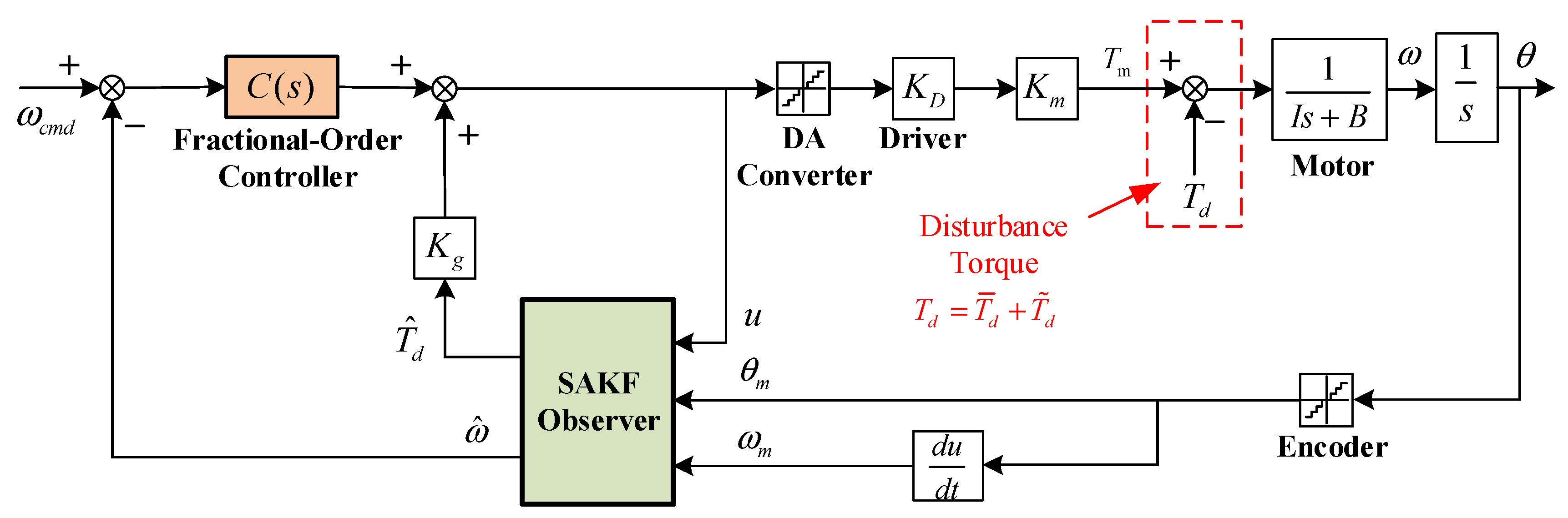
3.2. Design of SAKF Based Estimator
4. Experiment
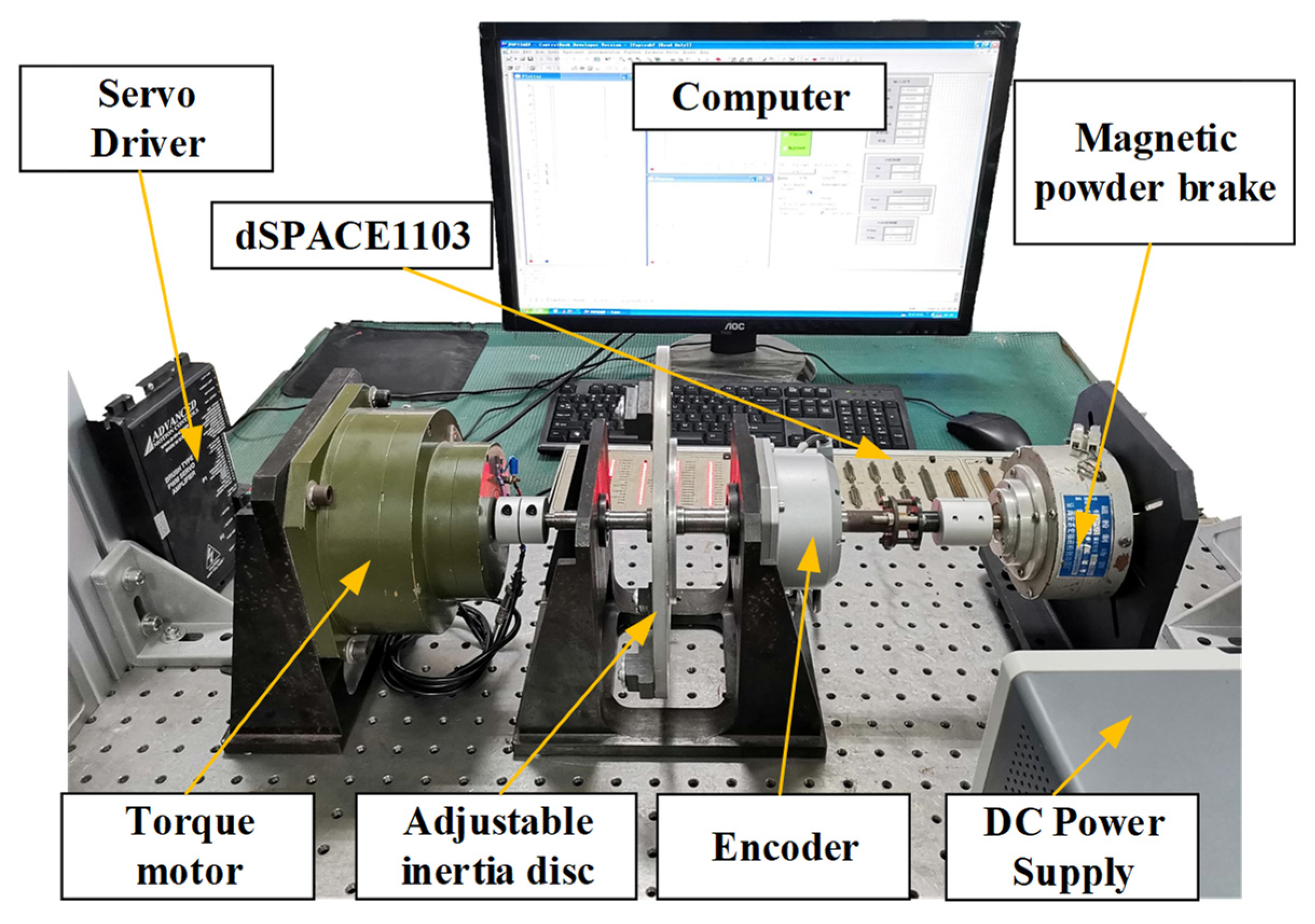
4.1. Experiment Setup
4.2. Control Parameters
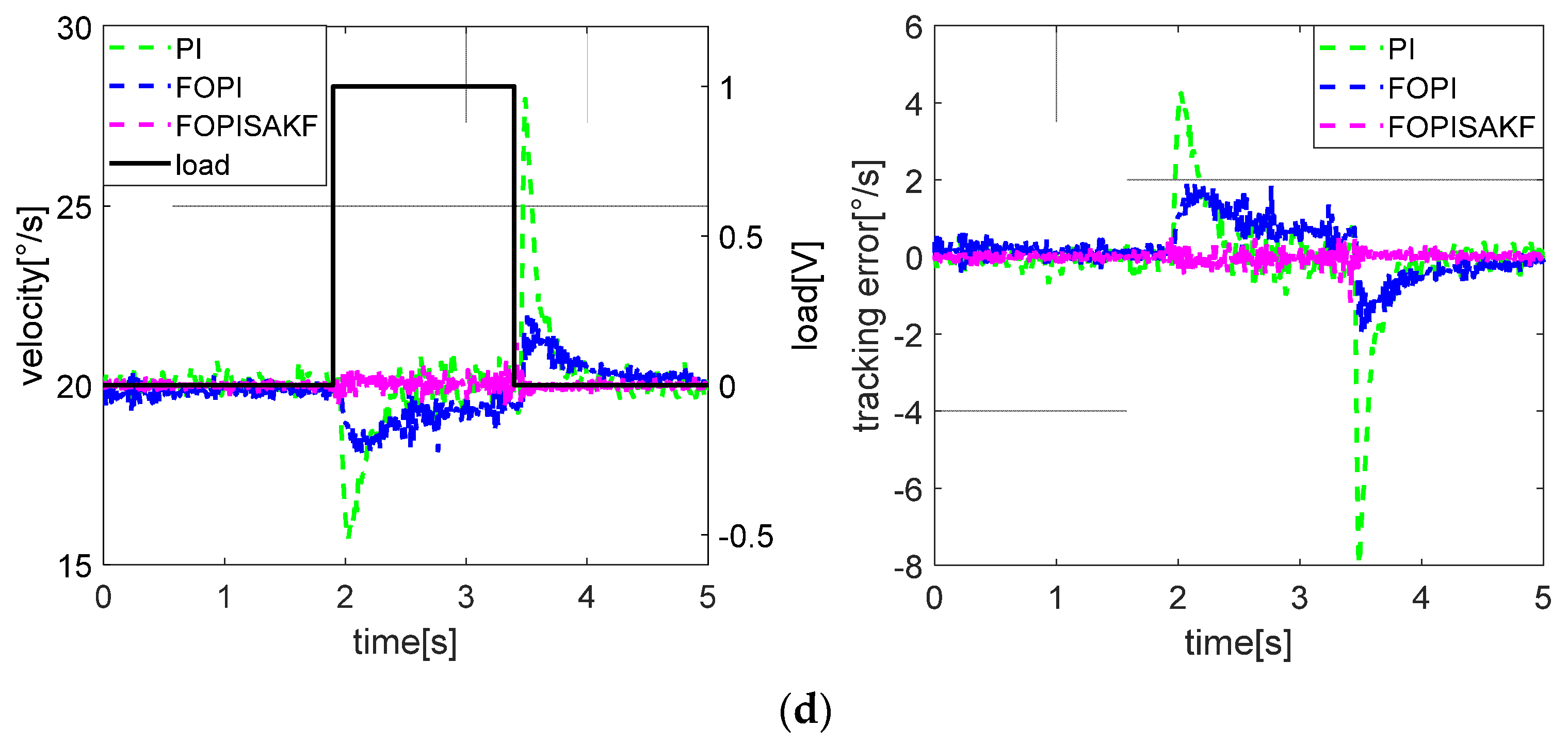
4.3. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, H. Design and Implementation of Brushless DC Motor Drive and Control System. Procedia Eng. 2012, 29, 2219–2224. [Google Scholar]
- Wang, Y.; Yu, Y.; Zhang, G.; Sheng, X. Fuzzy Auto-adjust PID Controller Design of Brushless DC Motor. Phys. Procedia 2012, 33, 1533–1539. [Google Scholar]
- Jocelyn, S.; Om, P.A.; Machado, J.T. Advances in Fractional Calculus; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Marinangeli, L.; Alijani, F.; HosseinNia, S.H. Fractional-order positive position feedback compensator for active vibration control of a smart composite plate. J. Sound Vib. 2018, 412, 1–16. [Google Scholar] [CrossRef]
- HosseinNia, S.H.; Tejado, I.; Vinagre, B.M. Fractional-order reset control: Application to a servomotor. Mechatronics 2013, 23, 781–788. [Google Scholar] [CrossRef]
- Shah, P.; Agashe, S. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
- Jakovljević, B.; Lino, P.; Maione, G. Control of double-loop permanent magnet synchronous motor drives by optimized fractional and distributed-order PID controllers. Eur. J. Control 2021, 58, 232–244. [Google Scholar] [CrossRef]
- Liu, N.; Cao, S.; Fei, J. Fractional-Order PID Controller for Active Power Filter Using Active Disturbance Rejection Control. Math. Probl. Eng. 2019, 2019, 1–10. [Google Scholar] [CrossRef]
- Bingi, K.; Ibrahim, R.; Karsiti, M.N.; Hassan, S.M.; Harindran, V.R. Real-Time Control of Pressure Plant Using 2DOF Fractional-Order PID Controller. Arab. J. Sci. Eng. 2018, 44, 2091–2102. [Google Scholar] [CrossRef]
- Seyedtabaii, S. New flat phase margin fractional order PID design: Perturbed UAV roll control study. Robot. Auton. Syst. 2017, 96, 58–64. [Google Scholar] [CrossRef]
- Costa, D.V.; Da, J.S. Tuning of fractional PID controllers with Ziegler-Nichols-type rules. Signal Process. 2006, 86, 2771–2784. [Google Scholar]
- Monje, C.A.; Calderon, A.J.; Vinagre, B.M.; Chen, Y.; Feliu, V. On Fractional PIλ Controllers: Some Tuning Rules for Robustness to Plant Uncertainties. Nonlinear Dyn. 2004, 38, 369–381. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.A. Optimal Tuning of Fractional Controllers Using Genetic Algorithms; Springer: Dordrecht, The Netherlands, 2010; p. 62. [Google Scholar]
- Padula, F. Optimal tuning rules for proportional-integral-derivative and fractional-order proportional-integral-derivative controllers for integral and unstable processes. Control Theory Appl. IET 2012, 6, 776–786. [Google Scholar] [CrossRef]
- Xue, D. Fractional-Order Control Systems: Fundamentals and Numerical Implementations; Ringgold, Inc.: Beaverton, OR, USA, 2017. [Google Scholar]
- Monje, C.A.; Vinagre, B.M.; Feliu, V.; Chen, Y. Tuning and auto-tuning of fractional order controllers for industry applications. Control Eng. Pract. 2008, 16, 798–812. [Google Scholar] [CrossRef] [Green Version]
- Luo, Y.; Chen, Y. Fractional order [proportional derivative] controller for a class of fractional order systems. Automatica 2009, 45, 2446–2450. [Google Scholar] [CrossRef]
- Xue, D.; Zhao, C.; Chen, Y. A Modified Approximation Method of Fractional Order System. In Proceedings of the IEEE International Conference on Mechatronics & Automation, Luoyang, China, 25–28 June 2006. [Google Scholar]
- Qi, C.; Jiang, X.; Xie, X.; Fan, D. A SAKF-Based Composed Control Method for Improving Low-Speed Performance and Stability Accuracy of Opto-Electric Servomechanism. Appl. Sci. 2019, 9, 4498. [Google Scholar] [CrossRef] [Green Version]
- Erkorkmaz, K.; Altintas, Y. High speed CNC system design. Part II: Modeling and identification of feed drives. Int. J. Mach. Tools Manuf. 2001, 41, 1487–1509. [Google Scholar] [CrossRef]
- Kaan, E.; Yusuf, A. High speed CNC system design. Part III: High speed tracking and contouring control of feed drives. Int. J. Mach. Tools Manuf. 2001, 41, 1637–1658. [Google Scholar]
- Åström, K.J.; Wittenmark, B. Computer-Controlled Systems: Theory and Design, 3rd ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Jiang, X.; Fan, D.; Fan, S.; Xie, X.; Chen, N. High-precision gyro-stabilized control of a gear-driven platform with a floating gear tension device. Front. Mech. Eng. 2021, 16, 487–503. [Google Scholar] [CrossRef]
- Li, S.; Zhong, M. High-Precision Disturbance Compensation for a Three-Axis Gyro-stabilized Camera Mount. IEEE/ASME Trans. Mechatron. 2015, 20, 3135–3147. [Google Scholar] [CrossRef]


| Symbol | Description | Value |
|---|---|---|
| Moment of inertia of motor rotor | 6.5 × 10−3 | |
| Moment of inertia of load | 2.3 × 10−3 | |
| Damping coefficient of motor rotor | 0.044 | |
| Motor torque constant | 0.73 | |
| Driver conversion factor | 0.47 | |
| DA conversion resolution | 20/(216) | |
| Encoder resolution | 0.02 |
| Methods | PI (°/s) | FOPI (°/s) | FOPISAKF (°/s) | Improvement (%) | |
|---|---|---|---|---|---|
| Experiments | |||||
| 20°/s and 1 Hz sinusoidal signal tracking experiment | 2.06 | 1.12 | 0.40 | 80.58 | |
| 20°/s and 5 Hz sinusoidal signal tracking experiment | 6.46 | 2.31 | 2.17 | 66.41 | |
| Step response experiment | 2.66 | 1.69 | 1.42 | 46.62 | |
| Anti-interference experiment | 1.22 | 0.63 | 0.13 | 89.34 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Jiang, X.; Ren, G.; Xie, X.; Fan, D. High-Precision Anti-Interference Control of Direct Drive Components. Actuators 2022, 11, 95. https://doi.org/10.3390/act11030095
Zheng J, Jiang X, Ren G, Xie X, Fan D. High-Precision Anti-Interference Control of Direct Drive Components. Actuators. 2022; 11(3):95. https://doi.org/10.3390/act11030095
Chicago/Turabian StyleZheng, Jieji, Xianliang Jiang, Guangan Ren, Xin Xie, and Dapeng Fan. 2022. "High-Precision Anti-Interference Control of Direct Drive Components" Actuators 11, no. 3: 95. https://doi.org/10.3390/act11030095
APA StyleZheng, J., Jiang, X., Ren, G., Xie, X., & Fan, D. (2022). High-Precision Anti-Interference Control of Direct Drive Components. Actuators, 11(3), 95. https://doi.org/10.3390/act11030095







