Influences of Parameter Deviation on the Vibration Isolation System of an End Effector
Abstract
:1. Introduction
2. Simplified System of the Vibration Isolation System for the End Effector
3. Simulation Analysis of the Vibration System with Different Parameter Deviations
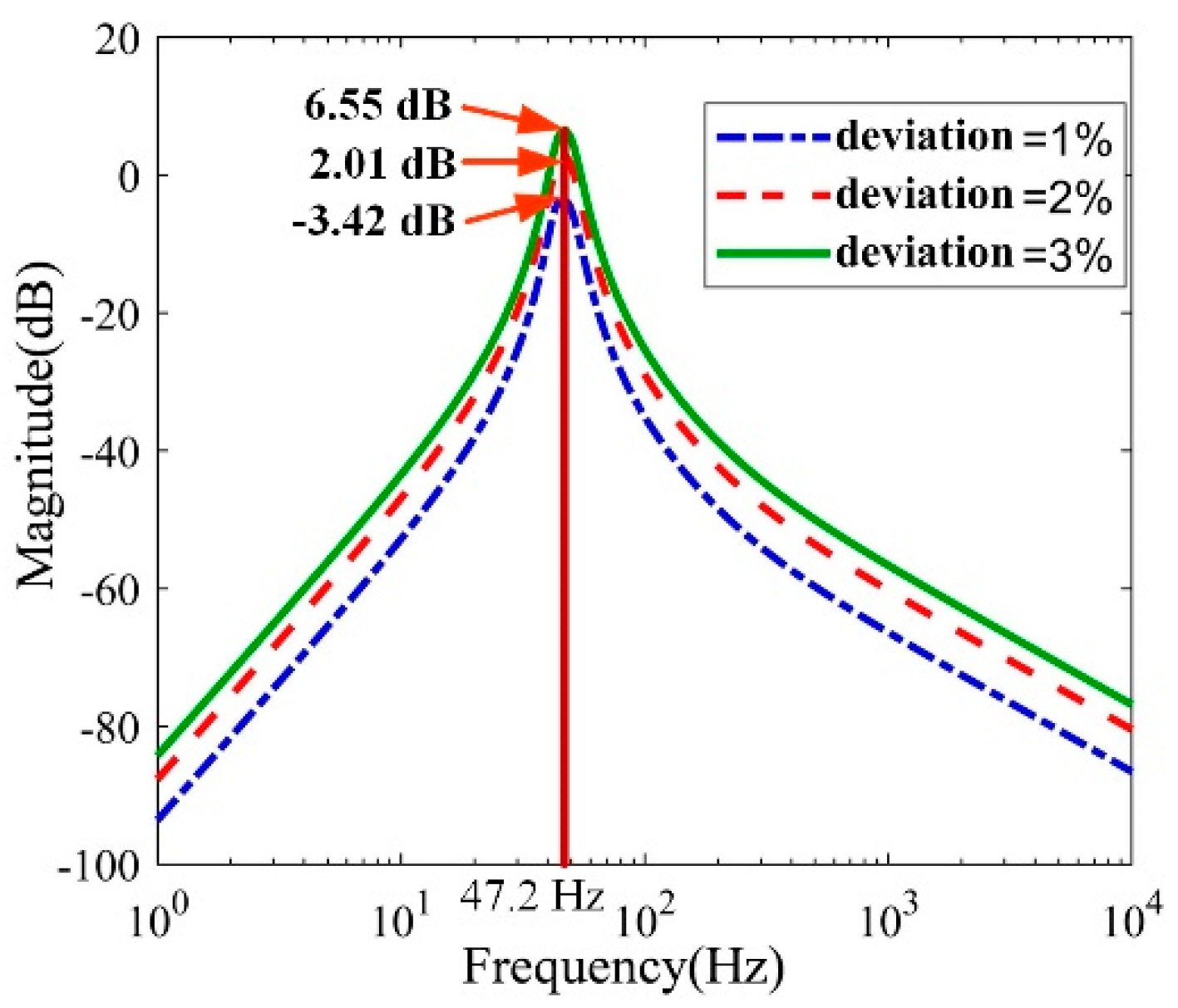
3.1. Influence of the Performance Parameter Deviation
3.2. Influence of the Distance Parameter Deviations between Two Vibration Isolations
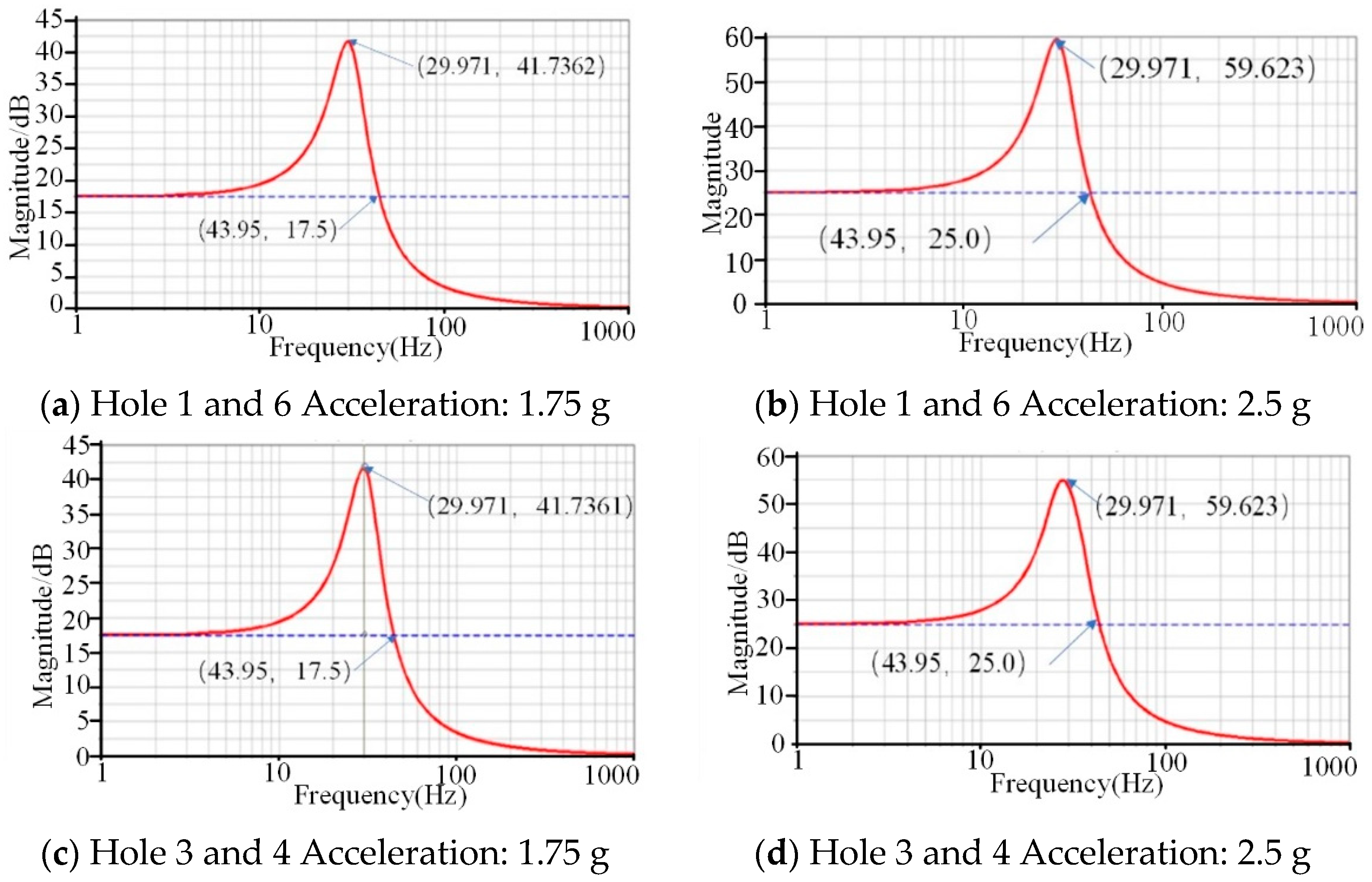
3.2.1. Symmetrical Distribution of the Vibration Isolators
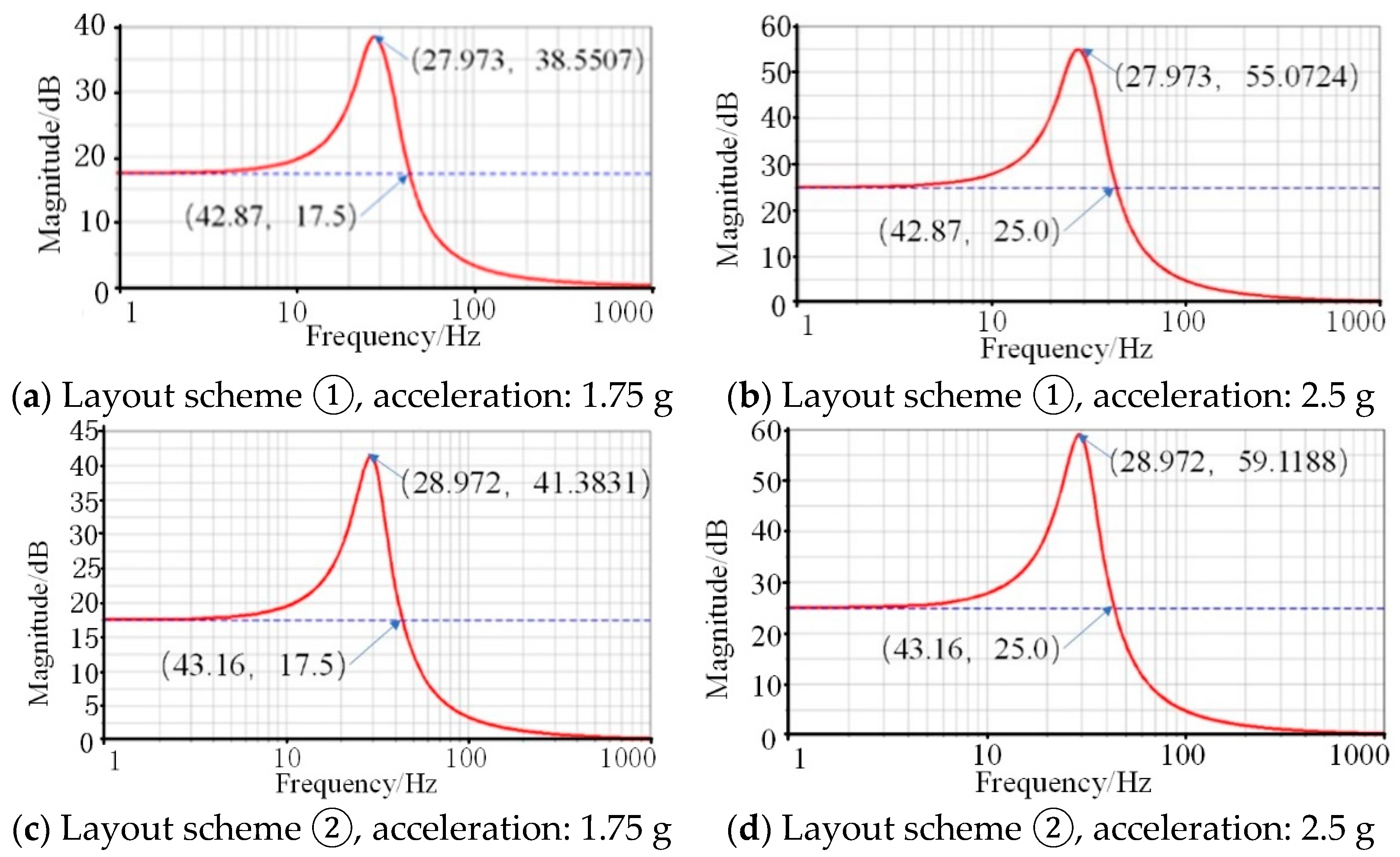
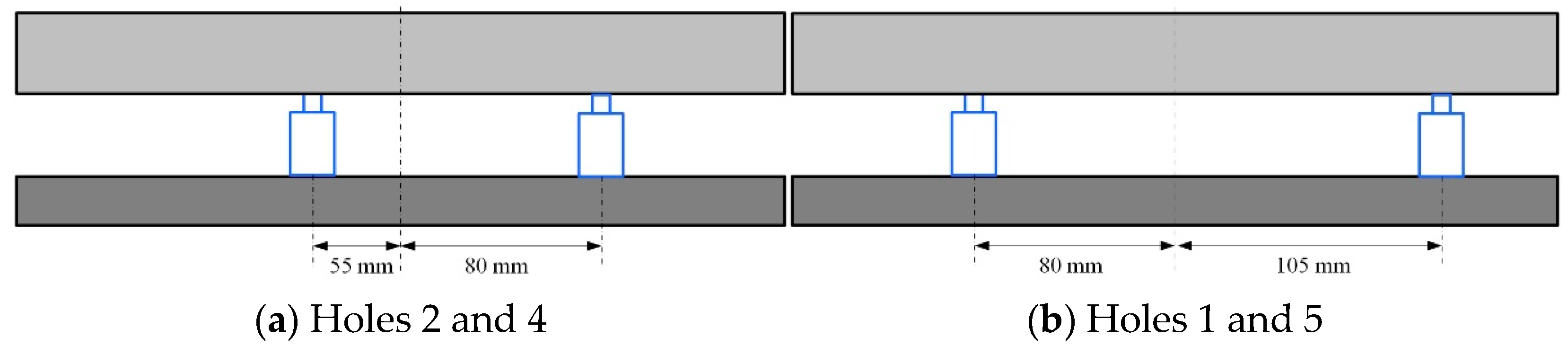
3.2.2. Asymmetric Distribution of the Vibration Isolators
4. Experimental Analysis
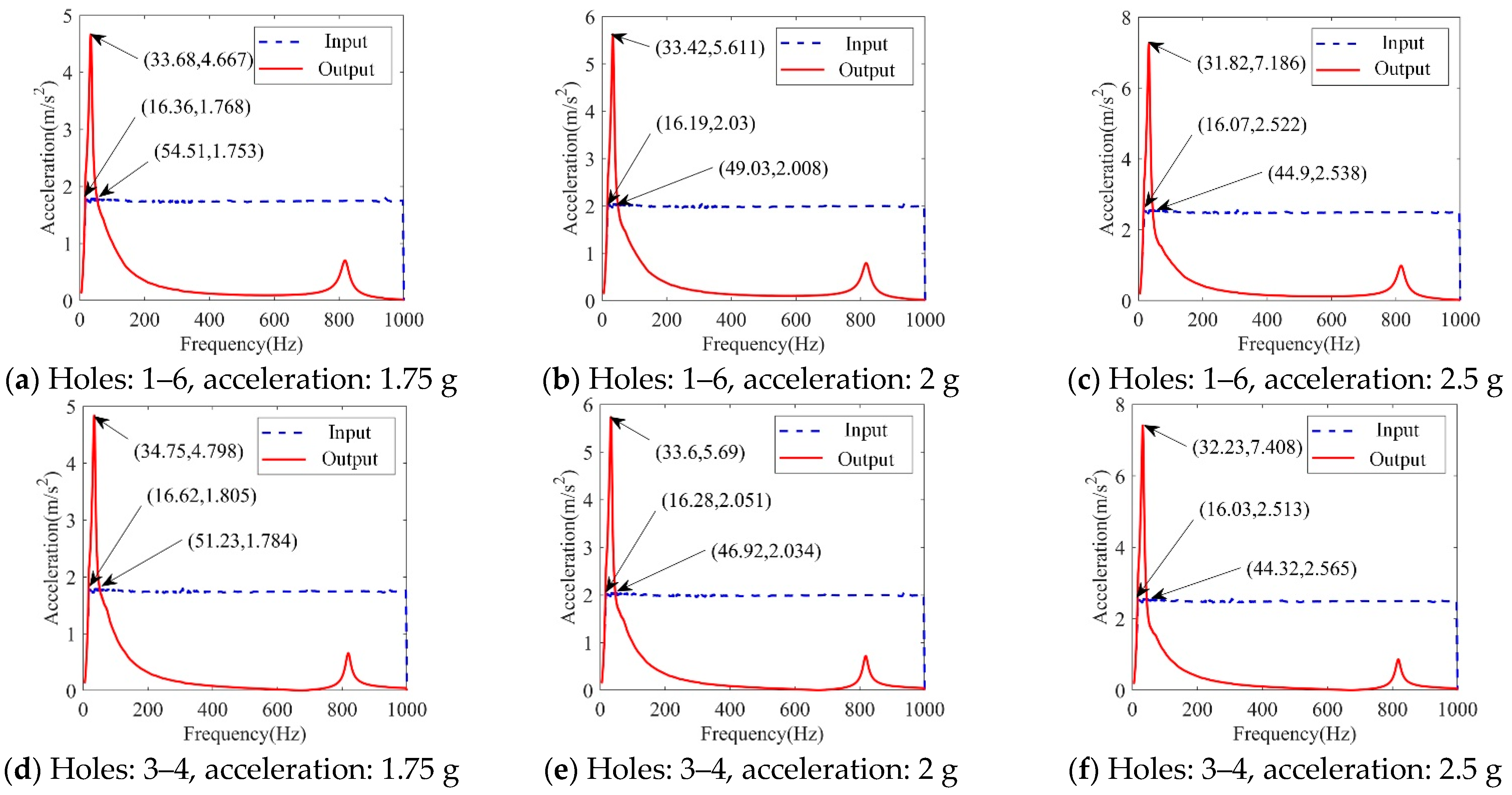
4.1. Dynamic Frequency Sweep Experiment of Symmetrically Arranged Vibration Isolators
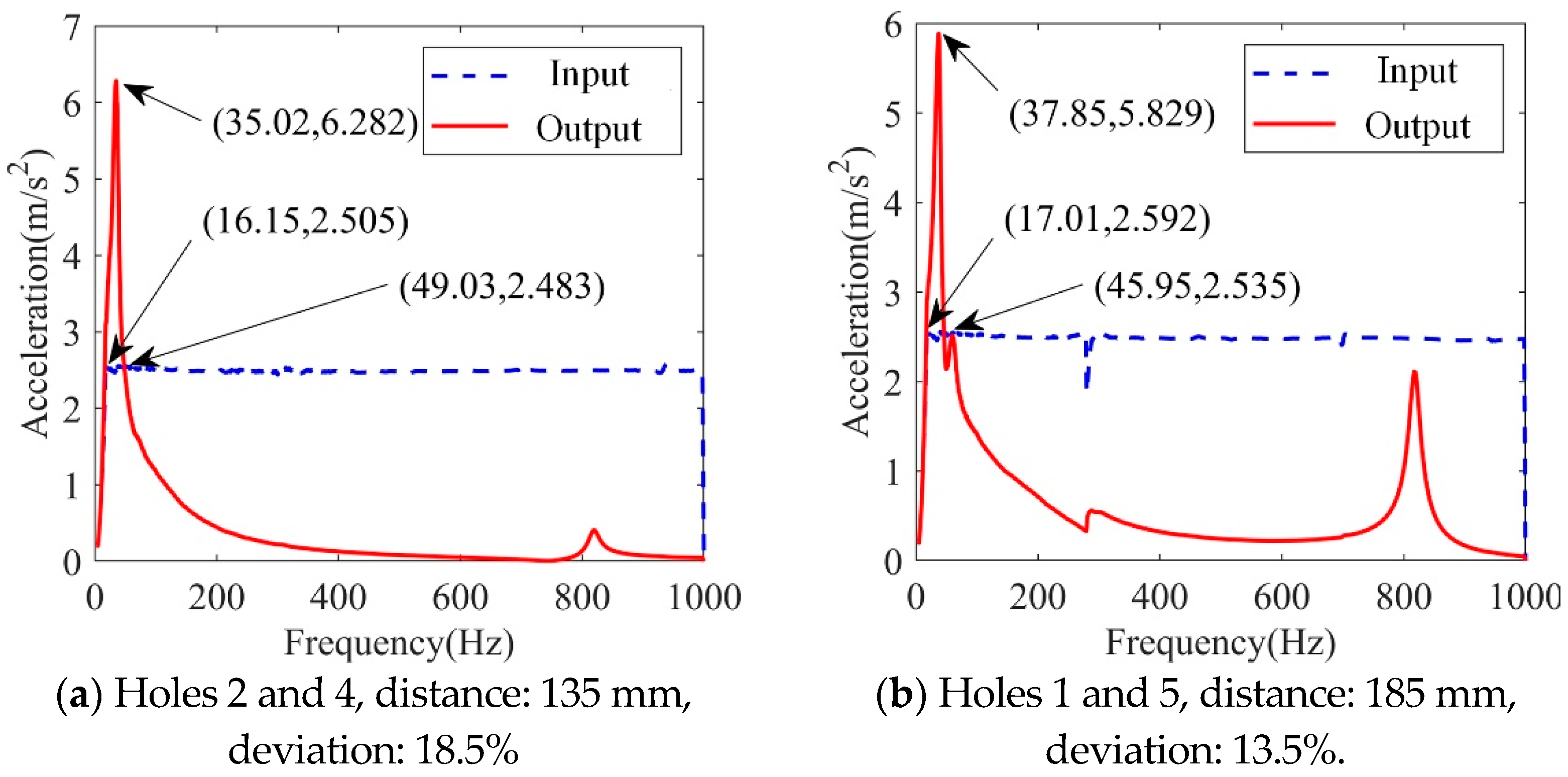
4.2. Dynamic Frequency Sweep Experiment of Asymmetrically Arranged Vibration Isolators
5. Discussion and Conclusions
5.1. The Discussion of the Experiment
5.2. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pan, X.; Lu, J.; Huo, J.; Gao, J.; Wu, H. A Review on Self-Recovery Regulation (SR) Technique for Unbalance Vibration of High-End Equipment. Chin. J. Mech. Eng. 2020, 33, 89. [Google Scholar] [CrossRef]
- Yu, H.; Yan, X. Principle and Application of Free Resonance Vibration Isolation Based on Dry Friction Damper. In Proceedings of the 2nd International Conference on Functional Manufacturing and Mechanical Dynamics, Hangzhou, China, 22–25 January 2012; p. 59. [Google Scholar]
- Hou, J.F.; Li, R.L.; Yu, G.C.; Luo, T.; He, H.W. Contrast Test Research on Application of Dry Friction Isolators to Vibration Isolation of Vehicle Electronic Devices. Appl. Mech. Mater. 2014, 505, 360–364. [Google Scholar] [CrossRef]
- Qu, D.; Liu, X.; Liu, G.; Bai, Y.; He, T. Analysis of vibration isolation performance of parallel air spring system for precision equipment transportation. Meas. Control 2019, 52, 291–302. [Google Scholar] [CrossRef] [Green Version]
- Bednarz, J. The New Methodology for Assessing of the Applicability of Elastomeric Materials in the Vibration Isolation Systems of Railway Lines. Arch. Acoust. 2016, 41, 573–578. [Google Scholar] [CrossRef] [Green Version]
- Jia, D.; Pang, F.-z.; Yin, X.-c.; Ye, X. Study on the vibro-acoustic characteristics of a vibration isolation mass structure with composite braces. In Proceedings of the International Conference on Applied Mechanics, Materials and Manufacturing (ICAMMM 2011), Shenzhen, China, 18–20 November 2012; p. 85. [Google Scholar]
- Bazinenkov, A.M.; Ivanova, D.A.; Efimov, I.A.; Rotar, A.P. Research of the mechanical properties of a magnetorheological elastomer for an active vibration isolation system. Vestn. Mashinostroeniya 2021, 41, 60–64. [Google Scholar] [CrossRef]
- Yarra, S.; Gordaninejad, F.; Behrooz, M.; Pekcan, G.; Itani, A.M.; Publicover, N. Performance of a large-scale magnetorheological elastomer-based vibration isolator for highway bridges. J. Intell. Mater. Syst. Struct. 2018, 29, 3890–3901. [Google Scholar] [CrossRef]
- Brancati, R.; Di Massa, G.; Pagano, S.; Petrillo, A.; Santini, S. A combined neural network and model predictive control approach for ball transfer unit-magnetorheological elastomer-based vibration isolation of lightweight structures. J. Vib. Control 2020, 26, 1668–1682. [Google Scholar] [CrossRef]
- Lu, Z.Q.; Zhao, L.; Ding, H.; Chen, L.Q. A dual-functional metamaterial for integrated vibration isolation and energy harvesting. J. Sound Vib. 2021, 509, 116251. [Google Scholar] [CrossRef]
- Hu, G.B.; Austin, A.C.M.; Sorokin, V.; Tang, L.H. Metamaterial beam with graded local resonators for broadband vibration suppression. Mech. Syst. Signal Process. 2021, 146, 106982. [Google Scholar] [CrossRef]
- Stearns, A.; Beck, B. An optimization problem for maximum vibration suppression in reconfigurable one dimensional metamaterials. New J. Phys. 2021, 23. [Google Scholar] [CrossRef]
- Perez-Aracil, J.; Pereira, E.; Aphale, S.S.; Reynolds, P. Vibration Isolation and Alignment of Multiple Platforms on a Non-Rigid Supporting Structure. Actuators 2020, 9, 108. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, B.; Chen, Y.; Wang, L. Performance Analysis of Discrete Whole-Spacecraft Vibration Isolation Platforms for Flexible Spacecrafts. In Proceedings of the Conference on Active and Passive Smart Structures and Integrated Systems, San Diego, CA, USA, 8–11 March 2010. [Google Scholar]
- Hua, Y.L.; Jun, L.J.; Jian, Z.S. Researches on Nonlinear Hybrid Vibration Isolation System. In Proceedings of the 4th International Conference on Computing, Control and Industrial Engineering (CCIE 2013), Wuhan, China, 27–28 October 2013; pp. 222–227. [Google Scholar]
- Garcia-Perez, O.A.; Silva-Navarro, G.; Peza-Solis, J.F. Flexible-Link Robots with Combined Trajectory Tracking and Vibration Control. Appl. Math. Model. 2019, 70, 285–298. [Google Scholar] [CrossRef]
- Barjuei, E.S.; Boscariol, P.; Vidoni, R. Robust Control of Three-Dimensional Compliant Mechanisms. ASME J. Dyn. Sys. Meas. Control 2016, 10, 138. [Google Scholar] [CrossRef]
- Zhang, G.; Pang, H.; He, J. Selection and Optimization in Vibration Isolation Structure of Marine Podded SSP Propulsion. In Proceedings of the 4th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA 2012), Sanya, China, 6–7 January 2012; p. 280. [Google Scholar]
- Sohail, A.; Liu, C. Study on the vibration isolation characteristics of an anti-resonant hydropneumatic suspension. J. Eng. 2019, 13, 208–210. [Google Scholar] [CrossRef]
- Wang, J. Active vibration control: Design towards performance limit. Mech. Syst. Signal Processing 2022, 171, 108926. [Google Scholar] [CrossRef]
- Zhu, L.; Yuan, H.; Zhou, H.; Jiang, D.; Liu, B.; Fan, C.; Tang, L. Vibration Test and Shock Absorption of Coal Crusher Chambers in Thermal Power Plants (I): Field Test and Assessment. Shock Vib. 2020, 2020, 8816829. [Google Scholar] [CrossRef]
- Eem, S.; Kim, J.H. Sensitivity analysis for the distribution of maximum responses by seismic isolation system parameters using the stochastic response database. Nucl. Eng. Des. 2019, 347, 53–58. [Google Scholar] [CrossRef]
- Alhan, C.; Hisman, K. Seismic isolation performance sensitivity to potential deviations from design values. Smart Struct. Syst. 2016, 18, 293–315. [Google Scholar] [CrossRef]
- Gazi, H.; Alhan, C. Reliability of elastomeric-isolated buildings under historical earthquakes with/without forward-directivity effects. Eng. Struct. 2019, 195, 490–507. [Google Scholar] [CrossRef]
- Qian, Z.J.; Cao, M.G.; Ying, J.L.; Zhuang, W.D.; Zhang, H.; Shi, J.; Zhou, D.C. Vibration characteristics and vibration isolation design of oil-immersed power transformer. In Proceedings of the 2nd International Conference on Civil Engineering, Environment Resources and Energy Materials, Changsha, China, 18–20 September 2020. [Google Scholar]
- Lu, Z.Q.; Gu, D.H.; Ding, H.; Lacarbonara, W.; Chen, L.Q. Nonlinear vibration isolation via a circular ring. Mech. Syst. Signal Process. 2019, 136, 106490. [Google Scholar] [CrossRef]
- Tan, D.; Lu, Z.Q.; Gu, D.H.; Ding, H.; Chen, L.Q. A Ring Vibration Isolator Enhanced by a Nonlinear Energy Sink. J. Sound Vib. 2021, 508, 116201. [Google Scholar] [CrossRef]
- Li, Z.; Wu, Q.; Liu, B.; Gong, Z. Optimal Design of Magneto-Force-Thermal Parameters for Electromagnetic Actuators with Halbach Array. Actuators 2021, 10, 231. [Google Scholar] [CrossRef]
- Rossi, A.; Orsini, F.; Scorza, A.; Botta, F.; Belfiore, N.P.; Sciuto, S.A. A Review on Parametric Dynamic Models of Magnetorheological Dampers and Their Characterization Methods. Actuators 2018, 7, 16. [Google Scholar] [CrossRef] [Green Version]
- Markou, A.A.; Stefanou, G.; Manolis, G.D. Stochastic energy measures for hybrid base isolation systems. Soil Dyn. Earthq. Eng. 2019, 119, 454–470. [Google Scholar] [CrossRef]
- Hu, Y.Q.; Feng, Z.W.; Qin, J.; Yang, F.; Zhao, J. Design and Verification of Micro-Vibration Isolator for a CMG. In Proceedings of the 5th International Symposium of Space Optical Instruments and Applications, Sino Holland Space Opt Instruments Joint Lab, Beijing, China, 5–7 September 2018; pp. 281–286. [Google Scholar]
- Zhou, Y.; Chen, P. Investigations on a vertical isolation system with quasi-zero stiffness property. Smart Struct. Syst. 2020, 25, 543–557. [Google Scholar] [CrossRef]
- Anvar, V. Numerical and Experimental Analysis of Metamaterials With Quasi-Zero Effect for Vibration Isolation. In Proceedings of the International Conference on Functional Materials, Characterization, Solid State Physics, Power, Thermal and Combustion Energy (FCSPTC), Andhra Pradesh, India, 7–8 April 2017. [Google Scholar]
- Demir, M.U.; Yilmaz, C. Analysis and design of an adjustable stiffness three-axis horizontal vibration isolator using elastic columns and a string in tension. J. Sound Vib. 2022, 523, 116736. [Google Scholar] [CrossRef]
- Bian, J.; Jing, X. Analysis and design of a novel and compact X-structured vibration isolation mount (X-Mount) with wider quasi-zero-stiffness range. Nonlinear Dyn. 2020, 101, 2195–2222. [Google Scholar] [CrossRef]
- Jiang, Y.; Song, C.; Ding, C.; Xu, B. Design of magnetic-air hybrid quasi-zero stiffness vibration isolation system. J. Sound Vib. 2020, 477, 115346. [Google Scholar] [CrossRef]
- Lee, D.H.; Kim, Y.B.; Chakir, S.; Huynh, T.; Park, H.C. Noninteracting Control Design for 6-DoF Active Vibration Isolation Table with LMI Approach. Appl. Sci. 2021, 11, 7693. [Google Scholar] [CrossRef]
- Ito, S.; Lindner, B.; Schitter, G. Sample-tracking Vibration Isolation with Hybrid Reluctance Actuators for Inline Metrology. IFAC PapersOnLine 2019, 52, 537–542. [Google Scholar] [CrossRef]
- Yu, X.; Cong, W.; Yu, Z.; Tomizuka, M. Controller design and optimal tuning of a wafer handling robot. In Proceedings of the IEEE International Conference on Automation Science & Engineering, Mexico City, Mexico, 20–24 August 2022. [Google Scholar]

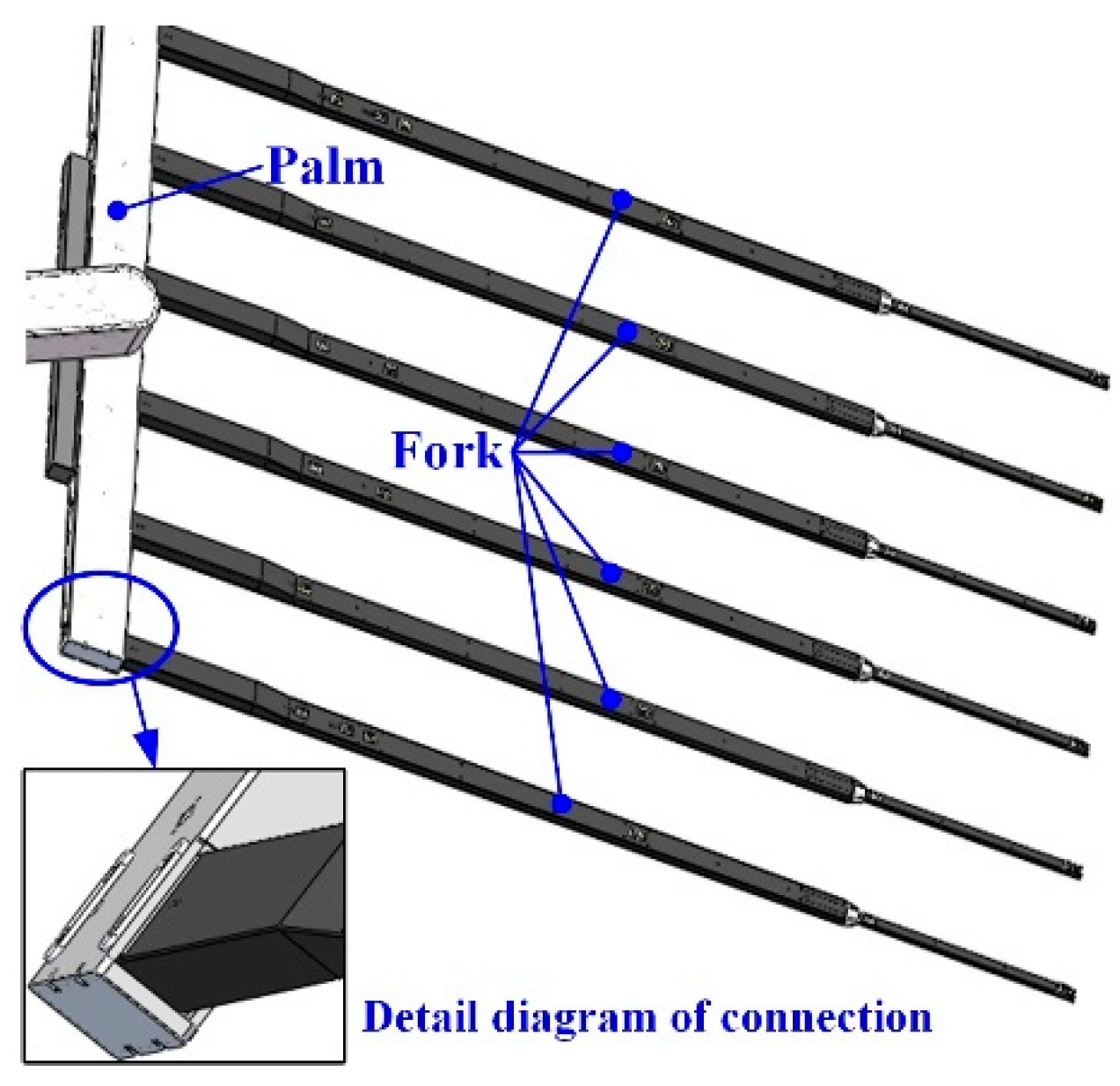
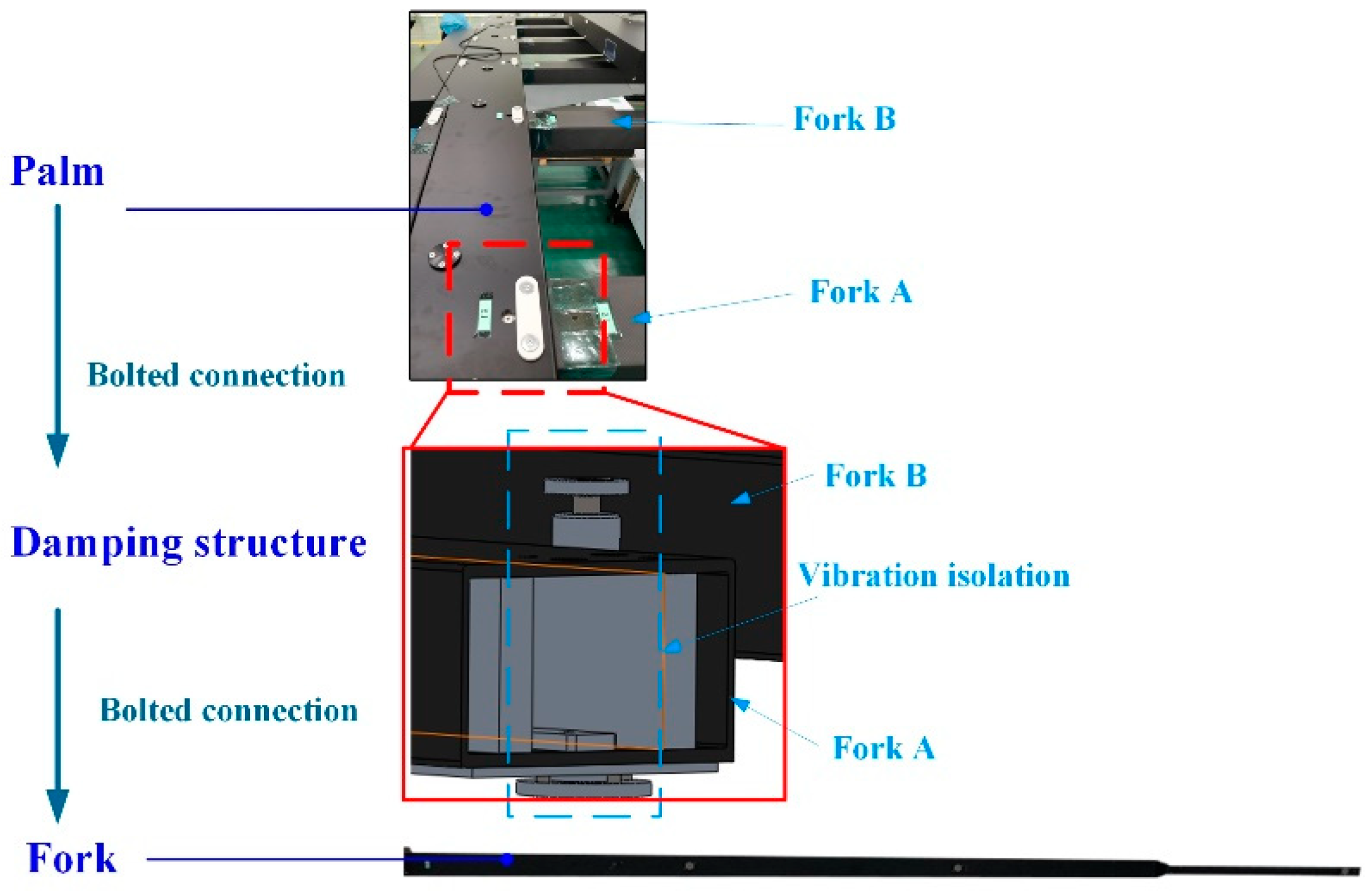
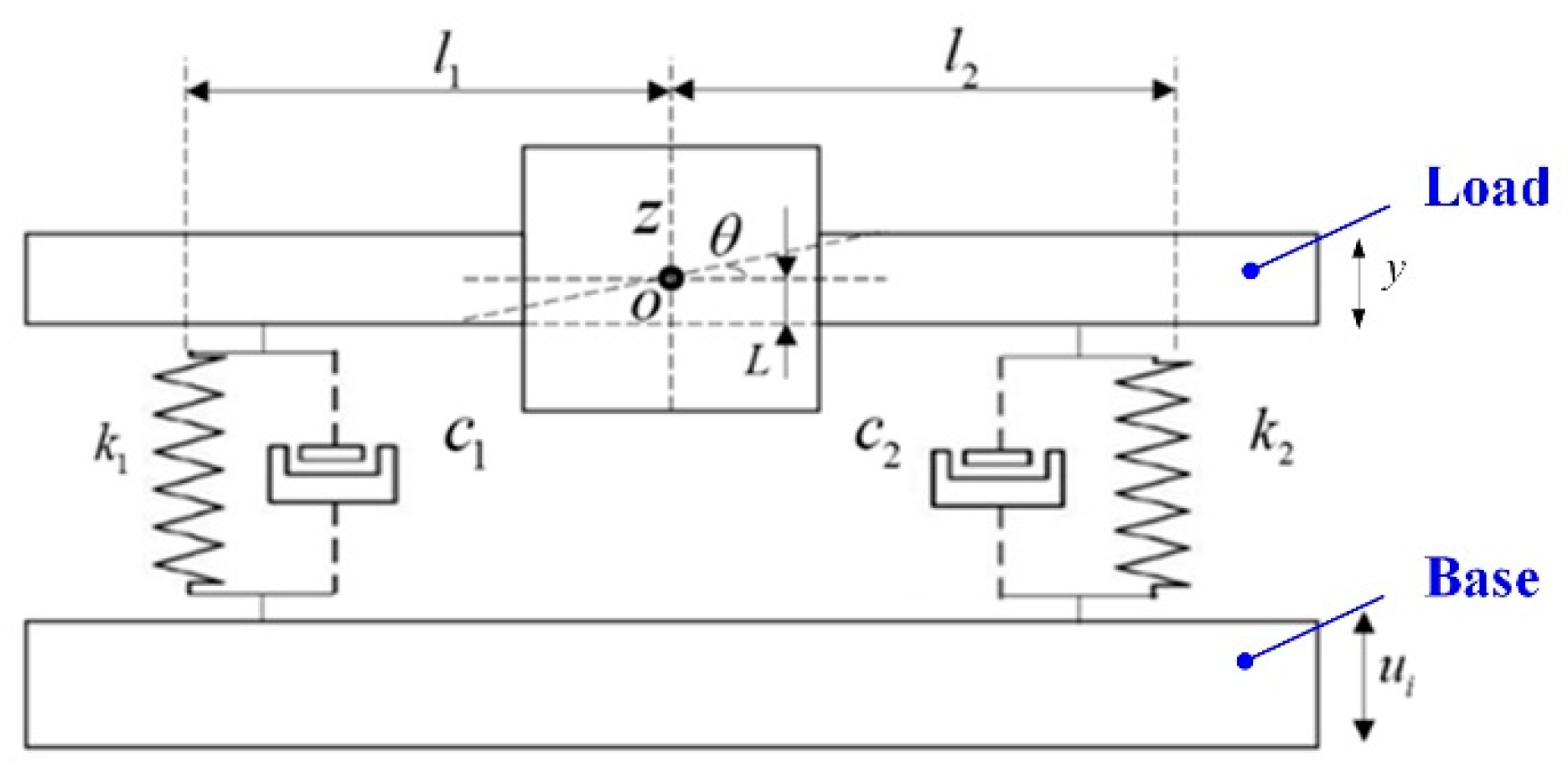
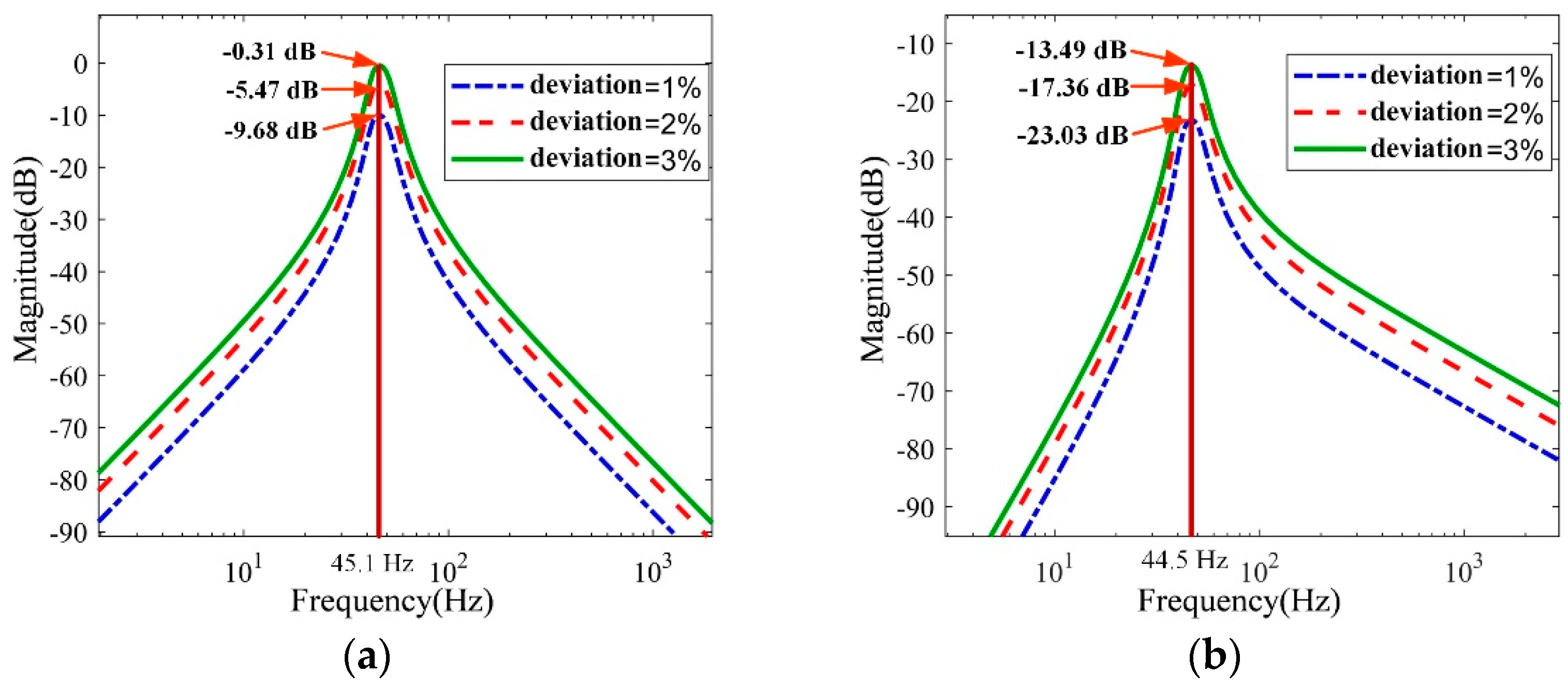



| Parameter | m | I0 | k1, k2 | c1, c2 | l1, l2 |
|---|---|---|---|---|---|
| Numerical value | 16 | 0.7789 | 20,000 | 95.0657 | 0.19 |
| Position | Acceleration/m/s2 | Natural Frequency/Hz | Amplitude of Resonance | Maximum Magnification |
|---|---|---|---|---|
| Holes 1 and 6 | 1.75 g | 29.97 | 41.74 | 2.38 |
| Holes 1 and 6 | 2.5 g | 29.97 | 59.62 | 2.38 |
| Holes 3 and 4 | 1.75 g | 29.97 | 41.74 | 2.38 |
| Holes 3 and 4 | 2.5 g | 29.97 | 59.62 | 2.38 |
| Position | Acceleration/m/s2 | Natural Frequency/Hz | Amplitude of Resonance | Maximum Magnification |
|---|---|---|---|---|
| Holes 1 and 5 | 1.75 g | 27.97 | 38.55 | 2.20 |
| Holes 1 and 5 | 2.5 g | 27.97 | 55.07 | 2.20 |
| Holes 2 and 4 | 1.75 g | 28.97 | 41.38 | 2.36 |
| Holes 2 and 4 | 2.5 g | 28.97 | 59.12 | 2.36 |
| Position | Acceleration/m/s2 | Natural Frequency/Hz | Maximum Magnification |
|---|---|---|---|
| Holes 1 and 6 | 1.75 g | 33.68 | 2.67 |
| Holes 1 and 6 | 2 g | 33.42 | 2.81 |
| Holes 1 and 6 | 2.5 g | 31.82 | 2.88 |
| Holes 3 and 4 | 1.75 g | 34.75 | 2.74 |
| Holes 3 and 4 | 2 g | 33.60 | 2.85 |
| Holes 3 and 4 | 2.5 g | 32.23 | 2.96 |
| Position | Acceleration/ m/s2 | Natural Frequency/Hz | Maximum Magnification | Deviation |
|---|---|---|---|---|
| Holes 1 and 6 | 2.5 g | 31.82 | 2.96 | 0 |
| Holes 1 and 5 | 2.5 g | 37.85 | 5.83 | 13.5% |
| Holes 3 and 4 | 2.5 g | 31.82 | 2.88 | 0 |
| Holes 2 and 4 | 2.5 g | 35.02 | 6.28 | 18.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, H.; Shan, X.; Yu, H.; Wang, G.; Fan, J. Influences of Parameter Deviation on the Vibration Isolation System of an End Effector. Actuators 2022, 11, 133. https://doi.org/10.3390/act11050133
Song H, Shan X, Yu H, Wang G, Fan J. Influences of Parameter Deviation on the Vibration Isolation System of an End Effector. Actuators. 2022; 11(5):133. https://doi.org/10.3390/act11050133
Chicago/Turabian StyleSong, Henan, Xiaobiao Shan, Han Yu, Guangyan Wang, and Jizhuang Fan. 2022. "Influences of Parameter Deviation on the Vibration Isolation System of an End Effector" Actuators 11, no. 5: 133. https://doi.org/10.3390/act11050133








