Performance-Optimized Dielectric Elastomer Actuator System with Scalable Scissor Linkage Transmission
Abstract
:1. Introduction
2. System Concept and Fundamentals
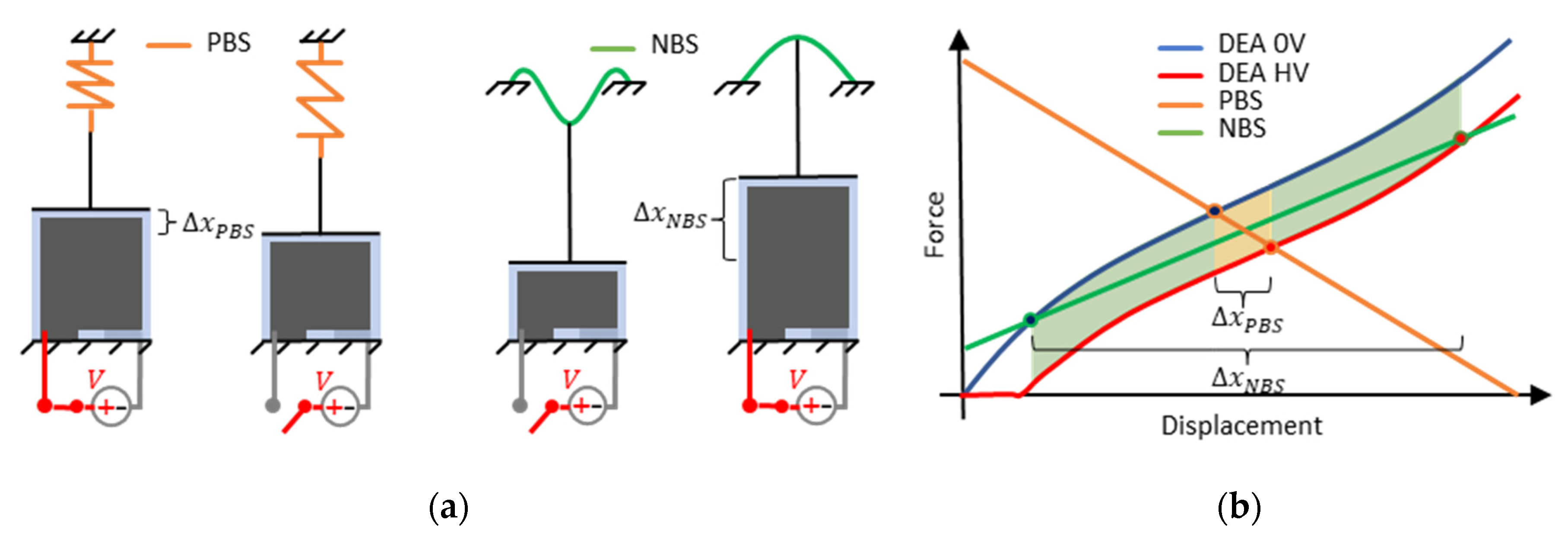
2.1. Performance-Optimized DEA Systems for Static Operation
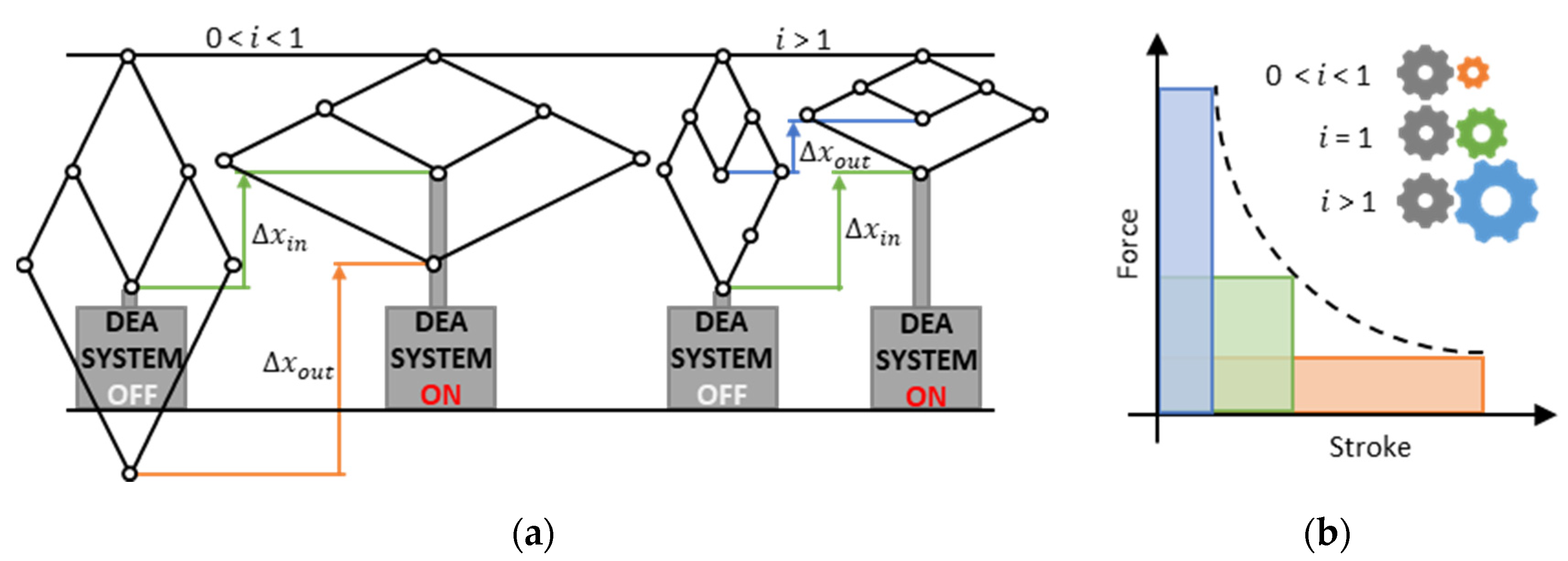
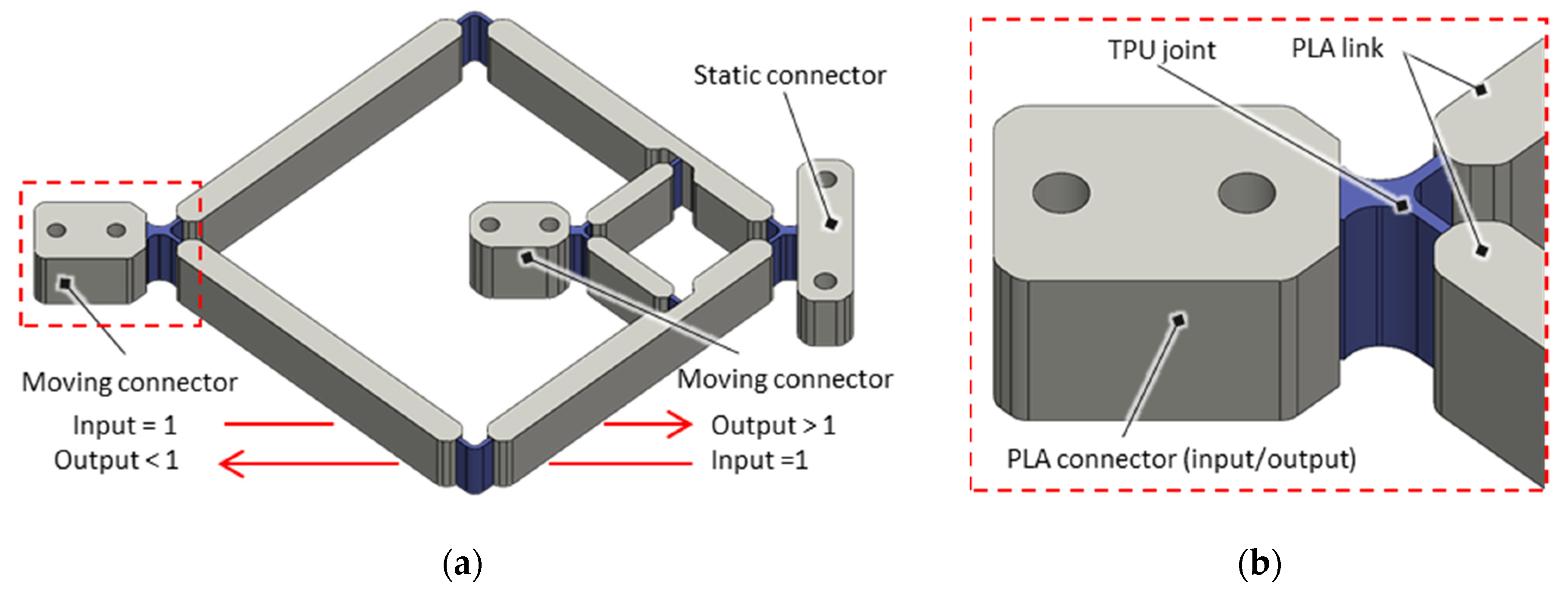
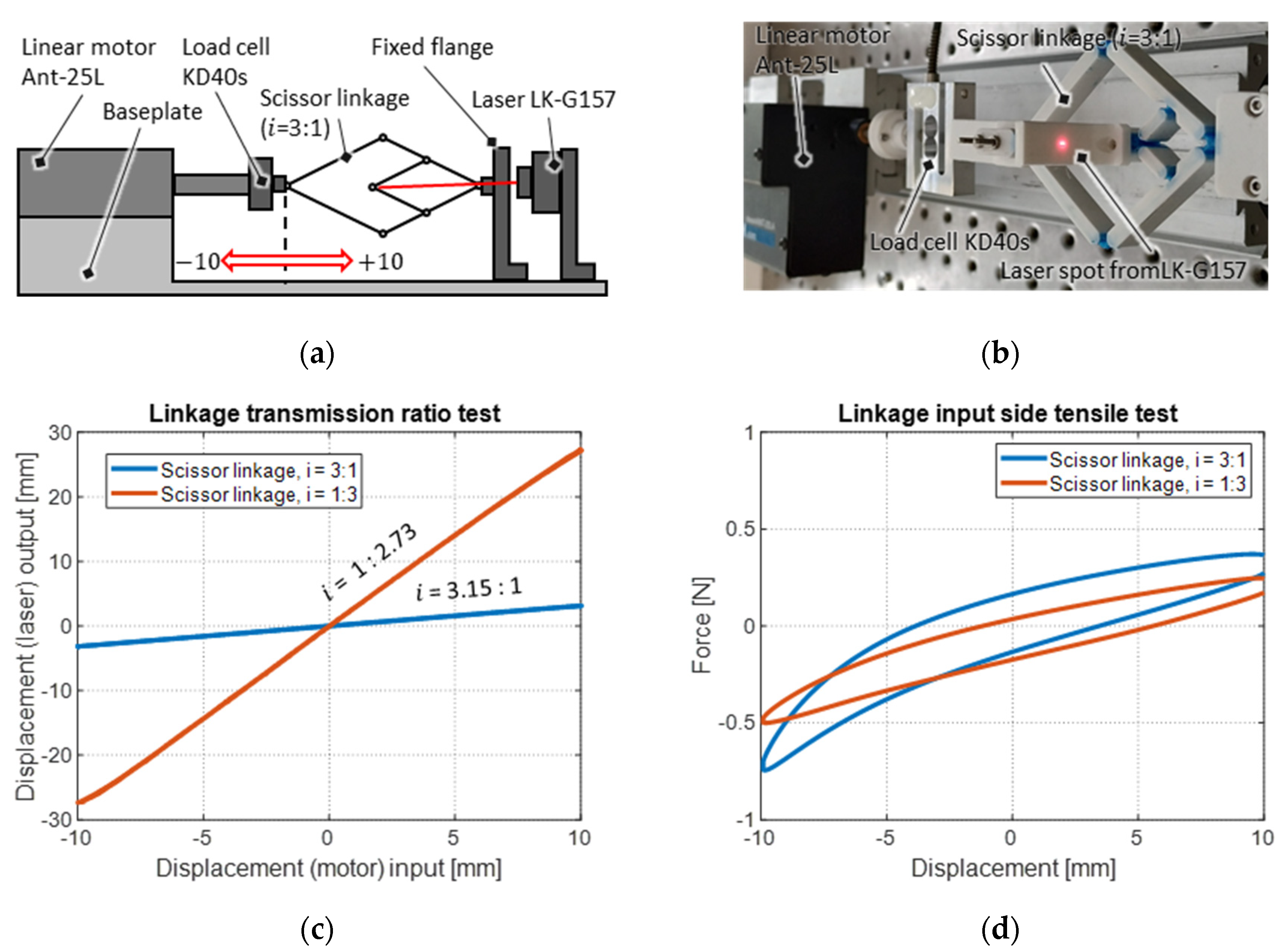
2.2. Scissor Linkage as Linear Transmission Mechanism
3. System Construction and Manufacturing
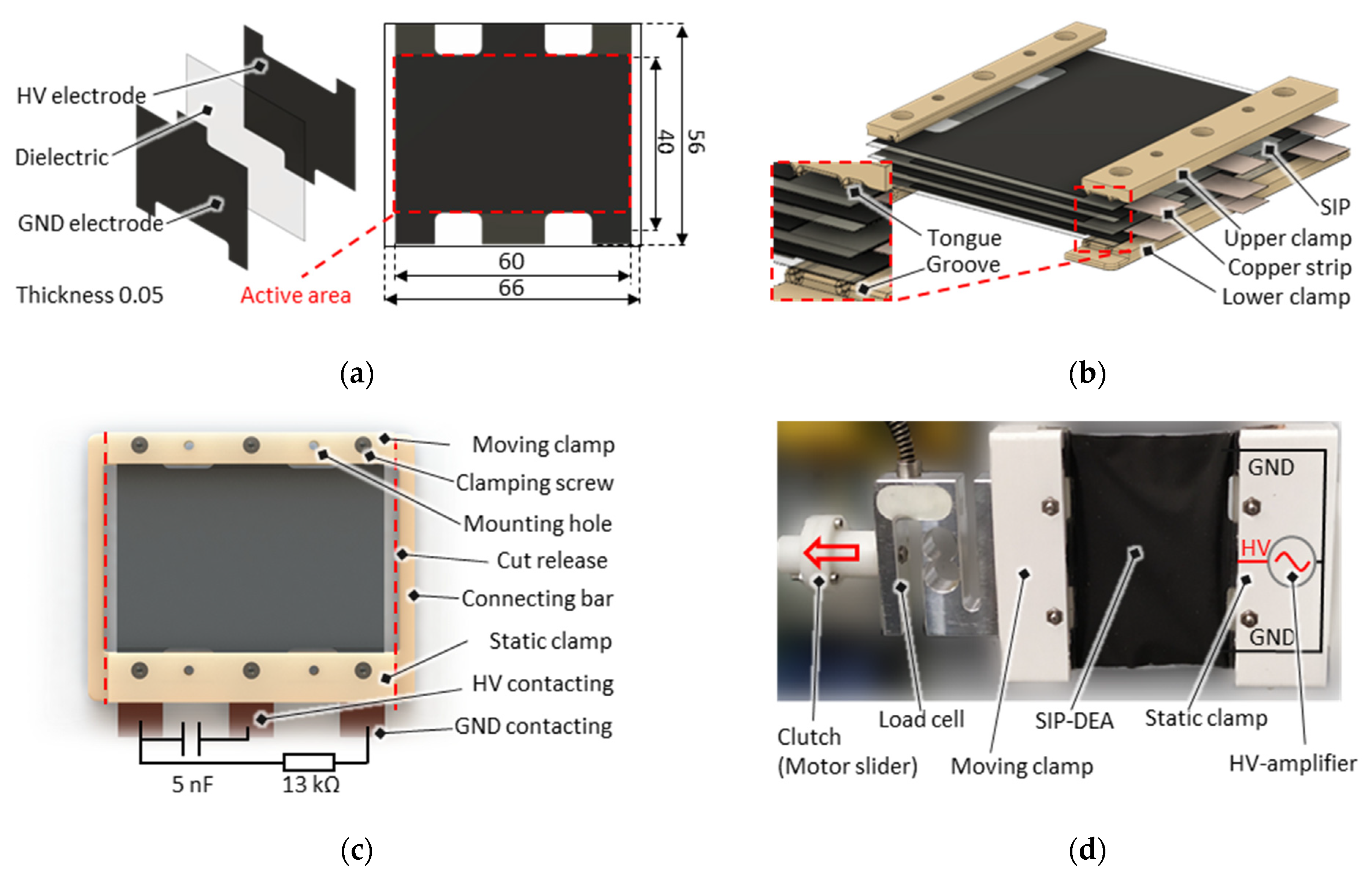
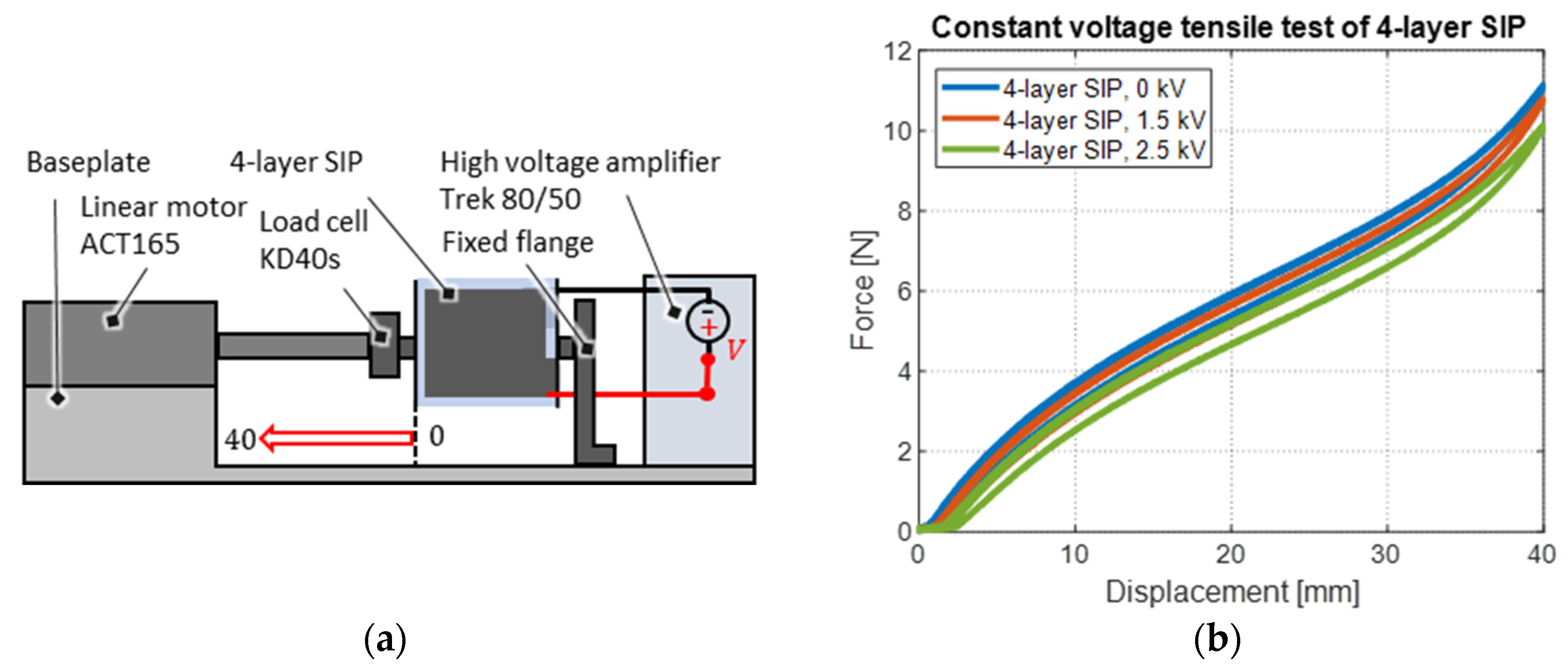
3.1. Multi-Layer SIP
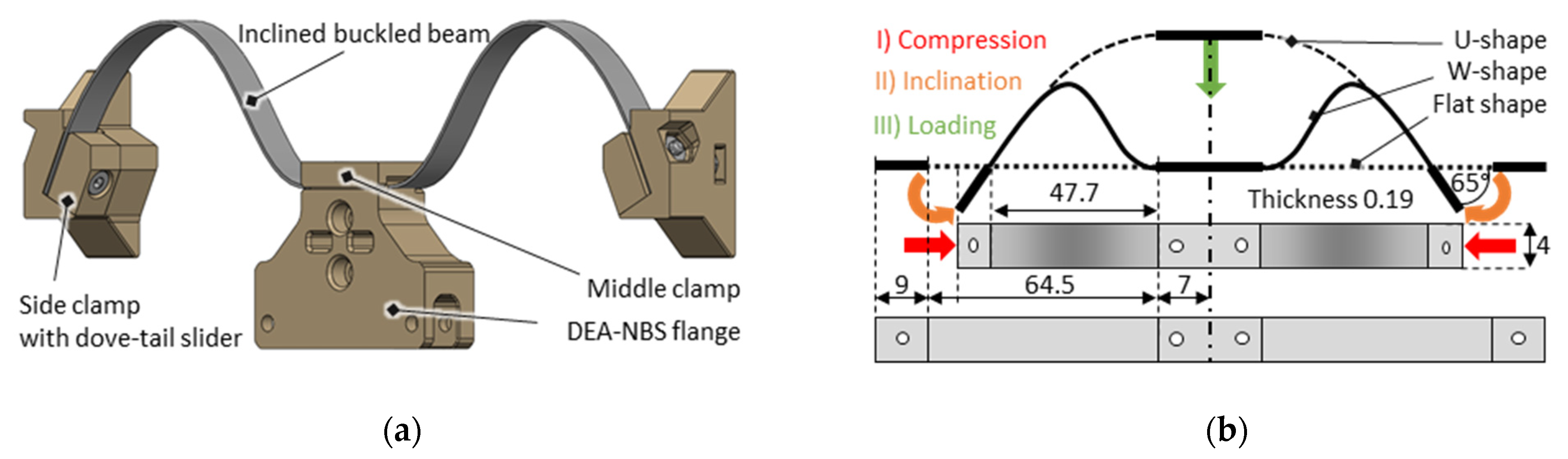
3.2. Inclined and Centrally Loaded Buckled Beam NBS
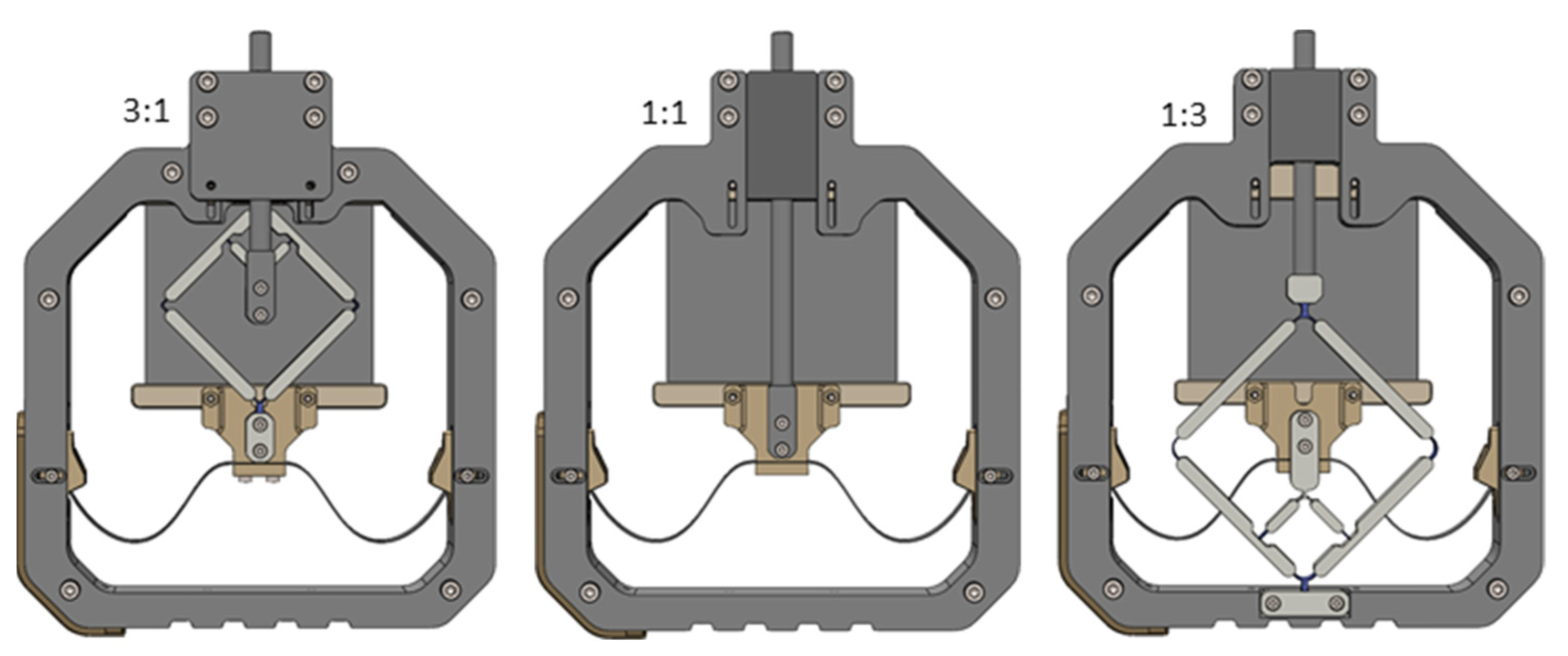
3.3. Non-Inversing Scissor Linkage Transmission Mechanism
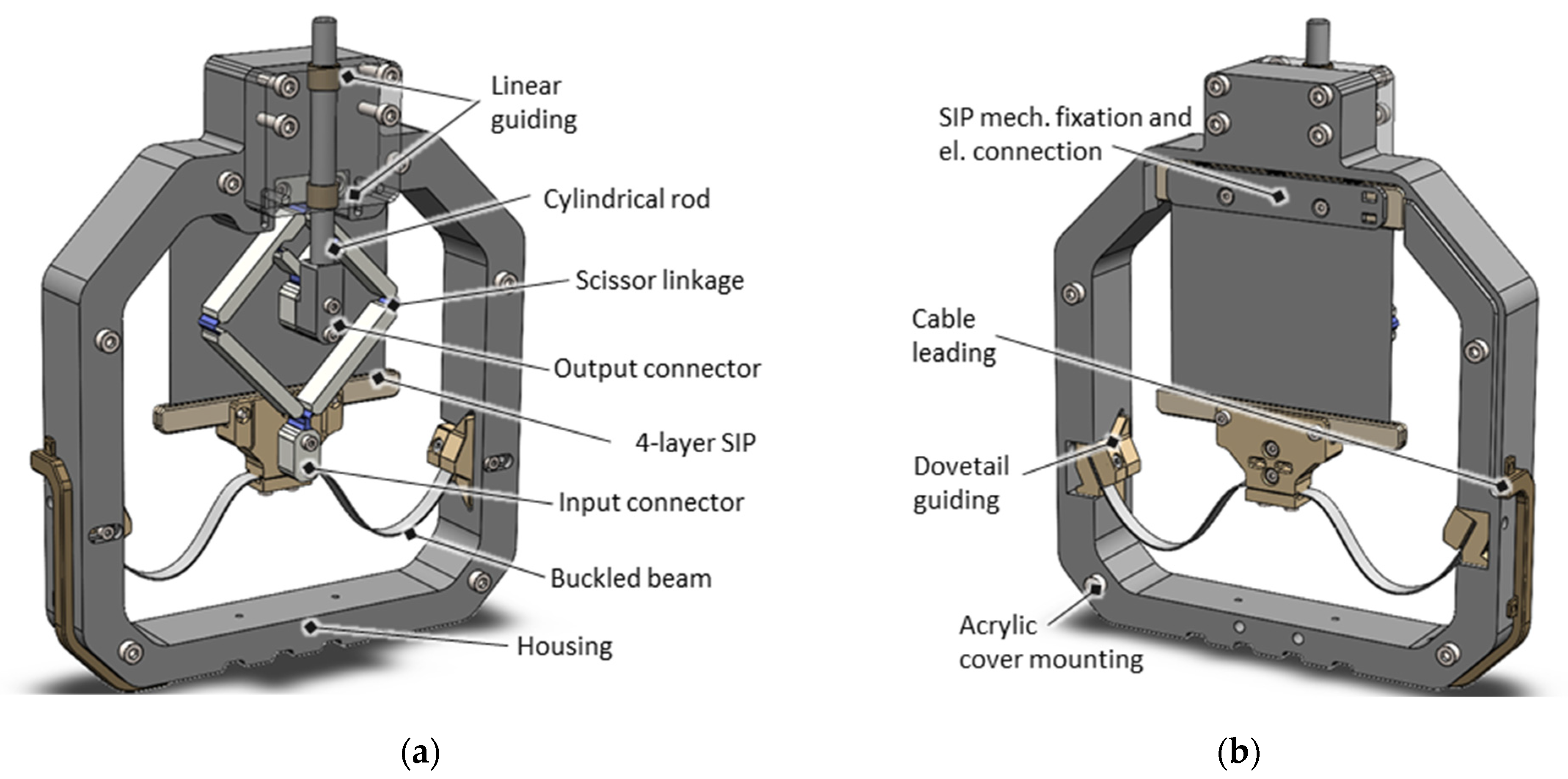
3.4. SIP Actuator System
4. System Characterization
4.1. Multi-Layer SIP
4.2. Inclined and Centrally Loaded Buckled Beam NBS
4.3. Non-Inversing Scissor Linkage Transmission Mechanism
4.4. SIP Actuator System
5. Discussion
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pelrine, R.E.; Kornbluh, R.D.; Joseph, J.P. Electrostriction of polymer dielectrics with compliant electrodes as a means of actuation. Sens. Actuators A Phys. 1998, 64, 77–85. [Google Scholar] [CrossRef]
- Pelrine, R.; Kornbluh, R.; Joseph, J.; Heydt, R.; Pei, Q.; Chiba, S. High-field deformation of elastomeric dielectrics for actuators. Mater. Sci. Eng. C 2000, 11, 89–100. [Google Scholar] [CrossRef]
- Carpi, F.; De Rossi, D.; Kornbluh, R.D.; Pelrine, R.; Sommer-Larson, P. Dielectric Elastomers as Electromechanical Transducers, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Chen, Y.; Agostini, L.; Moretti, G.; Fontana, M.; Vertechy, R. Dielectric elastomer materials for large-strain actuation and energy harvesting: A comparison between styrenic rubber, natural rubber and acrylic elastomer. Smart Mater. Struct. 2019, 28, 114001. [Google Scholar] [CrossRef]
- Madsen, F.B.; Yu, L.; Daugaard, A.E.; Hvilsted, S.; Skov, A.L. Silicone elastomers with high dielectric permittivity and high dielectric breakdown strength based on dipolar copolymers. Polymer 2014, 55, 6212–6219. [Google Scholar] [CrossRef]
- Wissler, M.; Mazza, E. Mechanical behavior of an acrylic elastomer used in dielectric elastomer actuators. Sens. Actuators A Phys. 2007, 134, 494–504. [Google Scholar] [CrossRef]
- Rosset, S.; Shea, H.R. Flexible and stretchable electrodes for dielectric elastomer actuators. Appl. Phys. A 2013, 110, 281–307. [Google Scholar] [CrossRef] [Green Version]
- Mose, F.; Pourazadi, S.; Wantono, C.; Menon, C. Study on electric properties of graphene and carbon black nanoparticles as compliant electrode for dielectric elastomer actuators. In Proceedings of the International Conference on Smart Materials and Structures (CANSMART), Vancouver, BC, Canada, 15–17 July 2015. [Google Scholar]
- Jones, R.W.; Wang, P.; Lassen, B.; Sarban, R. Dielectric elastomers and compliant metal electrode technology. In Proceedings of the Melecon 2010—2010 15th IEEE Mediterranean Electrotechnical Conference, Valletta, Malta, 26–28 April 2010; pp. 368–373. [Google Scholar] [CrossRef]
- Fasolt, B.; Hodgins, M.; Rizzello, G.; Seelecke, S. Effect of screen printing parameters on sensor and actuator performance of dielectric elastomer (DE) membranes. Sens. Actuators A Phys. 2017, 265, 10–19. [Google Scholar] [CrossRef]
- Araromi, O.; Conn, A.; Ling, C.; Rossiter, J.; Vaidyanathan, R.; Burgess, S. Spray deposited multilayered dielectric elastomer actuators. Sens. Actuators A Phys. 2011, 167, 459–467. [Google Scholar] [CrossRef]
- Hubertus, J.; Croce, S.; Neu, J.; Rizzello, G.; Seelecke, S.; Schultes, G. Influence of residual stresses of sputtered thin film electrodes for dielectric elastomer applications. Proceedings 2020, 64, 2. [Google Scholar]
- Zhu, Y.; Giffney, T.; Aw, K. A Dielectric elastomer-based multimodal capacitive sensor. Sensors 2022, 22, 622. [Google Scholar] [CrossRef]
- Rizzello, G.; Naso, D.; York, A.; Seelecke, S. A self-sensing approach for dielectric elastomer actuators based on online estimation algorithms. IEEE/ASME Trans. Mechatron. 2017, 2, 728–738. [Google Scholar] [CrossRef]
- Franke, M.; Ehrenhofer, A.; Lahiri, S.; Henke, E.-F.M.; Wallmersperger, T.; Richter, A. Dielectric elastomer actuator driven soft robotic structures with bioinspired skeletal and muscular reinforcement. Front. Robot. AI 2020, 7, 178. [Google Scholar] [CrossRef] [PubMed]
- Hau, S.; Rizzello, G.; Hodgins, M.; York, A.; Seelecke, S. Design and control of a high-speed positioning system based on dielectric elastomer membrane actuators. IEEE/ASME Trans. Mechatron. 2017, 22, 1259–1267. [Google Scholar] [CrossRef]
- Giousouf, M.; Kovacs, G. Dielectric elastomer actuators used for pneumatic valve technology. Smart Mater. Struct. 2013, 22, 104010. [Google Scholar] [CrossRef]
- Linnebach, P.; Rizzello, G.; Seelecke, S. Design and validation of a dielectric elastomer membrane actuator driven pneumatic pump. Smart Mater. Struct. 2020, 29, 75021. [Google Scholar] [CrossRef]
- Hosoya, N.; Masuda, H.; Maeda, S. Balloon dielectric elastomer actuator speaker. Appl. Acoust. 2019, 148, 238–245. [Google Scholar] [CrossRef]
- Bednar, S.; Modrak, J. Product variety management as a tool for successful mass customized product structure. Pol. J. Manag. Stud. 2015, 12, 16–25. [Google Scholar]
- Dombrowski, U.; Ebentreich, D.; Mielke, T.; Zahn, T.; Richter, T. Einführung lean development. In Lean Development: Aktueller Stand und Zukünftige Entwicklungen; Dombrowski, U., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 139–196. [Google Scholar] [CrossRef]
- Heim, J.R.; Polyakov, I.; Zarrabi, A.; Hui, O. Electroactive Polymer Transducers Biased for Increased Output. U.S. Patent 7915790B2, 29 March 2011. [Google Scholar]
- Hodgins, M.; Seelecke, S. Experimental Analysis of Biasing Elements for Dielectric Electro-Active Polymers. Proc. SPIE-Int. Soc. Opt. Eng. 2011, 7976, 797639. [Google Scholar] [CrossRef]
- Hau, S.; Bruch, D.; Rizzello, G.; Motzki, P.; Seelecke, S. Silicone based dielectric elastomer strip actuators coupled with nonlinear biasing elements for large actuation strains. Smart Mater. Struct. 2018, 27, 74003. [Google Scholar] [CrossRef]
- Berselli, G.; Vertechy, R.; Vassura, G.; Castelli, V.P. Design of a linear dielectric elastomer actuator of conical shape with quasi-constant available thrust. In Proceedings of the 2009 International Conference on Intelligent Engineering Systems, Bridgetown, Barbados, 16–18 April 2009; pp. 89–94. [Google Scholar]
- Liu, Y.; Liu, B.; Yin, T.; Xiang, Y.; Zhou, H.; Qu, S. Bistable rotating mechanism based on dielectric elastomer actuator. Smart Mater. Struct. 2019, 29, 15008. [Google Scholar] [CrossRef]
- Luo, B.; Li, B.; Yu, Y.; Yu, M.; Ma, J.; Yang, W.; Wang, P.; Jiao, Z. A Jumping robot driven by a dielectric elastomer actuator. Appl. Sci. 2020, 10, 2241. [Google Scholar] [CrossRef] [Green Version]
- Plante, J.-S.; Dubowsky, S. On the performance mechanisms of dielectric elastomer actuators. Sens. Actuators A 2007, 137, 96–109. [Google Scholar] [CrossRef]
- Chouinard, P.; Plante, J.-S. Bistable antagonistic dielectric elastomer actuators for binary robotics and mechatronics. Mechatron. IEEE/ASME Trans. 2012, 17, 1–9. [Google Scholar] [CrossRef]
- Conn, A.; Rossiter, J. Radially expanding mechanism for dielectric elastomers. Proc. SPIE-Int. Soc. Opt. Eng. 2010, 7642, 76420P. [Google Scholar] [CrossRef]
- Loew, P.; Rizzello, G.; Seelecke, S. Permanent magnets as biasing mechanism for improving the performance of circular dielectric elastomer out-of-plane actuators. Electroact. Polym. Actuators Devices 2017, 10163, 101630Y. [Google Scholar] [CrossRef]
- Bernat, J.; Kołota, J. DEAP Actuator composed of a soft pneumatic spring bias with pressure signal sensing. Energies 2021, 14, 1189. [Google Scholar] [CrossRef]
- McCarthy, J.M.; Soh, G.S. Planar kinematics. In Geometric Design of Linkages; Springer: Berlin/Heidelberg, Germany, 2011; pp. 75–92. [Google Scholar] [CrossRef] [Green Version]
- Chaudhary, N.; Gupta, A. Multi-body analysis for a four-bar mechanism using RecurDyn and MATLAB. In Machines, Mechanism and Robotics; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1813–1823. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruch, D.; Willian, T.P.; Schäfer, H.C.; Motzki, P. Performance-Optimized Dielectric Elastomer Actuator System with Scalable Scissor Linkage Transmission. Actuators 2022, 11, 160. https://doi.org/10.3390/act11060160
Bruch D, Willian TP, Schäfer HC, Motzki P. Performance-Optimized Dielectric Elastomer Actuator System with Scalable Scissor Linkage Transmission. Actuators. 2022; 11(6):160. https://doi.org/10.3390/act11060160
Chicago/Turabian StyleBruch, Daniel, Tobias Pascal Willian, Hendrik Cornelius Schäfer, and Paul Motzki. 2022. "Performance-Optimized Dielectric Elastomer Actuator System with Scalable Scissor Linkage Transmission" Actuators 11, no. 6: 160. https://doi.org/10.3390/act11060160
APA StyleBruch, D., Willian, T. P., Schäfer, H. C., & Motzki, P. (2022). Performance-Optimized Dielectric Elastomer Actuator System with Scalable Scissor Linkage Transmission. Actuators, 11(6), 160. https://doi.org/10.3390/act11060160






