Data-Based Security Fault Tolerant Iterative Learning Control under Denial-of-Service Attacks
Abstract
:1. Introduction
- •
- The nonlinear system is transformed into a linear data model by using the dynamic linearization technology under failures and DoS attacks. Then, a new data-based security fault tolerant iterative learning control (SFTILC) algorithm is designed to ensure the tracking performance of the system under the DoS attack.
- •
- The radial basis function neural network (RBFNN) is used to approximate the sensor failure function. A DoS attack compensation mechanism is proposed in the iterative domain to lessen the impacts of DoS attacks.
2. Preliminaries and Problem Formulations
2.1. System Description
2.2. Dynamic Linearization
3. Design Fault Tolerant Controller
3.1. Model Free Adaptive Iterative Learning Control
3.2. Sensor Failure
3.3. Attack Compensation
4. Stability Analysis
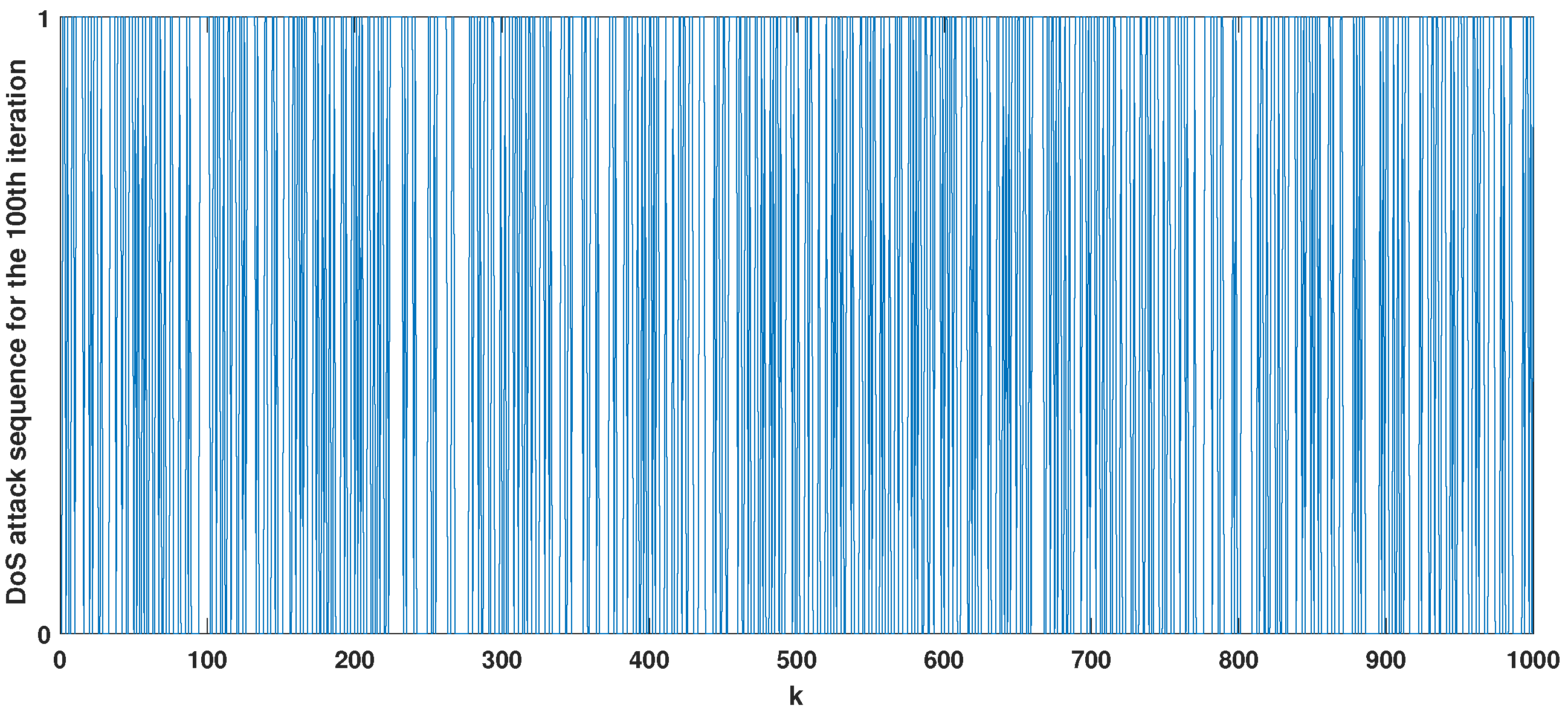
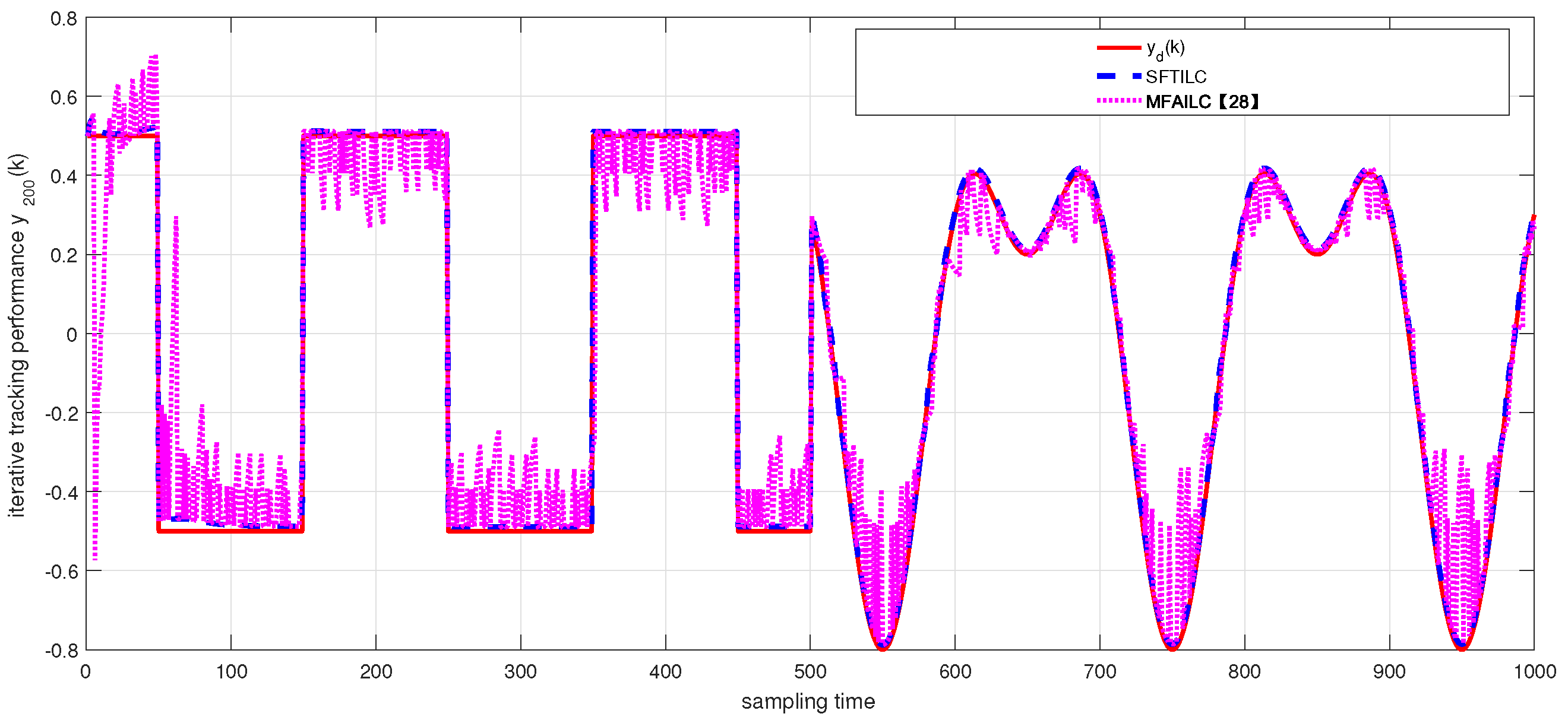
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gaid, M.; Cela, A.; Hamam, Y. Optimal integrated control and scheduling of networked control systems with communication constraints: Application to a car suspension system. IEEE Trans. Control Syst. Technol. 2006, 14, 776–787. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Yu, B. Output feedback stabilization of networked control systems with random delays modeled by markov chains. IEEE Trans. Autom. Control 2009, 54, 1668–1674. [Google Scholar]
- Xu, H.; Jagannathan, S. Neural network-based finite horizon stochastic optimal control design for nonlinear networked control systems. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 472–485. [Google Scholar] [CrossRef] [PubMed]
- Qiu, J.; Gao, H.; Ding, S. Recent advances on fuzzy-model-based nonlinear networked control systems: A survey. IEEE Trans. Ind. Electron. 2016, 63, 1207–1217. [Google Scholar] [CrossRef]
- Guardabassi, G.; Savaresi, S. Virtual reference direct design method: An off-line approach to data-based control system design. IEEE Trans. Autom. Control 2000, 45, 954–959. [Google Scholar] [CrossRef]
- Mahish, P.; Pradhan, A. Mitigating subsynchronous resonance using synchrophasor data based control of wind farms. IEEE Trans. Power Deliv. 2020, 35, 364–376. [Google Scholar] [CrossRef]
- Deng, C.; Wen, C.; Huang, J.; Zhang, X.; Zou, Y. Distributed observer-based cooperative control approach for uncertain nonlinear MASs under event-triggered communication. IEEE Trans. Autom. Control 2021, 67, 2669–2676. [Google Scholar] [CrossRef]
- Bu, X.; Hou, Z.; Zhang, H. Data-driven multiagent systems consensus tracking using model free adaptive control. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 1514–1524. [Google Scholar] [CrossRef]
- Meng, D.; Zhang, J. Design and analysis of data-driven learning control: An optimization-bBased approach. systems and control. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–15. [Google Scholar] [CrossRef]
- Jin, X. Nonrepetitive trajectory tracking for nonlinear autonomous agents with asymmetric output constraints using parametric iterative learning control. Int. J. Robust Nonlinear Control 2019, 29, 1941–1955. [Google Scholar] [CrossRef]
- Radac, M.; Lala, T. Hierarchical Cognitive Control for Unknown Dynamic Systems Tracking. Mathematics 2021, 9, 2752. [Google Scholar] [CrossRef]
- Memon, F.; Shao, C. Data-driven optimal PID type ILC for a class of nonlinear batch process. Int. J. Syst. Sci. 2020, 52, 263–276. [Google Scholar] [CrossRef]
- Hildebrand, R.; Lecchini, A.; Solari, G.; Gevers, M. Optimal prefiltering in iterative feedback tuning. IEEE Trans. Autom. Control 2005, 50, 1196–1200. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Hou, Z. Data-driven MFAC for a class of discrete-time nonlinear systems with RBFNN. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1013–1020. [Google Scholar] [CrossRef]
- Hou, Z.; Chi, R.; Gao, H. An overview of dynamic-linearization-based data-driven control and applications. IEEE Trans. Ind. Electron. 2017, 64, 4076–4090. [Google Scholar] [CrossRef]
- Liao, Y.; Du, T.; Jiang, Q. Model-free adaptive control method with variable forgetting factor for unmanned surface vehicle control. Appl. Ocean. Res. 2019, 93, 1141–1187. [Google Scholar] [CrossRef]
- Meng, D. Convergence conditions for solving robust iterative learning control problems under nonrepetitive model uncertainties. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1908–1919. [Google Scholar] [CrossRef]
- Meng, D.; Moore, K. Robust iterative learning control for nonrepetitive uncertain systems. IEEE Trans. Autom. Control 2017, 62, 907–913. [Google Scholar] [CrossRef]
- Zhou, C.; Che, W. Quantized data-based iterative learning control under denial-of-service attacks. Optim. Control. Appl. Methods 2021. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Q.; Ge, X.; Ding, L. Resilient control design based on a sampled-data model for a class of networked control systems under denial-of-service attacks. IEEE Trans. Cybern. 2020, 50, 3616–3626. [Google Scholar] [CrossRef]
- Liu, J.; Suo, W.; Zha, L.; Tian, E.; Xie, X. Security distributed state estimation for nonlinear networked systems against DoS attacks. Int. J. Robust Nonlinear Control 2020, 30, 1156–1180. [Google Scholar] [CrossRef]
- Li, J.; Yang, Z.; Mu, X.; Wu, X. Passivity-based Event-triggered Fault Tolerant Control for Nonlinear Networked Control System with Actuator Failures and DoS Jamming Attacks. J. Frankl. Inst. 2020, 357, 9288–9307. [Google Scholar] [CrossRef]
- Hu, L.; Wang, Z.; Han, Q.; Liu, X. State estimation under false data injection attacks: Security analysis and system protection. Automatica 2018, 87, 176–183. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Che, W.; Deng, C.; Wu, Z. Observer-based event-triggered containment control for MASs under DoS attacks. IEEE Trans. Cybern. 2021, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Che, W.; Deng, C.; Wu, Z. Distributed model-free adaptive control for learning nonlinear MASs under DoS attacks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–10. [Google Scholar] [CrossRef]
- Jin, X.; Che, W.; Wu, Z.; Wang, H. Analog control circuit designs for a class of continuous-time adaptive fault-tolerant control systems. IEEE Trans. Cybern. 2020, 52, 4209–4220. [Google Scholar] [CrossRef]
- Deng, C.; Jin, X.; Che, W.; Wang, H. Learning-based distributed resilient fault-tolerant control method for heterogeneous MASs under unknown leader dynamic. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–10. [Google Scholar] [CrossRef]
- Su, M.; Che, W. Fault-Tolerant control for model-free networked control systems under DoS attacks. J. Frankl. Inst. 2021, 358, 9023–9033. [Google Scholar] [CrossRef]
- Xing, J.; Li, N.; Chi, R.; Huang, B.; Hou, Z. Data-driven nonlinear ILC with varying trial lengths. J. Frankl. Inst. 2020, 357, 10262–10287. [Google Scholar] [CrossRef]
- Lian, J.; Hu, J.; Żak, S. Variable Neural Adaptive Robust Control: A Switched System Approach. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 903–915. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhou, C.; Che, W.; Deng, C.; Jin, X. Data-Based Security Fault Tolerant Iterative Learning Control under Denial-of-Service Attacks. Actuators 2022, 11, 178. https://doi.org/10.3390/act11070178
Li Z, Zhou C, Che W, Deng C, Jin X. Data-Based Security Fault Tolerant Iterative Learning Control under Denial-of-Service Attacks. Actuators. 2022; 11(7):178. https://doi.org/10.3390/act11070178
Chicago/Turabian StyleLi, Zengwei, Changren Zhou, Weiwei Che, Chao Deng, and Xiaozheng Jin. 2022. "Data-Based Security Fault Tolerant Iterative Learning Control under Denial-of-Service Attacks" Actuators 11, no. 7: 178. https://doi.org/10.3390/act11070178
APA StyleLi, Z., Zhou, C., Che, W., Deng, C., & Jin, X. (2022). Data-Based Security Fault Tolerant Iterative Learning Control under Denial-of-Service Attacks. Actuators, 11(7), 178. https://doi.org/10.3390/act11070178





