Fractional Order PID Control Based on Ball Screw Energy Regenerative Active Suspension
Abstract
:1. Introduction
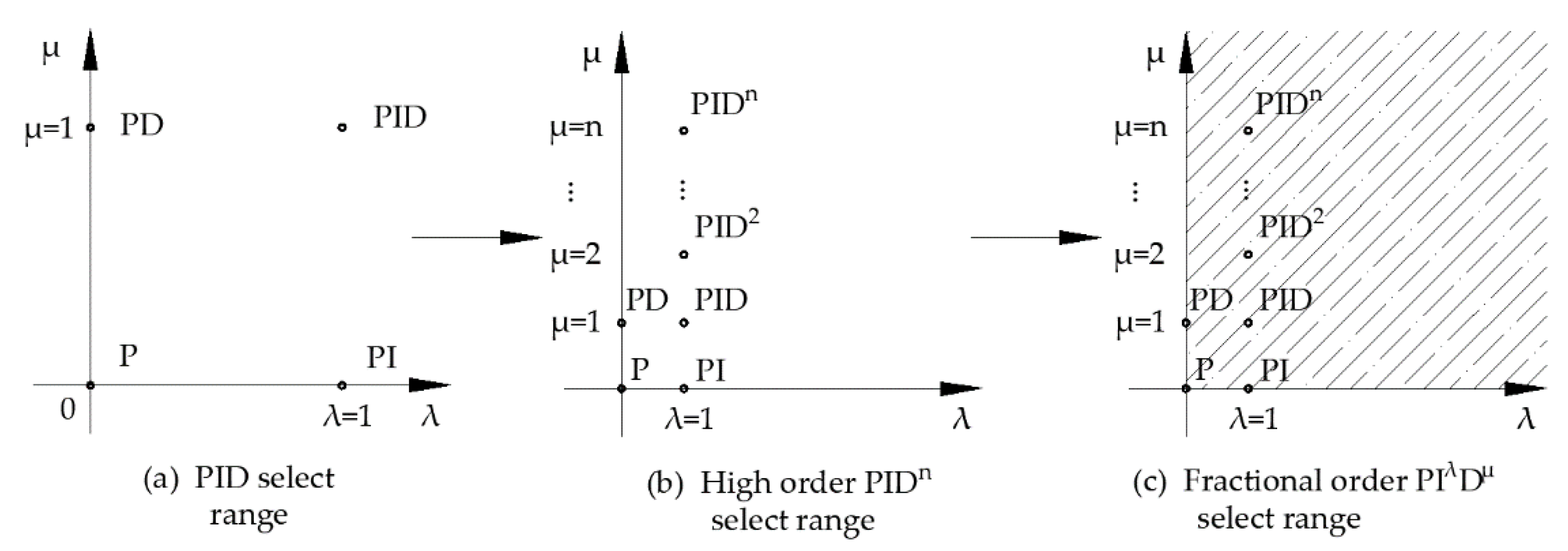
2. Advanced Fractional Order PID Controller
3. Principles and Modelling
3.1. Working Principle of Energy Regenerative Active Suspension
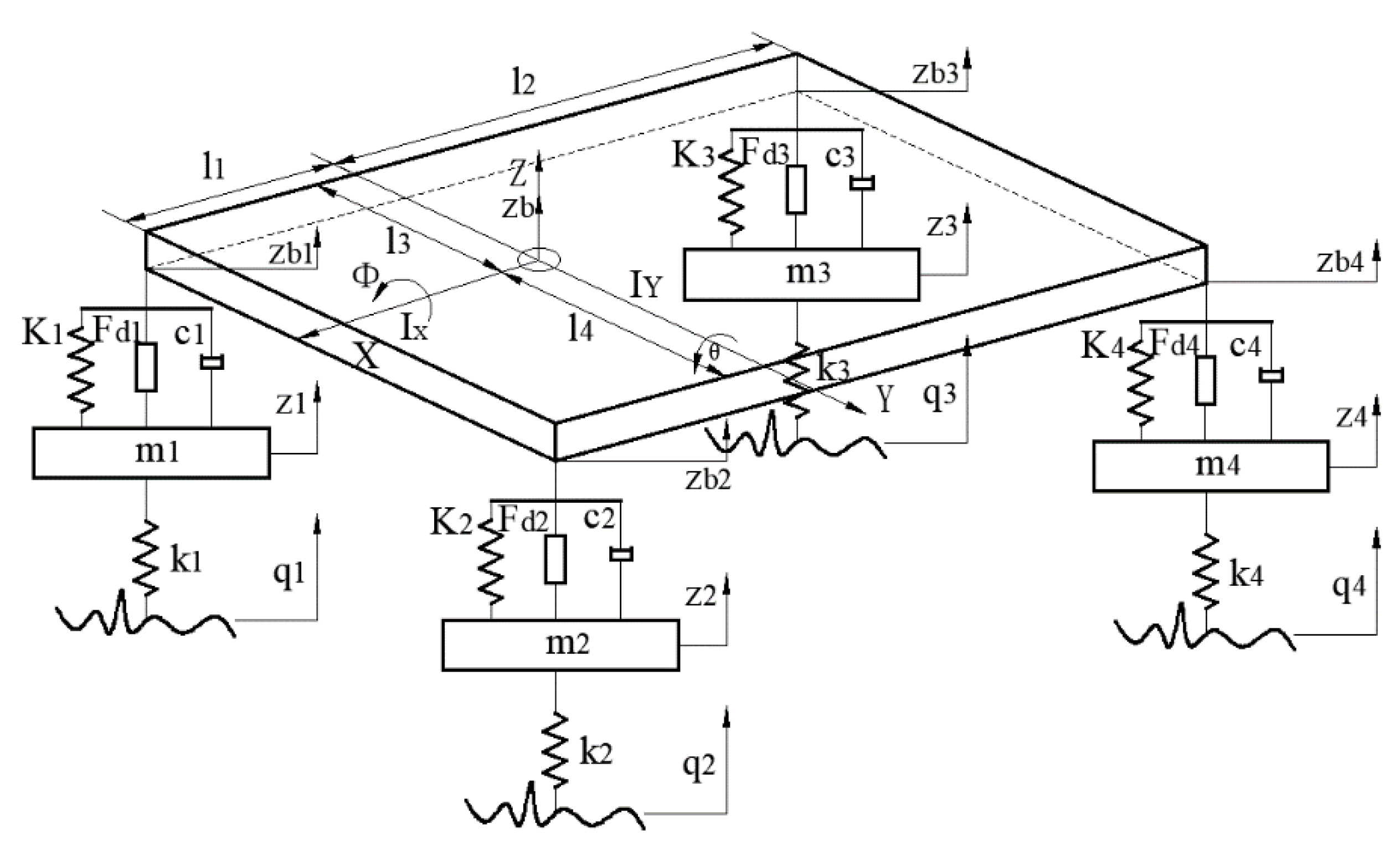
3.2. Dynamics Model of the Whole Vehicle Energy Regenerative Active Suspension System
3.3. Modelling of Road Excitation
3.4. Energy Regenerative Actuator Model
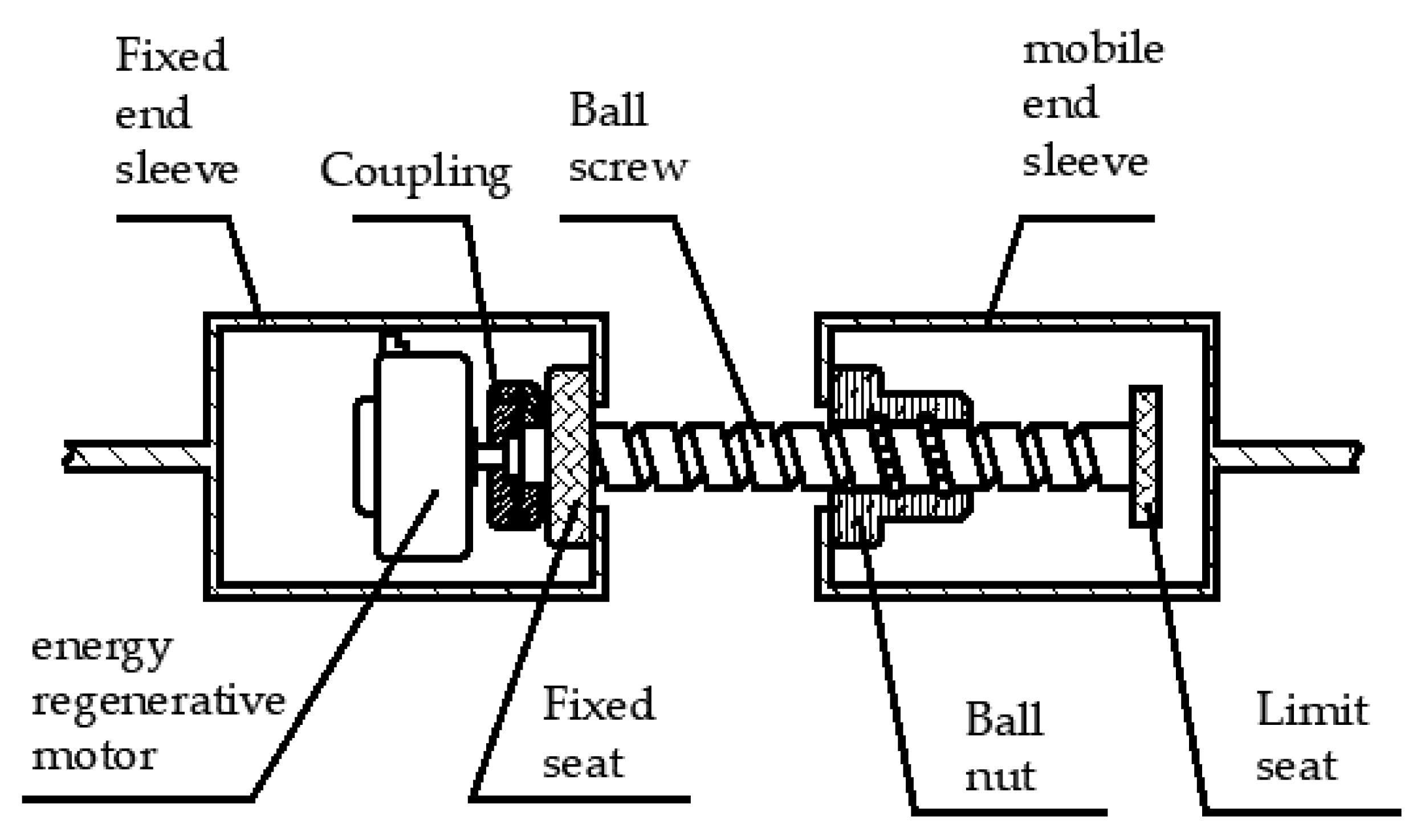
3.4.1. Design of Mechanical Structure of Energy Regenerative Actuator
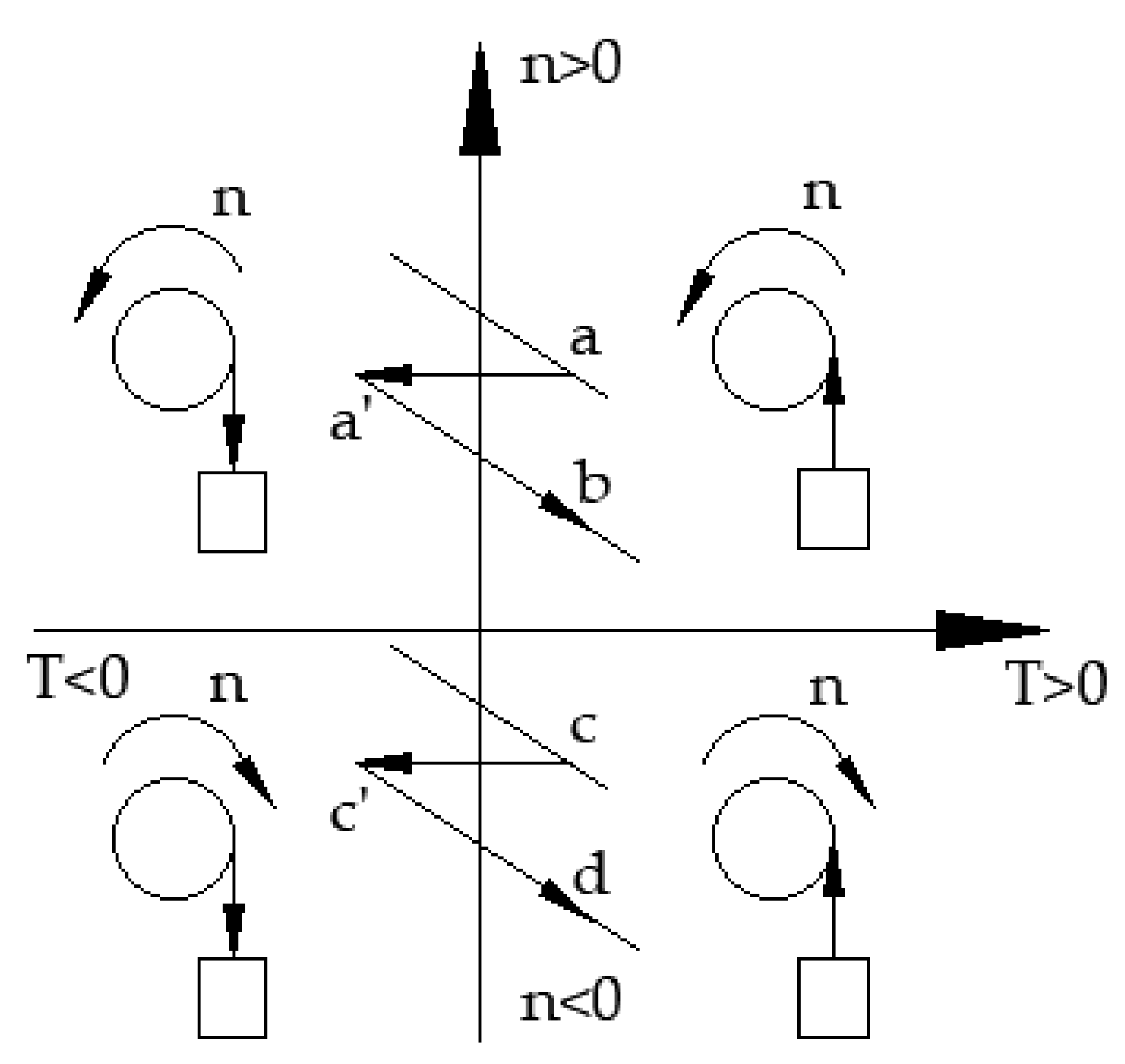
3.4.2. Four-Quadrant Operation Principle of Energy Regenerative Motor
3.4.3. Mathematical Model for Energy Recovery
3.4.4. Mathematical Model for Active Control
3.4.5. Analysis of the Relationship between Key Parameters and Performance of Actuator
3.4.6. Digital Implementation of Control Circuits
| Algorithm 1: FOPID |
| Input:, Ideal current value . Output: Actual current value . |
| 1: Limiting current amplitude to prevent integral saturation: If maximum motor operating current , . Else if minimum motor operating current , . 2: Calculation of error values: . 3: Setting of current accuracy: If ,. 4: For j=0: k − 1. 5: Update the binomial coefficients and from Equations (20), (21). 6: Updating the input motor voltage U from Equation (23). 7: . 8: End for. 9: Return I. |
4. Experimental Study of Energy Regenerative Actuators
4.1. Experimental Study of Energy Regenerative
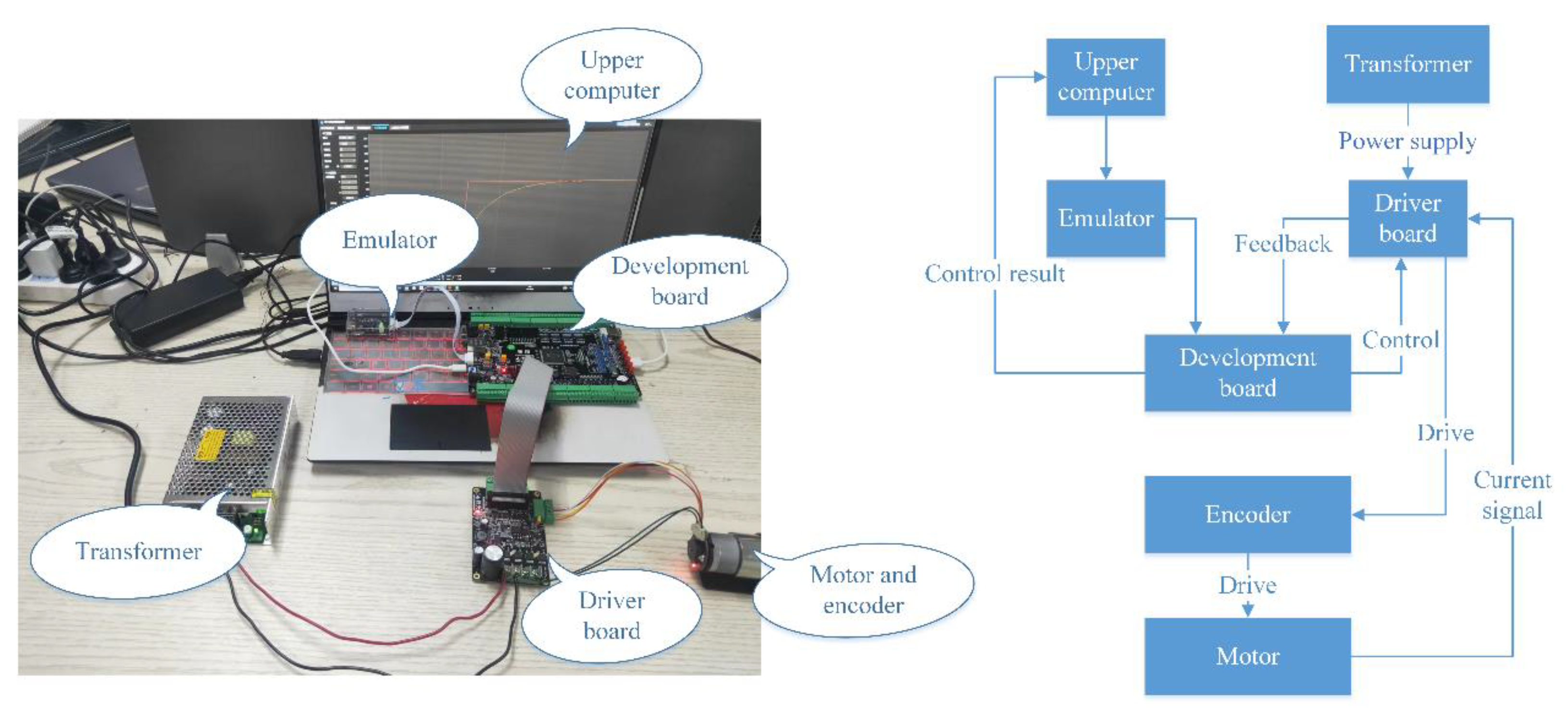
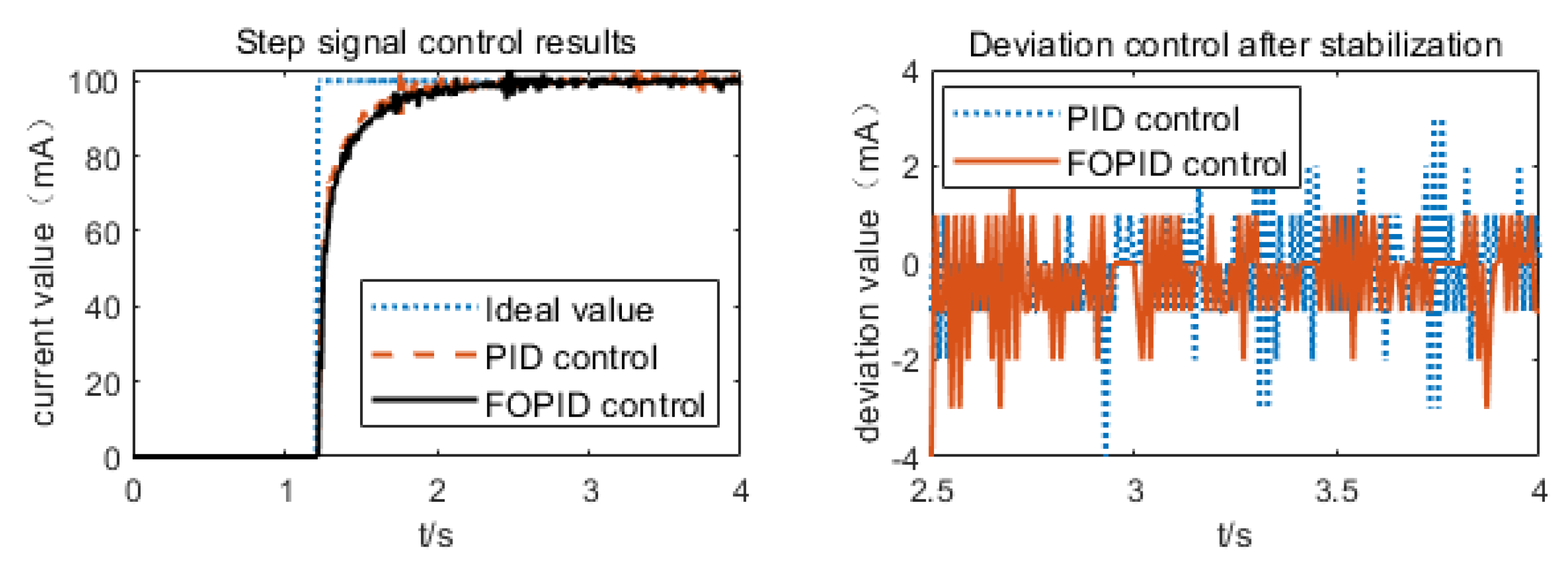
4.2. Experimental Study of Control Circuits
5. Principle of Active Control of the Whole Vehicle
5.1. Fractional Order PID Controller Simulation Model
5.2. Design of Objective Function
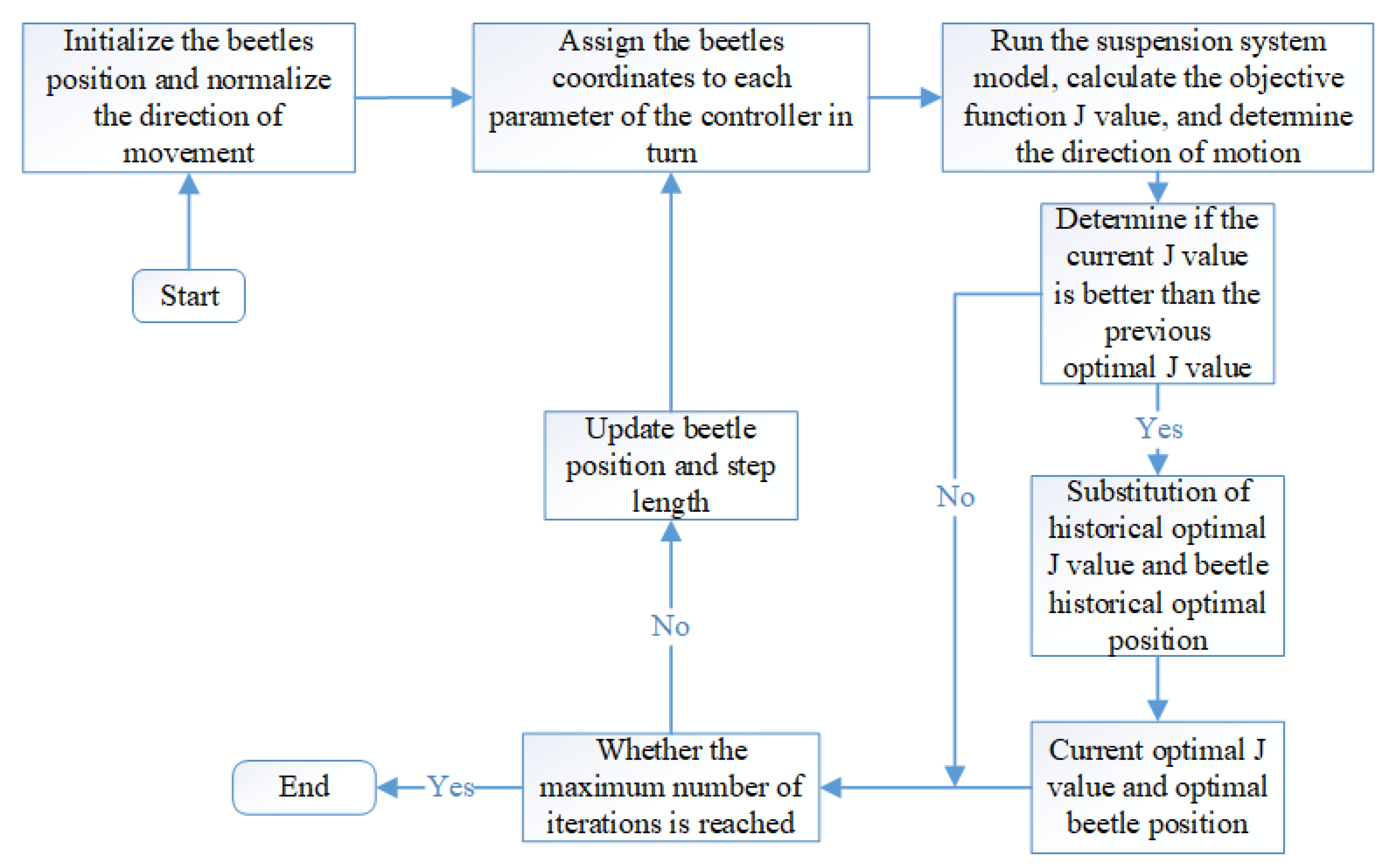
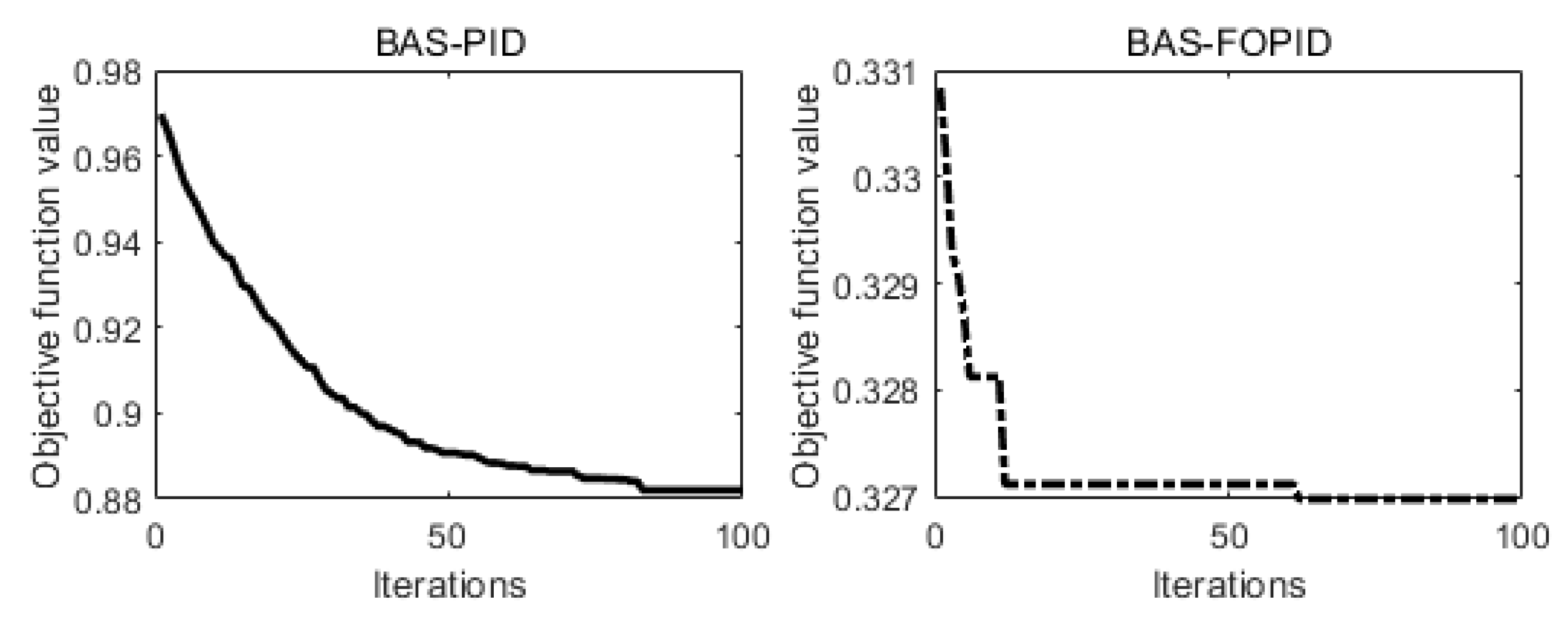
5.3. Beetle Antenna Search Algorithm
5.4. Parameter Adjustment Process and Results
6. Performance Simulation Analysis of Complete Vehicle Suspension System
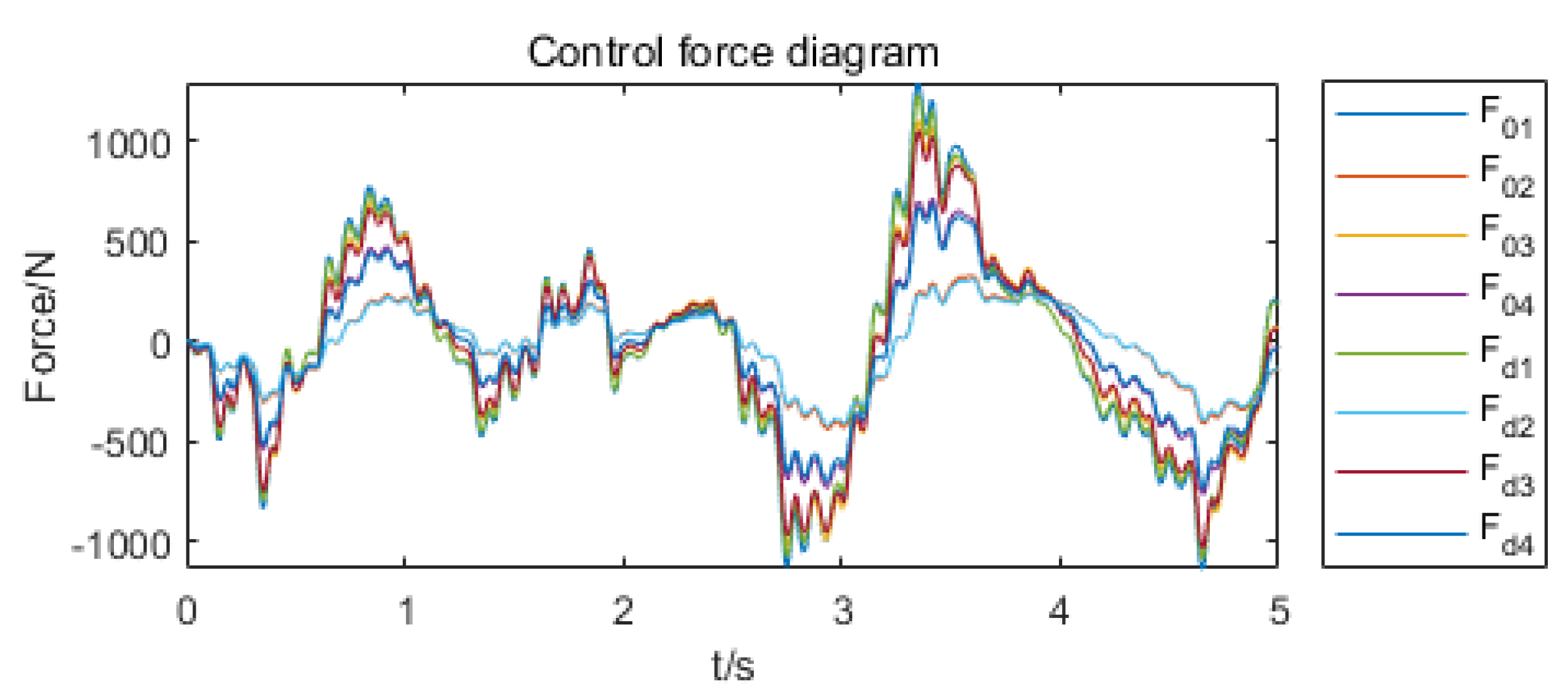
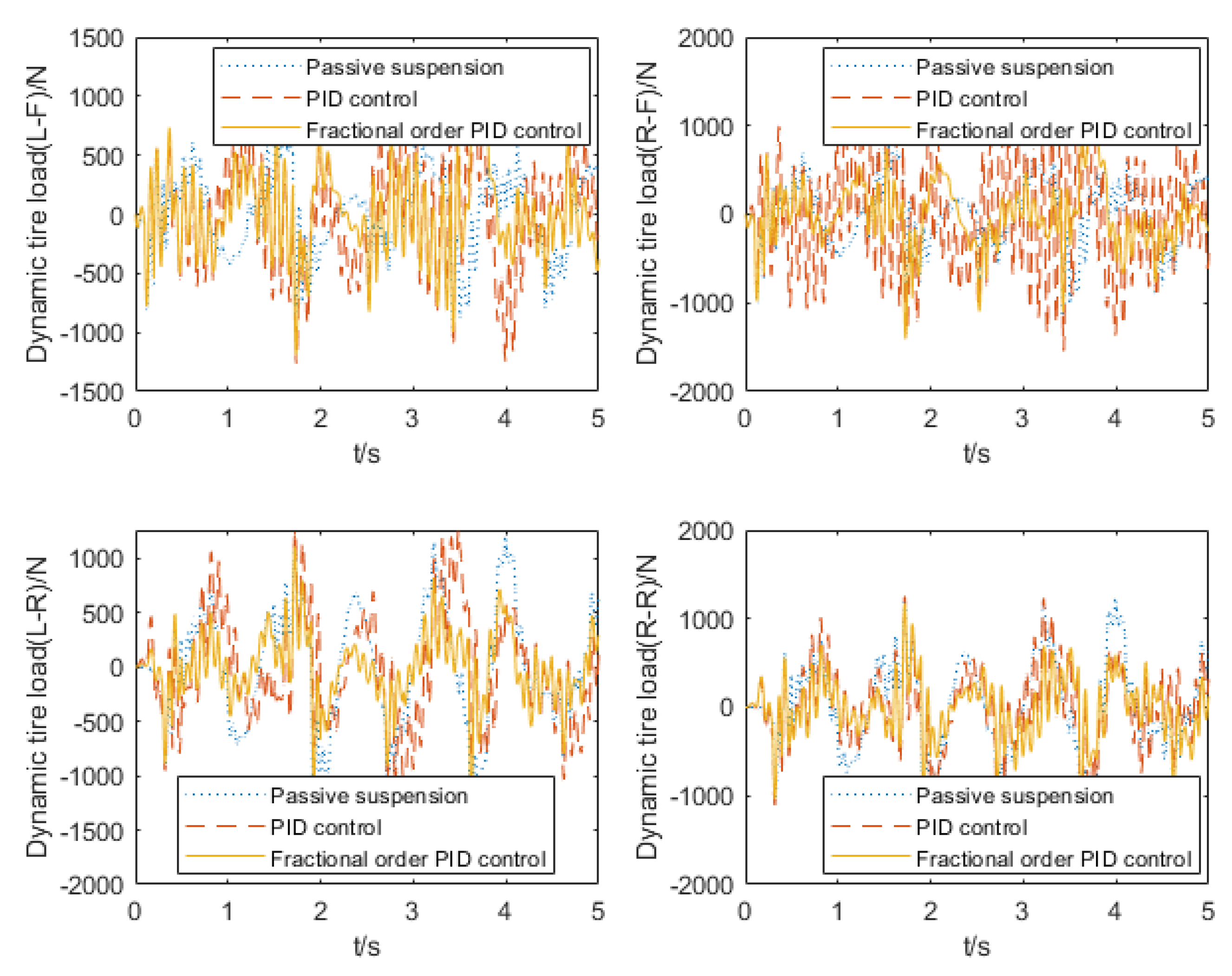
6.1. Actuator Control Force Simulation Analysis
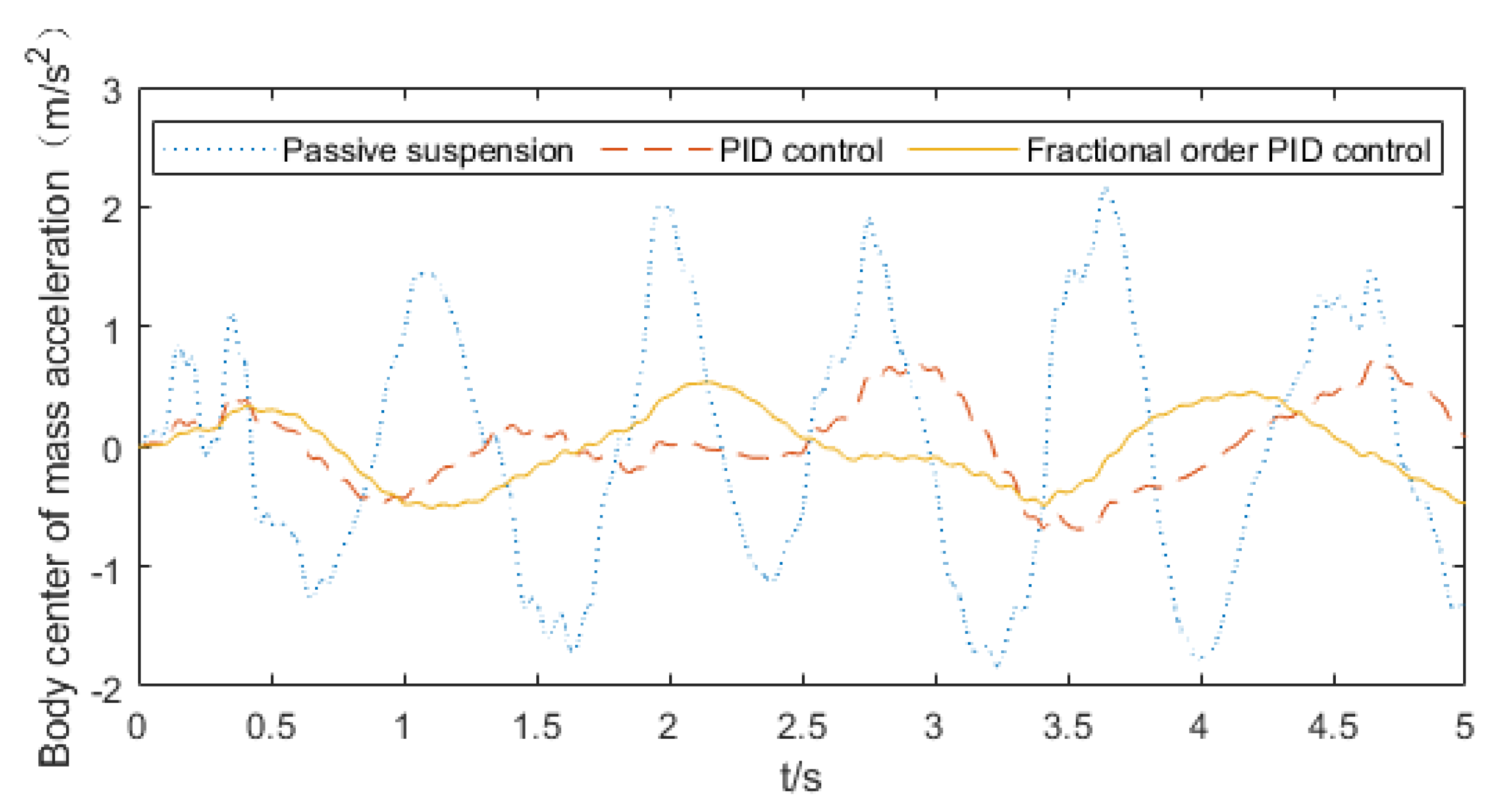
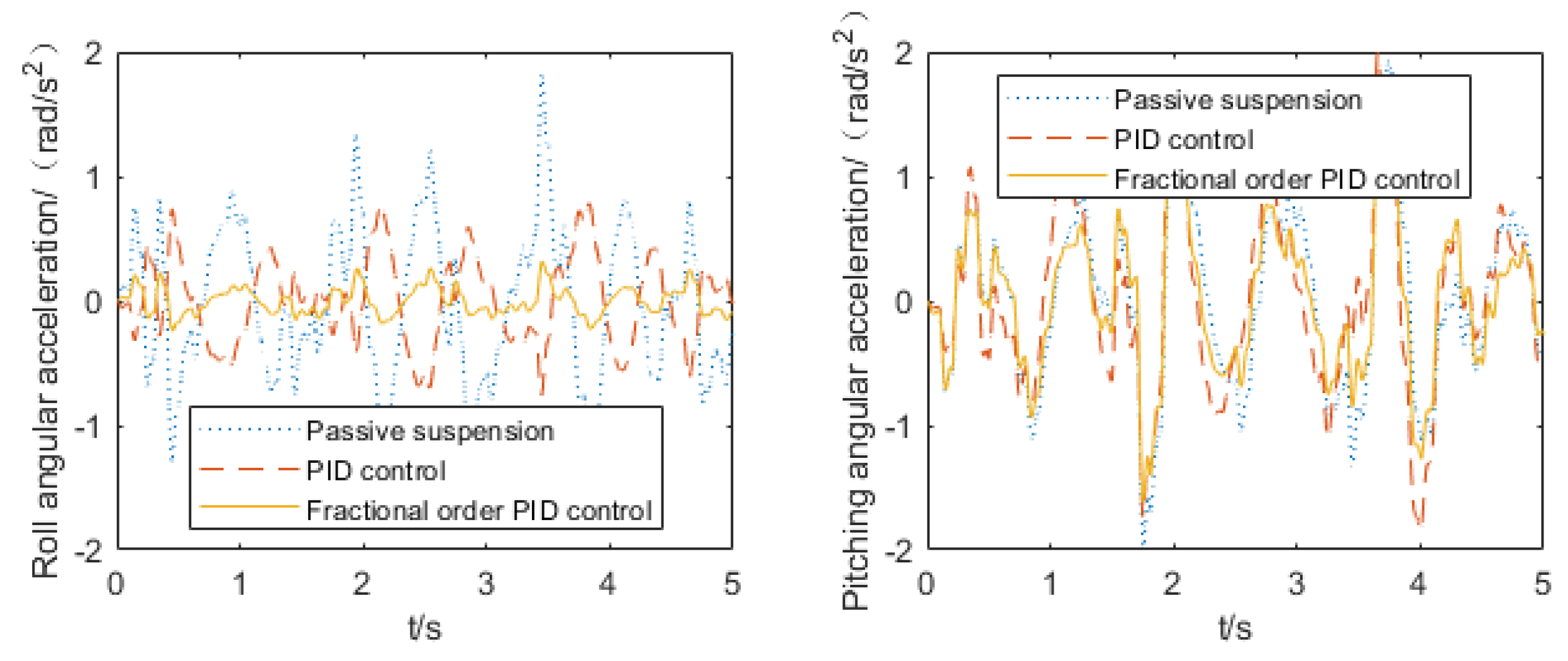
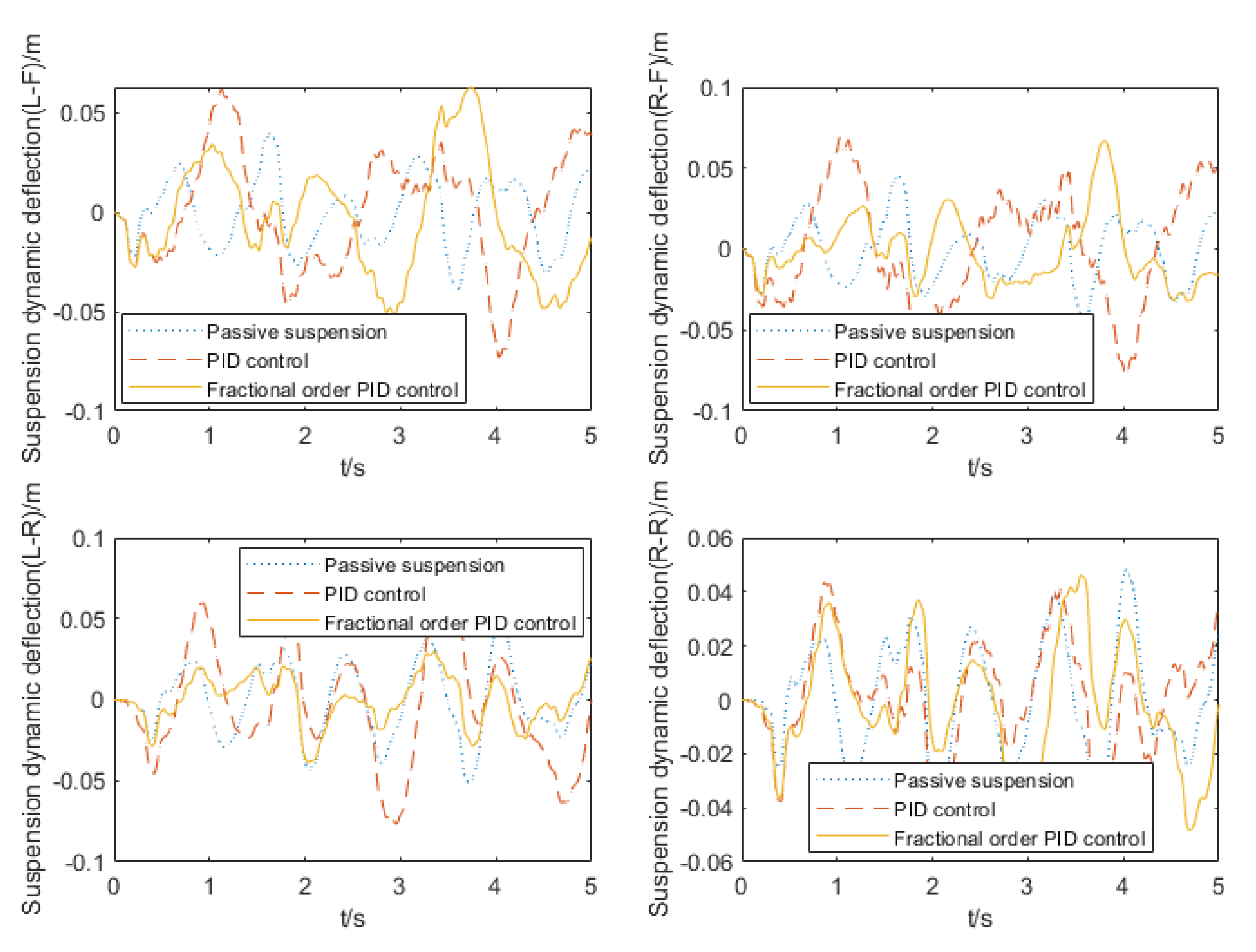
6.2. Simulation Analysis of Suspension System Vibration Damping Performance
7. Conclusions
- The electromagnetic torque constant of the energy regenerative motor was obtained through the energy regenerative test and the calculation of the formula, which provides a method for measuring the electromagnetic torque constant of the energy regenerative motor.
- The digital implementation method of the fractional order PID control circuit for motor current was proposed, which provides a way for the practical application of fractional order PID control in engineering. The feasibility of the ball screw type energy regenerative actuator, and the superiority of the designed fractional order PID control circuit over the PID control circuit, were verified through simulation and test of the actuator control circuit.
- The objective function optimization results showed that the BAS algorithm can effectively optimize the parameters of the PID controller and the fractional order PID controller for active suspension control, and the speed and effect of the fractional order PID controller were better than those of the PID controller.
- The vehicle suspension system dynamics model was established, and the PID controller and the fractional order PID controller were used for active control of the vehicle. The control results showed that both the PID controller and the fractional order PID controller could optimize the driving smoothness to a certain extent, and the fractional order PID controller had a better optimization effect. Optimization of acceleration of pitching angle and acceleration of roll angle was a problem not involved in the 1/4 suspension active control. Under PID control, the front suspension system had a certain degree of deterioration of tire dynamic load, and the rear suspension system achieved a certain degree of optimization. Each tire dynamic load was optimized under fractional order PID control, due to the coupling of each performance index of the suspension, leading to active control of the fractional order PID controller, suppressing increase to a certain extent, and further demonstrating the superiority of the fractional order PID controller compared with the PID controller in dealing with complex control objects.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fu, B.; Rocco, L.G.; Rickard, P.; Sebastian, S.; Stefano, B.; Roger, G. Active suspension in railway vehicles: A literature survey. Railw. Eng. Sci. 2020, 28, 3–35. [Google Scholar] [CrossRef] [Green Version]
- Khalid, E.M.; Fouad, G.; Fatima-Zahra, C. Adaptive Backstepping Control Design for Semi-Active Suspension of Half-Vehicle with Magnetorheological Damper. IEEE/CAA J. Autom. Sin. 2021, 8, 582–596. [Google Scholar] [CrossRef]
- Li, W.F.; Xie, Z.C.; Cao, Y.C.; Wong, P.K.; Zhao, J. Sampled-Data Asynchronous Fuzzy Output Feedback Control for Active Suspension Systems in Restricted Frequency Domain. IEEE/CAA J. Autom. Sin. 2021, 8, 1052–1066. [Google Scholar] [CrossRef]
- Yashar, M.; Alireza, A.; Ibrahim, B.K.; Afef, F. Tube-based Model Reference Adaptive Control for Vibration Suppression of Active Suspension Systems. IEEE/CAA J. Autom. Sin. 2022, 9, 728–731. [Google Scholar] [CrossRef]
- Chen, S.A.; Li, X.; Zhao, L.J. Development of a control method for an electromagnetic semi-active suspension reclaiming energy with varying charge voltage in steps. Int. J. Automot. Technol. 2015, 16, 765–773. [Google Scholar] [CrossRef]
- Huang, K.; Yu, F.; Zhang, Y. Active controller design for an electromagnetic energy-regenerative suspension. Int. J. Automot. Technol. 2011, 12, 877–885. [Google Scholar] [CrossRef]
- Amini, A.; Ekici, Ö.; Yakut, K. Experimental Study of Regenerative Rotational Damper in Low Frequencies. Int. J. Automot. Technol. 2020, 21, 83–90. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, H.; Guo, K.; Zhang, X.; Li, S. Electro-hydraulic damper for energy harvesting suspension: Modeling, prototyping and experimental validation. Appl. Energy 2017, 199, 1–12. [Google Scholar] [CrossRef]
- Zhu, S.; Shen, W.A.; Xu, Y.L. Linear electromagnetic devices for vibration damping and energy harvesting: Modeling and testing. Eng. Struct. 2012, 34, 198–212. [Google Scholar] [CrossRef] [Green Version]
- Shin, S.S.; Kim, B.S.; Lee, D.W.; Kwon, S.J. Vehicle Dynamic Analysis for the Ball-Screw Type Energy Harvesting Damper System. Recent Adv. Electr. Eng. Relat. Sci. 2016, 415, 853–862. [Google Scholar] [CrossRef]
- Narwade, P.; Deshmukh, R.; Nagarkar, M. Modeling and Simulation of a Semi-active Vehicle Suspension system using PID Controller. IOP Conf. Ser. Mater. Sci. Eng. 2020, 1004, 012003. [Google Scholar] [CrossRef]
- Nagarkar, M.P.; Bhalerao, Y.J.; Vikhe Patil, G.J. GA-based multi-objective optimization of active nonlinear quarter car suspension system—PID and fuzzy logic control. Int. J. Mech. Mater. Eng. 2018, 13, 10. [Google Scholar] [CrossRef]
- Wang, X.M. Microcontroller Control of Electric Motor, 4th ed.; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2015; pp. 84–85. [Google Scholar]
- Podlubny, I. Fractional-order systems and PIλDμ-controllers. IEEE Trans Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Huang, Y.F. The Ball Screw Type Feeder Can Shock Absorber Design and Dynamics Analysis. Master’s Thesis, Shenyang University of Technology, Shenyang, China, 2017. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD201801&filename=1017094149.nh (accessed on 6 July 2022).
- Jiang, X.; Li, S. BAS: Beetle Antennae Search Algorithm for Optimization Problems. Int. J. Robot. Control 2018, 1, 1–5. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Xu, B. Convergence analysis of beetle antennae search algorithm and its applications. Soft Comput. 2019, 25, 10595–10608. [Google Scholar] [CrossRef]
- Huba, M.; Vrancic, D.; Bistak, P. PID Control With Higher Order Derivative Degrees for IPDT Plant Models. IEEE Access 2021, 9, 2478–2495. [Google Scholar] [CrossRef]
- Yang, H.; Liu, J.; Li, M.; Zhang, X.; Liu, J.; Zhao, Y. Adaptive Kalman Filter with L2 Feedback Control for Active Suspension Using a Novel 9-DOF Semi-Vehicle Model. Actuators 2021, 10, 267. [Google Scholar] [CrossRef]
- Pakdelian, S. A compact and light-weight generator for backpack energy harvesting. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; Volume 1, pp. 1–8. [Google Scholar] [CrossRef]
- Li, Z.C. Structural Selection and Performance Simulation of Automotive Energy-Feeding Suspension. Master’s Thesis, Jilin University, Jilin, China, 2009. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD2009&filename=2009094256.nh (accessed on 6 July 2022).
- Ahamed, R.; Rashid, M.M.; Ferdaus, M.M. Design and modeling of energy generated magneto rheological damper. Korea-Aust. Rheol. J. 2016, 28, 67–74. [Google Scholar] [CrossRef]
- Liu, Q.Y. Research on Energy-Feeding Suspension Control Algorithm. Master’s Thesis, Jilin University, Jilin, China, 2019. Available online: https://kns.cnki.net/KCMS/detail/detail.aspx?dbname=CMFD201902&filename=1019155509.nh (accessed on 6 July 2022).
- Kou, F.R. Theory and Technology of Active Control of Automotive Vibration, 1st ed.; Huazhong University of Science and Technology Press: Wuhan, China, 2021; pp. 100–114. [Google Scholar]
- Kril, S.; Fedoryshyn, R.; Kril, O.; Pistun, Y. Investigation of Functional Diagrams of Step PID Controllers for Electric Actuators. Procedia Eng. 2015, 100, 1338–1347. [Google Scholar] [CrossRef] [Green Version]
- Li, X.J.; Liu, J.; Liu, Z.H. Research on BP Neural Network PID Control of Energy Regenerative Suspension. Mod. Manuf. Eng. 2020, 3, 60–65+135. [Google Scholar] [CrossRef]
- Pritesh, S.; Sudhir, A. Review of fractional PID controller. Mechatronics 2016, 38, 29–41. [Google Scholar] [CrossRef]
- Axtell, M.; Bise, M.E. Fractional calculus application in control systems. In Proceedings of the IEEE Conference on Aerospace and Electronics, Dayton, OH, USA, 21–25 May 1990; Volume 2, pp. 563–566. [Google Scholar] [CrossRef]
- Hamamci, S.E. Stabilization using fractional-order PI and PID controllers. Nonlinear Dyn. 2008, 51, 329–343. [Google Scholar] [CrossRef]
- Xue, D.Y.; Zhao, C.N.; Chen, Y.Q. A Modified Approximation Method of Fractional Order System. In Proceedings of the IEEE Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; pp. 1043–1048. [Google Scholar]
- Fan, Y.Q.; Shao, J.P.; Sun, G.T. Optimized PID Controller Based on Beetle Antennae Search Algorithm for Electro-Hydraulic Position Servo Control System. Sensors 2019, 19, 2727. [Google Scholar] [CrossRef] [PubMed] [Green Version]




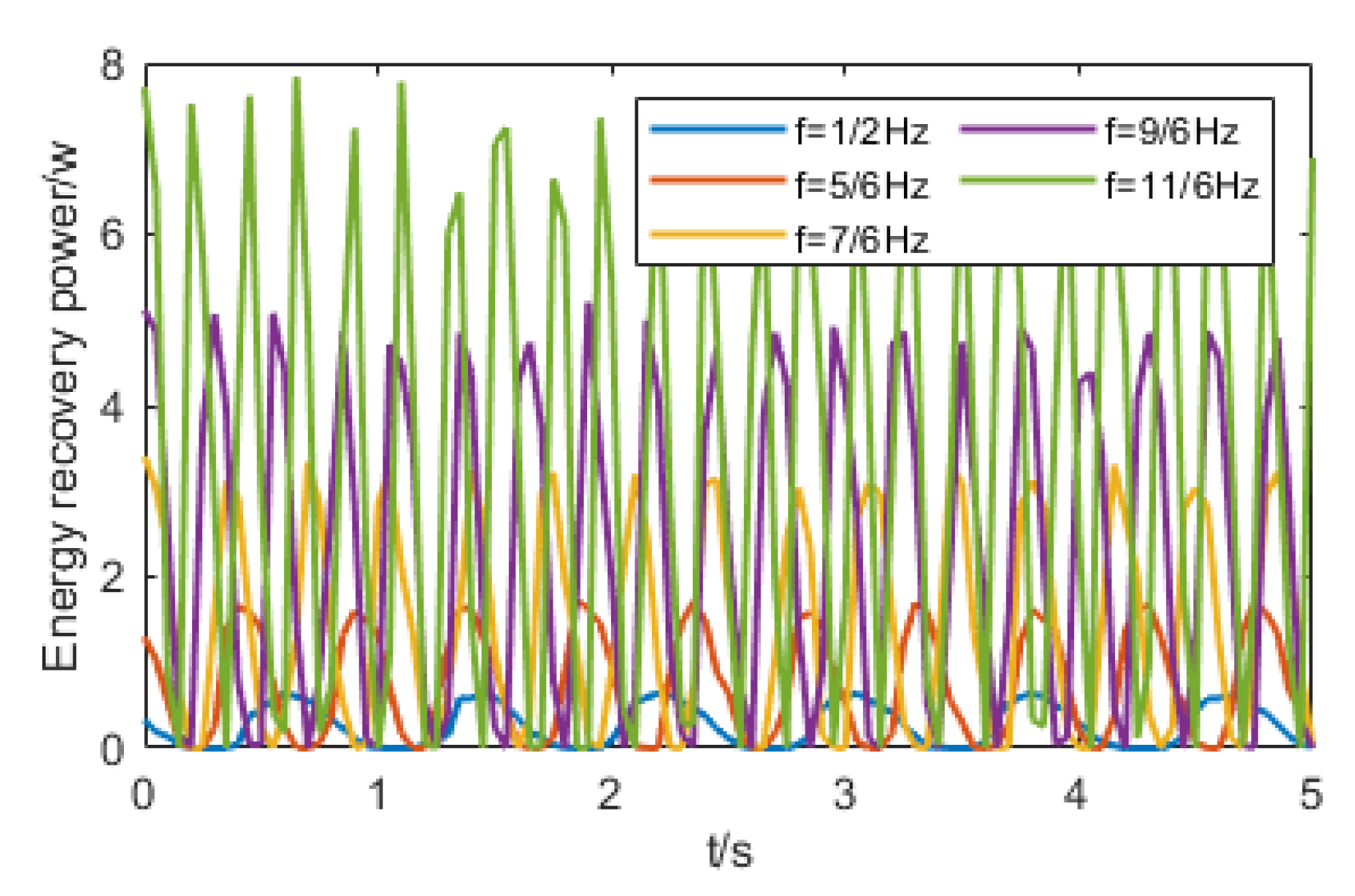

| Vibration Frequency/Hz | Mean Vibration Speed/ | Power Averages/W | Values of Electromagnetic Torque Constants |
|---|---|---|---|
| 1/2 | 0.0401 | 0.2637 | 0.2879 |
| 5/6 | 0.0672 | 0.7412 | 0.2884 |
| 7/6 | 0.0927 | 1.4553 | 0.2928 |
| 9/6 | 0.1204 | 2.3707 | 0.2878 |
| Parameter Name | Control Method | Parameter Name | Control Method | ||
|---|---|---|---|---|---|
| BAS-PID | BAS-FOPID | BAS-PID | BAS-FOPID | ||
| 807.4029 | 554.8152 | 540.1069 | 666.2706 | ||
| 936.2899 | 421.1504 | 83.3911 | 749.3380 | ||
| 228.4008 | 545.0502 | 64.5269 | 446.2735 | ||
| 1 | 0.4645 | 1 | 0.2909 | ||
| 1 | 0.1892 | 1 | 0.3609 | ||
| 788.5277 | 351.4805 | 521.3142 | 589.0160 | ||
| 164.5138 | 982.9772 | 93.6735 | 705.4344 | ||
| 444.9254 | 113.6506 | 151.8317 | 254.5784 | ||
| 1 | 0.1577 | 1 | 0.2135 | ||
| 1 | 0.2045 | 1 | 0.2033 | ||
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 1440 | 190,000 | ||
| 40 | 1.2 | ||
| 45 | 1.5 | ||
| 17,000 | 0.75 | ||
| 22,000 | 2440 | ||
| 1500 | 380 | ||
| 0.2885 | 30 | ||
| 0.3 | 0.02 |
| Performance Index | Control Method | ||
|---|---|---|---|
| Passive Suspension | PID Control | FOPID Control | |
| 1.0531 | 0.3409 | 0.2791 | |
| 0.5820 | 0.3321 | 0.1066 | |
| 0.7120 | 0.7120 | 0.5802 | |
| 0.0178 | 0.0288 | 0.0282 | |
| 0.0199 | 0.0342 | 0.0208 | |
| 0.0221 | 0.0367 | 0.0148 | |
| 0.0221 | 0.0231 | 0.0217 | |
| /N | 374.6207 | 444.1296 | 353.8659 |
| N | 427.0665 | 616.0492 | 390.4171 |
| N | 562.2558 | 526.5663 | 351.9963 |
| N | 576.0619 | 476.2702 | 376.7724 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Liu, J.; Liu, B.; Li, M. Fractional Order PID Control Based on Ball Screw Energy Regenerative Active Suspension. Actuators 2022, 11, 189. https://doi.org/10.3390/act11070189
Zhang J, Liu J, Liu B, Li M. Fractional Order PID Control Based on Ball Screw Energy Regenerative Active Suspension. Actuators. 2022; 11(7):189. https://doi.org/10.3390/act11070189
Chicago/Turabian StyleZhang, Jingming, Jiang Liu, Bilong Liu, and Min Li. 2022. "Fractional Order PID Control Based on Ball Screw Energy Regenerative Active Suspension" Actuators 11, no. 7: 189. https://doi.org/10.3390/act11070189
APA StyleZhang, J., Liu, J., Liu, B., & Li, M. (2022). Fractional Order PID Control Based on Ball Screw Energy Regenerative Active Suspension. Actuators, 11(7), 189. https://doi.org/10.3390/act11070189






