Analysis of the Notch Filter Insertion Position for Natural Frequency Vibration Suppression in a Magnetic Suspended Flywheel Energy Storage System
Abstract
:1. Introduction
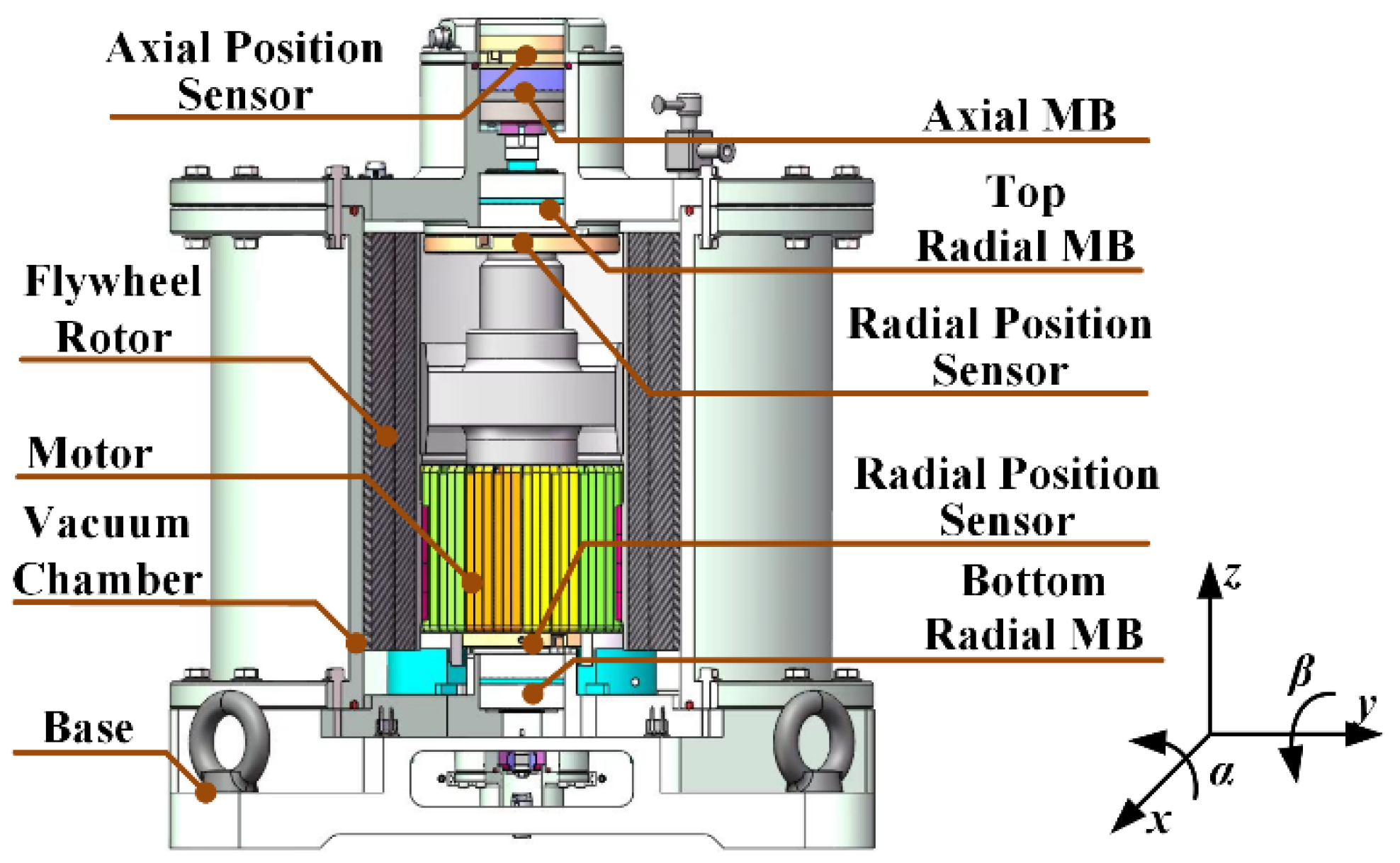
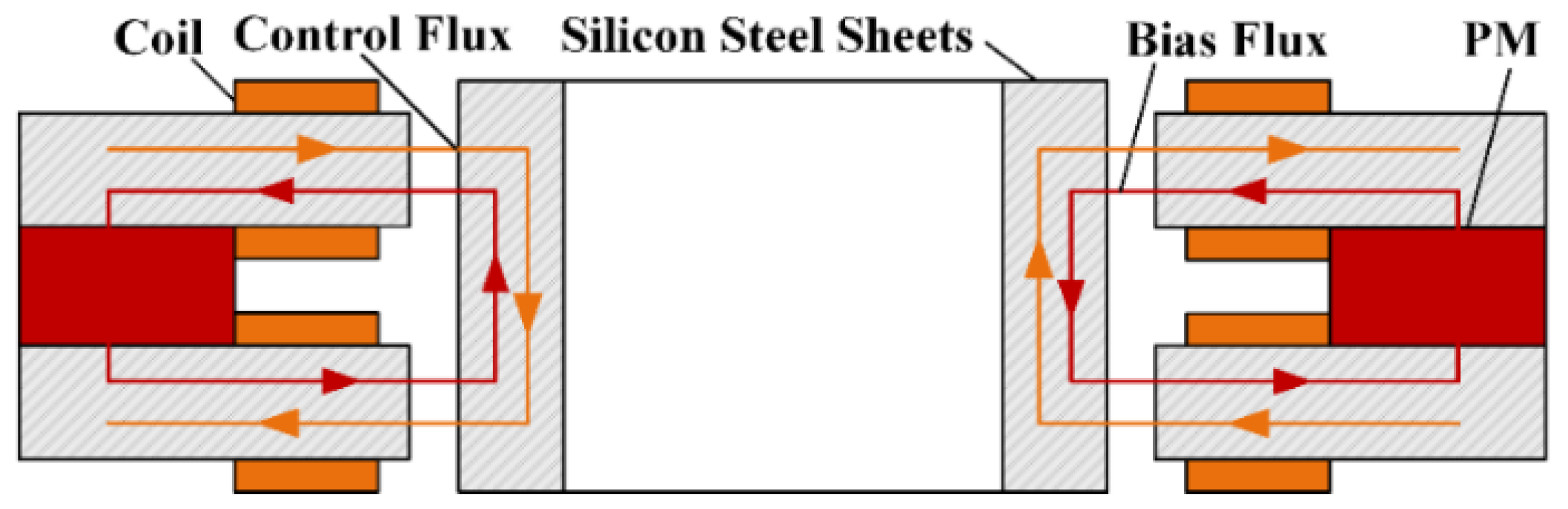
2. Structure of the FESS
3. Analysis of the Insertion Position of the Notch Filter
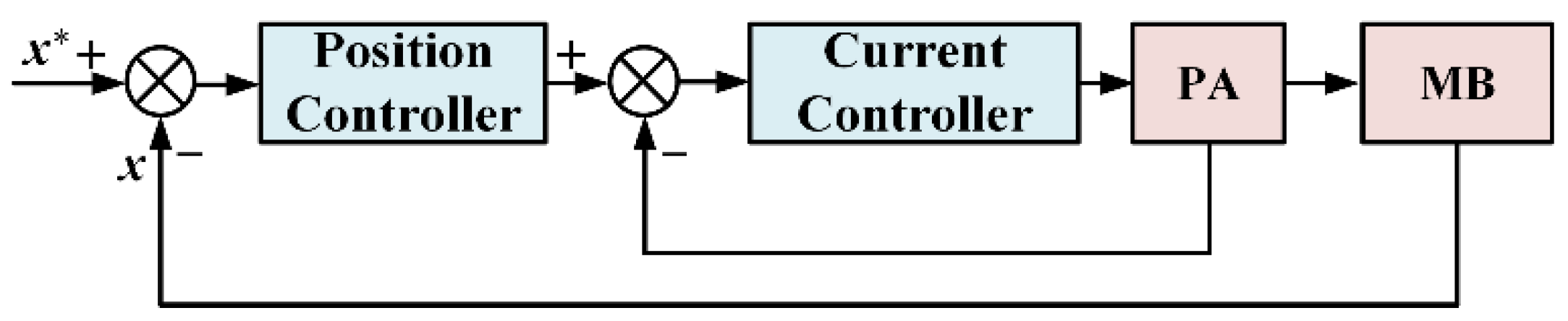
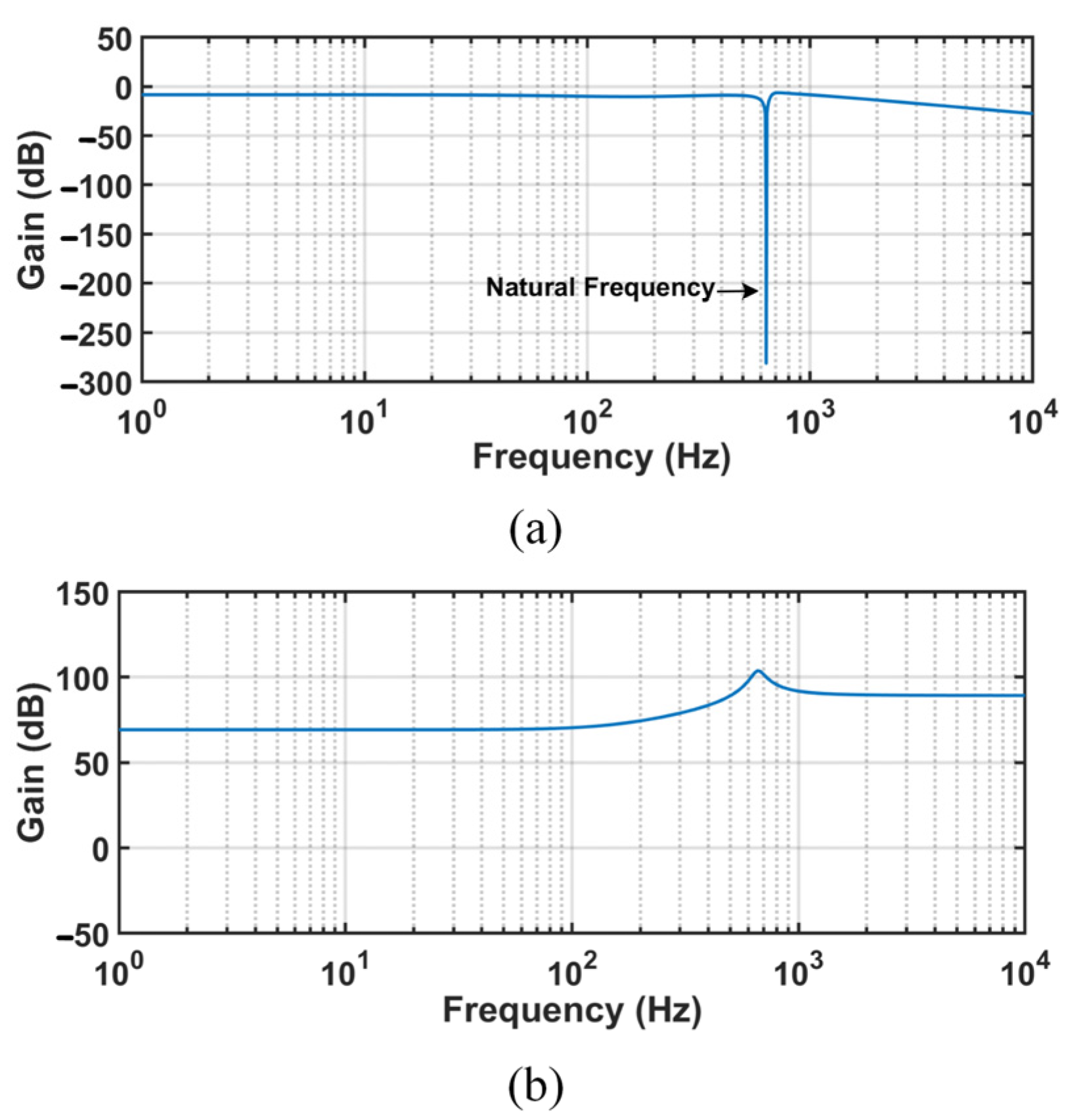
3.1. Model of the Magnetic Bearing Control System
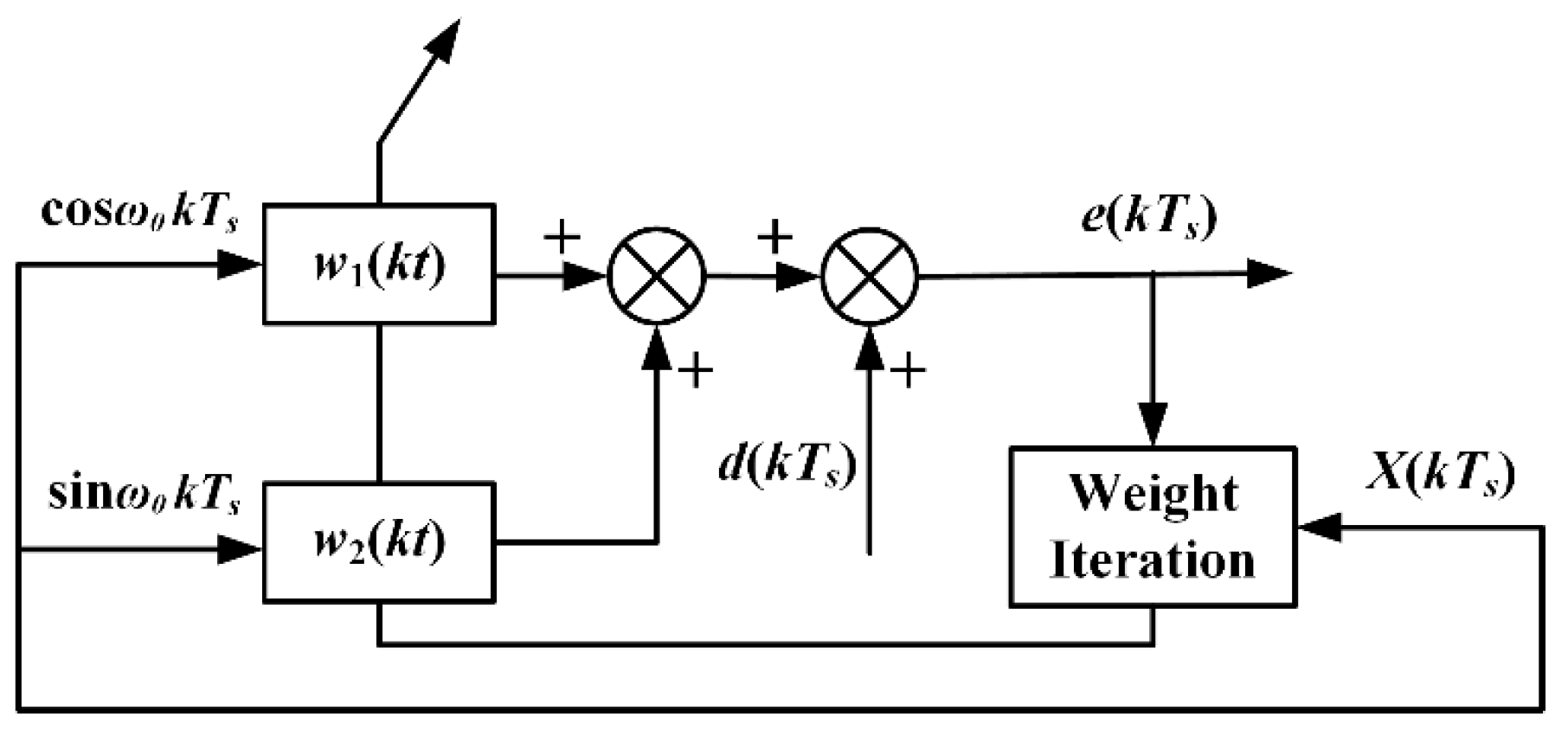
3.2. LMS Adaptive Notch Filter Algorithm
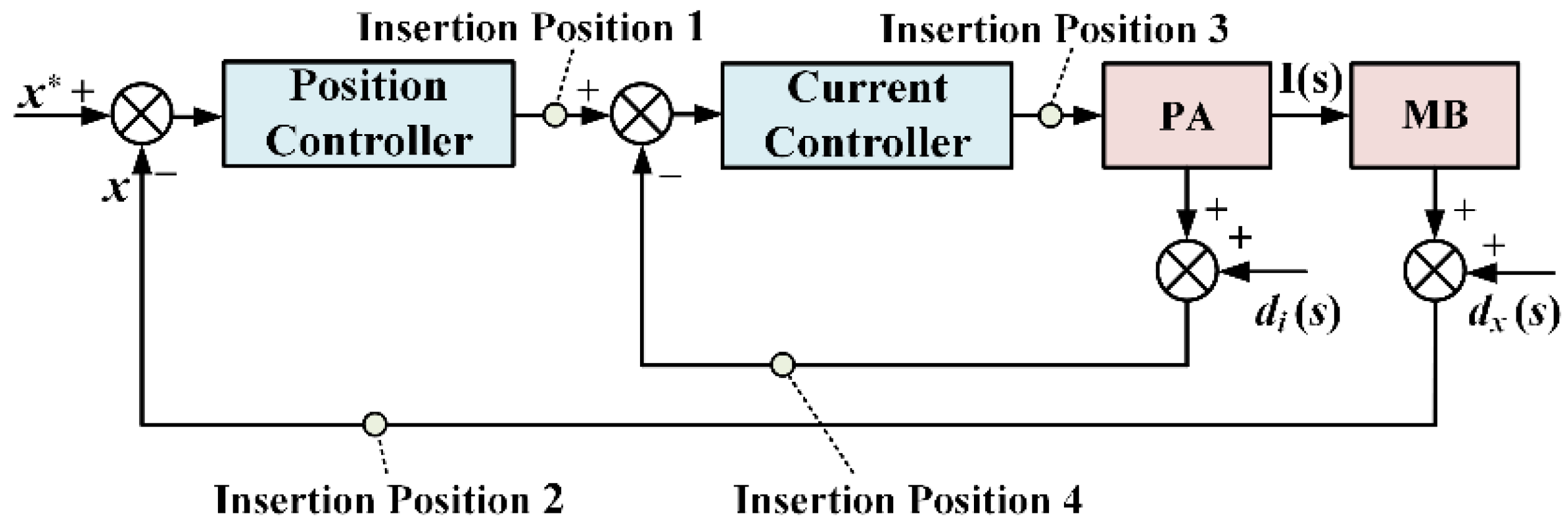
3.3. Insertion Position of the Notch Filter
4. Experimental Results
4.1. Experimental Platform
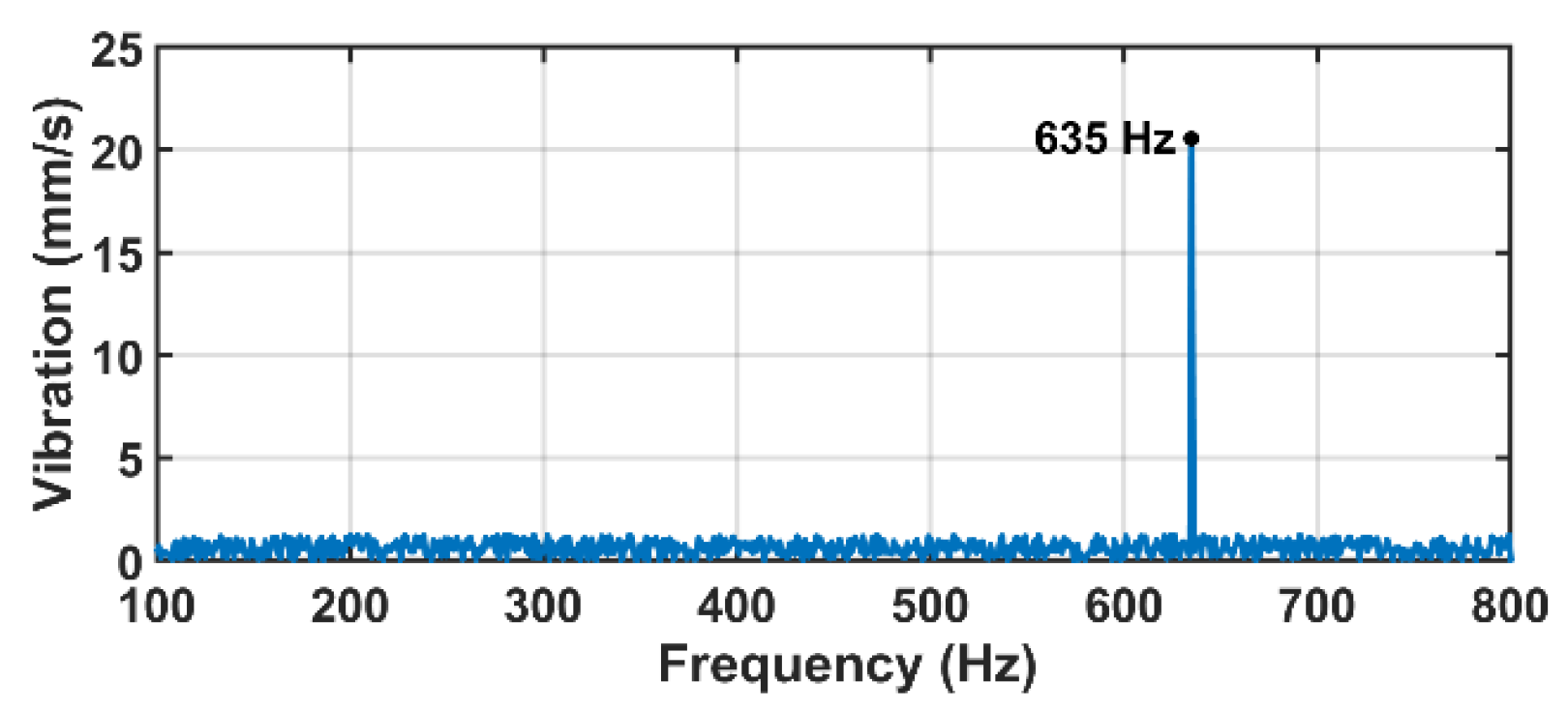
4.2. Experiment A: Test of the Natural Frequency of the Flywheel Rotor
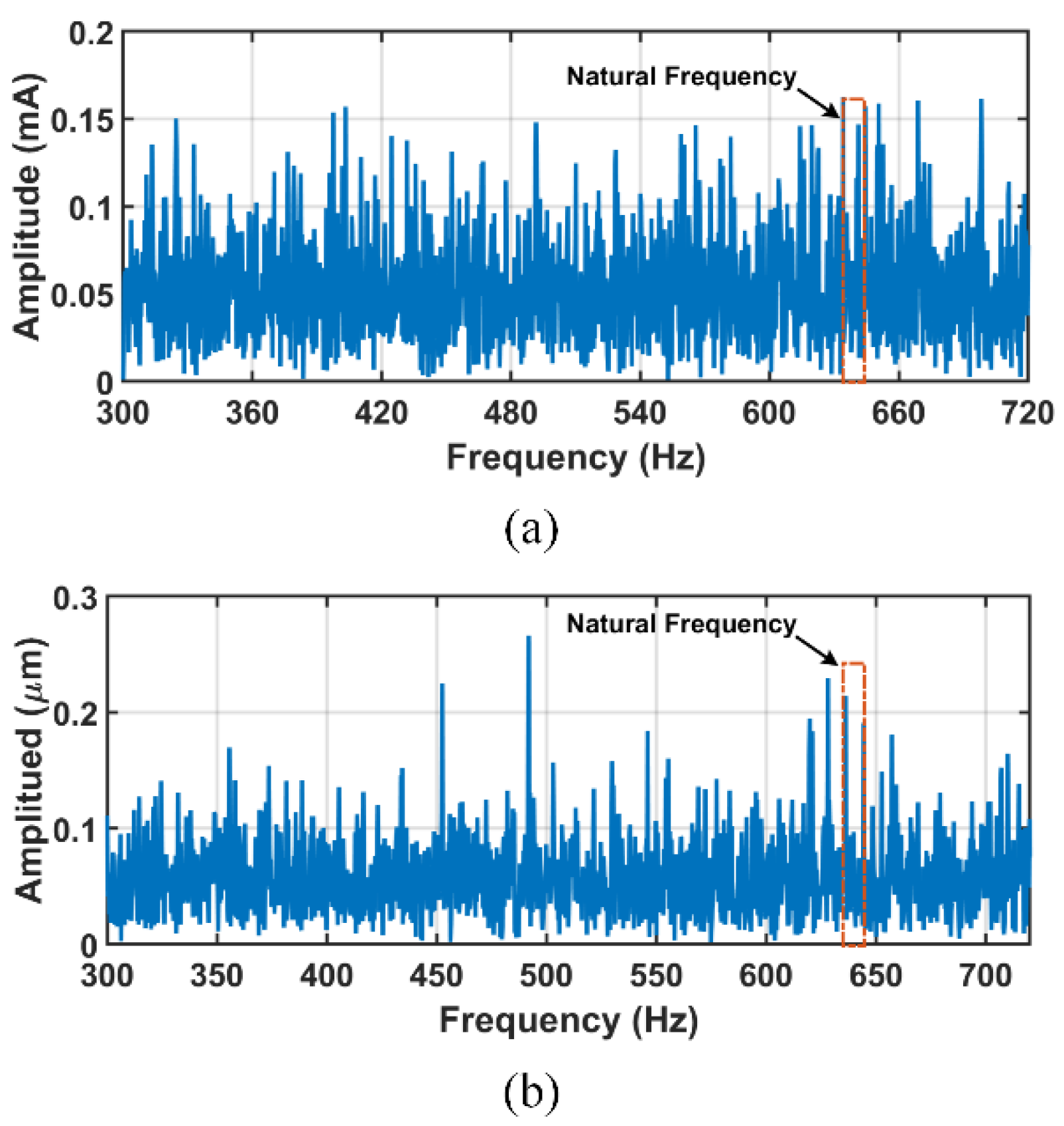
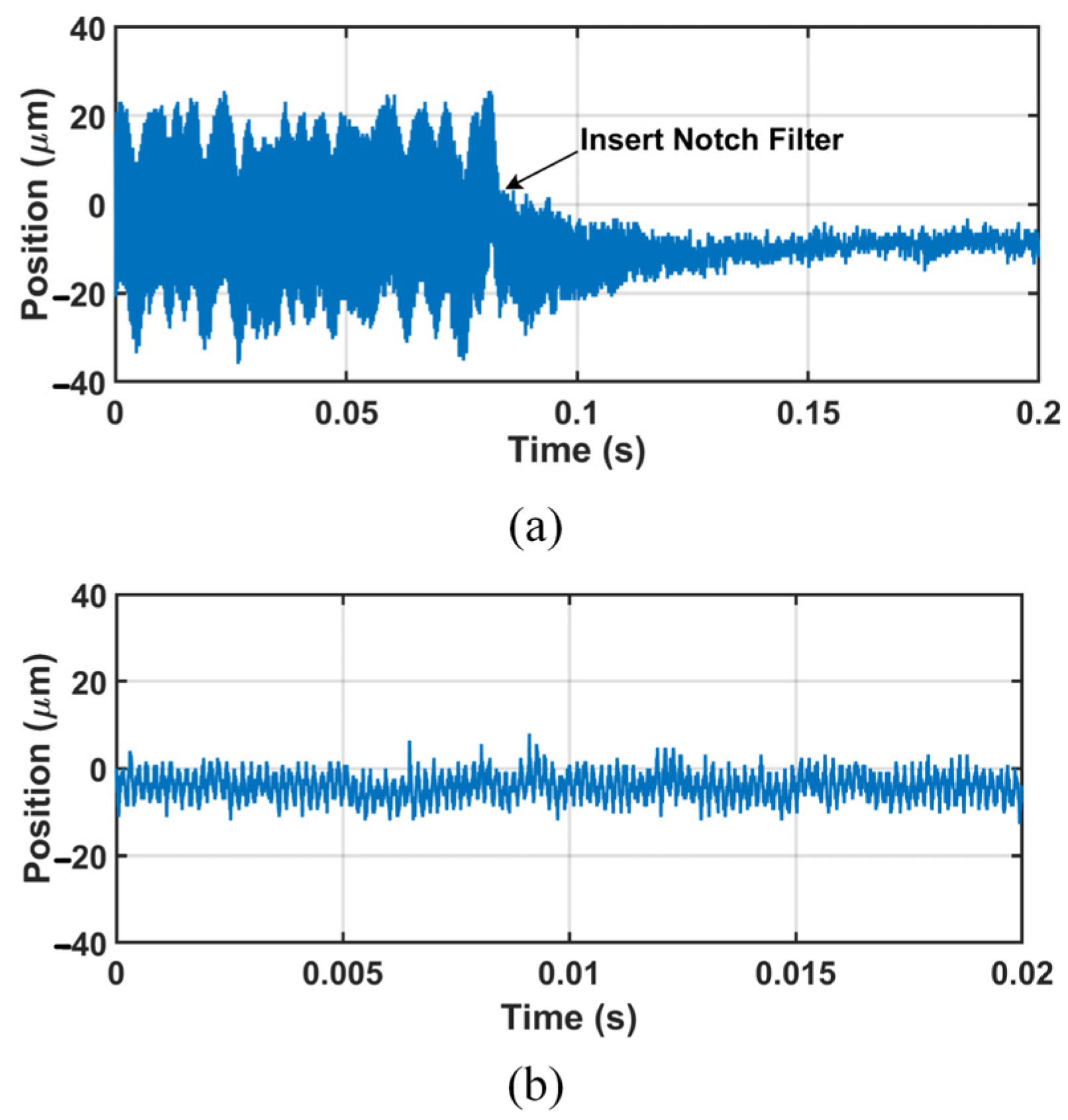
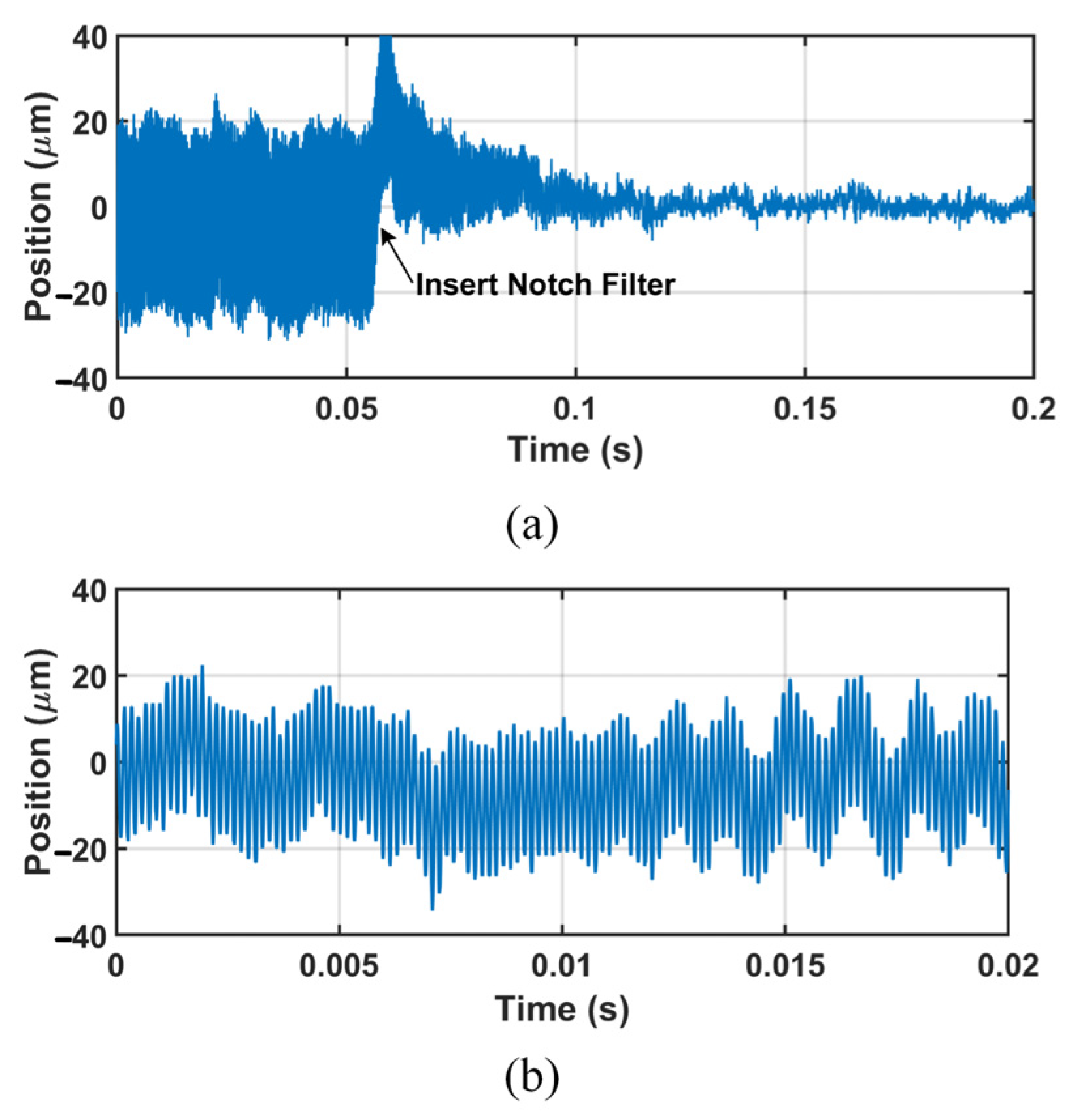
4.3. Experiment B: Position Responses of Different Insertion Positions
5. Conclusions
- (1)
- The vibration can be suppressed to some extent by inserting the notch filter into the forward and feedback path of the outer loop and the forward and feedback path of the inner loop.
- (2)
- When the notch filter is inserted into the forward and feedback path of the outer loop, the natural frequency noise of the position sensor can be filtered out; nevertheless, the natural frequency noise of the current sensor cannot be filtered out. When the notch filter is inserted into the feedback path of the inner loop, the natural frequency noise of the position sensor can be filtered out; nevertheless, the natural frequency noise of the current sensor cannot be filtered out.
- (3)
- When the notch filter is inserted into the forward path of the inner loop, the natural frequency noise of the position sensor and current sensor can be filtered out. Inserting the notch filter into the forward path of the inner loop is the most appropriate way to suppress the natural vibration.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Komori, M.; Kato, H.; Asami, K.-I. Suspension-Type of Flywheel Energy Storage System Using High Tc Superconducting Magnetic Bearing (SMB). Actuators 2022, 11, 215. [Google Scholar] [CrossRef]
- Hu, H.; Liu, K.; Wei, J.; Wang, H. Multirate model predictive current control of a permanent magnet synchronous machine for a flywheel energy storage system. Energy Rep. 2022, 8, 11579–11591. [Google Scholar] [CrossRef]
- Shadnam Zarbil, M.; Vahedi, A.; Azizi Moghaddam, H.; Khlyupin, P.A. Design and Sizing of Electric Bus Flash Charger Based on a Flywheel Energy Storage System: A Case Study. Energies 2022, 15, 8032. [Google Scholar] [CrossRef]
- Farrokhzad Ershad, N.; Tafazzoli Mehrjardi, R.; Ehsani, M. High-Performance 4WD Electric Powertrain with Flywheel Kinetic Energy Recovery. IEEE Trans. Power Electron. 2021, 36, 772–784. [Google Scholar] [CrossRef]
- Masouleh, M.I.; Limebeer, D.J.N. Fuel Minimization for a Vehicle Equipped With a Flywheel and Battery on a Three-Dimensional Track. IEEE Trans. Intell. Veh. 2017, 2, 161–174. [Google Scholar] [CrossRef]
- Li, J.; Han, Y.; Li, S. Flywheel-Based Boom Energy Recovery System for Hydraulic Excavators with Load Sensing System. Actuators 2021, 10, 126. [Google Scholar] [CrossRef]
- Hutchinson, A.; Gladwin, D.T. Optimisation of a wind power site through utilisation of flywheel energy storage technology. Energy Rep. 2020, 6, 259–265. [Google Scholar] [CrossRef]
- Adhikari, S.; Karki, R.; Piya, P. Recovery Risk Mitigation of Wind Integrated Bulk Power System With Flywheel Energy Storage. IEEE Trans. Power Syst. 2019, 34, 3484–3493. [Google Scholar] [CrossRef]
- Ghanaatian, M.; Lotfifard, S. Control of Flywheel Energy Storage Systems in the Presence of Uncertainties. IEEE Trans. Sustain. Energy 2019, 10, 36–45. [Google Scholar] [CrossRef]
- Mukoyama, S.; Nakao, K.; Sakamoto, H.; Matsuoka, T.; Nagashima, K.; Ogata, M.; Yamashita, T.; Miyazaki, Y.; Miyazaki, K.; Maeda, T.; et al. Development of Superconducting Magnetic Bearing for 300 kW Flywheel Energy Storage System. IEEE Trans. Appl. Supercond. 2017, 27, 3600804. [Google Scholar] [CrossRef]
- Werfel, F.N.; Floegel-Delor, U.; Riedel, T.; Rothfeld, R.; Wippich, D.; Goebel, B.; Reiner, G.; Wehlau, N. A Compact HTS 5 kWh/250 kW Flywheel Energy Storage System. IEEE Trans. Appl. Supercond. 2007, 17, 2138–2141. [Google Scholar] [CrossRef]
- Gengji, W.; Ping, W. Rotor Loss Analysis of PMSM in Flywheel Energy Storage System as Uninterruptable Power Supply. IEEE Trans. Appl. Supercond. 2016, 26, 0609905. [Google Scholar] [CrossRef]
- Nagorny, A.S.; Dravid, N.V.; Jansen, R.H.; Kenny, B.H. Design Aspects of a High Speed Permanent Magnet Synchronous Motor/Generator for Flywheel Applications. In Proceedings of the IEEE International Conference on Electric Machines & Drives, San Antonio, TX, USA, 15 May 2005. [Google Scholar]
- Wang, P.; Gu, T.; Sun, B.; Liu, R.; Zhang, T.; Yang, J. Design and Performance Analysis of Super Highspeed Flywheel Rotor for Electric Vehicle. World Electr. Veh. J. 2022, 13, 147. [Google Scholar] [CrossRef]
- Kale, V.; Secanell, M. A comparative study between optimal metal and composite rotors for flywheel energy storage systems. Energy Rep. 2018, 4, 576–585. [Google Scholar] [CrossRef]
- Wang, H.; Wu, Z.; Liu, K.; Wei, J.; Hu, H. Modeling and Control Strategies of a Novel Axial Hybrid Magnetic Bearing for Flywheel Energy Storage System. IEEE/ASME Trans. Mechatron. 2022, 27, 3819–3829. [Google Scholar] [CrossRef]
- Hu, H.; Liu, K.; Wang, H.; Wei, J. A Wide Bandwidth GaN Switching Power Amplifier of Active Magnetic Bearing for a Flywheel Energy Storage System. IEEE Trans. Power Electron. 2022, 38, 2589–2605. [Google Scholar] [CrossRef]
- Wu, D.; Zhang, D.; Han, Q.; Wang, H. Study on nonlinear force transmissibility of flywheel rotor system considering periodic base motions. J. Sound Vib. 2022, 529, 116953. [Google Scholar] [CrossRef]
- Herzog, R.; Buhler, P.; Gahler, C.; Larsonneur, R. Unbalance compensation using generalized notch filters in the multivariable feedback of magnetic bearings. IEEE Trans. Control. Syst. Technol. 1996, 4, 580–586. [Google Scholar] [CrossRef]
- Zheng, S.; Han, B.; Feng, R.; Jiang, Y. Vibration Suppression Control for AMB-Supported Motor Driveline System Using Synchronous Rotating Frame Transformation. IEEE Trans. Ind. Electron. 2015, 62, 5700–5708. [Google Scholar] [CrossRef]
- Cui, P.; Liu, Z.; Xu, H.; Zheng, S.; Han, B.; Zhang, D. Harmonic Vibration Force Suppression of Magnetically Suspended Rotor With Frequency-Domain Adaptive LMS. IEEE Sens. J. 2020, 20, 1166–1175. [Google Scholar] [CrossRef]
- Li, J.; Liu, G.; Zheng, S.; Cui, P.; Chen, Q. Micro-Jitter Control of Magnetically Suspended Control Moment Gyro Using Adaptive LMS Algorithm. IEEE/ASME Trans. Mechatron. 2022, 27, 327–335. [Google Scholar] [CrossRef]
- Chen, Q.; Liu, G.; Han, B. Unbalance vibration suppression for AMBs system using adaptive notch filter. Mech. Syst. Signal Process. 2017, 93, 136–150. [Google Scholar] [CrossRef]
- Cui, P.; Li, S.; Wang, Q.; Gao, Q.; Cui, J.; Zhang, H. Harmonic Current Suppression of an AMB Rotor System at Variable Rotation Speed Based on Multiple Phase-Shift Notch Filters. IEEE Trans. Ind. Electron. 2016, 63, 6962–6969. [Google Scholar] [CrossRef]
- He, J.; Deng, Z.; Peng, C.; Li, K. Reduction of the High-Speed Magnetically Suspended Centrifugal Compressor Harmonic Vibration Using Cascaded Phase-Shifted Notch Filters. IEEE Sens. J. 2021, 21, 1315–1323. [Google Scholar] [CrossRef]
- Moir Tom, J. Rudiments of Signal Processing and Systems; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]







| Symbol | Description | Value |
|---|---|---|
| VDC | Maximum voltage | 500 V |
| Pr | Maximum power | 500 kW |
| Em | Stored energy | 1.2 kWh |
| ωm | Maximum design speed | 27,000 rpm |
| Mr | Rotor weight | 58.0 kg |
| Sm | Prototype Size | Φ500 × 590 mm |
| Symbol | Description | Value |
|---|---|---|
| ω0 | Center frequency | 635 Hz |
| μ | Step length | 0.01 |
| fs | Sampling frequency | 5 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Wei, J.; Wang, H.; Xiao, P.; Zeng, Y.; Liu, K. Analysis of the Notch Filter Insertion Position for Natural Frequency Vibration Suppression in a Magnetic Suspended Flywheel Energy Storage System. Actuators 2023, 12, 22. https://doi.org/10.3390/act12010022
Hu H, Wei J, Wang H, Xiao P, Zeng Y, Liu K. Analysis of the Notch Filter Insertion Position for Natural Frequency Vibration Suppression in a Magnetic Suspended Flywheel Energy Storage System. Actuators. 2023; 12(1):22. https://doi.org/10.3390/act12010022
Chicago/Turabian StyleHu, Hongjin, Jingbo Wei, Haoze Wang, Peng Xiao, Yuan Zeng, and Kun Liu. 2023. "Analysis of the Notch Filter Insertion Position for Natural Frequency Vibration Suppression in a Magnetic Suspended Flywheel Energy Storage System" Actuators 12, no. 1: 22. https://doi.org/10.3390/act12010022
APA StyleHu, H., Wei, J., Wang, H., Xiao, P., Zeng, Y., & Liu, K. (2023). Analysis of the Notch Filter Insertion Position for Natural Frequency Vibration Suppression in a Magnetic Suspended Flywheel Energy Storage System. Actuators, 12(1), 22. https://doi.org/10.3390/act12010022






