Flexoelectric Effect of Ferroelectric Materials and Its Applications
Abstract
:1. Introduction
2. Measurement Methods of Flexoelectric Coefficients
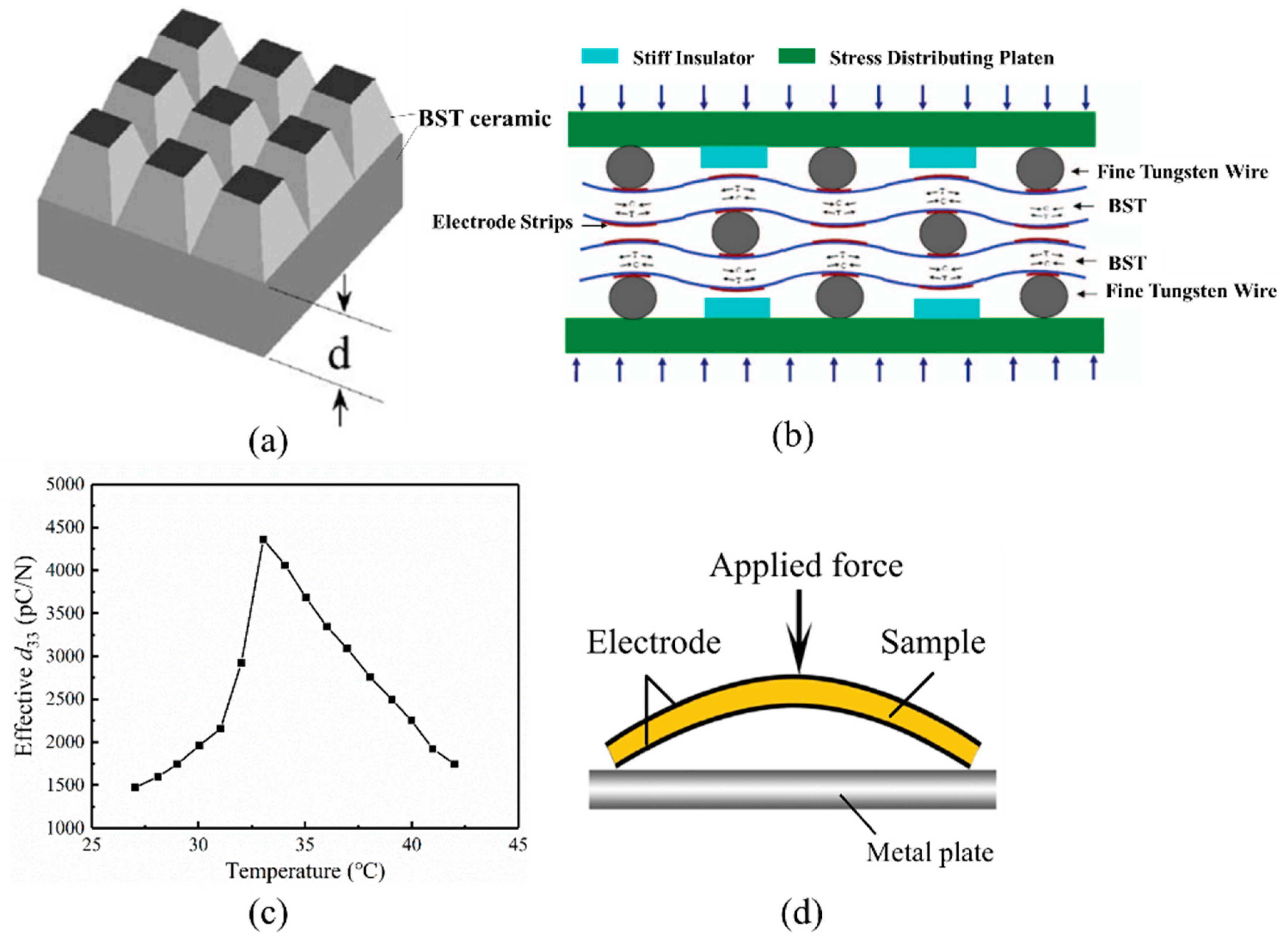
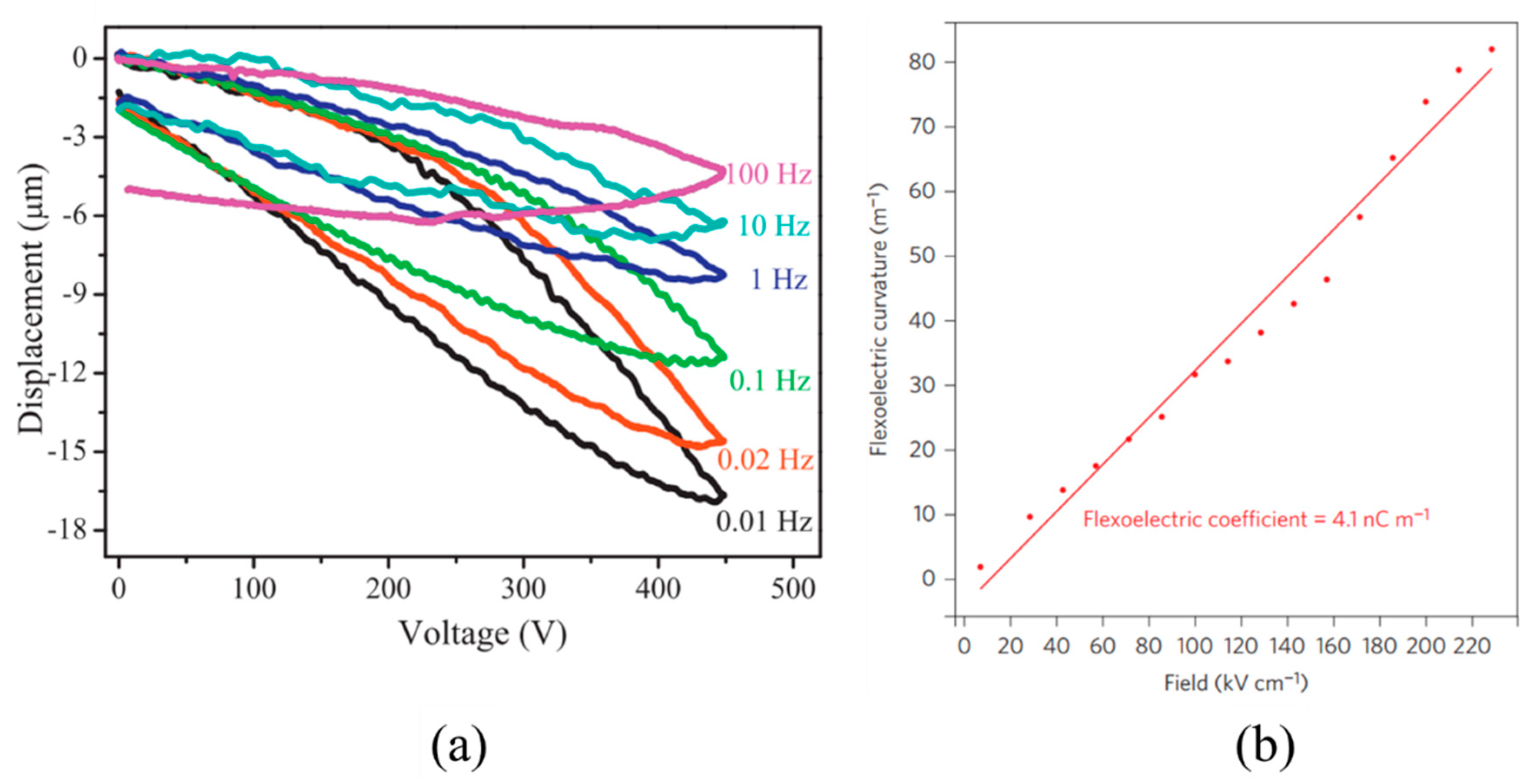
2.1. Cantilever Bending (CB)
2.2. Four-Point Bending (4PB)
2.3. Three-Point Bending (3PB)
2.4. Point-Ring Method (PR)
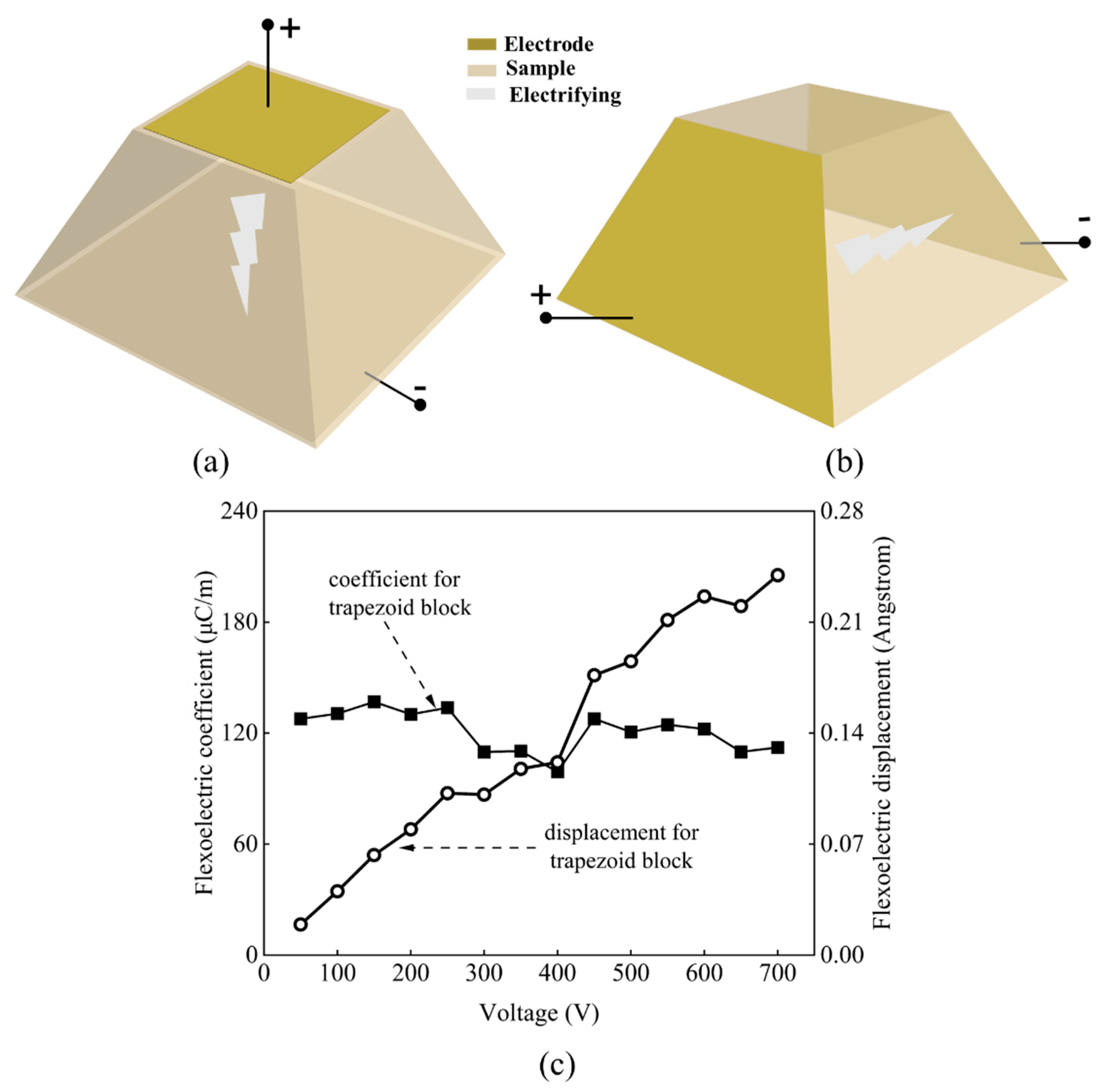
2.5. Pyramid Compression (PC)
2.6. Shock-Wave Method
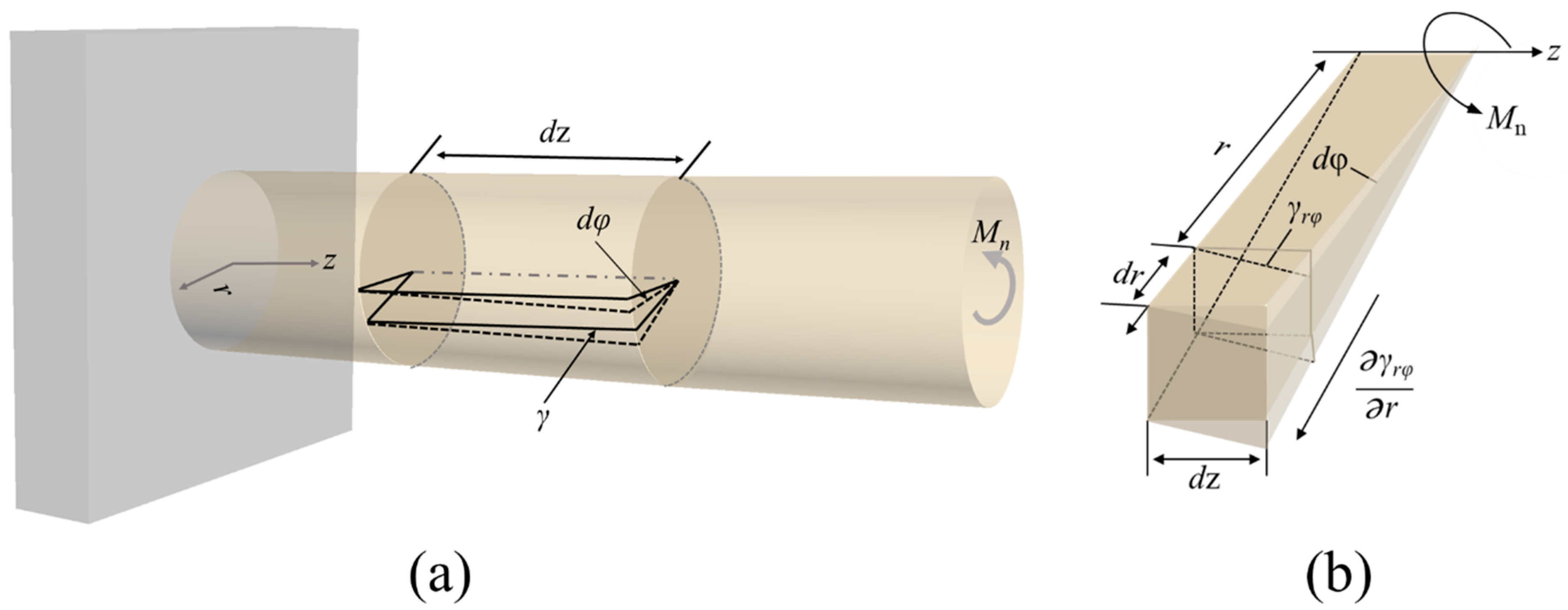
2.7. Cylinder Twisting (CT)
2.8. Converse Flexoelectric Effect (CFE)
3. The Magnitude of the Flexoelectric Coefficient
4. Theoretical Studies of Measured Flexoelectric Coefficients of Ferroelectric Materials
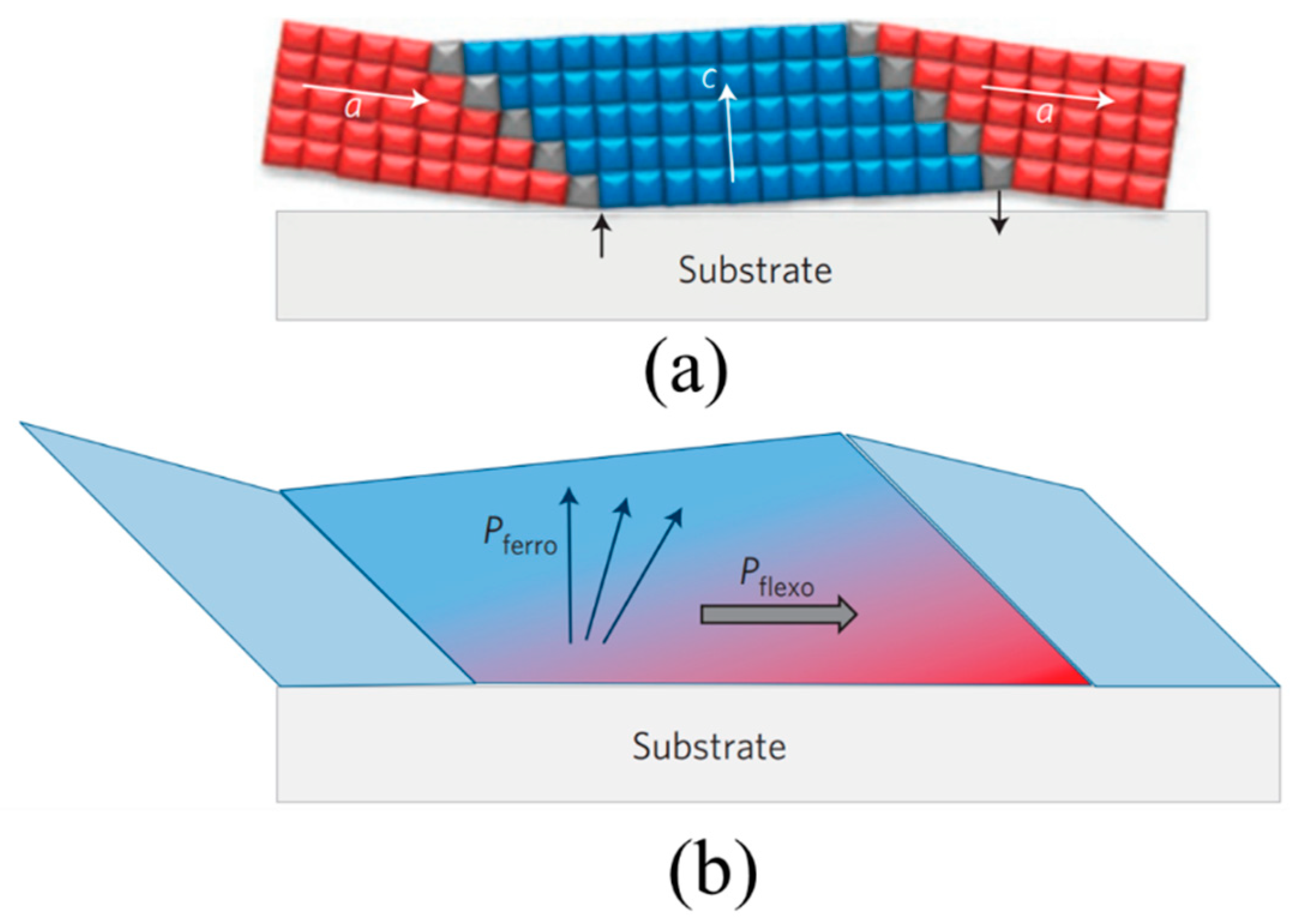
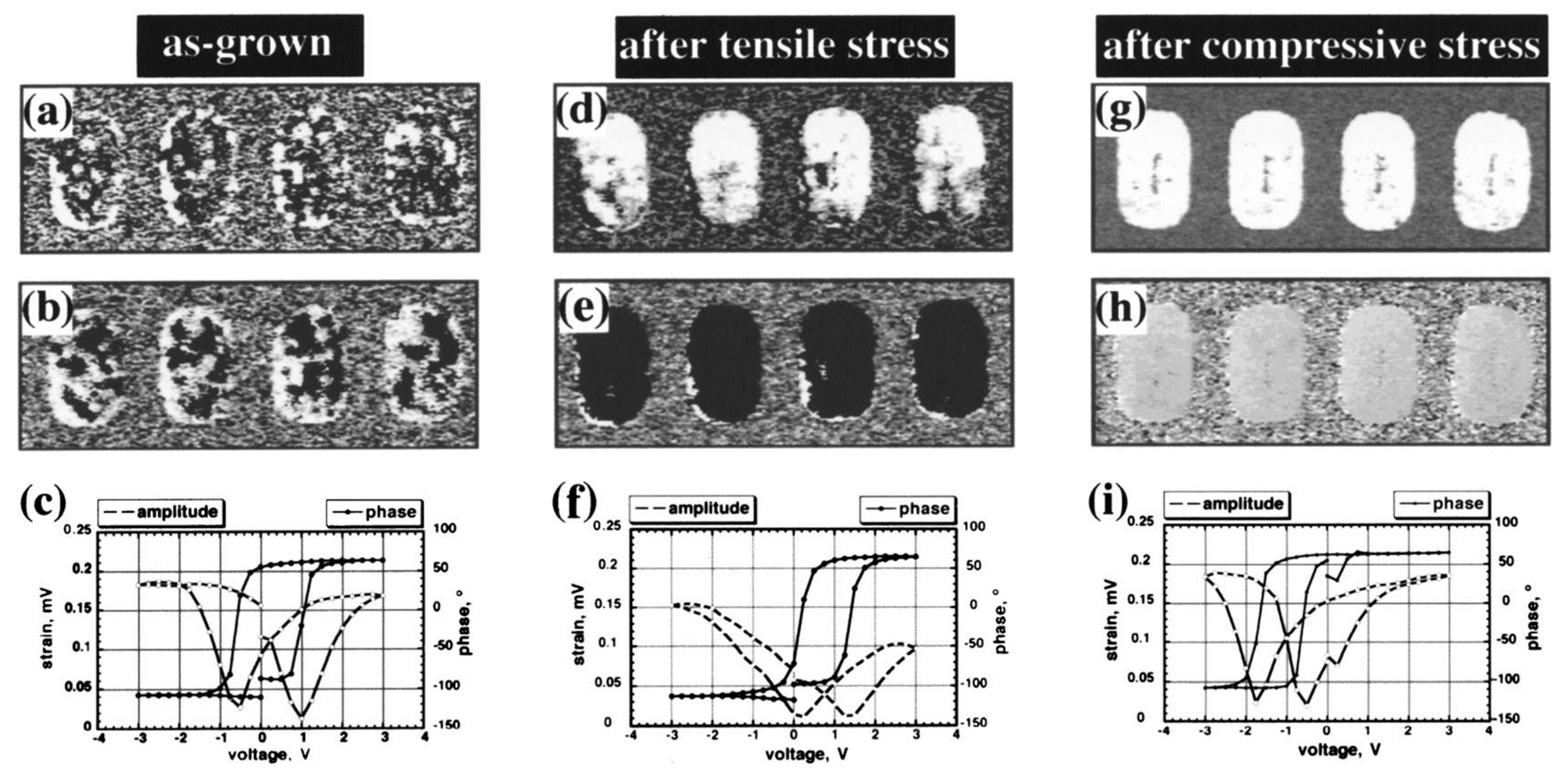
4.1. Theoretical Investigation of Spontaneously Polarized Surfaces
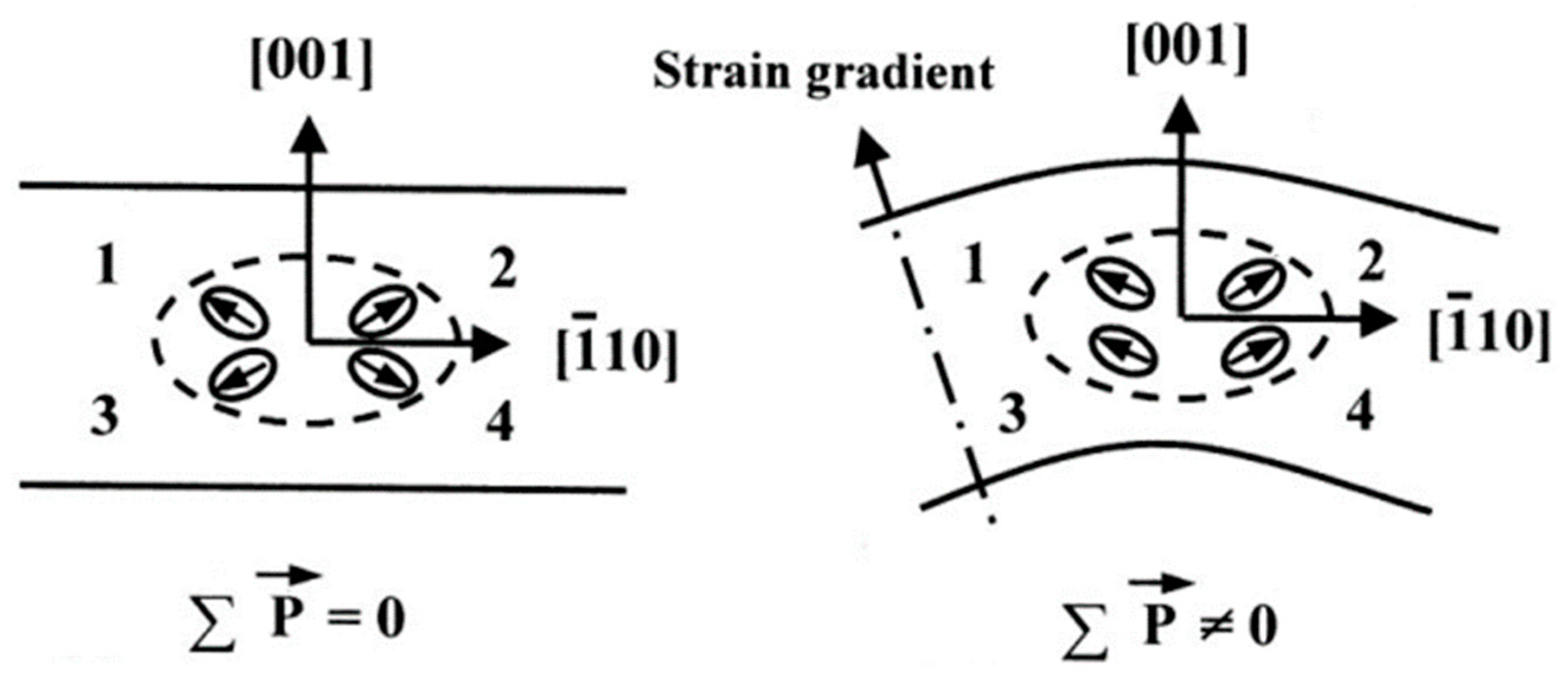
4.2. Theoretical Investigation of Nanopolar Region Orientation Regulated by Strain Gradient
4.3. Theoretical Investigation of Inhomogeneity Inducing Symmetry Breaking
4.4. Theoretical Investigation of Barrier Layer
4.5. Other Theoretical Investigations
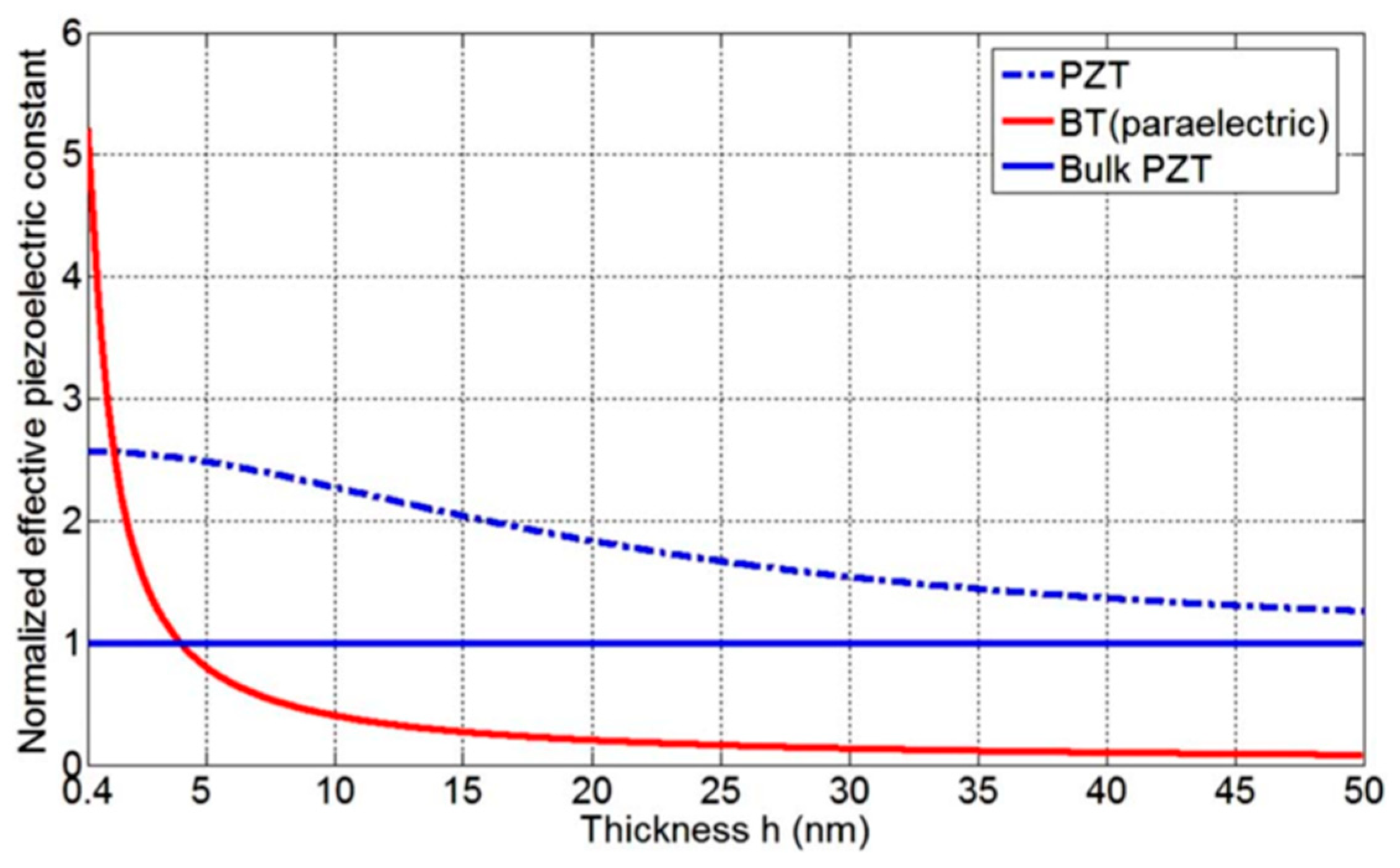
5. Flexoelectric Scaling Effect in Nanoscale Materials
6. Potential Applications of the Flexoelectric Effect
6.1. Flexoelectric Piezoelectric Composites
6.2. Sensors and Actuators
6.3. Mechanical Writing
6.4. Energy Harvester
6.5. Other Applications
7. Summary and Future Trends
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cross, L.E. Flexoelectric effects: Charge separation in insulating solids subjected to elastic strain gradients. J. Mater. Sci. 2006, 41, 53–63. [Google Scholar] [CrossRef]
- Quang, H.L.; He, Q.C. The number and types of all possible rotational symmetries for flexoelectric tensors. Proc. R. Soc. A Math. Phys. Eng. Sci. 2011, 467, 2369–2386. [Google Scholar] [CrossRef]
- Shu, L.; Wei, X.; Pang, T.; Yao, X.; Wang, C. Symmetry of flexoelectric coefficients in crystalline medium. J. Appl. Phys. 2011, 110, 104106. [Google Scholar] [CrossRef]
- Yudin, P.V.; Tagantsev, A.K. Fundamentals of flexoelectricity in solids. Nanotechnology 2013, 24, 432001. [Google Scholar] [CrossRef] [PubMed]
- Tagantsev, A.K. Electric polarization in crystals and its response to thermal and elastic perturbations. Phase Trans. 1991, 35, 119–203. [Google Scholar] [CrossRef]
- Zubko, P.; Catalan, G.; Tagantsev, A.K. Flexoelectric Effect in Solids. Annu. Rev. Mater. Res. 2013, 43, 387–421. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.; Cross, L.E. Observation of the flexoelectric effect in relaxor Pb(Mg1/3Nb2/3)O3 ceramics. Appl. Phys. Lett. 2001, 78, 2920–2921. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Large flexoelectric polarization in ceramic lead magnesium niobate. Appl. Phys. Lett. 2001, 79, 4420–4422. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Flexoelectric polarization of barium strontium titanate in the paraelectric state. Appl. Phys. Lett. 2002, 81, 3440–3442. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Strain-gradient-induced electric polarization in lead zirconate titanate ceramics. Appl. Phys. Lett. 2003, 82, 3293–3295. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Chen, P.; Chu, B. Flexoelectricity in ferroelectric materials. IET Nanodielectr. 2019, 2, 83–91. [Google Scholar] [CrossRef]
- Wang, B.; Gu, Y.; Zhang, S.; Chen, L.-Q. Flexoelectricity in solids: Progress, challenges, and perspectives. Prog. Mater. Sci. 2019, 106, 100570. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Mao, S.; Yeh, Y.W.; Purohit, P.K.; McAlpine, M.C. Nanoscale flexoelectricity. Adv. Mater. 2013, 25, 946–974. [Google Scholar] [CrossRef]
- Deng, Q.; Kammoun, M.; Erturk, A.; Sharma, P. Nanoscale flexoelectric energy harvesting. Int. J. Solids Struct. 2014, 51, 3218–3225. [Google Scholar] [CrossRef] [Green Version]
- Shu, L.; Liang, R.; Rao, Z.; Fei, L.; Ke, S.; Wang, Y. Flexoelectric materials and their related applications: A focused review. J. Adv. Ceram. 2019, 8, 153–173. [Google Scholar] [CrossRef] [Green Version]
- Tripathy, A.; Saravanakumar, B.; Mohanty, S.; Nayak, S.K.; Ramadoss, A. Comprehensive Review on Flexoelectric Energy Harvesting Technology: Mechanisms, Device Configurations, and Potential Applications. ACS Appl. Electron. Mater. 2021, 3, 2898–2924. [Google Scholar] [CrossRef]
- Kwon, S.R.; Huang, W.B.; Zhang, S.J.; Yuan, F.G.; Jiang, X.N. Flexoelectric sensing using a multilayered barium strontium titanate structure. Smart Mater. Struct. 2013, 22, 115017. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Huang, W.; Ryung Kwon, S.; Yang, S.; Jiang, X.; Yuan, F.-G. A sensor for the direct measurement of curvature based on flexoelectricity. Smart Mater. Struct. 2013, 22, 085016. [Google Scholar] [CrossRef]
- Bhaskar, U.K.; Banerjee, N.; Abdollahi, A.; Wang, Z.; Schlom, D.G.; Rijnders, G.; Catalan, G. A flexoelectric microelectromechanical system on silicon. Nat. Nanotechnol. 2016, 11, 263–266. [Google Scholar] [CrossRef]
- Wang, K.F.; Wang, B.L. Non-linear flexoelectricity in energy harvesting. Int. J. Eng. Sci. 2017, 116, 88–103. [Google Scholar] [CrossRef]
- Chu, B.; Salem, D.R. Flexoelectricity in several thermoplastic and thermosetting polymers. Appl. Phys. Lett. 2012, 101, 103905. [Google Scholar] [CrossRef]
- Zubko, P.; Catalan, G.; Buckley, A.; Welche, P.R.; Scott, J.F. Strain-gradient-induced polarization in SrTiO3 single crystals. Phys. Rev. Lett. 2007, 99, 167601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chu, B.; Zhu, W.; Li, N.A.N.; Cross, L.E. Flexoelectric Composite—A New Prospect for Lead-Free Piezoelectrics. Funct. Mater. Lett. 2011, 03, 79–81. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, J.; Chu, M.; Chu, B. Flexoelectric piezoelectric metamaterials based on the bending of ferroelectric ceramic wafers. Appl. Phys. Lett. 2016, 109, 072903. [Google Scholar] [CrossRef]
- Abdollahi, A.; Millán, D.; Peco, C.; Arroyo, M.; Arias, I. Revisiting pyramid compression to quantify flexoelectricity: A three-dimensional simulation study. Phys. Rev. B 2015, 91, 104103. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Lv, J.; Liang, X.; Xu, M.; Shen, S. Improved approach to measure the direct flexoelectric coefficient of bulk polyvinylidene fluoride. J. Appl. Phys. 2016, 119, 094104. [Google Scholar] [CrossRef]
- Biancoli, A.; Fancher, C.M.; Jones, J.L.; Damjanovic, D. Breaking of macroscopic centric symmetry in paraelectric phases of ferroelectric materials and implications for flexoelectricity. Nat. Mater. 2015, 14, 224–229. [Google Scholar] [CrossRef]
- Baskaran, S.; Ramachandran, N.; He, X.; Thiruvannamalai, S.; Lee, H.J.; Heo, H.; Chen, Q.; Fu, J.Y. Giant flexoelectricity in polyvinylidene fluoride films. Phys. Lett. A 2011, 375, 2082–2084. [Google Scholar] [CrossRef]
- Baskaran, S.; He, X.; Chen, Q.; Fu, J.Y. Experimental studies on the direct flexoelectric effect in α-phase polyvinylidene fluoride films. Appl. Phys. Lett. 2011, 98, 242901. [Google Scholar] [CrossRef]
- Hu, T.; Deng, Q.; Liang, X.; Shen, S. Measuring the flexoelectric coefficient of bulk barium titanate from a shock wave experiment. J. Appl. Phys. 2017, 122, 055106. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, M.; Liang, X.; Shen, S. Shear flexoelectric coefficient μ1211 in polyvinylidene fluoride. J. Appl. Phys. 2015, 117, 204102. [Google Scholar] [CrossRef]
- Zhang, S.; Liang, X.; Xu, M.; Feng, B.; Shen, S. Shear flexoelectric response along 3121 direction in polyvinylidene fluoride. Appl. Phys. Lett. 2015, 107, 142902. [Google Scholar] [CrossRef]
- Fu, J.Y.; Zhu, W.; Li, N.; Cross, L.E. Experimental studies of the converse flexoelectric effect induced by inhomogeneous electric field in a barium strontium titanate composition. J. Appl. Phys. 2006, 100, 024112. [Google Scholar] [CrossRef]
- Shu, L.; Huang, W.; Ryung Kwon, S.; Wang, Z.; Li, F.; Wei, X.; Zhang, S.; Lanagan, M.; Yao, X.; Jiang, X. Converse flexoelectric coefficient f1212 in bulk Ba0.67Sr0.33TiO3. Appl. Phys. Lett. 2014, 104, 232902. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.; Ji, Y.; Liu, Y.; Wu, L.; Yang, Y. Controllable Piezo-flexoelectric Effect in Ferroelectric Ba0.7Sr0.3TiO3 Materials for Harvesting Vibration Energy. ACS Appl. Mater. Interfaces 2022, 14, 36763–36770. [Google Scholar] [CrossRef]
- Hou, Y.; Tian, D.; Chu, B. Flexoelectric response of (1-x)BaTiO3-xSrTiO3 ceramics. Ceram. Int. 2020, 46, 12928–12932. [Google Scholar] [CrossRef]
- Chu, B.; Zhu, W.; Li, N.; Cross, L.E. Flexure mode flexoelectric piezoelectric composites. J. Appl. Phys. 2009, 106, 104109. [Google Scholar] [CrossRef]
- Huang, W.; Kim, K.; Zhang, S.; Yuan, F.-G.; Jiang, X. Scaling effect of flexoelectric (Ba,Sr)TiO3 microcantilevers. Phys. Status Solidi RRL 2011, 5, 350–352. [Google Scholar] [CrossRef]
- Li, Y.; Shu, L.; Huang, W.; Jiang, X.; Wang, H. Giant flexoelectricity in Ba0.6Sr0.4TiO3/Ni0.8Zn0.2Fe2O4 composite. Appl. Phys. Lett. 2014, 105, 162906. [Google Scholar] [CrossRef]
- Dai, Z.; Guo, S.; Gong, Y.; Wang, Z. Semiconductor flexoelectricity in graphite-doped SrTiO3 ceramics. Ceram. Int. 2021, 47, 6535–6539. [Google Scholar] [CrossRef]
- Mizzi, C.A.; Guo, B.; Marks, L.D. Experimental determination of flexoelectric coefficients in SrTiO3, KTaO3, TiO2, and YAlO3 single crystals. Phys. Rev. Mater. 2022, 6, 055005. [Google Scholar] [CrossRef]
- Tian, D.; Hou, Y.; Zhou, W.; Chu, B. Flexoelectric response of ferroelectric ceramics with reduced surface layer effect. J. Appl. Phys. 2021, 129, 194103. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Flexoelectricity of barium titanate. Appl. Phys. Lett. 2006, 88, 232902. [Google Scholar] [CrossRef]
- Narvaez, J.; Saremi, S.; Hong, J.; Stengel, M.; Catalan, G. Large Flexoelectric Anisotropy in Paraelectric Barium Titanate. Phys. Rev. Lett. 2015, 115, 037601. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Pan, Q.; Tian, D.; Zhou, W.; Chen, P.; Zhang, H.; Chu, B. Large Flexoelectriclike Response from the Spontaneously Polarized Surfaces in Ferroelectric Ceramics. Phys. Rev. Lett. 2018, 121, 057602. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Kim, T.; Hou, D.; Cann, D.; Jones, J.L.; Jiang, X. Flexoelectric characterization of BaTiO3-0.08Bi(Zn1/2Ti1/2)O3. Appl. Phys. Lett. 2017, 110, 222904. [Google Scholar] [CrossRef]
- Shu, L.; Wei, X.; Jin, L.; Li, Y.; Wang, H.; Yao, X. Enhanced direct flexoelectricity in paraelectric phase of Ba(Ti0.87Sn0.13)O3 ceramics. Appl. Phys. Lett. 2013, 102, 152904. [Google Scholar] [CrossRef] [Green Version]
- Shu, L.; Wan, M.; Wang, Z.; Wang, L.; Lei, S.; Wang, T.; Huang, W.; Zhou, N.; Wang, Y. Large flexoelectricity in Al2O3-doped Ba(Ti0.85Sn0.15)O3 ceramics. Appl. Phys. Lett. 2017, 110, 192903. [Google Scholar] [CrossRef]
- Hana, P. Study of Flexoelectric Phenomenon from Direct and from Inverse Flexoelectric Behavior of PMNT Ceramic. Ferroelectrics 2007, 351, 196–203. [Google Scholar] [CrossRef]
- Hana, P.; Marvan, M.; Burianova, L.; Zhang, S.J.; Furman, E.; Shrout, T.R. Study of the Inverse Flexoelectric Phenomena in Ceramic Lead Magnesium Niobate-Lead Titanate. Ferroelectrics 2011, 336, 137–144. [Google Scholar] [CrossRef]
- Narvaez, J.; Catalan, G. Origin of the enhanced flexoelectricity of relaxor ferroelectrics. Appl. Phys. Lett. 2014, 104, 162903. [Google Scholar] [CrossRef] [Green Version]
- Shu, L.; Wan, M.; Jiang, X.; Li, F.; Zhou, N.; Huang, W.; Wang, T. Frequency dispersion of flexoelectricity in PMN-PT single crystal. AIP Adv. 2017, 7, 015010. [Google Scholar] [CrossRef] [Green Version]
- Shu, L.; Li, T.; Wang, Z.; Li, F.; Fei, L.; Rao, Z.; Ye, M.; Ke, S.; Huang, W.; Wang, Y.; et al. Flexoelectric behavior in PIN-PMN-PT single crystals over a wide temperature range. Appl. Phys. Lett. 2017, 111, 162901. [Google Scholar] [CrossRef]
- Li, C.; Wang, Z.; Li, F.; Rao, Z.; Huang, W.; Shen, Z.; Ke, S.; Shu, L. Large flexoelectric response in PMN-PT ceramics through composition design. Appl. Phys. Lett. 2019, 115, 142901. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, Z.; Shu, S.; Tian, T.; Huang, W.; Li, C.; Ke, S.; Shu, L. Local structural heterogeneity induced large flexoelectricity in Sm-doped PMN–PT ceramics. J. Appl. Phys. 2021, 129, 174103. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Flexoelectric effect in ceramic lead zirconate titanate. Appl. Phys. Lett. 2005, 86, 072905. [Google Scholar] [CrossRef]
- Henmi, N.; Tohyama, M. Measurement of Flexoelectric Effect in Lead Zirconate Titanate Ceramics. J. Adv. Mech. Design Syst. Manuf. 2011, 5, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Vales-Castro, P.; Roleder, K.; Zhao, L.; Li, J.-F.; Kajewski, D.; Catalan, G. Flexoelectricity in antiferroelectrics. Appl. Phys. Lett. 2018, 113, 132903. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Hou, Y.; Chen, P.; Zhang, H.; Chu, B. The surface mechanism for the flexoelectric response in sodium bismuth titanate-based ferroelectric ceramics. J. Am. Ceram. Soc. 2019, 102, 5454–5464. [Google Scholar] [CrossRef]
- Zhang, H.; Chu, B. Energy harvesting by exploiting the enhanced flexoelectric-like response of reduced (Na0.5Bi0.5)0.92Ba0.08TiO3 ceramics. J. Eur. Ceram. Soc. 2018, 38, 2520–2525. [Google Scholar] [CrossRef]
- Zhou, W.; Chen, P.; Pan, Q.; Zhang, X.; Chu, B. Lead-Free Metamaterials with Enormous Apparent Piezoelectric Response. Adv. Mater. 2015, 27, 6349–6355. [Google Scholar] [CrossRef] [PubMed]
- Pan, Q.; Fang, C.; Luo, H.; Chu, B. Magnetoelectric response from the enhanced ferromagnetism and flexoelectric response in reduced BiFeO3–based ceramics. J. Eur. Ceram. Soc. 2019, 39, 1057–1064. [Google Scholar] [CrossRef]
- Li, Y.; Shu, L.; Zhou, Y.; Guo, J.; Xiang, F.; He, L.; Wang, H. Enhanced flexoelectric effect in a non-ferroelectric composite. Appl. Phys. Lett. 2013, 103, 142909. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, T.; Shu, L.; Wang, Z.; Huang, W.; Fei, L.; Li, F.; Rao, Z.; Ke, S.; Li, B.; et al. Flexoelectric fatigue in (K,Na,Li)(Nb,Sb)O3 ceramics. Appl. Phys. Lett. 2018, 113, 182901. [Google Scholar] [CrossRef]
- Poddar, S.; Ducharme, S. Measurement of the flexoelectric response in ferroelectric and relaxor polymer thin films. Appl. Phys. Lett. 2013, 103, 202901. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Xu, M.; Ma, G.; Liang, X.; Shen, S. Experimental method research on transverse flexoelectric response of poly(vinylidene fluoride). Jpn. J. Appl. Phys. 2016, 55, 071601. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, J.; Hu, X.; Chu, B.; Chen, S.; Salem, D. Flexoelectric effect in PVDF-based polymers. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 727–731. [Google Scholar] [CrossRef]
- Hu, X.; Zhou, Y.; Liu, J.; Chu, B. Improved flexoelectricity in PVDF/barium strontium titanate (BST) nanocomposites. J. Appl. Phys. 2018, 123, 154101. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, Y.; Hu, X.; Chu, B. Flexoelectric effect in PVDF-based copolymers and terpolymers. Appl. Phys. Lett. 2018, 112, 232901. [Google Scholar] [CrossRef]
- Wen, X.; Yang, G.; Ma, Q.; Tian, Y.; Liu, X.; Xue, D.; Deng, Q.; Shen, S. Flexoelectricity in compositionally graded Ba1-xSrxTiO3 ceramics. J. Appl. Phys. 2021, 130, 074102. [Google Scholar] [CrossRef]
- Tagantsev, A.K. Piezoelectricity and flexoelectricity in crystalline dielectrics. Phys. Rev. B 1987, 36, 6177. [Google Scholar] [CrossRef] [PubMed]
- Tagantsev, A.K.; Yurkov, A.S. Flexoelectric effect in finite samples. J. Appl. Phys. 2012, 112, 044103. [Google Scholar] [CrossRef] [Green Version]
- Stengel, M. Microscopic response to inhomogeneous deformations in curvilinear coordinates. Nat. Commun. 2013, 4, 2693. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stengel, M. Surface control of flexoelectricity. Phys. Rev. B 2014, 90, 201112. [Google Scholar] [CrossRef] [Green Version]
- Hong, J.; Vanderbilt, D. First-principles theory of frozen-ion flexoelectricity. Phys. Rev. B 2011, 84, 180101. [Google Scholar] [CrossRef] [Green Version]
- Tian, D.; Chen, P.; Yang, X.; Chu, B. Thickness dependence of dielectric and piezoelectric properties from the surface layer effect of BaTiO3-based ceramics. Ceram. Int. 2021, 47, 17262–17267. [Google Scholar] [CrossRef]
- Narvaez, J.; Vasquez-Sancho, F.; Catalan, G. Enhanced flexoelectric-like response in oxide semiconductors. Nature 2016, 538, 219–221. [Google Scholar] [CrossRef]
- Shu, L.; Ke, S.; Fei, L.; Huang, W.; Wang, Z.; Gong, J.; Jiang, X.; Wang, L.; Li, F.; Lei, S.; et al. Photoflexoelectric effect in halide perovskites. Nat. Mater. 2020, 19, 605–609. [Google Scholar] [CrossRef]
- Garten, L.M.; Trolier-McKinstry, S. Enhanced flexoelectricity through residual ferroelectricity in barium strontium titanate. J. Appl. Phys. 2015, 117, 094102. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Tan, P.; Ma, X.; Wang, D.; Jin, X.; Liu, Y.; Xu, B.; Qiao, L.; Qiu, C.; Wang, B.; et al. Ferroelectric crystals with giant electro-optic property enabling ultracompact Q-switches. Science 2022, 376, 371–377. [Google Scholar] [CrossRef]
- Wu, M.; Zhang, X.; Li, X.; Qu, K.; Sun, Y.; Han, B.; Zhu, R.; Gao, X.; Zhang, J.; Liu, K.; et al. Engineering of atomic-scale flexoelectricity at grain boundaries. Nat. Commun. 2022, 13, 216. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Yoon, A.; Jang, S.Y.; Yoon, J.G.; Chung, J.S.; Kim, M.; Scott, J.F.; Noh, T.W. Giant flexoelectric effect in ferroelectric epitaxial thin films. Phys. Rev. Lett. 2011, 107, 057602. [Google Scholar] [CrossRef]
- Wang, Z.; Li, C.; Zhang, Z.; Hu, Y.; Huang, W.; Ke, S.; Zheng, R.-K.; Li, F.; Shu, L. Interplay of defect dipole and flexoelectricity in linear dielectrics. Scr. Mater. 2022, 210, 114427. [Google Scholar] [CrossRef]
- Li, Q.; Liu, Y.; Liu, J.; Song, K.; Guo, H.; Li, F.; Xu, Z. Enhanced Piezoelectric Properties and Improved Property Uniformity in Nd-Doped PMN-PT Relaxor Ferroelectric Single Crystals. Adv. Funct. Mater. 2022, 32, 202201719. [Google Scholar] [CrossRef]
- Das, S.; Wang, B.; Paudel, T.R.; Park, S.M.; Tsymbal, E.Y.; Chen, L.Q.; Lee, D.; Noh, T.W. Enhanced flexoelectricity at reduced dimensions revealed by mechanically tunable quantum tunnelling. Nat. Commun. 2019, 10, 537. [Google Scholar] [CrossRef] [Green Version]
- Yamada, T.; Astafiev, K.F.; Sherman, V.O.; Tagantsev, A.K.; Muralt, P.; Setter, N. Strain relaxation of epitaxial SrTiO3 thin films on LaAlO3 by two-step growth technique. Appl. Phys. Lett. 2005, 86, 142904. [Google Scholar] [CrossRef]
- Catalan, G.; Noheda, B.; McAneney, J.; Sinnamon, L.J.; Gregg, J.M. Strain gradients in epitaxial ferroelectrics. Phys. Rev. B 2005, 72, 020102. [Google Scholar] [CrossRef] [Green Version]
- Karthik, J.; Mangalam, R.V.K.; Agar, J.C.; Martin, L.W. Large built-in electric fields due to flexoelectricity in compositionally graded ferroelectric thin films. Phys. Rev. B 2013, 87, 024111. [Google Scholar] [CrossRef] [Green Version]
- Park, S.M.; Wang, B.; Paudel, T.; Park, S.Y.; Das, S.; Kim, J.R.; Ko, E.K.; Lee, H.G.; Park, N.; Tao, L.; et al. Colossal flexoresistance in dielectrics. Nat. Commun. 2020, 11, 2586. [Google Scholar] [CrossRef]
- Sun, L.; Zhu, L.; Zhang, C.; Chen, W.; Wang, Z. Mechanical Manipulation of Silicon-based Schottky Diodes via Flexoelectricity. Nano Energy 2021, 83, 105855. [Google Scholar] [CrossRef]
- Guo, R.; You, L.; Lin, W.; Abdelsamie, A.; Shu, X.; Zhou, G.; Chen, S.; Liu, L.; Yan, X.; Wang, J.; et al. Continuously controllable photoconductance in freestanding BiFeO3 by the macroscopic flexoelectric effect. Nat. Commun. 2020, 11, 2571. [Google Scholar] [CrossRef] [PubMed]
- Park, S.M.; Wang, B.; Chen, L.-Q.; Noh, T.W.; Yang, S.M.; Lee, D. Flexoelectric control of physical properties by atomic force microscopy. Appl. Phys. Rev. 2021, 8, 041327. [Google Scholar] [CrossRef]
- Lee, D.; Yang, S.M.; Yoon, J.G.; Noh, T.W. Flexoelectric rectification of charge transport in strain-graded dielectrics. Nano Lett. 2012, 12, 6436–6440. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Lv, P.; Zhang, Y.; Huang, S.; Wong, C.M.; Yau, H.M.; Chen, X.; Wen, Z.; Jiang, X.; Zeng, C.; et al. Modulating the Electrical Transport in the Two-Dimensional Electron Gas at LaAlO3/SrTiO3 Heterostructures by Interfacial Flexoelectricity. Phys. Rev. Lett. 2019, 122, 257601. [Google Scholar] [CrossRef] [PubMed]
- Majdoub, M.S.; Sharma, P.; Cagin, T. Enhanced size-dependent piezoelectricity and elasticity in nanostructures due to the flexoelectric effect. Phys. Rev. B 2009, 79, 119904. [Google Scholar] [CrossRef]
- Liu, C.; Wu, H.; Wang, J. Giant piezoelectric response in piezoelectric/dielectric superlattices due to flexoelectric effect. Appl. Phys. Lett. 2016, 109, 192901. [Google Scholar] [CrossRef]
- Catalan, G.; Lubk, A.; Vlooswijk, A.H.; Snoeck, E.; Magen, C.; Janssens, A.; Rispens, G.; Rijnders, G.; Blank, D.H.; Noheda, B. Flexoelectric rotation of polarization in ferroelectric thin films. Nat. Mater. 2011, 10, 963–967. [Google Scholar] [CrossRef] [Green Version]
- Gruverman, A.; Rodriguez, B.J.; Kingon, A.I.; Nemanich, R.J.; Tagantsev, A.K.; Cross, J.S.; Tsukada, M. Mechanical stress effect on imprint behavior of integrated ferroelectric capacitors. Appl. Phys. Lett. 2003, 83, 728–730. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.-H.; Chen, X.; Li, Y.; Guo, X.; Ge, H.-X.; Shen, Q.-D. Ferroelectric polymer nanostructure with enhanced flexoelectric response for force-induced memory. Appl. Phys. Lett. 2018, 113, 042903. [Google Scholar] [CrossRef]
- Lee, D.; Jeon, B.C.; Yoon, A.; Shin, Y.C.; Lee, M.H.; Song, T.K.; Bu, S.D.; Kim, M.; Chung, J.-S.; Yoon, J.G.; et al. Flexoelectric Control of Defect Formation in Ferroelectric Epitaxial Thin Films. Adv. Mater. 2014, 26, 5005–5011. [Google Scholar] [CrossRef]
- Das, S.; Wang, B.; Cao, Y.; Rae Cho, M.; Jae Shin, Y.; Mo Yang, S.; Wang, L.; Kim, M.; Kalinin, S.V.; Chen, L.Q.; et al. Controlled manipulation of oxygen vacancies using nanoscale flexoelectricity. Nat. Commun. 2017, 8, 615. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jia, T.; Kimura, H.; Cheng, Z.; Zhao, H.; Kim, Y.-H.; Osada, M.; Matsumoto, T.; Shibata, N.; Ikuhara, Y. Mechanical force involved multiple fields switching of both local ferroelectric and magnetic domain in a Bi5Ti3FeO15 thin film. NPG Asia Mater. 2017, 9, e349. [Google Scholar] [CrossRef] [Green Version]
- Gharbi, M.; Sun, Z.H.; Sharma, P.; White, K.; El-Borgi, S. Flexoelectric properties of ferroelectrics and the nanoindentation size-effect. Int. J. Solids Struct. 2011, 48, 249–256. [Google Scholar] [CrossRef] [Green Version]
- Hu, T.; Deng, Q.; Shen, S. Probing flexoelectricity via a split Hopkinson pressure bar experiment. Appl. Phys. Lett. 2018, 112, 242902. [Google Scholar] [CrossRef]
- Wu, M.; Jiang, Z.; Lou, X.; Zhang, F.; Song, D.; Ning, S.; Guo, M.; Pennycook, S.J.; Dai, J.Y.; Wen, Z. Flexoelectric Thin-Film Photodetectors. Nano Lett. 2021, 21, 2946–2952. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Zhang, H.; Chu, B. Strain gradient induced thermal-electrical response in paraelectric Na0.5Bi0.5TiO3-based ceramics. Phys. Rev. Mater. 2018, 2, 034401. [Google Scholar] [CrossRef]
- Chen, P.; Zhou, W.; Zhang, H.; Pan, Q.; Zhang, X.; Chu, B. Large Thermal–Electrical Response and Rectifying Conduction Behavior in Asymmetrically Reduced Ferroelectric Ceramics. ACS Appl. Electron. Mater. 2019, 1, 478–484. [Google Scholar] [CrossRef]
- Qi, M.; Yang, Z.; Chen, S.; Lin, S.; Jin, Q.; Hong, H.; Rong, D.; Guo, H.; Wang, C.; Wang, Z.; et al. Asymmetric ground states in La0.67Sr0.33MnO3/BaTiO3 heterostructures induced by flexoelectric bending. Appl. Phys. Lett. 2022, 120, 233103. [Google Scholar] [CrossRef]
- Mizzi, C.A.; Lin, A.Y.W.; Marks, L.D. Does Flexoelectricity Drive Triboelectricity? Phys. Rev. Lett. 2019, 123, 116103. [Google Scholar] [CrossRef] [Green Version]
- Persson, B.N.J. On the role of flexoelectricity in triboelectricity for randomly rough surfaces. EPL 2020, 129, 10006. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Fu, J.Y.; Li, N.; Cross, L. Piezoelectric composite based on the enhanced flexoelectric effects. Appl. Phys. Lett. 2006, 89, 192904. [Google Scholar] [CrossRef]
- Tian, D.; Hou, Y.; Pan, Q.; Chu, B. Large Piezoelectriclike Response from Inhomogeneously Deformed Silicon Crystals. Phys. Rev. Appl. 2020, 14, 034008. [Google Scholar] [CrossRef]
- Jiang, X.; Huang, W.; Zhang, S. Flexoelectric nano-generator: Materials, structures and devices. Nano Energy 2013, 2, 1079–1092. [Google Scholar] [CrossRef]
- Huang, W.; Yan, X.; Kwon, S.R.; Zhang, S.; Yuan, F.-G.; Jiang, X. Flexoelectric strain gradient detection using Ba0.64Sr0.36TiO3 for sensing. Appl. Phys. Lett. 2012, 101, 252903. [Google Scholar] [CrossRef]
- Huang, W.; Kwon, S.-R.; Zhang, S.; Yuan, F.-G.; Jiang, X. A trapezoidal flexoelectric accelerometer. J. Intell. Mater. Syst. Struct. 2013, 25, 271–277. [Google Scholar] [CrossRef]
- Kwon, S.R.; Huang, W.B.; Zhang, S.J.; Yuan, F.G.; Jiang, X.N. Study on a flexoelectric microphone using barium strontium titanate. J. Micromech. Microeng. 2016, 26, 045001. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Chu, B. Sodium bismuth titanate-based lead-free RAINBOW piezoelectric devices. J. Eur. Ceram. Soc. 2017, 37, 2373–2377. [Google Scholar] [CrossRef]
- Zhang, S.; Zhai, C.; Liu, K.; Song, S.; Ji, H.; Shao, S.; Xu, M. Quantitative evaluation of energy harvesting capabilities on flexoelectric and piezoelectric materials. J. Appl. Phys. 2022, 131, 064101. [Google Scholar] [CrossRef]
- Qi, Y.; Jafferis, N.T.; Lyons, K., Jr.; Lee, C.M.; Ahmad, H.; McAlpine, M.C. Piezoelectric ribbons printed onto rubber for flexible energy conversion. Nano Lett. 2010, 10, 524–528. [Google Scholar] [CrossRef] [Green Version]
- Xu, R.; Chen, P.; Chen, C.; Hou, Y.; Chu, B. Thermal-electrical like response in doped sodium bismuth titanate-based ferroelectric ceramics. Ceram. Int. 2022, 48, 27568–27574. [Google Scholar] [CrossRef]
- Jiang, J.; Chen, Z.; Hu, Y.; Xiang, Y.; Zhang, L.; Wang, Y.; Wang, G.C.; Shi, J. Flexo-photovoltaic effect in MoS2. Nat. Nanotechnol. 2021, 16, 894–901. [Google Scholar] [CrossRef]
- Jiang, Z.; Xu, Z.; Xi, Z.; Yang, Y.; Wu, M.; Li, Y.; Li, X.; Wang, Q.; Li, C.; Wu, D.; et al. Flexoelectric-induced photovoltaic effects and tunable photocurrents in flexible LaFeO3 epitaxial heterostructures. J. Mater. 2022, 8, 281–287. [Google Scholar] [CrossRef]
- Jin, Y.; Zhang, F.; Zhou, K.; Suen, C.H.; Zhou, X.Y.; Dai, J.-Y. Oxygen vacancy and photoelectron enhanced flexoelectricity in perovskite SrTiO3 crystal. Appl. Phys. Lett. 2021, 118, 164101. [Google Scholar] [CrossRef]
- Qiao, H.; Zhao, P.; Kwon, O.; Sohn, A.; Zhuo, F.; Lee, D.-M.; Sun, C.; Seol, D.; Lee, D.; Kim, S.-W.; et al. Mixed triboelectric and flexoelectric charge transfer at the nanoscal. Adv. Sci. 2021, 8, 2101793. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Chen, W.; Zheng, Y. Flexoresponses of Synthetic Antiferromagnetic Systems Hosting Skyrmions. Phys. Rev. Lett. 2022, 128, 257201. [Google Scholar] [CrossRef] [PubMed]
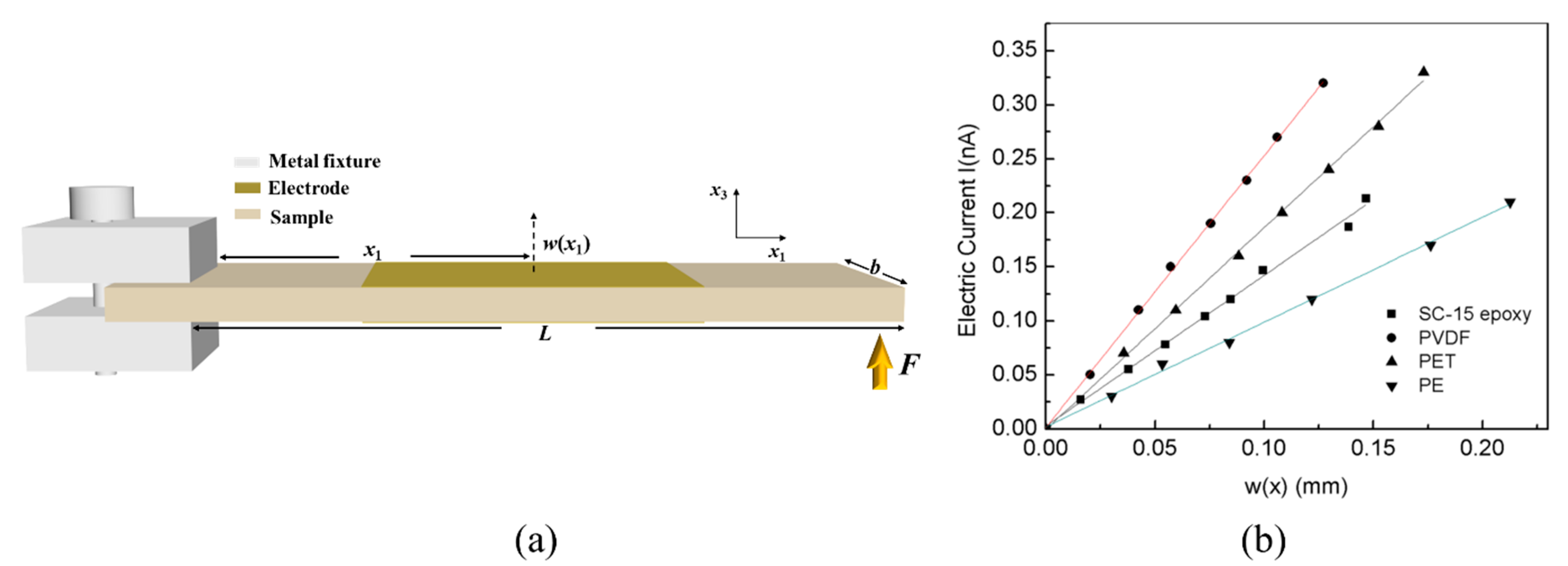
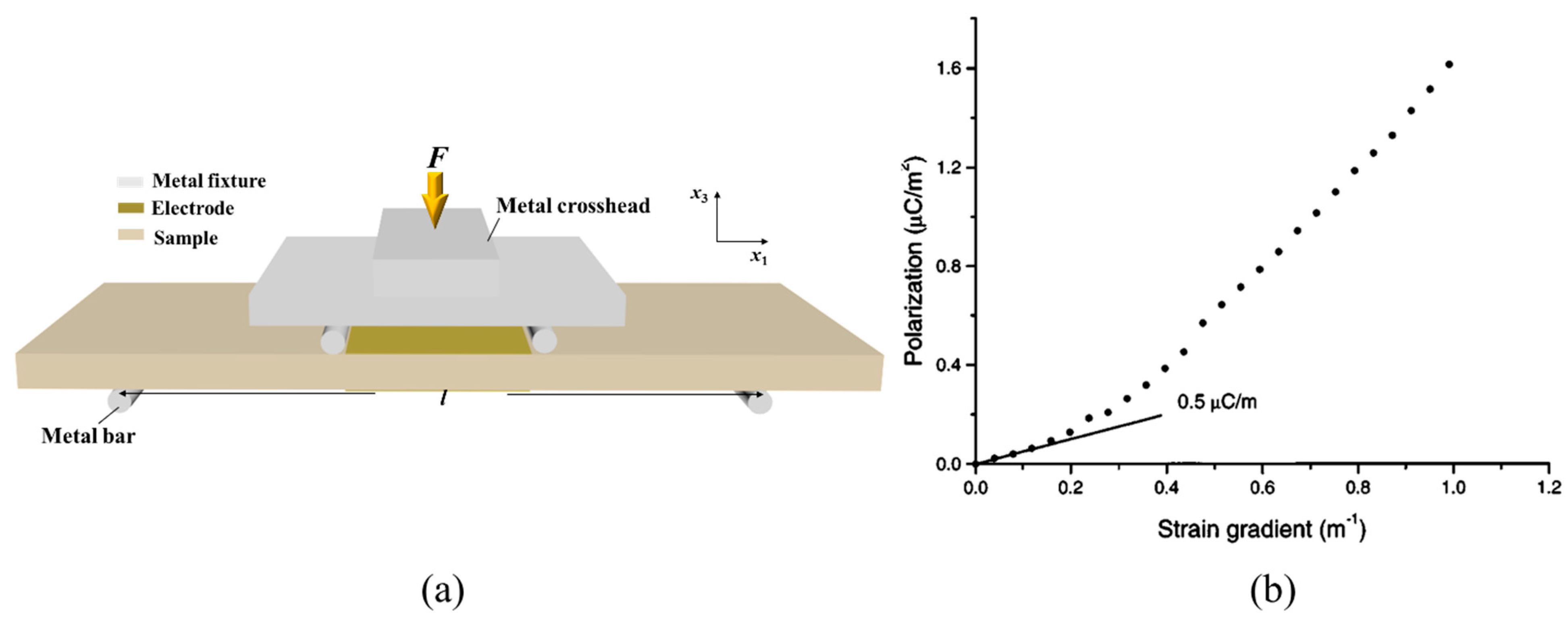
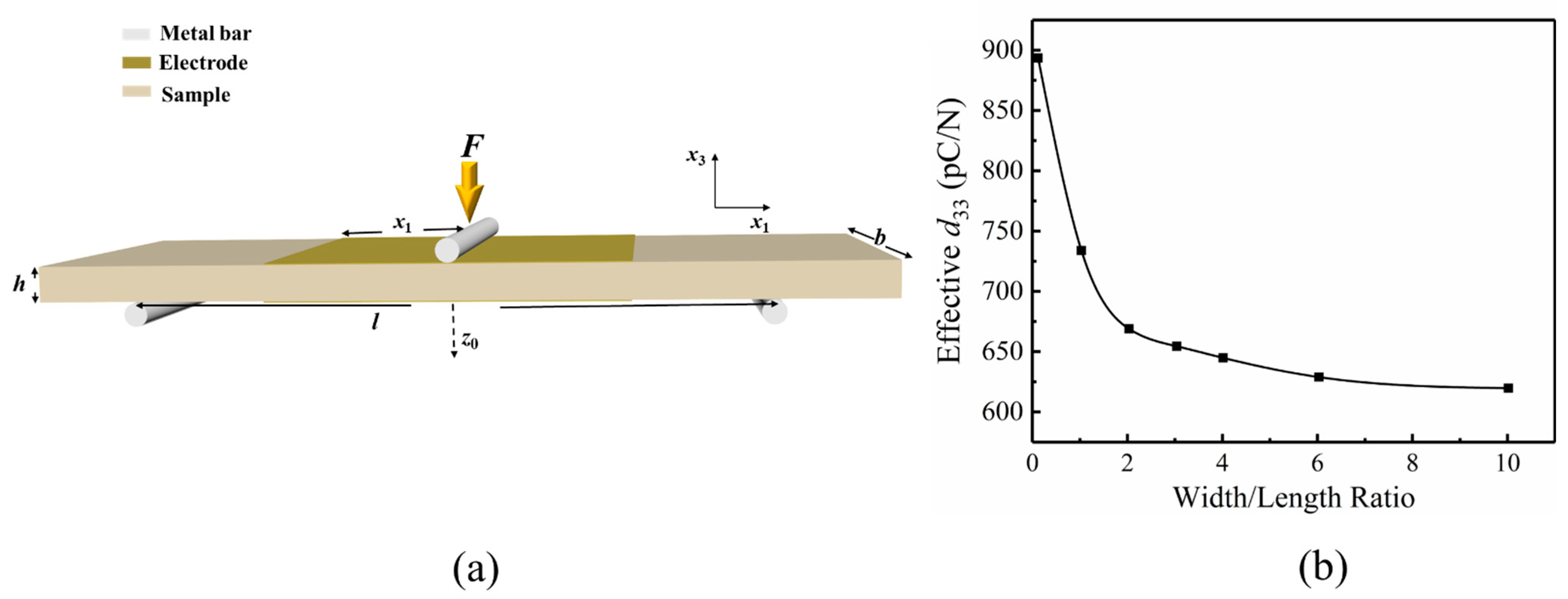
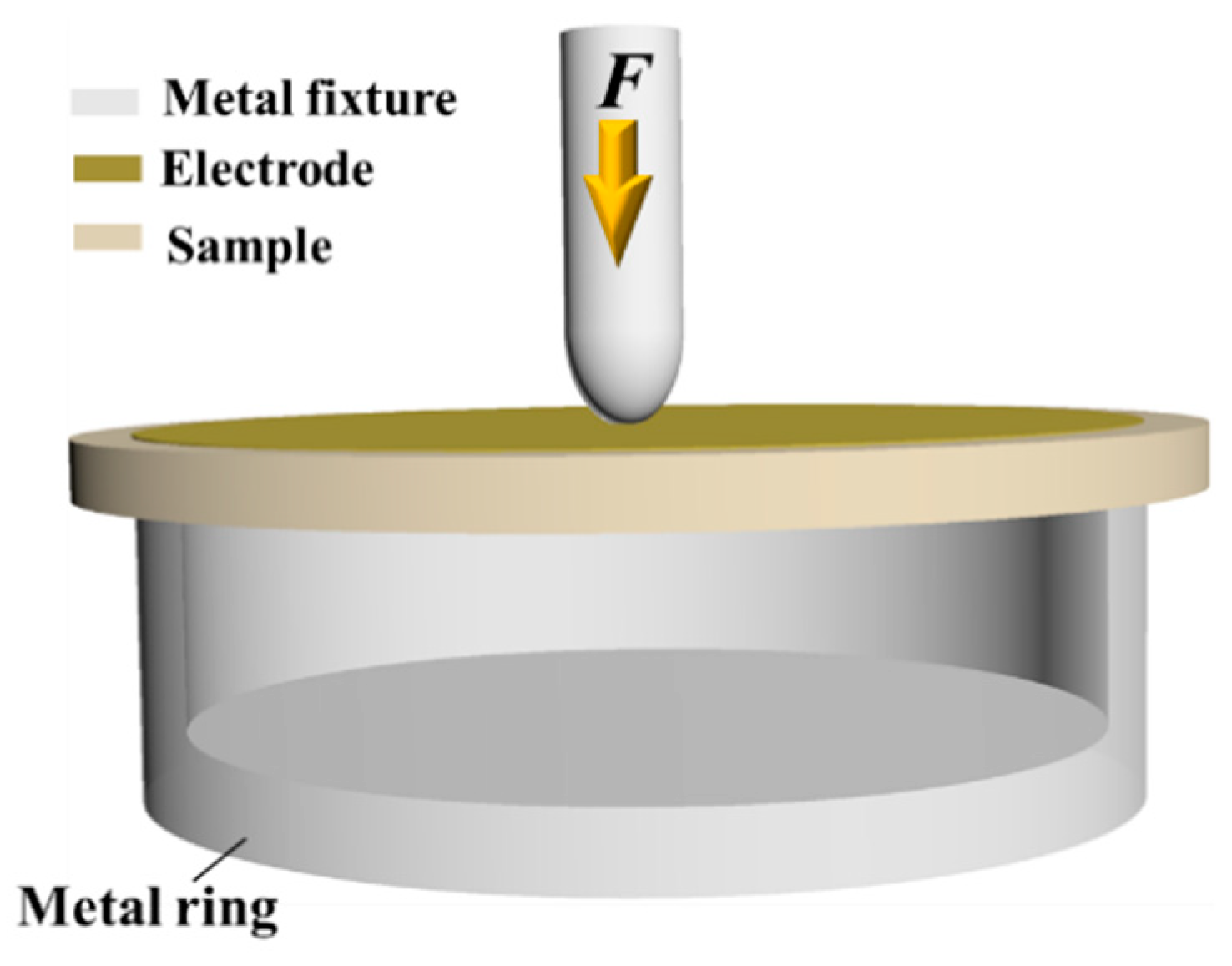







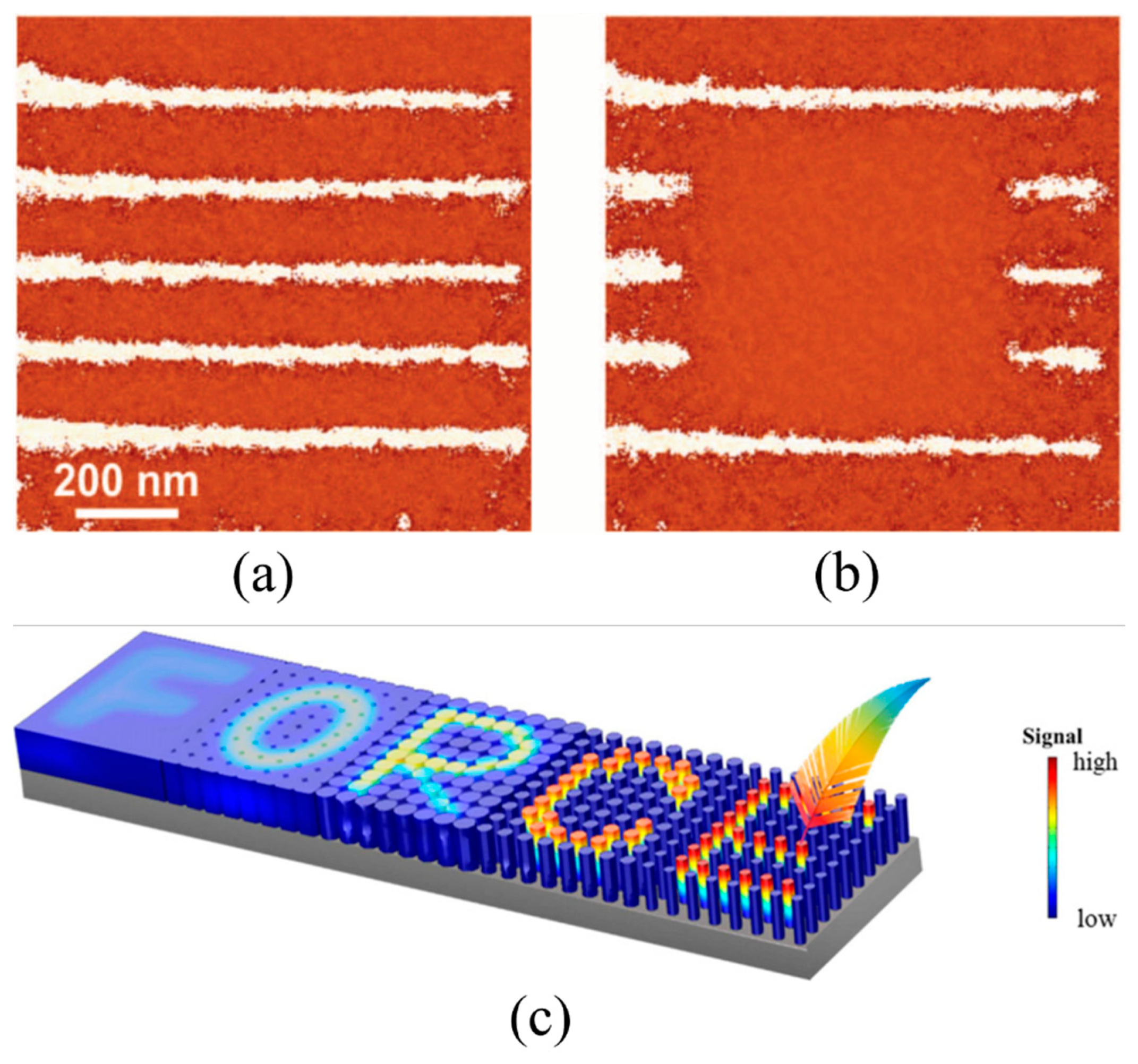


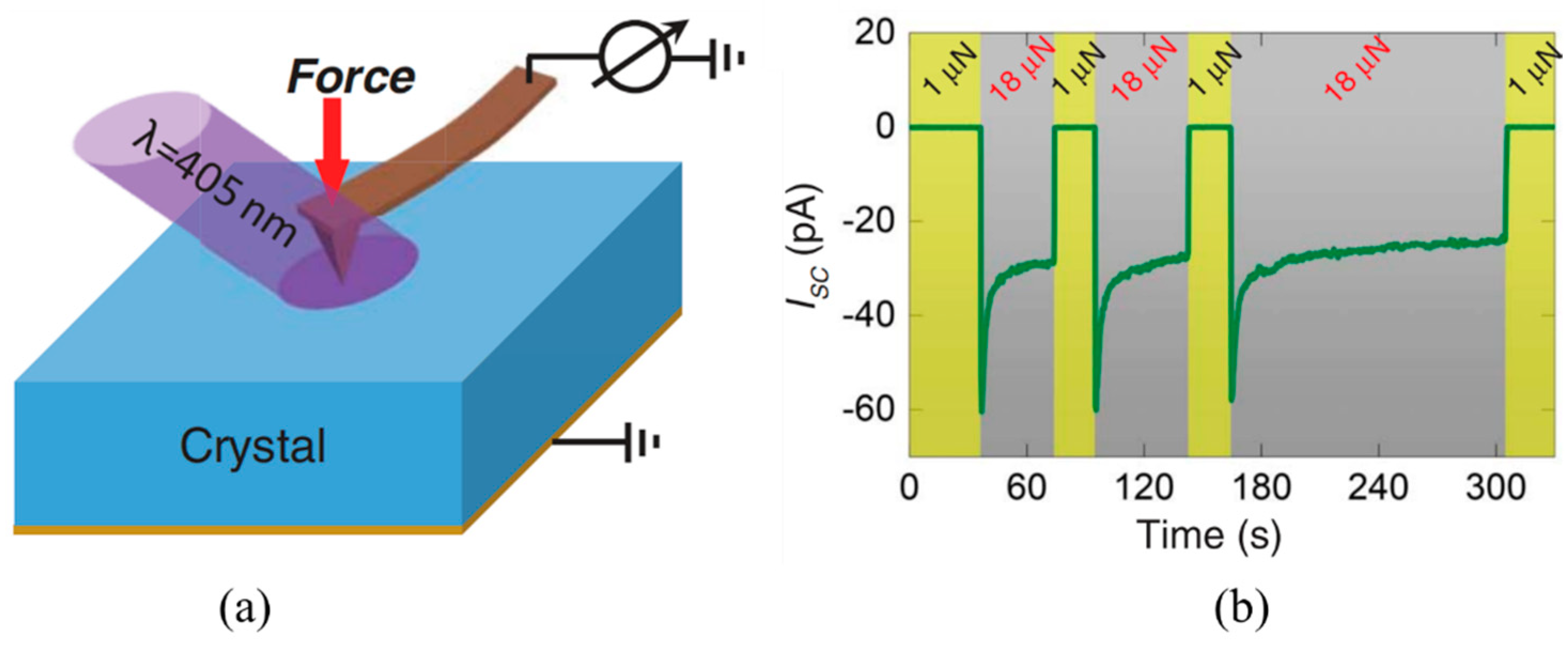

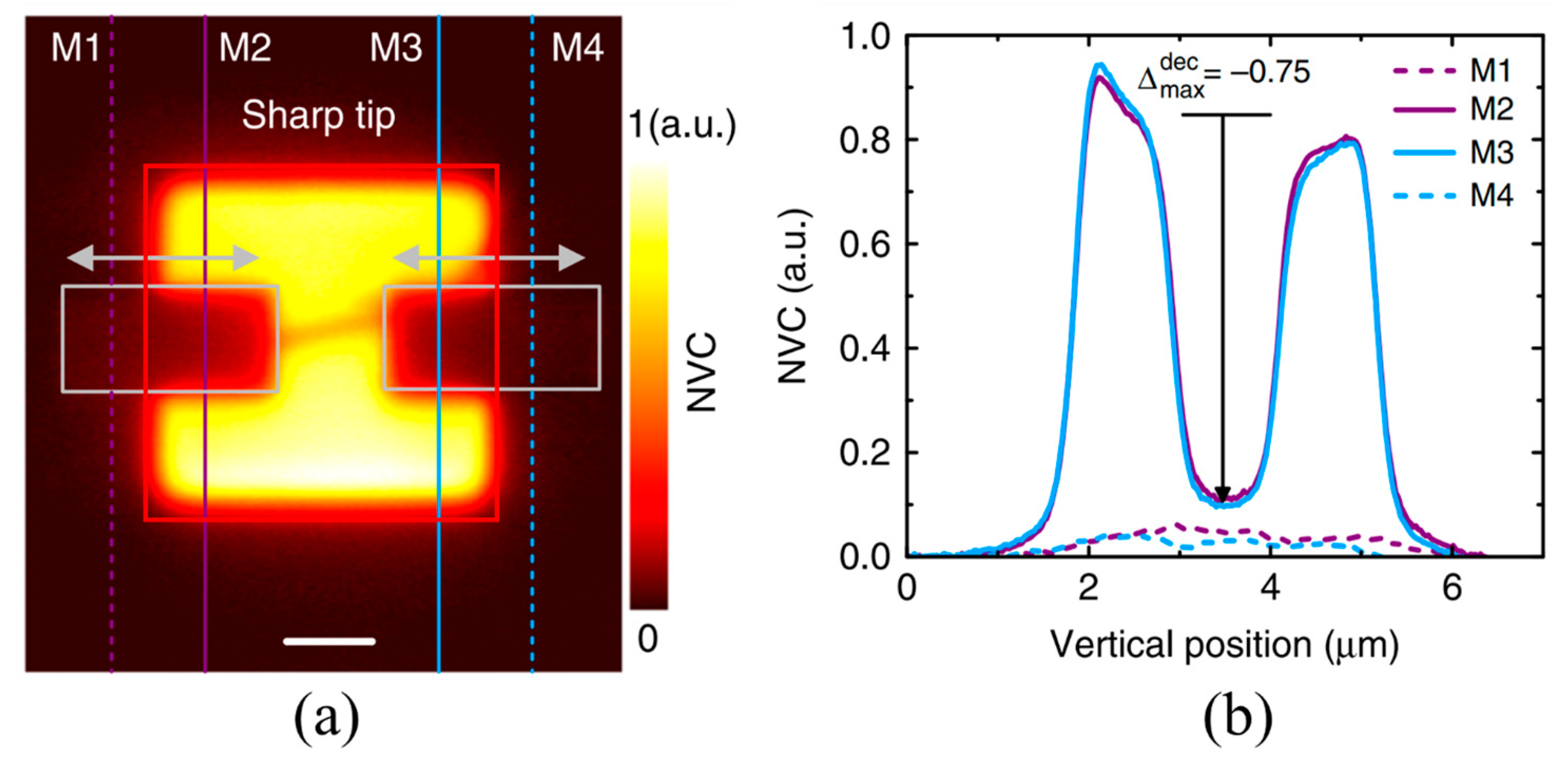
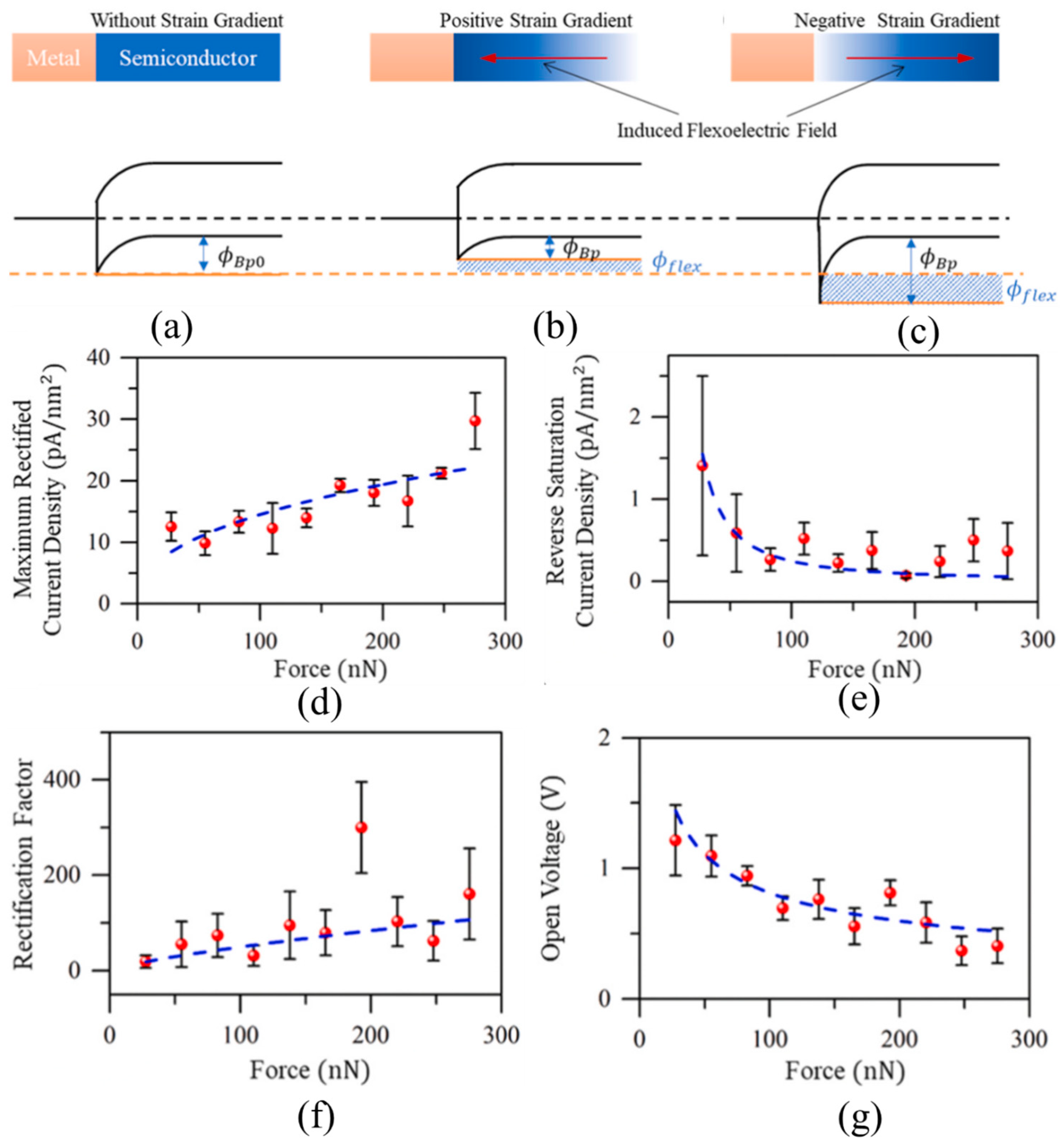
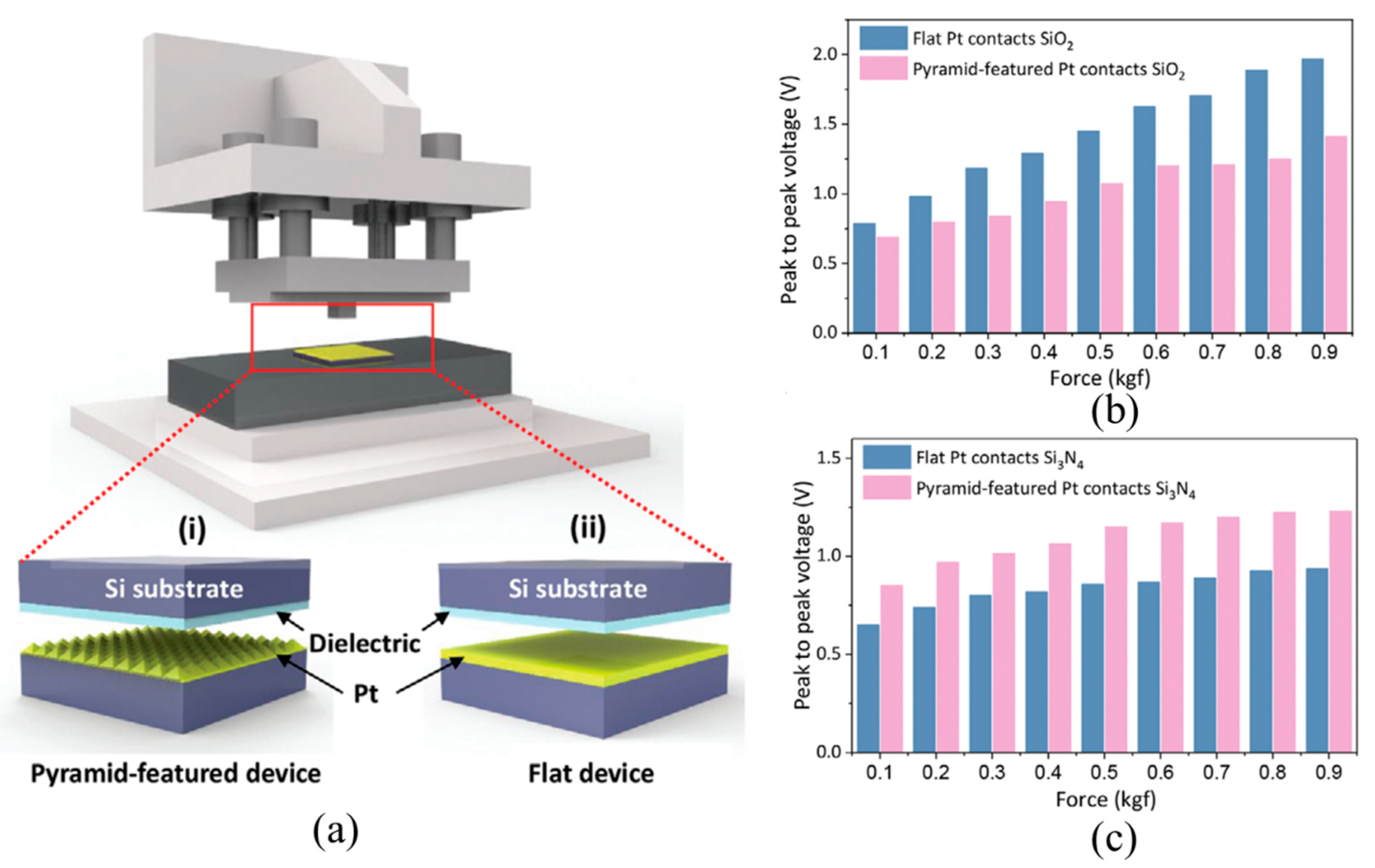
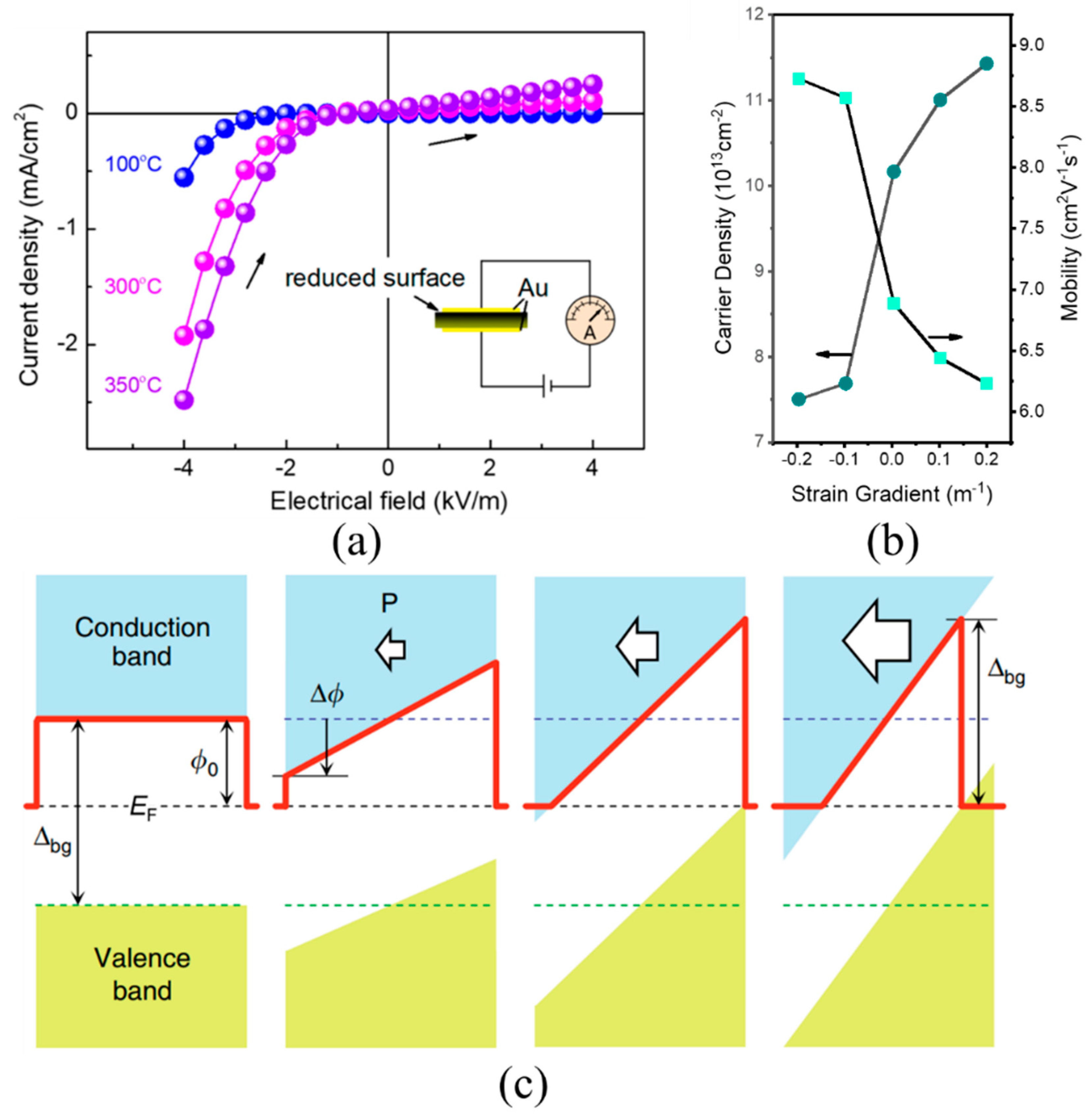
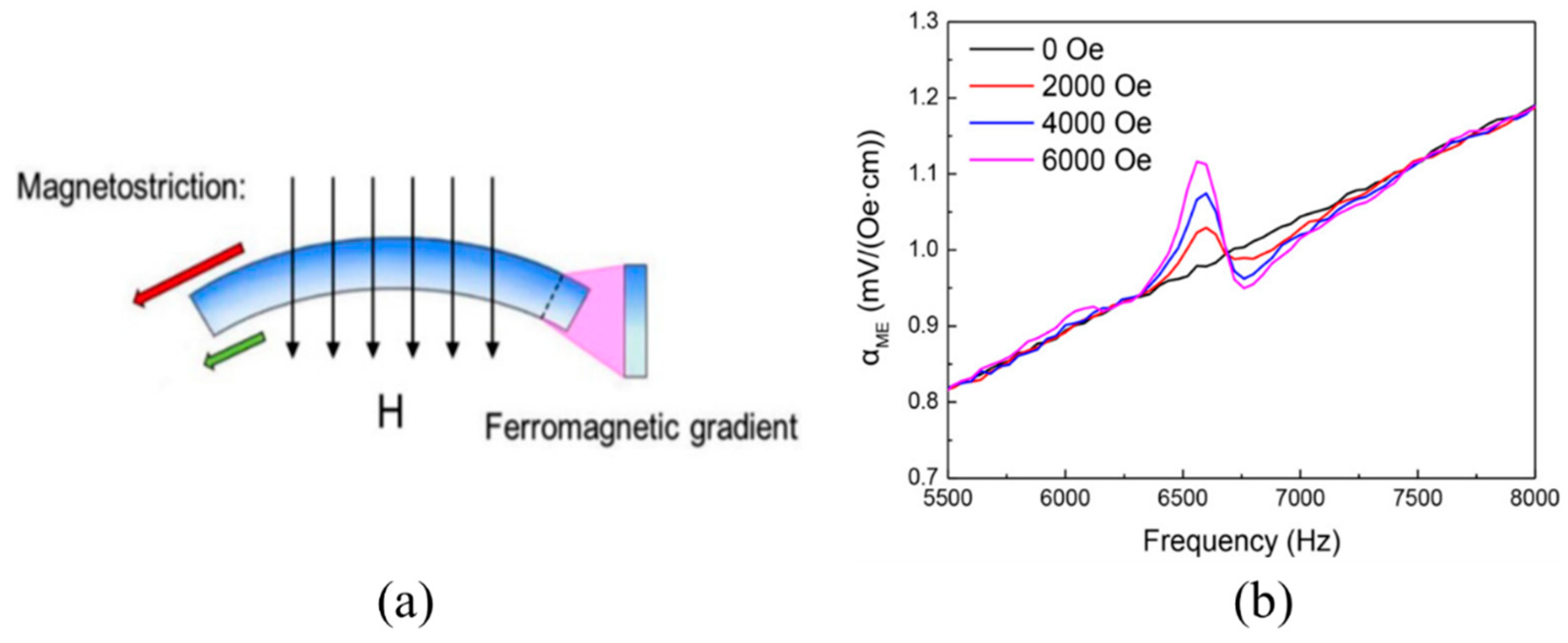
| Parameters | Meaning | Parameters | Meaning |
|---|---|---|---|
| F | Force | w(x1) | Displacement of point x1 for a cantilever beam |
| Strain gradient | P | Polarization | |
| i | Current | f | Measurement frequency |
| A | Electrode area | L | Distance from the free end to the clamping end of a cantilever beam |
| μijkl | Flexoelectric coefficient | b | Width of a plate sample or edge length of the bottom square surface of a sample with a truncated pyramid-like shape |
| s | Speed of the top metal crosshead | t | Time |
| l | Distance of the outer span of a plate sample | Q | Charge |
| z0 | Displacement of the center point of a three-point bending sample | σ | Poisson ratio |
| h | Thickness of the sample | c11 | Elastic modulus |
| d33 | Piezoelectric coefficient | r | Distance of a point from the center of a disc sample |
| RD | Radius of a disc sample | a | Edge length of the top square surface of a sample with a truncated pyramid-like shape |
| u(x,t) | Displacement of the particle at point x and time t using the shock-wave method | c | Shock-wave velocity |
| v | Speed of impacted sample by a flying plate | Ratio of the flying plate to the sample mass | |
| ρ | Mass density | Umax | Induced voltage from flexoelectric response |
| R | Resistance of a loading resistor | Ds | Diameter of a disc sample |
| γ | A deflecting micro-angle along the parallel lines of a cylinder-shaped sample | dφ | A rotating micro-angle along the diameter line of a cylinder-shaped sample |
| γrφ | Shear strain | Mn | Applied torque |
| J | Polar moment of inertia | G | Shear modulus |
| Material | Flexoelectric Coefficient (Frequency) | Value, μC/m | Method |
|---|---|---|---|
| Ba0.7Sr0.3TiO3 [35] | μ12 (17 Hz) | ~7 | CB |
| Ba0.67Sr0.33TiO3 [1] | μ11 (0.5 Hz) | ~150 | PC |
| Ba0.67Sr0.33TiO3 [33] | μ11 (400 Hz) | 121 ± 20 | CFE |
| Ba0.67Sr0.33TiO3 [9] | μ12 (1 Hz) | ~100 | CB |
| Ba0.67Sr0.33TiO3 [34] | μ12 (10 Hz) | 124 ± 14 | CFE |
| Ba0.67Sr0.33TiO3 [36] | μρ (110 Hz) | 284 ± 20 | PR |
| Ba0.67Sr0.33TiO3 [37] | μ12 | 6 ~10 | 3PB |
| Ba0.65Sr0.35TiO3 [38] | μ12 (2 Hz) | ~8 | CB |
| Ba0.6Sr0.4TiO3 [24] | μρ (110 Hz) | 10 ± 2 | PR |
| Ba0.6Sr0.4TiO3/Ni0.8Zn0.2Fe2O4 [39] | μ12 (30 Hz) | ~128 | CB |
| Ba0.5Sr0.5TiO3 [36] | μρ (110 Hz) | 2 ± 0.5 | PR |
| SrTiO3 [36] | μρ (110 Hz) | 0.3 ± 0.02 | PR |
| SrTiO3 [40] | μ12 (9 Hz) | ~0.008 | CB |
| SrTiO3 single crystals [22,41] | μ | 0.001~0.01 | 3PB |
| 20% C doped SrTiO3 [40] | μ12 (9 Hz) | ~0.16 | CB |
| Ba0.75Sr0.25TiO3 [42] | μρ (110 Hz) | 120 ± 20 | PR |
| BaTiO3 [43] | μ12 | ~10 | CB |
| BaTiO3 [30] | μ11 | ~17 | Shock wave |
| BaTiO3 single crystals [44] | (13 Hz) | 1~10 | 3PB |
| As prepared BaTiO3 [45] | μρ (110 Hz) | 120 ± 20 | PR |
| Abraded BaTiO3 [45] | μρ (110 Hz) | 30 ± 5 | PR |
| Quenched BaTiO3 [45] | μρ (110 Hz) | 45 ± 5 | PR |
| Heat-treated BaTiO3 [45] | μρ (110 Hz) | 200 ± 20 | PR |
| BaTiO3-0.08Bi(Zn0.5Ti0.5)O3 [46] | μ12 (20 Hz) | ~25 | CB |
| BaTi0.87Sn0.13O3 [47] | μ12 (30 Hz) | ~53 | CB |
| BaTi0.85Sn0.15O3 [48] | μ12 (10 Hz) | ~18 | CB |
| 0.5 wt%Al2O3-doped BaTi0.85Sn0.15O3 [48] | μ12 (10 Hz) | ~40 | CB |
| 0.2 wt%Al2O3-doped BaTi0.85Sn0.15O3 [48] | μ12 (10 Hz) | ~2 | CB |
| (Pb0.3 Sr0.7)TiO3 [1] | μ11 (0.5 Hz) | ~21 | PC |
| PMN [7] | μ12 (1 Hz) | ~4 | CB |
| 0.9PMN-0.1PT [49] | μ11 | 6~12 | PC |
| 0.9PMN-0.1PT [49] | μ11 | 20~50 | PC |
| 0.9PMN-0.1PT [50] | μ33 (0.2 Hz) | ~1000 | CFE |
| PMN-PT single crystals [51] | (13 Hz) | ~10 | 3PB |
| PMN-PT single crystals [52] | μeff (3 Hz) | ~71 | CB |
| PMN-PT single crystals [52] | μeff (6 Hz) | ~81 | CB |
| PMN-PT single crystals [52] | μeff (9 Hz) | ~99 | CB |
| PMN-PT single crystals [52] | μeff (12 Hz) | ~101 | CB |
| PIN-PMN-PT single crystals [53] | μeff (9 Hz) | ~50 | CB |
| 2.5% Bi-doped 0.7PMN-0.3PT [54] | μ12 (7 Hz) | ~260 | CB |
| 2.5% Bi-doped 0.68PMN-0.32PT [54] | μ12 (7 Hz) | ~300 | CB |
| 2.5% Bi-doped 0.66PMN-0.34PT [54] | μ12 (7 Hz) | ~220 | CB |
| 2.5% Bi-doped 0.64PMN-0.36PT [54] | μ12 (7 Hz) | ~80 | CB |
| 2.5% Sm-doped 0.70PMN-0.30PT [55] | μ12 | ~430 | CB |
| 2.5% Sm-doped 0.68PMN-0.32PT [55] | μ12 | ~550 | CB |
| 2.5% Sm-doped 0.66PMN-0.34PT [55] | μ12 | ~490 | CB |
| 2.5% Eu-doped 0.66PMN-0.32PT [55] | μ12 | ~380 | CB |
| Pb(Zr,Ti)O3 [10] | μ12 | 0.5~2 | 4PB |
| Pb(Zr,Ti)O3 [56] | μ12 (1 Hz) | ~1.4 | CB |
| Abraded PZT-81[45] | μρ (110 Hz) | 5 ± 0.5 | PR |
| Heat-treated PZT-81[45] | μρ (110 Hz) | 25 ± 2.5 | PR |
| Poled soft PZT [57] | μ12 (0.5 Hz) | ~49 | 4PB |
| PbZrO3 [58] | (13 Hz) | ~0.002 | 3PB |
| AgNbO3 [58] | μ (13 Hz) | ~0.005 | 3PB |
| NBT [59] | μρ (110 Hz) | 0.43 ± 0.02 | PR |
| NBBT2 [59] | μρ (110 Hz) | 0.83 ± 0.14 | PR |
| NBBT6 [24,59] | μρ (110 Hz) | 6.1 ± 1.22 | PR |
| NBBT8 [59] | μρ (110 Hz) | 4.19 ± 0.49 | PR |
| Heat-treated NBBT8 [42] | μρ (110 Hz) | 20 ± 5 | PR |
| Reduced NBBT8 [60] | μρ (110 Hz) | 1350 ± 100 | PR |
| NBBT10 [59] | μρ (110 Hz) | 4.24 ± 0.95 | PR |
| NBBT15 [59] | μρ (110 Hz) | 3.29 ± 0.2 | PR |
| NBBT20 [59] | μρ (110Hz) | 3.25 ± 0.38 | PR |
| NBBT20 [61] | μ12 | 2.4 ± 0.5 | CB |
| Reduced NBBT20 [61] | μ12 | 100 ± 10 | CB |
| 0.75BiFeO3-0.25BaTiO3 [62] | μρ (110 Hz) | 1 ± 0.5 | PR |
| Reduced 0.75BiFeO3-0.25BaTiO3 [62] | μρ (110 Hz) | 140 ± 20 | PR |
| (Bi1.5Zn0.5)(Zn0.5Nb1.5)O7/Ag [63] | μ12 (10 Hz) | ~0.17 | CB |
| (K0.4Na0.58Li0.02)(Nb0.96Sb0.04)O3 [64] | μ12 | ~1 | CB |
| KTaO3 single crystals [41] | μeff | ~0.004 | 3PB |
| YAlO3 single crystals [41] | μeff | ~−0.004 | 3PB |
| DyScO3 single crystals [41] | μeff | ~−0.008 | 3PB |
| LaAlO3 single crystals [41] | μeff | ~−0.003 | 3PB |
| Material | Flexoelectric Coefficient (Frequency) | Value, μC/m | Method |
|---|---|---|---|
| PVDF [21] | μ12 (21 Hz) | 0.013 ± 0.001 | CB |
| Oriented PET [21] | μ12 (21 Hz) | 0.0099 ± 0.0004 | CB |
| P(VDF-TrFE) [65] | μ12 | ≤0.191 ± 0.017 | CB |
| P(VDF-TrFE-CFE) [65] | μ12 | 0.03 ± 0.0015 | CB |
| PVDF [31] | μ12 | ~0.00073 | CT |
| -phase bulk PVDF [26] | μ11 | ~0.016 | PC |
| PVDF [66] | μ12 | ~0.015 | CB |
| PVDF [66] | μ12 | ~0.01 | 3PB |
| PVDF [66] | μ12 | ~0.014 | 4PB |
| PVDF [67] | μ12 (6 Hz) | 0.00582 ± 0.00043 | CB |
| P(VDF-CTFE) [67] | μ12 (6 Hz) | 0.00216 ± 0.00027 | CB |
| P(VDF-HFP) [67] | μ12 (6 Hz) | 0.00257 ± 0.00026 | CB |
| PVDF/10 vol% BST [68] | μ12 (6 Hz) | 0.00436 ± 0.00093 | 3PB |
| PVDF/15 vol% BST [68] | μ12 (6 Hz) | 0.00681 ± 0.0007 | 3PB |
| PVDF/20 vol% BST [68] | μ12 (6 Hz) | 0.00877 ± 0.00119 | 3PB |
| PVDF/25 vol% BST [68] | μ12 (6 Hz) | 0.0135 ± 0.00176 | 3PB |
| P(VDF-TrFE) (70/30) [69] | μ12 (6 Hz) | 0.00304 ± 0.00055 | 3PB |
| P(VDF-TrFE) (55/45) [69] | μ12 (6 Hz) | 0.00418 ± 0.00067 | 3PB |
| P(VDF-TrFE-CTFE) [69] | μ12 (6 Hz) | 0.00352 ± 0.0005 | 3PB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, D.; Jeong, D.-Y.; Fu, Z.; Chu, B. Flexoelectric Effect of Ferroelectric Materials and Its Applications. Actuators 2023, 12, 114. https://doi.org/10.3390/act12030114
Tian D, Jeong D-Y, Fu Z, Chu B. Flexoelectric Effect of Ferroelectric Materials and Its Applications. Actuators. 2023; 12(3):114. https://doi.org/10.3390/act12030114
Chicago/Turabian StyleTian, Dongxia, Dae-Yong Jeong, Zhenxiao Fu, and Baojin Chu. 2023. "Flexoelectric Effect of Ferroelectric Materials and Its Applications" Actuators 12, no. 3: 114. https://doi.org/10.3390/act12030114
APA StyleTian, D., Jeong, D.-Y., Fu, Z., & Chu, B. (2023). Flexoelectric Effect of Ferroelectric Materials and Its Applications. Actuators, 12(3), 114. https://doi.org/10.3390/act12030114






