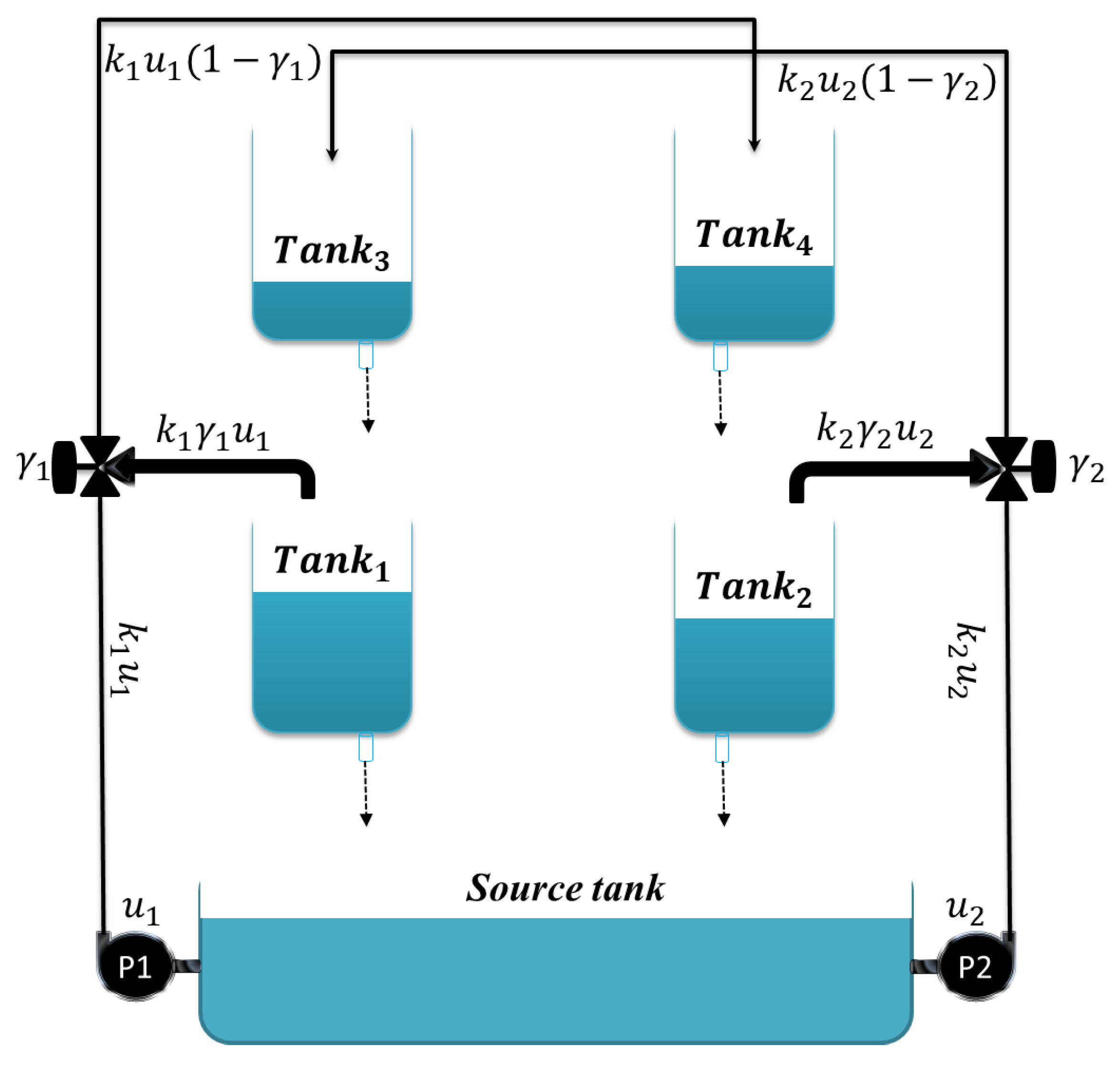
1. Introduction
Industrial processes are physical systems that comprise a group of operations to complete a specific requirement. Interaction during the industrial process is essential to most industrial processes; this interaction may cause multiple variables which increase the complexity of nonlinear systems. One of these industrial processes is the chemical industry, which has become significant to other industries in the last century such as the transport and pharmaceutical industries, in turn contributing to the development of the economy [
1]. The four-tank system is an example of the industrial chemical process proposed by [
1] at the end of 1995. It is considered one of the multivariable systems with strong nonlinearity and is used as a laboratory process for understanding the control concept for the multivariable control system [
1,
2].
At present, several control strategies have been proposed to study and control the performance of the four-tank system, from conventional simple methods to more accurate and complex methods. The author of [
3] presented four controllers: the linear quadratic regulator (LQR), linear quadratic Gaussian regulator (LQGR),
controller, and
controller. Simulation results showed the effectiveness of the LQR in providing a good percentage with regard to settling time. However, it showed a noticeable overshoot in the output response. Recently, some researchers considered the problem of disturbance and delay in the four-tank system and studied the performance of the system under these conditions. Authors in [
4] developed a decentralized nonlinear robust model predictive control (MPC). A comparison between the decentralized MPC, a centralized MPC, and a cascaded PI controller was conducted. Moreover, the author of [
5] proposed a second-order sliding mode controller, which is a twisting algorithm (TA) based controller. A comparison between the TA and a conventional sliding mode controller (SMC) was undertaken, and the simulation results showed that the TA performed better than the SMC in chattering reduction and disturbance rejection. In addition, the author of [
6] designed and implemented two controllers: the adaptive pole placement controller (APPC) and robust adaptive sliding mode controller (ASMC). A comparison between the APPC, ASMC, and the conventional PID was conducted under different conditions such as with reference tracking, exogenous disturbance applied to the four-tank system, and parameter uncertainties. The results showed that the ASMC has better transient and disturbance attenuation and a faster response than both APPC and PID. Furthermore, the author of [
7] presented a developed version of the four-tank system with SMC-based feedback linearization to stabilize the system within a specific range. The time-delayed four-tank system has been controlled using various techniques, such as SMC,
observer-based robust control, fuzzy control, and neural control [
8,
9,
10,
11,
12], while some authors have used the disturbance rejection technique as in [
13], wherein the author presented the design of a nonlinear disturbance observer-based port-controlled Hamiltonian (PCH) with a basic feedback controller. Simulation results showed that the proposed method had a better response and was more robust to the disturbance than the terminal sliding mode control. A nonlinear disturbance observer has been introduced to estimate disturbance along with a novel input/output feedback linearization controller. In [
14], a comparison between this proposed method, PID, and a disturbance observer-based sliding mode controller (DOBSMC) was conducted and showed that the proposed method improves the robustness of the system against disturbance and has superior performance compared with both PID and DOBSMC. The authors in [
15] studied a sliding mode observer (SMO) to estimate the valve ratios and higher-order sliding mode controller (HOSM) to ensure accurate performance and to attenuate chattering. The simulation results of the sliding mode observer based on the higher-order sliding mode controller showed that the proposed method was stable and accurately estimated the unknown parameter. Moreover, a comparison between the super twisting controller (STA) and the conventional sliding mode controller has been conducted and showed the robustness and the smoothing feature of the STA. In addition, the authors in [
16] proposed a new linear active disturbance rejection control (LADRC) with a nonlinear function. A comparison between the PID, LADRC, and ADRC was conducted. The simulation results showed that the proposed LADRC provides good steady-state performance, fast-tracking, and eliminates disturbance more accurately than PID and conventional LADRC. Finally, in [
17], the authors proposed two disturbance rejection control laws which were designed and tuned using Embedded Model Control to solve two problems, the first being the regulation of the water levels of the lower tanks, and the second being the regulation of the water levels of the four tanks. Although all the above studies proposed excellent and accurate controllers for the four-tank system, there are still some drawbacks in their work. Some of the above studies used a linearized model of the four-tank system [
1,
2]. As a result, these controllers were incapable of following the nonlinear dynamics of the system, especially in practical implementation. Moreover, the controllers could not handle the nonlinearity or cancel the effect of the applied disturbance in a sufficient way. Thus, the main goal of this research is to design robust control laws with the nonlinear four-tank system and in consideration of the problems of disturbance, uncertainty, and reference tracking.
Motivated by the aforementioned studies, two schemes of modified active disturbance rejection control (MADRC) are proposed with the nonlinear model of the four-tank system. The modification part of the MADRC is presented as follows:
- i.
The proposed tracking differentiator is used in the control unit to provide the error signal and its derivative.
- ii.
The proposed super twisting sliding mode controller (STC-SM), nonlinear proportional derivative (NLPD), and modified nonlinear state error feedback (MNLSEF) are used as nonlinear state error feedback (NLSEF) instead of the conventional NLSEF proposed by [
18].
- iii.
The modified nonlinear extended state observer (MNLESO) and
fal function ESO are used instead of the linear extended state observer (LESO) [
19].
The advantages of our proposal are that it may overcome problems presented previously such as nonlinearity, strong interacting, disturbance, uncertainty of the parameters and that it is able to track any applied reference.
To the best of our knowledge, a super twisting controller with improved active disturbance rejection control has not yet been proposed in the literature. This model solves the problem of the four-tank system in a significant and accurate way, which is our incentive for continuing this research endeavor.
The rest of this paper is organized as follows:
Section 2 presents the problem statement. The modeling of the four-tank system is presented in
Section 3, and the design of the modified ADRC is introduced in
Section 4. The convergence of the proposed control schemes is then demonstrated in
Section 5.
Section 6 demonstrates the simulation results and provides a discussion. Finally, the conclusions of this paper are given in
Section 7.
6. Simulation Results and Discussion
This section presents the simulation results and discussion. The four-tank model with the modified ADRC was tested and implemented using MATLAB/SIMULINK. Moreover, all the obtained results of the proposed method were compared with different methods. In this study, the genetic algorithm was utilized as an optimization technique to tune the parameters. The genetic algorithm (GA) is an optimization algorithm that was first proposed by Holland in [
28]. There are three steps to generating the next generation from the current generation, the implementation of which is used to select the best generation with the best genes. Mutation is the step that generates a new offspring with a random mutation in its genes. Finally, crossover is the step that generates offspring by exchanging the genes of the parents randomly until crossover is available. In addition, the four-tank parameters used for simulation are listed in
Table 4. Furthermore, a summary of all the proposed methods used in this work along with the other methods is given in
Table 5. The optimization processes were achieved by means of function (GA) within the MATLAB simulation.
Figure 3 shows the MADRC with GA.
Table 4.
Sampled parameters of the four-tank system [
1].
Table 4.
Sampled parameters of the four-tank system [
1].
| Parameters | Description | Value | Unit | Reference |
|---|
| The water level of | | | Estimated |
| The water level of | | | Estimated |
| The water level of | | | Estimated |
| The water level of | | | Estimated |
| The cross-section area of the outlet hole of | | | [1] |
| The cross-section area of the outlet hole of | | | [1] |
| The cross-section area of the outlet hole of | | | [1] |
| The cross-section area of the outlet hole of | | | [1] |
| The cross-section area of | | | [1] |
| The cross-section area of | | | [1] |
| The cross-section area of | | | [1] |
| The cross-section area of | | | [1] |
| The ratio of the flow in the | | | [1] |
| The ratio of the flow in the | | | [1] |
| Pump proportionality constant | | | [1] |
| Pump proportionality constant | | | [1] |
| Gravity constant | | | [1] |
| The calibrated constant | | | Estimated |
| The maximum height | | | Estimated |
Table 5.
Summary of all the proposed methods used in this work.
Table 5.
Summary of all the proposed methods used in this work.
| Scheme | TD | SEF | ESO |
|---|
| Linear active disturbance rejection control LADRC | - | LPID that can be given as | Linear extended state observer (LESO) [19] |
| (24) | | (25) |
| ADRC | - | NLSEF [18] |
| (26) |
| Improved active disturbance rejection control (IADRC) | - | Improved nonlinear state error feedback (INLSEF) [29] | Sliding mode extended state observer (SMESO) [30] |
| (27) | | (28) |
| ) are the controller parameters | is a nonlinear function |
| S fal-ADRC | - | NLSEF Equation (26) | Symmetrical fal ESO Equation (11) |
| D fal-ADRC | - | Different fal ESO Equation (12) |
MADRC scheme
(NLP-ADRC) and
(STC-ADRC) | Equation (3a) | Proposed NLPD Equation (5) | scheme Equation (7) |
| Equation (3b) | Proposed STC-SM Equation (6) | scheme Equation (8) |
MADRC scheme
(D fal-ADRC-TD) | Equation (8) | Proposed MNLSEF Equations (9) and (10) | Different fal ESO Equation (12) |
The multi-objective performance index (OPI) was used in this work to tune the parameters of the modified ADRC (MADRC) and the methods in
Table 4 in order to find the optimal value. It is expressed as follows:
The value of
and
were set to
and the weighted factor of each subsystem was set to
. The nominal values of the individual objectives that contain the (OPI) were set to
, and
. After the tuning process was conducted using GA [
31,
32], the parameter values of the modified ADRC and all the methods mentioned previously in
Table 5 were obtained and are given in
Table 6,
Table 7,
Table 8,
Table 9,
Table 10,
Table 11,
Table 12 and
Table 13.
To check the effectiveness of the proposed method, three tests were applied to the four-tank model as follows:
- A.
Case study 1. Exogenous disturbance
In this test, a step function was applied as a desired reference for both subsystems. Moreover, to investigate the effectiveness and robustness of the designed ADRC against the applied disturbance, a step function was applied as an exogenous disturbance. The water levels of both subsystems while applying an exogenous disturbance after
of starting the simulation for the first subsystem and after
of starting the simulation for the second subsystem are shown in
Figure 4. The output response of the first subsystem is given in
Figure 4a. The results show that in applying disturbance for the first subsystem at
, LADRC, ADRC, and IADRC exhibited an output response with an undershoot which reached nearly
,
,
, and
of the steady-state value, respectively, and lasted about
for LADRC,
for ADRC, and
for IADRC until the output response reached its steady state. For the second subsystem as shown in
Figure 4b, at
the output response exhibited an undershoot which reached nearly
,
, and
of its steady-state value for LADRC, ADRC and IADRC, respectively, and lasted about
for LADRC,
for ADRC, and
for IADRC until it reached its steady state. However, the proposed methods rejected the disturbance very quickly. It is observed that the output response of the proposed methods (i.e., NLPD-ADRC, STC-ADRC) is faster, smoother, and without overshooting when compared with the other methods. It took less than approximately
to reach the steady state (desired value), while a longer settling time was clearly observed in the output responses of the other methods.
The output response when using the second MADRC scheme is shown in
Figure 5. As can be seen from
Figure 5a, the output response reached a steady state with a smooth and fast response. However, it took approximately
and
for S
-ADRC and D
-ADRC to attenuate the disturbance and return to the steady state, respectively. Furthermore, under the effect of the disturbance, the output showed an undershoot of
and
of the steady state value for S
-ADRC and D
-ADRC, respectively. By contrast, the output response of the proposed method (i.e., D
-ADRC-TD) is smooth and more accurate, representing an improvement in terms of disturbance attenuation compared with D
-ADRC and S
-ADRC, which proves the effectiveness of the designed controller and observer. Further, as can be seen from
Figure 5b, the output response of the proposed method (i.e., D
-ADRC-TD) under the disturbance effect shows an improvement and robustness in canceling the disturbance effect in a short time, while the other methods, LADRC, ADRC, and S
-ADRC, take about
,
, and
to remove the disturbance effect and return to the steady state, respectively. Moreover, the output responses of the methods under the effect of the disturbance showed an undershoot of
,
,
,
, and
of the steady-state value for LADRC, ADRC, IADRC, and S
-ADRC, respectively.
Figure 6a,b show the control signal of the first subsystem and the second subsystem respectively. It is observed that the first MADRC scheme (i.e., STC-ADRC) is chattering-free with a smooth response; moreover, the NLPD-ADRC shows a reduction in chattering, while the other methods, such as ADRC, show chattering in the control signal. This proves the effectiveness of the proposed method.
Figure 7a,b show the control signal of the first subsystem and the second subsystem, respectively. It is observed that the second MADRC scheme (i.e., D
-ADRC-TD) is chattering-free with a smooth response, while the other methods, such as ADRC, show chattering in the control signal. This proves the effectiveness of the proposed method.
- B.
Case study 2. Parameter uncertainty
In this test, the system’s parameter uncertainty is taken into consideration to observe its effect on the nonlinear system. One of the parameters that affects the performance of the four-tank model is uncertainty in the design of the outlet hole of the first tank.
Figure 8 show the output response of the first tank under the presence of the parameter uncertainties (
) after
from starting the simulation. It appears that the proposed methods (i.e., NLPD-ADRC, STC-ADRC) can cope with parameter variation easily, while the other methods give undershoots of
of the steady state, respectively, and it takes LADRC, ADRC, and IADRC approximately
to weaken and reduce the uncertainty effect, respectively. By contrast, the proposed methods attenuate the effect of the parameter variation in less than
.
- C.
Case study 3. Reference tracking
In this test, a step function was applied for both subsystems with different amplitude and time to check the robustness and validation of the designed MNLESO and controllers in tracking references applied at different times.
Figure 9a shows the output response of the first subsystem when using NLPD-ADRC and STC-ADRC, while
Figure 9b shows the output response of the second subsystem. It is clear for both subsystems that the proposed methods (i.e., NLPD-ADRC and STC-ADRC) exhibit a smooth, fast-tracking, chattering-free, and accurate response without any visible over or undershoot (STC-ADRC), which reflects the effectiveness of the designed ESO and controller in coping with the time-varying reference.
Figure 10a shows the output response of the first subsystem when using S
-ADRC, D
-ADRC, and D
-ADRC-TD, while
Figure 10b shows the output response of the second subsystem. It is clear for both subsystems that the proposed method (D
-ADRC-TD) exhibits a smooth, fast-tracking, and accurate response without any peaking, which proves the effectiveness of the designed ESO and controller under the time-varying references.
Table 14 below proves that the STC-ADRC method provides the best result in terms of OPI reduction and steady-state error, while the other methods, such as NLPD-TD, D
fal-ADRC, and D
fal-ADRC-TD exhibit noticeable reduction in the OPI.
Remark 1. The intelligent PID (iPID) is a PID controller where the nonlinearity, unknown parts of the plant, and time-varying parameters are considered but do not appear in the modeling (see [33]). The ADRC is a robust control which estimates the total disturbance and rejects it in an online manner (see, for example, Equation (7) and [18,20,21]).