Transfer Learning-Based Fault Diagnosis Method for Marine Turbochargers
Abstract
:1. Introduction
2. Turbocharger Simulation Model Building
2.1. Turbocharger Bench Test
2.2. Turbocharger Model
2.2.1. Whole Machine Model
2.2.2. Input of Model Parameters
2.2.3. Finite Element Division and Modal Reduction of Turbocharger Substructure
2.2.4. EHD Bearing Modelling
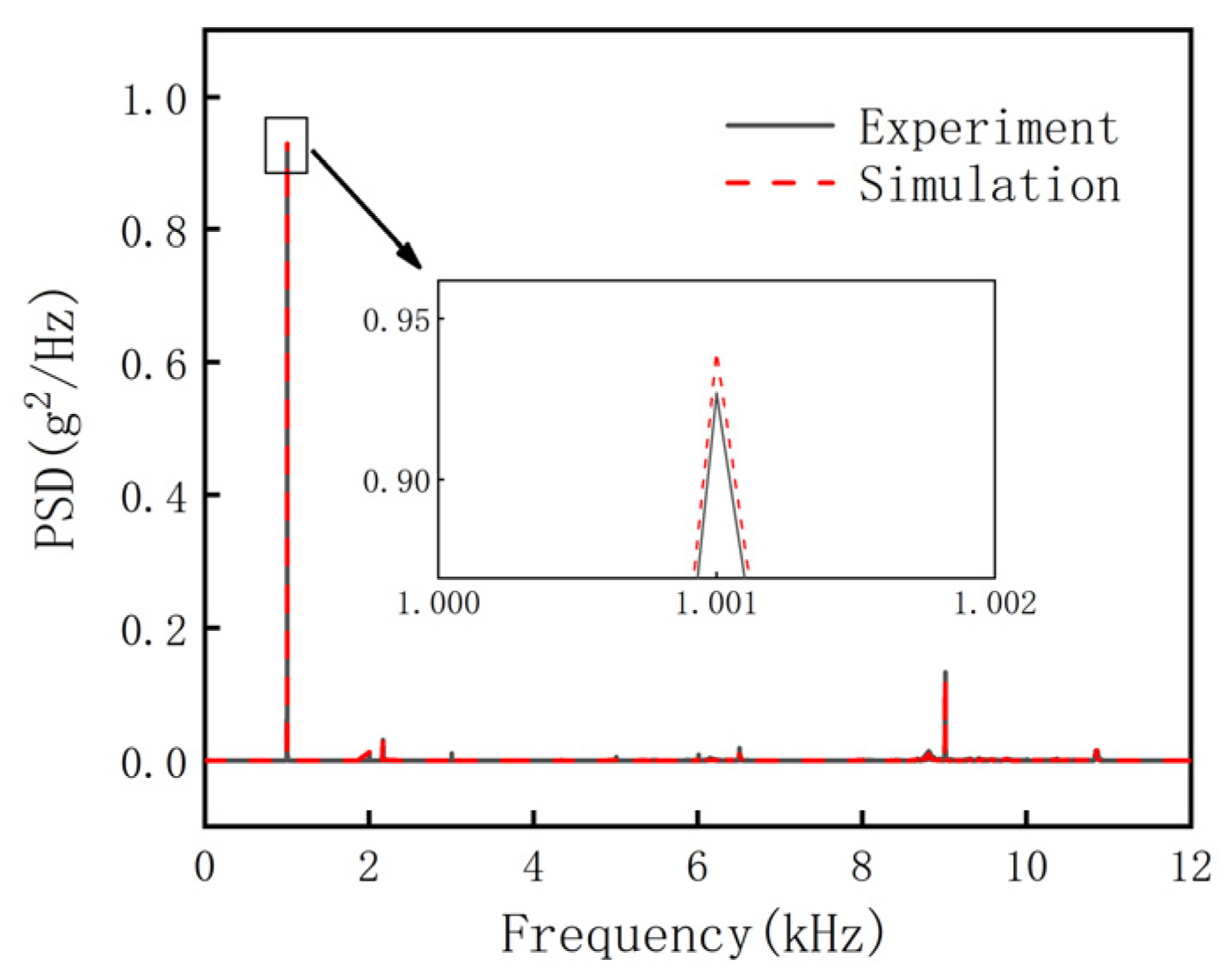
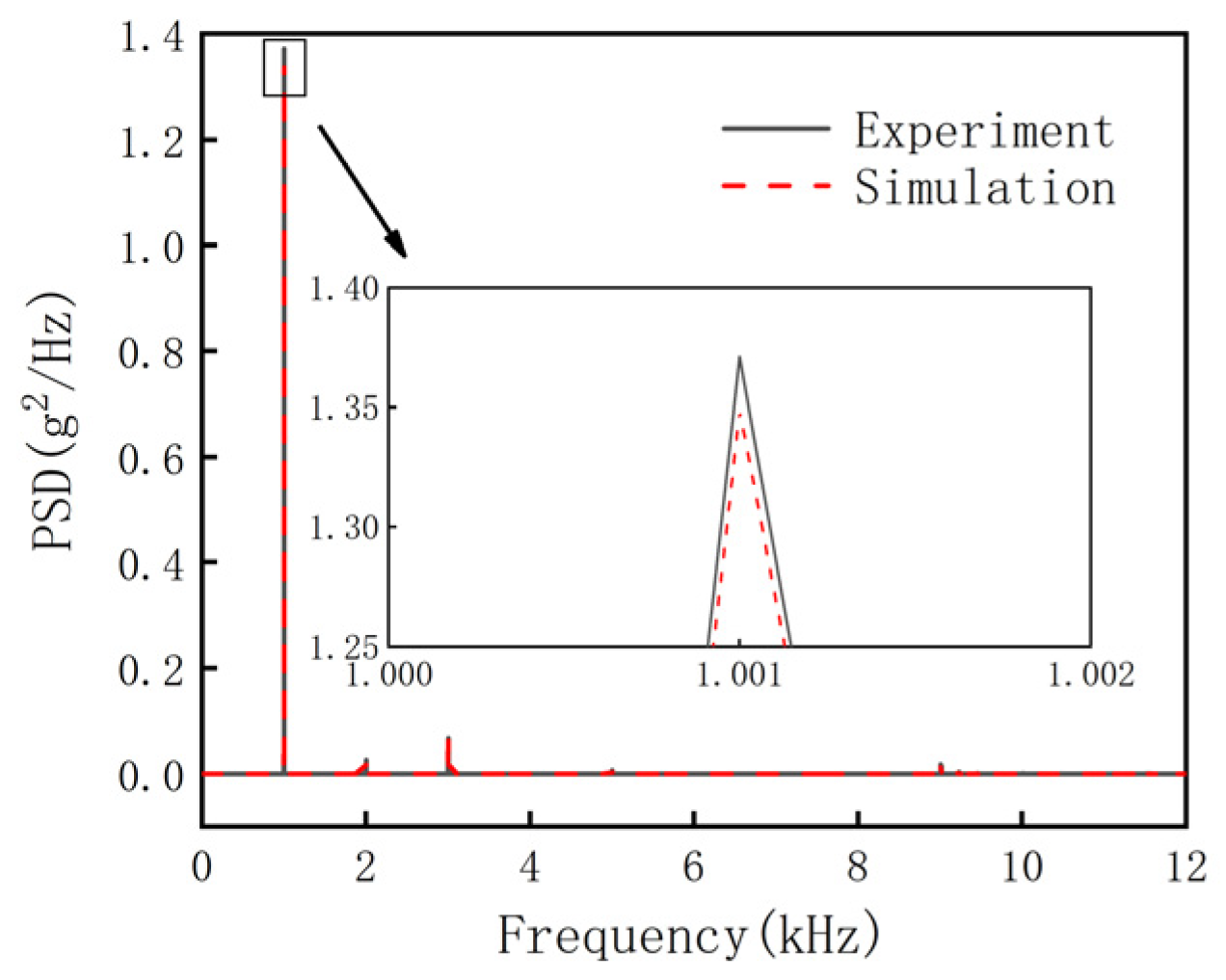
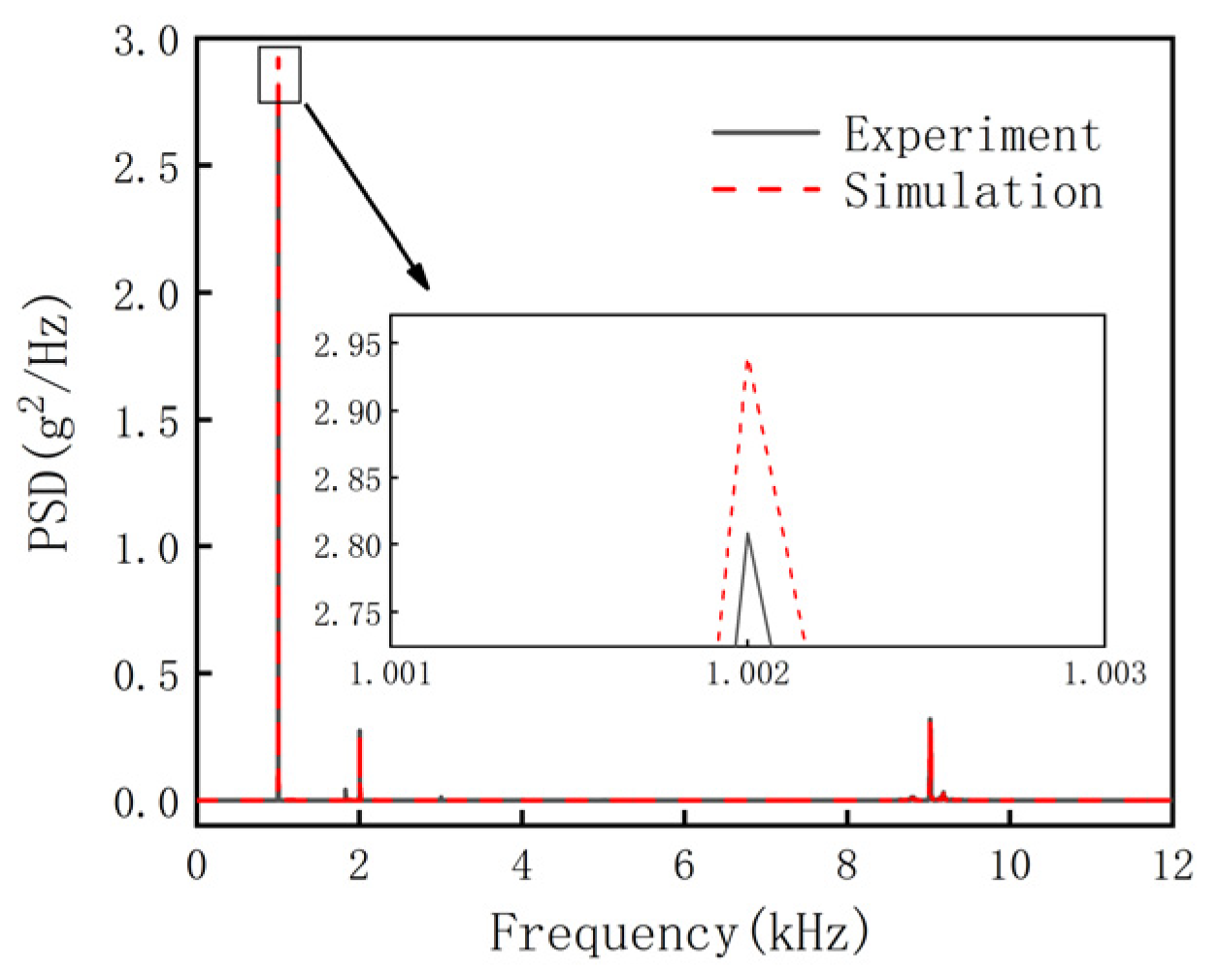
2.3. Model Validation
3. Fault Simulation and Its Data Analysis
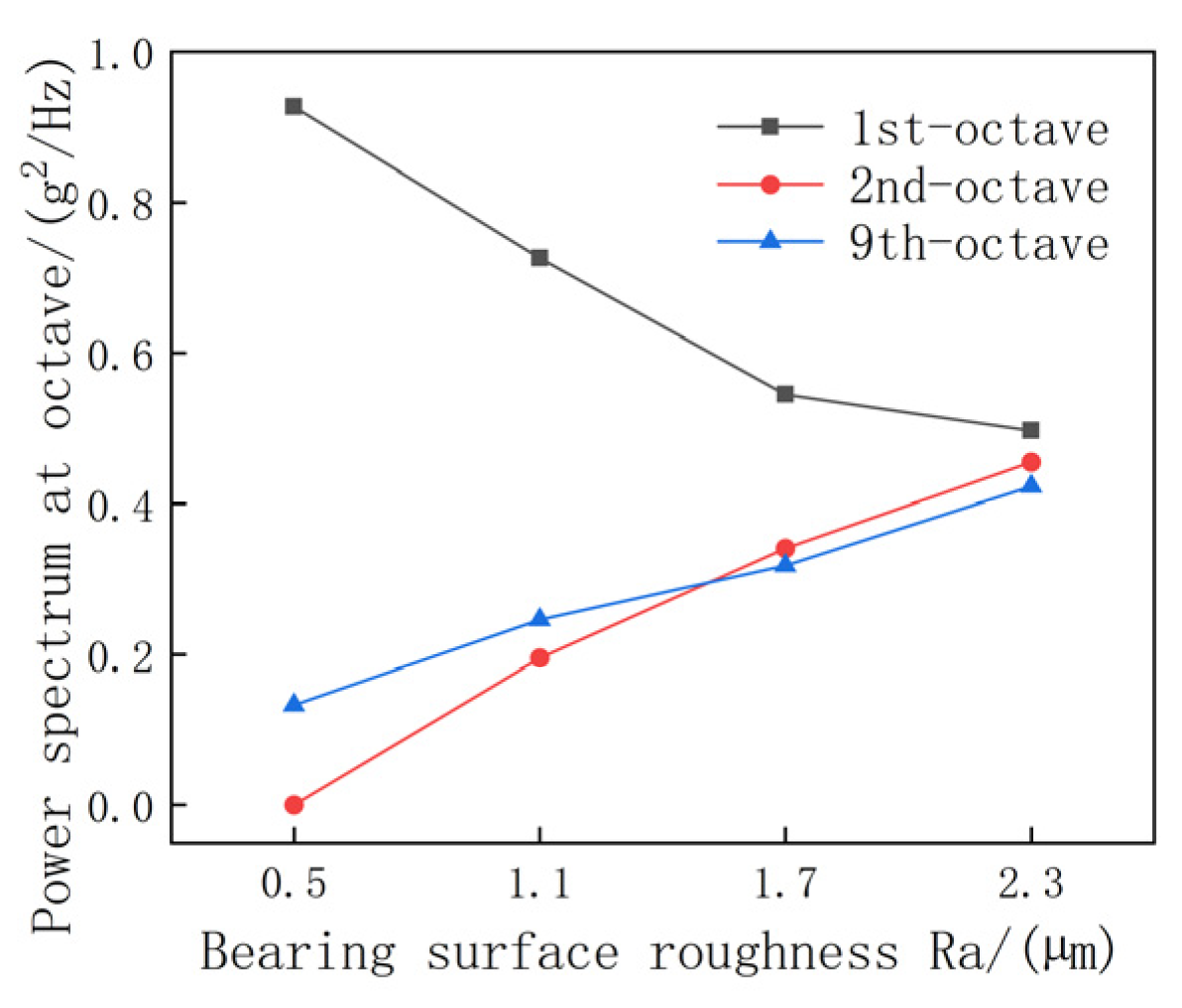
3.1. Bearing Wear Simulation
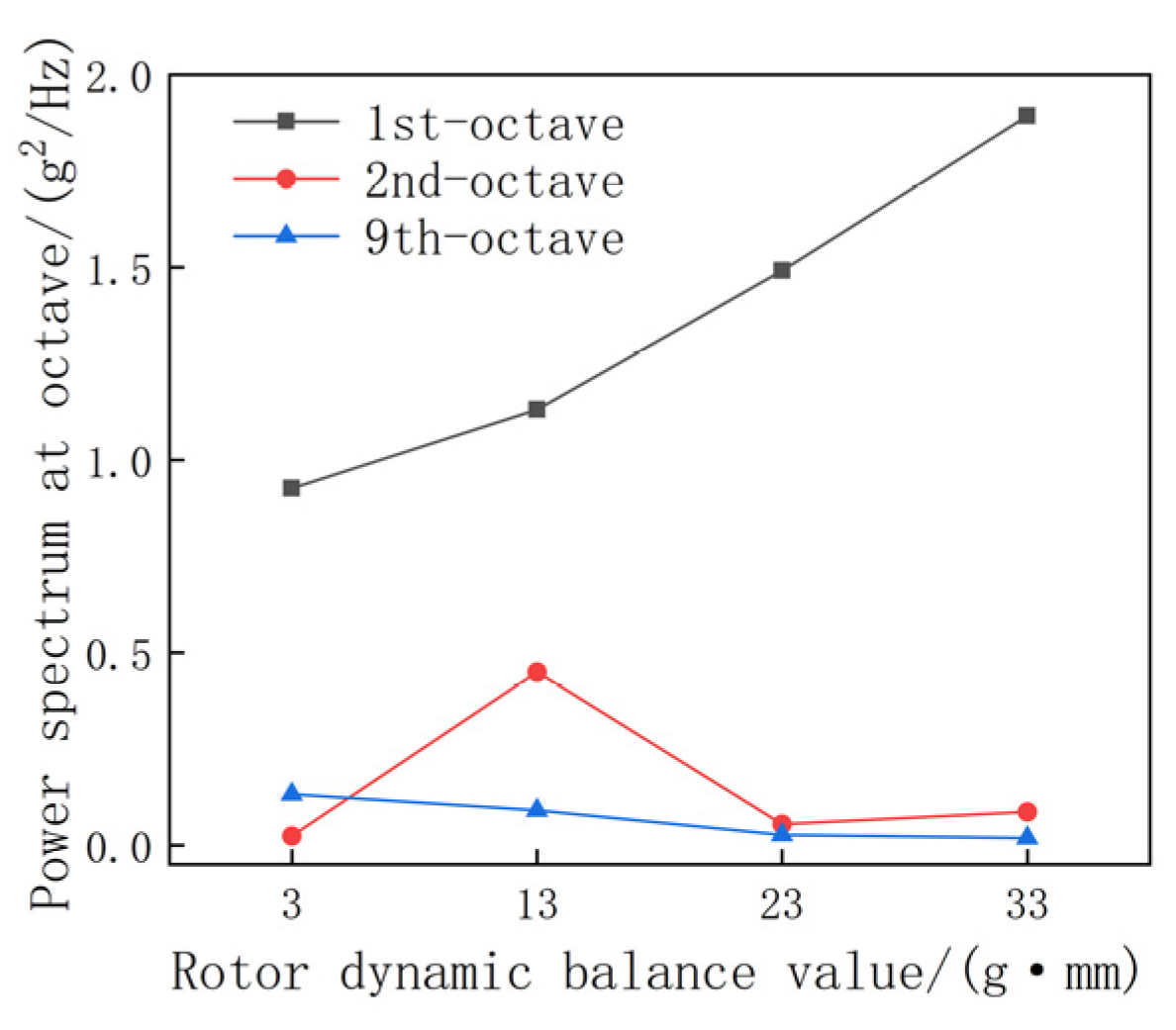
3.2. Dynamic Unbalance Simulation
4. Turbocharger Fault Feature Extraction
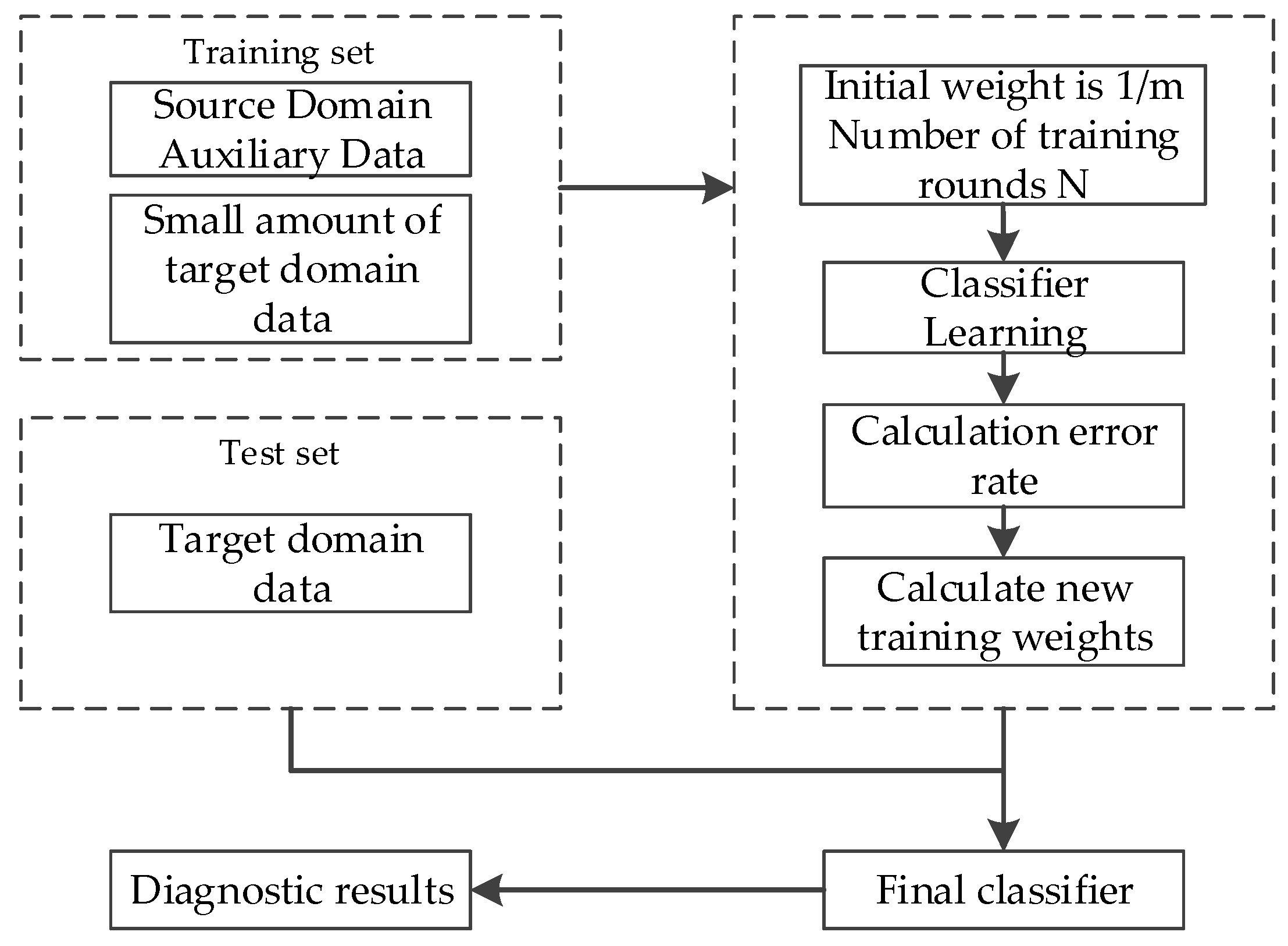
5. Transfer Learning Based Turbocharger Fault Diagnosis Method
5.1. TrAdaBoost Algorithm
| Algorithm 1 TrAdaBoost |
| Step 1: Initialization Input N, X, S and by Equation (20). Step 2: Update weight for t = 1:N Calculate , ht, by Equation (21) and (22). If , take . Use the value of and ht to calculate , and by Equations (23)~(25). end for Step 3: Output the hypothesis Calculate by Equation (26). |
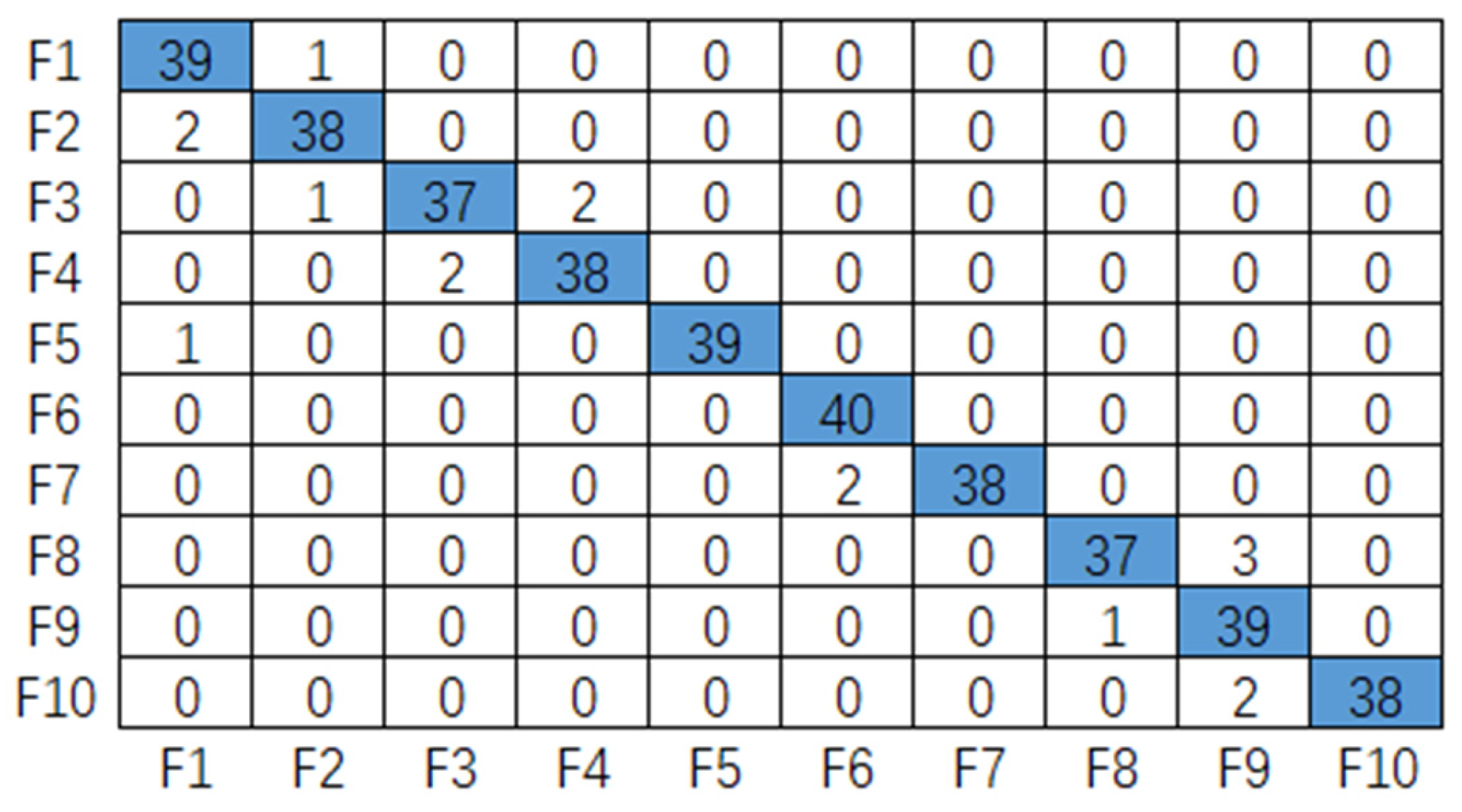
5.2. Model Diagnostic Effect
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Result of linear chirplet transform | |
| Time domain signal | |
| Window function | |
| c | Demodulation rate |
| β | Rotation angle |
| Sampling rate | |
| Sampling time | |
| Nc | Number of demodulation rates |
| RE | Rayleigh entropy |
| SNR | Signal-to-noise ratio |
| RMSE | Root mean square error |
| PSNR | Peak signal-to-noise ratio |
| x | Effective signal |
| m | Number of sampling points |
| Instantaneous phase of the kth component of the signal | |
| Amplitude of the kth component of the signal | |
| Result of linear MOMSSCT | |
| δ | The dirichlet function |
| Δ | Band width |
| RMS value of rotor n× frequency vibration | |
| xnk | The rotor n× frequency vibration component waveform |
| Rotor unbalance factor | |
| Rotor 1× frequency | |
| Bearing wear factor | |
| X | Joint training set |
| Xa | Auxiliary domain sample space |
| Xb | Source domain sample space |
| S | Test set |
| Initial weight vector | |
| Distribution | |
| ht | Output prediction |
| Error | |
| γ | Weight calculation factor |
| Learning machine weights | |
| N | The maximum number of iterations |
| Hypothesis | |
| n | Number of samples |
| m | Number of samples in the source domain training set |
| True label value of the data | |
| xi (i = 1, 2, …, n) | Sample in Xa |
| xi (i = n + 1, …, n + m) | Sample in Xb |
| TFR | Time–frequency representation |
References
- Varbanets, R.; Fomin, O.; Píštěk, V.; Klymenko, V.; Minchev, D.; Khrulev, A.; Zalozh, V.; Kučera, P. Acoustic Method for Estimation of Marine Low-Speed Engine Turbocharger Parameters. J. Mar. Sci. Eng. 2021, 9, 321. [Google Scholar] [CrossRef]
- Knežević, V.; Orović, J.; Stazić, L.; Čulin, J. Fault Tree Analysis and Failure Diagnosis of Marine Diesel Engine Turbocharger System. J. Mar. Sci. Eng. 2020, 8, 1004. [Google Scholar] [CrossRef]
- Mashhadi, P.S.; Nowaczyk, S.; Pashami, S. Stacked Ensemble of Recurrent Neural Networks for Predicting Turbocharger Remaining Useful Life. Appl. Sci. 2020, 10, 69. [Google Scholar] [CrossRef] [Green Version]
- Marelli, S.; Carraro, C.; Marmorato, G.; Zamboni, G.; Capobianco, M. Experimental analysis on the performance of a turbocharger compressor in the unstable operating region and close to the surge limit. Exp. Therm. Fluid Sci. 2014, 53, 154–160. [Google Scholar] [CrossRef]
- Li, C.H. Dynamics of rotor bearing systems supported by floating ring bearings. J. Tribol. 1982, 104, 469–477. [Google Scholar] [CrossRef]
- Peixoto, T.F.; Nordmann, R.; Cavalca, K.L. Dynamic analysis of turbochargers with thermo-hydrodynamic lubrication bearings. J. Sound Vib. 2021, 505, 116140. [Google Scholar] [CrossRef]
- Ntonas, K.; Aretakis, N.; Roumeliotis, I.; Pariotis, E.; Paraskevopoulos, Y.; Zannis, T. Integrated simulation framework for assessing turbocharger fault effects on diesel-engine performance and operability. J. Energy Eng. 2020, 146, 04020023. [Google Scholar] [CrossRef]
- Koutsovasilis, P. Automotive turbocharger rotordynamics: Interaction of thrust and radial bearings in shaft motion simulation. J. Sound Vib. 2019, 455, 413–429. [Google Scholar] [CrossRef]
- Wang, J.; Wen, H.; Qian, H.; Guo, J.; Zhu, J.; Dong, J.; Shen, H. Typical Fault Modeling and Vibration Characteristics of the Turbocharger Rotor System. Machines 2023, 11, 311. [Google Scholar] [CrossRef]
- Bin, G.-F.; Huang, Y.; Guo, S.-P.; Li, X.-J.; Wang, G. Investigation of induced unbalance magnitude on dynamic characteristics of high-speed turbocharger with floating ring bearings. Chin. J. Mech. Eng. 2018, 31, 88. [Google Scholar] [CrossRef] [Green Version]
- Barrett, J.D. Diagnosis and fault-tolerant control. IEEE Trans. Autom. Control 2012, 49, 493–494. [Google Scholar] [CrossRef]
- Maliuk, A.S.; Prosvirin, A.E.; Ahmad, Z.; Kim, C.H.; Kim, J.-M. Novel bearing fault diagnosis using gaussian mixture model-based fault band selection. Sensors 2021, 21, 6579. [Google Scholar] [CrossRef] [PubMed]
- Fonte, M.; Reis, L.; Infante, V.; Freitas, M. Failure analysis of cylinder head studs of a four stroke marine diesel engine. Eng. Fail. Anal. 2019, 101, 298–308. [Google Scholar] [CrossRef]
- Dalla Vedova, M.D.; Germanà, A.; Berri, P.C.; Maggiore, P. Model-based fault detection and identification for prognostics of electromechanical actuators using genetic algorithms. Aerospace 2019, 6, 94. [Google Scholar] [CrossRef] [Green Version]
- Sharma, V.; Parey, A. Extraction of weak fault transients using variational mode decomposition for fault diagnosis of gearbox under varying speed. Eng. Fail. Anal. 2020, 107, 104204. [Google Scholar] [CrossRef]
- Ma, L.; Dong, J.; Peng, K. A novel hierarchical detection and isolation framework for quality-related multiple faults in large-scale processes. IEEE Trans. Ind. Electron. 2019, 67, 1316–1327. [Google Scholar] [CrossRef]
- Yin, S.; Wang, G.; Gao, H. Data-driven process monitoring based on modified orthogonal projections to latent structures. IEEE Trans. Control Syst. Technol. 2015, 24, 1480–1487. [Google Scholar] [CrossRef]
- Palmer, F.S.; Luber, B.; Fuchs, J.; Kern, T.; Rosenberger, M. Data-driven fault diagnosis of bogie suspension components with on-board acoustic sensors. In Proceedings of the Fifth European Conference on the Prognostics and Health Management Society, Turin, Italy, 1–3 July 2020; pp. 1–13. [Google Scholar]
- Li, L.; Ding, S.X.; Yang, Y.; Peng, K.; Qiu, J. A fault detection approach for nonlinear systems based on data-driven realizations of fuzzy kernel representations. IEEE Trans. Fuzzy Syst. 2017, 26, 1800–1812. [Google Scholar] [CrossRef]
- Said, M.; Abdellafou, K.; Taouali, O. Machine learning technique for data-driven fault detection of nonlinear processes. J. Intell. Manuf. 2020, 31, 865–884. [Google Scholar] [CrossRef]
- Lundgren, A.; Jung, D. Data-driven fault diagnosis analysis and open-set classification of time-series data. Control Eng. Pract. 2022, 121, 105006. [Google Scholar] [CrossRef]
- Stubbs, S.; Zhang, J.; Morris, J. BioProcess performance monitoring using multiway interval partial least squares. Comput. Aided Chem. Eng. 2018, 41, 243–259. [Google Scholar]
- He, Z.; Yang, Y.; Qiao, L.; Zhang, Y.; Han, H.; Li, H.; Liu, Z.; Yang, Y. Canonical correlation analysis and key performance indicator based fault detection scheme with application to marine diesel supercharging systems. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 5156–5160. [Google Scholar]
- Peng, K.; Zhang, K.; You, B.; Dong, J. Quality-relevant fault monitoring based on efficient projection to latent structures with application to hot strip mill process. IET Control Theory Appl. 2015, 9, 1135–1145. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.; Ma, X.; Liang, W.; Liang, W.H. Fault tree analysis using bayesian optimization: A reliable and effective fault diagnosis approaches. J. Fail. Anal. Prev. 2021, 21, 619–630. [Google Scholar]
- Zhou, T.; Han, T.; Droguett, E.L. Towards trustworthy machine fault diagnosis: A probabilistic Bayesian deep learning framework. Reliab. Eng. Syst. Saf. 2022, 224, 108525. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Qin, K.; Xu, Y. Diesel engine fault diagnosis using intrinsic time-scale decomposition and multistage Adaboost relevance vector machine. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 881–894. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Jumnake, G.F.; Mahalle, P.N.; Shinde, G.R.; Thakre, P.A. Deep and Transfer Learning in Malignant Cell Classification for Colorectal Cancer. In Information Systems for Intelligent Systems: Proceedings of ISBM 2022; Springer: Singapore, 2023; pp. 319–329. [Google Scholar]
- Chen, W.; Qiu, Y.; Feng, Y.; Li, Y.; Kusiak, A. Diagnosis of wind turbine faults with transfer learning algorithms. Renew. Energy 2021, 163, 2053–2067. [Google Scholar] [CrossRef]
- Yao, Y.; Doretto, G. Boosting for transfer learning with multiple sources. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1855–1862. [Google Scholar]
- Hu, J.; Yu, Y.; Yang, J.; Jia, H. Research on the Generalisation Method of Diesel Engine Exhaust Valve Leakage Fault Diagnosis Based on Acoustic Emission. Measurement 2023, 210, 112560. [Google Scholar] [CrossRef]
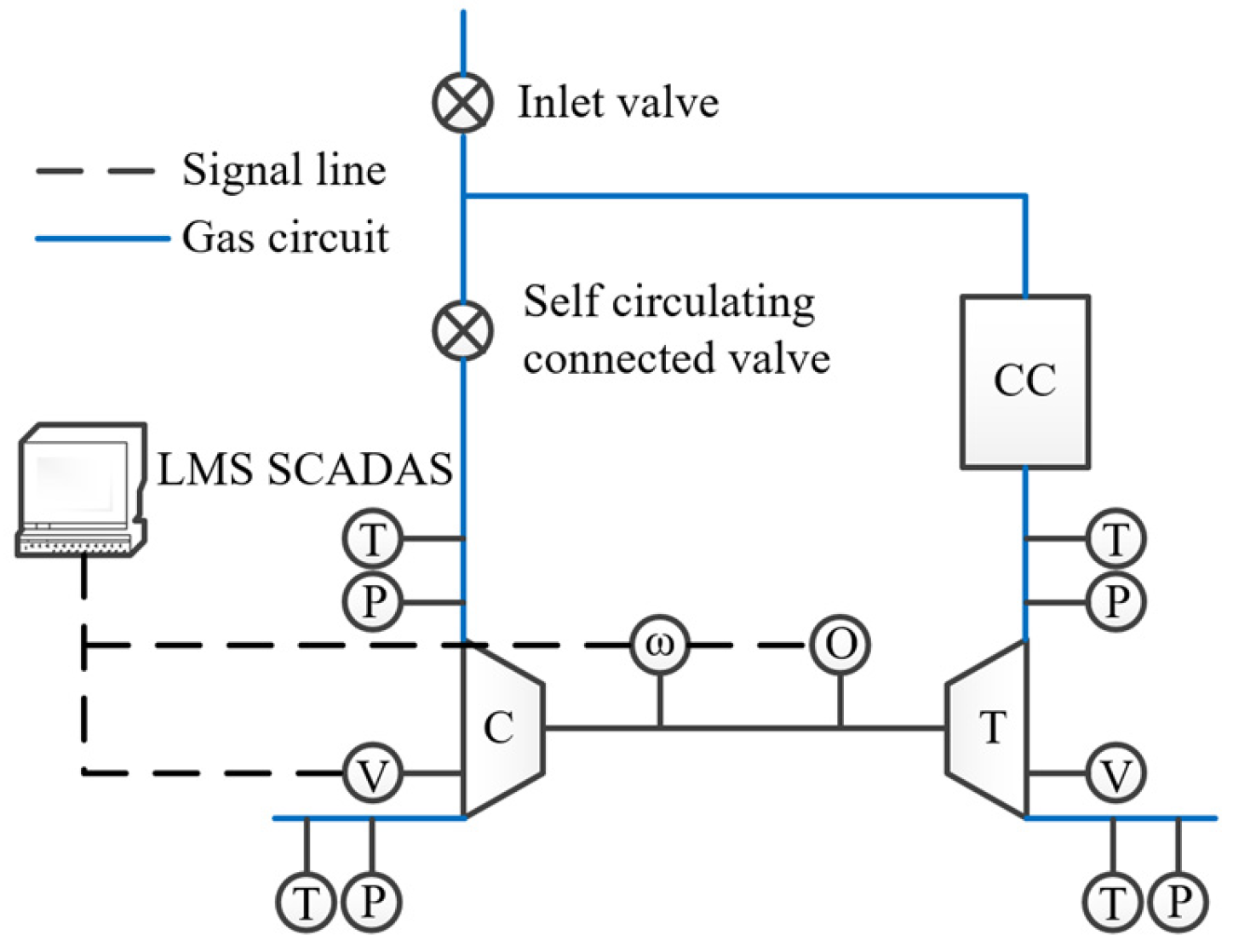
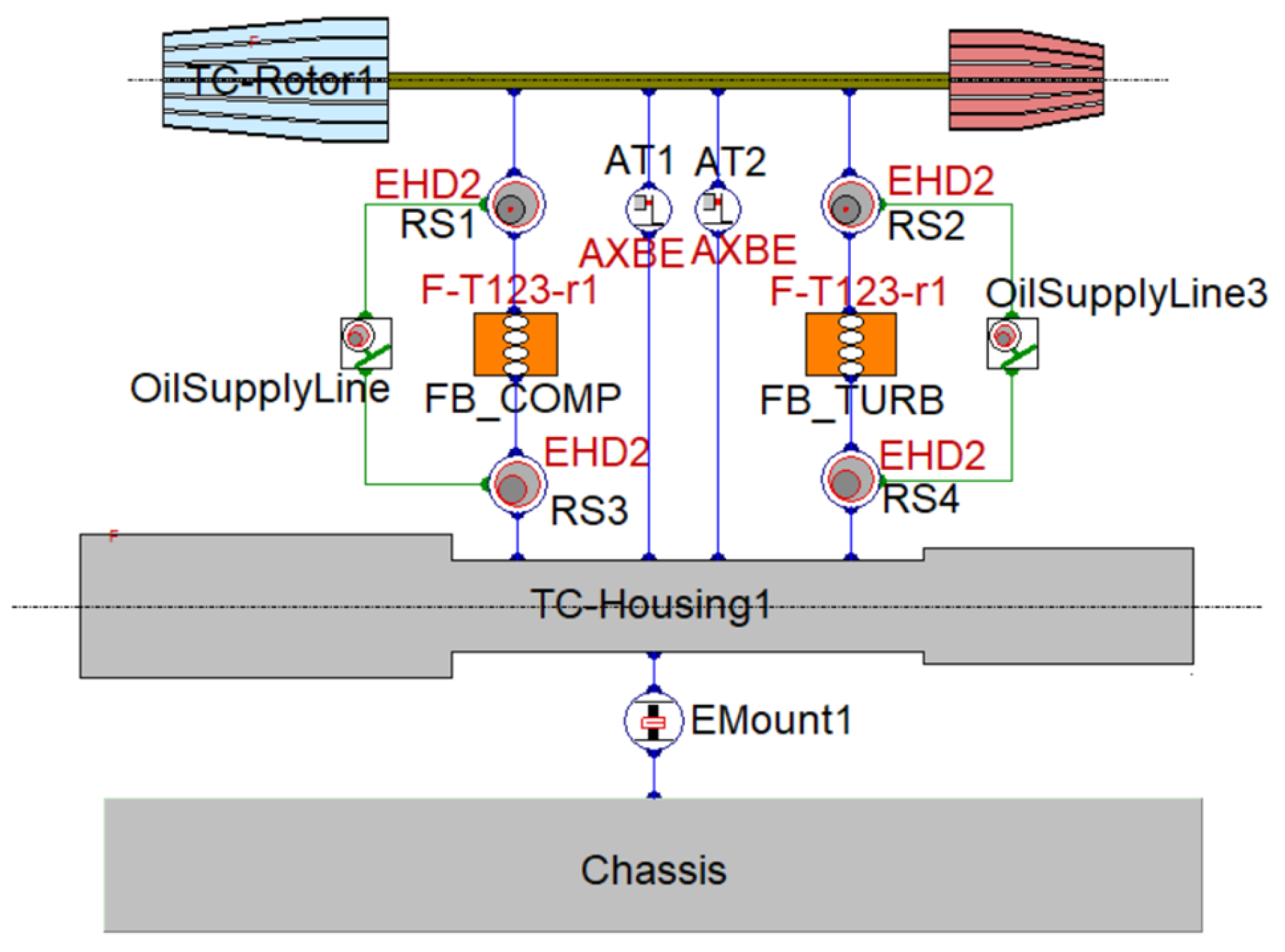
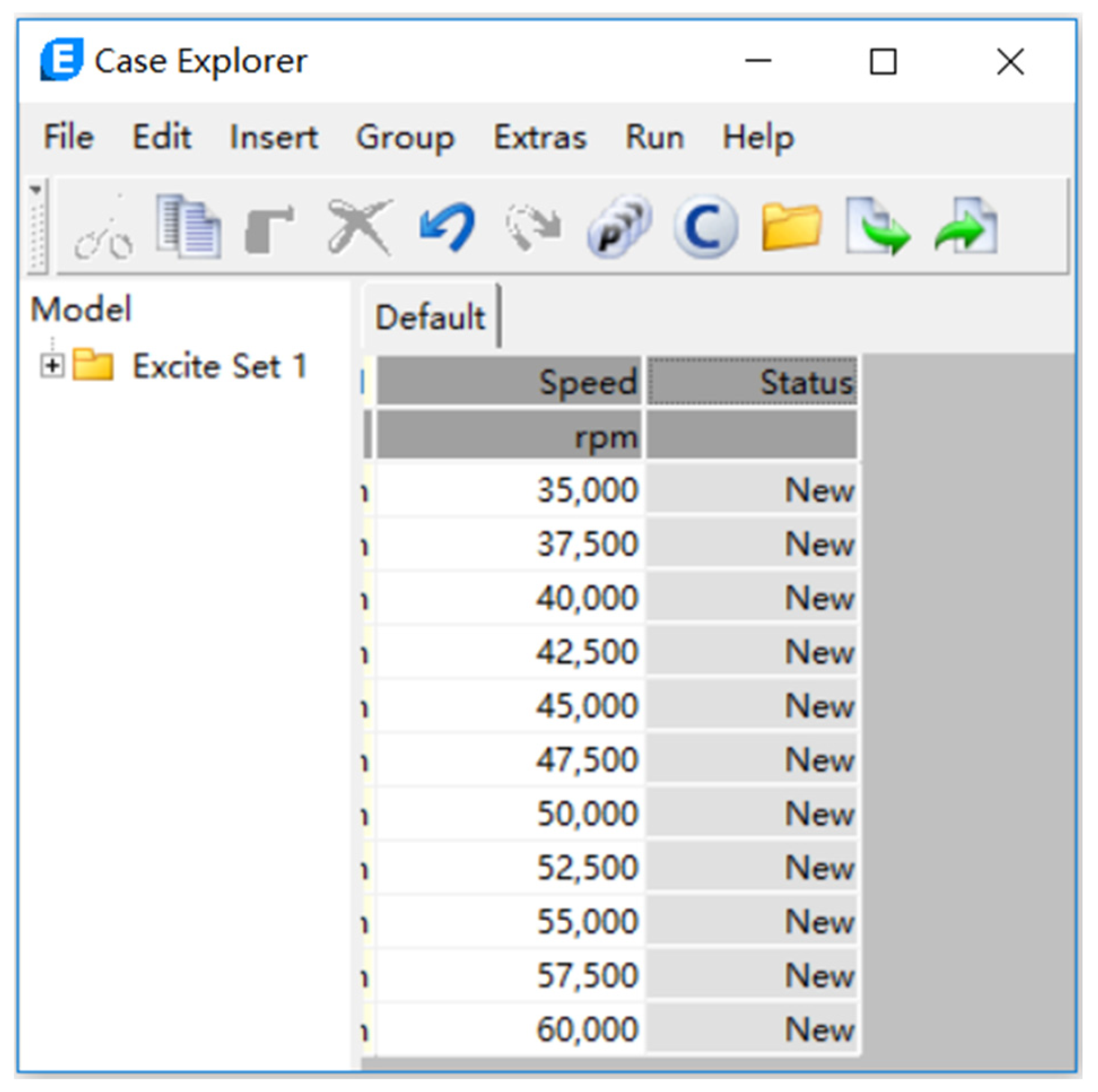
| Equipment Name | Model | Range | Precision |
|---|---|---|---|
| Turbocharger measurement and control system | NI | — | — |
| Vibration test system | LMS SCADAS Mobile | — | — |
| Acceleration sensor | B&K 4534-B | ±700 g | — |
| orbit of the shaft centre Eddy current sensor | Bently3300 | 10~100 mils | — |
| Rotational speed sensor | EM3309 | — | ±0.5% |
| Temperature sensors | K index thermocouple | 0~1000 °C | ±2% |
| Pressure sensors | Y-153BF | 0~1.6 MPa | ±0.4% |
| Turbocharger Status | Condition Characterization Parameters | Unit | Tests |
|---|---|---|---|
| Dynamic unbalance condition | Rotor dynamic unbalance and Bearing surface roughness Ra value | mg·mm and μm | (1) 10.0 mg·mm 0.5 μm (2) 7.6 mg·mm 0.5 μm |
| Dynamic unbalance and bearing wear condition | Rotor dynamic unbalance and Bearing surface roughness Ra value | mg·mm and μm | (1) 10.0 mg·mm 1.2 μm |
| Normal status | Rotor dynamic unbalance and Bearing surface roughness Ra value | mg·mm and μm | (1) 3.1 mg·mm 0.5 μm |
| Parameter | Value | Unit |
|---|---|---|
| The diameter of the rotor shaft | 12.4 | mm |
| Eccentricity of the compressor impeller | 2 | mm |
| Eccentricity of the turbine impeller | 3 | mm |
| Inner diameter of the floating ring | 12.4 | mm |
| Outer diameter of the floating ring | 17.7 | mm |
| Size of the floating ring | 20.2 | mm |
| The density of oil | 827.9 | kg/m3 |
| The initial temperature of the oil film | 373 | K |
| The viscosity of the lubricant | 11.3 | mPa·s |
| Specific heat of the oil film | 1950 | J/kg·K |
| Thermal conductivity of the oil film | 0.14 | W/m·K |
| Constant α of viscosity-pressure | 2.2 × 10−8 | m2/K |
| Constant β of viscosity-temperature | 0.03 | K−1 |
| Normal | Minor Failure | Moderate Failure | Severe Failure | |
|---|---|---|---|---|
| Time domain acceleration peak/g | 4.89 | 8.16 | 11.89 | 16.64 |
| Peak to peak acceleration/g | 13.55 | 21.44 | 31.39 | 42.29 |
| Root mean square value/g | 2.74 | 4.14 | 5.84 | 7.57 |
| 0–2 k band energy ratio | 28.13% | 12.96% | 11.03% | 10.73% |
| 2–4 k band energy ratio | 3.42% | 5.51% | 6.72% | 8.06% |
| 4–6 k band energy ratio | 2.43% | 1.56% | 1.50% | 1.43% |
| 6–8 k band energy ratio | 11.12% | 9.48% | 9.08% | 8.68% |
| 8–10 k band energy ratio | 40.89% | 53.23% | 55.13% | 55.30% |
| 10–12 k band energy ratio | 14.01% | 17.26% | 16.54% | 15.80% |
| Normal | Minor Failure | Moderate Failure | Severe Failure | |
|---|---|---|---|---|
| Time domain acceleration peak/g | 4.89 | 18.73 | 34.83 | 48.55 |
| Peak to peak acceleration/g | 13.55 | 31.31 | 46.39 | 61.94 |
| Root mean square value/g | 2.74 | 7.59 | 13.93 | 19.57 |
| 0–2 k band energy ratio | 28.13% | 31.52% | 35.26% | 72.32% |
| 2–4 k band energy ratio | 3.42% | 3.40% | 0.96% | 6.29% |
| 4–6 k band energy ratio | 2.43% | 2.42% | 2.33% | 2.48% |
| 6–8 k band energy ratio | 11.12% | 11.06% | 16.92% | 1.20% |
| 8–10 k band energy ratio | 40.89% | 37.67% | 22.93% | 9.87% |
| 10–12 k band energy ratio | 14.01% | 13.92% | 21.60% | 7.85% |
| Source Domain Auxiliary Data (Simulation) | Target Domain Data (Measured) | |
|---|---|---|
| Normal | 160 | 40 |
| dynamic unbalance | 480 | 120 |
| bearing wear | 480 | 120 |
| Dynamic unbalance combined with bearing wear | 480 | 120 |
| Training Set | Test Set | ||
|---|---|---|---|
| Data content | Source domain auxiliary data | Small amount of target domain data | Target domain data |
| Data quantity | 1600 | 20 or 40 | 400 |
| Source Domain → Target Domain | Data1 | Data2 |
|---|---|---|
| Number of target samples in the training set | 20 | 40 |
| TrAdaBoost algorithm accuracy | 0.87 | 0.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, F.; Yang, J.; Cai, Y.; Xie, L. Transfer Learning-Based Fault Diagnosis Method for Marine Turbochargers. Actuators 2023, 12, 146. https://doi.org/10.3390/act12040146
Dong F, Yang J, Cai Y, Xie L. Transfer Learning-Based Fault Diagnosis Method for Marine Turbochargers. Actuators. 2023; 12(4):146. https://doi.org/10.3390/act12040146
Chicago/Turabian StyleDong, Fei, Jianguo Yang, Yunkai Cai, and Liangtao Xie. 2023. "Transfer Learning-Based Fault Diagnosis Method for Marine Turbochargers" Actuators 12, no. 4: 146. https://doi.org/10.3390/act12040146
APA StyleDong, F., Yang, J., Cai, Y., & Xie, L. (2023). Transfer Learning-Based Fault Diagnosis Method for Marine Turbochargers. Actuators, 12(4), 146. https://doi.org/10.3390/act12040146






