Improvements on the Dynamical Behavior of a HiL-Steering System Test Bench

Abstract

Shorter available development times and fewer available vehicle prototypes have increased the subsystem-based investigation on test rigs within the automotive development process. Steering systems exhibit a direct interface to the driver, therefore, posing high requirements to the control performance of a test bench, especially for the perception of steering feel. This work proposes three approaches to improve the force control performance of permanent magnet linear motors incorporated on a steering test bench. The first method improves control accuracy when a harmonic force signal is introduced into the steering system by adjusting the reference force signal based on the identified peak values of the measured and reference forces. The second method allows the inclusion of the actuator’s inertia and the occurring ratios between steering wheel angle and rack displacement into the control scheme to reduce performance deterioration due to inertia. The third approach considers delay time in the actuator control and estimates its future position for delay compensation. A validation of the proposed methods is conducted, displaying an improvement for all three applications. The proposed methods extend the applicability of a steering test bench within the automotive development process by enabling more accurate and reproductible control performance.

1. Introduction

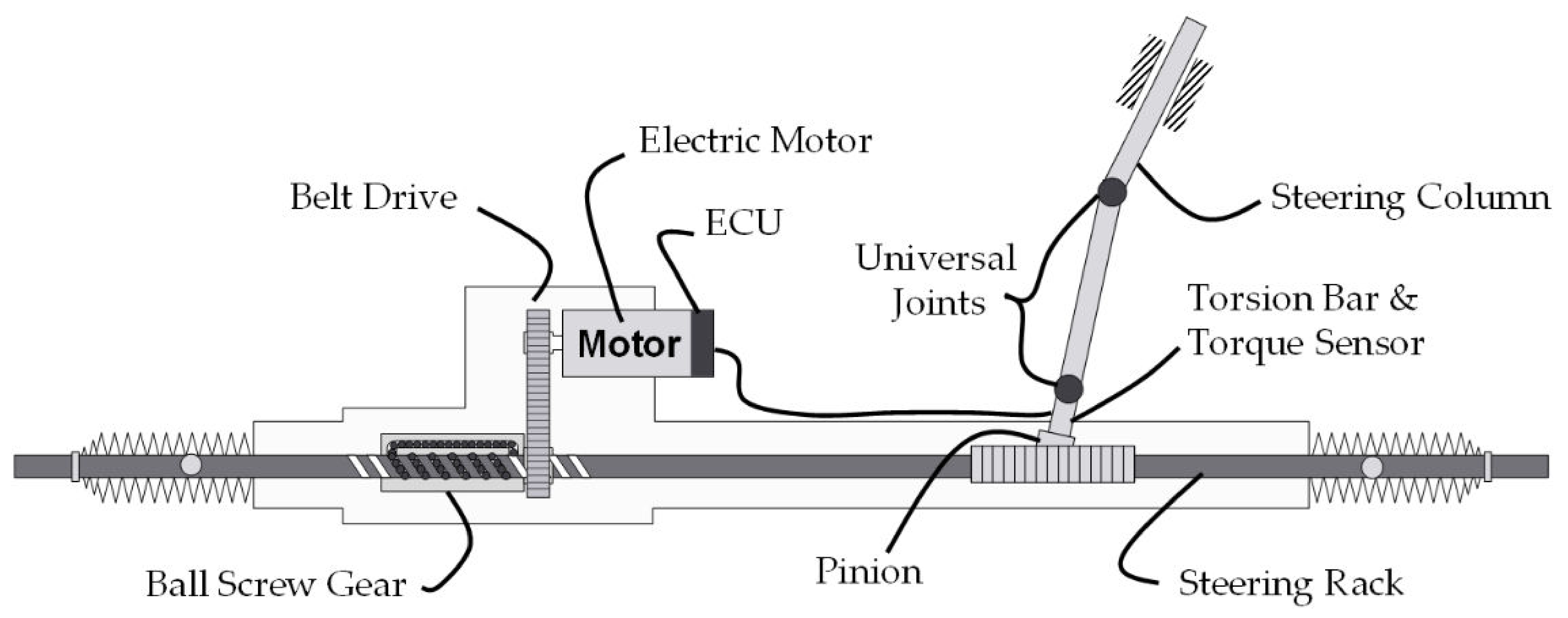
Modern steering systems for passenger vehicle cars possess an electric motor, which provides the necessary servo force to support the driver during steering maneuvers. During the automotive development process, the steering feel is improved, often in full vehicle tests. An alternative to road tests is the utilization of a steering system test bench, which allows the objective investigation of the steering system, without the requirement of a vehicle prototype.

Typical tests on steering test benches range from measurements of mechanical characteristics, such as the friction force of the steering gear, to approximations of full vehicle tests. Since electric power steering (EPS) systems exhibit large servo forces during parking, steering test benches for the investigation of such systems are required to provide sufficiently large actuator forces to imitate the wheel–road contact for real word applications. Currently, this goal is achieved by the usage of one or two permanent magnet linear synchronous motors (PMLSM).

Due to the high-power requirements, the utilized PMLSMs exhibit non-neglectable moving masses, deteriorating the dynamic behavior of the system. This is especially relevant when rapid steering wheel angle inputs are present. Furthermore, EPS systems represent nonlinear characteristics with friction, backlash, and natural frequencies within the investigated frequency range, which negatively influence the control performance, exemplarily when harmonic rack forces are introduced into the steering system. These shortcomings limit the applicability of steering test benches along the development process and require optimization.

Common approaches utilized to improve the dynamic control of regulated systems incorporate the inverse plant model into the control scheme [1,2]. In [3,4], a combined offline and online estimated transfer function is utilized to adapt the reference signal to the dynamics of the system under test, which is represented as a shaking table. For the online implementation, a recursive extended least square algorithm is used. A similar approach is described in [5], wherein an online recursive extended least square algorithm adaptively alters the transfer function for acceleration, force and position control of a shaking table. Another force control approach is introduced in [6], where the inverse model approach was successfully implemented within a flight simulator.

The estimation of a control transfer function on a steering test bench is connected to high efforts. Since the steering system represents an active component with friction, backlash and a variable driver input, steering systems are nonlinear systems. Consequently, the transfer function is only valid for one system state. Due to a great variety of variations in the system, transfer function-based approaches are not applicable for this purpose.

Similar, but alternative, approaches to control harmonic reference signals on a shaking table were introduced in [7,8]. Both methods utilize a least mean square filtering approach to weigh or adapt the input signal to compensate phase and amplitude deviation in the system response. Here, the adaptation occurs due to a comparison of the resulting and measured signals of the shaking table, without the explicit knowledge of the transfer function. Therefore, a similar approach can also be used on a steering test bench, where harmonic excitations are inserted into the steering rack.

Alternative approaches for the improvement of the dynamic characteristics of control systems are the usage of feedforward control signals based on velocity or acceleration information. In the discipline of hard disc drive control, there exist high requirements for the dynamic control performance, since the distance between a storage and the write/read pin needs to be small, but physical contact must not occur, even in the presence of external disturbances. For this purpose, [9] introduced an acceleration feedforward control (AFC), which detects external disturbances to improve the control performance. In [10], a similar approach was utilized to reduce the impact of external shocks to the drive system by an AFC in combination with a double disturbance observer, which successfully enhanced the control quality.

Within machining control applications, feedforward control approaches are exposed to changing boundary conditions, introduced by the workpiece characteristics, tool degradation and travel speed. Therefore, [11] implemented an adaptive feedforward control based on the reference position signal and the occurring error together with friction compensation to reduce the resulting position error. Approaches for inertia compensation by a feedforward control are even further restricted since the workpiece and direction of excitation vary over time. Consequently, [12] developed a velocity and AFC in combination with a jerk disturbance observer to compensate for varying inertia during the machining process. Similar approaches were conducted in [13,14,15], where observers and artificial intelligence are implemented to estimate the current inertia of the system.

Previously described approaches for enhanced dynamics are implemented for position or velocity control and for predefined reference signals. A torque control application with feedforward control for friction and inertia compensation was proposed in [16] on a rehabilitation device. The compensation is based on the currently measured angular velocity and the motor inertia, which successfully improves the control performance. A similar approach is also applicable for the implementation on a steering test bench, where the PMSLM is normally operated in force control mode.

Since steering system test benches are required to function within real-time applications, exemplarily together with a vehicle model, there are not only dynamic requirements in terms of magnitude accuracy but also concerning the time delay between the reference and measured signal. Such effects originate from dead time and the dynamic properties of the PMLSM control. A common method to deal with and improve the control performance of systems with dead time is the implementation of a Smith predictor [17]. Here, a model of the process is utilized to derive a mathematical formulation without a delay in the system, enabling the use of standard PID control tuning processes for systems without dead time. The work in [18] proposed an adaptation of a Smith predictor in combination with a fuzzy-PI controller on a brushless DC motor to account for modelling uncertainties, while an approach with an automatic dead time calculation is introduced in [19].

Another method to improve the dynamic behavior of a brushless DC motor incorporates time-shifting the voltage signal according to the electrical characteristics of the motor in terms of inductance and resistance [20]. The identification of the shifting time for the voltage signal is performed for different goals, such as performance [20] or acoustics [21]. A similar approach is proposed in [22], wherein a phase delay compensation is utilized to improve the efficiency of the electric motor and its generated torque. Here, the optimum shifting time is estimated based on a Fourier series. These approaches utilize information of the current system state to alter the control strategy to improve performance. The basic principle is also applicable for steering test bench applications in real-time operation.

For PMLSMs implemented in steering system test benches, the prevailing operation mode is force control, which can be subdivided into two categories, based on the origin of the reference force signal. First, a reference force signal is provided in advance of the test to the PMLSM for the excitation of the steering system. This setup is exemplarily utilized for the harmonic force excitation of the steering rack. Second, the force is calculated based on a vehicle model, where the rack displacement measured within the PMLSM functions as the input for the reference rack force calculation. For the most basic case, the PMLSM operates as a virtual spring and, therefore, provides a reference force proportional to the measured rack displacement.

In this paper, drawbacks of the control performance occurring for both control categories are identified, and associated improvement approaches are proposed. For a previously known harmonic reference signal, a similar methodology as in [7] is implemented to calculate a weighing factor to adapt the reference signal. Two additional methods, which are applicable for real-time testing, exemplarily combined with a vehicle model, use the steering wheel angle and steering rack-velocity information to provide the PMLSM control with a compensation signal for inertia and time delay.

The remaining article is structured as follows: Section 2 gives an overview of the steering system and the relevant steering test bench, followed by a problem formulation and the proposal of compensation approaches in Section 3. Results of the implemented control improvements are displayed and discussed in Section 4. Section 5 summarizes the conducted investigations.

2. Steering System and Test Bench

This section introduces both the structure and function of electric power steering systems as well as the steering system test bench used for the investigations.

2.1. Electric Power Steering System

Modern steering systems in vehicles are equipped with an electrical motor to assist the driver during driving maneuvers. Depending on the positioning of the electric motor, different variations of EPS exist [23]. In this work, the motor of the steering system is located parallel to the rack of the system, representing an axle parallel (apa) EPS. A simplified sketch of the system is displayed in Figure 1.

The rotational driver input is introduced through the steering wheel into the steering column. Within the adjacent torsion bar, a sensor detects the applied steering torque. Universal joints in this path allow adjustment of the steering wheel position. Within the contact between the pinion and the steering rack, the rotational movement of the pinion is transformed into a translatory displacement of the steering rack. The ratio of the steering gear can be variable over the whole stroke, where the center range is generally less direct compared to larger steering wheel angles. This allows the reduction of steering angle demand during parking, while maintaining high stability under high-speed driving [23]. The translatory movement of the steering rack is then transferred by the tie rods to the wheel carrier, introducing a wheel rotation. Based on the measured steering torque at the steering systems torsion bar sensor and by different steering functions, a servo torque is calculated within the ECU and supplied by the electric motor. A belt drive and ball screw gear convert the assistance torque into an assistance force on the steering rack.

Due to the occurring inertia of the electric motor and the ball screw gear in combination with its elastic connection, the steering system exhibits a low-pass character for external excitations, originating from the tie rods [25,26]. In addition to the reduction of relevant road feedback to the driver [25], investigations also showed that this combination leads to a dominant natural frequency [26,27], complicating the force control during tests on a steering test bench.

2.2. Steering System Test Bench

Within this investigation, an electromechanical steering system test bench by dSPACE is utilized, which is described in [28], and consists of two PMLSMs for the introduction of road excitations to the steering rack and one steering wheel actuator (SWA) representing the driver input. Both PMLSMs are named according to their side of implementation, namely rod left actuator (RLA) and rod right actuator (RRA). The technical data are displayed in

Table 1. Characteristics of the steering system test bench.

PMLSM			SWA
Characteristic	Unit	Value	Characteristic	Unit	Value
max. Force	kN	20	max. Torque	Nm	50
max. Velocity	m/s	1	max. Velocity	°/s	3000
max. Frequency	Hz	30

.

The PMLSM can be operated in position, velocity and force control. Here, only force control is considered. The SWA provides similar operation modes as position, velocity and torque control. These control tasks in addition to the relevant signal measurements are performed by a dSPACE Hardware-in-the-Loop (HiL) simulator [28]. A matlab/Simulink model allows the operator to adapt and extend the implemented control structures to match the requirements. Within this work, the Simulink model interface is utilized to implement the dynamic optimization methods.

Measurements on the steering system test bench range from the evaluation of the occurring friction in the passive system to HiL tests on full vehicle level, including a real-time vehicle dynamic model [26,27]. The setup of the test rig for HiL testing is shown in Figure 2.

Based on the selected driving maneuver, the reference steering wheel angle ${\delta }_{Ref,SWA}$ is provided to the SWA. Further maneuver information, such as the surface geometry and pedal position, are sent to the vehicle model. The residual bus simulation provides the steering system with the necessary bus communication signals, such as vehicle speed $v_{veh}$, for a proper function, such as within the actual vehicle.

As a response to the reference steering wheel angle, the SWA excites the steering column and induces a steering maneuver. Angle, velocity and torque sensors adjacent to the SWA detect the relevant quantities. Sensors incorporated within the PMLSMs measure the occurring rack displacement of the steering system, $x_{meas,RLA}$ as well as $x_{Meas,RRA}$, and send this information to the vehicle model. Based on the rack displacement, the vehicle dynamic model calculates the wheel carrier rotation and the associated tire and rack forces. The latter are then utilized as the reference force signals $F_{ref,RRA}$ and $F_{ref,RLA}$ for the RRA and RLA, respectively. A load cell within the force path between the steering rack and the PMLSM detects the contact force for the closed-loop control. As a result, the required steering torque for the SWA to reach the reference angle, measured by an additional torque and angle sensor of the test rig close to the SWA, coincides with the steering torque perceived by a driver in a vehicle test.

Since the required rack forces for the previously described setup may originate from a vehicle model, the reference force signal is not known in advance to the test because it is derived from the occurring rack displacement, vehicle speed and surface condition. Alternative investigations, exemplarily the characterization of the feedback behavior of the steering system as explained in [26,27], utilize reference force signals with specific characteristics, which are defined as a time sequence before the test. Therefore, the reference force is not dependent on the steering system behavior and other surrounding conditions. Therefore, in this case, the displacement of the steering rack does not influence the desired reference force. The setup from Figure 2 remains similar, but the vehicle model is replaced by a time dependent signal generator, which provides a predefined reference force signal without incorporating the steering system behavior.

3. Problem Formulation and Compensation Approaches

In this section, two applications for the investigation of steering systems on a test bench are introduced, where dynamic insufficiencies deteriorate the measurement result. The first application describes the identification of the feedback behavior of the steering system, wherein a previously defined harmonic reference force signal is introduced into the steering rack. Due to the steering system’s characteristics, the measured force exhibits deviation from the reference force. A second application investigates the guidance behavior of the steering system, where both the magnitude as well as the phase delay between the reference signal and the measured force do not adhere to the requirements. Solution approaches for both applications are motivated and derived.

3.1. Steering System Feedback

This subsection describes the feedback investigation test, motivates the occurring deviations and introduces a compensation approach.

3.1.1. Test Description

For the investigation of the feedback behavior of the steering system, only one PMLSM (the RLA) is connected to the steering rack, while the steering wheel is either swinging freely or locked at a constant angle, controlled by the SWA. Due to the high control performance of the SWA, the steering wheel is approximately fixed at its position and not rotating. Oscillations do occur for the case of a freely swinging steering wheel. A sine sweep signal with constant amplitude and increasing frequency is then used as the reference force signal for the connected PMLSM [26]. Based on the measured input force $F_{meas,RLA}$ and the steering torque sensed by the torsion bar $M_{tb}$, a transfer function $G_{FB,Steer}$ is calculated by a Fast Fourier Transformation (FFT) [29] of the input and output signal:

$$G_{FB,Steer}=\frac{FFT\left(M_{tb}\right)}{FFT\left(F_{meas,RLA}\right)}.$$

(1)

An exemplary bode plot of the identification result for a passive steering system is displayed in Figure 3, where a resonance frequency at 6 Hz is detected.

3.1.2. Motivation and Problem Formulation

Due to the occurring friction and backlash in the system in combination with an active servo motor, steering systems are nonlinear, which means that the identified transfer function is only valid for the exact condition of the test. To compare the results of different applications of whole steering systems, the boundary conditions of the measurement, such as the force amplitude, need to be held constant, requiring high dynamic performance control. Extrapolating the results outside the reference state is only valid for linear, time-invariant systems [29]. This requirement becomes clear when considering the support force of the servo motor, which does not correlate linearly to the rack force. Therefore, reduced or increased rack forces lead to different torsion bar torques and, therefore, to varying assistance forces, which change the share of the required steering torque of the driver. Consequently, the magnitude of the transfer functions increases or decreases, complicating a comparison for different rack force amplitudes.

As a result of the steering system characteristics, the resulting rack force amplitude exhibits deviations from the reference amplitude along the frequency range. An exemplarily resulting normed rack force course in the time domain is presented in Figure 4. Here, the reference amplitude indicates the desired amplitude of the input force sine sweep reference signal from 1 Hz to 30 Hz and ideally coincides with the amplitudes of the measured rack forces. At 13.8 s, the rack force displays an overshoot of 43.6% compared to the reference amplitude. For increasing time, which is equivalent to increasing frequency, the amplitude drops to 81% of the reference signal. These deviations hinder reliable comparison.

3.1.3. Solution Approach

As the force control performance is strongly influenced by the characteristics of the steering system, a transfer-function-based approach, as introduced in [1,2,3,4], represents a valid compensation approach. Since the steering system is a nonlinear component, a transfer function for the test bench control must be derived for each operating point of the steering system, which is associated with a large effort. Therefore, an online approach which solely requires the reference and the measured force signal is proposed. To allow for wide applicability of the solution approach, an improvement is required for the following conditions:

• Harmonic signal with constant and/or increasing frequency;
• Harmonic signal with constant and/or varying amplitude;
• Harmonic signal with or without a varying and previously unknown offset value and their combination.

The latter case is especially important when the steering test bench is used in combination with a vehicle model and external disturbances are superposed to the rack forces from the vehicle model.

The basic principle of the proposed solution approach is, similar to [7], the adaption of the reference signal to consider the current dynamic properties of the complete control system. This means that the amplitude of the reference signal is increased for decreased measured rack force amplitudes and vice versa. The magnitude of the correction factor depends on the detected difference between the reference and measured rack force amplitudes. Therefore, a real-time capable algorithm is introduced which calculates a correction factor for the reference signal based on the currently measured force amplitudes, estimated by a peak value identification (PVID). A visualization of the PVID algorithm to detect a high point is displayed in Figure 5.

If the search for a new high point is triggered, a comparison of the current value $F\left(i\right)$ and the stored maximum value $F_{max,det}$ is performed for each timestep (see Figure 5a).

An update happens if the current value is larger than the previously stored value, otherwise the update is suspended (see Figure 5b). Since the force measurement is accompanied with measurement noise from the load cell, a threshold value is defined, which allows a distinction between the discovery of a new high point and noise-induced force reductions. As soon as the measured force value drops below a threshold, represented as the value which is $F_{thres}$ lower than the currently stored maximum, a high point detection is triggered to update the currently reached force amplitude $F_{HP}$, as displayed in Figure 5c. Furthermore, the currently detected minimum value $F_{min,det}$ is initialized with the high point value. Then, the search for a low point is performed identically.

The presented algorithm can be applied to the measured force signal as well as the reference signal to obtain both the desired $L{P}_{ref}$, $H{P}_{ref}$ and achieved $L{P}_{meas}$, $H{P}_{meas}$ force amplitudes. Here, $H{P}_i$ and $L{P}_i$ stand for the force high point and low point, respectively. Subsequently, the correction ratio $\lambda \left(i+1\right)$ for both amplitudes is updated according to

$$\lambda \left(i+1\right)=\frac{\lambda \left(i\right)·H{P}_{ref}}{H{P}_{meas}}$$

(2)

or

$$\lambda \left(i+1\right)=\frac{\lambda \left(i\right)·L{P}_{ref}}{L{P}_{meas}}$$

(3)

and used to adapt the reference signal to the current situation (see Equation (4)). Since this approach adapts the reference signal based on the occurring maximum and minimum values, it is called peak value control (PVC).

$$F_{harm,ref,new}=F_{harm,ref}·\lambda \left(i+1\right)$$

(4)

Here, $F_{harm,ref}$ and $F_{harm,ref,new}$ stand for the harmonic reference signal and the adapted harmonic reference signal, respectively.

Note that the harmonic signal without offset $F_{harm,ref}$ is separated from the reference offset force $F_{off,ref}$. This distinction allows the previously introduced superposition of rack forces from a vehicle model and the harmonic signal. A block model of the whole algorithm together with the force control structure of the steering test bench is displayed in Figure 6.

The adaption of the reference signal is conducted before the PI control structure of the test bench and includes information from the measured force $F_{meas}$ and the reference forces $F_{off,ref}$ and $F_{harm,ref}$ (see Figure 6a). Figure 6b displays a block diagram of the peak value control implementation). The harmonic reference signal is a multiplication with the currently active correction ratio, directly fed to the PVID algorithm, whereas the measured force is offset adjusted by subtracting the reference offset value before being analyzed by the PVID. The correction ratio λ is calculated according to Equation (2) or Equation (3) and multiplied with the harmonic reference signal. Finally, the adapted harmonic reference signal is added to the offset reference value, representing the adapted reference signal, which is fed to the control structure. The separated analysis is conducted to only adapt the high-frequency inputs, since the low-frequency signals possess high control accuracy.

The advantages of this approach are that no further information other than the measured and reference force value are required. Furthermore, the calculation can be performed for any steering system with different applications and boundary conditions (e.g., vehicle speed). A disadvantage is that the calculation of a correction factor is only possible when a new peak value is updated. Firstly, this leads to a time delay since the threshold value must first be undershot. Secondly, it results in a lower limit up to which amplitudes can be resolved. This value is determined by the measurement noise and the resulting threshold parameter.

Here, phase correction is not implemented, since only the transfer from the measured rack force to the measured steering wheel torque is considered. A phase delay between the measured and reference force signal is, therefore, irrelevant for the feedback characterization of the steering system.

3.2. Steering System Guidance Dynamics

In this subsection, a description of the test setup and the derived control performance limitation are explained. The description of two solution approaches, one for magnitude improvement and another for delay compensation, conclude the subsection.

3.2.1. Test Description

For the investigation of the dynamic guidance behavior of steering systems, one or two PMLSMs are connected to the steering rack. In contrast to the previously described feedback investigation, the reference force signal is calculated based on the rack displacement of the steering system and is not previously defined. For simplicity in the evaluation of the results, a virtual spring is implemented in the control scheme instead of a vehicle model. Consequently, the reference force generated is proportional to the rack displacement.

The identification of the guidance behavior of the steering system is adapted from a standard full vehicle test, the frequency response test as described in ISO 7401 [30]. For this maneuver, a sine steer input with slowly increasing frequency is introduced into the steering wheel. For the investigation of the steering system, exemplary relevant objective parameters are the transfer function from steering wheel angle to lateral acceleration and from the steering wheel angle to the vehicle yaw velocity [27]. Consequently, the frequency response test represents a relevant investigation for a steering test bench.

3.2.2. Motivation and Problem Formulation

To demonstrate the occurring control performance deterioration during the test, measurements with a steering wheel angle of 20° and an implemented virtual spring stiffness $k_{virt}$ of 400 N/mm are conducted. Within 50 s, the frequency is exponentially increased from 0.1 Hz up to 5 Hz, which lays above the reported frequency input ranges of 2.0 Hz in [30], 2.8 Hz in [27], 3 Hz in [23,31] and 4 Hz in [32] and is, therefore, considered sufficiently dynamic. Figure 7 depicts the bode plot of the transfer function from measured rack displacement $x_{meas,RLA}$ to the measured rack force $F_{meas,RLA}$, introduced by the RLA, calculated as the feedforward control performance $G_{FF,Perf}$

$$G_{FF,Perf}=\frac{FFT\left(F_{meas,RLA}\right)}{FFT\left(x_{meas,RLA}\right)}.$$

(5)

Ideally, the magnitude course equals the defined spring stiffness, and the phase delay is zero.

Two deviations from the desired test bench behavior can be observed. First, the effective stiffness decreases for increasing input frequency. At 3 Hz, a stiffness reduction of 20% is measured which increases up to 50% at 5 Hz. That means that the desired rack forces are not reached for the setup. Second, the phase delay increases in magnitude over the frequency range. Consequently, the force applied to the steering system no longer matches the steering wheel angle and the rack position, which negatively influences the steering torque buildup and, therefore, the overall impression.

3.2.3. Solution Approach

Since the proposed approach is required for applications where the reference force signal is not known in advance, adjustments to the reference signal cannot be conducted beforehand. To overcome the previously introduced deficits, a two-part approach is presented. The first method allows an improvement of the magnitude course over the frequency range, whereas the second solution reduces the occurring time or phase delay.

Inertia Compensation

The basic assumption to improve the magnitude control performance of the PMLSM is that its moving mass is not incorporated in the control scheme and, therefore, deteriorates the performance during high-dynamic maneuvers. To improve these dynamic properties, inertia compensation (IC) is implemented in the control scheme by considering the acceleration of the steering system, similar to [16]. For this purpose, two locations for acceleration measurement are available. The first is located directly at the PMLSM and detects the acceleration of the RLA or RRA. A second possibility measures the steering wheel angle and derives the currently occurring steering wheel angle acceleration. For the investigated setup, the acceleration of the steering rack represents the result of the steering wheel input. Due to the elasticity of the torsion bar and the inertia of the steering rack, a time delay is expected to occur within the transfer path. As the acceleration information should be available as soon as possible, the steering wheel angle ${\phi }_{SW}$ and, more concrete, the steering wheel angle speed ${\dot{\phi }}_{SW}$ is selected as the relevant signal.

Since the angular velocity is transformed into a translatory displacement of the steering rack, the steering ratio as well as the gimbal error due to the universal joints within the steering column need to be incorporated in the control structure. For this purpose, the steering system is steered from the maximum to the minimum steering wheel angle after the initial setup, and the resulting overall steering ratio is measured and mapped to a position dependent lookup table.

The measured steering wheel velocity ${\dot{\phi }}_{SW}$ is then multiplied with the relevant steering ratio, resulting in the estimated rack speed ${\dot{\widehat{x}}}_{RLA}$ or ${\dot{\widehat{x}}}_{RRA}$. To receive an estimated rack acceleration signal ${\ddot{\widehat{x}}}_{RLA}$ and ${\ddot{\widehat{x}}}_{RRA}$, a derivative transfer function, according to the recommendation in [33], is utilized as

$$\frac{s{K}_D}{1-s{T}_D}.$$

(6)

$K_D$ and $T_D$ stand for the gain and time constant of the filter, respectively. For the implementation, a discrete transfer function for a sample time of 125 µs is derived, setting $K_D=1$ and $T_D=1.25$ ms.

To reduce the influence of the PMLSMs inertia, the estimated acceleration is then multiplied with the mass of the respective motor $m_{RLA}$ or $m_{RRA}$, resulting in the inertia compensation force signal $F_{comp,in}$, which is added to the reference force signal from the spring model $F_{spring}$. The overall implementation of the approach is displayed in Figure 8a and the more detailed representation of the IC in Figure 8b.

In cases of active steering with steer-by-wire systems, as in [34], where rack displacement occurs without steering wheel movement, the rack acceleration signal can be utilized instead of the steering wheel angle displacement. The rack acceleration is then directly available without the incorporation of a steering ratio in the control structure. Since EPS systems with a mechanical link between the steering wheel and steering gear represent the state of the art, this work focuses on a fixed and predefined ratio between steering wheel angle and rack displacement.

Delay Compensation

The second approach aims to reduce the phase delay between the rack displacement and the resulting contact force and is referred to as delay compensation (DC). Therefore, a similar basic principle, as in [22], is incorporated. To compensate for the resulting delay, the currently available reference signal is adapted so that the dynamic limitations of the PMLSMs and the overlying control structure are considered. Therefore, the following considerations are made exemplarily for a connected RLA.

Assuming the occurring displacement for the investigation of the dynamic guidance behavior of the steering system can be expressed as a harmonic sine in the form of

$$x_{meas,RLA}\left(t\right)=s_{\max }·\sin \left(2\pi ft\right),$$

(7)

where $s_{\max }$ is the amplitude of the excitation, $f$ the current frequency and $t$ is the time. The phase delay in the resulting measured rack force $F_{meas}\left(t\right)$ is then

$$F_{meas}\left(t\right)=k_{virt}·s_{\max }\sin \left(2\pi f\left(t-t_{delay}\right)\right)=k_{virt}{x}_{meas,RLA}\left(t-t_{delay}\right).$$

(8)

The phase delay is considered here by incorporating $t_{delay}$ into the formulation. The goal is to introduce an additional term $\Delta x\left(t\right)$ to the measured position $x_{meas,RLA}\left(t\right)$ to compensate the delay, so that

$$F_{meas}\left(t\right)=k_{virt}·(x_{meas,RLA}\left(t-t_{delay}\right)+\Delta x\left(t-t_{delay}\right){)}^{!};=k_{virt}{x}_{meas,RLA}\left(t\right).$$

(9)

Together with the phase delay ${\phi }_{delay}$

$${\phi }_{delay}=2\pi f{t}_{delay}$$

(10)

and the previously introduced definitions, the two right hand terms in Equation (9) can be written as

$$s_{\max }\sin \left(2\pi ft-{\phi }_{delay}\right)+\Delta x(t-t_{delay}{)}^{!};=s_{\max }·\sin \left(2\pi ft\right).$$

(11)

Adding a zero in the sine term on the right side, it can be reformulated as

$$s_{\max }\sin \left(2\pi ft-{\phi }_{delay}+{\phi }_{delay}\right)=s_{\max }\left(\sin \left(2\pi ft-{\phi }_{delay}\right)\cos \left({\phi }_{delay}\right)+\cos \left(2\pi ft-{\phi }_{delay}\right)\sin \left({\phi }_{delay}\right)\right)$$

(12)

For small delay angles ${\phi }_{delay}$, the approximations $\sin \left({\phi }_{delay}\right)\approx {\phi }_{delay}$ and $\cos \left({\phi }_{delay}\right)=1$ can be implemented. For the investigated delay here, a maximum deviation of 1.15% for the sine term and 3.5% for the cosine term at 15° phase delay is observed, which is sufficiently accurate. Therefore, Equation (11) can be simplified to

$$s_{\max }\sin \left(2\pi ft-{\phi }_{delay}\right)+\Delta x(t-t_{delay}{)}^{!};=s_{\max }\left(\sin \left(2\pi ft-{\phi }_{delay}\right)·1+\cos \left(2\pi ft-{\phi }_{delay}\right)·{\phi }_{delay}\right),$$

(13)

and further to

$$\Delta x(t-t_{delay}{)}^{!};=\cos \left(2\pi ft-{\phi }_{delay}\right)·{\phi }_{delay}.$$

(14)

Replacing the phase delay by its definition from Equation (10)

$$\Delta \mathrm{x}(\mathrm{t}-{\mathrm{t}}_{\mathrm{delay}}{)}^{!};=s_{\max }\cos \left(2\pi f\left(t-t_{delay}\right)\right)·2\pi f·t_{delay}$$

(15)

with the derivative of the measured rack position

$$\frac{d}{dt}{\dot{x}}_{meas,RLA}\left(\mathrm{t}-{\mathrm{t}}_{\mathrm{delay}}\right)=\frac{d}{dt}\left(s_{\max }\sin \left(2\pi f\left(t-t_{delay}\right)\right)\right)=s_{\max }\cos \left(2\pi f\left(t-t_{delay}\right)\right)·2\pi f$$

(16)

Equation (15) can be rewritten as

$$\Delta x(t-t_{delay}{)}^{!};={\dot{x}}_{meas,RLA}\left(t-t_{delay}\right)·t_{delay}.$$

(17)

Consequently, the additional term from Equation (9) can be introduced by considering the current velocity of the RLA multiplied with the occurring delay time.

$$\Delta x(t{)}^{!};={\dot{x}}_{meas,RLA}\left(t\right)·t_{delay}.$$

(18)

Therefore, the derived term represents an estimation of the future position of the steering rack. To incorporate a frequency-dependent delay time, a simple frequency estimation model, which is valid for sinusoidal excitation, is introduced. Since both the acceleration ${\ddot{x}}_{meas,RLA}$ and position of the PMLSM $x_{meas,RLA}$ are measured, their ratio is utilized for frequency estimation

$$\frac{{\ddot{x}}_{meas,RLA}}{x_{meas,RLA}}=\frac{s_{\max }{\left(2\pi f\right)}^2\sin \left(2\pi ft\right)}{s_{\max }\sin \left(2\pi ft\right)}$$

(19)

with a zero-value exception, the frequency is calculated as

$$f_{estim}=\frac{\sqrt{\left|\frac{{\ddot{x}}_{meas,RLA}}{x_{meas,RLA}}\right|}}{2\pi }$$

(20)

The approach with a variable delay time is called variable delay compensation and is abbreviated as DCvar for distinction from the constant delay time solution.

For the DC and DCvar approach, the measured position of the PMLSM is added to the look ahead term $\Delta x$ and utilized for the evaluation of the spring force $F_{spring}$, as displayed in Figure 9a. The calculation of the look ahead term is illustrated in detail in Figure 9b for a frequency-dependent estimated delay time ${\widehat{t}}_{delay}$. In case of a constant delay time, the lookup table is replaced by the constant value.

Both DC and DCvar can be utilized for steer-by-wire systems, since only rack information and no steering wheel information are required. That means that there is no need for a fixed link between steering wheel angle and rack displacement.

4. Results and Discussion

In this section, the comparison of the proposed approaches and the reference state is conducted.

4.1. Feedback Control Performance

For the evaluation of the control performance during feedback characterization, the transfer function from the reference force signal to the measured force is utilized as the objective criteria. Identical to previously introduced transfer functions, the estimation is performed with an FFT to receive the feedback control performance $G_{FB,Perf}$

$$G_{FB,Perf}=\frac{FFT\left(F_{meas,RLA}\right)}{FFT\left(F_{ref,RLA}\right)}.$$

(21)

Here, the magnitude of $G_{FC,Perf}$ represents the relevant parameter. For a setup where the steering wheel is fixed in its position, the vehicle velocity is set to 70 km/h and a force excitation amplitude of 600 N is defined; the magnitude of the feedback control performance is displayed in Figure 10. The PVC successfully reduces the deviation from the desired amplitude, which is indicated by the red horizontal line with a magnitude of one. To display the improvement for multiple setups, the maximum and minimum magnitude are identified for all available setups. The relevant values for the displayed setup are marked with a triangle in Figure 10.

An overview on the boundary conditions for four investigated setups is displayed in

Table 2. Overview of the investigated setups for feedback evaluation.

	Setup Abbreviation
Parameter	S1	S2	S3	S4
Velocity [km/h]	70	70	120	Passive EPS
Amplitude [N]	600	800	800	600
Offset Value [N]	0	0	1000	0
Steering Lock	Blocked	Free Steering	Angle Control	Angle Control

. The results in Figure 10 represent S1.

Table 3. Resulting maximum and minimum control magnitudes for the investigated setups with the initial control structure and the PVC.

	S1		S2		S3		S4		Average/Median
	noComp	PVC	noComp	PVC	noComp	PVC	noComp	PVC	noComp		PVC
Min	0.668	0.930	0.687	0.913	0.810	0.828	0.766	0.915	0.733	0.727	0.896	0.914
Max	1.024	1.035	1.028	1.098	1.028	1.051	1.294	1.052	1.094	1.028	1.059	1.052
Total	0.332	0.070	0.313	0.098	0.190	0.172	0.294	0.085	0.267	0.273	0.104	0.090

summarizes the minimum and maximum occurring magnitudes for the initial control structure without compensation (noComp) and the PVC for four setups. Additionally, the last row displays the maximum deviation from the reference course. The average and median for the investigated setups are calculated in the last column. On average, the PVC is able to maintain the amplitude within a range of ±10.4% deviation compared to the reference signal. For the reference setup, an average deviation of 26.7% is detected. This means that the control performance is improved by more than 50%.

Despite the improvement in the average control performance, the maximum magnitudes when PVC is applied are larger compared to the initial control approach. This means that the maximum occurring force amplitudes exhibit increased deviation from the reference signal in comparison to the reference setup. Since the PVC is able to limit the maximum positive deviations for all applications below 10%, especially for setup S3, where the reference exhibits overshoot of 30%, the performance of the control scheme is improved by the application of PVC.

Figure 10 and Figure 11 display the control performance for the feedback investigation for an alternative steering system with different inertia, friction and application. An improvement in the control performance for the whole frequency range and the peak values is achieved by the implementation of PVC. The qualitative deviation of the magnitude course over the frequency range between Figure 10 and Figure 11 is a result of the altered dynamic behavior of the new steering system.

To demonstrate the performance of the PVC for time-varying offset values, a low-frequency sine for the offset force is superposed with a high-frequency sine, representing the harmonic excitation. The offset force reference signal is a sine function with an amplitude of 1000 N and 0.5 Hz frequency, while the harmonic signal possesses an amplitude of 600 N and an increasing frequency from 3 Hz to 30 Hz. The time course of the reference signal displayed in Figure 12a. Figure 12b shows the objective control performance. An improvement by the PVC control for both maximum and average deviation is achieved. Consequently, the PVC is also applicable for these investigations.

After the verification of improved control performance by the PVC, a final experiment is conducted to demonstrate the importance of the feedback characterization of steering systems. Figure 13a depicts the identified feedback behavior of a steering system for three different excitations, while Figure 13b represents the associated control performance.

In Figure 13a, two different feedback magnitudes for the same excitation force amplitude of 600 N are calculated, which mainly differ at 16.5 Hz, where one result exhibits a resonance phenomenon, while the other solution remains constant. The difference between the results is the implementation of PVC. An explanation for the deviation can be found when considering the occurring control performance. At 16.5 Hz, where the peak in the feedback behavior is located, the measured rack force without PVC is 25% larger than the reference value. Therefore, instead of 600 N, a force of 750 N is present at the steering rack. For PVC, the deviation is less than 5%. A second experiment with 800 N amplitude and PVC is introduced. It displays a similar resonance at 16.5 Hz like the course for 600 N without PVC, while the control performance is close to one due to PVC implementation. Consequently, the measured peak without the PVC with an amplitude of 600 N is not a characteristic of the steering system but a result of the test bench control performance, because the higher prevailing force amplitude is responsible for the behavior. If we now consider benchmark investigations with different steering systems where the amplitude setpoint is derived based on vehicle applications, the importance of the implementation of an approach, such as PVC, is obvious to avoid unwanted influences.

4.2. Feedforward Control Performance

Since the derived IC, DC and DCvar approaches exhibit various parameters, a parameterization process is conducted.

For the selection of an adequate inertia compensation mass, a variation study of the PMLSMs mass is performed. The experimental setup for the investigation of the dynamic guidance behavior is utilized. Based on information from the test bench manufacturer, a physical mass of 200 kg is assumed. Therefore, a range from 150 kg to 250 kg is considered for identification. Figure 14a displays the sum of the root square error of the resulting spring stiffness according to Equation (5), from the reference value of 400 N/mm, normed to the solution without inertia compensation.

The occurring minimum error from the reference stiffness is obtained for a mass of 210 kg, where the error is reduced by more than 95%. This improvement is also visible for the resulting stiffness in Figure 14b. Note that the phase delay is still identical to the initial result, where no compensation is introduced. Consequently, a second identification is performed to define the relevant delay time $\Delta t_{delay}$ for the DC and DCvar approach. The results of the parameter optimization for a delay time variation between 5.7 ms and 6.2 ms are displayed in Figure 15.

Based on the results from Figure 15a, the constant delay time $\Delta t_{delay}$ is set to 6 ms. The frequency-dependent lookup table is identified as the inverse phase delay from Figure 14b and exhibits a reduced error in comparison to the constant time delay compensation. The resulting bode plot in Figure 15b now displays good agreement for the desired spring stiffness due to IC, as well as phase delay for the DC and DCvar approaches. The values for the phase delay compensation for the frequency-dependent lookup table are displayed in

Table 4. Frequency breakpoints and lookup values for the frequency-dependent delay time.

Breakpoint	1	2	3	4	5	6	7	8	9
Frequency [Hz]	0.52	1.02	1.52	2.02	2.52	3.02	3.52	4.02	4.52
$\Delta t_{delay}$ [ms]	5.6	5.7	5.7	5.8	5.8	5.9	6	6.1	6.2

.

To obtain an objective comparison of the different control performances,

Table 5. Summary of the measured magnitudes of the transfer function from rack displacement to measured rack force and the difference from the spring stiffness for the compensation methods.

Compensation	None		IC		IC + DC		IC + DCvar
Test	Max	Avg.	Max	Avg.	Max	Avg.	Max	Avg.
V1	207.46	74.75	23.47	3.15	10.12	3.43	11.68	3.44
V2	220.9	78.39	25.06	4.24	22.56	8.62	21.74	8.69
V3	229.78	78.82	25.40	8.50	38.23	14.42	36.99	14.5
V4	234.81	84.97	56.72	26.79	79.43	33.12	77.56	32.62
Average	223.24	79.23	32.66	10.67	37.59	14.90	36.99	14.81

and

Table 6. Summary of the phase delay of the transfer function from rack displacement to measured rack force for the compensation methods.

Compensation	None		IC		IC + DC		IC + DCvar
Test	Max	Avg.	Max	Avg.	Max	Avg.	Max	Avg.
V1	12.32	5.62	11.35	5.53	1.11	0.21	0.74	0.17
V2	10.84	5.72	11.94	5.85	0.97	0.34	1.28	0.36
V3	10.97	5.74	11.45	5.50	1.00	0.15	0.89	0.17
V4	10.83	5.47	10.79	4.89	2.93	1.23	2.97	1.14
Average	11.24	5.64	11.38	5.44	1.50	0.48	1.47	0.46

summarize the maximum and average deviations of the control performance magnitude and phase delay from the desired behavior, respectively. In total, four different setups for the steering guidance test are investigated where the vehicle velocity $v_{veh}$, the spring stiffness $k_{virt}$ and the steering wheel angle amplitude ${\phi }_{SW}$ are varied. The setups are abbreviated as

• V1: $v_{veh}$ = 70 km/h    $k_{virt}$ = 400 N/mm  ${\phi }_{SW}$ = 20°
• V2: $v_{veh}$ = 70 km/h    $k_{virt}$ = 800 N/mm  ${\phi }_{SW}$ = 20°
• V3: $v_{veh}$ = 180 km/h  $k_{virt}$ = 800 N/mm  ${\phi }_{SW}$ = 20°
• V4: $v_{veh}$ = 180 km/h  $k_{virt}$ = 800 N/mm  ${\phi }_{SW}$ = 10°

Table 5 demonstrates that the IC approach successfully reduces the resulting deviations between the measured magnitude and the reference spring stiffness. The best solution concerning the magnitude accuracy is derived for IC without phase compensation. Incorporating the DC and DCvar approach leads to an increase of 15% and 13.3% for the maximum deviation, respectively. On average, the phase compensation exhibits a 50% increase compared to IC alone. Still, all three approaches reduce the maximum occurring stiffness error by at least 83% and on average by 81.2%, demonstrating the improved control performance for the investigated application.

For the phase deviation in Table 6, the same observation as in Figure 14b is valid. Although the resulting measured spring stiffness is thoroughly improved by the implementation of IC alone, the phase delay is maintained at a constant level compared to the reference measurement without compensation. For the integration of DC and DCvar, the phase delay is reduced by 86.7% for the maximum and up to 91.5% for the average phase delays of the measured force signal to the displacement signal. Here, DCvar exhibits slightly improved performance if compared to DC, but the added value is neglectable. Therefore, the following comparisons exclude the IC + DCvar approach and concentrate on the IC and IC methods. Still, both DC and DCvar improve the phase accuracy of the test bench.

A second experiment is conducted to validate the applicability of the control improvements for applications, wherein their parameters are not optimized. Here, $k_{virt}$ = 400 N/mm and $v_{veh}$ = 70 km/h are chosen for the maneuver conditions. Instead of a sine sweep input, which is utilized for guidance behavior identification, a steering wheel reference signal is implemented, which is derived from a real driving maneuver from a driving simulator. The complete reference force signal for the maneuver is depicted in Figure 16a, wherein the relevant regions are highlighted with the indices “A” and “B”. In “A”, a steering wheel excitation similar to an impulse is introduced, while region “B” represents a high-frequency sine excitation. The resulting measured forces for the relevant regions A and B are displayed in detail in Figure 16b,c to demonstrate the performance of the different compensation approaches.

The contribution of the individual compensation approaches can be understood by the measured courses. In the case of no implemented compensation approach, the PMLSM inertia causes deviations at 14.3 s in Figure 16b, where an increase of the contact force is observed in advance to the rise of the reference force. Here, negative contact forces represent pressure on the load cell. When the steering maneuver is initiated at 14.3 s, the steering system moves to the center region, therefore, reducing the rack force. Since the PMLSM is not able to follow the movement immediately, an overshoot occurs where the decrease in the rack force is primarily caused by the missing movement due to inertia of the PMLSM. At the maximum reference force of the time course at 14.4 s, both the amplitude and phase deviation of the measured force without compensation are visible. When incorporating the IC approach, the measured force deviation is reduced for both previously described points, resulting in a better approximation of the reference signal. The phase delay, as evaluated earlier, is still present. When IC and DC are implemented simultaneously, the reference force is represented accurately by the measured force for both amplitude accuracy and the phase delay. A similar tendency can be observed in Figure 16c. Here, due to the implemented control improvements, the reference signal and the measured force with IC + DC are almost indistinguishable. These observations also underline the improved dynamic performance of the force control for an application where the tuning parameters were not derived.

For the third comparison, a basic setup is investigated, which is utilized for the evaluation of the steering power on a test bench (see [27]). For these tests, the steering wheel angle is defined to obtain a constant steering wheel velocity over a large portion of the complete steering stroke. The rack force is held at a constant value. For each new test, the rack force is increased until the torsion bar torque exceeds a predefined limit. At this point, the steering power limit is reached. For the herein investigated test setup, a constant force of 0 N is predefined, while the steering wheel maneuvers at 800°/s. Since the rack force reference signal is constant over time, no DC is implemented since it has no effect on the control performance. The time courses of the measured rack force with and without IC is displayed in Figure 17.

The fluctuations of the measured forces without compensation originate from the gimbal fault and the steering wheel angle acceleration and deceleration at the beginning and at the end of the steering wheel movement. Since the IC incorporates both the steering ratio as well as the gimbal fault and provides an inertia compensation signal, these influences are successfully reduced.

5. Conclusions

Within this paper, an automotive steering system testbench, consisting of two PMLSMs and one steering wheel actuator, is examined concerning its dynamic performance. The study presents three methods, each of which improves one defined use case. The first approach deals with the situation when a harmonic reference signal is previously known but the steering system characteristics hinder the PMLSM from reaching the desired force course. An online real-time capable algorithm uses the peak value information of the harmonic reference signal and the measured peak forces to calculate a ratio and adapt the input signal accordingly to receive a good amplitude accuracy. A second approach is applicable when the steering test bench operates in closed loop operation, meaning that the rack force is calculated based on the rack displacement. Due to high inertia of the PMLSM, the magnitude and phase delay of the PMLSM are deteriorated. Therefore, the steering wheel angle signal is used to provide an inertia compensation signal, which incorporates not only the moving mass of the PMLSM but also the occurring steering ratio and gimbal error in the column. It is demonstrated that the approach successfully improves the dynamic control performance by reaching the desired force amplitudes. To compensate for the phase delay in the same setup, a phase delay compensation approach is motivated, which ideally avoids the occurrence of phase delay between the reference and measured force signal. The latter approach can be combined with the inertia compensation to significantly improve the test bench control. Final validation tests demonstrate the applicability of the proposed methods, also for new applications where the parameterization was not performed. The introduced methods represent an improvement of the steering test bench control to allow subsystem-based development, even for the investigation of steering feel, which poses strict requirements due to the close contact to the human driver. Future improvements in the dynamic control performance may include model predictive control approaches for the closed loop operation of the steering system test bench. Additionally, automated, online transfer function estimation represents an approach to include the system behavior into the control of previously defined excitation signals. In this method, the representative transfer function can be selected based on information of the surrounding conditions of the experiment and used to alter the reference signal accordingly.