Dual Synthetic Jets Actuator and Its Applications Part V: Novel Valveless Continuous Micropump Based on Dual Synthetic Jets with a Tesla Structure
Abstract
:1. Introduction
2. Structure and Numerical Methods
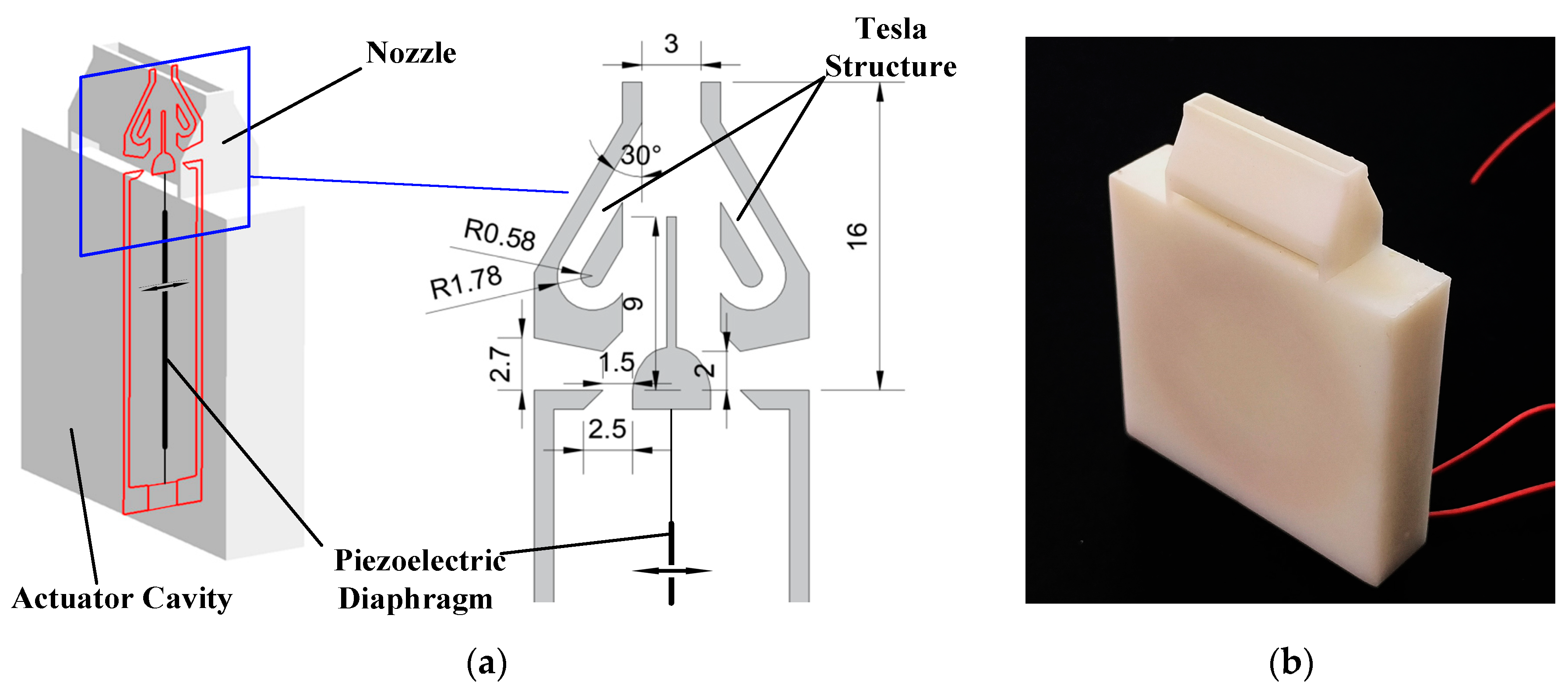
2.1. Structure and Mechanism
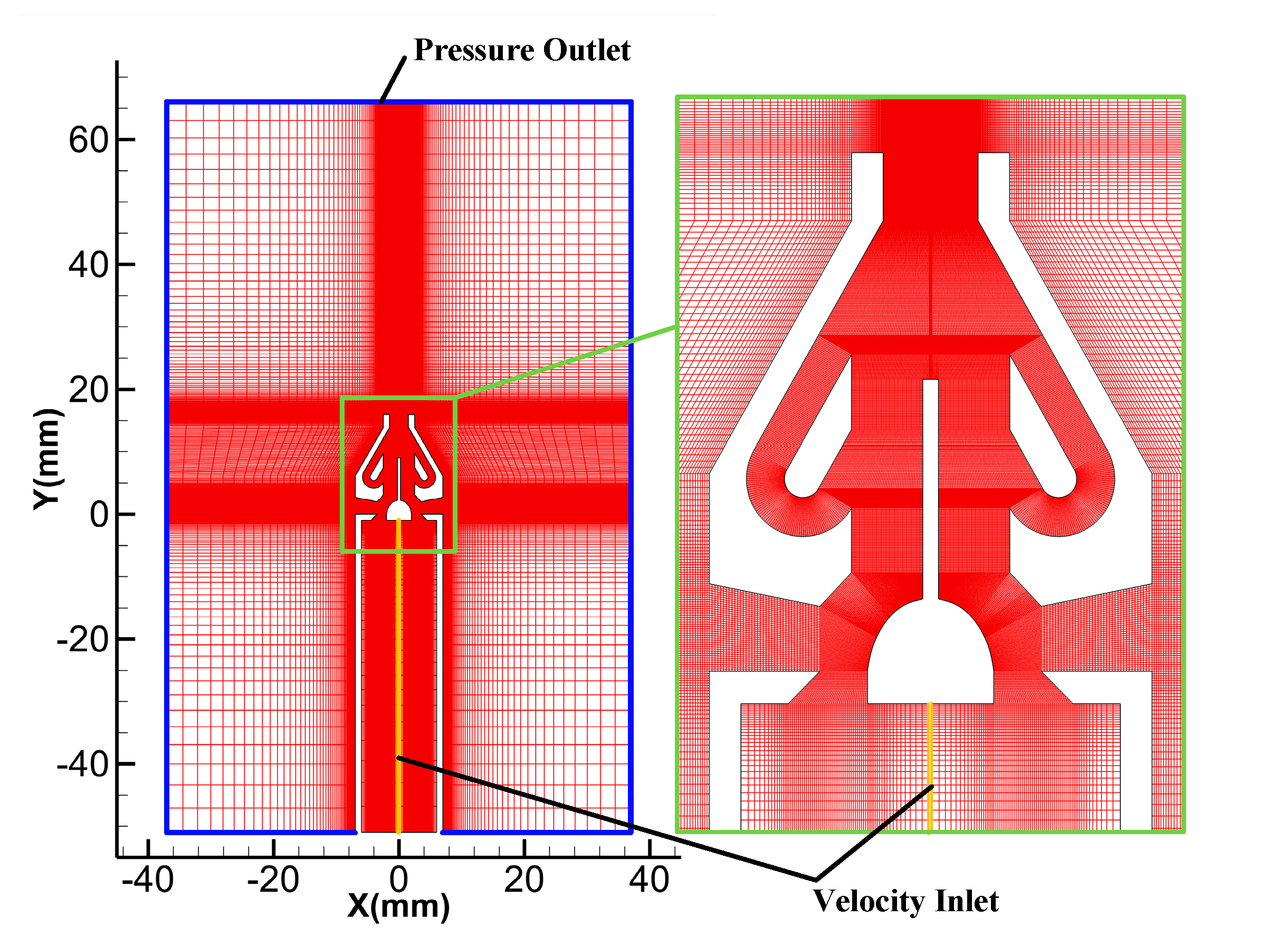
2.2. Numerical Model and CFD Method
2.3. Grid Independence Verification
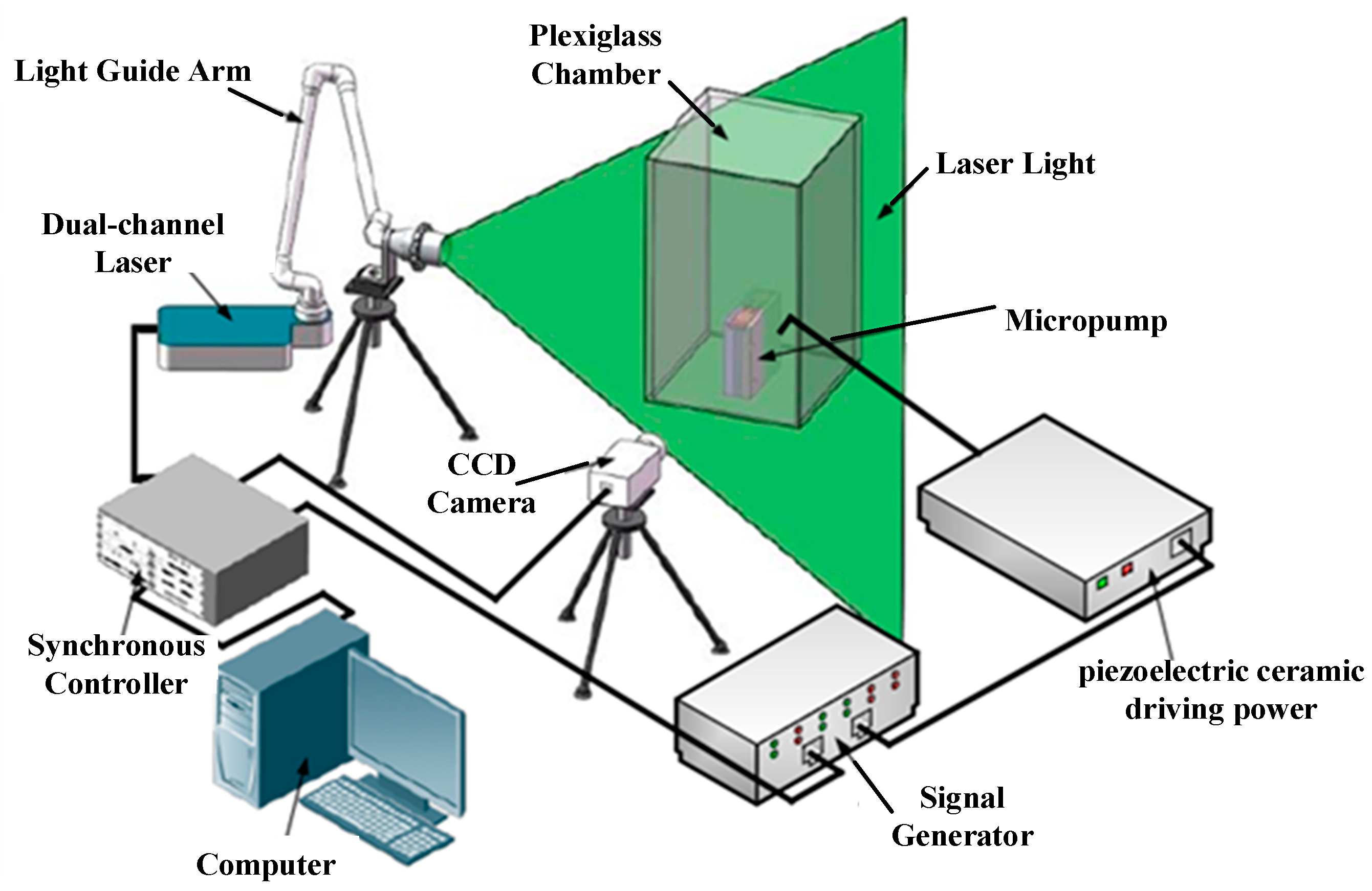
2.4. PIV Experimental Method
3. Results and Analysis
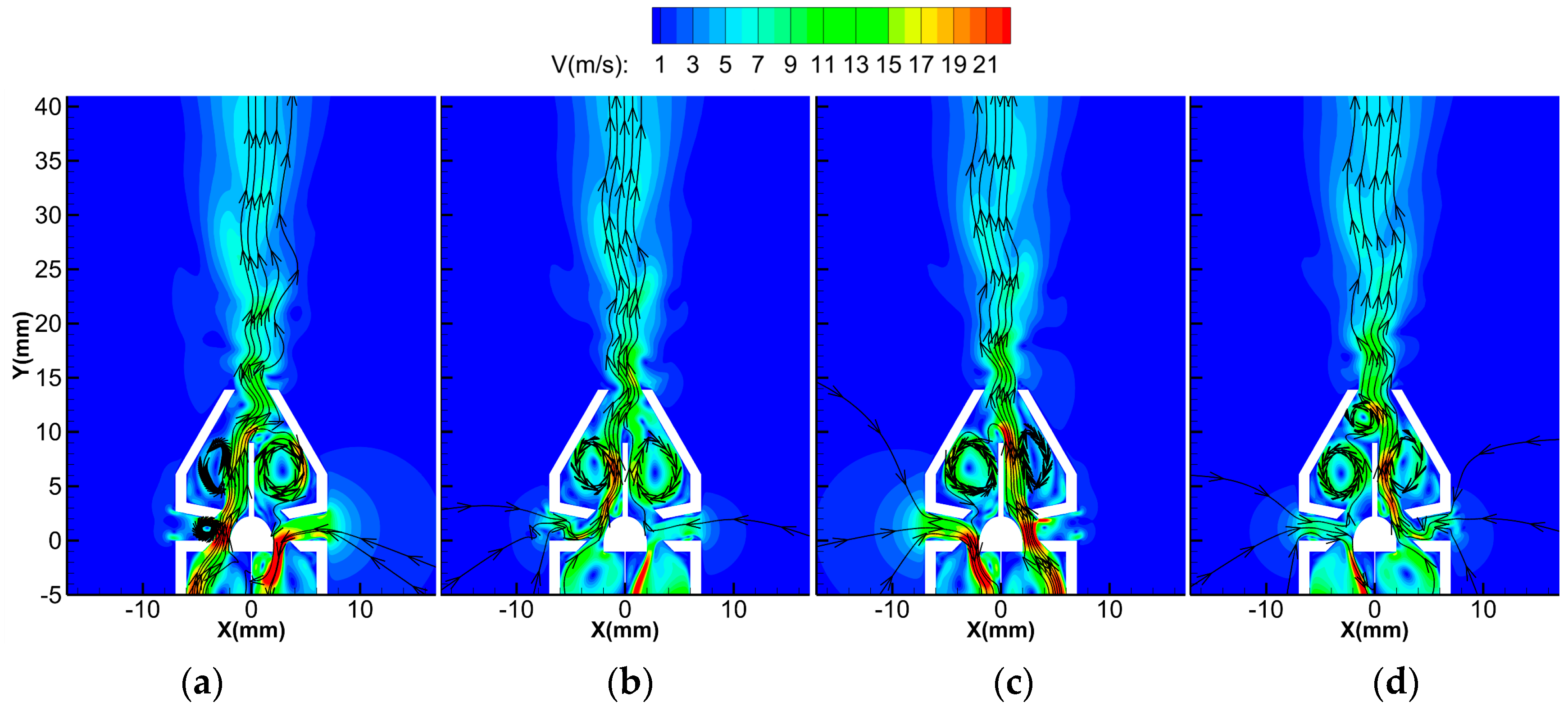
3.1. Instantaneous Flow Field
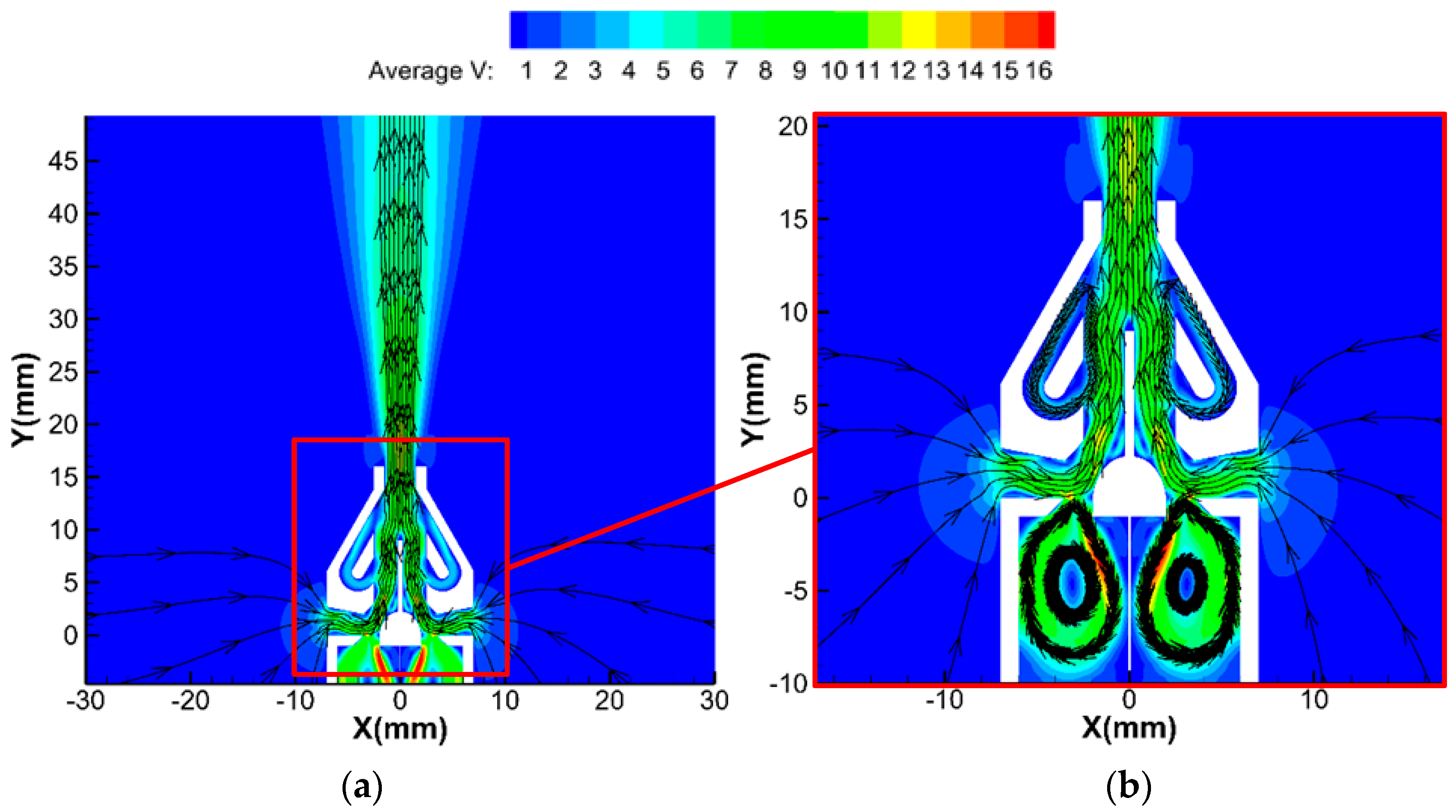
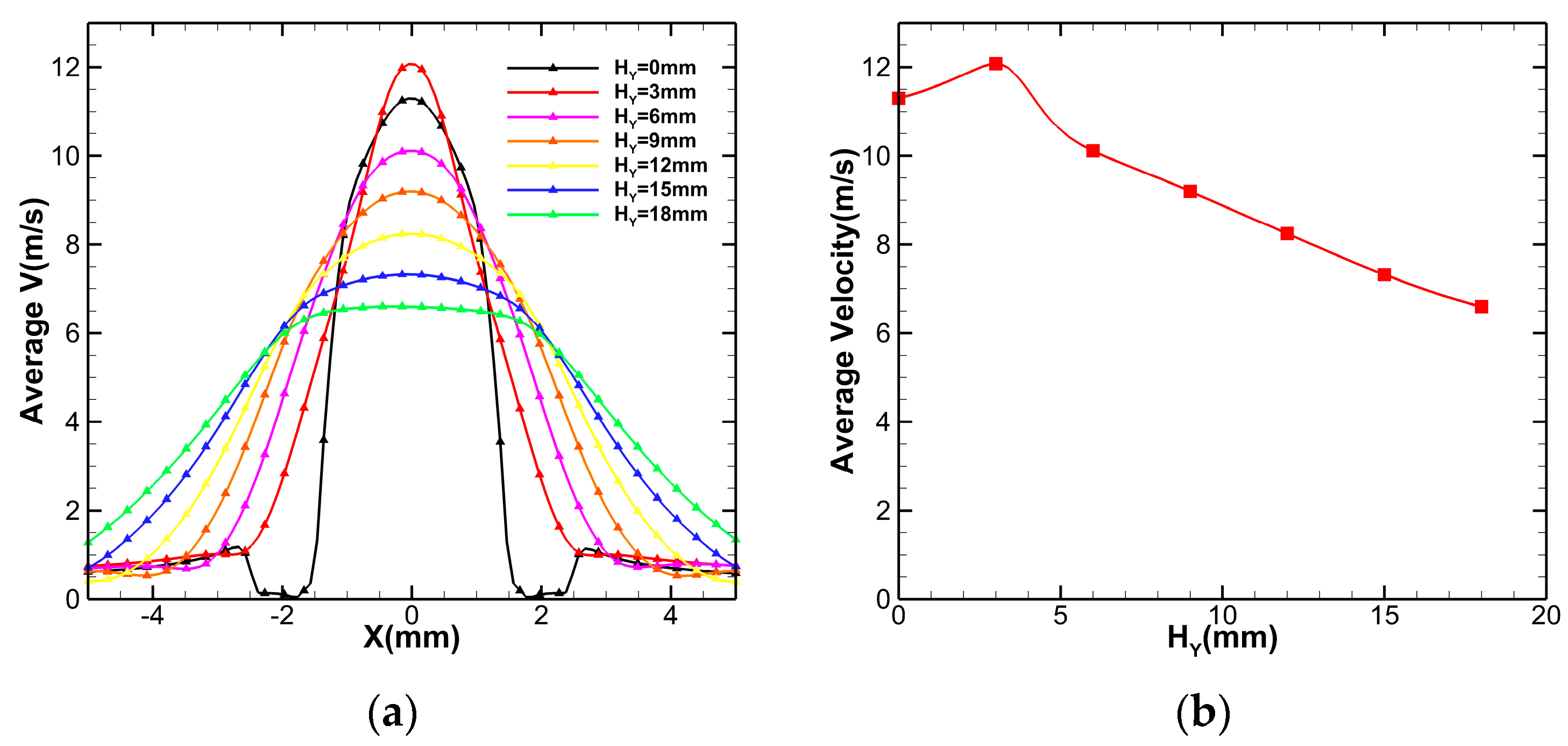
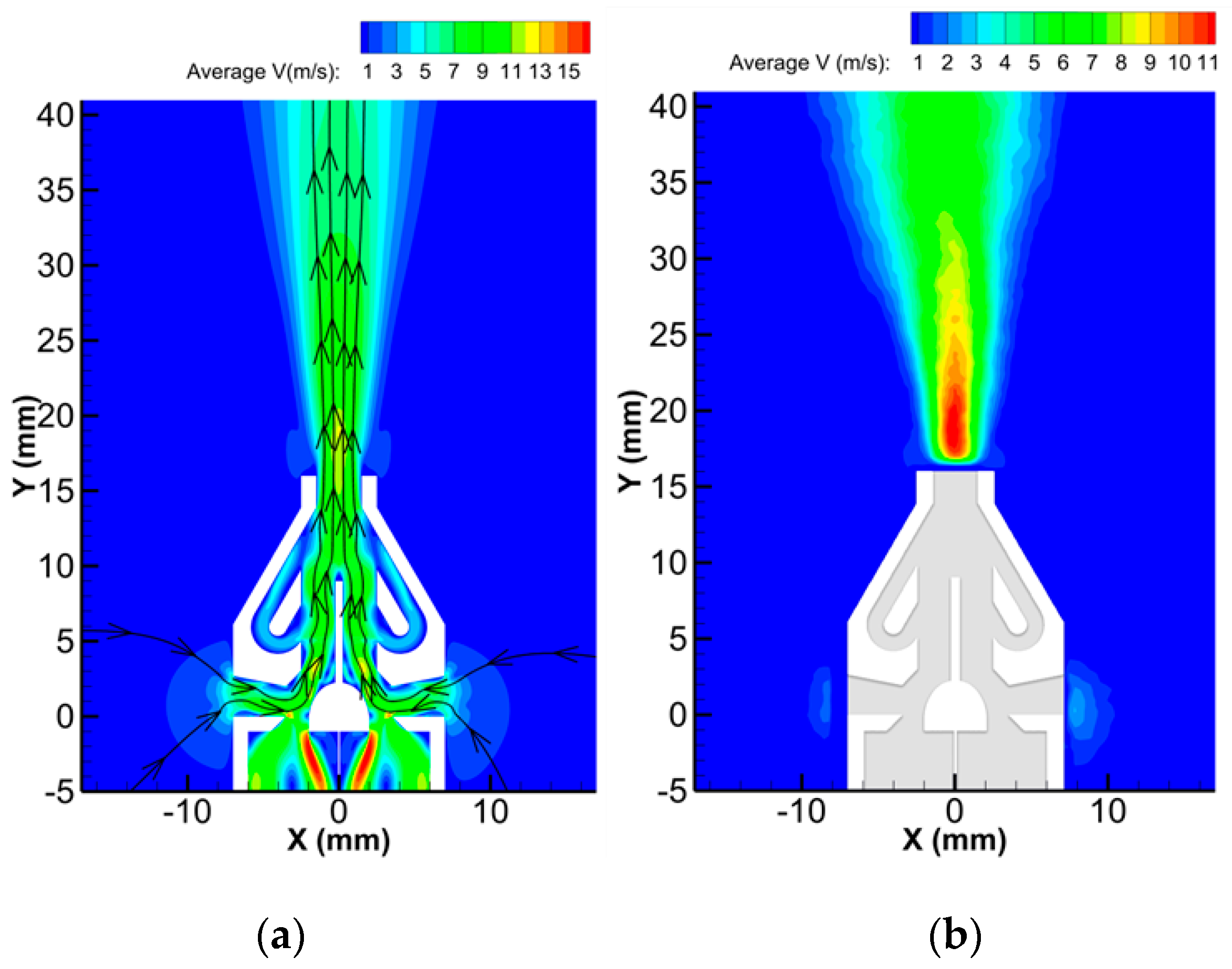
3.2. TimeMean Flow Field
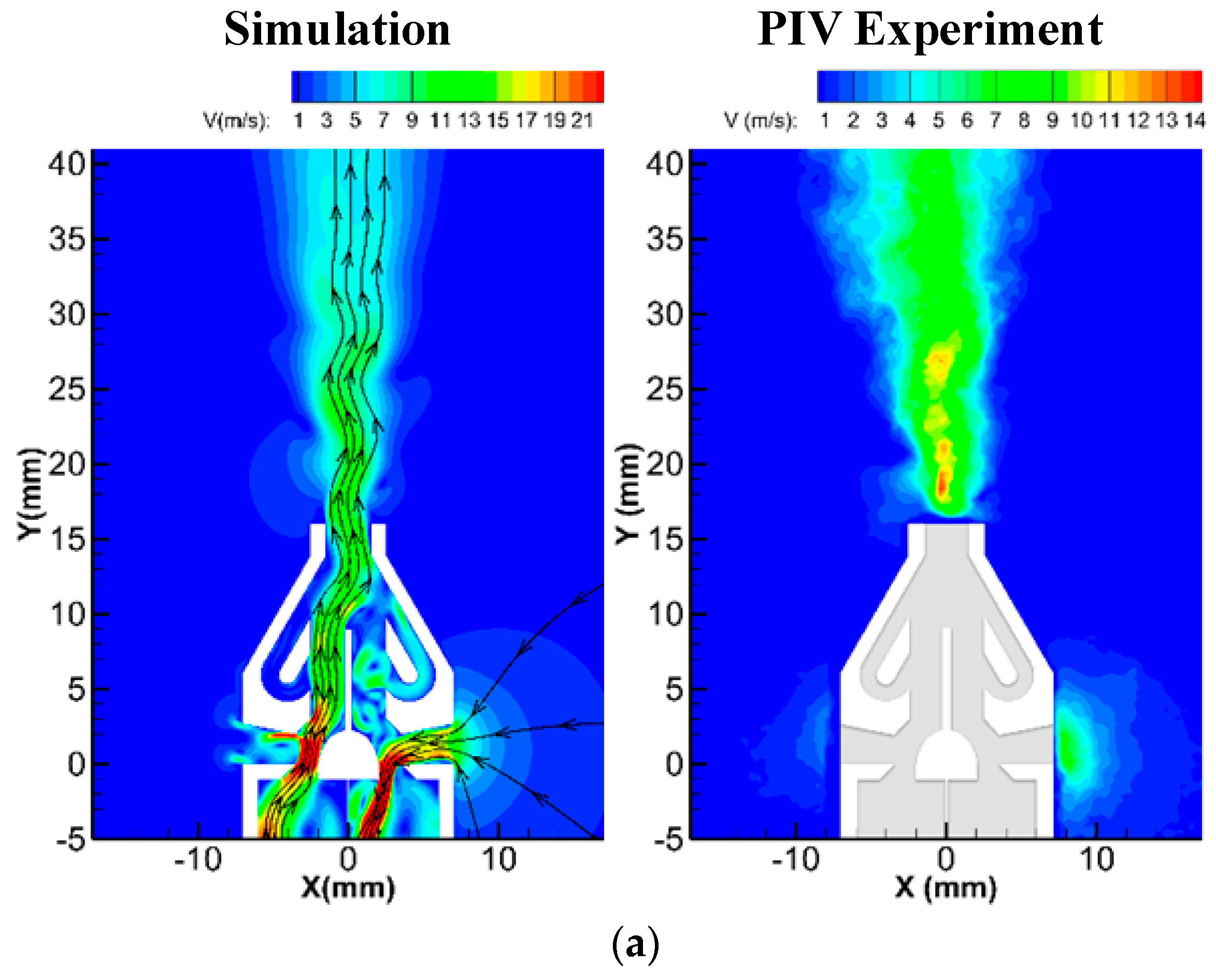
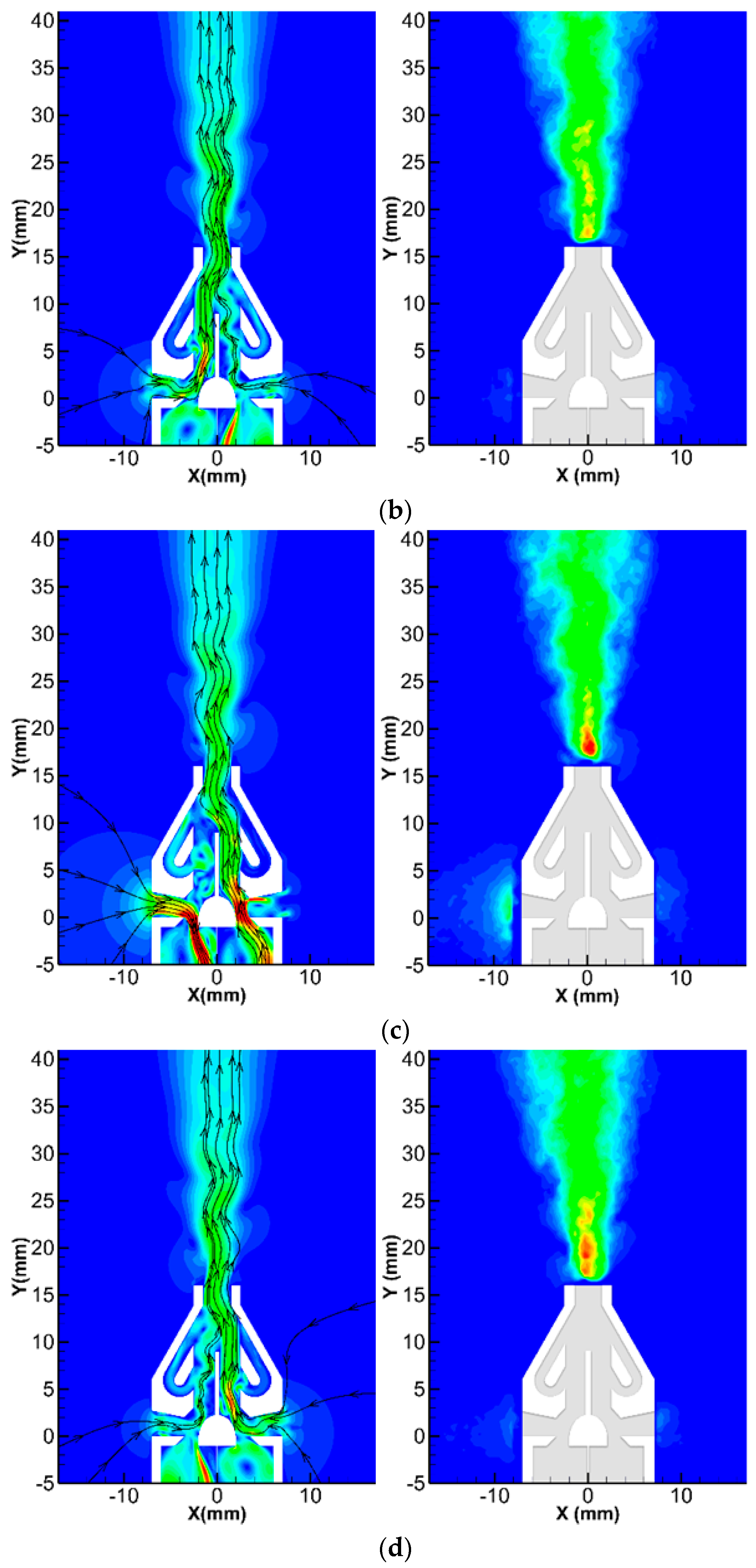
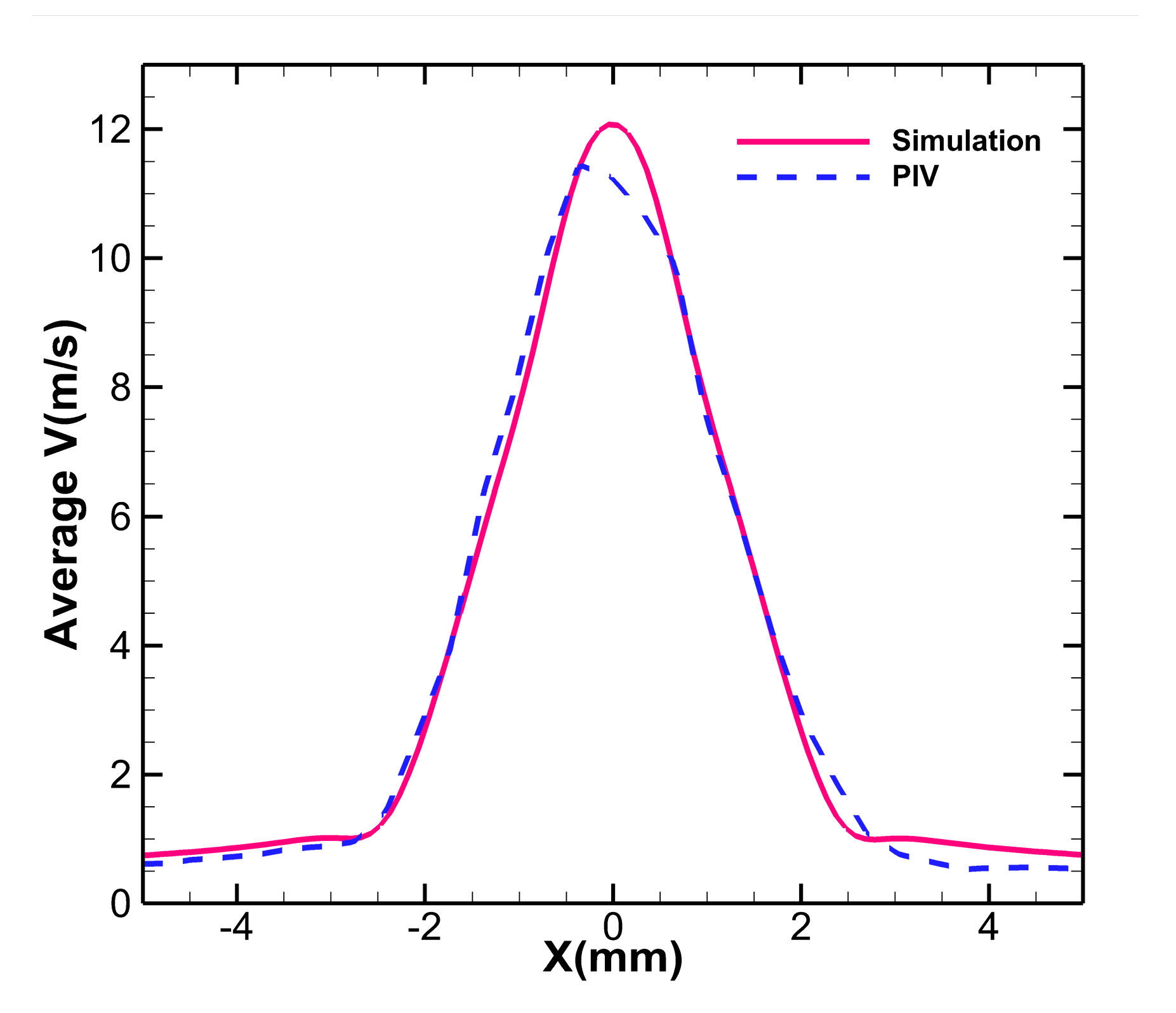
3.3. PIV Results Analysis
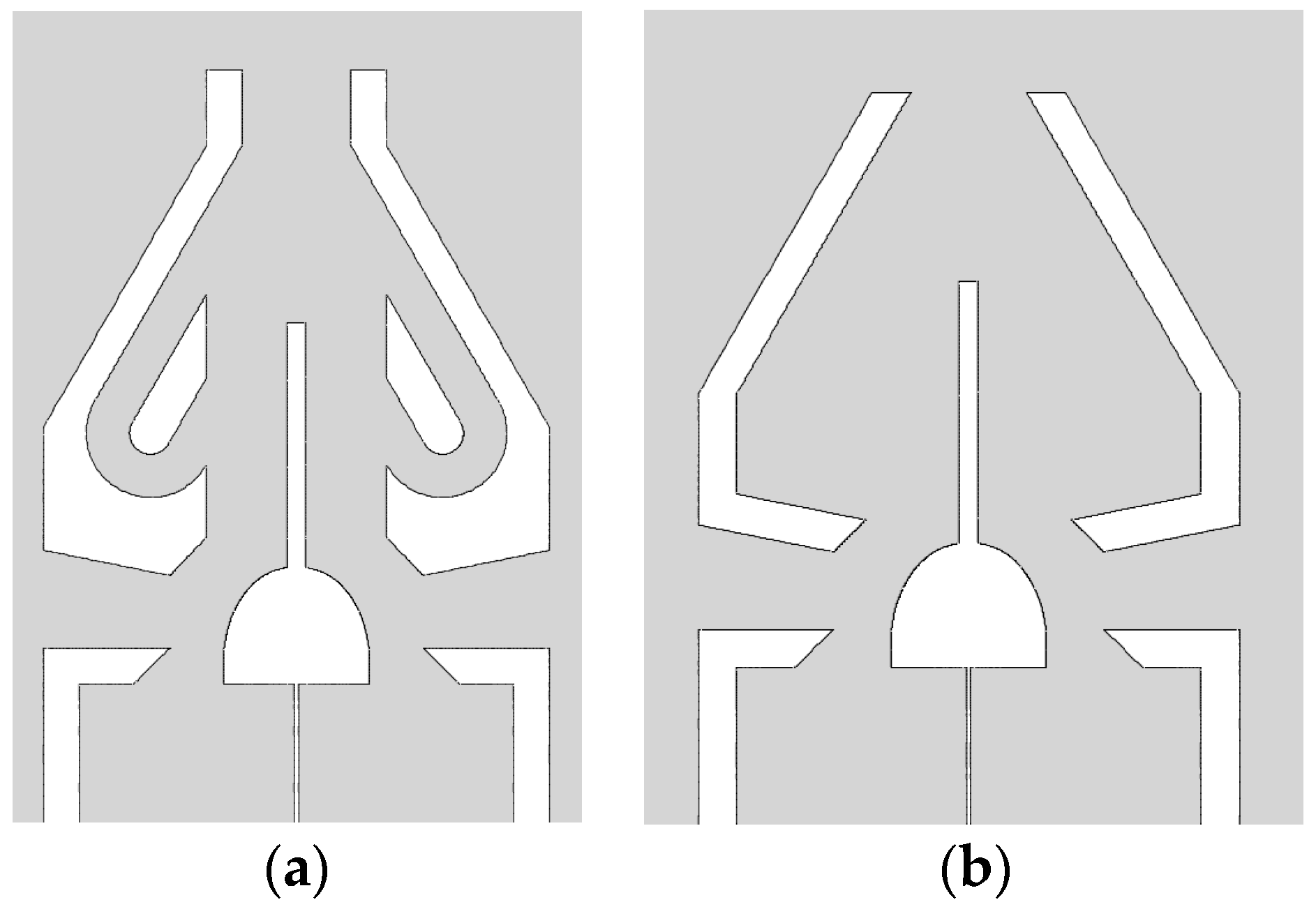
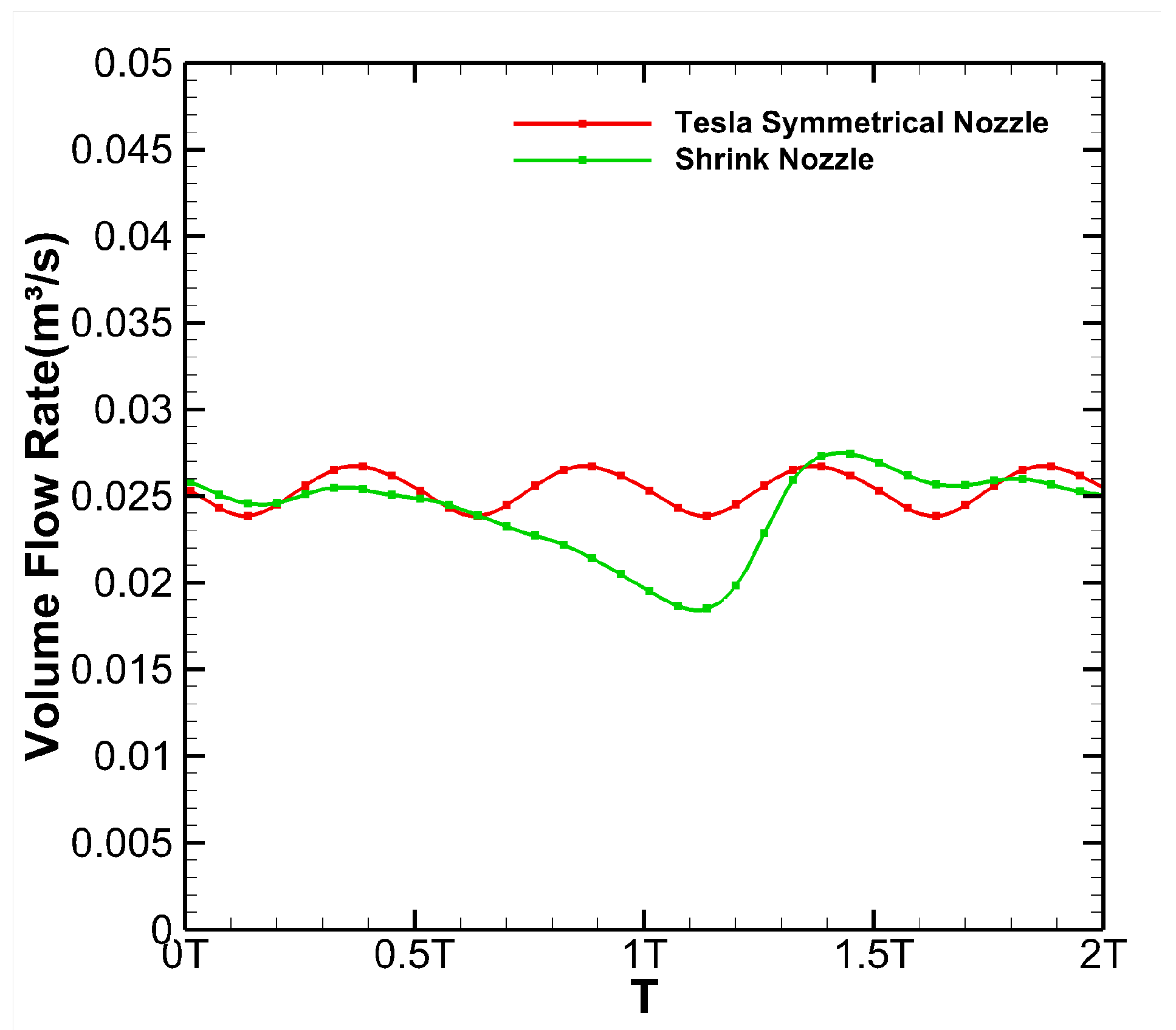
3.4. Comparison with the Traditional Shrink Nozzle
4. Conclusions
- (1)
- The novel valveless continuous micropump based on dual synthetic jets with a Tesla structure could realize the directional transport of fluid. Through the reciprocating vibration of the diaphragm, the micropump could periodically inhale fluid from both sides and alternately eject the jet from the nozzle. It was able to continuously eject the fluid within one cycle and the pumping flow rate was relatively stable.
- (2)
- The numerical simulation results showed that the downstream time-mean flow field of the micropump presented a unimodal symmetry pattern. The maximum velocity on the center line of the flow field increased first and then decreased as the distance from the nozzle outlet grew. It appeared at a distance of 3 mm from the nozzle outlet and reached 12 m/s. Even at a distance of 24 mm, the velocity reached 6 m/s.
- (3)
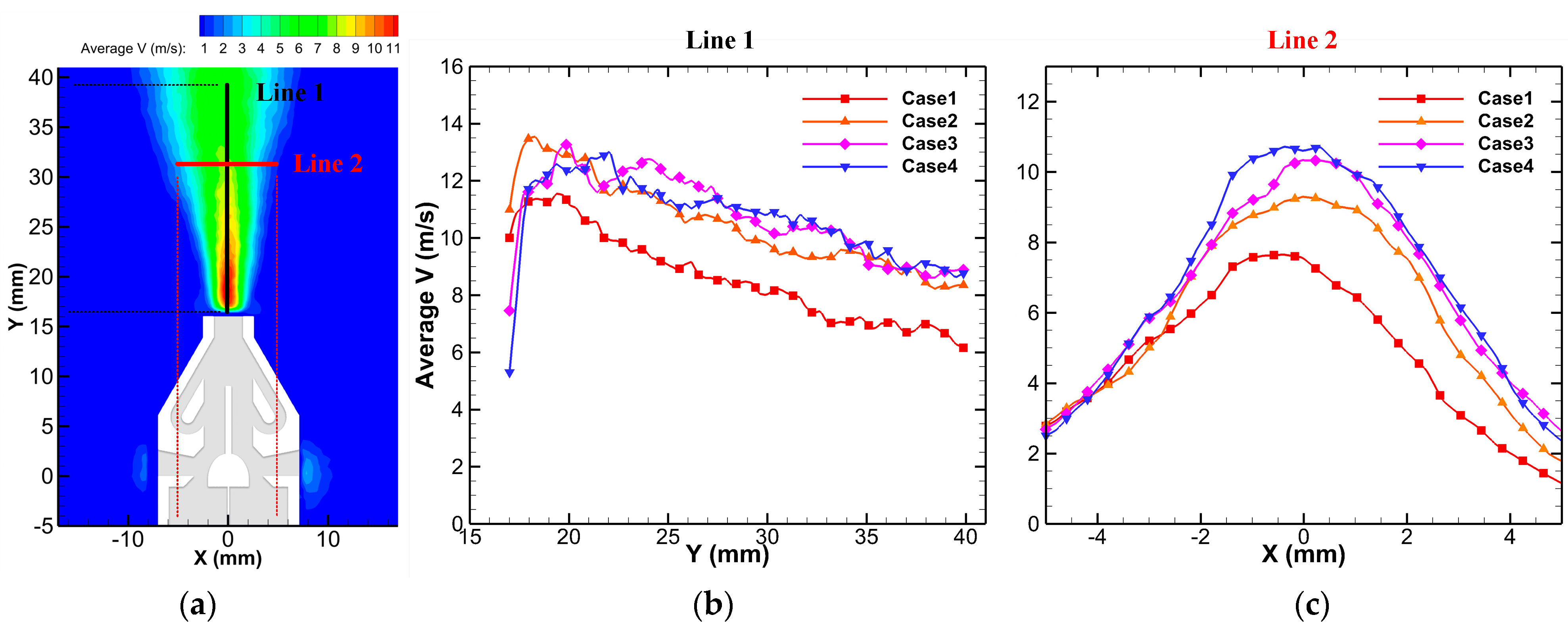
- The PIV results showed that the influence range of the micropump jet could be effectively enlarged by increasing the driving voltage amplitude within a certain range (±150 V~±210 V), and the maximum influence range was 43.1°. With the increase in driving voltage amplitude, the maximum velocity of the micropump jet first increased and then remained at a stable value. At 180 V driving voltage, the maximum velocity reached 13.5 m/s. Although the increase in the voltage could not effectively improve the maximum velocity of the jet, it could enhance the transport capability of the micropump.
- (4)
- Compared with the traditional shrinking nozzle, the double Tesla symmetrical nozzle could eliminate the internal vortex and enhance the flow rate by 5.27%, making the flow rate more stable and periodic.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cobo, A.; Sheybani, R.; Tu, H.; Meng, E. A wireless implantable micropump for chronic drug infusion against cancer. Sens. Actuator A Phys. 2016, 239, 18–25. [Google Scholar] [CrossRef]
- Bußmann, A.; Leistner, H.; Zhou, D.; Wackerle, M.; Congar, Y.; Richter, M.; Hubbuch, J. Piezoelectric Silicon Micropump for Drug Delivery Applications. Appl. Sci. 2021, 11, 8008. [Google Scholar] [CrossRef]
- Rubayet, H.; Sevki, C.; Mahmoud, B.; Anthony, P.; Austin, R. A Magnetorheological Duckbill Valve Micropump for Drug Delivery Applications. Micromachines 2022, 13, 723. [Google Scholar]
- Atsushi, T.; Kenichi, K.; Hiroaki, S. Autonomous microfluidic control by chemically actuated micropumps and its application to chemical analyses. Anal. Chem. 2010, 82, 6870–6876. [Google Scholar]
- Do, V.K.; Yamamoto, T.; Ukita, Y.; Takamura, Y. Precise flow control with internal pneumatic micropump for highly sensitive solid-phase extraction liquid electrode plasma. Sens. Actuators B Chem. 2015, 221, 1561–1569. [Google Scholar] [CrossRef]
- Kant, R.; Singh, D.; Bhattacharya, S. Digitally controlled portable micropump for transport of live micro-organisms. Sens. Actuators A Phys. 2017, 265, 138–151. [Google Scholar] [CrossRef]
- Vedran, B.; Denis, D. All Silica Micro-Fluidic Flow Injection Sensor System for Colorimetric Chemical Sensing. Sensors 2021, 21, 4082. [Google Scholar]
- Bußmann, A.; Thalhofer, T.; Hoffmann, S.; Daum, L.; Surendran, N.; Hayden, O.; Hubbuch, J.; Richter, M. Microfluidic Cell Transport with Piezoelectric Micro Diaphragm Pumps. Micromachines 2021, 12, 1459. [Google Scholar] [CrossRef]
- Liu, J.H.; Yan, W.X.; Zhao, Y.Z. A Micropump Sucker Using a Piezo-Driven Flexible Mechanism. J. Mech. Robot. 2019, 11, 041009. [Google Scholar] [CrossRef]
- Chang, X.; Chen, C.; Li, J.; Lu, X.; Liang, Y.; Zhou, D.; Wang, H.; Zhang, G.; Li, T.; Wang, J.; et al. Motile Micropump Based on Synthetic Micromotors for Dynamic Micropatterning. ACS Appl. Mater. 2019, 11, 28507–28514. [Google Scholar] [CrossRef]
- Pramod, K.; Sen, A.K. Flow and Heat Transfer Analysis of an Electro-Osmotic Flow Micropump for Chip Cooling. J. Electron. Packag. 2014, 136, 031012. [Google Scholar] [CrossRef]
- Tang, Y.; Jia, M.; Ding, X.; Li, Z.; Wan, Z.; Lin, Q.; Fu, T. Experimental investigation on thermal management performance of an integrated heat sink with a piezoelectric micropump. Appl. Therm. Eng. 2019, 161, 114053. [Google Scholar] [CrossRef]
- Peng, Y.H.; Wang, D.H.; Li, X.Y.; Zhang, Y. Cooling chip on PCB by embedded active microchannel heat sink. Int. J. Heat Mass Transf. 2022, 196, 123251. [Google Scholar] [CrossRef]
- Abhari, F.; Jaafar, H.; Yunus, N.A. A Comprehensive Study of Micropumps Technologies. Int. J. Electrochem. Sci. 2012, 7, 9765–9780. [Google Scholar]
- Smith, B.L.; Glezer, A. The formation and evolution of synthetic jets. Phys. Fluids 1998, 10, 2281–2297. [Google Scholar] [CrossRef]
- Ikhlaq, M.; Yasir, M.; Demiroğlu, M.; Arik, M. Synthetic Jet Cooling Technology for Electronics Thermal Management—A Critical Review. IEEE Trans. Compon. Packag. Manuf. Technol. 2021, 8, 1156–1170. [Google Scholar] [CrossRef]
- Luo, X.B.; Li, Z.X.; Guo, Z.Y. Principle and Numerical Simulation of A New Valve-less Micropump. China Mech. Eng. 2002, 15, 1261–1263. (In Chinese) [Google Scholar]
- Luo, Z.B.; Xia, Z.X. A novel valve-less synthetic-jet-based micro-pump. Sens. Actuator A Phys. 2005, 122, 131–140. [Google Scholar] [CrossRef]
- Dau, V.T.; Dinh, T.X.; Sugiyama, S. A MEMS-based silicon micropump with intersecting channels and integrated hotwires. J. Micromech. Microeng. 2009, 19, 125016. [Google Scholar] [CrossRef]
- Choi, J.P.; Kim, K.S.; Seo, Y.H.; Kim, B.H. Design and Fabrication of Synthetic Air-Jet Micropump. Int. J. Precis. Eng. Manuf. 2011, 12, 355–360. [Google Scholar] [CrossRef]
- He, X.H.; Zhu, X.B. Performances of Valve-less Synthetic Jet-based Piezoelectric Pumps. J. Beijing Univ. Technol. 2015, 4, 493–500. (In Chinese) [Google Scholar]
- Munas, F.R.; Melroy, G.; Abeynayake, C.B. Development of PZT Actuated Valveless Micropump. Sensors 2018, 18, 1302. [Google Scholar] [CrossRef]
- Le Van, L.; Bui, T.T.; Nhu, C.N.; Ngoc, A.N.; Dinh, T.X.; Dang, L.B.; Tran, C.D.; Duc, T.C. Simulation and Experimental Study of a Synthetic Jet Valveless Pump. IEEE ASME Trans. Mechatron. 2019, 25, 1162–1170. [Google Scholar] [CrossRef]
- Tran, C.D.; Pham, P.H.; Nguyen, T.K.; Phan, H.P.; Dinh, T.; Nguyen, T.V.; Bui, T.T.; Chu, D.T.; Nguyen, N.T.; Dao, D.V. A new structure of Tesla coupled nozzle in synthetic jet micro-pump. Sens. Actuator A Phys. 2020, 315, 112296. [Google Scholar] [CrossRef]
- Luo, Z.B.; Xia, Z.X.; Liu, B. New Generation of Synthetic Jet Actuators. AIAA J. 2006, 44, 2418–2420. [Google Scholar] [CrossRef]
- Luo, Z.B.; Zhao, Z.J.; Deng, X.; Wang, L.; Xia, Z.X. Dual Synthetic Jets Actuator and Its Applications—Part I: PIV Measurements and Comparison to Synthetic Jet Actuator. Actuators 2022, 11, 205. [Google Scholar] [CrossRef]
- Luo, Z.B. Principle of Synthetic Jet and Dual Synthetic Jets, and Their Applications in Jet Vectoring and Micro-Pump. Ph.D. Thesis, National University of Defense Technology, Changsha, China, October 2006. [Google Scholar]
- Luo, Z.B.; Xia, Z.X. Luo-Xia Model, A Computing Model of PZT-Driven Synthetic Jet Actuator. In Proceedings of the CCCM 2010, Mianyang, China, 20 August 2010. (In Chinese). [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 7, 078001. [Google Scholar]

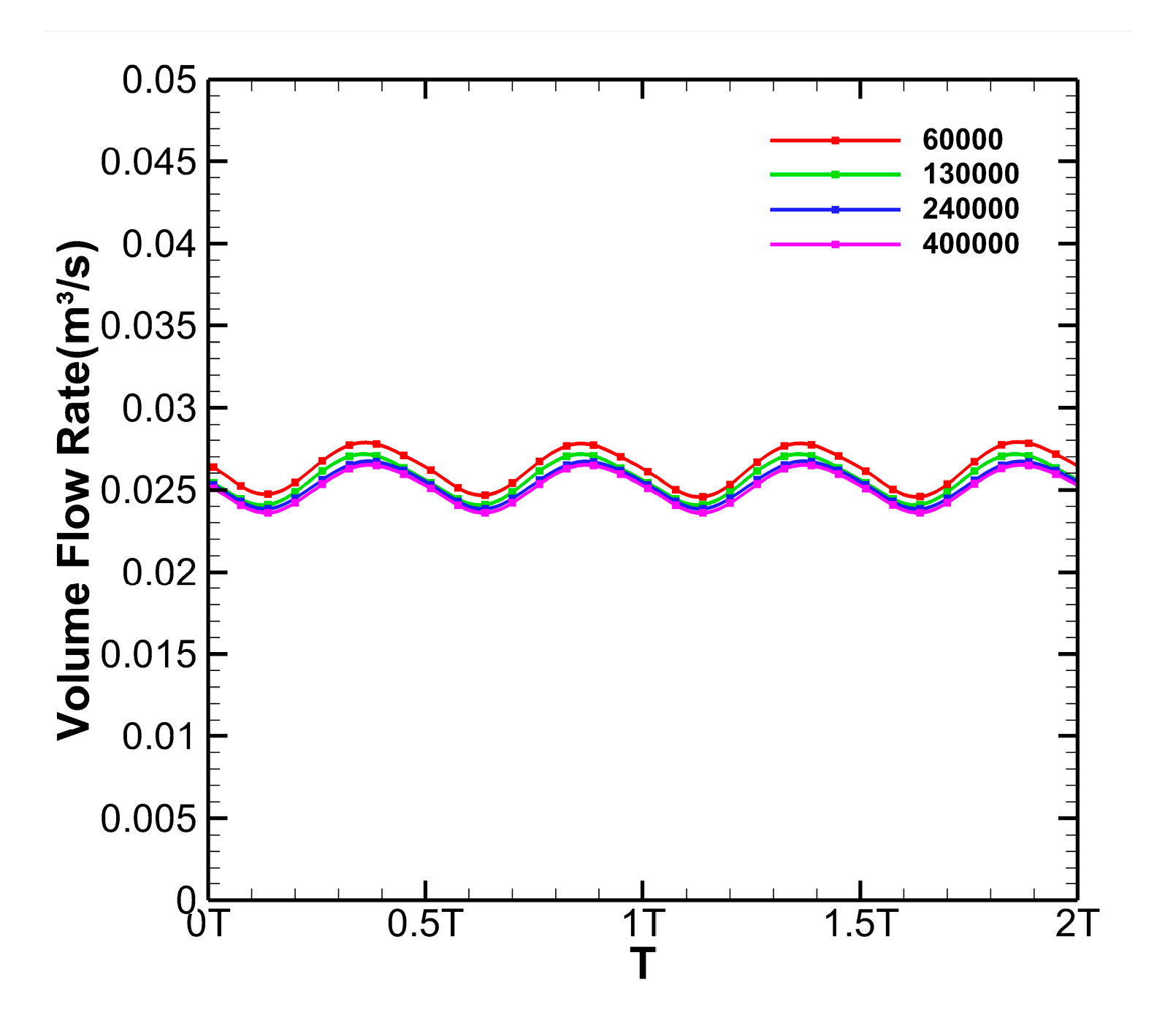

| Number of Grids | Difference from 400,000 Results (%) | |
|---|---|---|
| 60,000 | 0.02632 | 4.74 |
| 130,000 | 0.02567 | 2.15 |
| 240,000 | 0.02536 | 0.92 |
| 400,000 | 0.02513 | —— |
| Experimental Serial Number | Driving Voltage Amplitude (±V) | Influence Area Size (°) |
|---|---|---|
| Case1 | 150 | 38.5 |
| Case2 | 180 | 40.5 |
| Case3 | 210 | 43.1 |
| Case4 | 240 | 42.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.-Y.; Peng, W.-Q.; Luo, Z.-B.; Zhao, Z.-J.; Gong, J.-Y.; Dong, Z.-F. Dual Synthetic Jets Actuator and Its Applications Part V: Novel Valveless Continuous Micropump Based on Dual Synthetic Jets with a Tesla Structure. Actuators 2023, 12, 226. https://doi.org/10.3390/act12060226
Zhang J-Y, Peng W-Q, Luo Z-B, Zhao Z-J, Gong J-Y, Dong Z-F. Dual Synthetic Jets Actuator and Its Applications Part V: Novel Valveless Continuous Micropump Based on Dual Synthetic Jets with a Tesla Structure. Actuators. 2023; 12(6):226. https://doi.org/10.3390/act12060226
Chicago/Turabian StyleZhang, Jian-Yuan, Wen-Qiang Peng, Zhen-Bing Luo, Zhi-Jie Zhao, Jian-Yu Gong, and Zhao-Feng Dong. 2023. "Dual Synthetic Jets Actuator and Its Applications Part V: Novel Valveless Continuous Micropump Based on Dual Synthetic Jets with a Tesla Structure" Actuators 12, no. 6: 226. https://doi.org/10.3390/act12060226
APA StyleZhang, J.-Y., Peng, W.-Q., Luo, Z.-B., Zhao, Z.-J., Gong, J.-Y., & Dong, Z.-F. (2023). Dual Synthetic Jets Actuator and Its Applications Part V: Novel Valveless Continuous Micropump Based on Dual Synthetic Jets with a Tesla Structure. Actuators, 12(6), 226. https://doi.org/10.3390/act12060226







