Design, Topology Optimization, and Additive Manufacturing of a Pneumatically Actuated Lightweight Robot
Abstract
:1. Introduction
1.1. Motivation
1.2. AM and Topology Optimization
1.3. AM of Fluidic Systems and Components
1.4. AM of Pneumatic Actuators
1.5. Research Gap, Overall Aim and Manufacturing Technologies
1.6. The DIMAP Project and Parallel Publications
1.7. Organization of This Paper
2. Mechanical System
2.1. Kinematics and Conceptual Design
2.2. Topology Optimization
2.2.1. The Density Method
2.2.2. Simulation Model
2.2.3. Optimization Setup and Constraints
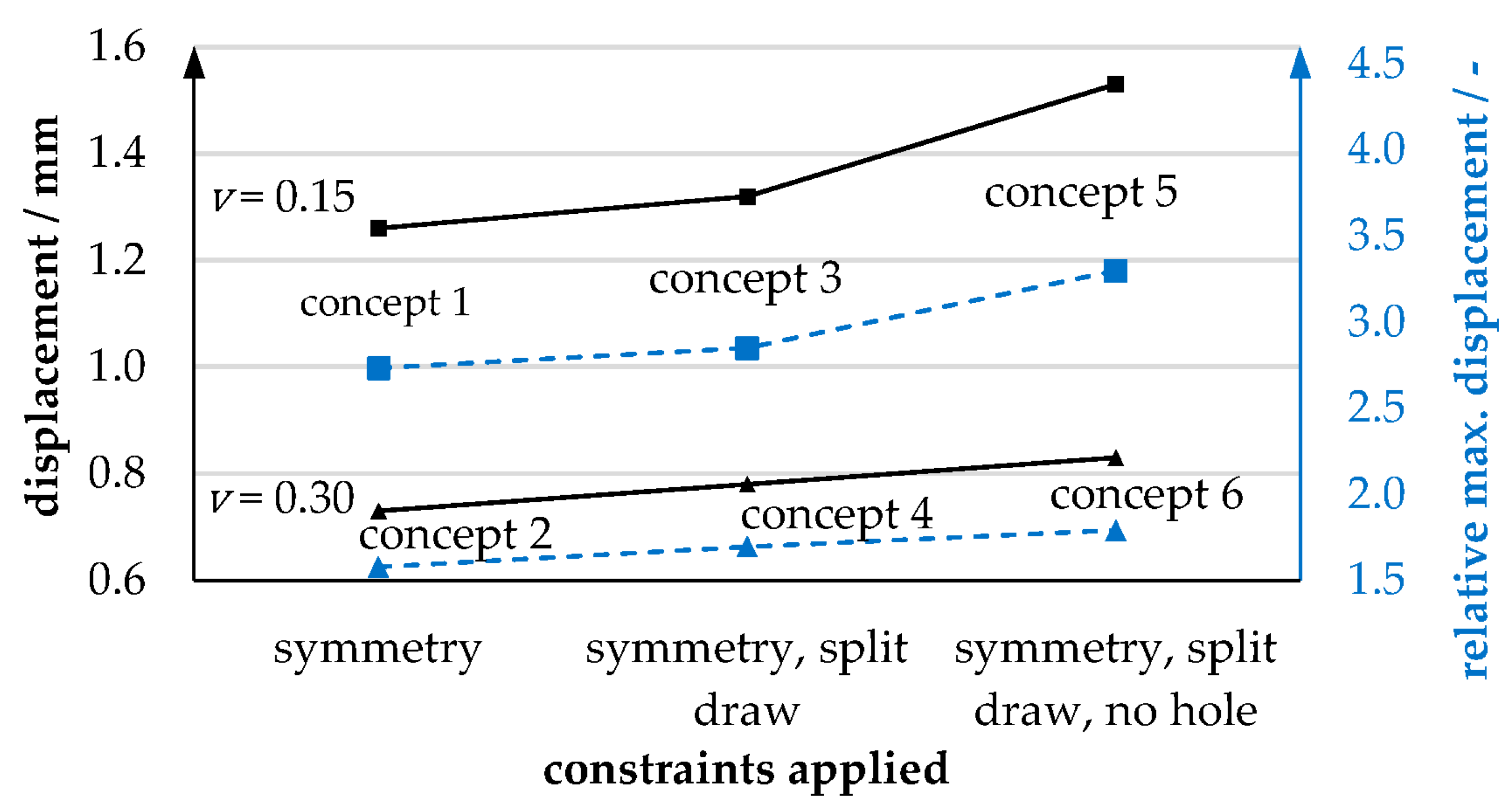
2.2.4. Optimization Results
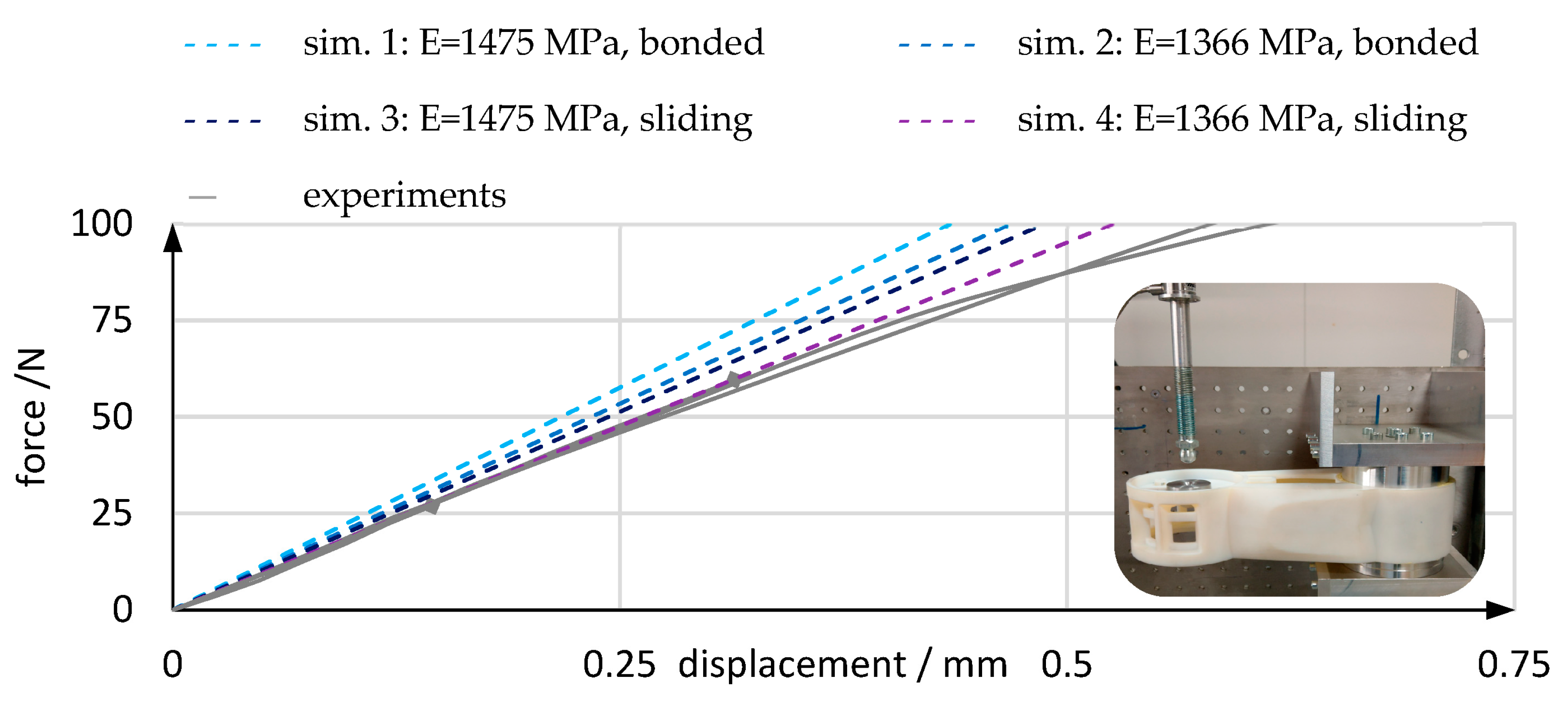
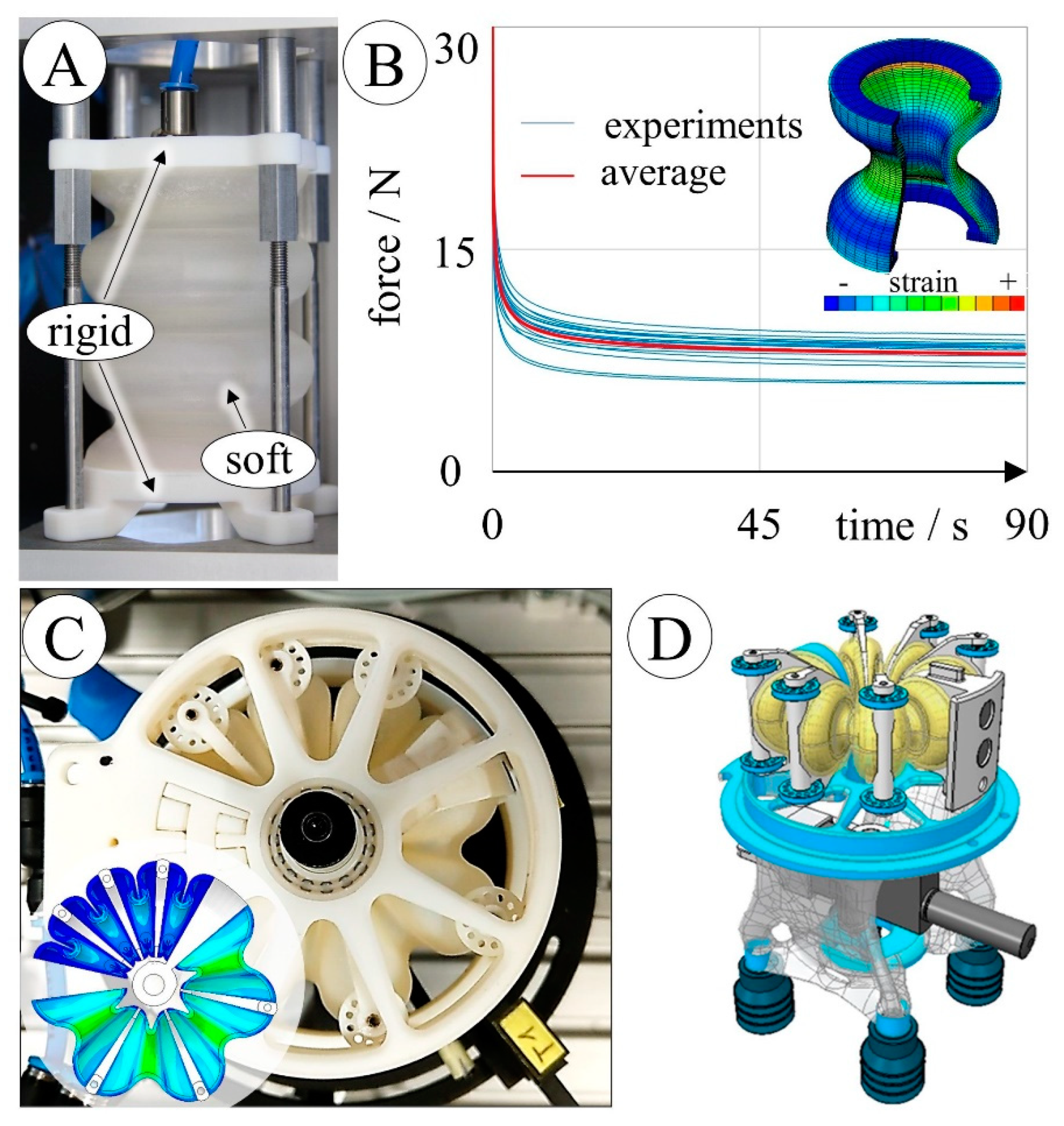
2.3. Validation Experiment
3. Pneumatic System
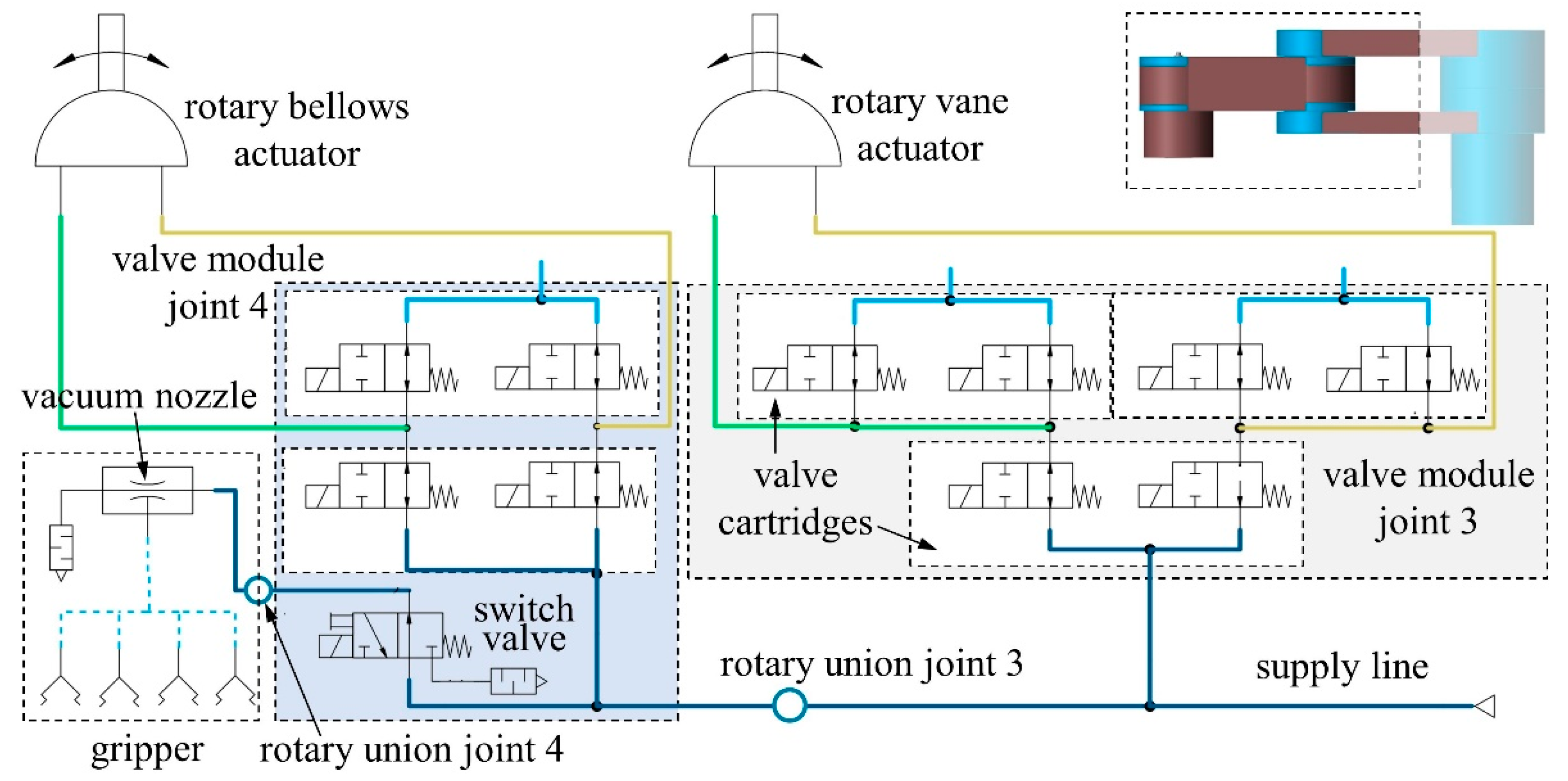
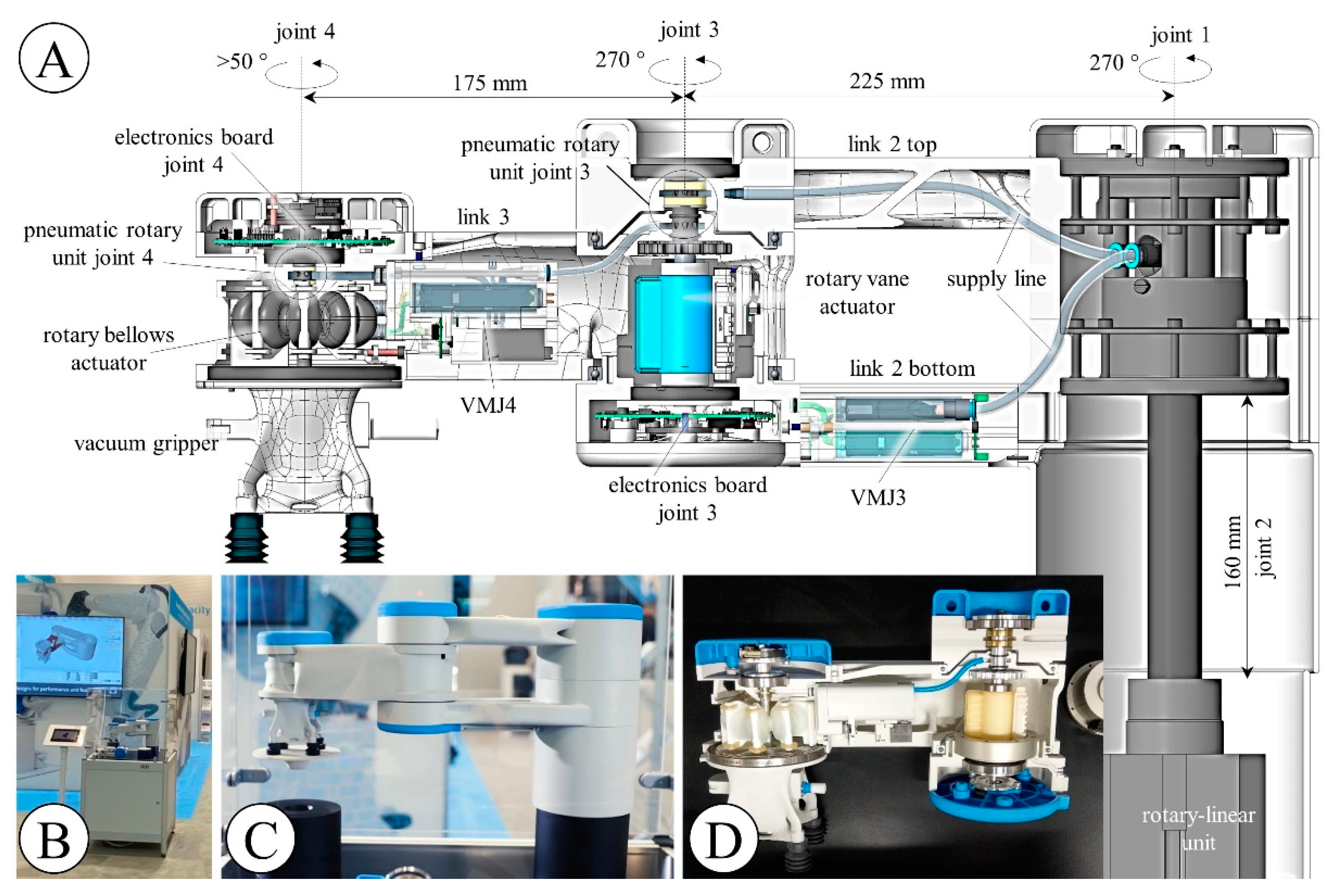
3.1. Pneumatic System—Conceptual Design
3.2. Pneumatic Actuators
3.2.1. Integration of Rotary Bellows Actuator
3.2.2. Integration of RVA
3.2.3. Comparison of AM-Based Actuators
3.3. Pneumatic Valve Modules
3.3.1. Mechanical Design and Manufacturing
3.3.2. Component Testing
4. Final Robot Design
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Load Case 1 | Load Case 2 | Load Case 3 | ||||||
|---|---|---|---|---|---|---|---|---|
| F1/N | F2/N | F3/N | F4/N | F5/N | F6/N | F7/N | F8/N | |
| x | 0 | 0 | −46.8 | 0 | −60.1 | 0 | −12.7 | −12.7 |
| y | −31.4 | −31.4 | 0 | 0 | 0 | 0 | 0 | 0 |
| z | 0 | 0 | 0 | 19.8 | −46.8 | −60.1 | −9.9 | 0 |
| Structure | Constraints | Actual Volume Fraction | Relative Compliance | Relative Max. TCP Displacement | TCP Displacement/mm | Solver Iterations | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Split Draw | No Hole | Volume Fraction | LC1 | LC2 | LC3 | |||||
| 1 | no | no | 0.150 | 0.137 | 3.80 | 2.73 | 1.04 | 0.69 | 1.26 | 33 |
| 2 | no | no | 0.300 | 0.300 | 1.90 | 1.58 | 0.52 | 0.40 | 0.73 | 24 |
| 3 | yes | no | 0.150 | 0.135 | 3.81 | 2.85 | 1.08 | 0.72 | 1.32 | 33 |
| 4 | yes | no | 0.300 | 0.294 | 1.94 | 1.70 | 0.55 | 0.43 | 0.78 | 28 |
| 5 | yes | yes | 0.150 | 0.165 | 4.62 | 3.30 | 1.18 | 0.81 | 1.53 | 50 |
| 6 | yes | yes | 0.300 | 0.295 | 2.09 | 1.79 | 0.57 | 0.45 | 0.83 | 36 |
| 7 | - | - | - | 1.000 | 1.00 | 1.00 | 0.25 | 0.25 | 0.46 | - |
| 8 | - | - | - | 0.437 | 1.29 | 1.36 | 0.39 | 0.34 | 0.63 | - |
References
- Gealy, D.V.; McKinley, S.; Yi, B.; Wu, P.; Downey, P.R.; Balke, G.; Zhao, A.; Guo, M.; Thomasson, R.; Sinclair, A.; et al. Quasi-direct drive for low-cost compliant robotic manipulation. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 437–443. [Google Scholar] [CrossRef] [Green Version]
- Sariyildiz, E.; Mutlu, R.; Roberts, J.; Kuo, C.-H.; Ugurlu, B. Design and Control of a Novel Variable Stiffness Series Elastic Actuator. IEEE/ASME Trans. Mechatron. 2023, 28, 1534–1545. [Google Scholar] [CrossRef]
- Covestro, A.G. Effective Shoe Manufacturing with 3D Printing. 2019. Available online: https://www.covestro.com/press/effective-shoe-manufacturing-with-3D-printing/ (accessed on 25 June 2023).
- Mahle GmbH. MAHLE Produces High-Performance Aluminum Pistons Using 3D Printing for the First Time. 2020. Available online: https://www.jp.mahle.com/global/media/global_news/2020/07-additive_manufacturing/press_release_mahle-additive_manufacturing.pdf (accessed on 25 June 2023).
- Bendsøe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer Science + Business Media: Norwell, MA, USA, 2013; ISBN 978-3-662-05086-6. [Google Scholar] [CrossRef]
- Zuo, K.-T.; Chen, L.-P.; Zhang, Y.-Q.; Yang, J. Manufacturing-and machining-based topology optimization. Int. J. Adv. Manuf. Technol. 2006, 27, 531–536. [Google Scholar] [CrossRef]
- Mantovani, S.; Presti, I.L.; Cavazzoni, L.; Baldini, A. Influence of manufacturing constraints on the topology optimization of an automotive dashboard. Procedia Manuf. 2017, 11, 1700–1708. [Google Scholar] [CrossRef]
- Liu, J.; Ma, Y. A survey of manufacturing oriented topology optimization methods. Adv. Eng. Softw. 2016, 100, 161–175. [Google Scholar] [CrossRef]
- Liu, J.; Gaynor, A.T.; Chen, S.; Kang, Z.; Suresh, K.; Takezawa, A.; Li, L.; Kato, J.; Tang, J.; Wang, C.C.L.; et al. Current and future trends in topology optimization for additive manufacturing. Struct. Multidiscip. Optim. 2018, 57, 2457–2483. [Google Scholar] [CrossRef] [Green Version]
- Zegard, T.; Paulino, G.H. Bridging topology optimization and additive manufacturing. Struct. Multidiscip. Optim. 2016, 53, 175–192. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Pancheri, F.; Lueth, T.C. Larg: A lightweight robotic gripper with 3-D topology optimized adaptive fingers. IEEE/ASME Trans. Mechatron. 2022, 27, 2026–2034. [Google Scholar] [CrossRef]
- Kohn, R.V.; Strang, G. Optimal design and relaxation of variational problems, I. Commun. Pure Appl. Math. 1986, 39, 113–137. [Google Scholar] [CrossRef]
- Bendsøe, M.P. Optimal Shape Design as a material distribution Problem. Struct. Multidiscip. Optim. 1989, 1, 193–202. [Google Scholar] [CrossRef]
- Junk, S.; Klerch, B.; Nasdala, L.; Hochberg, U. Topology optimization for additive manufacturing using a component of a humanoid robot. In Proceedings of the 28th CIRP Design Conference, Nantes, France, 23–25 May 2018; pp. 102–107. [Google Scholar] [CrossRef]
- Grzesiak, A.; Becker, R.; Verl, A. The bionic handling assistant: A success story of additive manufacturing. Assem. Autom. 2011, 31, 329–333. [Google Scholar] [CrossRef]
- Richardson, B.S.; Lind, R.F.; Lloyd, P.D.; Noakes, M.W.; Love, L.J.; Post, B.K. The design of an additive manufactured dual arm manipulator system. Addit. Manuf. 2018, 24, 467–478. [Google Scholar] [CrossRef]
- MacCurdy, R.; Katzschmann, R.; Youbin, K.; Rus, D. Printable hydraulics: A method for fabricating robots by 3D co-printing solids and liquids. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 9 June 2016. [Google Scholar] [CrossRef]
- Mazzolai, B.; Mattoli, V. Robotics: Generation soft. Nature 2016, 536, 400–401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sochol, R.D.; Sweet, E.; Glick, C.C.; Venkatesh, S.; Avetisyan, A.; Ekman, K.F.; Raulinaitis, A.; Tsai, A.; Wienkers, A.; Korner, K.; et al. 3D printed microfluidic circuitry via multijet-based additive manufacturing. Lab A Chip 2016, 16, 668–678. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barasuol, V.; Villarreal-Magaña, O.A.; Sangiah, D.; Frigerio, M.; Baker, M.; Morgan, R.; Medrano-Cerda, G.A.; Caldwell, D.G.; Semini, C. Highly-integrated hydraulic smart actuators and smart manifolds for high-bandwidth force control. Front. Robot. AI 2018, 5, 51. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Diegel, O.; Schutte, J.; Ferreira, A.; Chan, Y.L. Design for additive manufacturing process for a lightweight hydraulic manifold. Addit. Manuf. 2020, 36, 101446. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, S.; Li, J.; Zhu, Y.; Peng, T.; Yang, H. Additive manufacturing of products with functional fluid channels: A review. Addit. Manuf. 2020, 36, 101490. [Google Scholar] [CrossRef]
- Li, I.-H.; Lin, Y.-S.; Lee, L.-W.; Lin, W.-T. Design, manufacturing, and control of a pneumatic-driven passive robotic gait training system for muscle-weakness in a lower limb. Sensors 2021, 21, 6709. [Google Scholar] [CrossRef]
- Chiou, S.-J.; Chu, H.-R.; Li, I.-H.; Lee, L.-W. A Novel Wearable Upper-Limb Rehabilitation Assistance Exoskeleton System Driven by Fluidic Muscle Actuators. Electronics 2022, 12, 196. [Google Scholar] [CrossRef]
- Gaiser, I.; Wiegand, R.; Ivlev, O.; Andres, A.; Breitwieser, H.; Schulz, S.; Bretthauer, G. Compliant Robotics and Automation with Flexible Fluidic Actuators and Inflatable Structures; InTech Open Access Publisher: Rijeka, Croatia, 2012. [Google Scholar] [CrossRef] [Green Version]
- Festo AG & Co. KG. BionicCobot—Sensitive Helper for Human-Robot Collaboration. 2017. Available online: https://www.festo.com/net/SupportPortal/Files/462251/Festo_BionicCobot_en.pdf (accessed on 25 June 2023).
- Krause, J.; Bhounsule, P. A 3D printed linear pneumatic actuator for position, force and impedance control. Actuators 2018, 7, 24. [Google Scholar] [CrossRef] [Green Version]
- Varga, M.; Filakovsky, F. Design, manufacturing and problem analysis of an entirely FDM 3D printed linear pneumatic actuator. Tech. Sci. Technol. 2020, 3, 98–105. [Google Scholar] [CrossRef]
- Remmers, R.; Cook, D.; Gervasi, V. Custom, integrated, pneumatic, rotary actuator for an active ankle-foot orthosis. In Proceedings of the 2010 SFF Symposium, Austin, TX, USA, 9–11 August 2010; pp. 816–827. [Google Scholar]
- Siegfarth, M.; Pusch, T.P.; Pfeil, A.; Renaud, P.; Stallkamp, J. Multi-material 3D printed hydraulic actuator for medical robots. Rapid Prototyp. J. 2020, 26, 1019–1026. [Google Scholar] [CrossRef]
- Neitzert, T.R. Accuracy of Additive Manufactured Parts. Key Eng. Mater. 2015, 661, 113–118. [Google Scholar] [CrossRef]
- Rebong, R.E.; Stewart, K.T.; Utreja, A.; Ghoneima, A.A. Accuracy of three-dimensional dental resin models created by fused deposition modeling, stereolithography, and Polyjet prototype technologies: A comparative study. Angle Orthod. 2018, 88, 363–369. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Walker, J.; Zidek, T.; Harbel, C.; Yoon, S.; Strickland, F.S.; Kumar, S.; Shin, M. Soft robotics: A review of recent developments of pneumatic soft actuators. Actuators 2020, 9, 3. [Google Scholar] [CrossRef] [Green Version]
- Gorissen, B.; Reynaerts, D.; Konishi, S.; Yoshida, K.; Kim, J.-W.; De Volder, M. Elastic inflatable actuators for soft robotic applications. Adv. Mater. 2017, 29, 1604977. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, F.; Piccin, O.; Barb, L.; Laurent, B. Soft robots manufacturing: A review. Front. Robot. AI 2018, 5, 84. [Google Scholar] [CrossRef] [Green Version]
- Wallin, T.J.; Pikul, J.; Shepherd, R.F. 3D printing of soft robotic systems. Nat. Rev. Mater. 2018, 3, 84–100. [Google Scholar] [CrossRef]
- Hu, W.; Mutlu, R.; Li, W.; Alici, G. A structural optimisation method for a soft pneumatic actuator. Robotics 2018, 7, 24. [Google Scholar] [CrossRef] [Green Version]
- Yap, Y.L.; Sing, S.L.; Swee Yeong, W.Y. A review of 3D printing processes and materials for soft robotics. Rapid Prototyp. J. 2020, 26, 1345–1361. [Google Scholar] [CrossRef]
- Zolfagharian, A.; Kouzani, A.Z.; Khoo, S.Y.; Moghadam, A.A.A.; Gibson, I.; Kaynak, A. Evolution of 3D printed soft actuators. Sens. Actuators A Phys. 2016, 250, 258–272. [Google Scholar] [CrossRef]
- Gul, J.Z.; Sajid, M.; Rehman, M.M.; Siddiqui, G.U.; Shah, I.; Kim, K.-H.; Lee, J.-W.; Choi, K.H. 3D printing for soft robotics—A review. Sci. Technol. Adv. Mater. 2018, 19, 243–262. [Google Scholar] [CrossRef] [Green Version]
- Polygerinos, P.; Correll, N.; Morin, S.A.; Mosadegh, B.; Onal, C.D.; Petersen, K.; Cianchetti, M.; Tolley, M.T.; Shepherd, R.F. Soft Robotics: Review of Fluid-Driven Intrinsically Soft Devices; Manufacturing, Sensing, Control, and Applications in Human-Robot Interaction. Adv. Eng. Mater. 2017, 19, 1700016. [Google Scholar] [CrossRef]
- Liu, C.-H.; Chen, L.-J.; Chi, J.-C.; Wu, J.-Y. Topology optimization design and experiment of a soft pneumatic bending actuator for grasping applications. IEEE Robot. Autom. Lett. 2022, 7, 2086–2093. [Google Scholar] [CrossRef]
- Kaminski, R.; Knubben, E.M. Fluid-Actuated Rotary Drive. European Patent Application 619 EP 2 497 959 A1, 12 September 2012. [Google Scholar]
- Dämmer, G.; Gablenz, S.; Hildebrandt, A.; Major, Z. Design of an Additively Manufacturable Multi-Material Light-Weight Gripper with integrated Bellows Actuators. Adv. Sci. Technol. Eng. Syst. J. 2019, 4, 23–33. [Google Scholar] [CrossRef] [Green Version]
- Dämmer, G.; Lackner, M.; Laicher, S.; Neumann, R.; Major, Z. Design of an Inkjet-Printed Rotary Bellows Actuator and Simulation of its Time-Dependent Deformation Behavior. Front. Robot. AI 2021, 8, 663158. [Google Scholar] [CrossRef]
- Dämmer, G.; Bauer, H.; Neumann, R.; Major, Z. Design, Additive Manufacturing and Component Testing of Pneumatic Rotary Vane Actuators for Lightweight Robots. Rapid Prototyp. J. 2021, 28, 20–32. [Google Scholar] [CrossRef]
- Dämmer, G.; Gablenz, S.; Hildebrandt, A.; Major, Z. PolyJet-Printed Bellows Actuators: Design, Structural Optimization and Experimental Investigation. Front. Robot. AI 2019, 6, 34. [Google Scholar] [CrossRef] [Green Version]
- Makino, H.; Furuya, N. Selective compliance assembly robot arm. In Proceedings of the First International Conference on Assembly Automation (ICAA), Brighton, England, 25–27 March 1980; pp. 77–86. [Google Scholar]
- OptiStruct, Altair. OptiStruct 11.0 User Manual; Altair Engineering Inc.: Troy, MI, USA, 2011. [Google Scholar]
- Stratasys Ltd. PolyJet Materials Data Sheet. 2018. Available online: https://www.cirp.de/verfahren/Materialdaten/PolyJet-Materials-Data-Sheet.pdf (accessed on 25 June 2023).



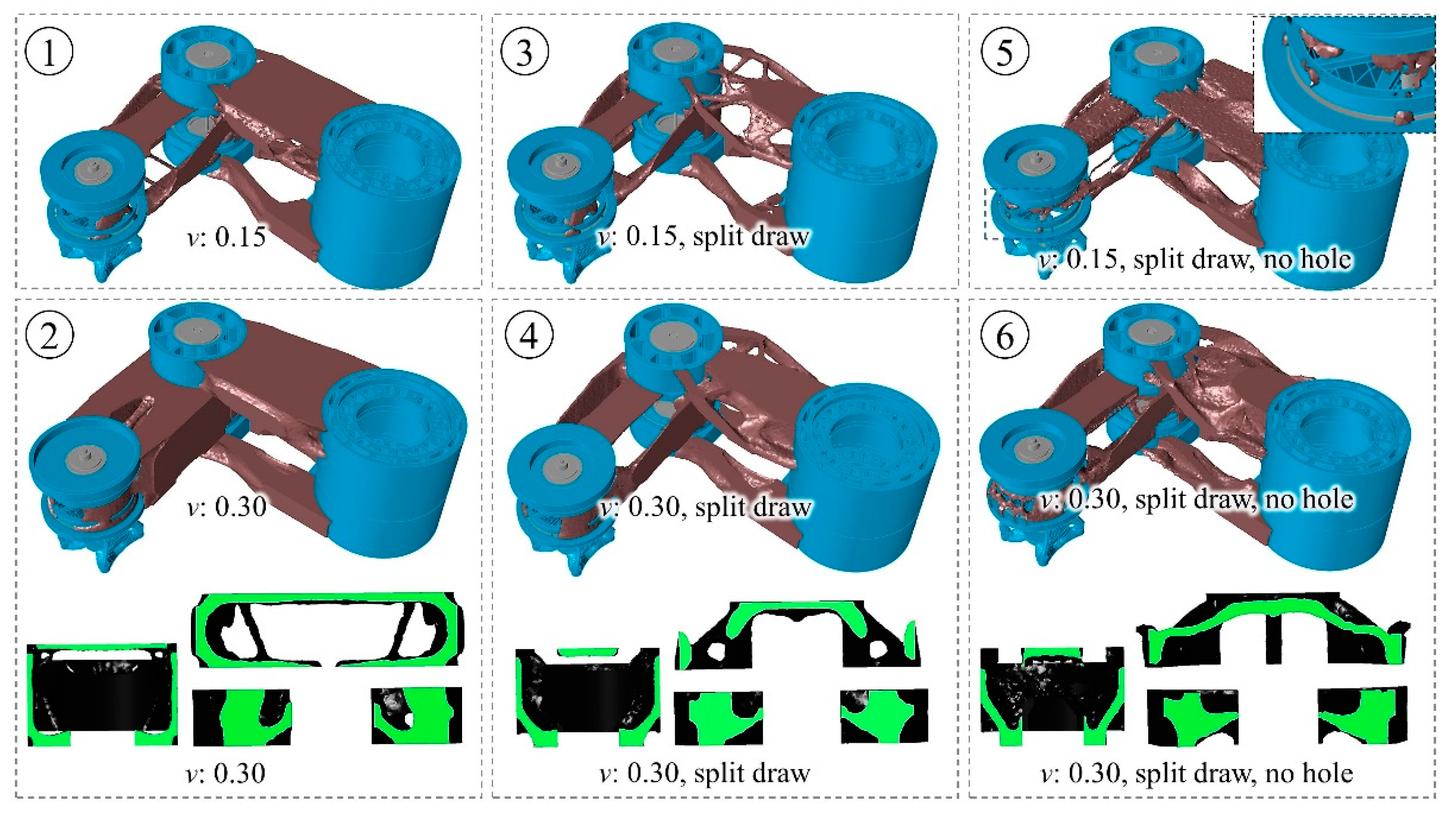



| TO Run | Constraints | ||
|---|---|---|---|
| Split Draw | No Hole | Volume Fraction | |
| 1 | no | no | 0.15 |
| 2 | no | no | 0.30 |
| 3 | yes | no | 0.15 |
| 4 | yes | no | 0.30 |
| 5 | yes | yes | 0.15 |
| 6 | yes | yes | 0.30 |
| Rotary Bellows Actuator | RVA | |
|---|---|---|
| purpose | PolyJet technology demonstrator; research into design for multi-material AM and materials sciences of PolyJet elastomers | functional prototyping in research and pre-development of robotics and automation |
| manufacturing technologies | PolyJet | SLS/PolyJet, elastomer molding, CNC machining |
| materials (non-standard components) | soft and rigid thermosetting acrylate-based photopolymers | thermoplastic PA12/ thermosetting acrylate-based photopolymer, SIL/PU elastomers |
| no. of parts | 23 in total, 1 main part and 22 small parts for guiding and bearings | 48 in total, 4 main parts and 44 small parts for housing bolt connections |
| diameter/height | 80 mm/44 mm | 64 mm/60 mm |
| range of motion | >48° (90 mbar) | 270° |
| maximum torque, breakaway torque | 20 Nmm (90 mbar), <3 Nmm | 5 Nm (6 bar), 0.5 Nm |
| mass | 105 g | 202.9–225.3 g |
| max. load cycles | >20,000 | >40,000, up to 1,000,000 |
| advantages | highly integrated design; low friction; no leakage; single-technology manufacturing | high performance; no mass-production technologies required; immediately usable |
| limitations | low performance due to low resilience of elastomer | CNC machining required, multi-step manufacturing |
| main results | proof of concept, time-dependent FE simulation of A30 bellows structures | proof of concept, prototyping of RVAs using simple and accessible technologies |
| future improvements and potential | use of higher-performance materials, AM of highly integrated robotic systems | structural optimization, application-specific RVAs for tailored lightweight robots |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dämmer, G.; Gablenz, S.; Neumann, R.; Major, Z. Design, Topology Optimization, and Additive Manufacturing of a Pneumatically Actuated Lightweight Robot. Actuators 2023, 12, 266. https://doi.org/10.3390/act12070266
Dämmer G, Gablenz S, Neumann R, Major Z. Design, Topology Optimization, and Additive Manufacturing of a Pneumatically Actuated Lightweight Robot. Actuators. 2023; 12(7):266. https://doi.org/10.3390/act12070266
Chicago/Turabian StyleDämmer, Gabriel, Sven Gablenz, Rüdiger Neumann, and Zoltán Major. 2023. "Design, Topology Optimization, and Additive Manufacturing of a Pneumatically Actuated Lightweight Robot" Actuators 12, no. 7: 266. https://doi.org/10.3390/act12070266
APA StyleDämmer, G., Gablenz, S., Neumann, R., & Major, Z. (2023). Design, Topology Optimization, and Additive Manufacturing of a Pneumatically Actuated Lightweight Robot. Actuators, 12(7), 266. https://doi.org/10.3390/act12070266





