Modelling the Periodic Response of Micro-Electromechanical Systems through Deep Learning-Based Approaches
Abstract
1. Introduction
2. Problem Formulation
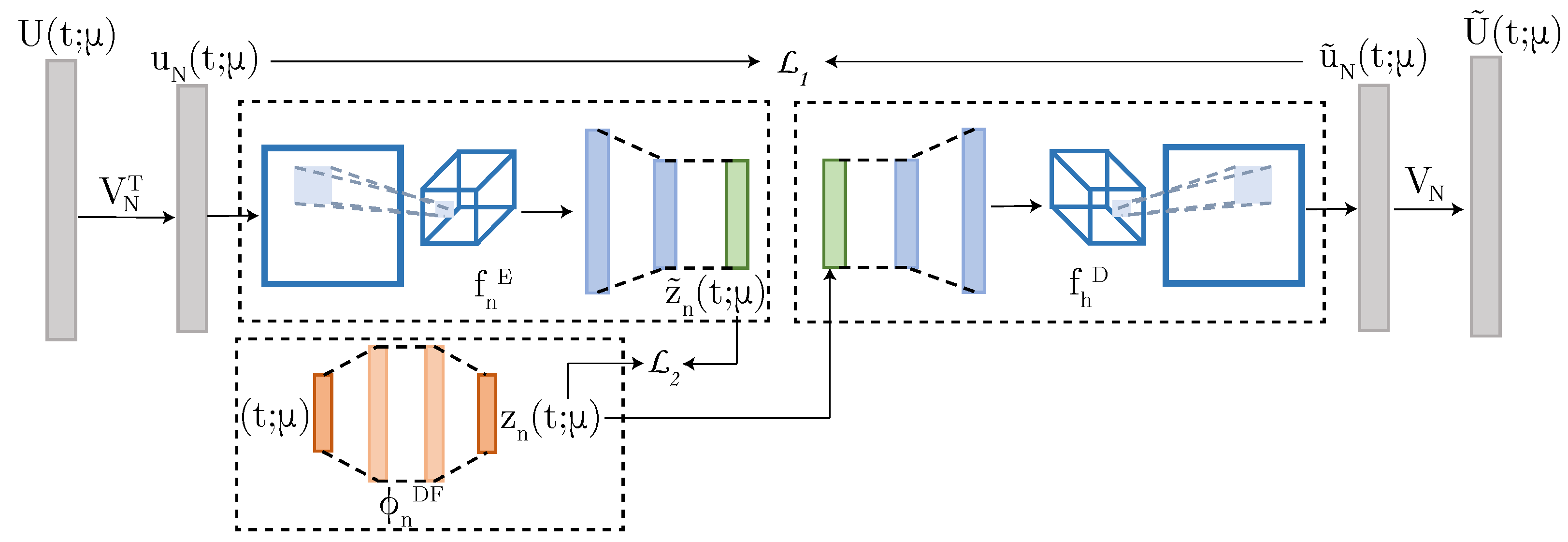
3. POD-DL-ROM Technique: Outline and Critical Issues
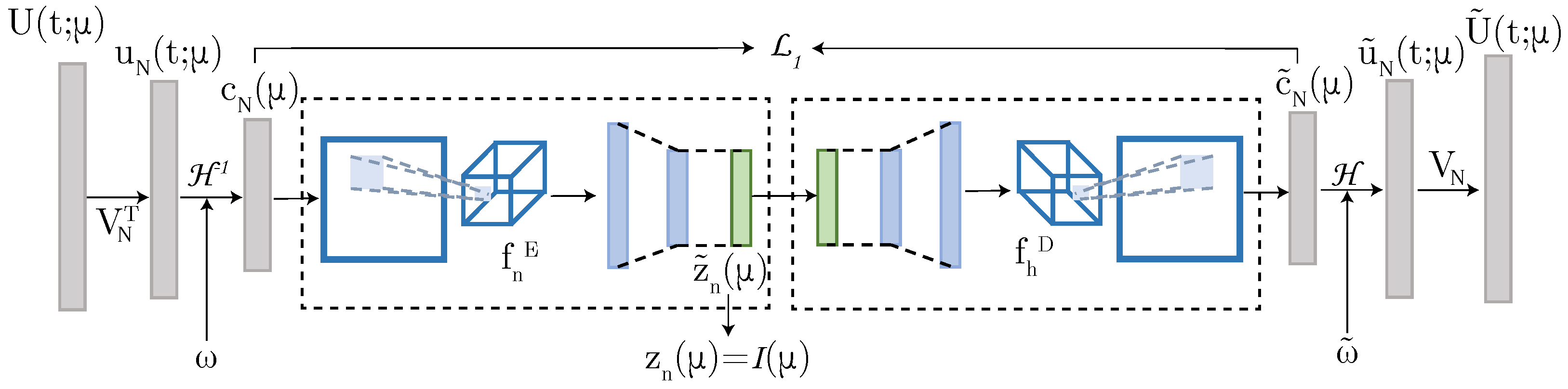
4. Periodic DL-ROM Technique
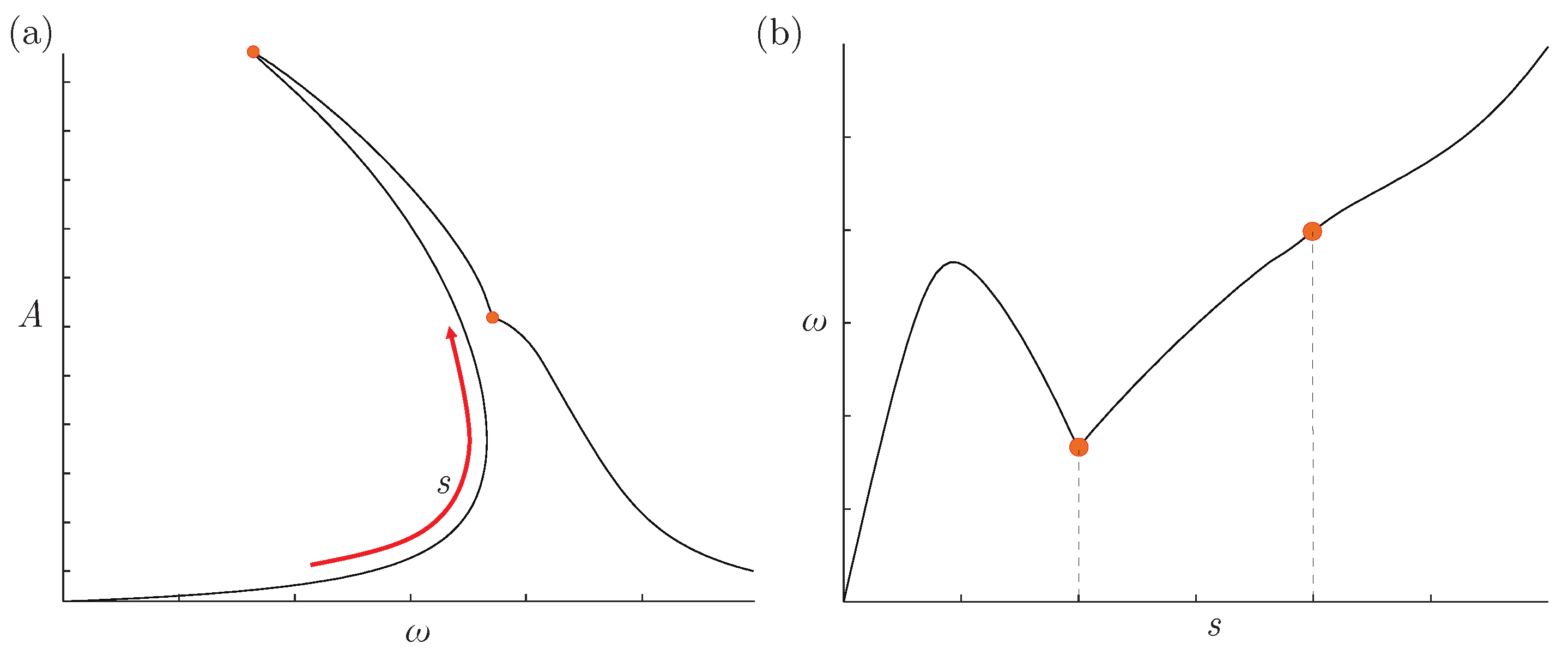
5. Frequency Response Function Modelling: Arch Length Abscissa
6. Application: Electromechanical Disk Resonating Gyroscope
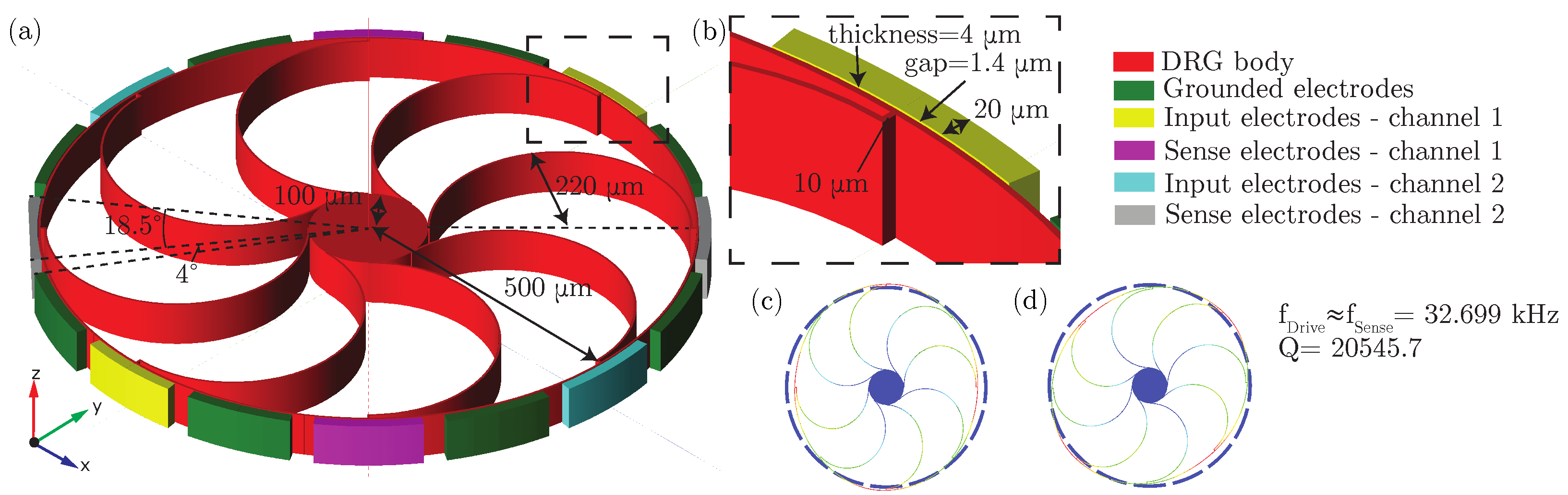
6.1. Problem Description
6.2. Hyperparameters and Training
6.3. Latent Coordinates and Frequency Features
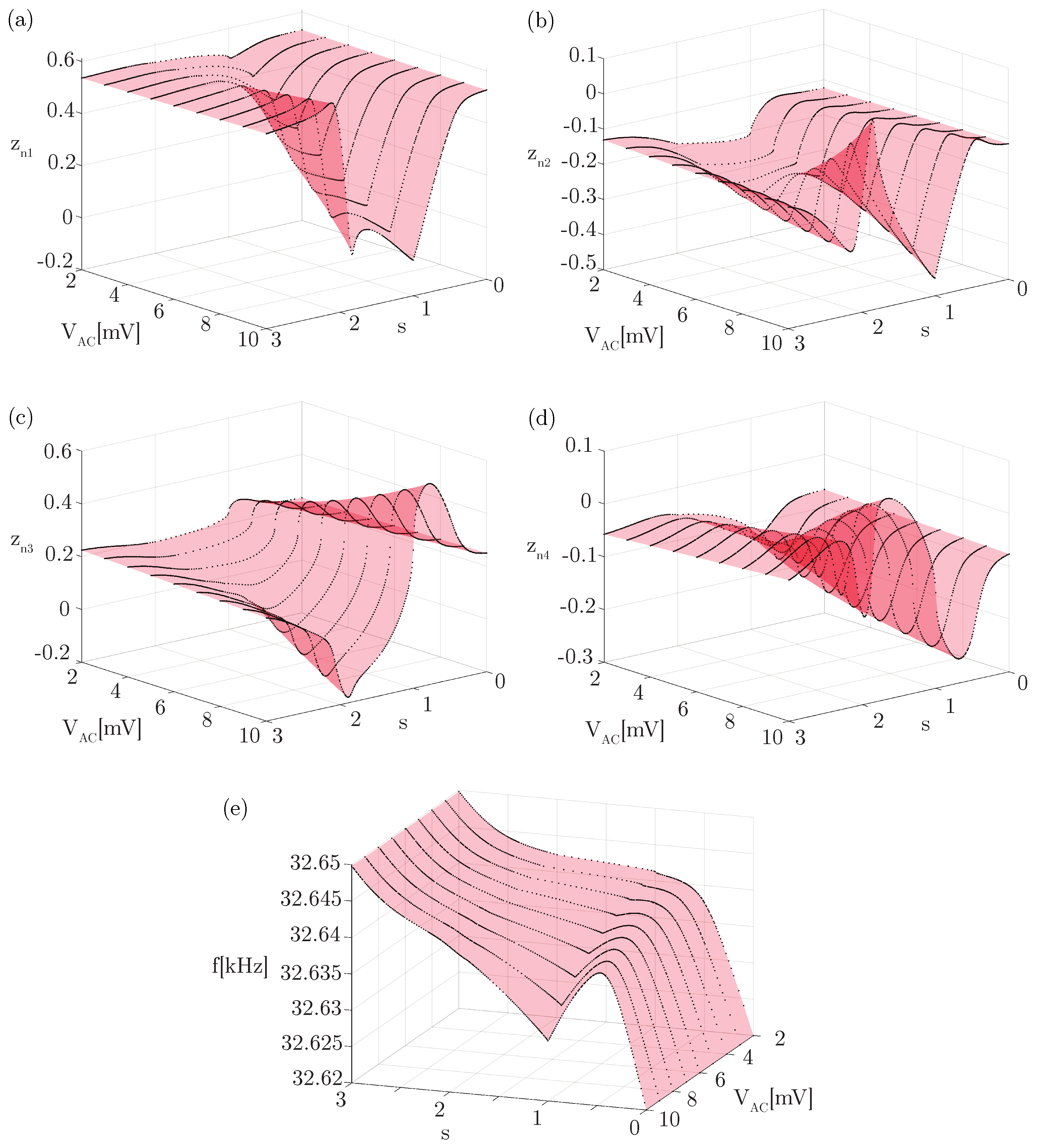
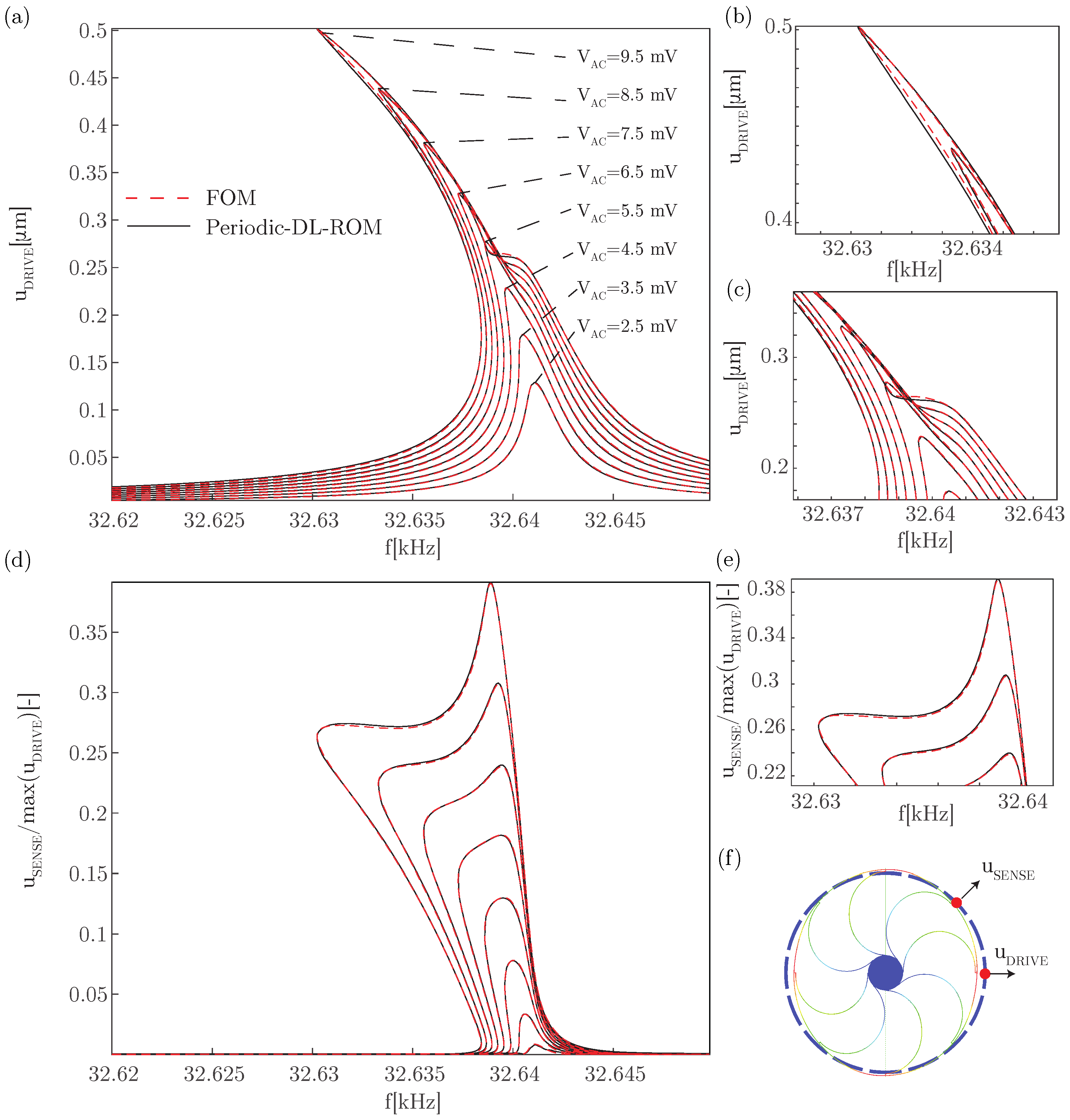
6.4. Results
6.5. Key Advantages and Comparison with POD-DL-ROM
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vizzaccaro, A.; Givois, A.; Longobardi, P.; Shen, Y.; Deü, J.F.; Salles, L.; Touzé, C.; Thomas, O. Non-intrusive reduced order modelling for the dynamics of geometrically nonlinear flat structures using three-dimensional finite elements. Comput. Mech. 2020, 66, 1293–1319. [Google Scholar] [CrossRef]
- Touzé, C.; Vizzaccaro, A.; Thomas, O. Model order reduction methods for geometrically nonlinear structures: A review of nonlinear techniques. Nonlinear Dyn. 2021, 105, 1141–1190. [Google Scholar] [CrossRef]
- Kerschen, G.; Golinval, J.C.; Vakakis, A.F.; Bergman, L.A. The method of proper orthogonal decomposition for dynamical characterization and order reduction of mechanical systems: An overview. Nonlinear Dyn. 2005, 41, 147–169. [Google Scholar] [CrossRef]
- Amabili, M.; Touzé, C. Reduced-order models for nonlinear vibrations of fluid-filled circular cylindrical shells: Comparison of POD and asymptotic nonlinear normal modes methods. J. Fluids Struct. 2007, 23, 885–903. [Google Scholar] [CrossRef]
- Amabili, M.; Sarkar, A.; Paıdoussis, M. Reduced-order models for nonlinear vibrations of cylindrical shells via the proper orthogonal decomposition method. J. Fluids Struct. 2003, 18, 227–250. [Google Scholar] [CrossRef]
- Gobat, G.; Opreni, A.; Fresca, S.; Manzoni, A.; Frangi, A. Reduced order modeling of nonlinear microstructures through Proper Orthogonal Decomposition. Mech. Syst. Signal Process. 2022, 171, 108864. [Google Scholar] [CrossRef]
- Frangi, A.; Gobat, G. Reduced order modelling of the non-linear stiffness in MEMS resonators. Int. J. -Non-Linear Mech. 2019, 116, 211–218. [Google Scholar] [CrossRef]
- Zega, V.; Gobat, G.; Fedeli, P.; Carulli, P.; Frangi, A.A. Reduced Order Modelling in a Mems Arch Resonator Exhibiting 1: 2 Internal Resonance. In Proceedings of the 2022 IEEE 35th International Conference on Micro Electro Mechanical Systems Conference (MEMS), Tokyo, Japan, 9–13 January 2022; IEEE: Piscataway Township, NJ, USA; pp. 499–502. [Google Scholar]
- Gobat, G.; Zega, V.; Fedeli, P.; Guerinoni, L.; Touzé, C.; Frangi, A. Reduced order modelling and experimental validation of a MEMS gyroscope test-structure exhibiting 1: 2 internal resonance. Sci. Rep. 2021, 11, 16390. [Google Scholar] [CrossRef]
- Gobat, G.; Guillot, L.; Frangi, A.; Cochelin, B.; Touzé, C. Backbone curves, Neimark-Sacker boundaries and appearance of quasi-periodicity in nonlinear oscillators: Application to 1: 2 internal resonance and frequency combs in MEMS. Meccanica 2021, 56, 1937–1969. [Google Scholar] [CrossRef]
- Mahdiabadi, M.K.; Tiso, P.; Brandt, A.; Rixen, D.J. A non-intrusive model-order reduction of geometrically nonlinear structural dynamics using modal derivatives. Mech. Syst. Signal Process. 2021, 147, 107126. [Google Scholar] [CrossRef]
- Wu, L.; Tiso, P. Nonlinear model order reduction for flexible multibody dynamics: A modal derivatives approach. Multibody Syst. Dyn. 2016, 36, 405–425. [Google Scholar] [CrossRef]
- Vizzaccaro, A.; Salles, L.; Touzé, C. Comparison of nonlinear mappings for reduced-order modelling of vibrating structures: Normal form theory and quadratic manifold method with modal derivatives. Nonlinear Dyn. 2021, 103, 3335–3370. [Google Scholar] [CrossRef]
- Shaw, S.; Pierre, C. Non-linear normal modes and invariant manifolds. J. Sound Vib. 1991, 150, 170–173. [Google Scholar] [CrossRef]
- Shaw, S.W.; Pierre, C. Normal modes for non-linear vibratory systems. J. Sound Vib. 1993, 164, 85–124. [Google Scholar] [CrossRef]
- Ponsioen, S.; Pedergnana, T.; Haller, G. Automated computation of autonomous spectral submanifolds for nonlinear modal analysis. J. Sound Vib. 2018, 420, 269–295. [Google Scholar] [CrossRef]
- Vizzaccaro, A.; Shen, Y.; Salles, L.; Blahoš, J.; Touzé, C. Direct computation of nonlinear mapping via normal form for reduced-order models of finite element nonlinear structures. Comput. Methods Appl. Mech. Eng. 2021, 384, 113957. [Google Scholar] [CrossRef]
- Opreni, A.; Vizzaccaro, A.; Frangi, A.; Touzé, C. Model Order Reduction based on Direct Normal Form: Application to Large Finite Element MEMS Structures Featuring Internal Resonance. Nonlinear Dyn. 2021, 105, 1237–1272. [Google Scholar] [CrossRef]
- Vizzaccaro, A.; Opreni, A.; Salles, L.; Frangi, A.; Touzé, C. High order direct parametrisation of invariant manifolds for model order reduction of finite element structures: Application to large amplitude vibrations and uncovering of a folding point. Nonlinear Dyn. 2022, 110, 525–571. [Google Scholar] [CrossRef]
- Jain, S.; Haller, G. How to compute invariant manifolds and their reduced dynamics in high-dimensional finite element models. Nonlinear Dyn. 2022, 107, 1417–1450. [Google Scholar] [CrossRef]
- Opreni, A.; Vizzaccaro, A.; Touzé, C.; Frangi, A. High-order direct parametrisation of invariant manifolds for model order reduction of finite element structures: Application to generic forcing terms and parametrically excited systems. Nonlinear Dyn. 2023, 111, 5401–5447. [Google Scholar] [CrossRef]
- Hesthaven, J.S.; Ubbiali, S. Non-intrusive reduced order modeling of nonlinear problems using neural networks. J. Comput. Phys. 2018, 363, 55–78. [Google Scholar] [CrossRef]
- San, O.; Maulik, R. Neural network closures for nonlinear model order reduction. Adv. Comput. Math. 2018, 44, 1717–1750. [Google Scholar] [CrossRef]
- Dutta, S.; Rivera-Casillas, P.; Styles, B.; Farthing, M.W. Reduced order modeling using advection-aware autoencoders. Math. Comput. Appl. 2022, 27, 34. [Google Scholar] [CrossRef]
- Wang, Q.; Ripamonti, N.; Hesthaven, J.S. Recurrent neural network closure of parametric POD-Galerkin reduced-order models based on the Mori-Zwanzig formalism. J. Comput. Phys. 2020, 410, 109402. [Google Scholar] [CrossRef]
- Fatone, F.; Fresca, S.; Manzoni, A. Long-time prediction of nonlinear parametrized dynamical systems by deep learning-based reduced order models. arXiv 2022, arXiv:2201.10215. [Google Scholar]
- Hernández, Q.; Badías, A.; Chinesta, F.; Cueto, E. Thermodynamics-informed graph neural networks. arXiv 2022, arXiv:2203.01874. [Google Scholar] [CrossRef]
- Nguyen, T.; Li, Z.; Silander, T.; Leong, T.Y. Online feature selection for model-based reinforcement learning. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; PMLR, 2013; pp. 498–506. [Google Scholar]
- Cai, S.; Mao, Z.; Wang, Z.; Yin, M.; Karniadakis, G.E. Physics-informed neural networks (PINNs) for fluid mechanics: A review. Acta Mech. Sin. 2021, 37, 1727–1738. [Google Scholar] [CrossRef]
- Wu, P.; Qiu, F.; Feng, W.; Fang, F.; Pain, C. A non-intrusive reduced order model with transformer neural network and its application. Phys. Fluids 2022, 34, 115130. [Google Scholar] [CrossRef]
- Sitapure, N.; Kwon, J.S.I. Exploring the potential of time-series transformers for process modeling and control in chemical systems: An inevitable paradigm shift? Chem. Eng. Res. Des. 2023, 194, 461–477. [Google Scholar] [CrossRef]
- Sitapure, N.; Kwon, J.S. CrystalGPT: Enhancing system-to-system transferability in crystallization prediction and control using time-series-transformers. arXiv 2023, arXiv:2306.03099. [Google Scholar] [CrossRef]
- Fresca, S.; Dede, L.; Manzoni, A. A comprehensive deep learning-based approach to reduced order modeling of nonlinear time-dependent parametrized PDEs. J. Sci. Comput. 2021, 87, 1–36. [Google Scholar] [CrossRef]
- Fresca, S.; Manzoni, A. POD-DL-ROM: Enhancing deep learning-based reduced order models for nonlinear parametrized PDEs by proper orthogonal decomposition. Comput. Methods Appl. Mech. Eng. 2022, 388, 114181. [Google Scholar] [CrossRef]
- Cicci, L.; Fresca, S.; Manzoni, A. Deep-HyROMnet: A Deep Learning-Based Operator Approximation for Hyper-Reduction of Nonlinear Parametrized PDEs. J. Sci. Comput. 2022, 93, 57. [Google Scholar] [CrossRef]
- Fresca, S.; Gobat, G.; Fedeli, P.; Frangi, A.; Manzoni, A. Deep learning-based reduced order models for the real-time simulation of the nonlinear dynamics of microstructures. Int. J. Numer. Methods Eng. 2022, 123, 4749–4777. [Google Scholar] [CrossRef]
- Gobat, G.; Fresca, S.; Manzoni, A.; Frangi, A. Reduced Order Modeling of Nonlinear Vibrating Multiphysics Microstructures with Deep Learning-Based Approaches. Sensors 2023, 23, 3001. [Google Scholar] [CrossRef]
- Yu, J.; Wen, Y.; Yang, L.; Zhao, Z.; Guo, Y.; Guo, X. Monitoring on triboelectric nanogenerator and deep learning method. Nano Energy 2022, 92, 106698. [Google Scholar] [CrossRef]
- Bangi, M.S.F.; Kwon, J.S.I. Deep reinforcement learning control of hydraulic fracturing. Comput. Chem. Eng. 2021, 154, 107489. [Google Scholar] [CrossRef]
- Singh Sidhu, H.; Siddhamshetty, P.; Kwon, J.S. Approximate dynamic programming based control of proppant concentration in hydraulic fracturing. Mathematics 2018, 6, 132. [Google Scholar] [CrossRef]
- Lee, J.H.; Wong, W. Approximate dynamic programming approach for process control. J. Process. Control 2010, 20, 1038–1048. [Google Scholar] [CrossRef]
- Malvern, L. Introduction to the Mechanics of a Continuous Medium; Prentice-Hall Series in Engineering of the Physical Sciences; Prentice-Hall: Englewood Cliffs, NJ, USA, 1969. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Hinton, G.E.; Zemel, R. Autoencoders, minimum description length and Helmholtz free energy. Adv. Neural Inf. Process. Syst. 1993, 6, 3–10. [Google Scholar]
- Fresca, S.; Manzoni, A.; Dedè, L.; Quarteroni, A. Deep learning-based reduced order models in cardiac electrophysiology. PLoS ONE 2020, 15, e0239416. [Google Scholar] [CrossRef]
- Fresca, S.; Manzoni, A. Real-time simulation of parameter-dependent fluid flows through deep learning-based reduced order models. Fluids 2021, 6, 259. [Google Scholar] [CrossRef]
- Ayazi, F.; Najafi, K. A HARPSS polysilicon vibrating ring gyroscope. J. Microelectromech. Syst. 2001, 10, 169–179. [Google Scholar] [CrossRef]
- Coventor Inc., A Lam Research Company. Coventor MEMS+TM. Available online: https://www.coventor.com/ (accessed on 1 March 2023).
- Parent, A.; Krust, A.; Lorenz, G.; Favorskiy, I.; Piirainen, T. Efficient nonlinear simulink models of MEMS gyroscopes generated with a novel model order reduction method. In Proceedings of the 2015 Transducers-2015 18th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Anchorage, Alaska, 21–25 June 2015; IEEE: Piscataway Township, NJ, USA, 2015; pp. 2184–2187. [Google Scholar]
- Parent, A.; Krust, A.; Lorenz, G.; Piirainen, T. A novel model order reduction approach for generating efficient nonlinear verilog-a models of mems gyroscopes. In Proceedings of the 2015 IEEE International Symposium on Inertial Sensors and Systems (ISISS) Proceedings, Hapuna Beach, HI, USA, 23–26 March 2015; IEEE: Piscataway Township, NJ, USA, 2015; pp. 1–4. [Google Scholar]
- Innes, M.; Saba, E.; Fischer, K.; Gandhi, D.; Rudilosso, M.C.; Joy, N.M.; Karmali, T.; Pal, A.; Shah, V. Fashionable modelling with flux. arXiv 2018, arXiv:1811.01457. [Google Scholar]


| Layer | Input | Output | Kernel | # of Filters |
|---|---|---|---|---|
| Dimension | Dimension | Size | ||
| 1 | [N, , 2] | [, , 3] | [2, 2] | 3 |
| 2 | [, , 3] | [, , 5] | [5, 5] | 5 |
| 3 | [, , 5] | [, , 5] | [5, 5] | 5 |
| 5 | 10 | |||
| 6 | 10 | n |
| Layer | Input | Output | Kernel | # of Filters |
|---|---|---|---|---|
| Dimension | Dimension | Size | ||
| 1 | n | 10 | ||
| 2 | 10 | |||
| 3 | [, , 5] | [, , 5] | [2, 2] | 5 |
| 4 | [, , 5] | [, , 3] | [2, 2] | 3 |
| 5 | [, , 3] | [N, , 2] | [2, 2] | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gobat, G.; Baronchelli, A.; Fresca, S.; Frangi, A. Modelling the Periodic Response of Micro-Electromechanical Systems through Deep Learning-Based Approaches. Actuators 2023, 12, 278. https://doi.org/10.3390/act12070278
Gobat G, Baronchelli A, Fresca S, Frangi A. Modelling the Periodic Response of Micro-Electromechanical Systems through Deep Learning-Based Approaches. Actuators. 2023; 12(7):278. https://doi.org/10.3390/act12070278
Chicago/Turabian StyleGobat, Giorgio, Alessia Baronchelli, Stefania Fresca, and Attilio Frangi. 2023. "Modelling the Periodic Response of Micro-Electromechanical Systems through Deep Learning-Based Approaches" Actuators 12, no. 7: 278. https://doi.org/10.3390/act12070278
APA StyleGobat, G., Baronchelli, A., Fresca, S., & Frangi, A. (2023). Modelling the Periodic Response of Micro-Electromechanical Systems through Deep Learning-Based Approaches. Actuators, 12(7), 278. https://doi.org/10.3390/act12070278







