Dynamic Performance of a Magnetic Energy-Harvesting Suspension: Analysis and Experimental Verification

Abstract

The advantages of the proposed novel magnetic energy-harvesting suspension (MEHS) are high safety, compact structure and convenient maintenance, compared with the previous studies. However, the force generated by the energy harvester with harvesting energy can affect the motion of the mechanical system. Therefore, this paper aims to analyze the ride comfort and road handling of the MEHS, and investigates the dynamic performance of the MEHS. Firstly, the structure and the working principle of the MEHS are illustrated and introduced, and the dynamic mechanism of the quarter-vehicle with the MEHS is revealed and investigated. Secondly, the effects of the electromechanical coupling coefficient and external load resistance on the dynamic performance are investigated by numerical calculation. An experimental setup is established to verify the dynamic performance of the proposed MEHS. According to the experimental results, the dynamic performance of the suspension is contradictory with the increase of the external load resistance at the periodic frequency 7 Hz. And compared with the passive suspension, the dynamic performance of the MEHS is changed at various excitations, in which the sprung displacement and relative dynamic load of the tire of MEHS at the periodic frequency 3.3 Hz are reduced by 39.45% and 41.18%, respectively. Overall, the external load resistance of the proposed MEHS can be utilized to realize the variable damping of the suspension system and reduce the effect of vibration on the suspension system at the resonance frequency. And the dynamic performance has been verified in the laboratory, which lays the foundation for the dynamic analysis in a real vehicle.

1. Introduction

Due to the irregularities of the road surface, the vehicle occurs vibration when the vehicle travels on the road, which causes discomfort to the driver and reduces the handling stability of the vehicle [1]. Meanwhile, the vehicle suspension for suppressing sprung vibration dissipates the vibration energy into heat energy [2]. Various vibration harvesters applied to the vehicle are designed to harvest the vibration energy, which mainly includes mechanical energy harvester [3,4], electro-hydraulic energy harvester [5,6] and electromagnetic energy harvester [7,8]. Furthermore, the energy-harvesting systems are extensively designed, in which the energy is harvested using piezoelectric technology [9,10,11] and triboelectric technology [12]. Active suspension and semi-active suspension are designed by many researchers [13,14] to achieve better ride comfort and road handling. Meanwhile, magnetorheological suspension technology has been widely studied due to the development of magnetic fluid technology [15,16]. In the energy harvesting system, the harvested energy from suspension vibration is transformed into electrical energy to power the electronic equipment, which is a self-powered technology [17,18], and the generated reaction force from the harvester can reduce the vibration of the system.

The energy-harvesting technologies from the vibration environment have been widely investigated for decades [19,20]. Yang et al. [21] designed a hybrid vehicle suspension system that can regenerate energy from vibrations and verified the energy harvesting performance. The structure of regenerative suspension combined with the linear generator was considered by Kim et al. [22], and the maximum power and the average power were 586.43 W, 214.98 W, respectively. Arroyo et al. [23] designed and tested a new electromagnetic generator, and the vibration energy harvesting with a nonlinear energy extraction circuit was optimized. Sapiński et al. [24,25] designed an energy-harvesting linear MR damper that can harvest energy from the excitations, and the performance of the energy harvesting and damping were investigated and analyzed. A compact stiffness controllable magnetorheological damper was proposed and prototyped by Zhu et al. [26], which can achieve self-powered capacity. The testing results indicated that the power generated by the damper was 2.595 W at a harmonic excitation with 0.15 Hz frequency and 30 mm displacement. Firoozy et al. [27] investigated quasiperiodic energy harvesting in a nonlinear vibration-based harvester. A novel hydraulic energy-regenerative shock absorber was presented by Zou et al. [28], which was applied to the vehicle suspension to generate electrical power. The results showed that the regenerated energy’s root-mean-squared (RMS) was up to 107.94 W at 50 km/h. Wu et al. [29] proposed a hydraulic energy-harvesting shock absorber prototype. An energy-harvesting suspension integrated in a hydraulically interconnected suspension system was introduced by Chen et al. [30], which can generate up to 421 W at 4 Hz frequency and 40 mm displacement. Guntur et al. [31] designed a hydro-magneto-electric regenerative shock absorber, and the maximum generated output power was 14 W at periodical input 1.5 Hz frequency. A cable dynamics energy-harvesting shock absorber using cable transmission was presented by Bowen et al. [32], and the mechanical efficiency of the designed system was around 60%. Salman et al. [33] presented a regenerative absorber integrated helical gears and dual-tapered roller clutches; the designed system can reach a peak efficiency of 52% and an average efficiency of 40%. A novel regenerative absorber using an arm-teeth mechanism was designed by Zhang et al. [34], which can convert linear to rotational motion to improve energy harvesting. However, based on the above research, these energy-harvesting devices replace the damper of the passive suspension (PS), which can affect the driving safety of vehicles when the energy-harvesting devices do not work, and the devices have issues of complex structure and difficult maintenance. Therefore, a magnetic energy-harvesting suspension (MEHS) was presented by Zhou et al. [35,36,37,38]; its advantages are high safety, simple structure and convenient maintenance compared with the previous studies.

Although many energy harvesters have been designed, prototyped and studied in the suspension system, the electromechanical coupling between the energy harvesting and the dynamic performance of the suspension system also needs to be analyzed. Liu et al. [39] proposed a mechanical-motion-rectifier-based, energy-harvesting shock absorber, among a ball-screw mechanism and two one-way clutches were applied to replace conventional oil dampers. Furthermore, the chassis acceleration increased 11.12% and the average power was 13.3 W for a representative period of 8 s. According to the system energy flow mechanism, Gao et al. [40] designed different control strategies for active suspension, which can achieve compatibility between ride comfort and energy harvesting efficiency under different road conditions. The harvesting energy from the vehicle suspension system was assessed by Zuo et al. [41], and the tradeoffs among energy harvesting, ride comfort, and road handling were analyzed.

According to the above studies, the force generated by the energy harvester with harvesting energy has a certain influence on the motion of the suspension, which can change the motion state of the system; therefore, it is necessary to analyze the dynamic performance of the system. To obtain the dynamic performance of the MEHS in energy harvesting mode, this paper analyzes the effect of system parameters on the dynamic performance of the MEHS, and the harvested power, vehicle body acceleration and relative dynamic load of the tire of the suspension system are obtained as performance indexes.

The content of this paper is organized as follows. Section 2 introduces the structure and working principle of the MEHS. In Section 3, a two-degree-of-freedom, quarter-vehicle model with the MEHS is established, and the mathematical expressions of the harvesting power, vehicle body acceleration and relative dynamic load of the tire are calculated. Section 4 analyzes the dynamic performance of the MEHS under the various inputs, electromechanical coupling coefficients and external load resistances. In Section 5, the experiments are carried out to validate the coupling performance of the suspension system. The conclusion is presented in Section 6.

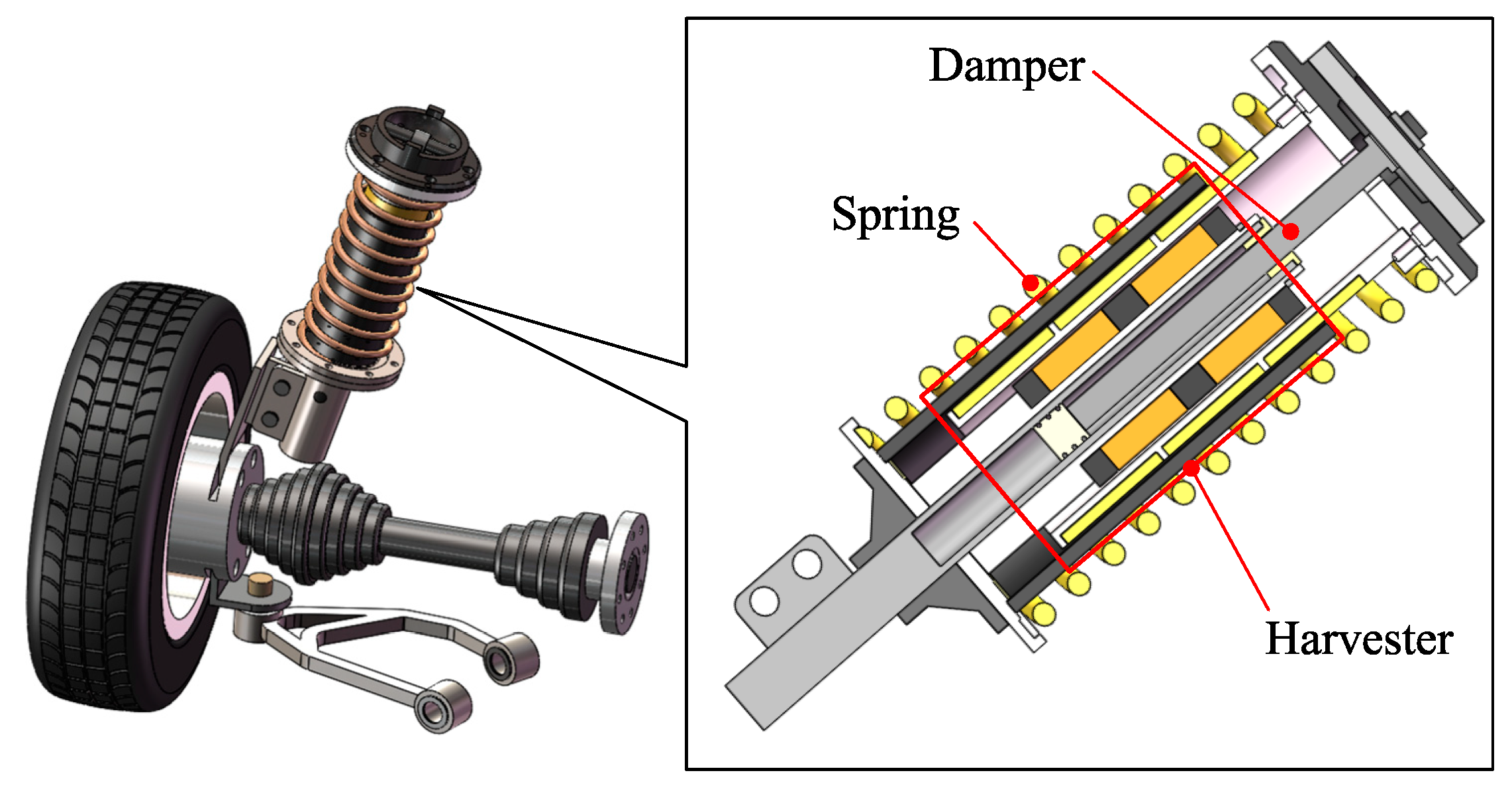
2. Structure and Working Principle of MEHS

2.1. Structure

A schematic diagram of a vehicle suspension system with the proposed MEHS is illustrated, as shown in Figure 1. The energy harvester is integrated into the PS in the MEHS, which provides the suspension system with advantages of high-vehicle safety and compact structure. Figure 1 shows that the structure of the MEHS mainly consists of a PS and an energy harvester. In the PS part, there is a spring and a damper, which can be utilized to absorb most of the vibration energy to maintain the ride comfort. In the energy harvester part, the structure of the harvester is designed based on the structure of the voice coil motor. The MEHS has both vibration reduction and energy harvesting functions through the above design.

2.2. Working Principle

The vehicle body will be vibrated and impacted due to the roughness of the road surface when the vehicle travels on the road. According to Faraday’s law of electromagnetic induction, the moved coils of the harvester can generate electric energy. However, when there is an induction current in the coils of the harvester, the coils generate electromagnetic force as the coils move. According to the above analysis, it can be obtained that the harvesting energy and electromagnetic force exist simultaneously. Therefore, the dynamic performance of the MEHS is investigated in the energy harvesting mode, and the variable damping characteristics of the device are realized by changing the external load resistance.

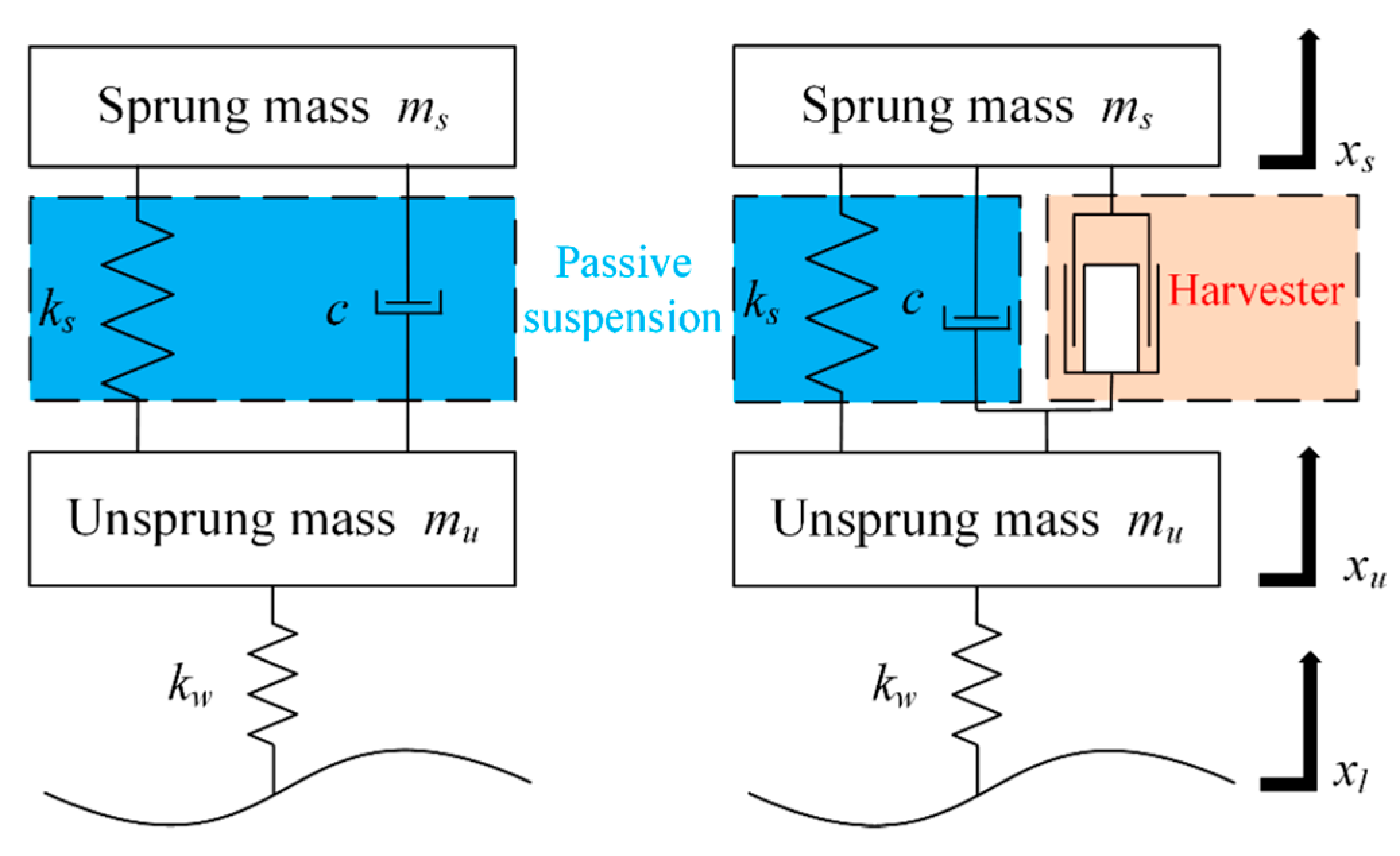
3. Theoretical Modeling

In this paper, the principle prototype and test platform for MEHS are designed and manufactured, and the dynamic performance of the principle prototype is investigated. This section introduces the modeling of the quarter-vehicle system, and the mathematical expression of the harvested energy, ride comfort and road handling for the vehicle with the MEHS are provided under periodic excitation.

3.1. Quarter-Vehicle Model

The wheel follows the profile of the road surface when the vehicle travels on the road, therefore, as the system input, the road surface excitation mainly includes periodic excitation and impact excitation and random excitation in this paper. Figure 2 shows the traditional quarter-vehicle model and the quarter-vehicle model with the MEHS; it can be seen that the structure of the PS is retained, and the installed energy harvester is connected in parallel with the PS in the MEHS. $x_s$, $x_u$ and $x_l$ are the displacements of the sprung, unsprung and road surface, respectively. $k_s$ and $c$ are the stiffness and damping coefficient of the PS, respectively. $k_w$ is the tire stiffness. In addition, the energy harvester of the MEHS is simplified into an inductance $L$ and a resistor $R_{coil}$, which is connected to the external load resistance $R_{load}$.

According to Figure 2, the dynamic equations of the traditional quarter-vehicle model and quarter-vehicle model with the MEHS can be written as

$$\left\{\begin{array}{l}{m}_s{\ddot{x}}_s+k_s\left(x_s-x_u\right)+c\left({\dot{x}}_s-{\dot{x}}_u\right)=0\\ m_u{\ddot{x}}_u+k_w\left(x_u-x_l\right)-k_s\left(x_s-x_u\right)-c\left({\dot{x}}_s-{\dot{x}}_u\right)=0\end{array}\right.$$

(1)

$$\left\{\begin{array}{l}{m}_s{\ddot{x}}_s+k_s\left(x_s-x_u\right)+c\left({\dot{x}}_s-{\dot{x}}_u\right)-k_{a}i=0\\ m_u{\ddot{x}}_u+k_w\left(x_u-x_l\right)-k_s\left(x_s-x_u\right)-c\left({\dot{x}}_s-{\dot{x}}_u\right)+k_{a}i=0\\ L\dot{i}+Ri+k_a\left({\dot{x}}_s-{\dot{x}}_u\right)=0\end{array}\right.$$

(2)

where $R=R_{coil}+R_{load}$. $m_s$ and $m_u$ are sprung mass and unsprung mass, respectively. $k_a$ is the electromechanical coupling coefficient of the MEHS. i is the induced current in the coil. $k_{a}i$ is the magnetic force generated by the MEHS. Furthermore, to analyze the energy harvesting and dynamic performance of the suspension system, the road surface model is simplified to periodic excitation $x_l=a\sin \left(\omega t\right)$ in this paper, and applying a Laplace transform to Equation (2) results in

$$\left\{\begin{array}{l}{m}_s{x}_s\left(z\right)z^2+k_s\left(x_s\left(z\right)-x_u\left(z\right)\right)+c\left(x_s\left(z\right)-x_u\left(z\right)\right)z-k_{a}i\left(z\right)=0\\ m_u{x}_u\left(z\right)z^2+k_w\left(x_u\left(z\right)-x_l\left(z\right)\right)-k_s\left(x_s\left(z\right)-x_u\left(z\right)\right)-c\left(x_s\left(z\right)-x_u\left(z\right)\right)z+k_{a}i\left(z\right)=0\\ Li\left(z\right)z+Ri\left(z\right)+k_a\left(x_s\left(z\right)-x_u\left(z\right)\right)z=0\end{array}\right.$$

(3)

3.2. Energy Harvesting

The vibration energy is converted into electric energy through the harvester when the vehicle travels on the road, and the energy harvesting performance of the MEHS is investigated based on the mean power. According to Equation (3), the current i in the system can be used to analyze the energy harvesting performance, and the output power is considered as an evaluation index. Hence, the transmission from the road surface displacement to the current can be obtained as

$$\frac{i\left(z\right)}{x_l\left(z\right)}=\frac{k_a{m}_s{k}_w{z}^3}{\Delta }$$

(4)

where $\Delta =a_1{z}^5+a_2{z}^4+a_3{z}^3+a_4{z}^2+a_{5}z+a_6$, $a_1=L{m}_s{m}_u$, $a_2=Lc\left(m_s+m_u\right)+R{m}_s{m}_u$, $a_3=L\left(m_s{k}_w+m_u{k}_s+m_s{k}_s\right)+k_a^2\left(m_s+m_u\right)+Rc\left(m_s+m_u\right)$,$a_4=Lc{k}_w+R\left(m_s{k}_w+m_u{k}_s+m_s{k}_s\right)$, $a_5=L{k}_s{k}_w+Rc{k}_w$, $a_6=R{k}_s{k}_w$. The amplitude of the current in the system can be expressed as

$${\sigma }_i=\frac{a{k}_a{m}_s{k}_w{\omega }^3}{\Delta \left(\omega \right)}$$

(5)

where $\Delta \left(\omega \right)=\sqrt{{\left(a_2{\omega }^4-a_4{\omega }^2+a_6\right)}^2+{\left(a_1{\omega }^5-a_3{\omega }^3+a_5\omega \right)}^2}$. According to Equation (5), the mean output power of the MEHS in one cycle can be calculated as

$$P=\frac{{\displaystyle {\int }_0^T{i}^2{R}_{load}dt}}{T}=\frac{{\sigma }_i^2{R}_{load}}{2}$$

(6)

3.3. Ride Comfort

In this paper, the dynamics of the seat and human are not considered, therefore, the human body is replaced by the vehicle body. Ride comfort is subjective to human perception, which is evaluated using the mean value of the vehicle body acceleration, and the vehicle body acceleration is inversely proportional to ride comfort. The transmission from the road surface displacement to the vehicle body acceleration can be obtained as

$$\frac{{\ddot{x}}_s\left(z\right)}{x_l\left(z\right)}=\frac{b_1{z}^4+b_2{z}^3+b_3{z}^2}{\Delta }$$

(7)

where $b_1=cL{k}_w$, $b_2=cR{k}_w+k_{s}L{k}_w+k_w{k}_a^2$, $b_3=k_{s}R{k}_w$. Therefore, the peak value of the vehicle body acceleration in the system can be calculated as

$${\sigma }_{{\ddot{x}}_s}=\frac{a{\Delta }_b\left(\omega \right)}{\Delta \left(\omega \right)}$$

(8)

where ${\Delta }_b\left(\omega \right)=\sqrt{{\left(b_1{\omega }^4-b_3{\omega }^2\right)}^2+{\left(-b_2{\omega }^3\right)}^2}$.

3.4. Road Handling

Road handling is an important vehicle driving performance, affecting vehicle driving safety. There is no contact force between the tire and the ground, leading to the loss of road handling. To reflect the road handling more directly, the relative dynamic load of the tire is calculated, which is the ratio of the tire force and gravity. The contact force between the tire and the ground will be lost when the relative dynamic load of the tire is equal or greater than one. Therefore, the relative dynamic load of the tire is considered as an important index to evaluate road handling. The transmission from the road surface displacement to the relative displacement of the tire can be provided as

$$\frac{x_u\left(z\right)-x_l\left(z\right)}{x_l\left(z\right)}=\frac{-\left(c_1{z}^5+c_2{z}^4+c_3{z}^3+c_4{z}^2\right)}{a_1{z}^5+a_2{z}^4+a_3{z}^3+a_4{z}^2+a_{5}z+a_6}$$

(9)

where $c_1=L{m}_s{m}_u$, $c_2=R{m}_s{m}_u+L{m}_{u}c+L{m}_{s}c$, $c_3=R{m}_{u}c+R{m}_{s}c+L{m}_u{k}_s+L{m}_s{k}_s+\left(m_u+m_s\right)k_a^2$, $c_4=R{m}_s{k}_s+R{m}_u{k}_s$. Therefore, the peak value of the relative change of the tire in the system can be obtained as

$${\sigma }_{\left(x_u-x_l\right)}=\frac{a{\Delta }_c\left(\omega \right)}{\Delta \left(\omega \right)}$$

(10)

where ${\Delta }_c\left(\omega \right)=\sqrt{{\left(-c_2{\omega }^4+c_4{\omega }^2\right)}^2+{\left(-c_1{\omega }^5+c_3{\omega }^3\right)}^2}$. According to Equation (10), the peak value of the relative dynamic load of the tire in the system can be calculated as

$${\sigma }_{F_{tire}}=\frac{k_w{\sigma }_{\left(x_u-x_l\right)}}{\left(m_s+m_u\right)g}$$

(11)

4. Parameters Analysis

It can be seen from Equation (6) that the generated power is related to excitation frequency $\omega$, excitation amplitude $a$, electromechanical coupling coefficient $k_a$ and external load resistance $R_{load}$ under the determined parameters of the suspension system, and the generated power affects the dynamic performance of the suspension. Therefore, the numerical parametric studies are conducted to analyze the effects of the parameters on the energy harvesting, ride comfort and road handling of the MEHS in this section. Furthermore, the parameters of the fabricated MEHS prototype are adopted from the reference [35]: sprung mass $m_s=4.2$ kg, unsprung mass $m_u=2$ kg, suspension stiffness $k_s=2920$ N/m, tire stiffness $k_w=4930$ N/m, suspension damping coefficient $c=16$ N·m/s, electromechanical coupling coefficient $k_a=33.9892$ and external load resistance $R_{load}=20$ Ω.

4.1. Influence of the Road Input

The excitation frequency 1–10 Hz and the excitation amplitude 2–3 mm are adopted as the input signals. Figure 3 and Figure 4 illustrate the harvested average power, sprung acceleration and relative dynamic load of the tire at various excitations, respectively. The main influence factor of energy harvesting is the relative velocity of the suspension. Figure 3 shows that the harvested power increases as the excitation amplitude increases, which tells us that the relative velocity of the suspension is greater at a higher amplitude. Furthermore, the maximum harvested power is obtained at the excitation frequency 3.3 Hz. When the excitation frequency is less than 2 Hz, the harvested power is basically zero.

The evaluation of the ride comfort is measured by the peak value of the sprung acceleration, the ride comfort is less when the sprung acceleration is larger. It can be seen that the changing trend of the sprung acceleration is the same as that of the harvested energy, as shown in Figure 4a, and the sprung acceleration of the vehicle with the MEHS increases as the excitation amplitude increases. Compared with the PS, the MEHS can suppress the sprung vibration and reduce the sprung acceleration; however, it can be found that the structure of the MEHS can increase the sprung acceleration when the range of the excitation frequency is 4–7.8 Hz. The road handling of the vehicle is affected by the relative dynamic load of the tire; the road handling is less with the increase of the relative dynamic load. Figure 4b illustrates that the relative dynamic load of the tire for the PS is greater than one when the range of the excitation frequency is 3.2–3.3 Hz, which will lose the contact force between the road and tire, however, the MEHS can increase the contact force between road and tire to eliminate the loss of the contact force. Furthermore, the relative dynamic load of the MEHS is greater than that of the PS at the excitation frequency 4–9 Hz and increases as the excitation amplitude increases. Hence, with respect to the excitation frequency and amplitude, the energy harvesting performance of suspension is the same as its dynamic performance.

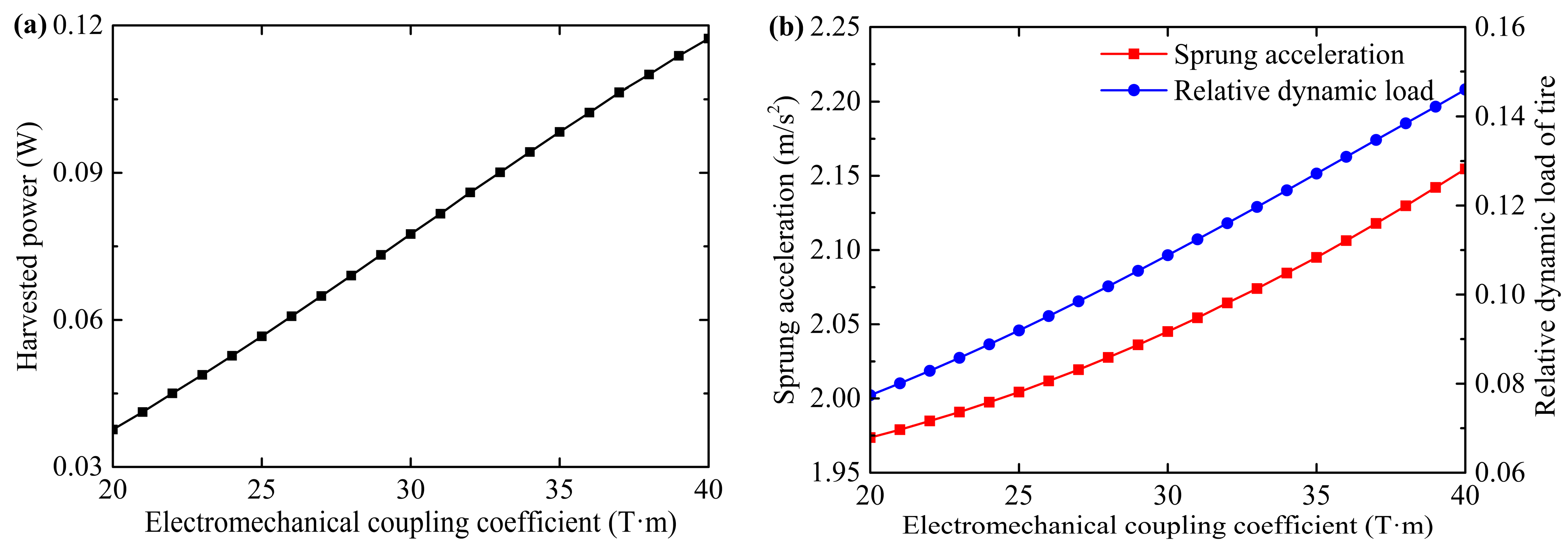
4.2. Influence of the Electromechanical Coupling Coefficient

The energy harvester obtains the electromechanical coupling coefficient, which is an important part of the MEHS. Since the coupling coefficient of the fabricated MEHS prototype is 33.9892, the coupling coefficient range from 20 to 40 is used to investigate the influence of the electromechanical coupling coefficient. And the effects of the electromechanical coupling coefficient on energy harvesting, ride comfort and road handling at the excitation frequency 7 Hz and excitation amplitude 2 mm are investigated, and the numerical results of the harvested power, sprung acceleration and relative dynamic load of the tire are plotted in Figure 5. It can be seen that the generated power, sprung acceleration and relative dynamic load of the tire increase with the increase of the electromechanical coupling coefficient, respectively. However, the effects of the increased sprung acceleration and relative dynamic load of the tire on the ride comfort and road handling are negative. Therefore, in terms of the electromechanical coupling coefficient, the energy harvesting performance and the dynamic performance of the MEHS are contradictory.

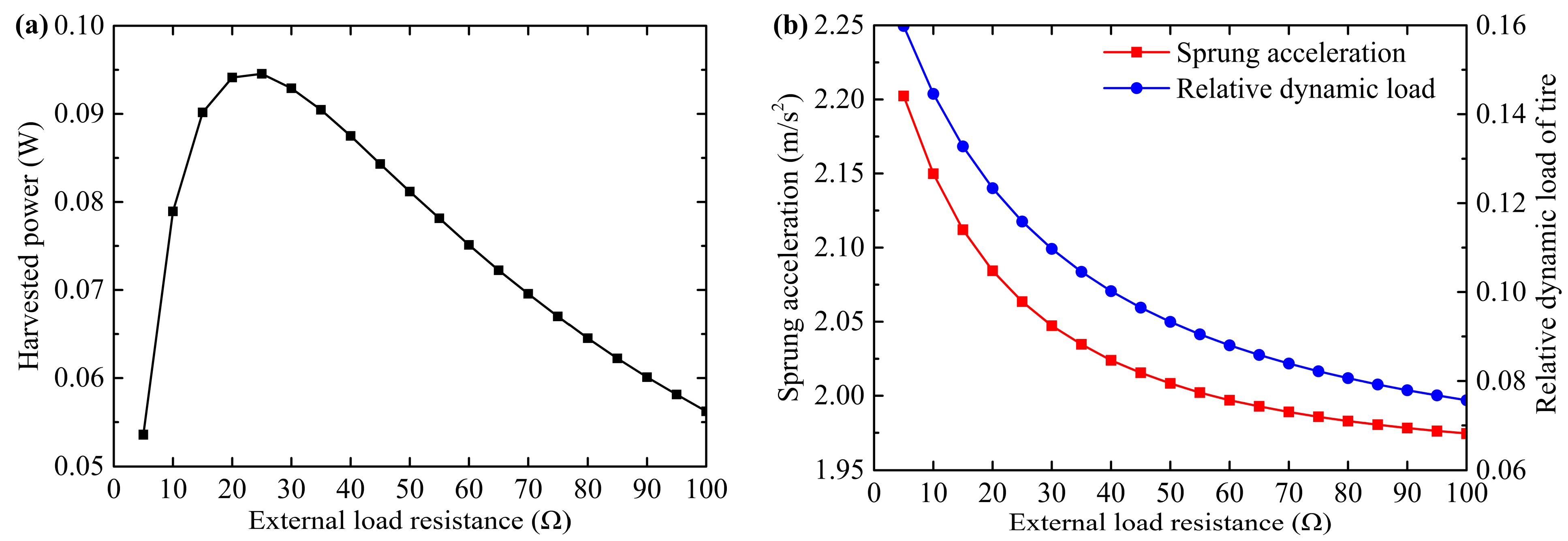
4.3. Influence of the External Load Resistance

Figure 6 illustrates the effects of the external load resistance on the energy harvesting and dynamic performance of the MEHS at the excitation frequency 7 Hz and excitation amplitude 2 mm. It can be found from Figure 6a that the maximum harvested power is obtained at the external load resistance 25 Ω, and the harvested power decreases with the increase of the sprung mass when the nominal external load resistance is greater than 25 Ω. Meanwhile, as shown in Figure 6b, the sprung acceleration and relative dynamic load of the tire decrease as the external load resistance increases, which makes the ride comfort and road handling of the vehicle gradually better. However, the energy harvesting and dynamic performance of the MEHS are contradictory with the increase of the external load resistance.

5. Experiment Verification

This section aims to verify the above analysis results and investigate the dynamic performance at the various excitations and external load resistances. The prototype is manufactured to simulate the quarter-vehicle system, and the experiment setup is built to measure the output voltage and the displacements of the sprung and unsprung for the suspension system. In addition, to investigate the effect of the energy harvester on the dynamic performance of the suspension system, comparison experiments between the PS and MEHS need to be carried out.

5.1. Experimental Setup

A view of the experimental setup is shown in Figure 7. The prototype is mounted on the frame by a linear bearing, and the laser displacement sensors (HG-C1100, Panasonic) are mounted on the frame to measure the displacements of the sprung and unsprung. The spring simulating tire stiffness is fixed on the shaker (m060, IMV), and the shaker is connected with the power amplifier (MA1, IMV) by a cable. The signal input port of the power amplifier is connected with a DAC port of the dSPACE 1103. The control block diagram is designed with MATLAB software on the PC, and the compiled file is loaded into the ControlDesk software: an experimental software used to develop the dSPACE 1103. Therefore, the excitation signal amplified by the power amplifier is transmitted to the shaker to obtain the objective excitation.

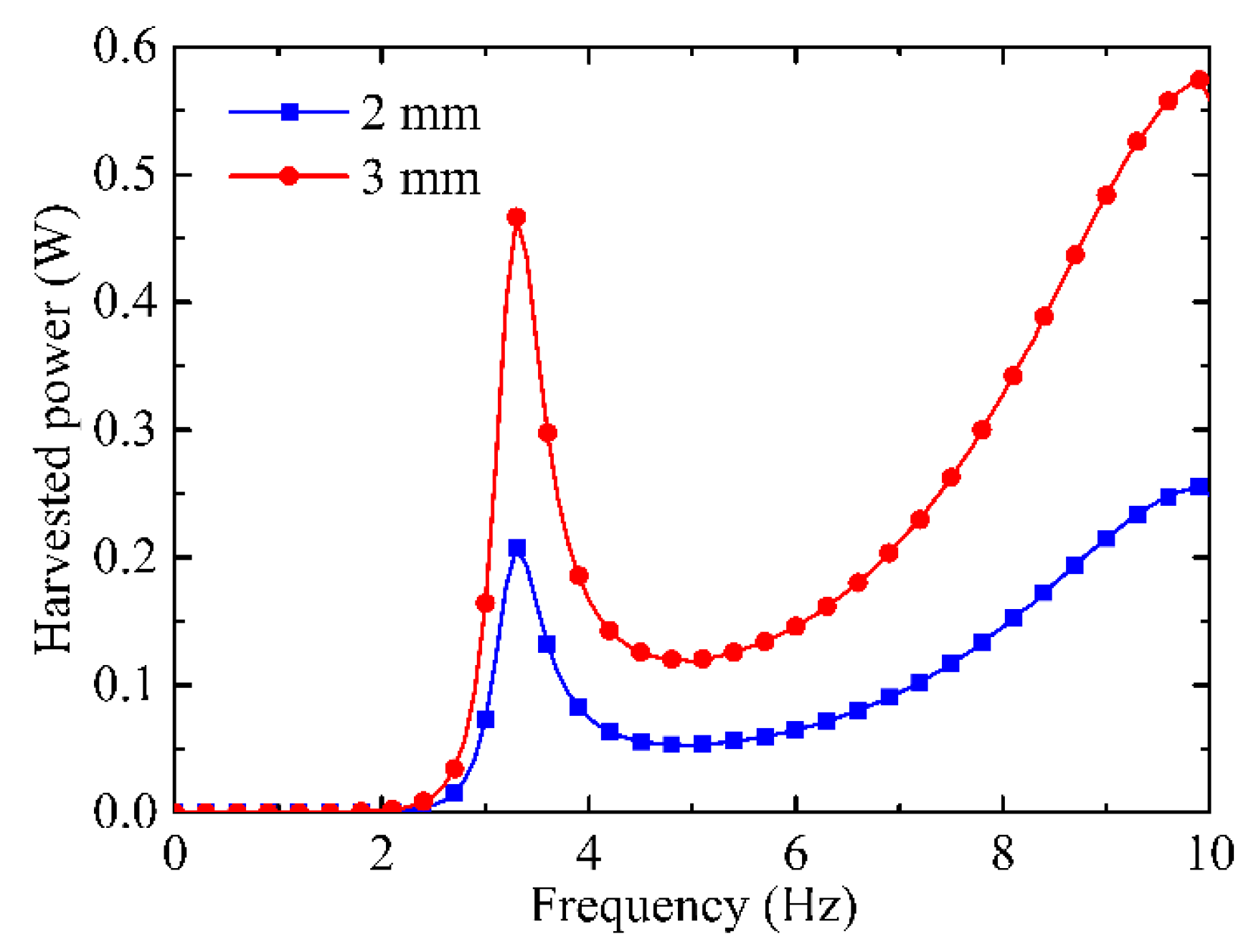
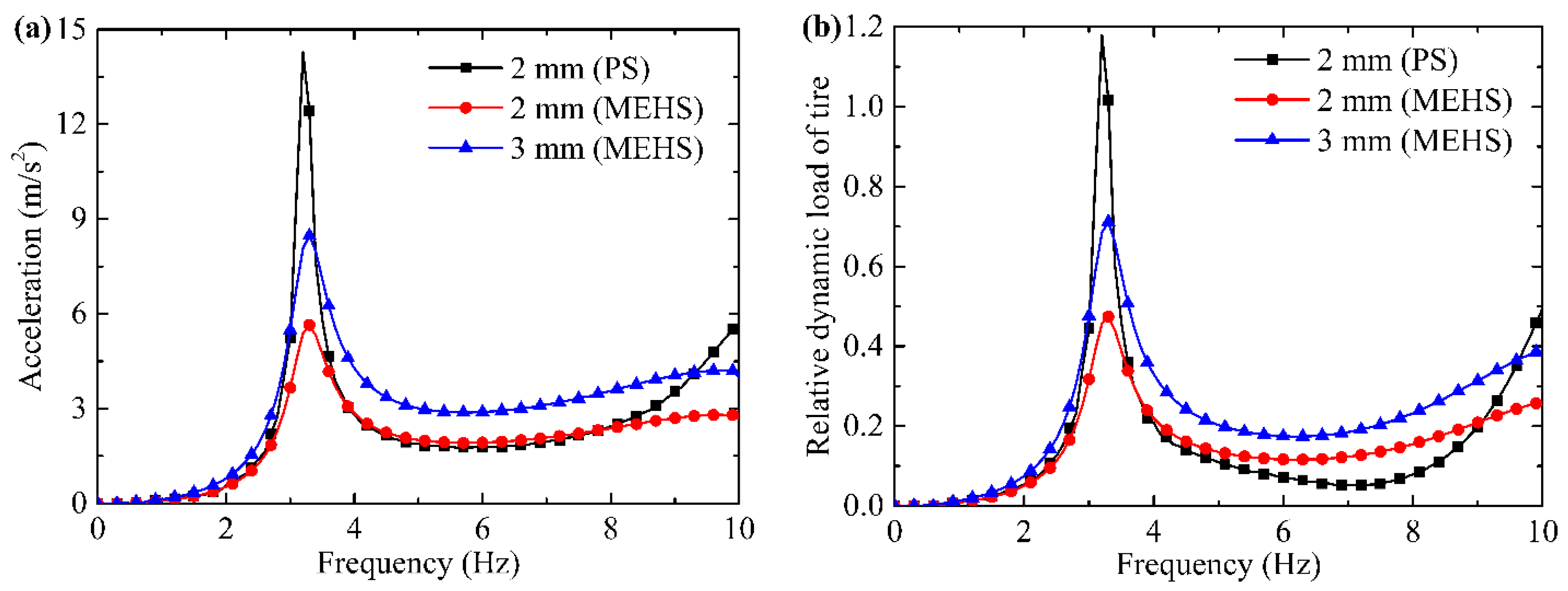
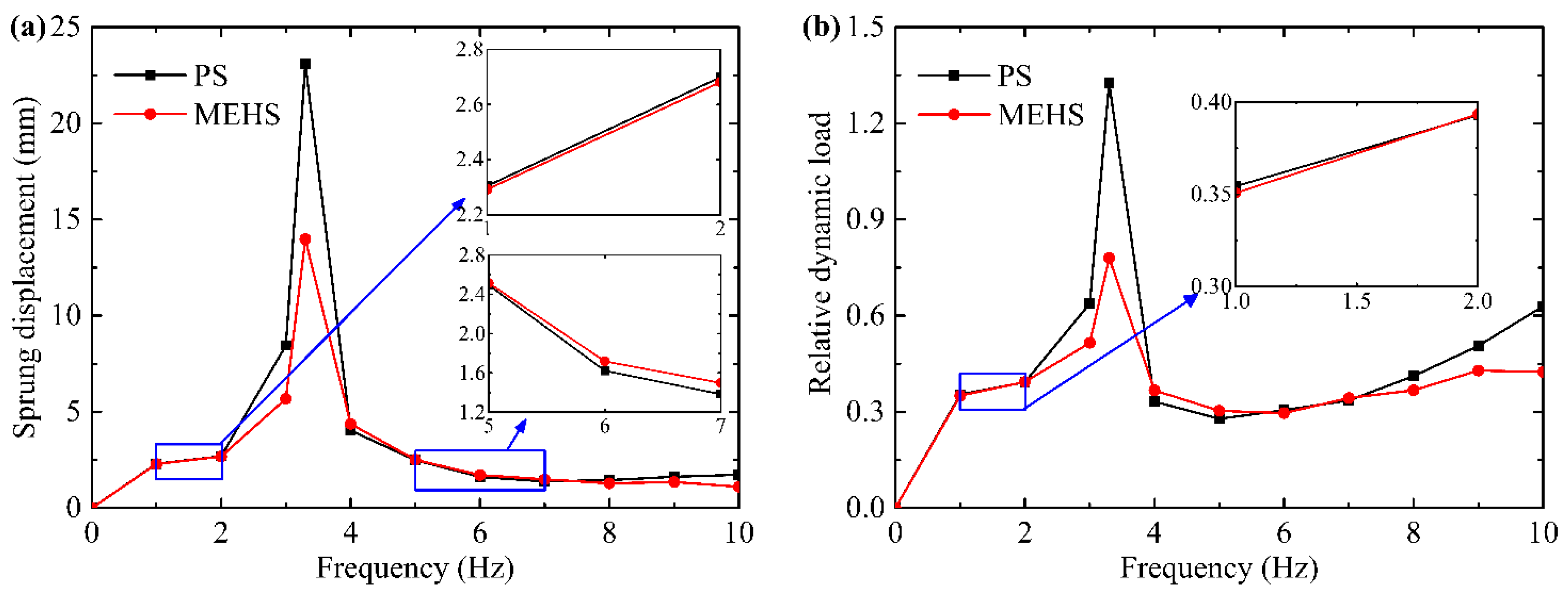
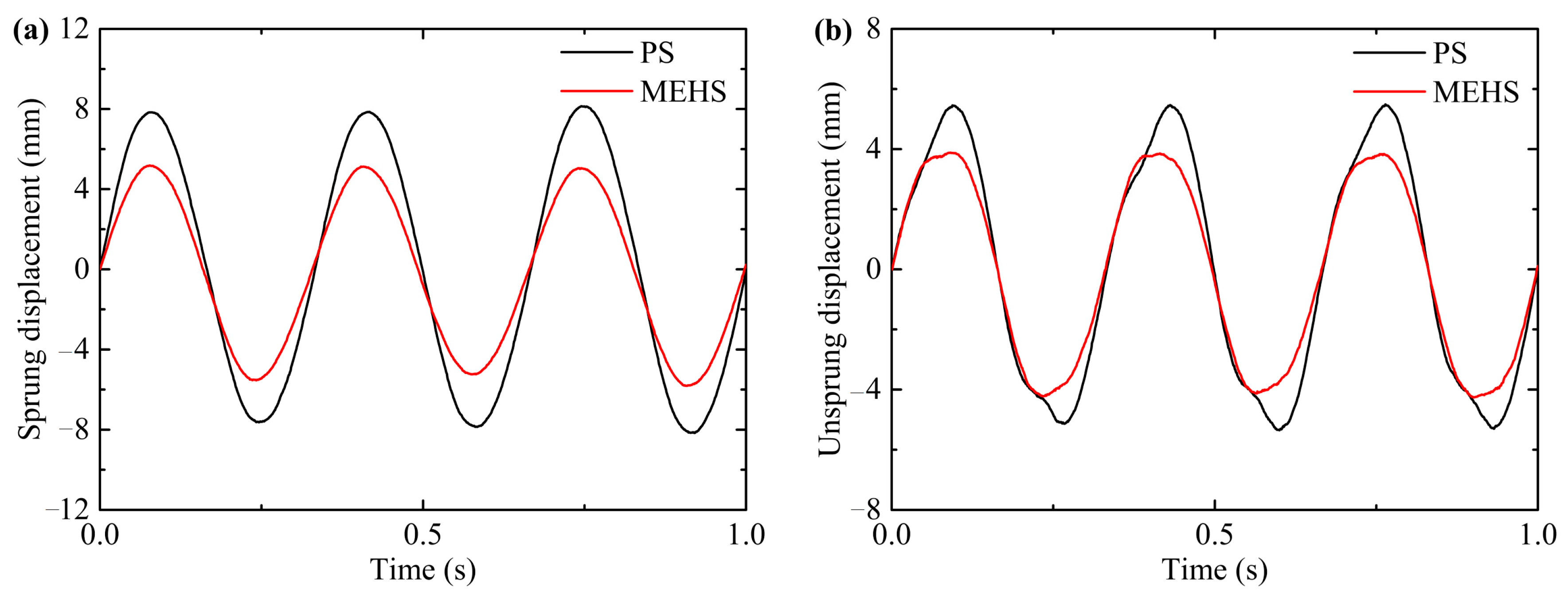
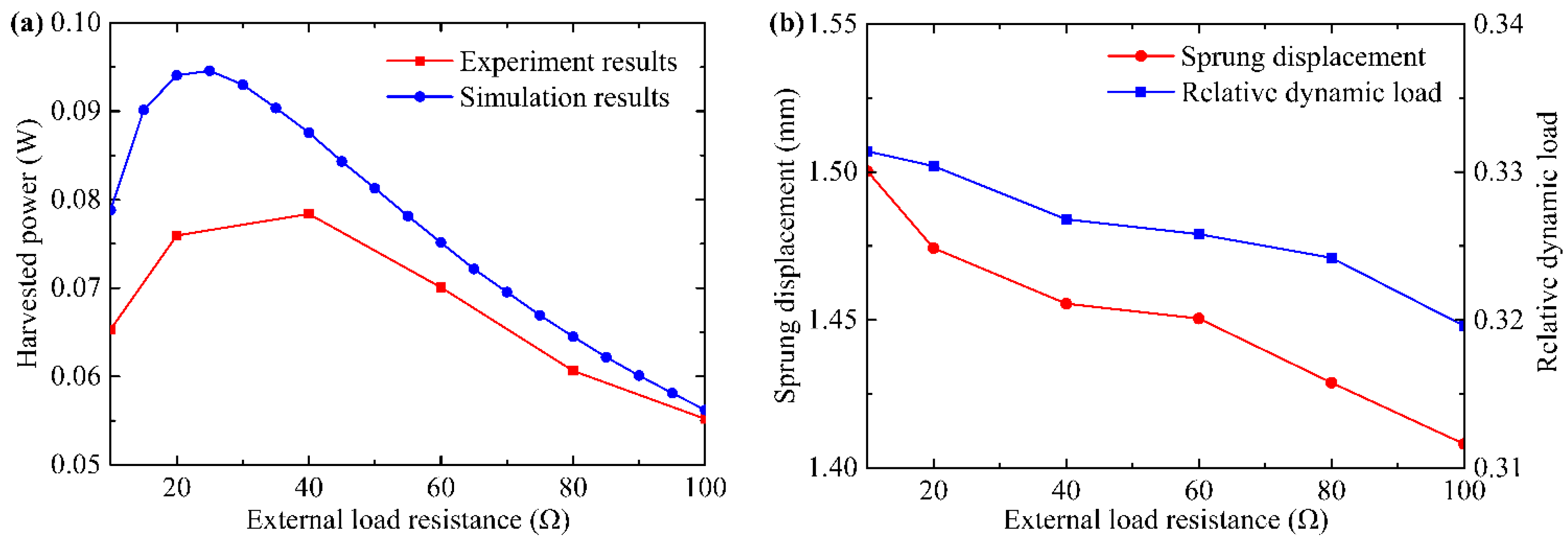
5.2. Experiment Results

In this experiment, the sprung, unsprung and shaker displacements are measured at the excitation frequencies 1–10 Hz, and the relative dynamic load of the prototype is calculated by Equation (11). To analyze the effect of the energy harvester on the dynamic performance of the suspension system, as shown in Figure 8, the measured sprung displacement and calculated relative dynamic load of the MEHS and PS are illustrated at the various excitation frequencies and amplitude 2 mm, and when the coils of MEHS are open circuit, the MEHS is regarded as a PS. It can be seen from Figure 8a that the sprung displacement is changed greatly when the excitation frequency is 3.3 Hz, and compared with the PS, the sprung displacement of the MEHS is reduced by 39.45% at the frequency 3.3 Hz, which can suppress the sprung vibration to increase the ride comfort. Furthermore, when the excitation frequency range is 4–7 Hz, the sprung displacement of the MEHS is greater than that of the PS, which can decrease ride comfort. As shown in Figure 8b, it can be found that the relative dynamic load of the PS is greater than one at the excitation frequency 3.3 Hz, which can lose the contact between ground and tire, and the relative dynamic load of the MEHS is reduced by 41.18% to maintain the contact force and improve road handling. Although, the relative dynamic load of the MEHS is greater than that of the PS at the excitation frequencies 4–5 Hz, the effect of the MEHS on road handling can be ignored. And the whole changing trend of the measurement is consistent with the numerical analysis. Meanwhile, the measured displacement profiles of the sprung and unsprung are obtained at the excitation frequency 3 Hz, as shown in Figure 9. It can be seen that, compared with PS, the effects of the MEHS on sprung and unsprung displacements are obvious to improve the vehicle performance, and the reduced rates of the sprung and unsprung displacements are 34.01% and 28.82%, respectively.

The external load resistance is a variable parameter; the harvested power, sprung displacement and relative dynamic load of various load resistances are obtained to analyze the energy harvesting and dynamic performance at the excitation frequency 7 Hz and amplitude 2 mm, as shown in Figure 10, in which the range of the load resistance is 10–100 Ω. It can be seen from Figure 10a that the harvested power is decreased with the increase of the external load resistance when the external load resistance is greater than 40 Ω. Compared with the numerical results, the whole changing trend of the measured results is consistent with the numerical analysis. Furthermore, the experiment results of the dynamic performance with various load resistances are plotted, as shown in Figure 10b, the sprung displacement and relative dynamic load decreases as the external load resistance increases, as well as dynamic performance.

Furthermore, it can be seen that there is a numerical difference between the experimental results and the numerical results. This is because the experimental device not only has the damper’s damping but also the experimental setup’s damping. The above reason leads to a decrease in the accuracy of the mathematical model. Therefore, the following work will investigate the damping characteristics of the experimental setup itself and add a new damping term to the mathematical model.

5.3. Discussion

The effect of the induced current on the dynamic performance of the MEHS has been presented in Section 5.2. Compared with the PS, the electromagnetic force generated by the MEHS with harvesting energy can affect the sprung and unsprung motion to change the dynamic performance of the vehicle. To explain the effect of the external load resistance on the suspension, according to Equation (3), the equivalent damping coefficient of the MEHS with various external load resistances is calculated as

$$c_e=\frac{\sqrt{{\left(k_{a}R\right)}^2+{\left(k_{a}L\omega \right)}^2}}{R^2+{\left(L\omega \right)}^2}+c$$

(12)

where the inductance $L$ is small, which can be ignored. Hence, Equation (12) can be simplified into

$$c_e=\frac{k_a}{R}+c$$

(13)

According to Equation (13), the damping coefficients of the MEHS and PS at the various external load resistances are plotted in Figure 11. It can be found that the damping coefficient of the MEHS is greater than that of the PS, however, the damping coefficient is decreased as the load resistance increases. Therefore, the external load resistance can be utilized to change the damping of the system, which can be sought as the tradeoff between energy harvesting and dynamic performance. Further research can design a control strategy, which can convert the vehicle suspension into the PS, MEHS and active suspension based on the requirements, in which the MEHS and active suspension can adjust the suspension damping.

6. Conclusions

The dynamic performance of the proposed magnetic energy-harvesting suspension (MEHS) is investigated in this paper. The expressions of the harvested average power, sprung acceleration and relative dynamic load of the tire at the periodic excitation are derived, and the effects of various inputs, electromechanical coupling coefficients and external load resistances on the vehicle performance are analyzed using the numerical calculation. Meanwhile, the prototype of the MEHS and the experimental setup are fabricated to verify the energy harvesting and the dynamic performance of the MEHS. Based on the numerical and experimental results, the following conclusions can be obtained:

(1)

Compared with the passive suspension (PS), the MEHS can effectively reduce the dynamic performance at the impact and periodic excitation. And the sprung displacement and relative dynamic load of the tire of MEHS are reduced by 39.45% and 41.18% at the periodic frequency 3.3 Hz, respectively.

(2)

In terms of the electromechanical coupling coefficient, the energy harvesting performance and the dynamic performance of the MEHS are contradictory.

(3)

With the increase of the external load resistance, the generated power and the dynamic performance of the suspension are contradictory at the periodic excitation 7 Hz.

(4)

Under the impact excitation and random excitation, the MEHS can change the damping characteristics to affect the dynamic performance of the suspension system.

The analysis results of the dynamic performance on the MEHS are used to guide the design of the real vehicle, which make the vehicle realize the tradeoff among energy harvesting, ride comfort and road handling. Meanwhile, the variable damping motion of the suspension system can be realized by changing the external load resistance during energy harvesting. In future work, the energy harvesting and dynamic performance of the real vehicle with the MEHS will be investigated.