A Non-Arrhenius Model for Mechanism Consistency Checking in Accelerated Degradation Tests
Abstract
:1. Introduction
1.1. A Brief Introduction to the Accelerated Lifetime and Degradation Tests
1.2. Literature Review
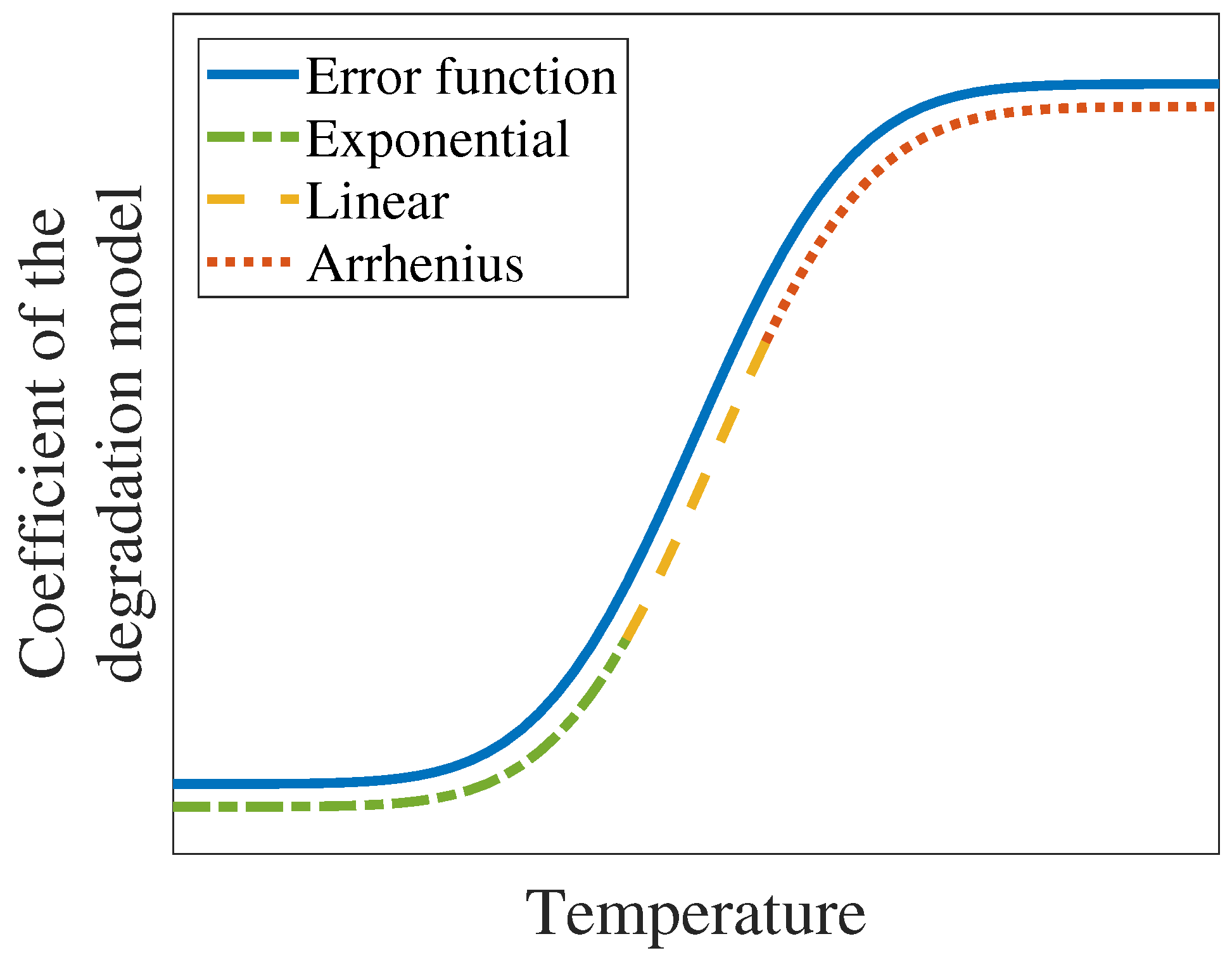
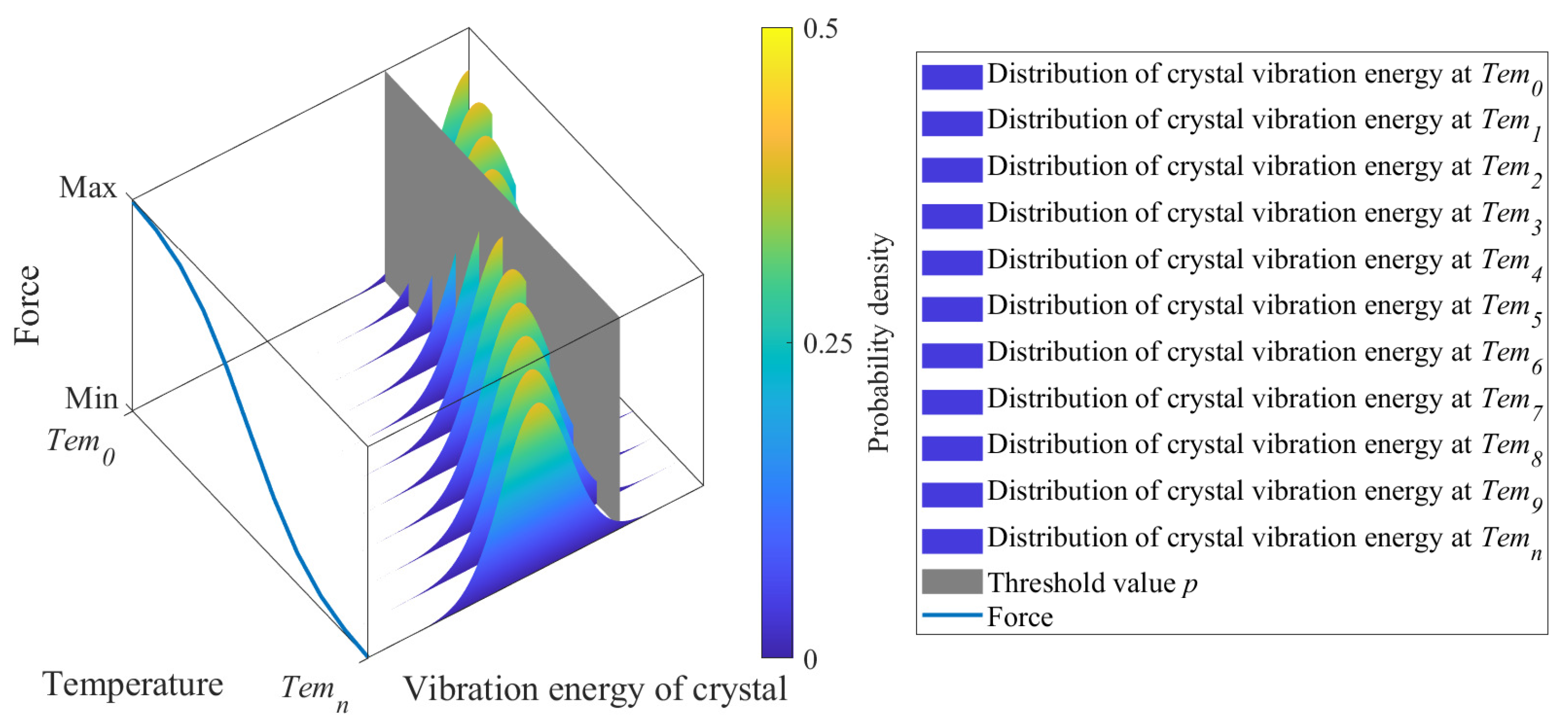
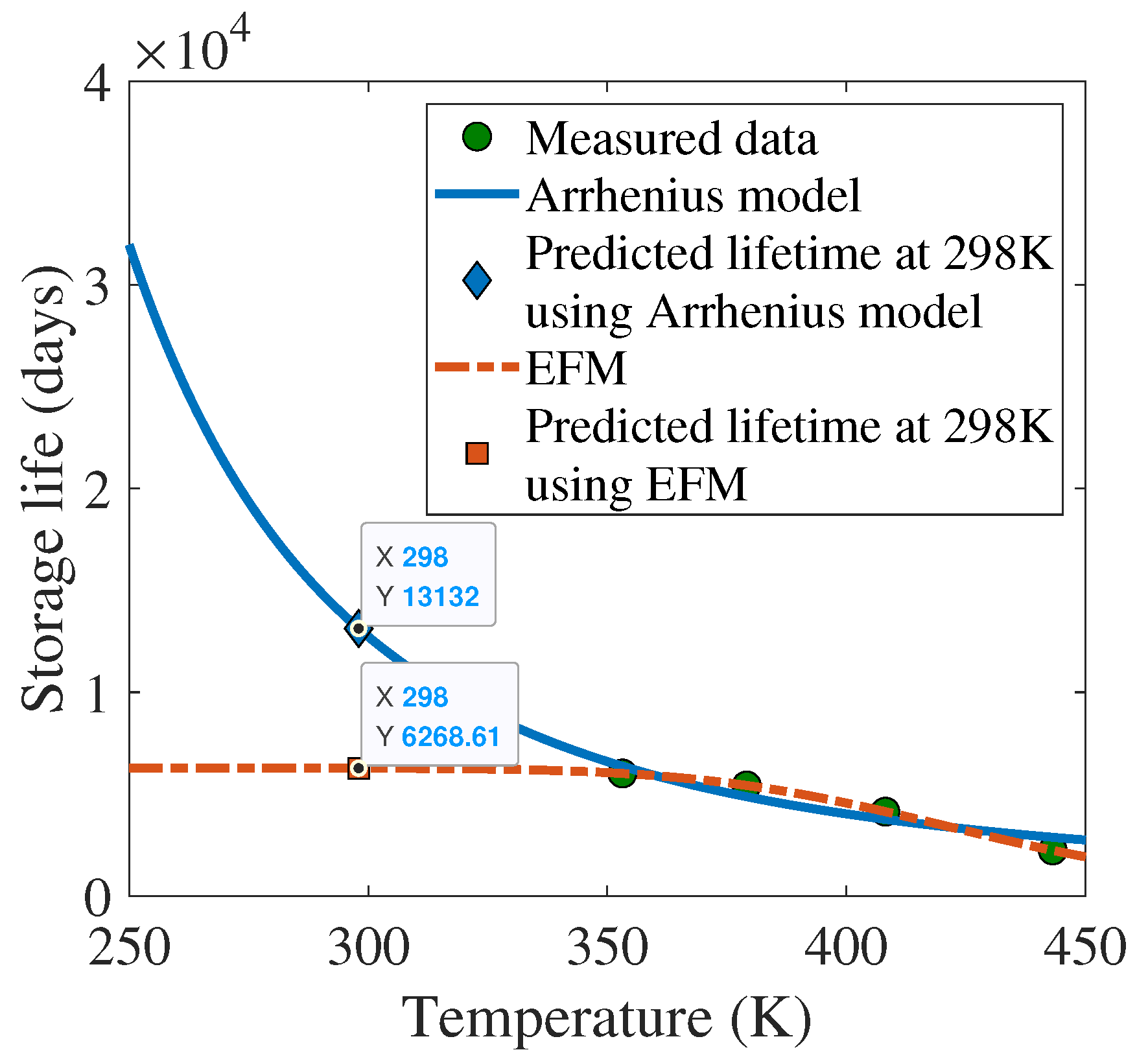
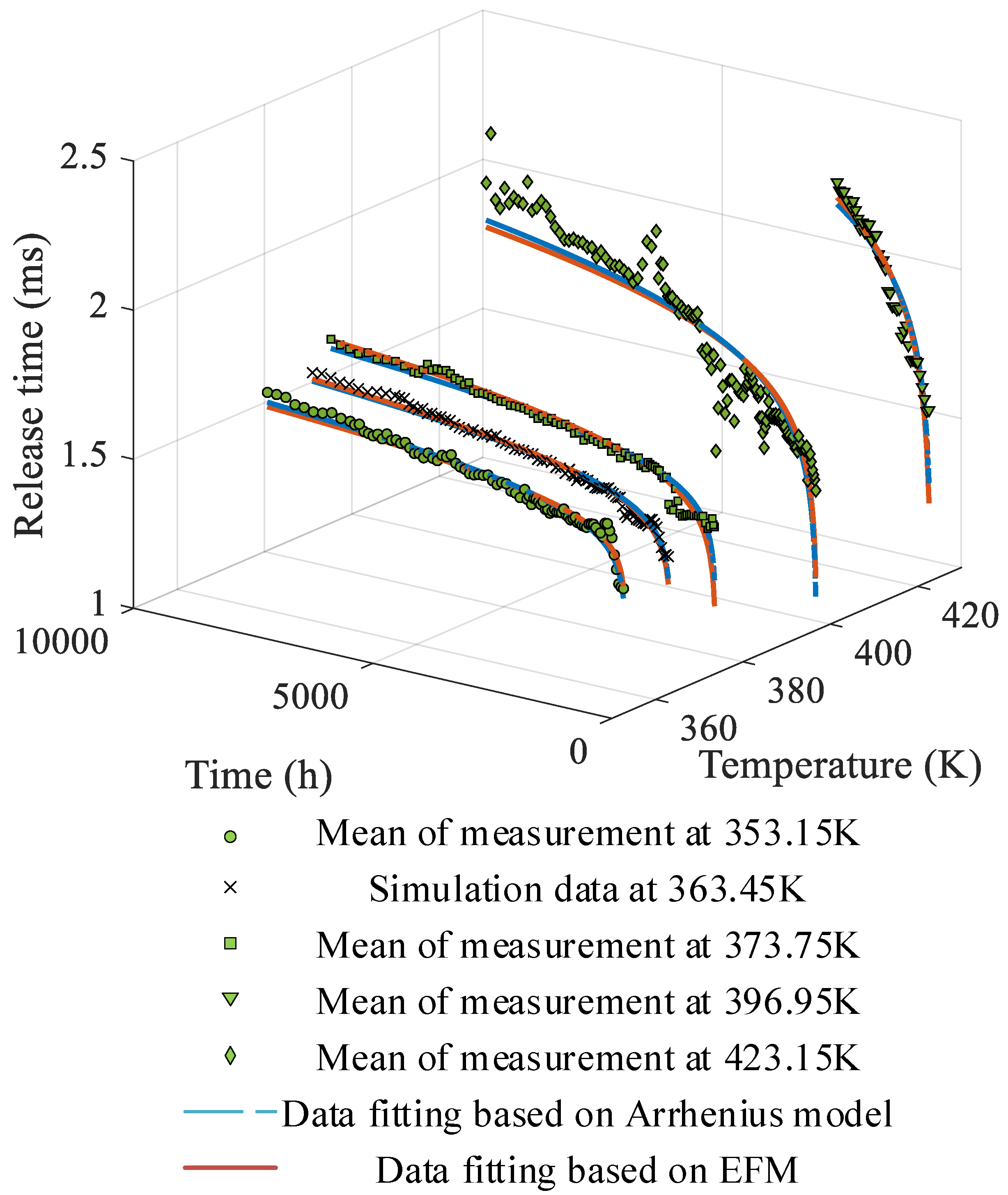
- A non-Arrhenius model is proposed to portray the degradation behavior of electromagnetic relays under ADT. The model is based on the theory of the crystal vibration energy of the material of the spring. As compared to the conventional Arrhenius-based degradation model, EFM is able to better capture the temperature characteristics of coefficients in the degradation model (TCCDM) over a much wide temperature range (see Figure 3).
- A procedure for degradation mechanism consistency checking is devised. The procedure leverages the statistical hypothesis (i.e., the test), and checks whether the parameter characterizing the degradation mechanism changes or not over temperature. Analytic expressions of the partial derivatives to the likelihood function are derived, and the Bayesian information criterion is employed to compare EFM- and Arrhenius-based degradation models.
- The proposed model can be used to explain the degradation of a wide range of materials and components, such as the capacitor or rubber.
2. Mathematical Description of the Arrhenius Model
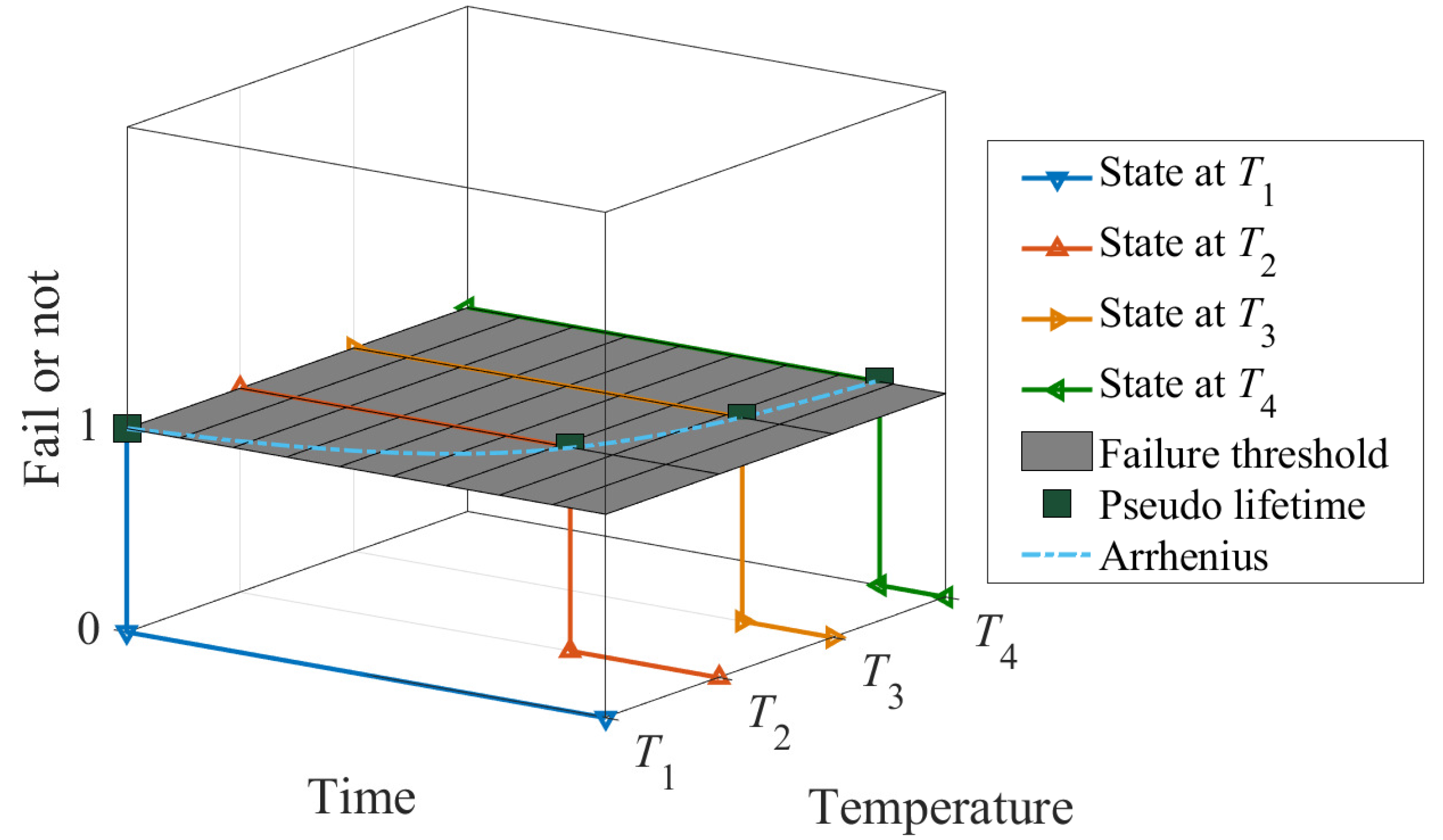
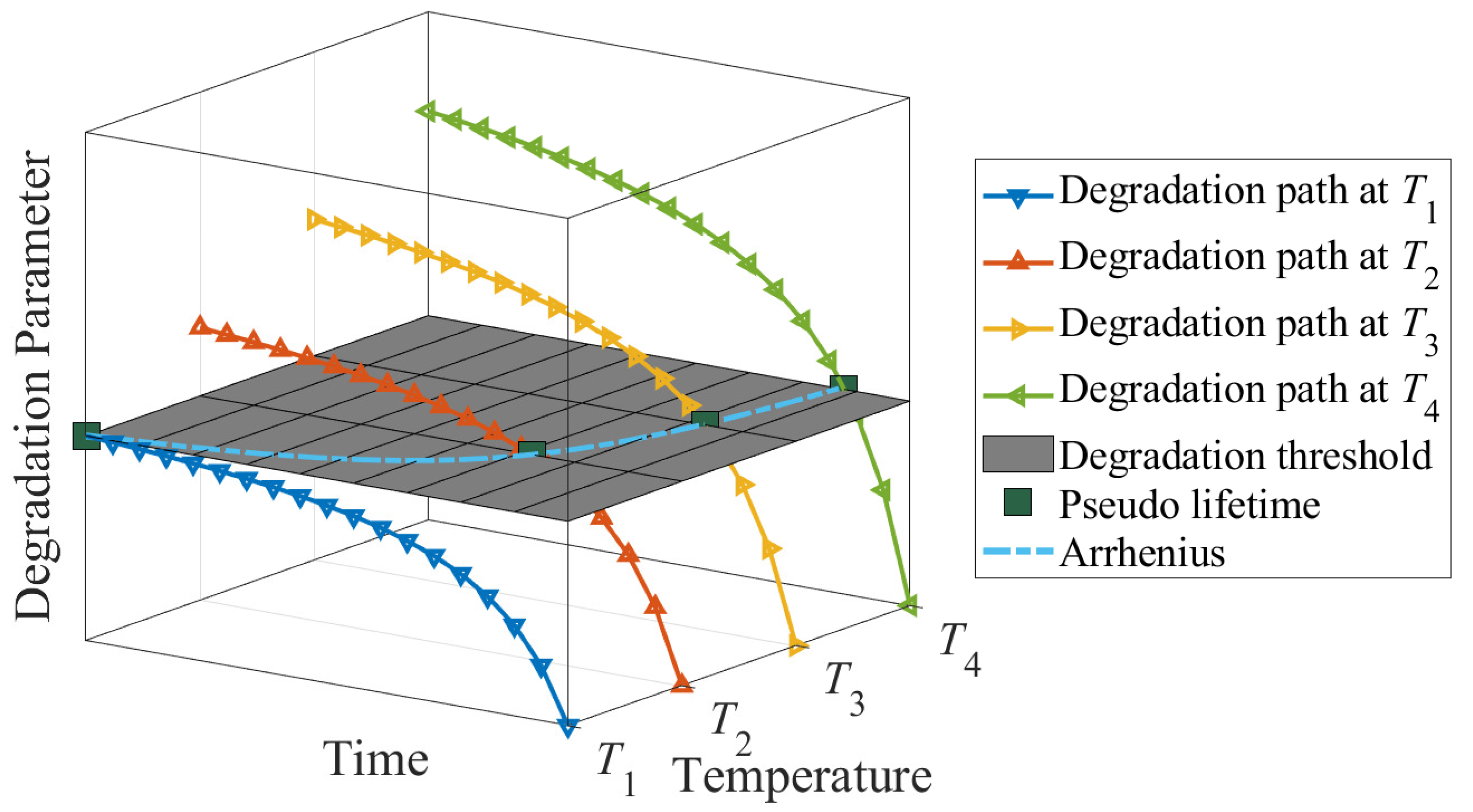
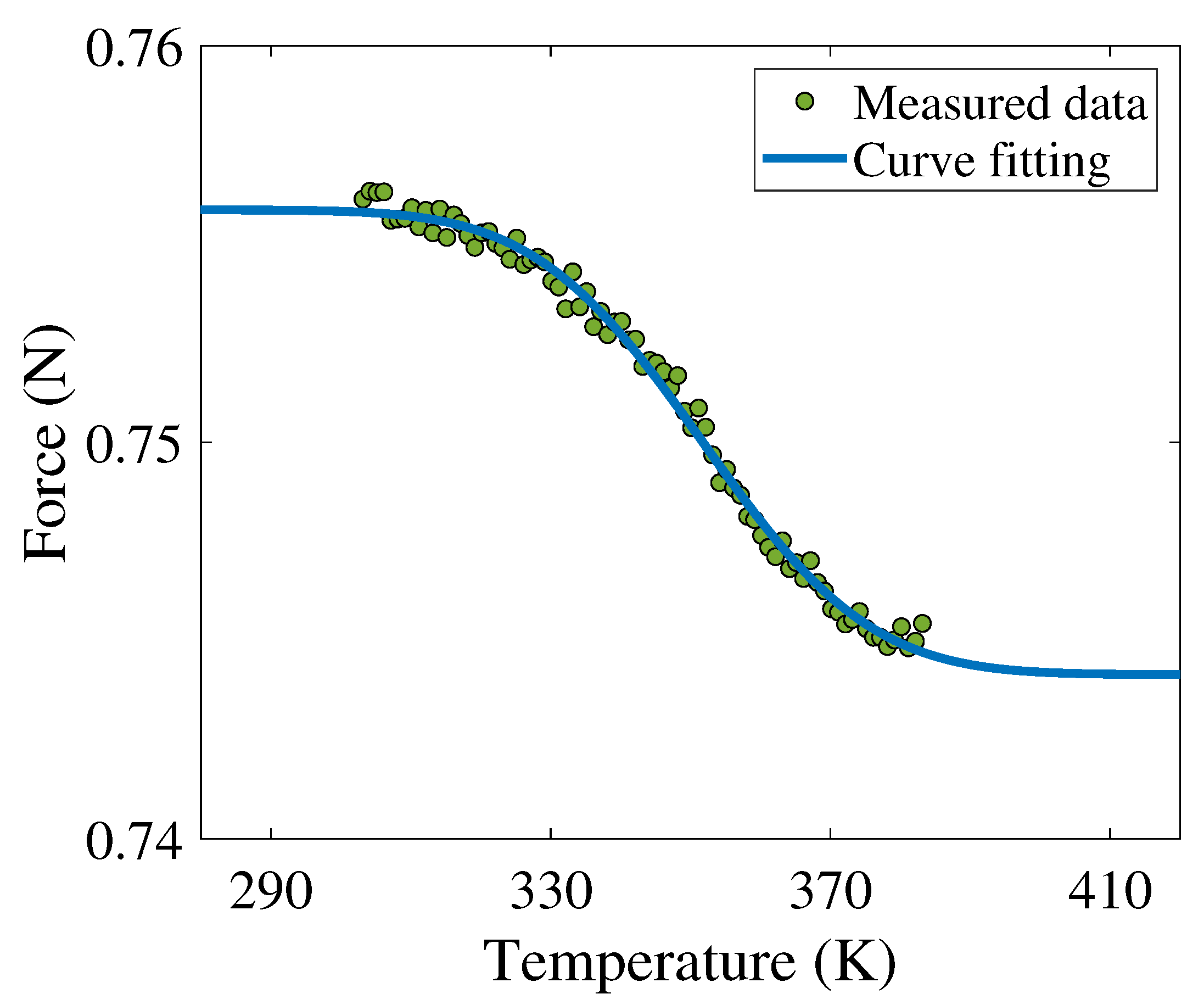
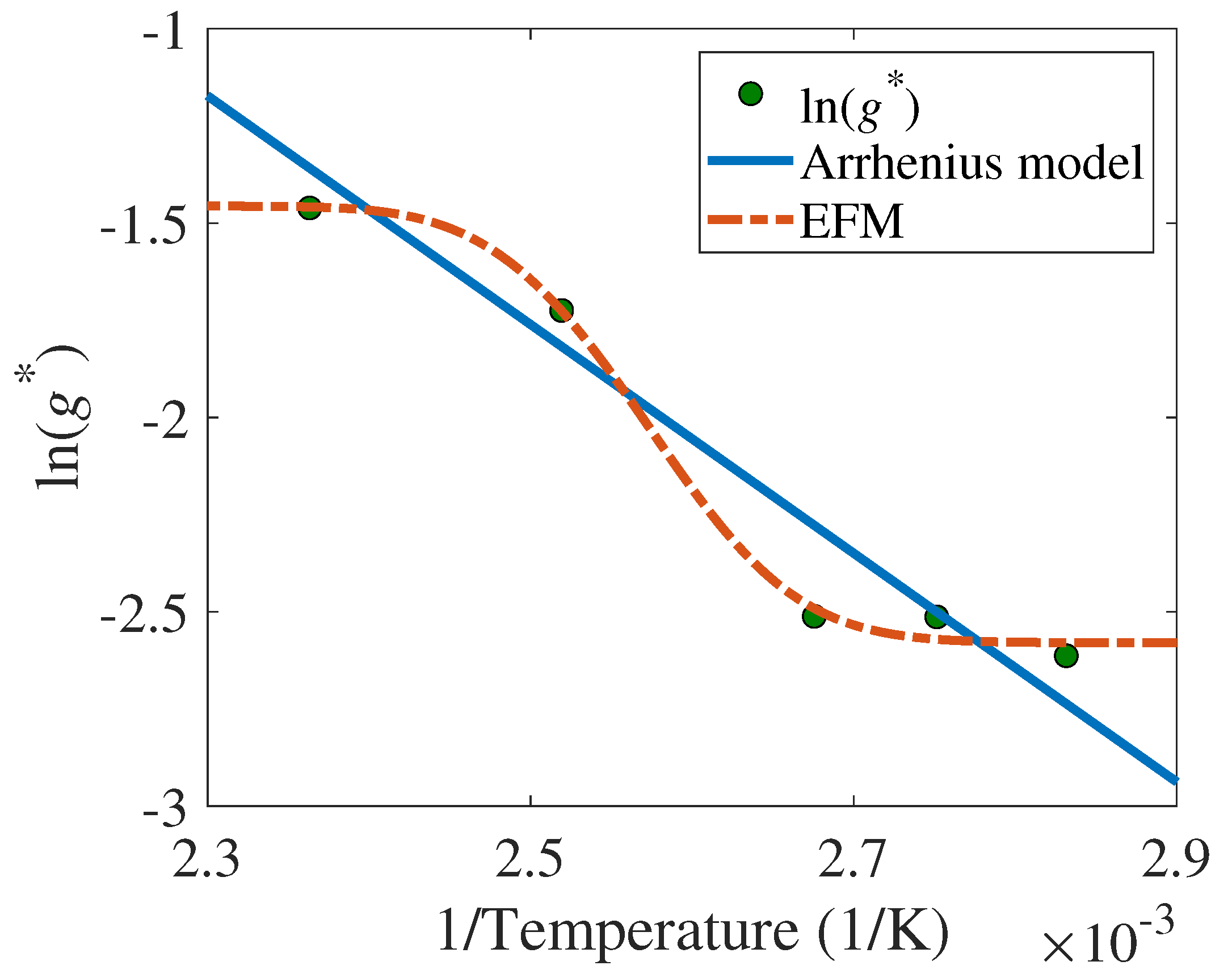
- The temperature characteristics of degradation parameters (TCDPs) (e.g., the force of the spring over temperature) align with the shape that the Arrhenius model prescribes.
- The temperature characteristics of coefficients in the degradation model (TCCDM) (e.g., d only changes with temperature) align with the shape of TCDP.
3. Theory of the EFM
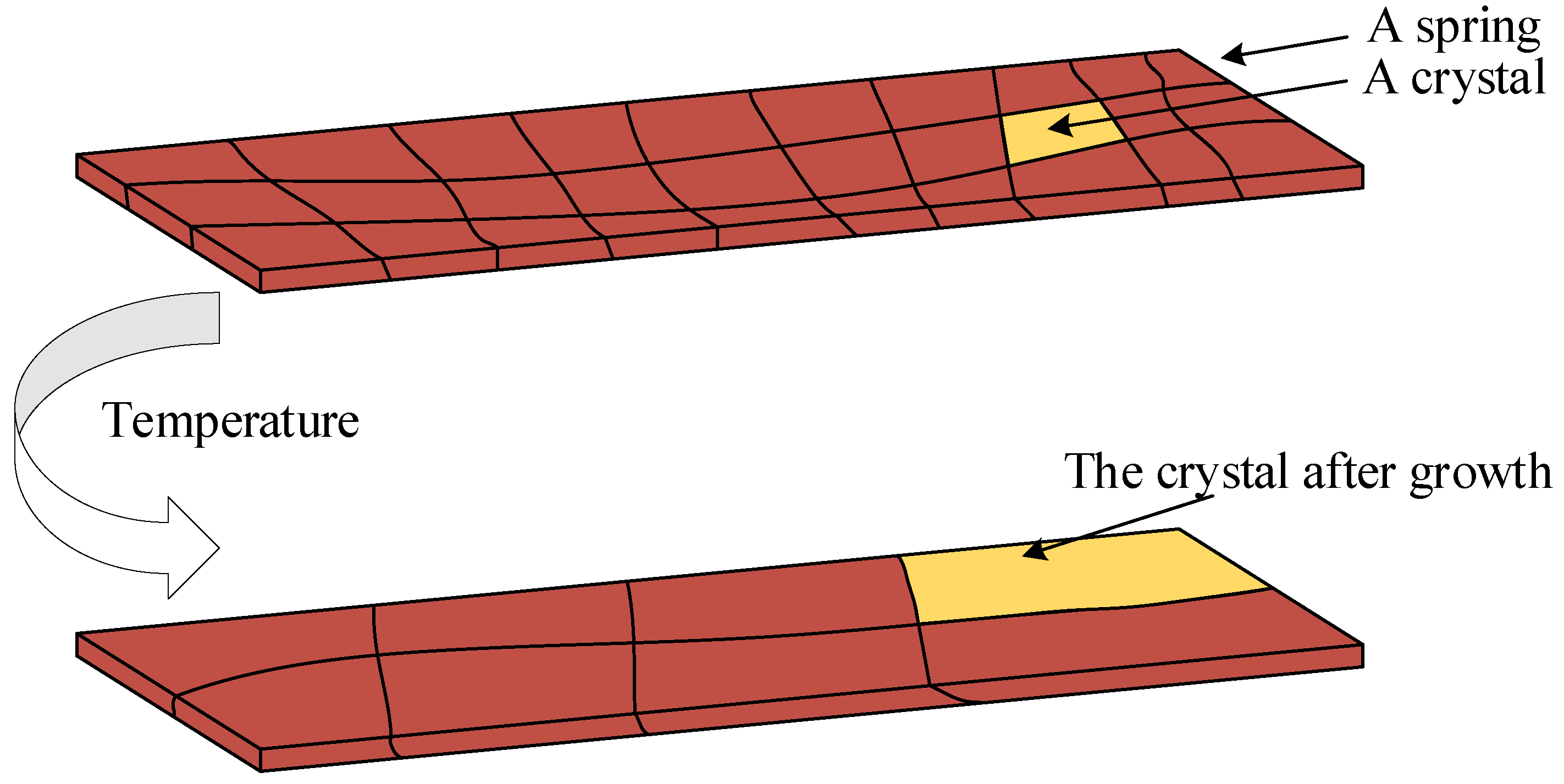
3.1. Temperature Characteristics Based on Crystal Vibration Energy
3.2. Comparison of the Arrhenius Model and EFM
4. Procedure for Mechanism Consistency Checking
- Establish a degradation model;
- Define a criterion for mechanism consistency checking.
4.1. Degradation Model
4.2. Criteria for Mechanism Consistency Checking
4.3. Parameter Estimation
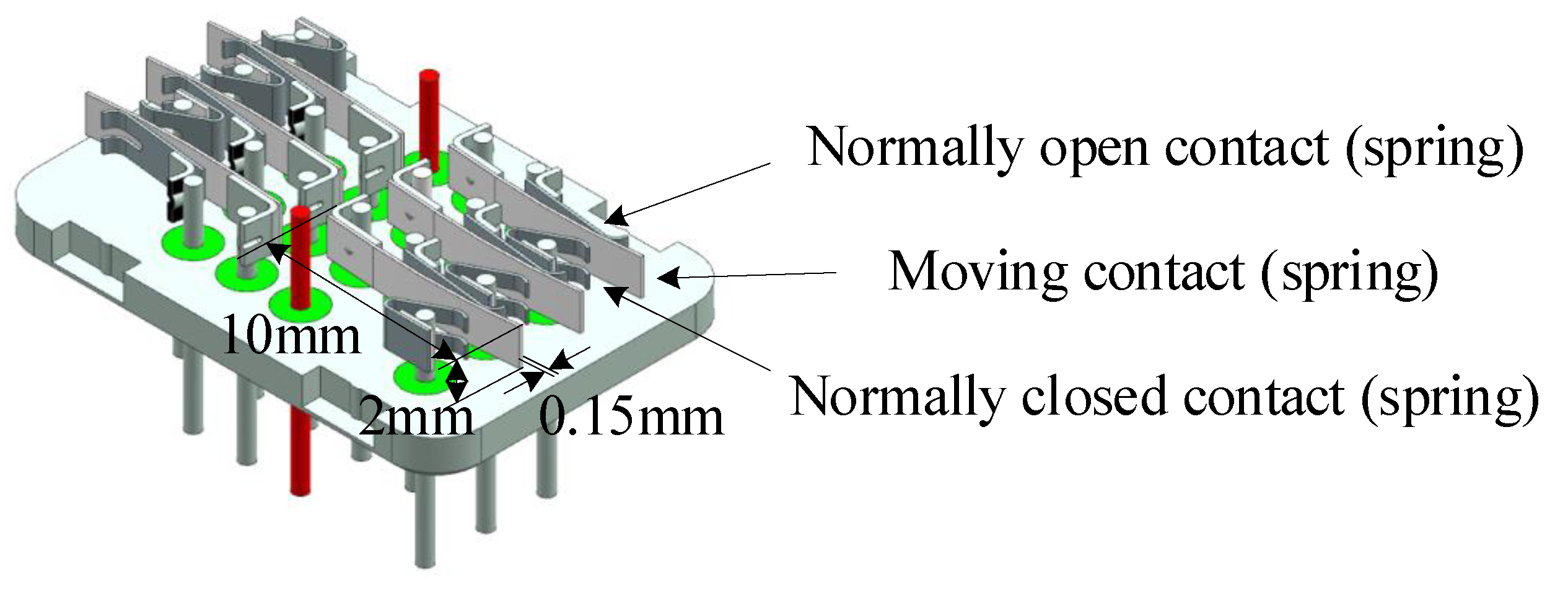
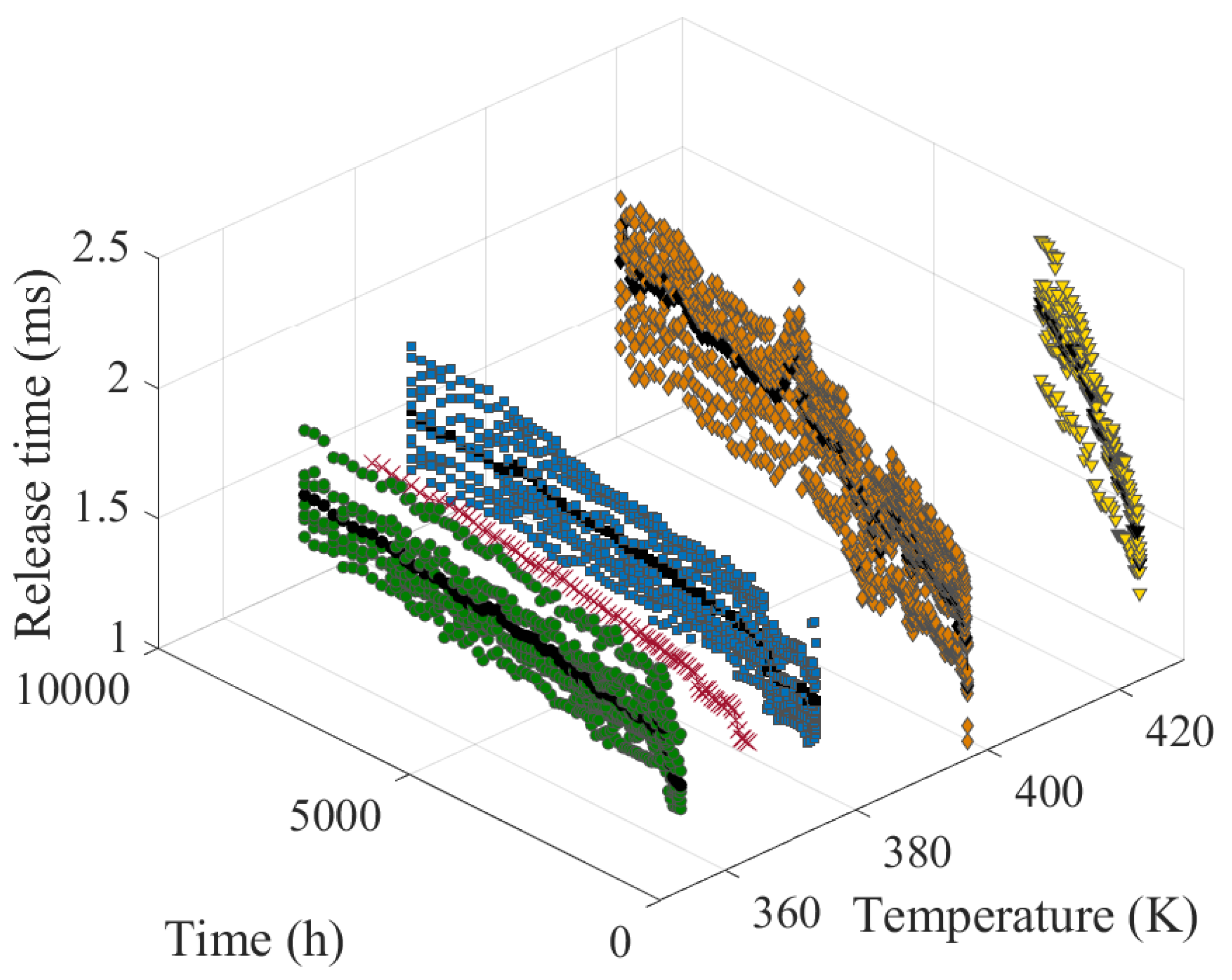
5. Case Study on the Degradation of Electromagnetic Relays
5.1. Stress Relaxation as the Degradation Parameter
5.2. Loss of Spring Force as the Degradation Parameter
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, T.; Peng, B.; Coit, D.W.; Yu, Z. Degradation Modeling and Lifetime Prediction Considering Effective Shocks in a Dynamic Environment. IEEE Trans. Reliab. 2019, 68, 819–830. [Google Scholar] [CrossRef]
- Xu, X.; Tang, S.; Yu, C.; Xie, J.; Han, X.; Ouyang, M. Remaining useful life prediction of lithium-ion batteries based on wiener process under time-varying temperature condition. Reliab. Eng. Syst. Saf. 2021, 214, 107675. [Google Scholar] [CrossRef]
- Qian, C.; Fan, X.; Fan, J.; Yuan, C.; Zhang, G. An accelerated test method of luminous flux depreciation for LED luminaires and lamps. Reliab. Eng. Syst. Saf. 2016, 147, 84–92. [Google Scholar] [CrossRef]
- Liu, D.D. Insulation resistance degradation in Ni–BaTiO3 multilayer ceramic capacitors. IEEE Trans. Comp. Packag. Manufact. Technol. 2015, 5, 40–48. [Google Scholar] [CrossRef]
- Moon, B.; Jun, N.; Park, S.; Seok, C.; Hong, U. A study on the modified arrhenius equation using the oxygen permeation block model of crosslink structure. Polymers 2019, 11, 136. [Google Scholar] [CrossRef] [Green Version]
- Woo, C.S.; Choi, S.S.; Lee, S.B.; Kim, H.S. Useful Lifetime Prediction of Rubber Components Using Accelerated Testing. IEEE Trans. Reliab. 2010, 59, 11–17. [Google Scholar] [CrossRef]
- Lu, X.; Chen, X.; Wang, Y.; Tan, Y. Consistency analysis of degradation mechanism in step-stress accelerated degradation testing. Eksploat. Niezawodn. 2017, 19, 302–309. [Google Scholar] [CrossRef]
- Wang, X.; Sun, Q. Consistency check of degradation mechanism between natural storage and enhancement test for missile servo system. J. Syst. Eng. Electron. 2019, 30, 415–424. [Google Scholar] [CrossRef]
- Zhai, G.; Zheng, B.; Ye, X.; Si, S.; Zio, E. A failure mechanism consistency test method for accelerated degradation test. Qual. Reliab. Engng. Int. 2021, 37, 464–483. [Google Scholar] [CrossRef]
- Guo, C.; Wan, N.; Ma, W.; Zhang, Y.; Feng, S. A fast method for judging the consistency of the failure mechanism of the constant temperature stress accelerated experiment. Acta. Phys. Sin.-Ch. Ed. 2013, 62, 478–482. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, H.; Yang, Z.; Kang, R.; Yang, Y. Consistency analysis of accelerated degradation mechanism based on gray theory. J. Syst. Eng. Electron. 2014, 25, 322–331. [Google Scholar] [CrossRef]
- Celina, M.; Gillen, K.; Assink, R. Accelerated aging and lifetime prediction: Review of non-Arrhenius behaviour due to two competing processes. Polym. Degrad. Stab. 2005, 90, 395–404. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Y.; Ma, X. Rubber lifetime prediction for ADT data considering non-arrhenius behavior. In Proceedings of the 2017 Annual Reliability and Maintainability Symposium (RAMS), Orlando, FL, USA, 23–26 January 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Liu, Q.; Cui, Z.; Wang, J. Analysis on the Non-Arrhennius life prediction method of rubber. Adv. Mater. Res. 2013, 683, 366–371. [Google Scholar] [CrossRef]
- Rapp, G.; Tireau, J.; Bussiere, P.O.; Chenal, J.M.; Rousset, F.; Chazeau, L.; Gardette, J.L.; Therias, S. Influence of the physical state of a polymer blend on thermal ageing. Polym. Degrad. Stab. 2019, 163, 161–173. [Google Scholar] [CrossRef]
- Guo, X.; Yuan, X.; Liu, G.; Hou, G.; Zhang, Z. Storage Life Prediction of Rubber Products Based on Step Stress Accelerated Aging and Intelligent Algorithm. Polymers 2023, 15, 157. [Google Scholar] [CrossRef]
- Guo, X.; Yuan, X.; Hou, G.; Zhang, Z.; Liu, G. Natural Aging Life Prediction of Rubber Products Using Artificial Bee Colony Algorithm to Identify Acceleration Factor. Polymers 2022, 14, 3439. [Google Scholar] [CrossRef]
- Macdonald, J.R. The Ngai coupling model of relaxation: Generalizations, alternatives, and their use in the analysis of non-Arrhenius conductivity in glassy, fast-ionic materials. J. Appl. Phys. 1998, 84, 812–827. [Google Scholar] [CrossRef]
- Zhao, L.; Liang, A.; Yuan, D.; Hu, Y.; Liu, D.; Huang, J.; He, S.; Shen, B.; Xu, Y.; Liu, X.; et al. Common electronic origin of superconductivity in (Li,Fe)OHFeSe bulk superconductor and single-layer FeSe/SrTiO3 films. Nat. Commun. 2016, 7, 10608. [Google Scholar] [CrossRef] [Green Version]
- Nakane, H.; Watanabe, T.; Nagata, C.; Fujiwara, S.; Yoshizawa, S. Measuring the temperature dependence of resistivity of high purity copper using a solenoid coil SRPM method. IEEE Trans. Instrum. Meas. 1992, 41, 107–110. [Google Scholar] [CrossRef]
- Celina, M.; Graham, A.C.; Gillen, K.T.; Assink, R.A.; Minier, L.M. Thermal Degradation Studies of a Polyurethane Propellant Binder. Rubber Chem. Technol. 2000, 73, 678–693. [Google Scholar] [CrossRef]
- Gao, L.; Chen, X.; Zhang, S.; Gao, H. Mechanical properties of anisotropic conductive film with strain rate and temperature. Mater. Sci. Eng. A 2009, 513–514, 216–221. [Google Scholar] [CrossRef]
- Gregorová, E.; Nečina, V.; Hříbalová, S.; Pabst, W. Temperature dependence of Young’s modulus and damping of partially sintered and dense zirconia ceramics. J. Eur. Ceram. Soc. 2020, 40, 2063–2071. [Google Scholar] [CrossRef]
- Chen, H.; Liu, N. Application of Non-Arrhenius Equations in Interpreting Calcium Carbonate Decomposition Kinetics: Revisited. J. Am. Ceram. Soc. 2010, 93, 548–553. [Google Scholar] [CrossRef]
- Maitra, S.; Bandyopadhyay, N.; Pal, J. Application of Non-Arrhenius Method for Analyzing the Decomposition Kinetics of SrCO3 and BaCO3. J. Am. Ceram. Soc. 2008, 91, 337–341. [Google Scholar] [CrossRef]
- Wang, J.; Ding, J.; Delaire, O.; Arya, G. Atomistic Mechanisms Underlying Non-Arrhenius Ion Transport in Superionic Conductor AgCrSe2. Appl. Energy Mater. 2021, 4, 7157–7167. [Google Scholar] [CrossRef]
- Campbell, F.J. Temperature dependence of hydrolysis of polyimide wire insulation. IEEE Trans. Electron. Insul. 1985, EI-20, 111–116. [Google Scholar] [CrossRef]
- Li, J. Identification Method Study for Degradation Mechanism Consistency of Springs In Accelerated Storage Testing. Master’s Thesis, National University of Defense Technology, Changsha, China, 2018. [Google Scholar]
- Tang, Y. Statistical Mechanics and Its Application in Physical Chemistry; China Science Publishing Media Ltd.: Beijing, China, 2010; pp. 6–7. [Google Scholar]
- Wang, Z. Storage Reliability Degradation Test and Evaluation Technologe of Aerospace Electromagnetic Relay. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2013. [Google Scholar]
- Lin, Y. Reliability Assessment Method of Relay Subsystem Based on Performance Degradation. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2020. [Google Scholar]
- Sun, B.; Fan, X.; Yuan, C.; Qian, C.; Zhang, G. A degradation model of aluminum electrolytic capacitors for LED drivers. In Proceedings of the 2015 16th International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems, Budapest, Hungary, 19–22 April 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Abdennadher, K.; Venet, P.; Rojat, G.; Rétif, J.; Rosset, C. A Real-Time Predictive-Maintenance System of Aluminum Electrolytic Capacitors Used in Uninterrupted Power Supplies. IEEE Trans. Ind. Appl. 2010, 46, 1644–1652. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Ye, X.; Zhai, G. Degradation model and maintenance strategy of the electrolytic capacitors for electronics applications. In Proceedings of the 22011 Prognostics and System Health Managment Confernece, Shenzhen, China, 24–25 May 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Sun, B.; Yan, M.; Feng, Q.; Li, Y.; Ren, Y.; Zhou, K.; Zhang, W. Gamma Degradation Process and Accelerated Model Combined Reliability Analysis Method for Rubber O-Rings. IEEE Access 2018, 6, 10581–10590. [Google Scholar] [CrossRef]
- Patel, M.; Skinner, A. Thermal ageing studies on room-temperature vulcanised polysiloxane rubbers. Polym. Degrad. Stab. 2001, 73, 399–402. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, B.; Bai, H.; Wang, W. Evolution of hidden localized flow during glass-to-liquid transition in metallic glass. Nat. Commun. 2014, 5, 5823. [Google Scholar] [CrossRef] [Green Version]

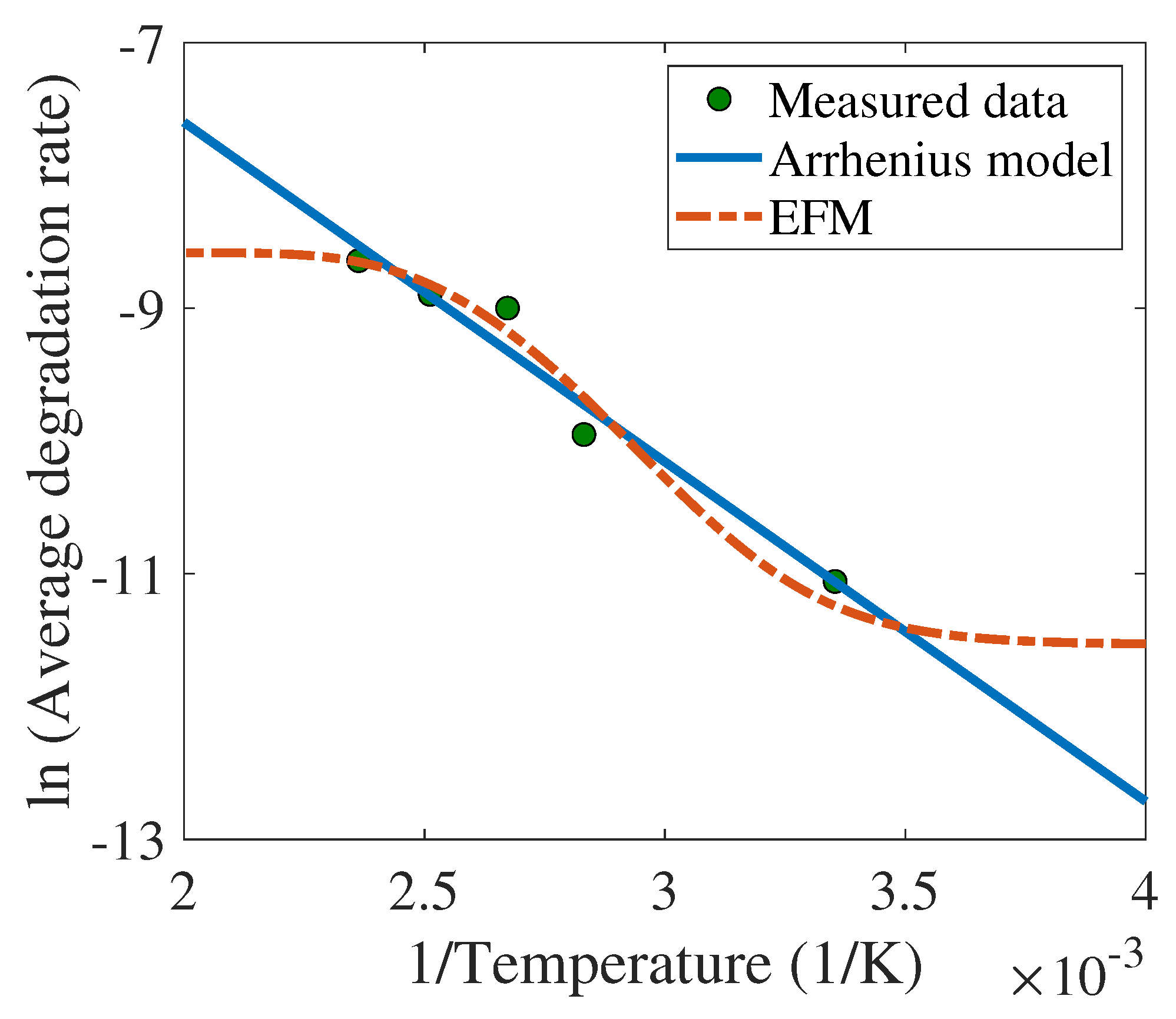
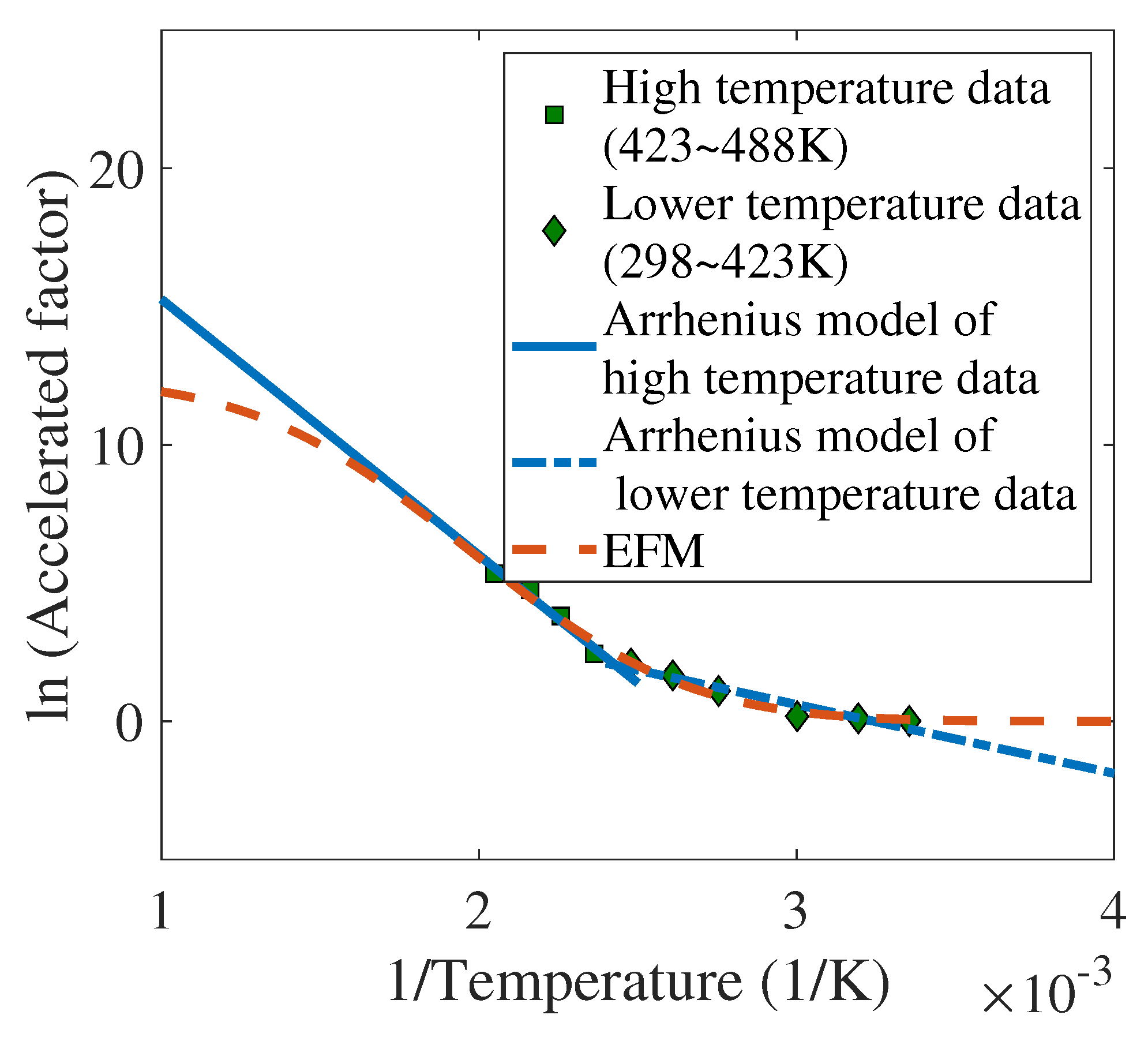
| Accelerated Model | Parameters | ||||
|---|---|---|---|---|---|
| Arrhenius model | A | - | - | - | |
| - | - | - | |||
| - | - | - | |||
| - | - | - | |||
| - | - | - | |||
| - | - | - | |||
| - | - | - | |||
| EFM | - | - | - | ||
| - | - | - | |||
| - | - | - | |||
| b | - | - | - | ||
| - | - | - | |||
| - | - | - | |||
| - | - | - | |||
| - | - | - | |||
| - | - | - | |||
| Accelerated Model | Outcome | ||||
|---|---|---|---|---|---|
| Arrhenius model | Reject | ||||
| EFM | Retain |
| Temperature | Time | Force Loss | Degradation Rate | Arrhenius | EFM |
|---|---|---|---|---|---|
| (K) | (h) | (N) | (N/h) | ||
| 3456 | |||||
| 3216 | |||||
| 3456 | |||||
| 3456 | |||||
| 3456 |
| Model | BIC | ||
|---|---|---|---|
| Arrhenius | −91.11 | ||
| EFM | −91.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, J.; Fu, R.; Liang, H.; Lin, Y. A Non-Arrhenius Model for Mechanism Consistency Checking in Accelerated Degradation Tests. Actuators 2023, 12, 319. https://doi.org/10.3390/act12080319
You J, Fu R, Liang H, Lin Y. A Non-Arrhenius Model for Mechanism Consistency Checking in Accelerated Degradation Tests. Actuators. 2023; 12(8):319. https://doi.org/10.3390/act12080319
Chicago/Turabian StyleYou, Jiaxin, Rao Fu, Huimin Liang, and Yigang Lin. 2023. "A Non-Arrhenius Model for Mechanism Consistency Checking in Accelerated Degradation Tests" Actuators 12, no. 8: 319. https://doi.org/10.3390/act12080319
APA StyleYou, J., Fu, R., Liang, H., & Lin, Y. (2023). A Non-Arrhenius Model for Mechanism Consistency Checking in Accelerated Degradation Tests. Actuators, 12(8), 319. https://doi.org/10.3390/act12080319







