Mechanism and Experimental Investigation of Vibration Reduction for Container Cranes Based on Particle Damping Technology
Abstract
:1. Introduction
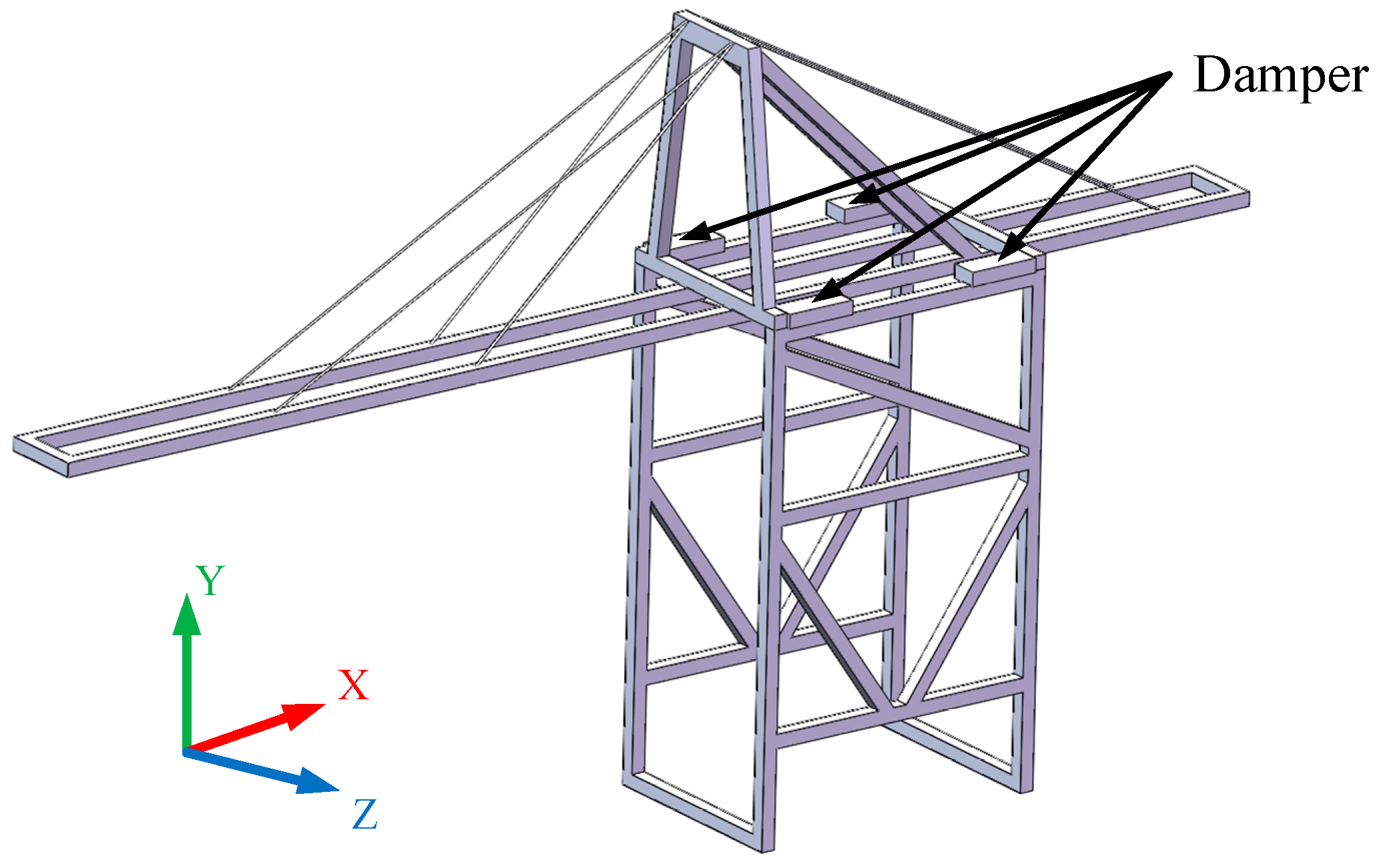
2. Similar Model of Crane
3. Theoretical Analysis
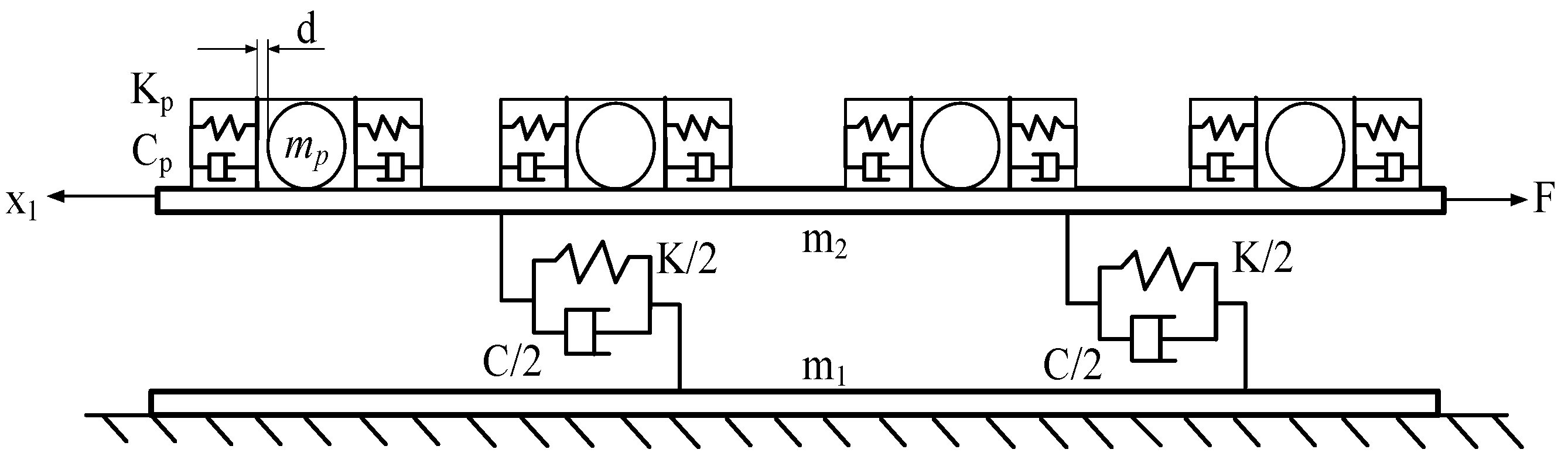
3.1. Design of Simplified Model and Calculation of Stiffness Equation
- (1)
- The gap of the damper cavity before and after equivalent simplification is equal;
- (2)
- The total mass of multiple particles before equivalent simplification is equal to the mass of individual particles after equivalent simplification;
- (3)
- The particle damper before the equivalent simplification is a cuboid, the single particle damper after the equivalent simplification is a cylinder, and the diameter of the cylinder is equal to the diameter of the single particle after the equivalent simplification;
- (4)
- The contact between the particle and the cavity wall is also expressed in terms of stiffness and damping.
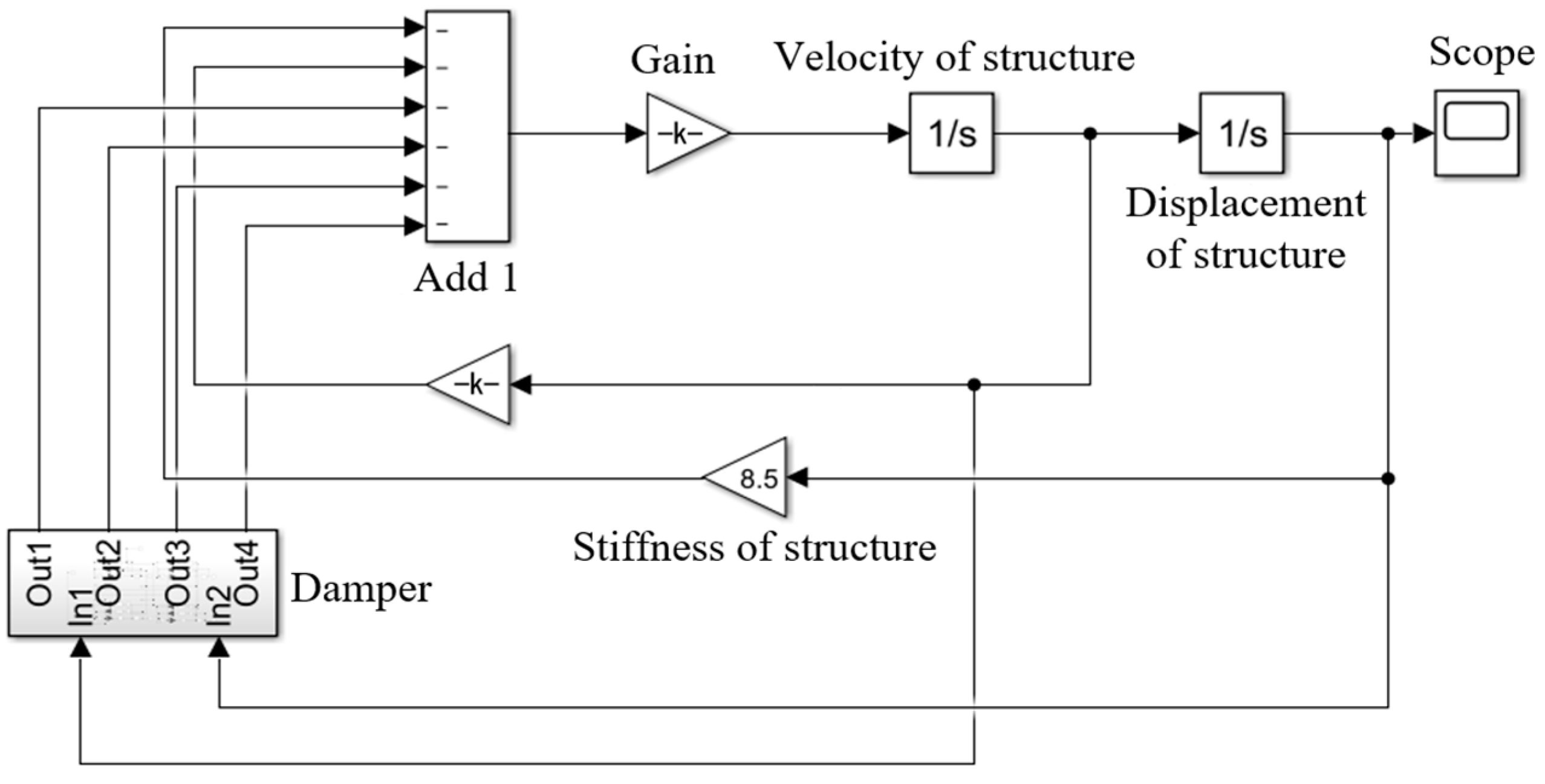
3.2. Simulink Modeling and Solution
- (1)
- The weight of the crane model is obtained by weighing;
- (2)
- A certain tension is applied to the upper part of the model, and the upper part of the model is offset under the action of the tension. The stiffness of the bracket structure is calculated by the offset and the indicator of the tension device;
- (3)
- The tension is released, the free vibration attenuation signal of the model is detected by the acceleration sensor, and the damping ratio of the model is identified by the envelope of the free vibration attenuation signal. The experiment layout is shown in Figure 4.
4. Experimental
4.1. Experimental Platform
4.2. Description of Experiment Process
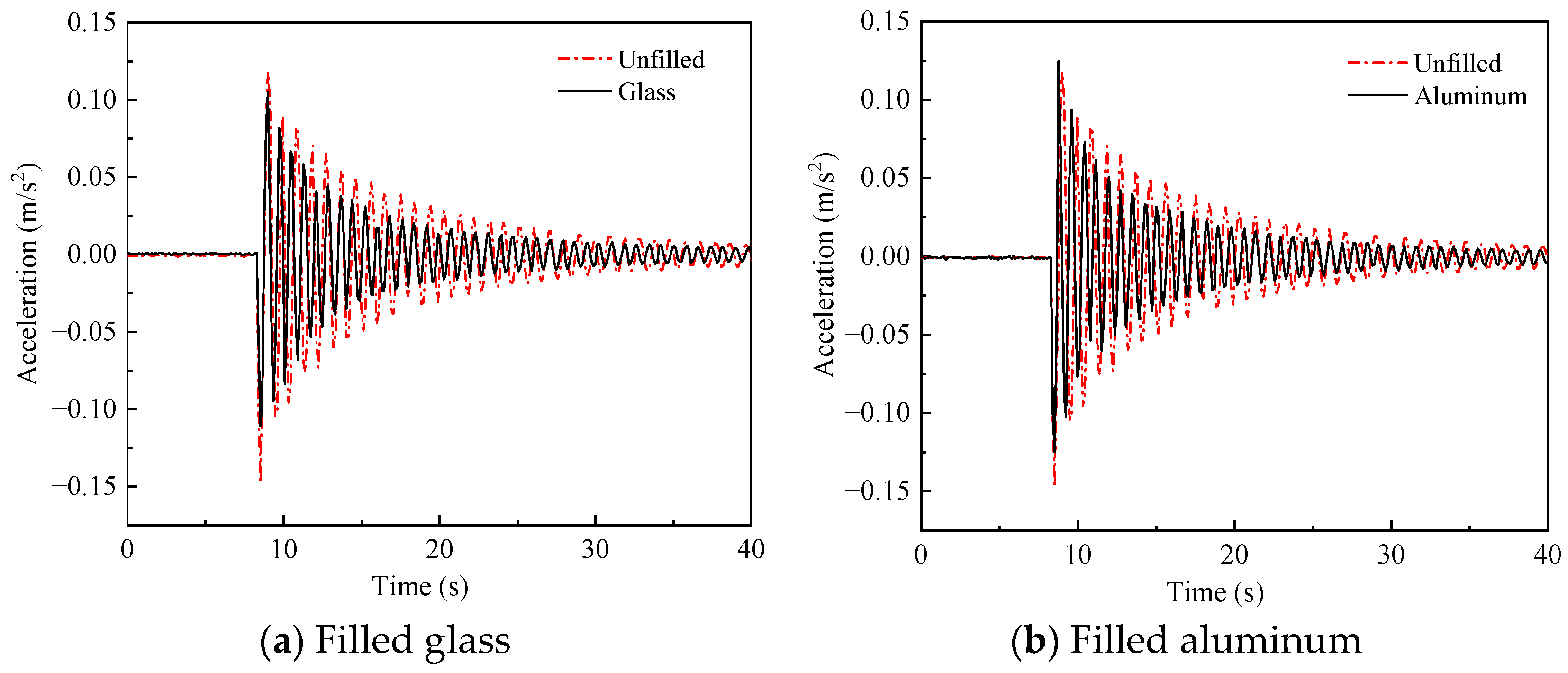
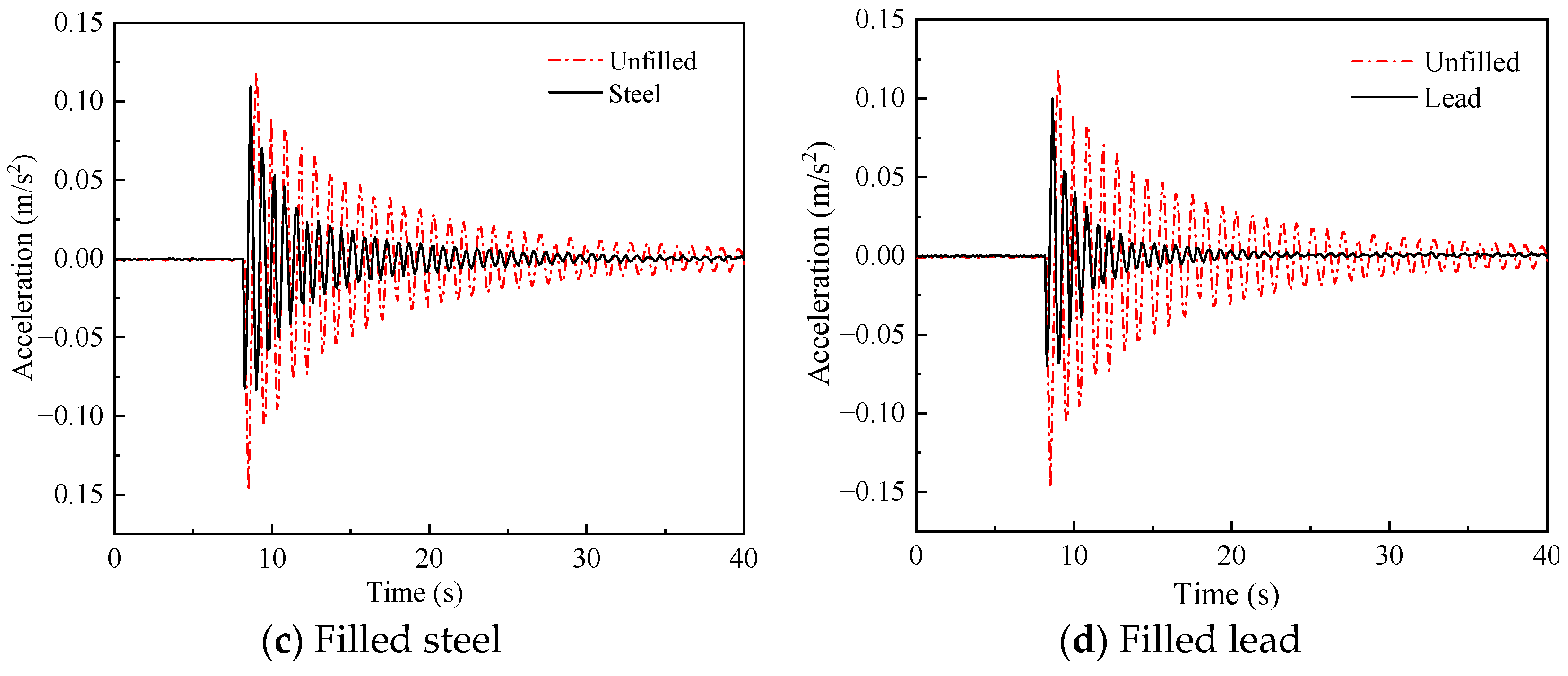
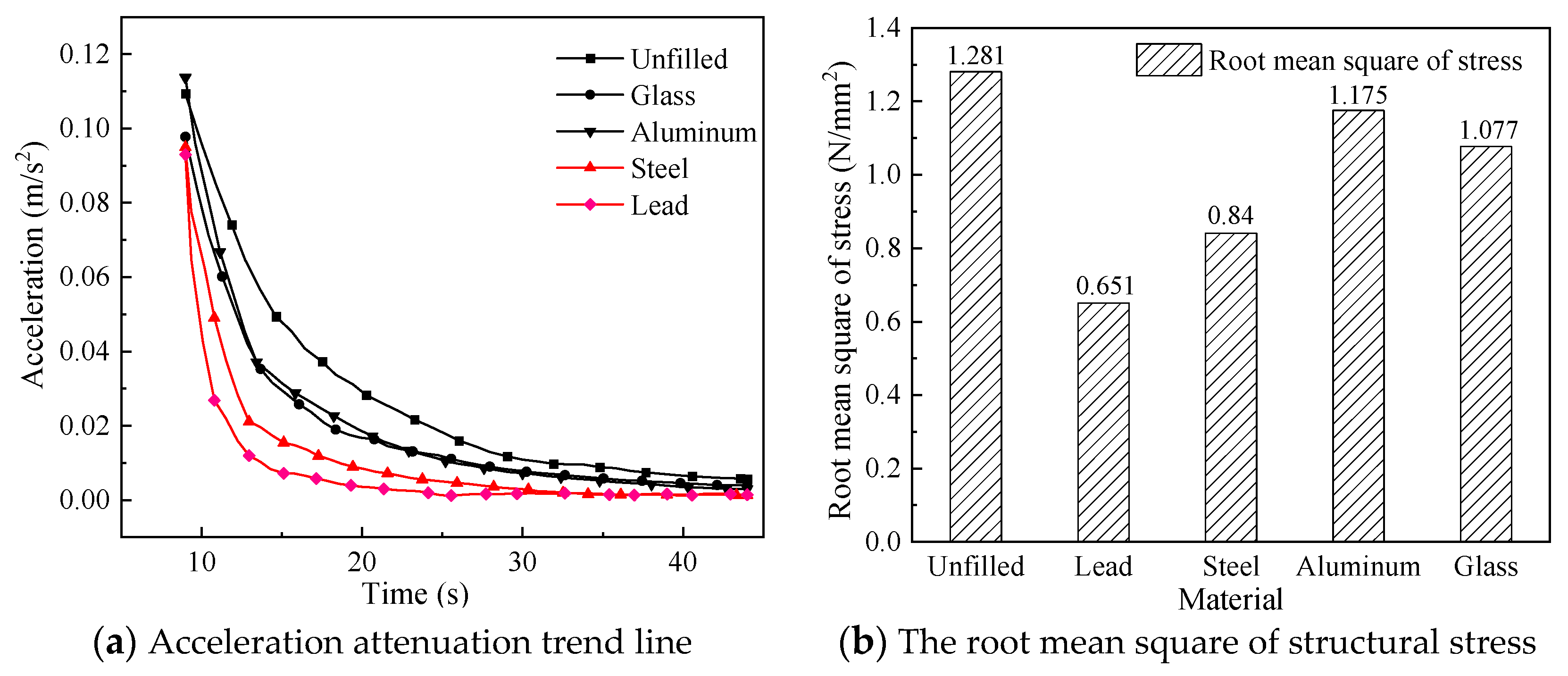
4.3. Effect of Different Materials on Vibration Suppression Characteristics
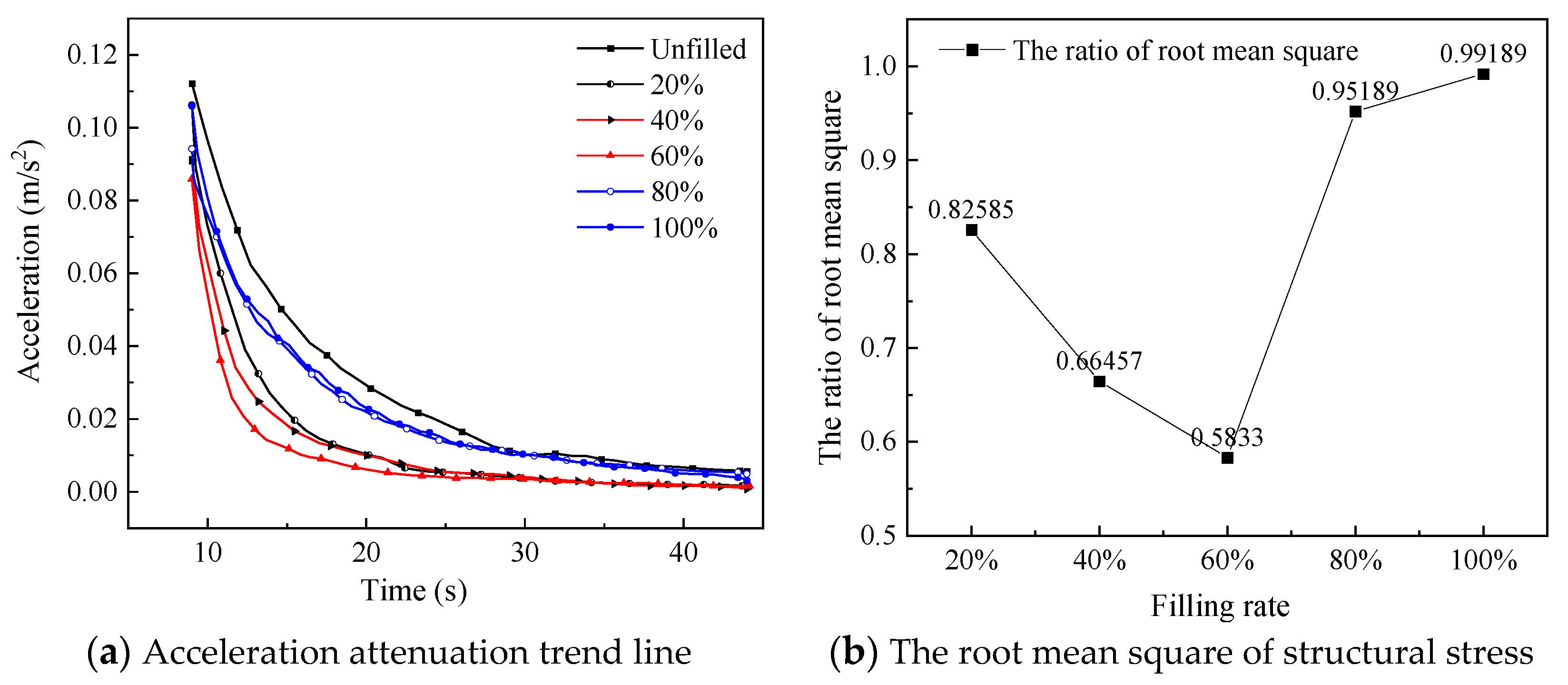
4.4. Effect of Different Filling Rates on Vibration Suppression Characteristics
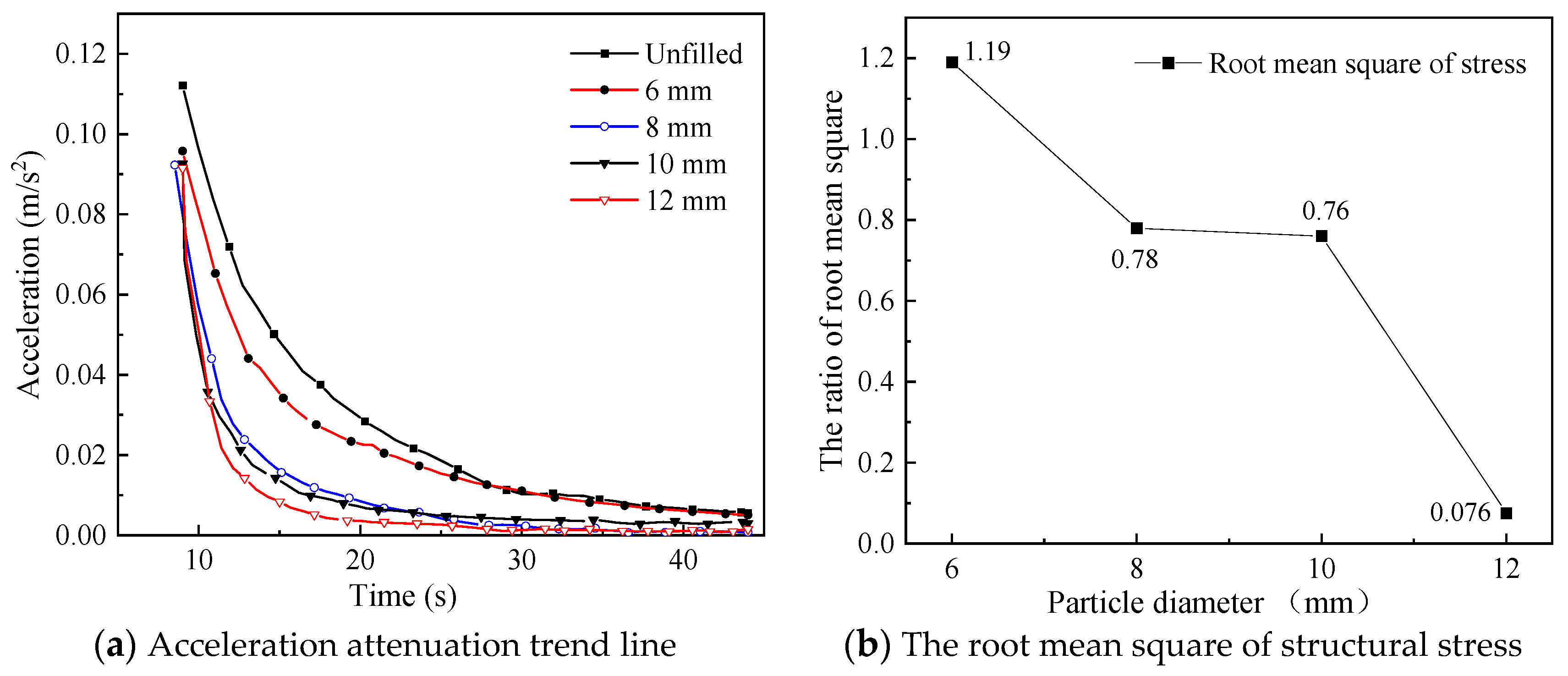
4.5. Effect of Different Particle Diameters on Vibration Suppression Characteristics
4.6. Effect of the Installation Position of the Damper on Vibration Suppression Characteristics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hebiba, A.M.; Bouferguene, A.; Moon, S. Automated Stability Analysis for Selection of Tower Crane and Location. J. Constr. Eng. Manag. 2022, 148, 04022127. [Google Scholar] [CrossRef]
- Zhang, W.; Xue, N.N.; Zhang, J.R. Identification of Critical Causal Factors and Paths of Tower-Crane Accidents in China through System Thinking and Complex Networks. J. Constr. Eng. Manag. 2021, 147, 04021174. [Google Scholar] [CrossRef]
- Tran, Q.H.; Huh, J.; Doan, N.S. Fragility Assessment of a Container Crane under Seismic Excitation Considering Uplift and Derailment Behavior. Appl. Sci. 2019, 9, 4660. [Google Scholar] [CrossRef]
- Xing, X.Y.; Liu, J.K. State-estimator-based robust vibration control of crane bridge system with trolley via PDE model. Commun. Nonlinear Sci. 2021, 99, 105799. [Google Scholar] [CrossRef]
- Al-Fadhli, A.; Khorshid, E. Payload oscillation control of tower crane using smooth command input. J. Vib. Control 2021, 29, 902–915. [Google Scholar] [CrossRef]
- Zhao, X.S.; Huang, J. Distributed-mass payload dynamics and control of dual cranes undergoing planar motions. Mech. Syst. Signal Pr. 2019, 126, 636–648. [Google Scholar] [CrossRef]
- Meyer, N.; Seifried, R. Damping prediction of particle dampers for structures under forced vibration using effective fields. Granul. Matter. 2021, 23, 64. [Google Scholar] [CrossRef]
- Rakhio, A.; Ido, Y.; Iwamoto, Y. Experimental and Numerical Analysis of Torque Properties of Rotary Elastomer Particle Damper considering the Effect of Gap and No Gap between Rotor and Body of the Damper. Shock. Vib. 2022, 2021, 7724156. [Google Scholar] [CrossRef]
- He, H.X.; Wang, B.S.; Yan, W.M. Mechanical Model and Optimization Analysis of Multiple Unidirectional Single-Particle Damper. J. Eng. Mech. 2021, 147, 04021040. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, Z.X.; Masri, S.M. Particle impact dampers: Past, present, and future. Struct. Control Health Monit. 2018, 25, 2058. [Google Scholar] [CrossRef]
- Yan, W.M.; Xu, W.B.; Wang, J. Experimental research on the effects of a tuned particle damper on a viaduct system under seismic loads. J. Bridge Eng. 2014, 19, 04013004. [Google Scholar] [CrossRef]
- Chockalingam, S.; Natarajan, U.; Cyril, A.G. Damping investigation in boring bar using hybrid copper-zinc particles. J. Vib. Control 2017, 23, 2128–2134. [Google Scholar] [CrossRef]
- Hassui, A.; Suyama, D.I.; Magri, A. Reduction of internal turning surface roughness by using particle damping aided by airflow. Int. J. Adv. Manuf. Technol. 2019, 106, 125–131. [Google Scholar]
- Meyer, N.; Schwartz, C.; Morlock, M. Systematic design of particle dampers for horizontal vibrations with application to a lightweight manipulator. J. Sound. Vib. 2021, 510, 116319. [Google Scholar] [CrossRef]
- Wang, J.; Juan, M.X.; Yang, S.G. Experimental Investigation of the Vibration Reduction of the Pipeline System with a Particle Impact Damper under Random Excitation. Appl. Sci. 2023, 13, 618. [Google Scholar] [CrossRef]
- Papaluo, A.; Strepelias, E.; Roubien, D. Seismic protection of monuments using particle dampers in multi-drum columns. Soil. Dyn. Earthq. Eng. 2015, 77, 360–368. [Google Scholar] [CrossRef]
- Li, Z.; Ye, F.P.; Wu, S.Y. Design and Experimental Verification of a 1/20 Scale Model of Quayside Container Crane Using Distortion Theory. Shock. Vib. 2019, 2019, 5893948. [Google Scholar] [CrossRef]
- Lu, Z.; Liao, Y.; Huang, Z.K. Stochastic response control of particle dampers under random seismic excitation. J. Sound. Vib. 2020, 481, 115439. [Google Scholar] [CrossRef]
- Masri, S.F.; Ibrahim, A.M. Response of the Impact Damper to Stationary Random Excitation. J. Acoust. Soc. Am. 1973, 53, 200–211. [Google Scholar] [CrossRef]








| Similarity Parameter | Similarity Ratio | Similarity Parameter | Similarity Ratio |
|---|---|---|---|
| Geometric dimension | 1/80 | Frequency | |
| Density | 1 | Time | |
| Mass | 1/803 | Elastic modulus | 1 |
| Displacement | 1/80 | Section inertia radius | 1/80 |
| Parameter | Symbol | Value |
|---|---|---|
| Mass of bracket structure | m1 | 2.5 kg |
| Mass of beam structure | m2 | 3.4 kg |
| Mass of sphere | mp | 0.135 kg |
| Structural stiffness of steel frame | K | 8.5 N/mm |
| Damping ratio of steel frame | ξ | 0.178 |
| Damping value of steel frame | C | 1.94 N/(mm/s) |
| External load | F | 10 N |
| Equivalent spring stiffness of the collision between the sphere and the cavity wall | Kp | 108,570 N/mm |
| The damping ratio of the sphere | ξp | 0.375 |
| Equivalent spring damping value of the collision between the sphere and the cavity wall | Cp | 4.54 N/(mm/s) |
| Equivalent displacement of sphere | xp | - |
| Distance between sphere and cavity wall | d | 3 mm |
| Part Name | Material | Density (kg/m³) | Young’s Modulus (GPa) | Poisson’s Ratio | Dimension (mm) |
|---|---|---|---|---|---|
| Crane structure | Al-Mg-Si | 2880 | 72 | 0.25 | h2 |
| Damper chamber | SS304 | 7930 | 11 | 0.29 | 40 × 100 × 20 |
| Steel bead | 45Cr | 7850 | 209 | 0.3 | r6/r5/r4/r3 |
| Aluminum bead | Al | 2700 | 10.9 | 0.32 | r5 |
| Lead bead | Pb | 11,343 | 70 | 0.42 | r5 |
| Glass bead | SiO2 | 2500 | 68 | 0.215 | r5 |
| Experiment Condition | Installation Position | Material | Filling Rate | Particle Size | Mass Ratio |
|---|---|---|---|---|---|
| 1 | Proximal end | Lead | 50% | 10 mm | 7.9% |
| Steel | 5.6% | ||||
| Aluminum | 1.9% | ||||
| Glass | 1.7% | ||||
| 2 | Proximal end | Steel | 20%~100% | 10 mm | 2.3%~11.2% |
| 3 | Proximal end | Steel | 50% | 6~12 mm | 1.2%~9.7% |
| 4 | Proximal end | Steel | 50% | 10 mm | 5.6% |
| Distal end | 5.6% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, F.; Xue, X.; Jiang, W.; Yin, X. Mechanism and Experimental Investigation of Vibration Reduction for Container Cranes Based on Particle Damping Technology. Actuators 2024, 13, 11. https://doi.org/10.3390/act13010011
Ye F, Xue X, Jiang W, Yin X. Mechanism and Experimental Investigation of Vibration Reduction for Container Cranes Based on Particle Damping Technology. Actuators. 2024; 13(1):11. https://doi.org/10.3390/act13010011
Chicago/Turabian StyleYe, Fangping, Xinyi Xue, Weijie Jiang, and Xiyan Yin. 2024. "Mechanism and Experimental Investigation of Vibration Reduction for Container Cranes Based on Particle Damping Technology" Actuators 13, no. 1: 11. https://doi.org/10.3390/act13010011
APA StyleYe, F., Xue, X., Jiang, W., & Yin, X. (2024). Mechanism and Experimental Investigation of Vibration Reduction for Container Cranes Based on Particle Damping Technology. Actuators, 13(1), 11. https://doi.org/10.3390/act13010011





