Research on Some Control Algorithms to Compensate for the Negative Effects of Model Uncertainty Parameters, External Interference, and Wheeled Slip for Mobile Robot
Abstract
:1. Introduction
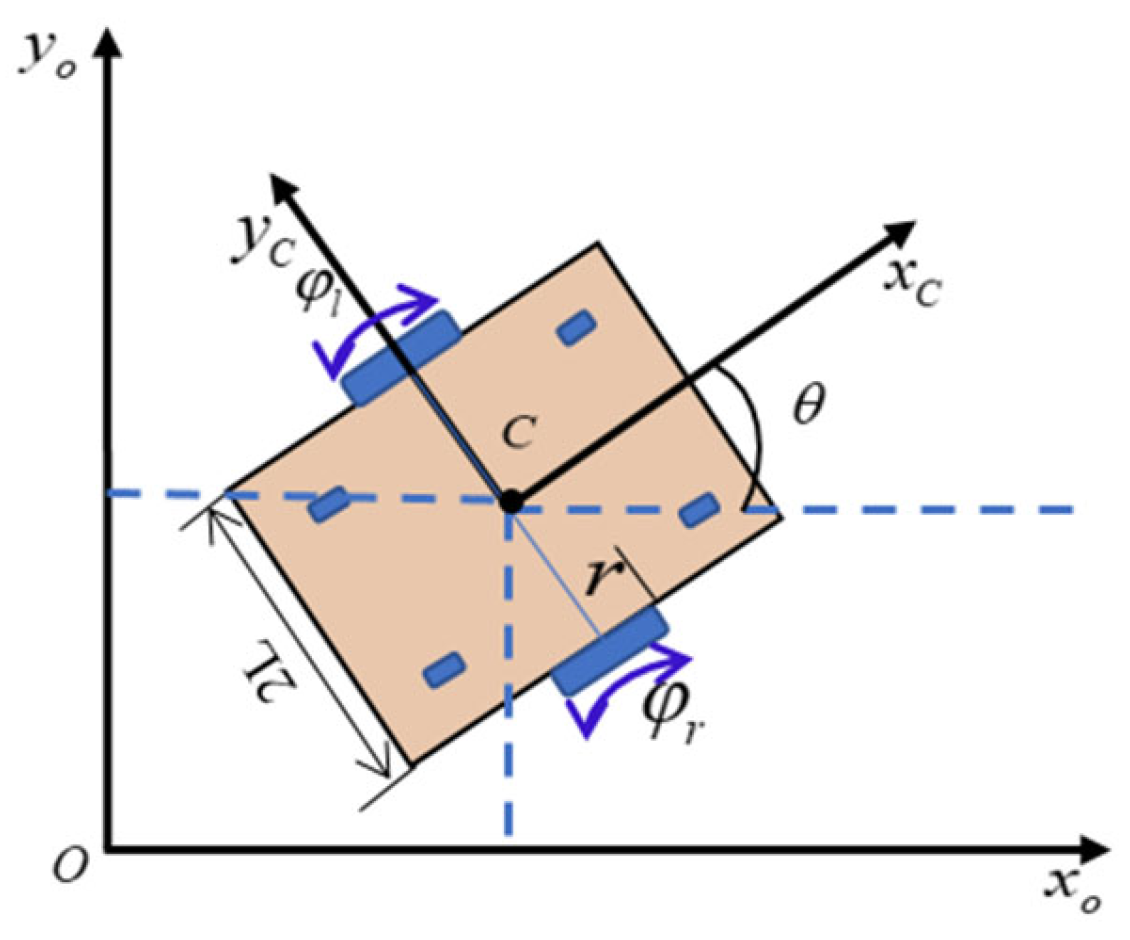
2. The Kinematics and Dynamic Model of Non-Holonomic Mobile Robots
2.1. The Kinematics of the Non-Holonomic Wheeled Mobile Robot (WMR)
2.2. Dynamics of Non-Holonomic Wheeled Mobile Robots (WMR)
- -
- Vehicle mass and moment of inertia are uncertain, so the inertia matrix is considered uncertain.
- -
- When the vehicle moves on different floors, especially slippery and wet floors, it is easy for the wheel to slip, affecting the road trajectory, or when the vehicle moves at a fast speed into curves, it can easily cause wheel slippage. The friction between the wheel and the floor will change, causing interference that greatly affects the position and direction of the vehicle.
- -
- In addition, there still exists noise due to model errors and measurement noise. These are also issues considered when designing the control for WMRs. In this study, we use the kinematic and dynamic model of a mobile robot when there is a side slip as the control object so that this WMR follows a given trajectory and can compensate for the side slip using DSC, AFDSC, and AFNNDSC.
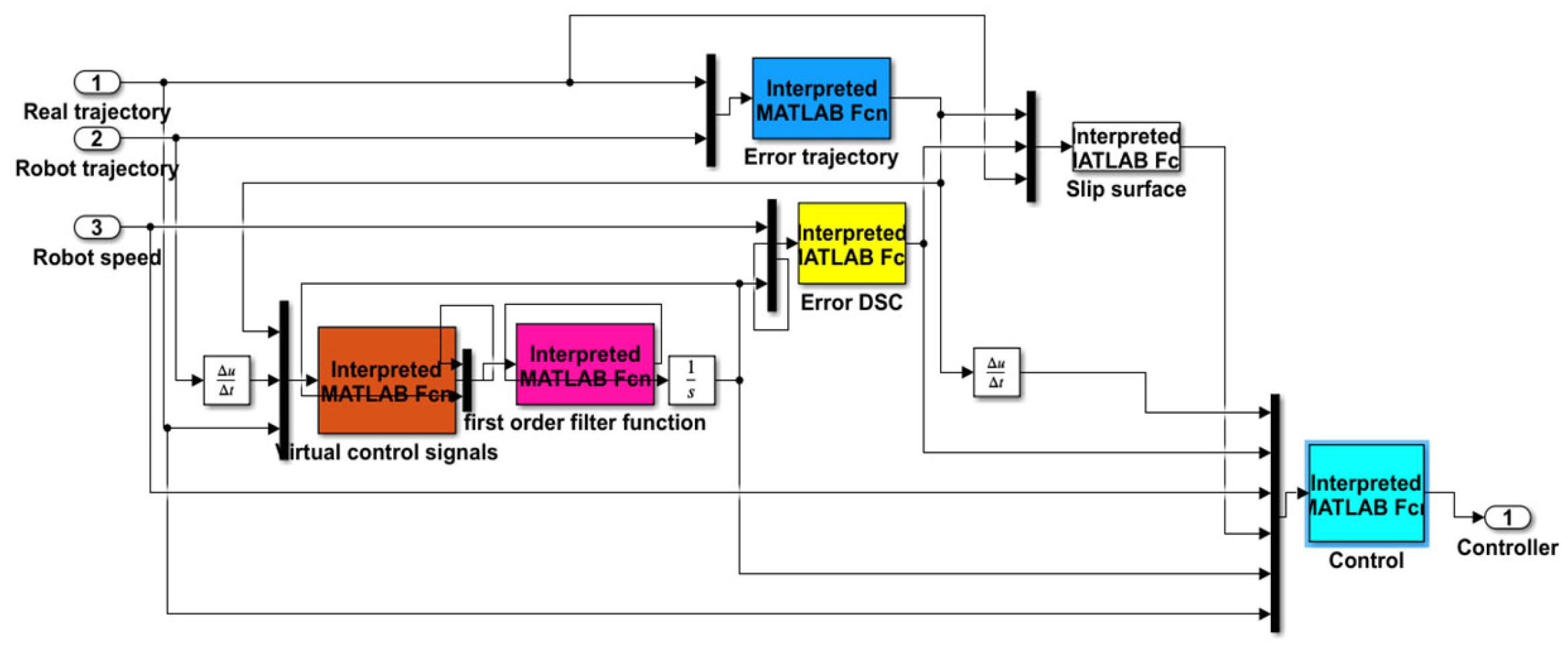
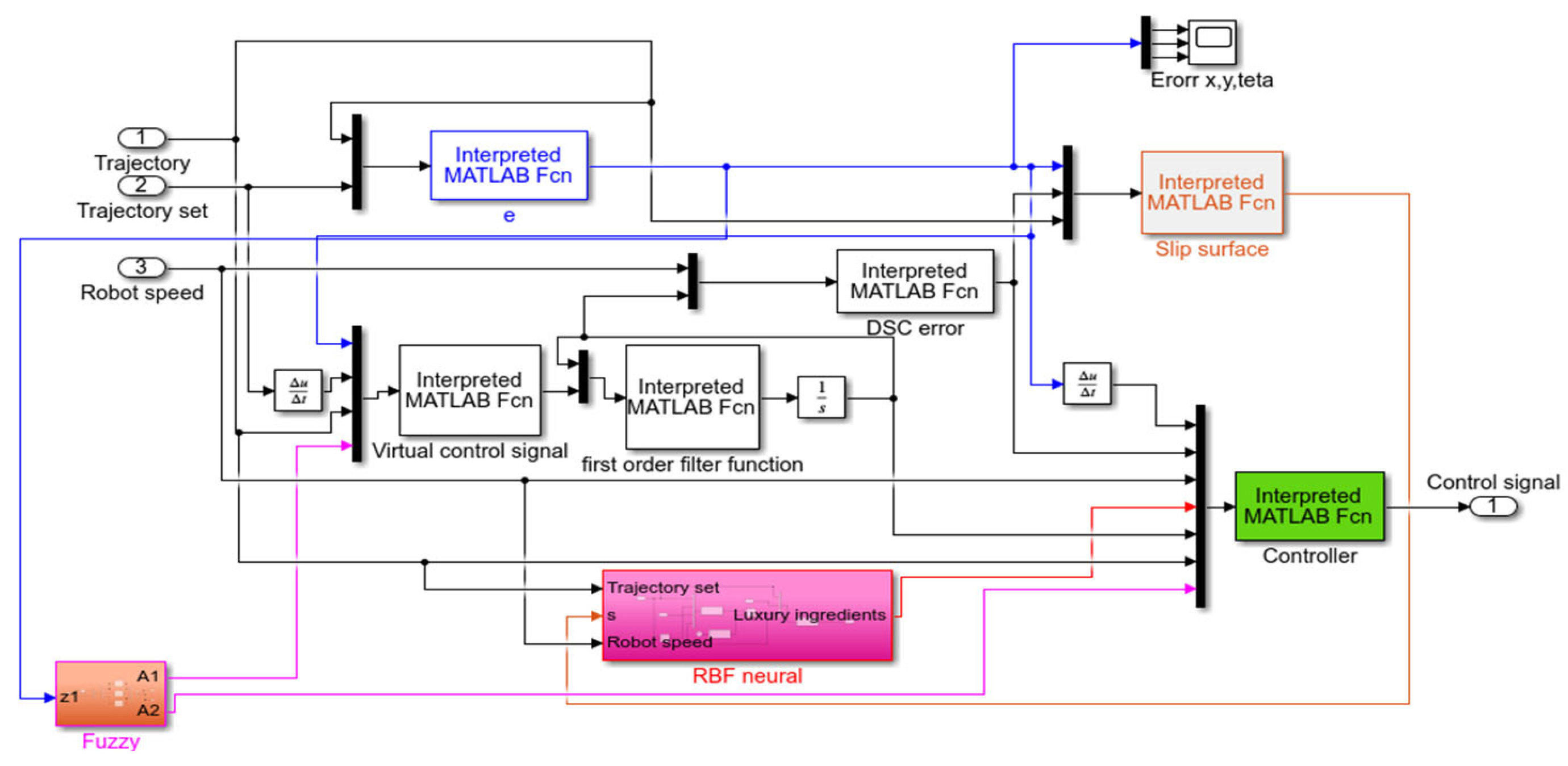
3. Design the Adaptive Fuzzy Neural Network Dynamic Surface Controller (AFNNDSC)
3.1. Dynamic Sliding Control Algorithm
3.1.1. Building a Dynamic Sliding Surface Trajectory Control Algorithm for WMRs
3.1.2. Simulation to Verify the Algorithm
- a.
- In case there is no interference
- b.
- In case of interference
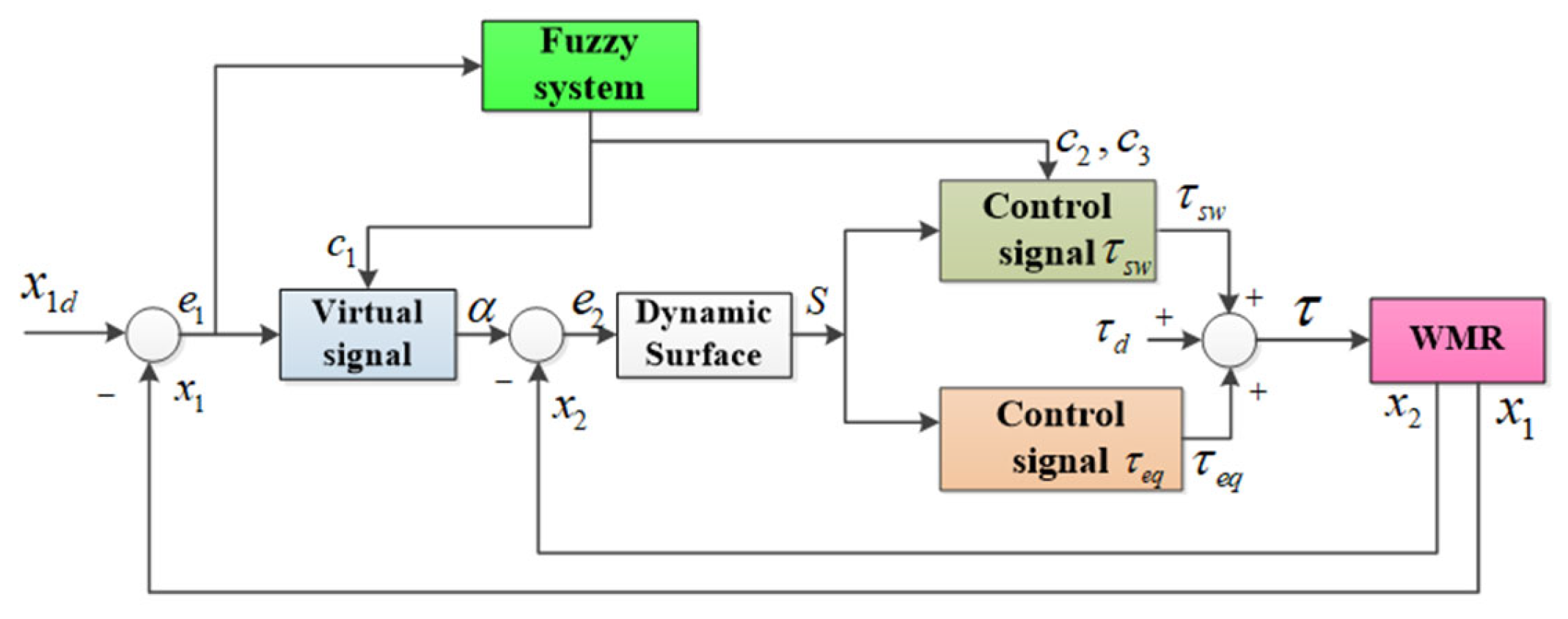
3.2. Adaptive Fuzzy Logic Dynamic Surface Controller for (AFDSC)
3.2.1. The Adaptive Fuzzy Logic Dynamic Surface Controller
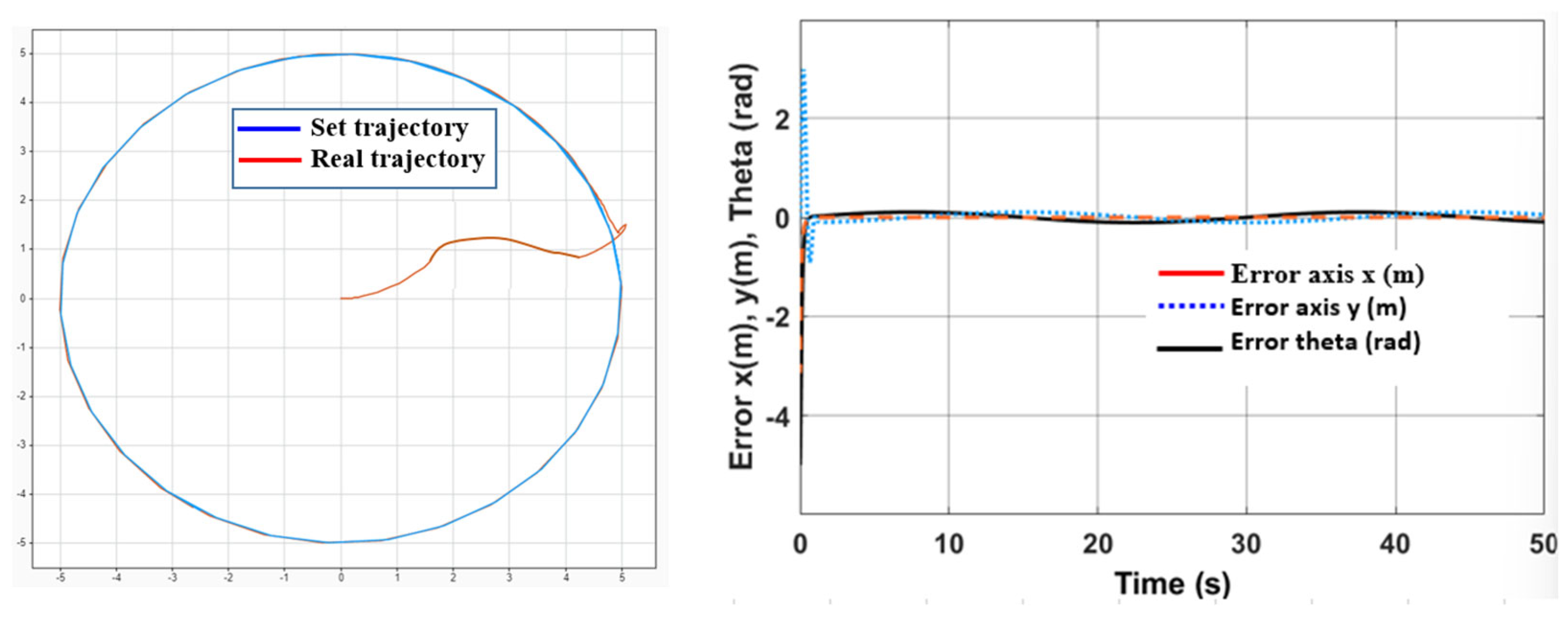
3.2.2. Simulation to Verify the Controller AFDSC
3.3. Adaptive Fuzzy Neural Network Dynamic Surface Controller for (AFNNDSC)
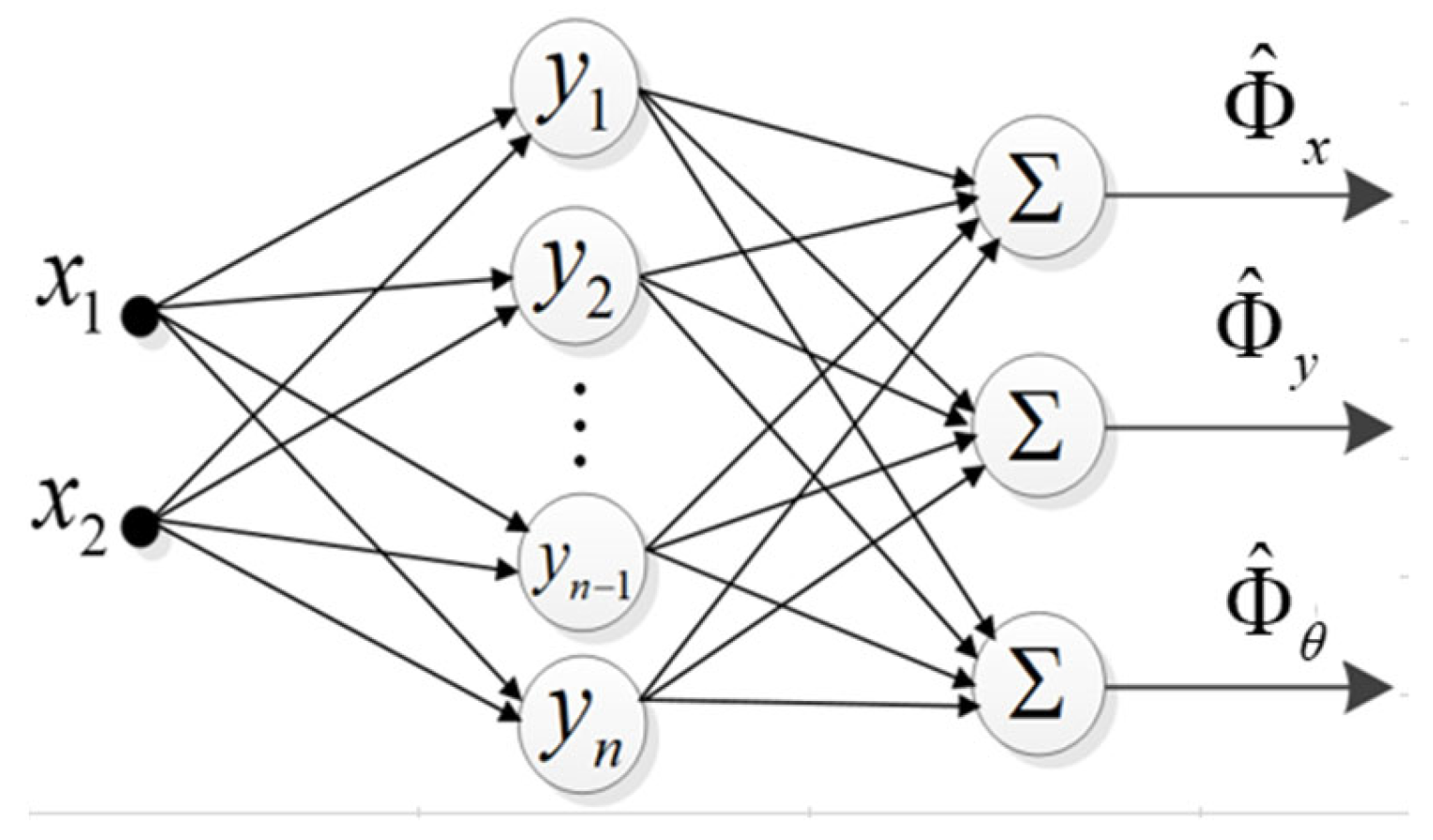
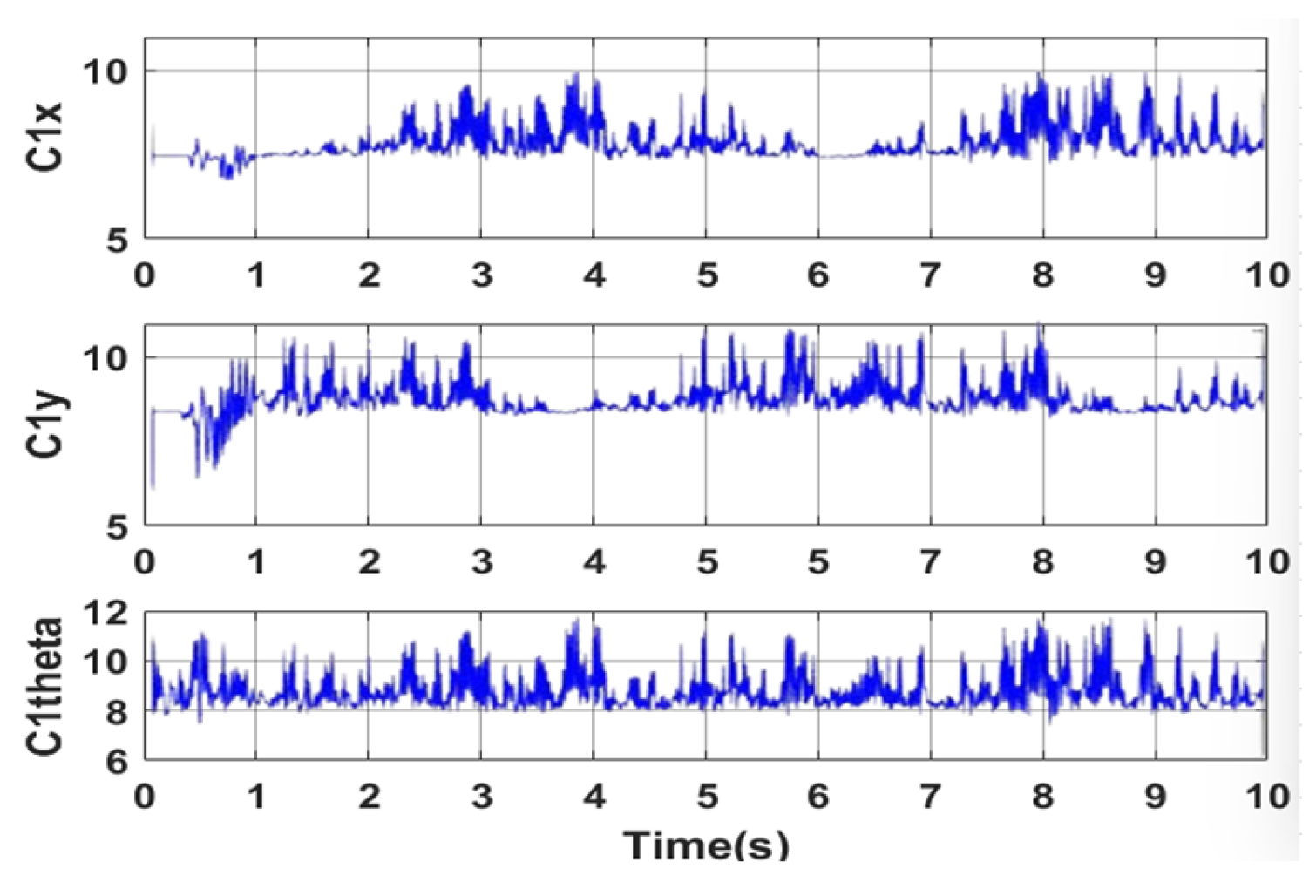
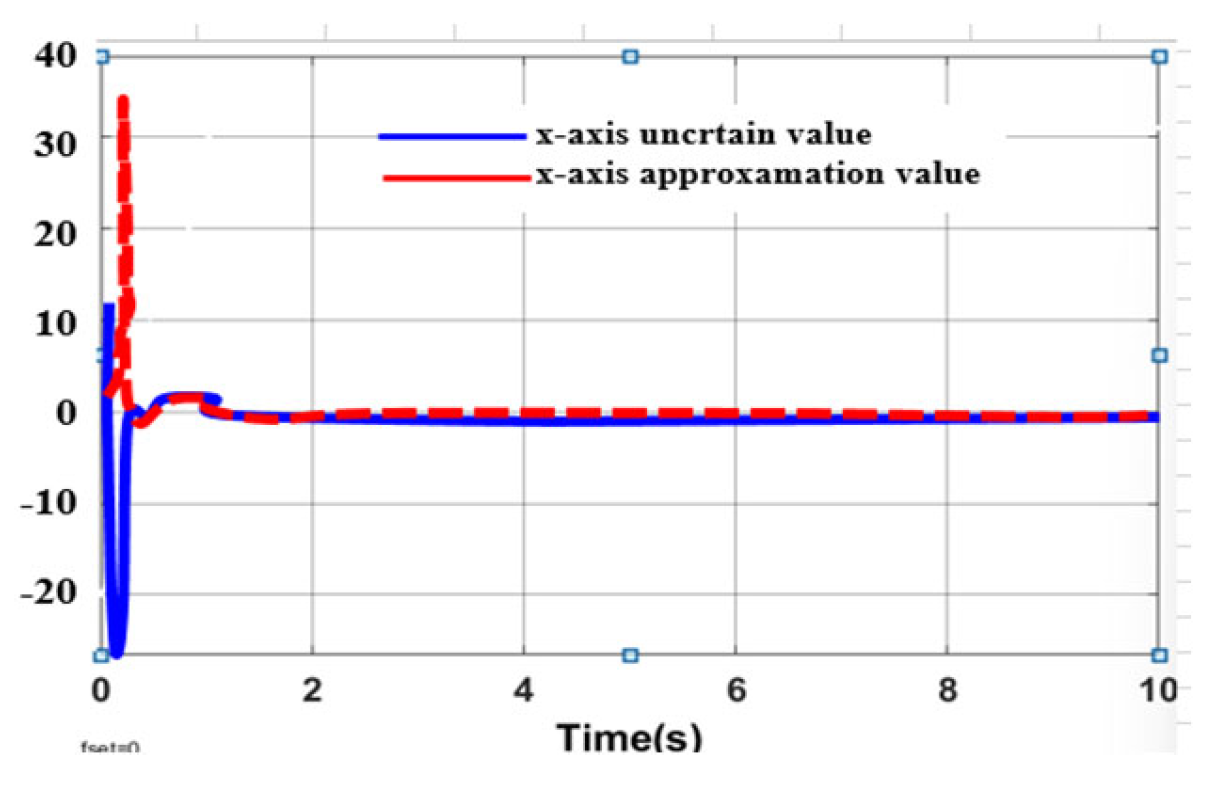
3.3.1. Approximation of WMR Model Uncertainty Component Using Radial Neural Network
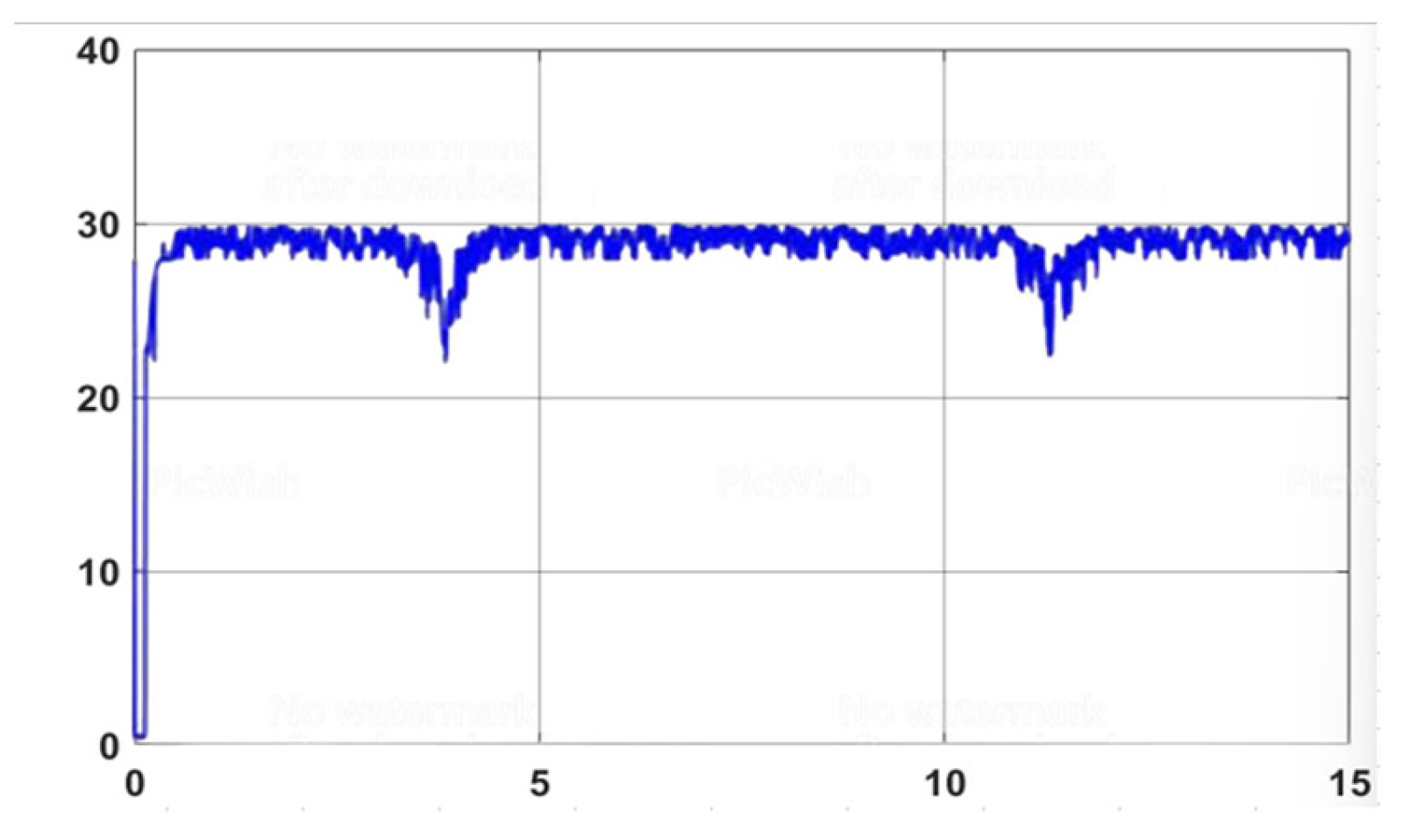
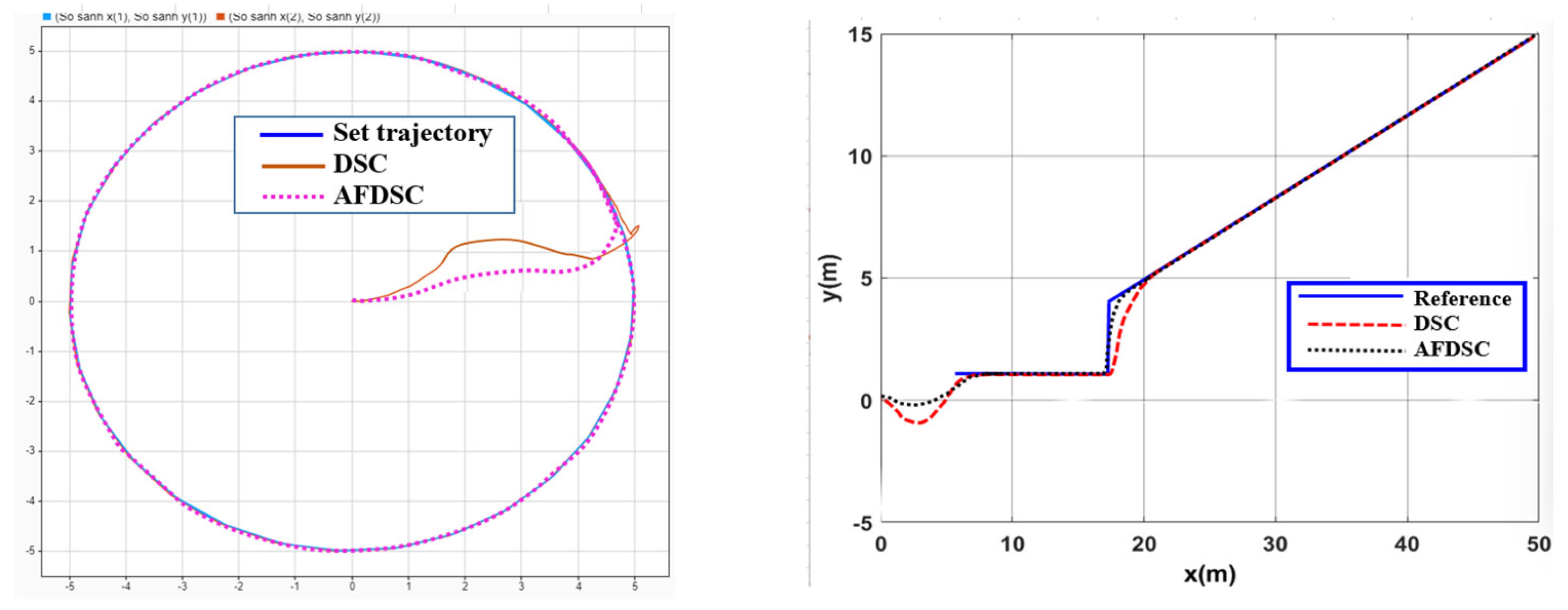
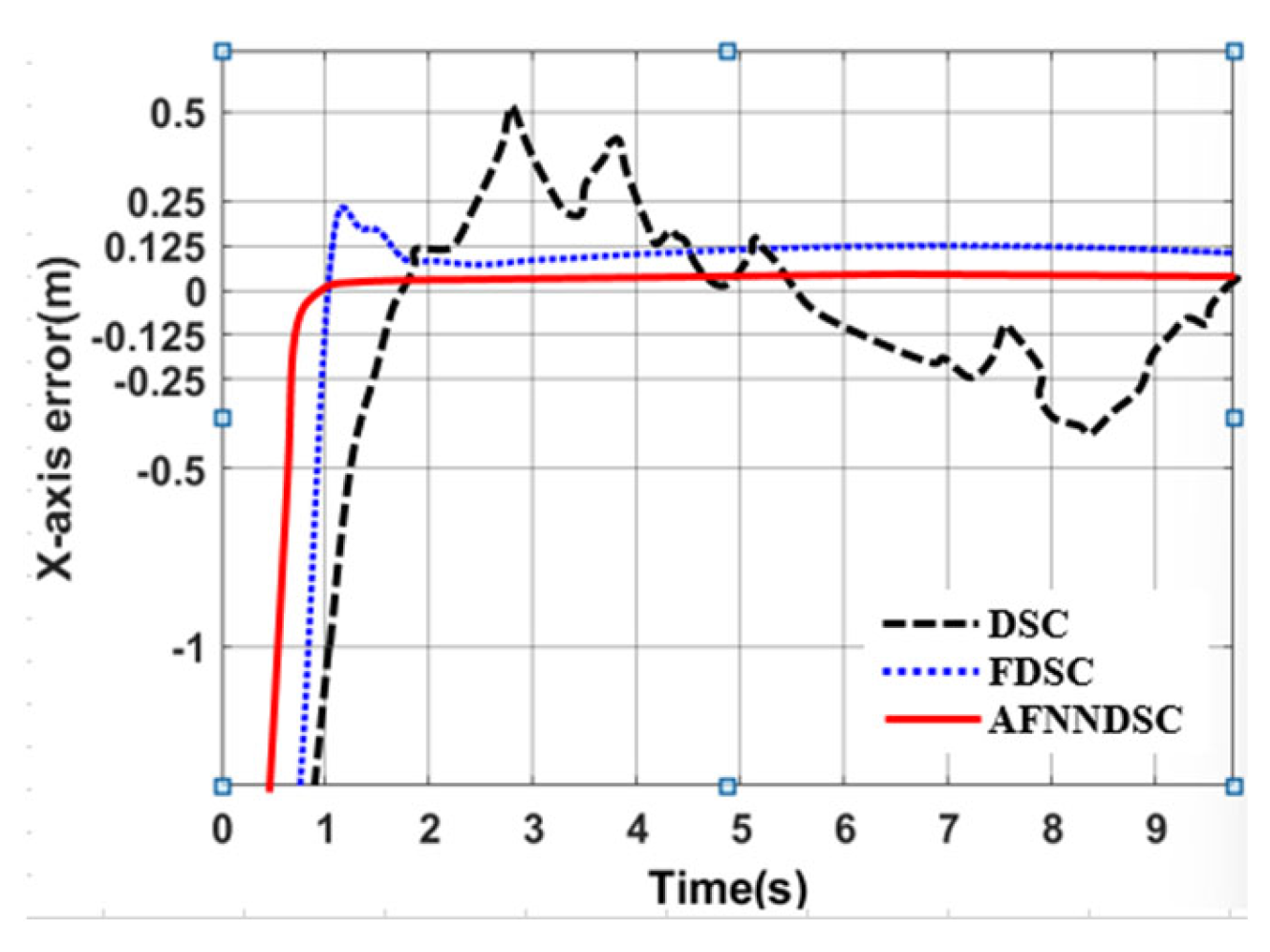
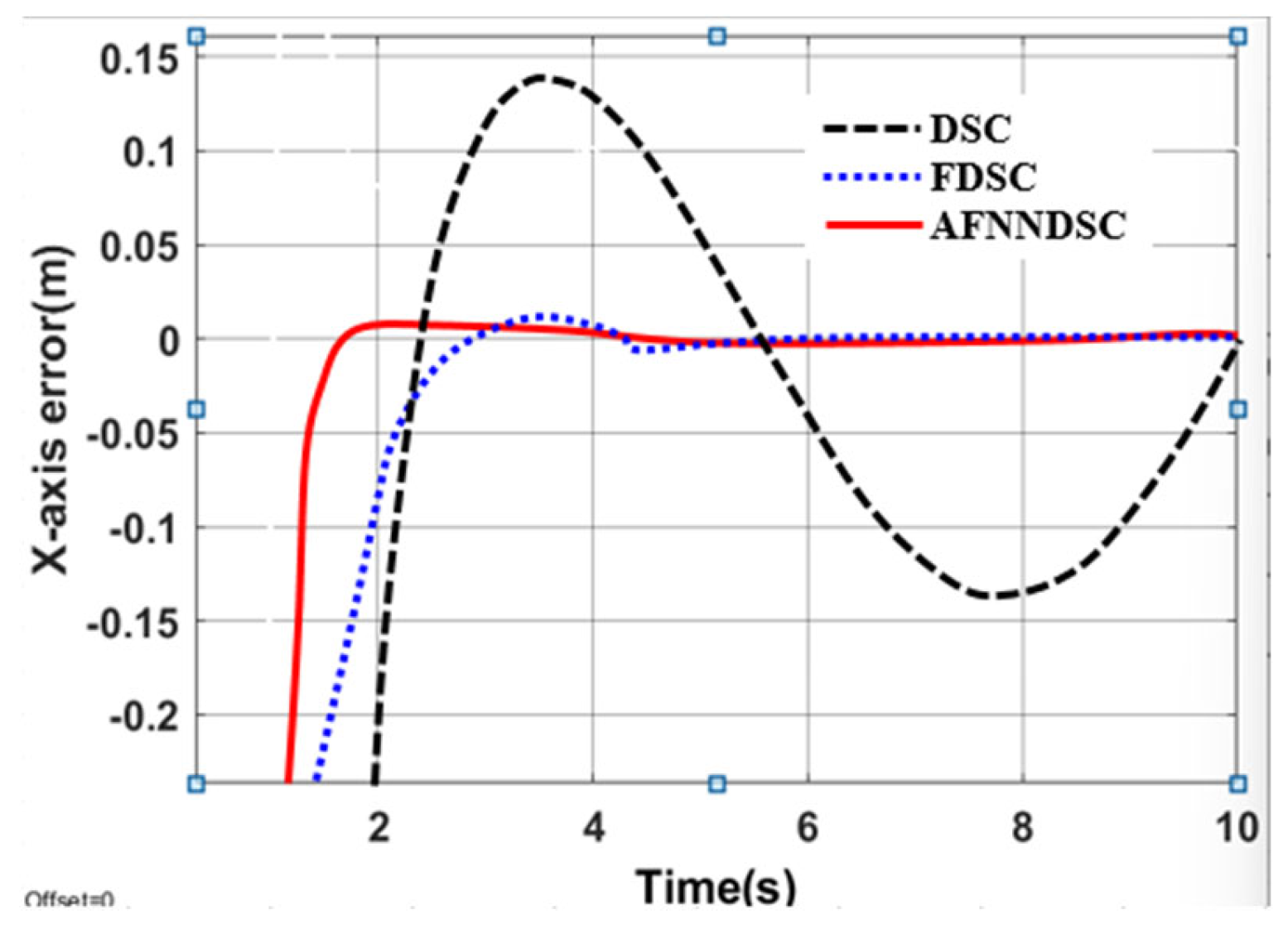
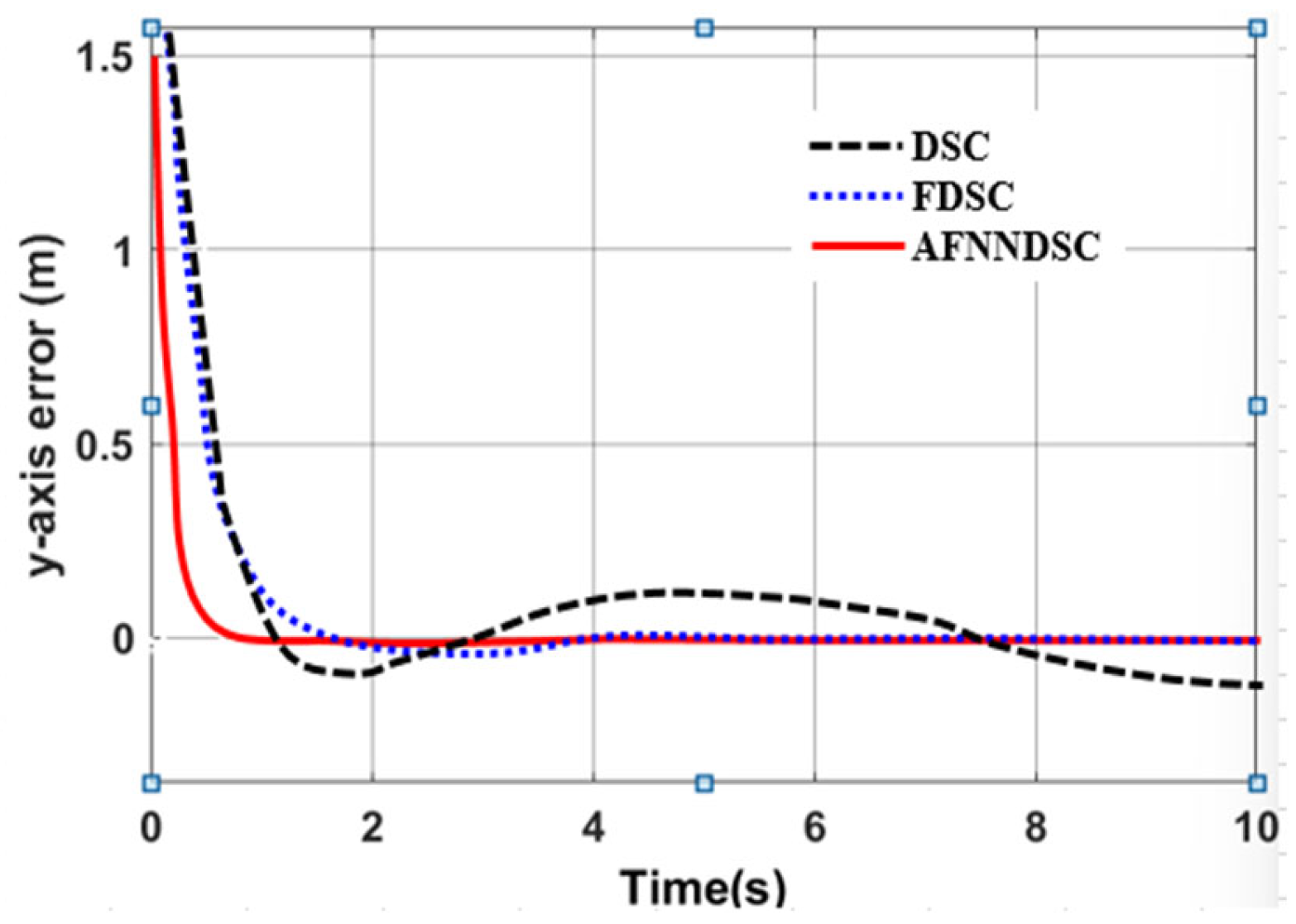
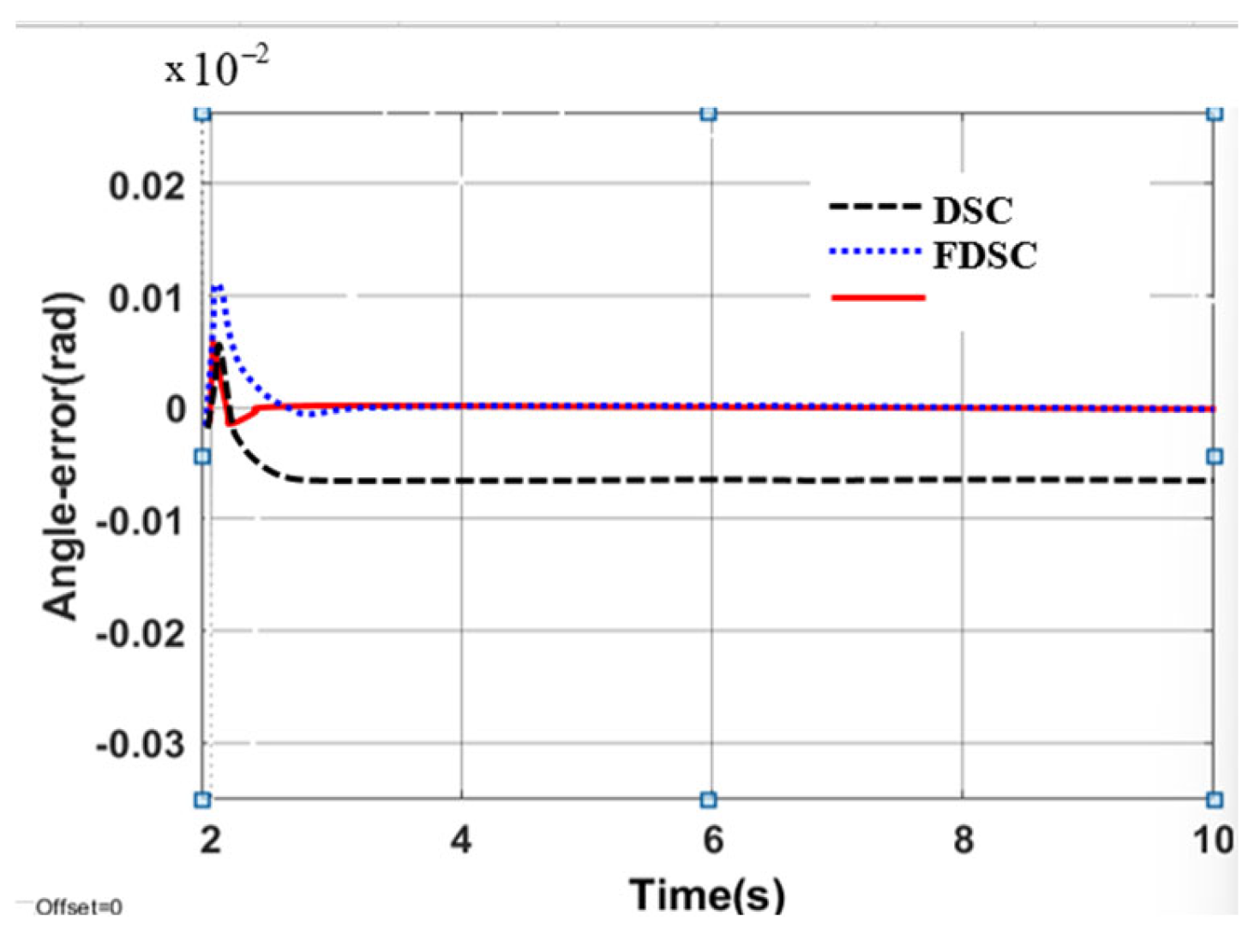
3.3.2. Result Simulation of Adaptive Fuzzy Neural Network Dynamic Surface Controller
The Robot Model Is Affected by External Disturbances
Impact of Variation in Friction Coefficient from the Environment
4. Fabrication and Experimental Operation of WMR with the Proposed Controller
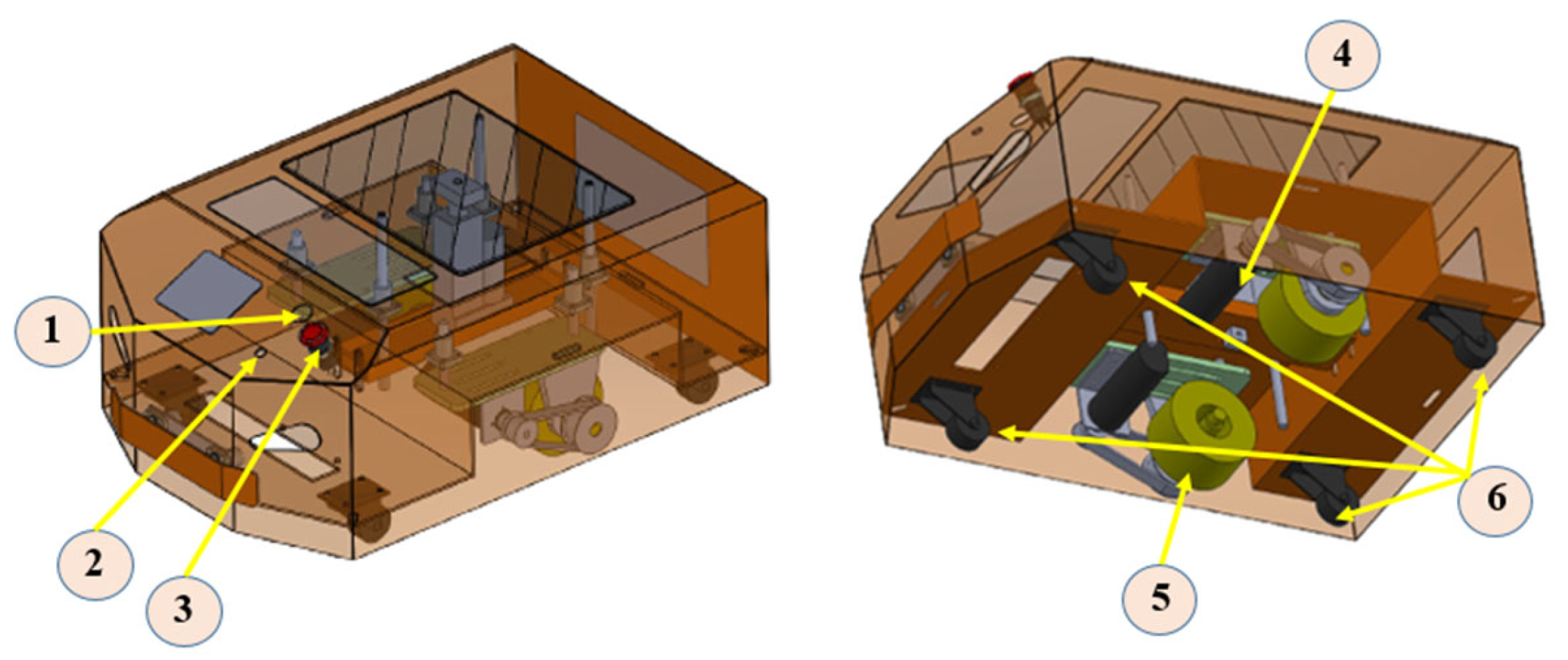
4.1. Manufacturing WMR Model
4.1.1. Mechanical Design of WMR
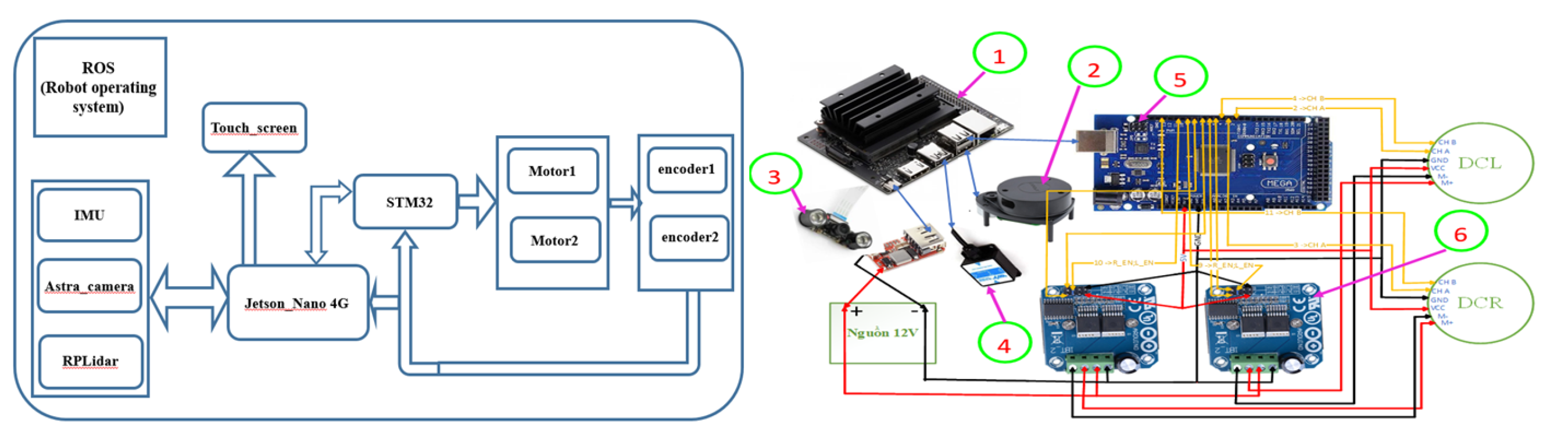
4.1.2. Design the Control Circuit Hardware Structure for the Robot
4.1.3. Robot Control Software
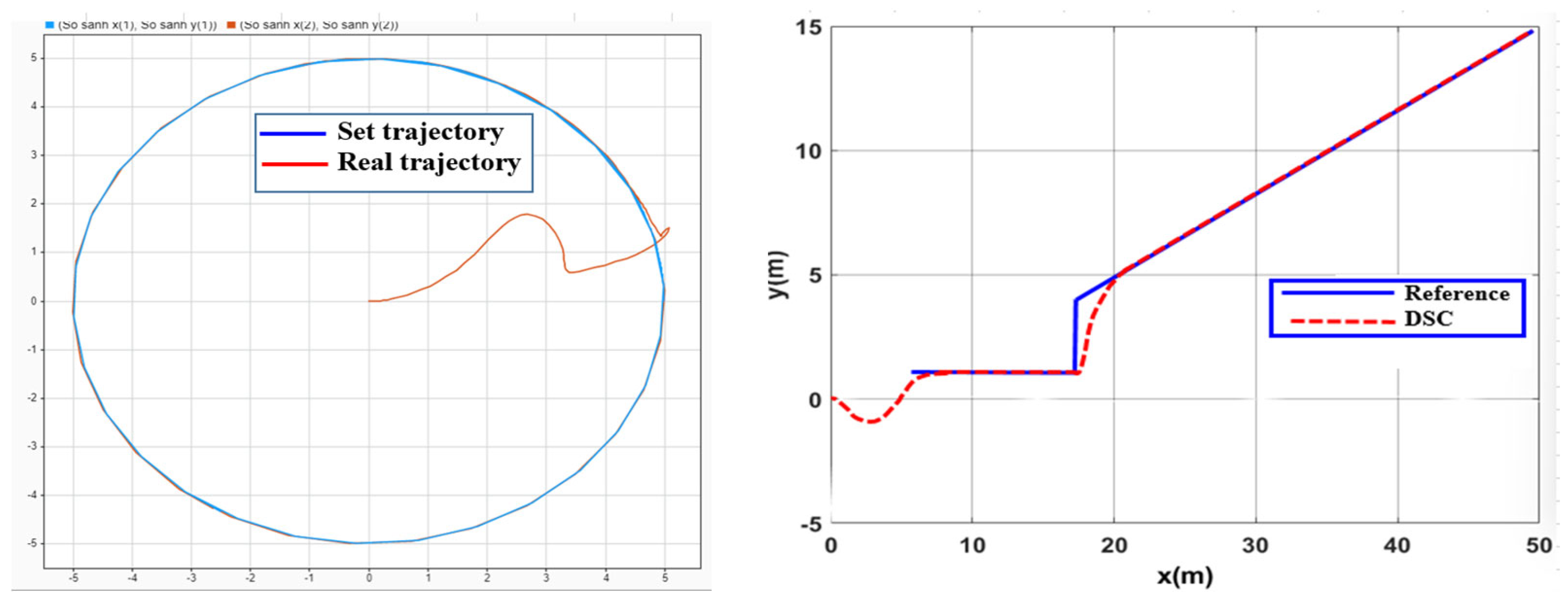
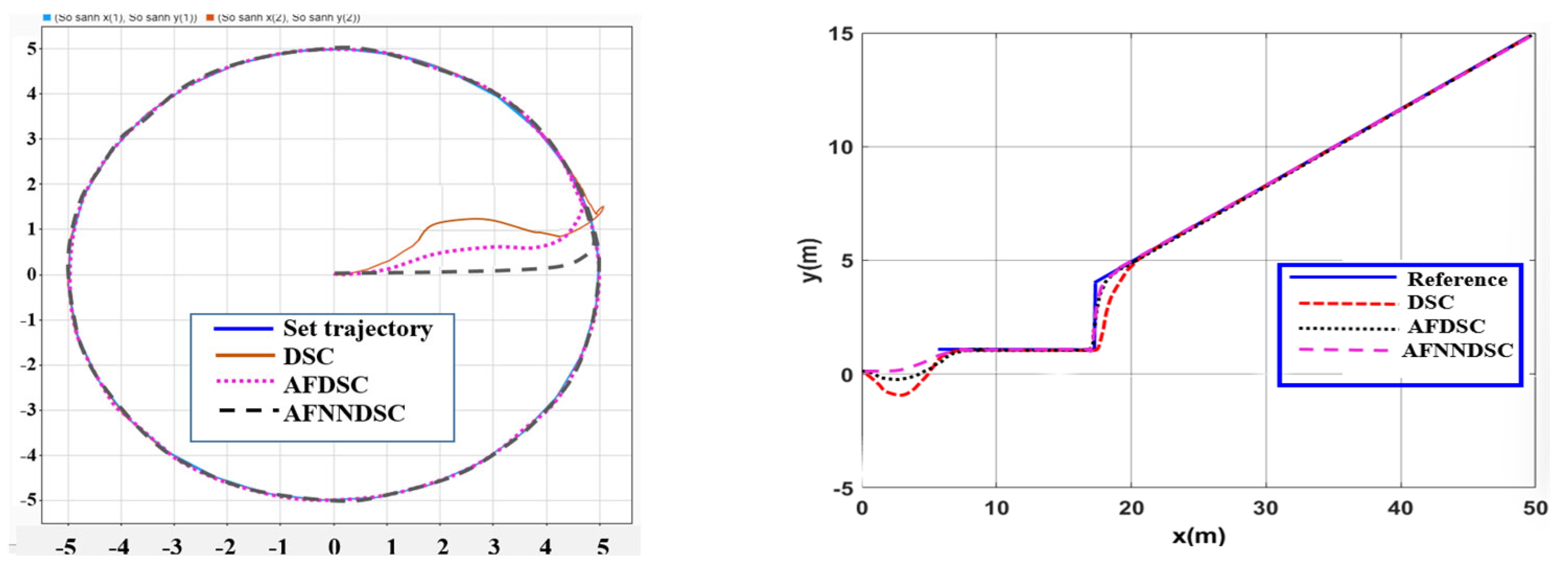
4.2. Simulate the Controller Tracking the Planned Trajectory on Gazebo
4.3. Experimental Model to Verify Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, T.; Yang, S.; Wang, F.; Mittal, G. A neural network for a non-holonomic mobile robot with unknown robot parameters. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation, ICRA 2002, Washington, DC, USA, 11–15 May 2002. [Google Scholar]
- Hu, T.; Yang, S. A novel tracking control method for a wheeled mobile robot. In Proceedings of the 2nd Workshop on Computational Kinematics, Seoul, Republic of Korea, 20–22 May 2001; pp. 104–116. [Google Scholar]
- Tiep, D.K.; Lee, K.; Im, D.-Y.; Kwak, B.; Ryoo, Y.-J. Design of Fuzzy-PID Controller for Path Tracking of Mobile Robot with Differential Drive. Int. J. Fuzzy Log. Intell. Syst. 2018, 18, 220–228. [Google Scholar] [CrossRef]
- Souma, M.; Alia, A.; Hall, E.L. Designing and simulation a motion Controller for a Wheeled Mobile Robot Autonomous Navigation). In Proceedings of the SPIE Intelligent Robots and Computer Vision Conference, Sydney, Australia, 3–6 December 2013. [Google Scholar]
- Zhao, L.; Wang, G.; Fan, X.; Li, Y. The Analysis of Trajectory Control of Non-holonomic Mobile Robots Based on Internet of Things Target Image Enhancement Technology and Backpropagation Neural Network. Front. Neurorobotics 2021, 15, 634340. [Google Scholar] [CrossRef]
- Rubio, F.; Valero, F.; Llopis-Albert, C. A review of mobile robots: Concepts, methods, theoretical framework, and applications. Sage J. 2019, 10, 172988141983959. [Google Scholar] [CrossRef]
- Wang, H.Y.; Wang, S. Trajectory Tracking Control for Nonholonomic Wheeled Mobile Robots with External Disturbances and Parameter Uncertainties. Int. J. Control Autom. Syst. 2020, 18, 3015–3022. [Google Scholar] [CrossRef]
- Tinh, N.V.; Kiem, N.T.; Tuan Hung, D.; Pham, T. Neural Network-based Adaptive Sliding Mode Control Method for Tracking of a Nonholonomic Wheeled Mobile Robot with Unknown Wheel Slips, Model Uncertainties, and Unknown Bounded External Disturbances. Acta Polytech. Hung. 2018, 15, 103–123. [Google Scholar]
- Liu, T.; Zhang, P.; Wang, M.; Jiang, Z.-P. New Results in Stabilization of Uncertain Nonholonomic Systems: An Event-Triggered Control Approach. J. Syst. Sci. Complex. 2021, 34, 1953–1972. [Google Scholar] [CrossRef]
- Wang, X.F.; Wang, C. Robust Adaptive Terminal Sliding Mode Control of an Omnidirectional Mobile Robot for Aircraft Skin Inspection. Int. J. Control Autom. Syst. 2021, 19, 1078–1088. [Google Scholar]
- Aldo, J.M.V.; Vicente, P.V.; Anand, S.O.; Juan, D.S.t. Adaptive Fuzzy Velocity Field Control for Navigation of Nonholonomic Mobile Robots. J. Intell. Robot. Syst. 2021, 101, 1–12. [Google Scholar]
- Liu, Y.; He, W.; Qiao, H.; Ji, H. Adaptive-Neural-Network-Based Trajectory Tracking Control for a Nonholonomic Wheeled Mobile Robot with Velocity Constraints. IEEE Trans. Ind. Electron. 2021, 68, 5057–5067. [Google Scholar]
- Zhang, J.-J.; Fang, Z.-L.; Zhang, Z.-Q.; Gao, R.-Z.; Zhang, S.-B. Trajectory Tracking Control of Nonholonomic Wheeled Mobile Robots Using Model Predictive Control Subjected to Lyapunov-Based Input Constraints. Int. J. Control Autom. Syst. 2022, 20, 1640–1651. [Google Scholar] [CrossRef]
- Wang, S.; Bao, X.; Zhang, S.; Shen, G. Trajectory Tracking Control of Wheeled Mobile Robots Using Backstepping; Lecture Notes in Computer Science book series; Springer: Cham, Switzerland, 2019; Volume 11744, pp. 1393–1399. [Google Scholar]
- Memon; Muhammad, J.R.; Attaullah, Y. Trajectory Tracking and Stabilization of Nonholonomic Wheeled Mobile Robot Using Recursive Integral Backstepping Control. Electronics 2021, 16, 1992. [Google Scholar]
- Cui, M. Observer-Based Adaptive Tracking Control of Wheeled Mobile Robots with Unknown Slipping Parameters. IEEE Access 2019, 7, 169646–169655. [Google Scholar] [CrossRef]
- Nourizadeh, P.; McFadden, F.J.S.; Browne, W.N. In situ slip estimation for mobile robots in outdoor environments. J. Field Robot. 2022, 40, 467–482. [Google Scholar] [CrossRef]
- Liang, D.; Sun, N.; Wu, Y.; Fang, Y. Differential Flatness-Based Robust Control of Self-Balanced Robots. Int. J. Robot. Res. 2018, 51, 949–954. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, S.; Lyu, W.; Wang, K. Backstepping sliding mode-based anti-skid braking control for a civil aircraft. Aerosp. Syst. 2023, 6, 187–197. [Google Scholar] [CrossRef]
- Sidek, N.; Sarkar, N. Dynamic modeling and control of nonholonomic mobile robot with lateral slip. In Proceedings of the 3rd International Conference on Systems, Cancun, Mexico, 13–18 April 2008; pp. 35–40. [Google Scholar]
- Motte, I.; Campion, G.A. Slow manifold approach for the control of mobile robots not satisfying the kinematic constraints. IEEE Trans. Robot. Autom. 2010, 16, 875–880. [Google Scholar] [CrossRef]
- Matveev, A.; Hoy, M.; Katupitiya, J.; Savkin, A. Nonlinear sliding mode control of an unmanned agricultural tractor in the presence of sliding and control saturation. Robot. Auton. Syst. 2013, 61, 973–987. [Google Scholar] [CrossRef]
- Chen, C.; Gao, H.; Ding, L.; Li, W.; Yu, H.; Deng, Z. Trajectory tracking control of WMRs with lateral and longitudinal slippage based on active disturbance rejection control. Robot. Auton. Syst. 2018, 107, 236–245. [Google Scholar] [CrossRef]
- Peña, C.; Cerqueira, J.J.F.; Lima, M.N. Control of wheeled mobile robots singularly perturbed by using the slipping and skidding variations: Curvilinear coordinates approach (Part I). IFAC-Papers-Online 2015, 48, 100–105. [Google Scholar] [CrossRef]
- Sasiadek, J. Space Robotics and its Challenges. In GeoPlanet: Earth and Planetary Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8, pp. 1–8. [Google Scholar] [CrossRef]
- Cordo, A.T.; Nicolae, C. Evaluation of the Vehicle Sideslip Angle According to Different Road Conditions. In Proceedings of the 4th International Congress of Automotive and Transport Engineering, Cluj, Romania, 17–19 October 2018; pp. 814–819. [Google Scholar]
- Zhang, L.; Chen, H.; Huang, Y.; Guo, H.; Sun, H.; Ding, H.; Wang, N. Model predictive control for integrated longitudinal and lateral stability of electric vehicles with in-wheel motors. Emerg. Trends LPV-Based Control Intell. Automot. Syst. 2020, 20, 1–19. [Google Scholar] [CrossRef]
- Thiago, B.B.; Iossaqui, J.G.; Juan, F.C. Kinematic control design for wheeled mobile robots with longitudinal and lateral slip. arXiv 2021, arXiv:2105.06501. [Google Scholar]
- Gao, X.; Yan, L.; Gerada, C. Modeling and Analysis in Trajectory Tracking Control for Wheeled Mobile Robots with Wheel Skidding and Slipping: Disturbance Rejection Perspective. Actuators 2021, 10, 222. [Google Scholar] [CrossRef]
- Yoo, S. Approximation-based adaptive control for a class of mobile robots with unknown skidding and slipping. Int. J. Control Autom. Syst. 2012, 85, 703–710. [Google Scholar] [CrossRef]
- Hoang, N.; Kang, H. Neural network-based adaptive tracking control of mobile robots in the presence of wheel slip and external disturbance force. Neurocomputing 2016, 188, 12–22. [Google Scholar] [CrossRef]
- Low, C.B.; Wang, D. GPS-based tracking control for a car-like wheeled mobile robot with skidding and slipping. IEEE/ASME Trans. Mechatron. 2008, 13, 480–484. [Google Scholar]
- Lenain, R.; Thuilot, B.; Cariou, C.; Martinet, P. Mixed kinematic and dynamic sideslip angle observer for accurate control of fast off-road mobile robots. J. Field Robot. 2010, 27, 181–196. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Zhang, L.; Walker, P. Sideslip angle estimation of ground vehicles: A comparative study. IET Control Theory Appl. 2021, 14, 3490–3505. [Google Scholar] [CrossRef]
- Bayar, G.; Bergerman, M.; Konukseven, E.; Koku, A. Improving the trajectory tracking performance of autonomous orchard vehicles using wheel slip compensation. Biosyst. Eng. 2016, 146, 149–164. [Google Scholar] [CrossRef]
- Grip, H.; Imsland, L.; Johansen, T.; Kalkkuhl, J.; Suissa, A. Vehicle sideslip estimation: Design, implementation and experimental validation. IEEE Control Syst. Mag. 2009, 29, 36–52. [Google Scholar]
- Dakhlallah, J.; Glaser, S.; Mammar, S.; Sebsadji, Y. Tire-Road Forces Estimation Using Extended Kalman Filter and Sideslip Angle Evaluation. In Proceedings of the 2008 American Control Conference, Washington, DC, USA, 11–13 June 2008; pp. 4597–4602. [Google Scholar]
- Fu, X.; Wang, S.; Yang, J.; Wang, Y.; Liu, Z. Adaptive Sliding Mode Control for Omnidirectional Mobile Robot Based on a New Friction Modeling. In Proceedings of the 2017 International Conference on Computer Technology, Electronics and Communication (ICCTEC), Dalian, China, 19–21 December 2017. [Google Scholar]
- Swaroop, D.; Hedrick, J.K.; Yip, P.P.; Gerdes, J.C. Dynamic surface control for a class of nonlinearsystems. IEEE Trans. Automat. Contr. 2000, 45, 1893–1899. [Google Scholar] [CrossRef]
- Tobergte, D.R.; Curtis, S. Dynamic Surface Control of Uncertain Nonlinear Systems; Springer: London, UK, 2013; Volume 53. [Google Scholar]
- Edalati, L.; Khaki Sedigh, A.; Aliyari Shooredeli, M.; Moarefianpour, A. Adaptive fuzzy dynamic surface control of nonlinear systems with input saturation and time-varying output constraints. Mech. Syst. Signal Process. 2018, 100, 311–329. [Google Scholar] [CrossRef]
- Gore, R.; Reynolds, P.F., Jr.; Kamensky, D.; Diallo, S.; Padilla, J. Statistical debugging for simulations. ACM Trans. Model. Comput. Simul. (TOMACS) 2015, 25, 1–26. [Google Scholar] [CrossRef]
- Qi, S.; Zhang, D.; Guo, L.; Wu, L. Adaptive Dynamic Surface Control of Nonlinear Switched Systems with Prescribed Performance. J. Dyn. Control Syst. 2018, 24, 269–286. [Google Scholar] [CrossRef]
- Wang, C.; Wang, D.; Han, Y. Neural Network Based Adaptive Dynamic Surface Control for Omnidirectional Mobile Robots Tracking Control with Full-State Constraints and Input Saturation. Int. J. Control Autom. Syst. 2021, 19, s4067–s4077. [Google Scholar] [CrossRef]
- Qin, P.; Zhao, T.; Liu, N.; Mei, Z.; Yan, W. Predefined-Time Fuzzy Neural Network Control for Omnidirectional Mobile Robot. Processes 2022, 11, 23. [Google Scholar] [CrossRef]
- Huang, S.N.; Tan, K.K.; Lee, T.H. Adaptive motion control using neural network approximations. Automatica 2002, 38, 227–233. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, M.; Zhang, J. Kinematic model identification of autonomous Mobile Robot using dynamical recurrent neural networks. In Proceedings of the 2005 IEEE International Conference Mechatronics and Automation, Niagara Falls, ON, Canada, 29 July 2005–1 August 2005; Volume 3, pp. 1447–1450. [Google Scholar]
- Ge, S.S.; Wang, C. Direct adaptive neural network control of a class of nonlinear systems. IEEE Trans. Neural Netw. 2002, 13, 214–221. [Google Scholar] [CrossRef]
- Wang, J.; Chen, J.; Ouyang, S.; Yang, Y. Trajectory tracking control based on adaptive neural dynamics for four-wheel drive Omnidirectional mobile robots. Eng. Rev. 2014, 34, 235–243. [Google Scholar]
- Yu, L.; Fei, S.; Yang, G. A Nơ ron Network Approach for Tracking Control of Uncertain Switched Nonlinear Systems with Unknown Dead-Zone Input. Circuits Syst. Signal Process 2015, 34, 2695–2710. [Google Scholar] [CrossRef]
- Rosillo, N.; Montés, N.; Ferreira, N. A Generalized Matlab/ROS/Robotic Platform Framework for Teaching Robotics. Robot. Educ. 2019, 25, 159–169. [Google Scholar]
- Araújo, A.; Portugal, D.; Couceiro, M.S.; Rocha, R.P. Integrating Arduino-Based Educational Mobile Robots in ROS. J. Intell. Robot. Syst. 2017, 77. [Google Scholar]
- Rajesh, K.M.; Chint, R.T.; Sarath, S.; Akhil, R. ROS based Autonomous Indoor Navigation Simulation Using SLAM Algorithm. Int. J. Pure Appl. Math. 2018, 7, 199–205. [Google Scholar]
- Yoshida, H.; Fujimoto, H.; Kawano, D.; Goto, Y.; Tsuchimoto, M.; Sato, K. ROS: An open-source Robot Operating System. In Proceedings of the 41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 4754–4759. [Google Scholar]


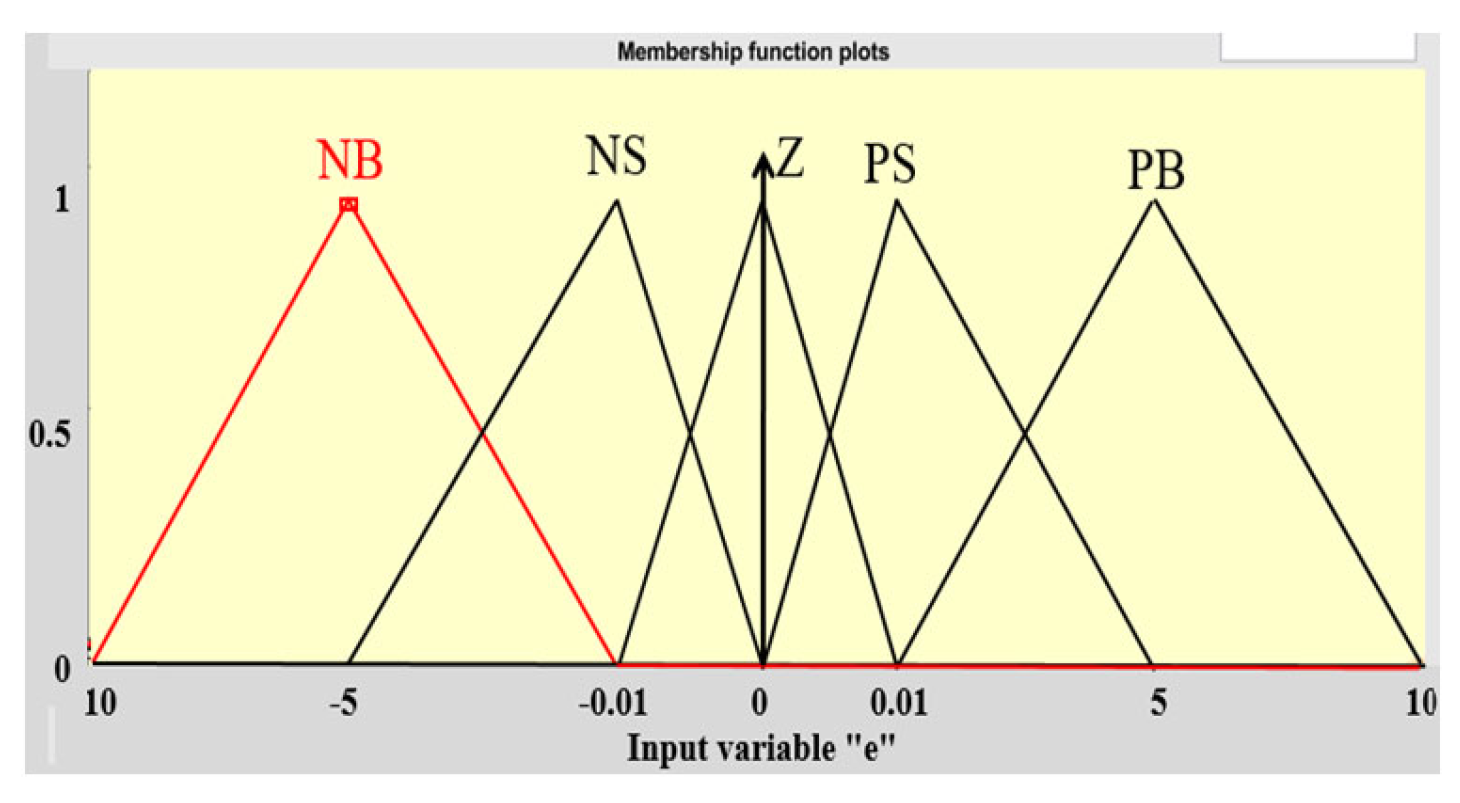



















| Language Variation e | Language Variation | Meaning |
|---|---|---|
| NB | NB | Negative big |
| NS | NS | Negative small |
| Z | Z | Zezo |
| PS | PS | Positive small |
| PB | PB | Positive big |
| NB | NS | Z | PS | PB | |
| NB | M(M) | S(B) | VS(VB) | S(B) | M(M) |
| NS | B(S) | M(M) | S(B) | M(M) | B(S) |
| Z | VS(VB) | B(S) | M(M) | B(S) | VS(VB) |
| PS | B(S) | M(M) | S(B) | M(M) | B(S) |
| PB | M(M) | S(B) | VS(VB) | S(B) | M(M) |
| Variable Output Language | Meaning | ||
|---|---|---|---|
| VS | Verry small | 1.5 | 20 |
| S | Small | 4.25 | 25 |
| M | medium | 6.5 | 30 |
| B | Big | 8 | 35 |
| VB | Verry big | 10 | 40 |
| Controller | The Largest Deviation Value When the Robot Follows the Trajectory | ||
|---|---|---|---|
| X-axis (m) | Y-axis (m) | Angle (rad) | |
| DSC | 0.1452 | 0.1683 | 0.00652 |
| AFDSC | 0.00136 | 0.00415 | 0.000452 |
| AFNNDSC | 0.000572 | 0.000523 | 0.000394 |
| Experimental Environment | DSC Controller | AFDSC Controller | AFDSC Controller | |
|---|---|---|---|---|
| 1 | Around the room | 0.04163 (m) | 0.00968 (m) | 0.000934 (m) |
| 2 | Along the corridor | 0.02431 (m) | 0.007217 (m) | 0.000763 (m) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hà, V.T.; Thuong, T.T.; Thanh, N.T.; Vinh, V.Q. Research on Some Control Algorithms to Compensate for the Negative Effects of Model Uncertainty Parameters, External Interference, and Wheeled Slip for Mobile Robot. Actuators 2024, 13, 31. https://doi.org/10.3390/act13010031
Hà VT, Thuong TT, Thanh NT, Vinh VQ. Research on Some Control Algorithms to Compensate for the Negative Effects of Model Uncertainty Parameters, External Interference, and Wheeled Slip for Mobile Robot. Actuators. 2024; 13(1):31. https://doi.org/10.3390/act13010031
Chicago/Turabian StyleHà, Vo Thu, Than Thi Thuong, Nguyen Thi Thanh, and Vo Quang Vinh. 2024. "Research on Some Control Algorithms to Compensate for the Negative Effects of Model Uncertainty Parameters, External Interference, and Wheeled Slip for Mobile Robot" Actuators 13, no. 1: 31. https://doi.org/10.3390/act13010031
APA StyleHà, V. T., Thuong, T. T., Thanh, N. T., & Vinh, V. Q. (2024). Research on Some Control Algorithms to Compensate for the Negative Effects of Model Uncertainty Parameters, External Interference, and Wheeled Slip for Mobile Robot. Actuators, 13(1), 31. https://doi.org/10.3390/act13010031






