Design of an Optical Path Scanning Control System in a Portable Fourier Transform Spectrometer Based on Adaptive Feedforward–Nonlinear Proportional-Integral Cascade Composite Control
Abstract
:1. Introduction
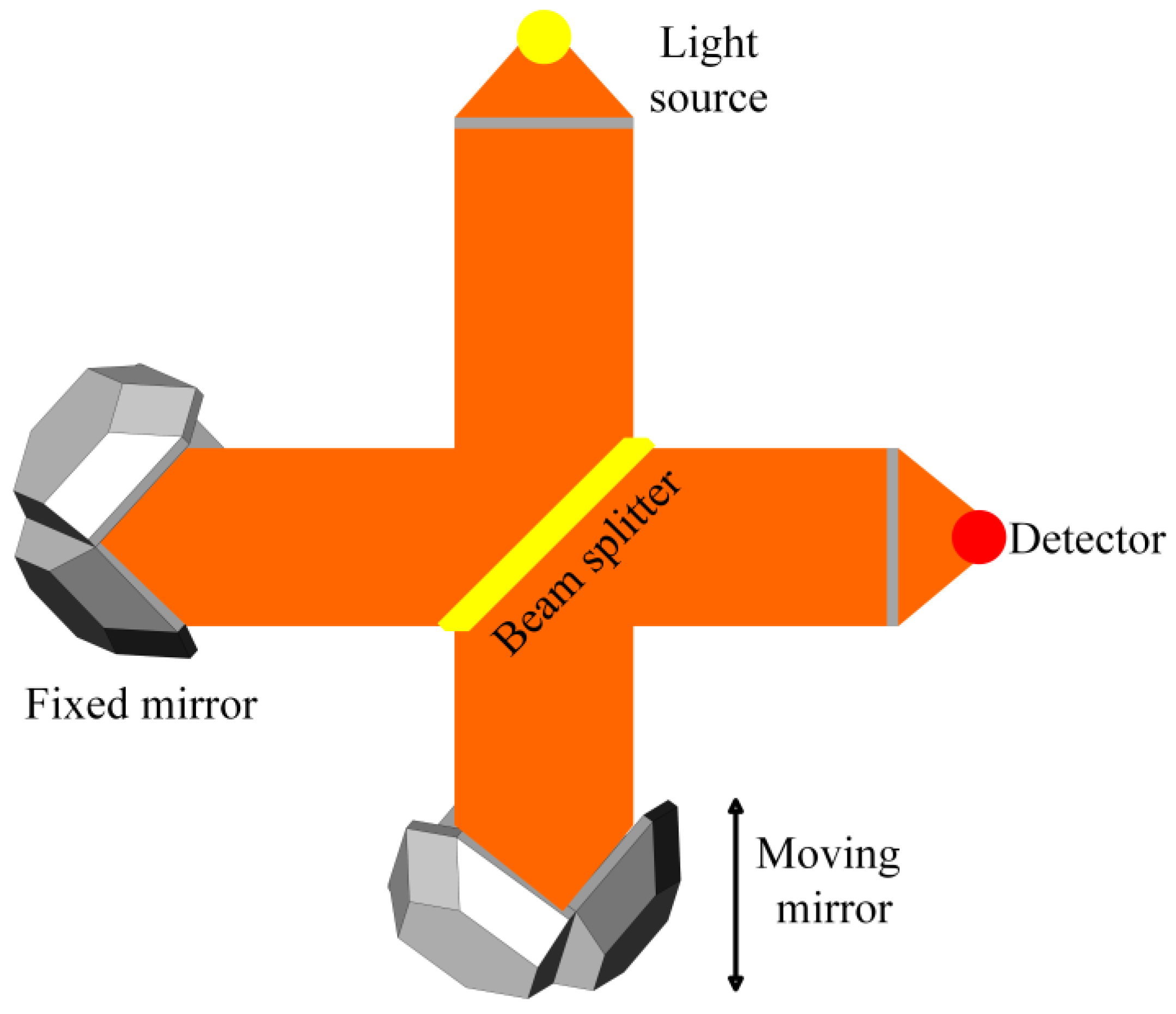
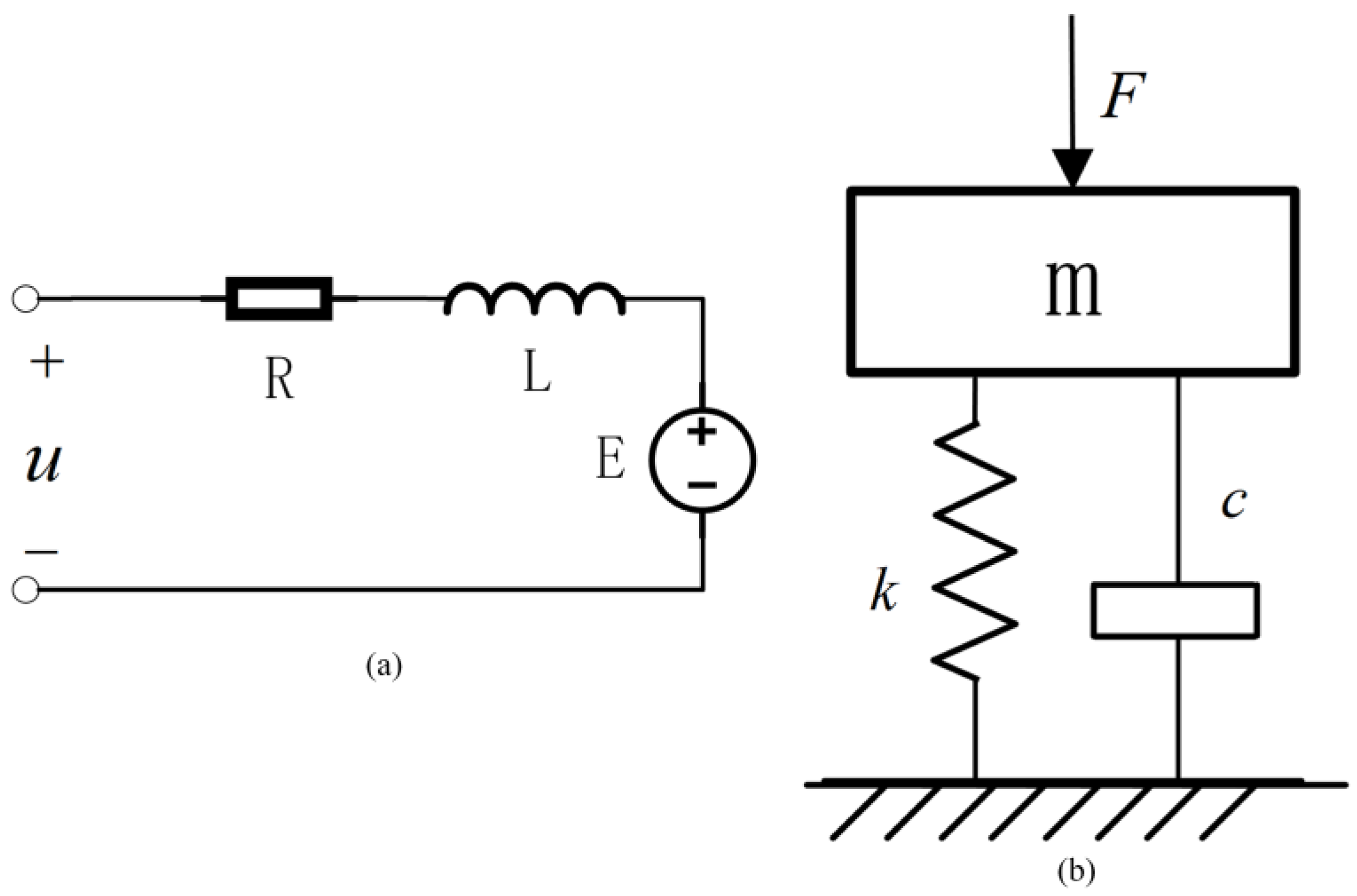
2. Problem Formulation of Optical Path Scanning System
3. Design of Adaptive Feedforward–Nonlinear PI Cascade Composite Controller
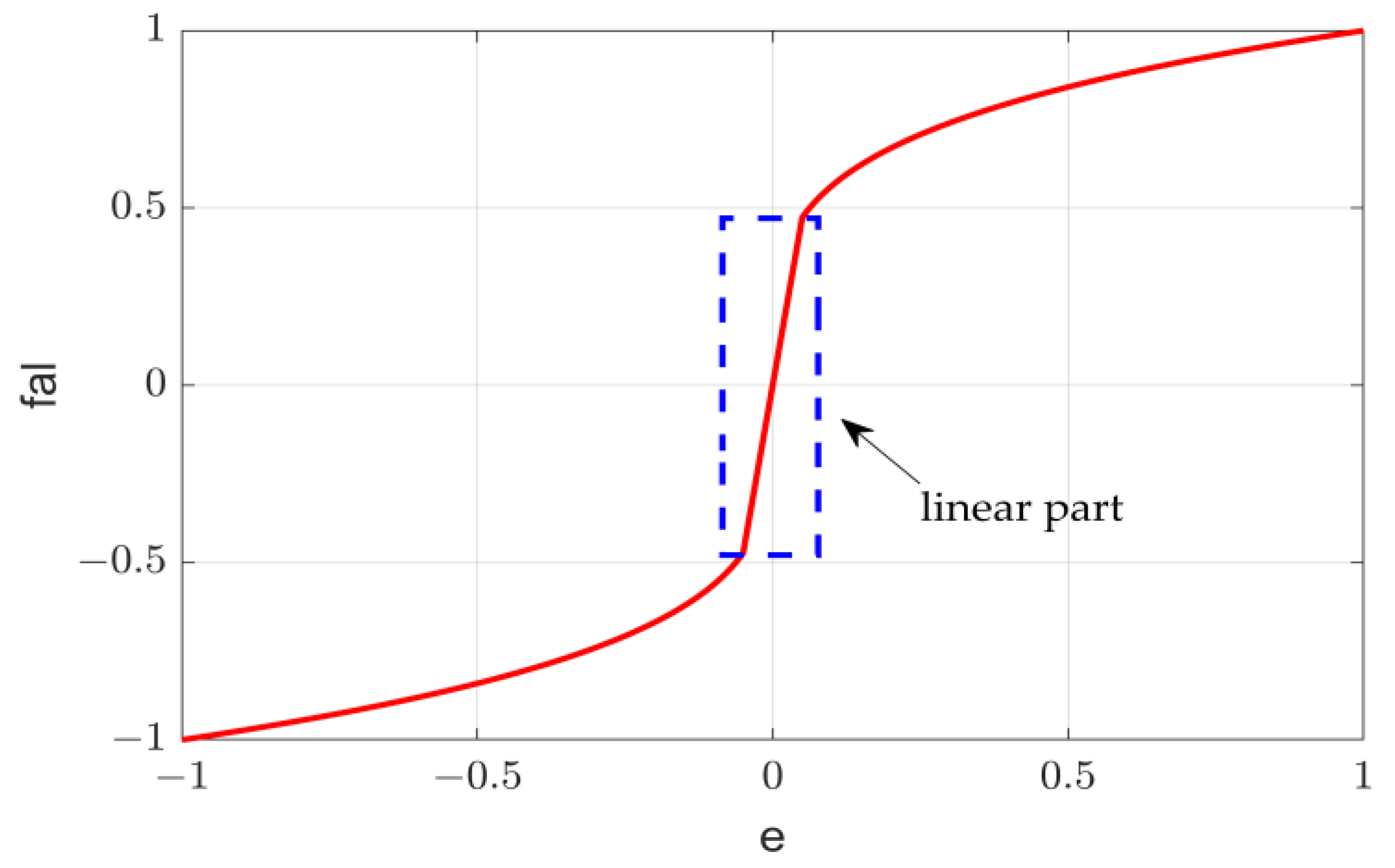
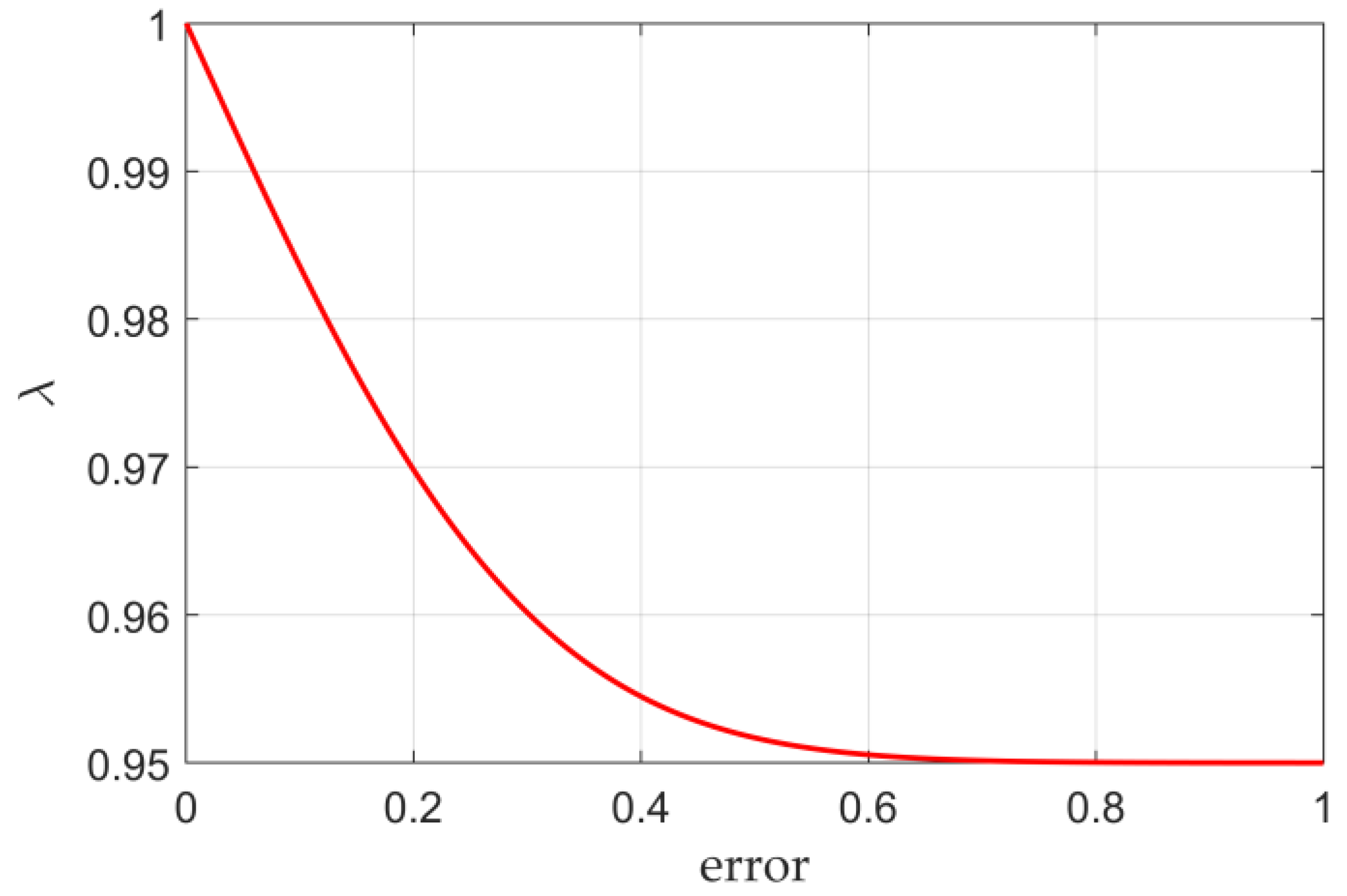
3.1. Nonlinear PI Cascade Controller
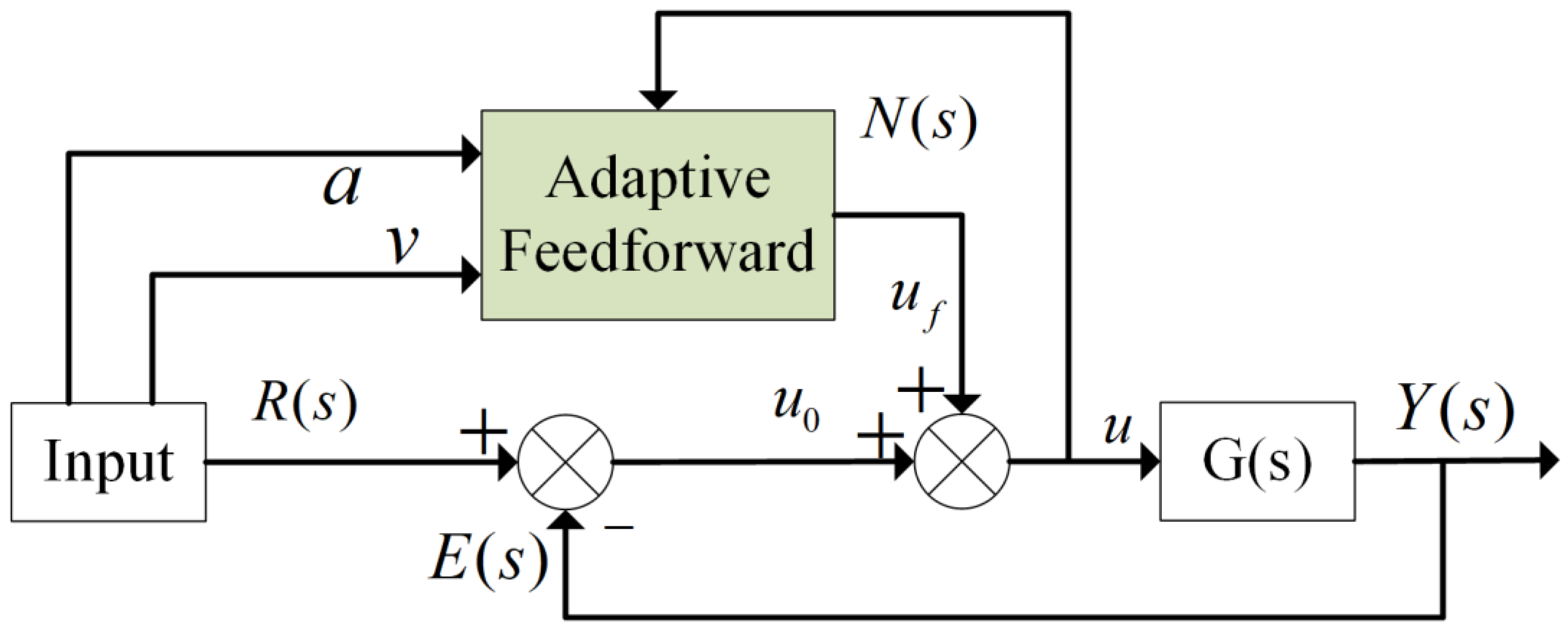
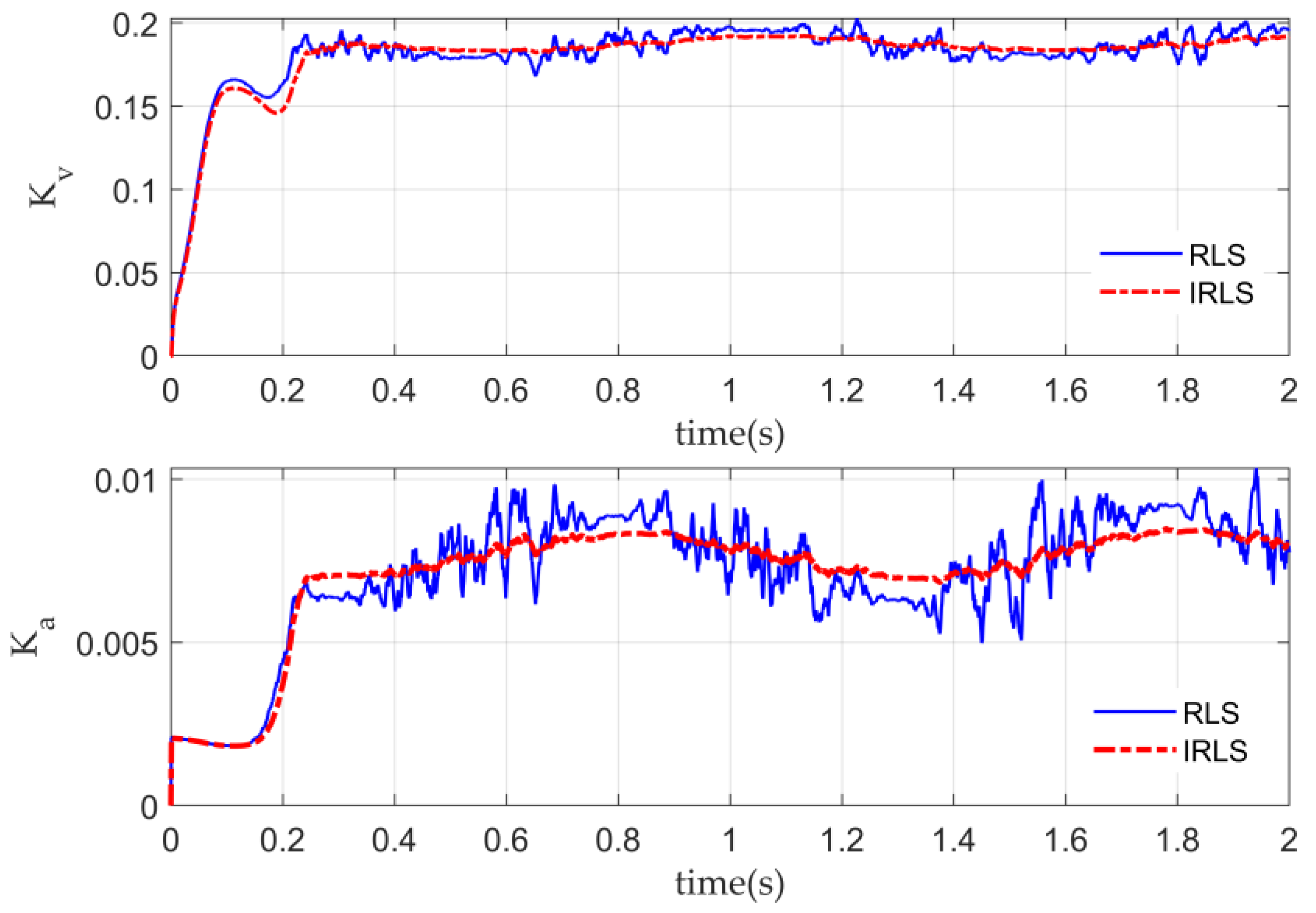
3.2. Adaptive Feedforward Compensator
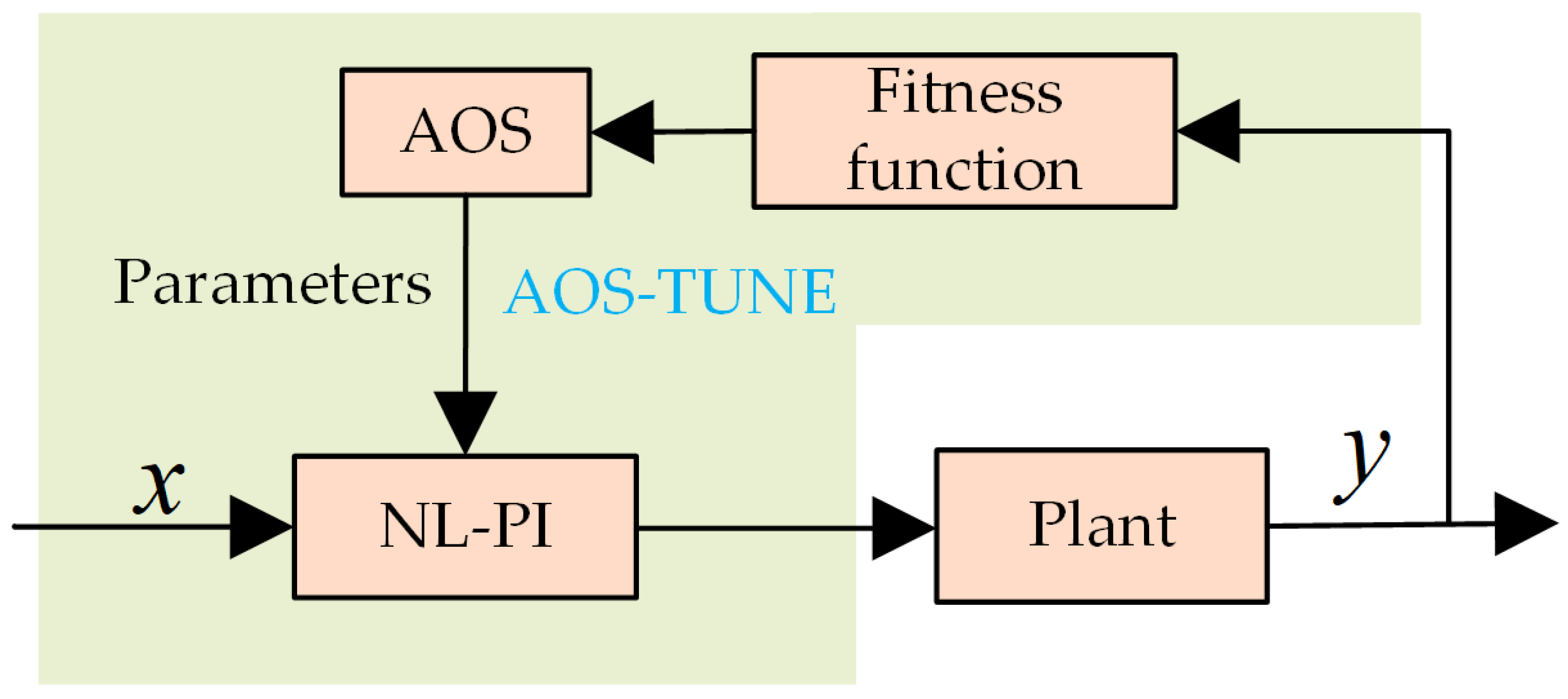
3.3. Adaptive Feedforward–Nonlinear PI Cascade Composite Controller and Parameter Tuning
4. Simulation and Results Analysis
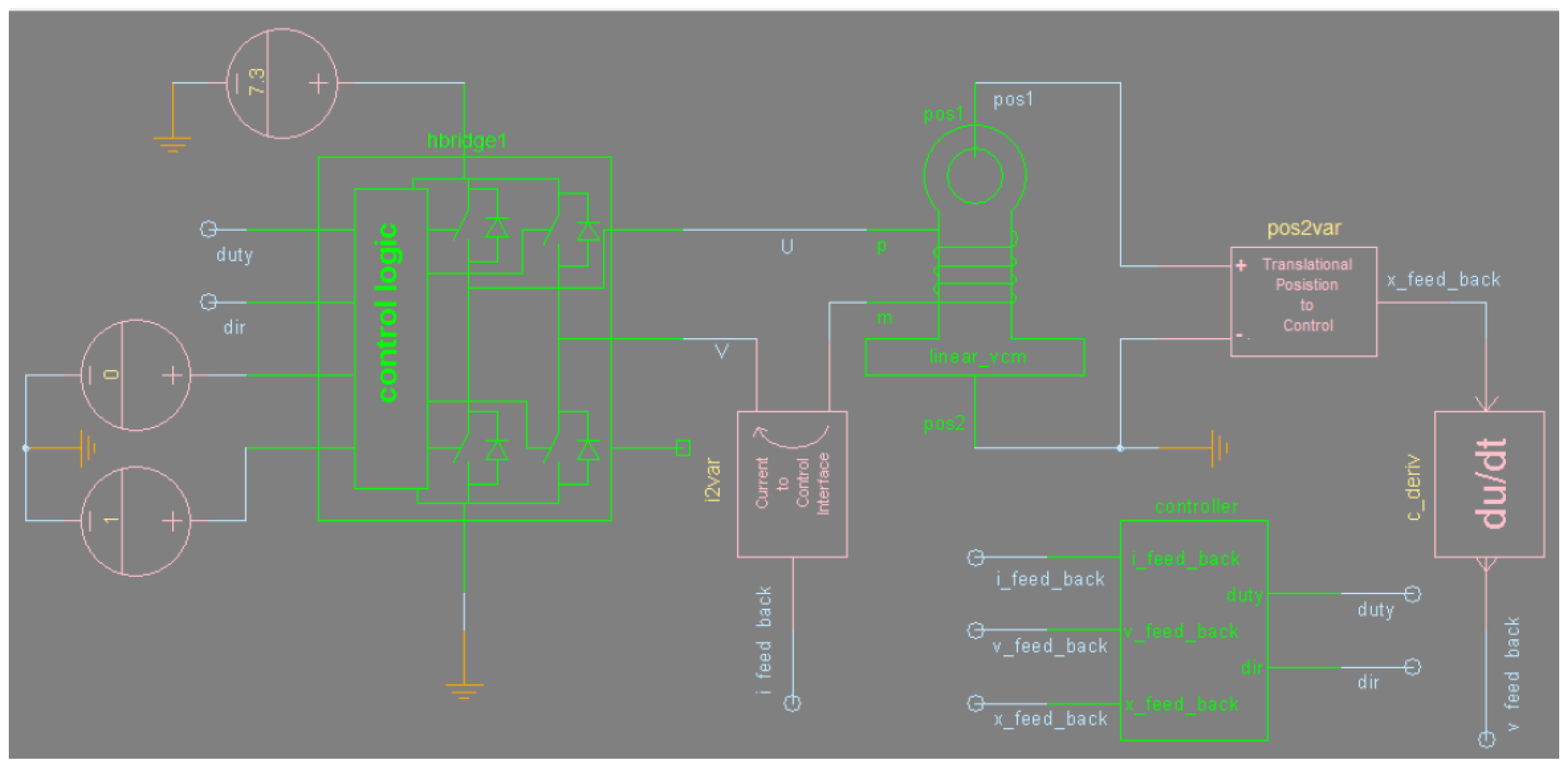
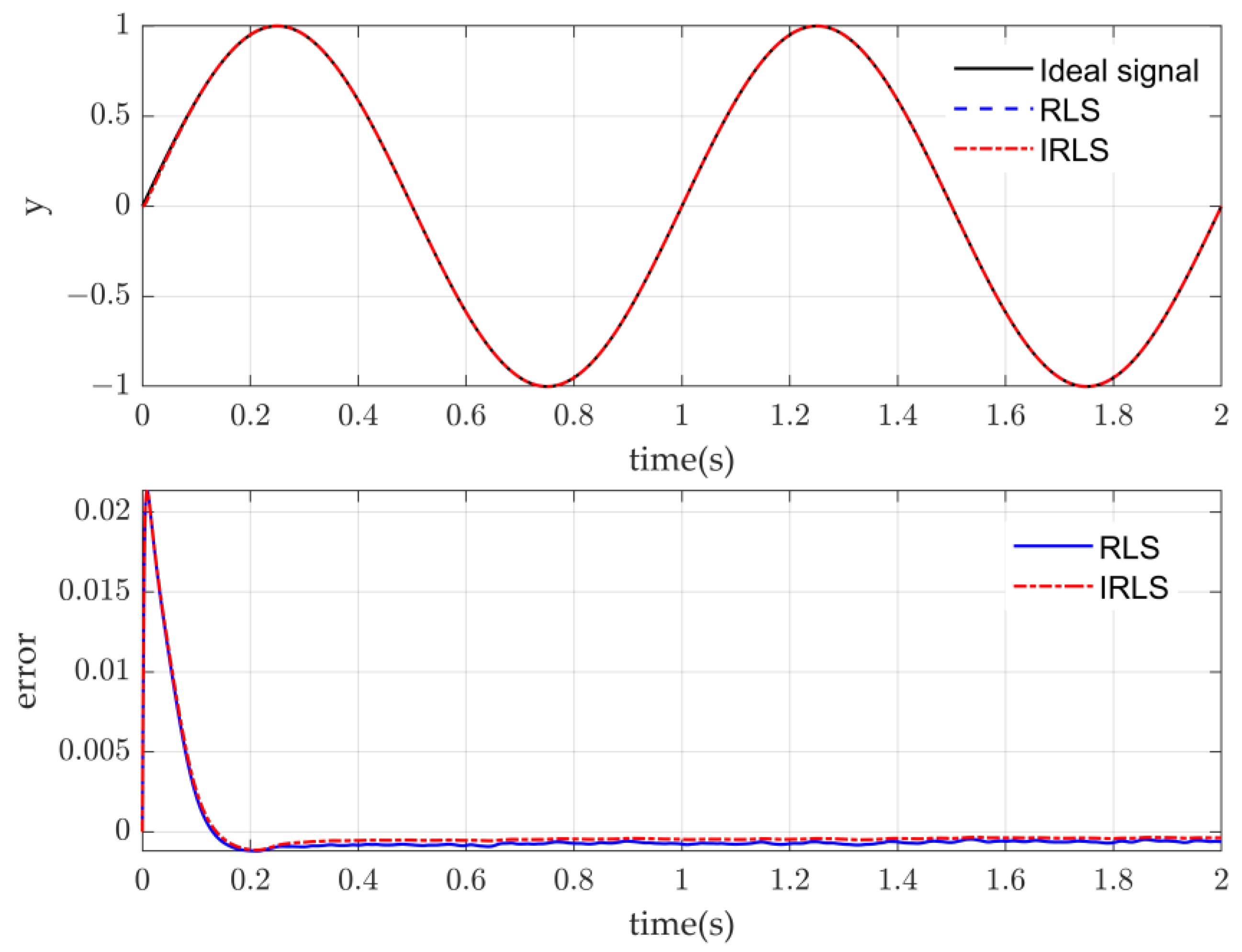
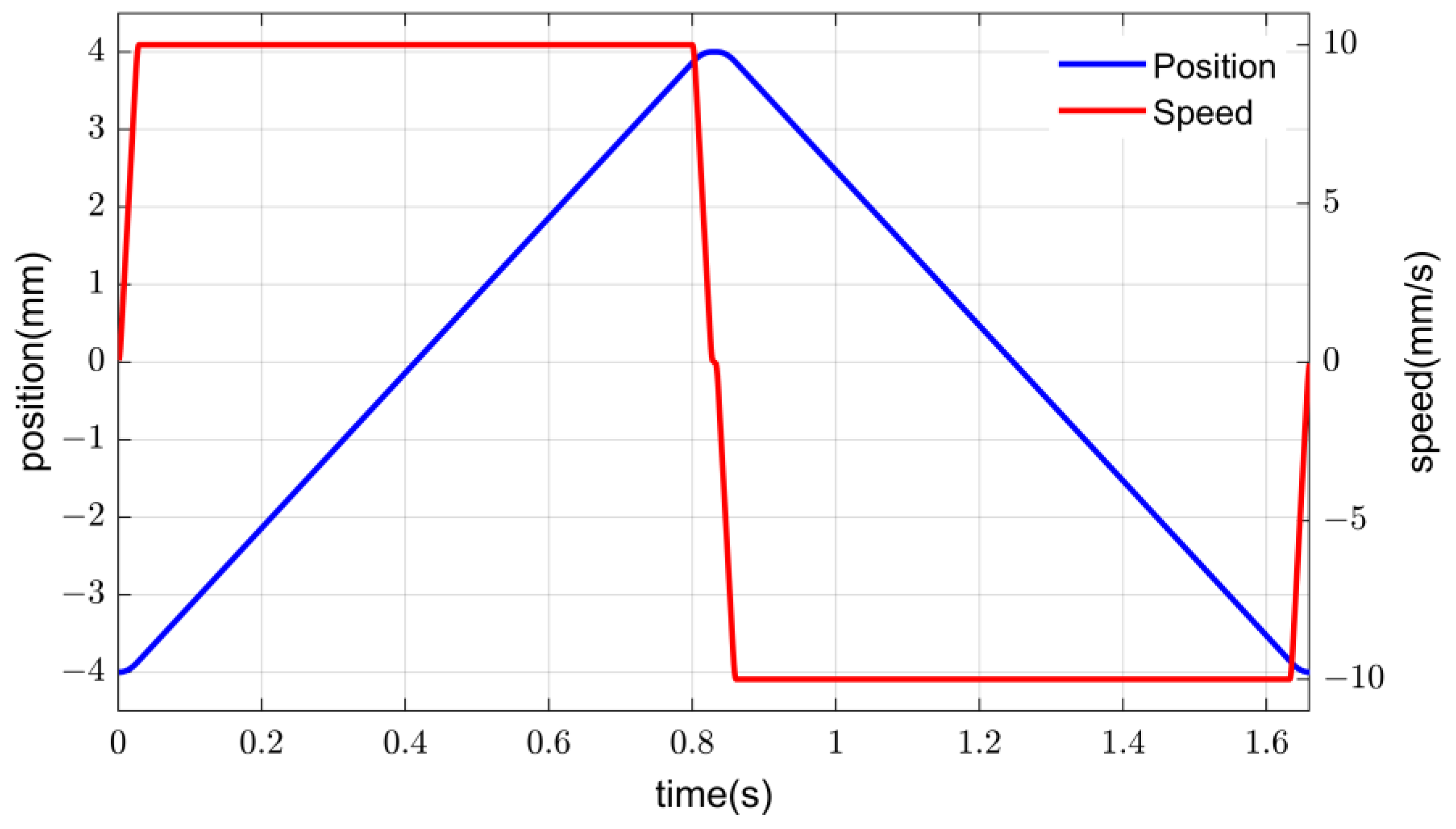
4.1. Parameter Setting and Model Building
4.2. Simulation Results and Analysis
4.2.1. Performance of the Composite Controller
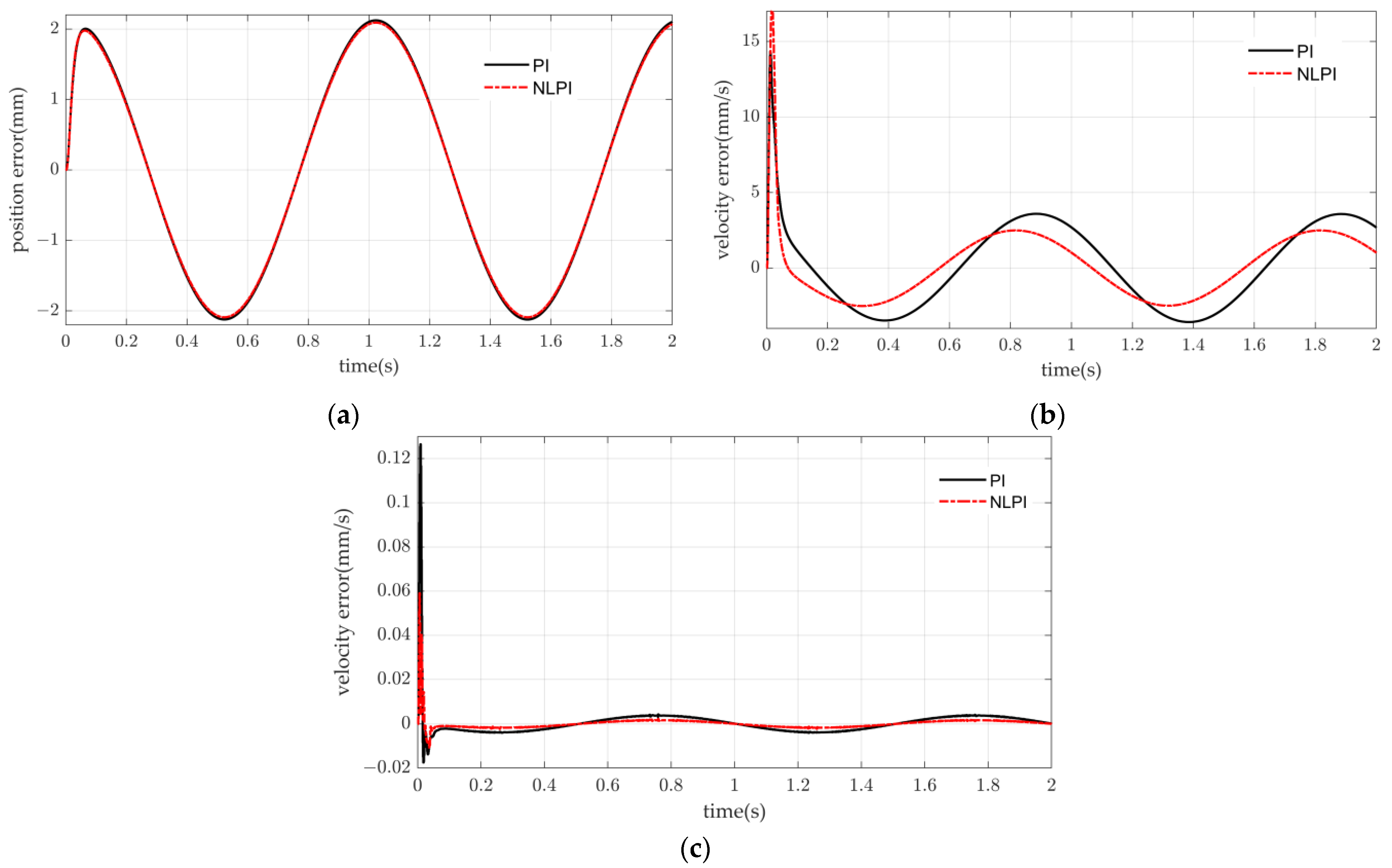
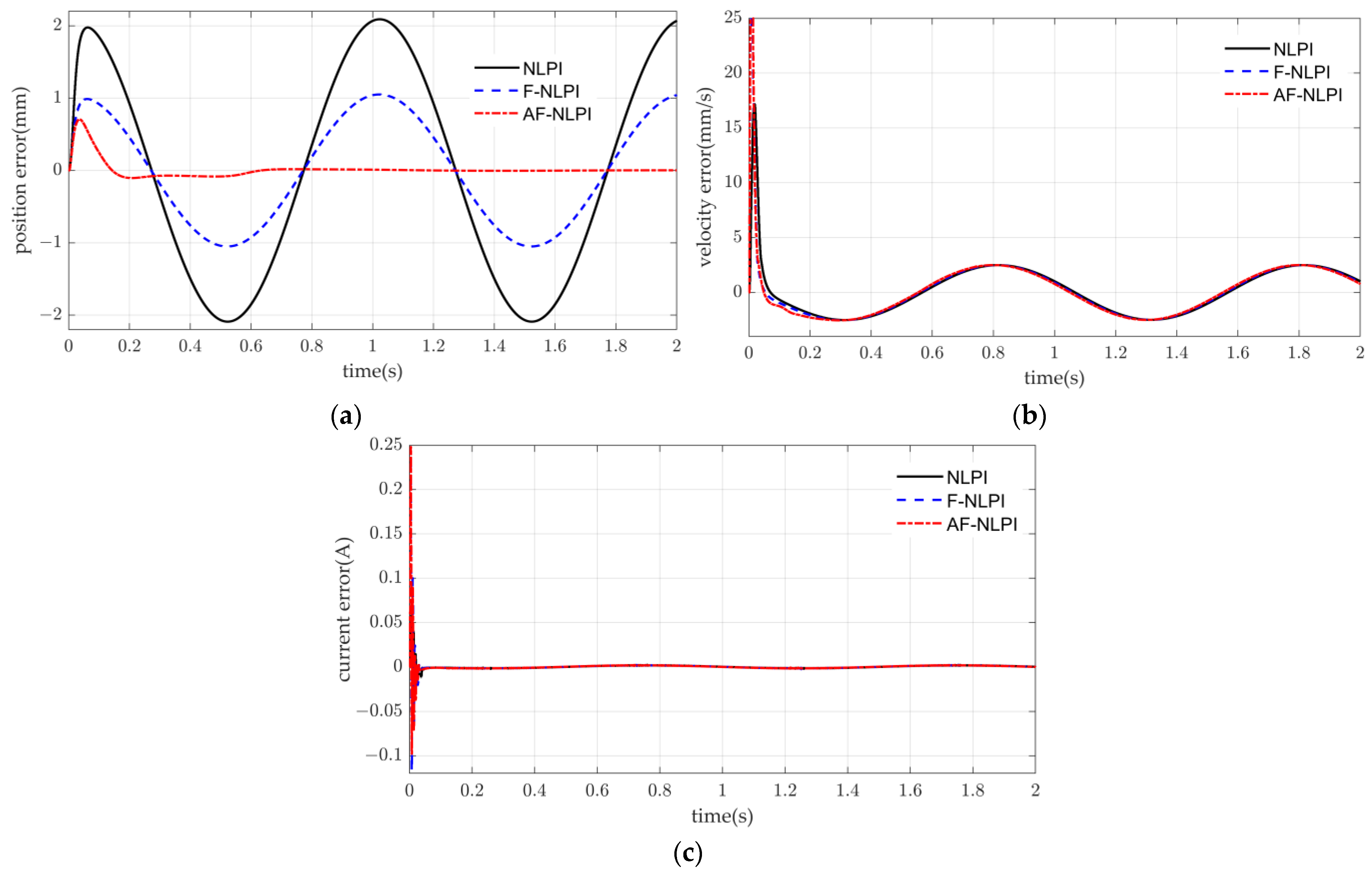
4.2.2. Comparison of Simulation Results for Different Controllers
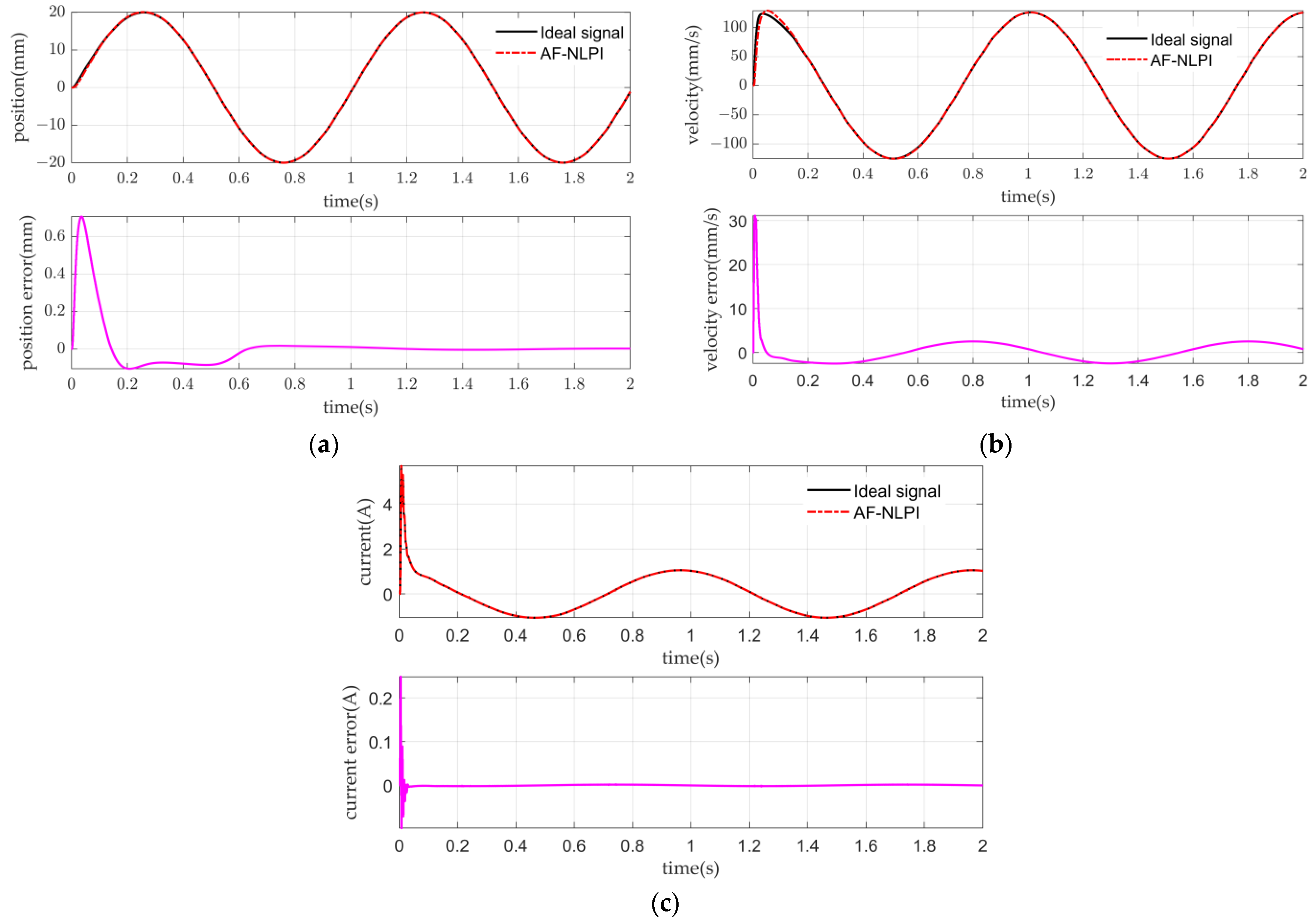
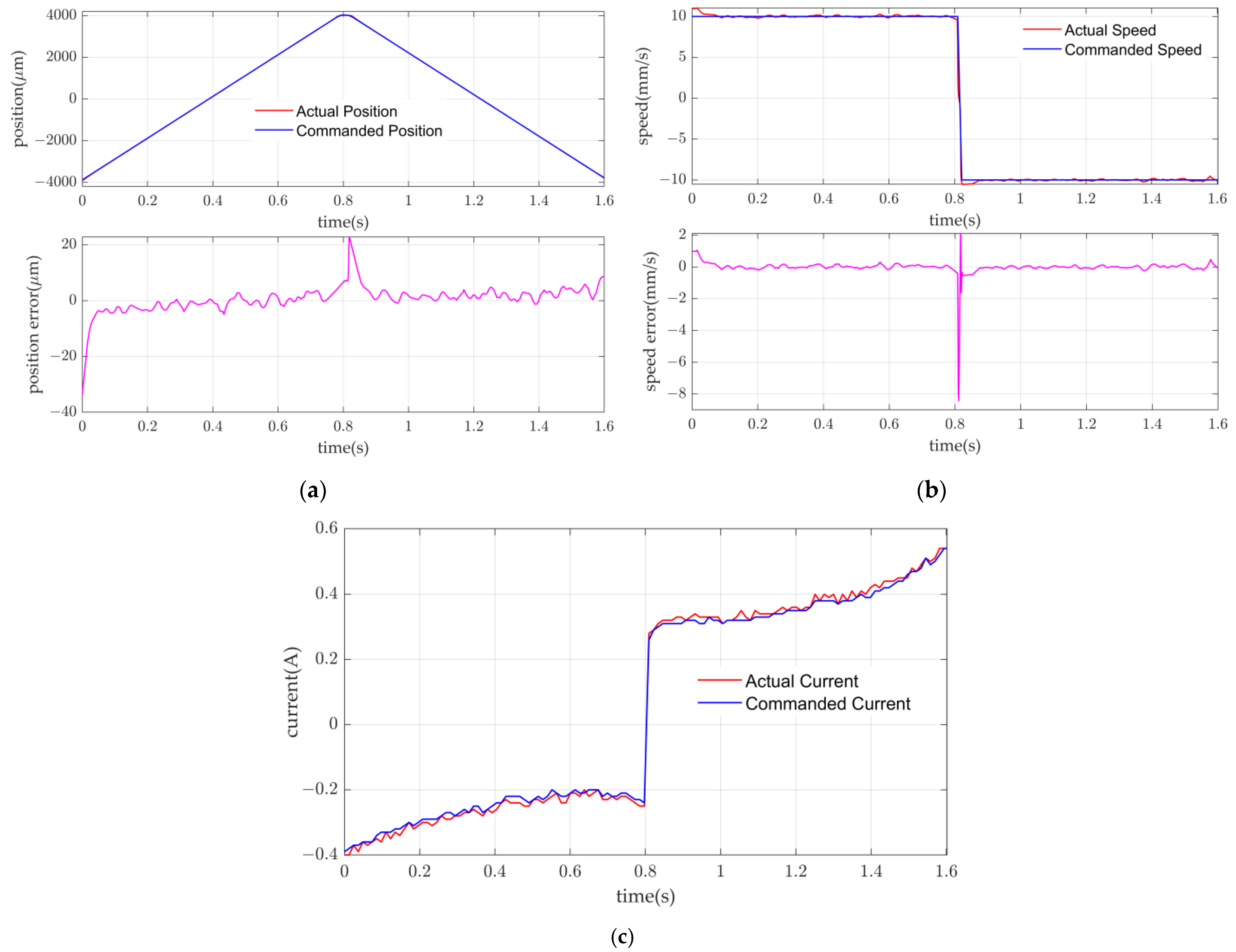
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.; Yuan, M.; Liu, X.; Su, M.; Wang, L.; Zeng, Y.; Zang, H.; Nie, L. Comparative analysis of rapid quality evaluation of Salvia miltiorrhiza (Danshen) with Fourier transform near-infrared spectrometer and portable near-infrared spectrometer. Microchem. J. 2020, 159, 105492–105502. [Google Scholar] [CrossRef]
- Jahromi, K.E.; Nematollahi, M.; Krebbers, R.; Abbas, M.A.; Khodabakhsh, A.; Harren, F.J.M. Fourier transform and grating-based spectroscopy with a mid-infrared supercontinuum source for trace gas detection in fruit quality monitoring. Opt. Express 2021, 29, 12381–12397. [Google Scholar] [CrossRef]
- Luo, S.; Tian, J.; Liu, Z.; Lu, Q.; Zhong, K.; Yang, X. Rapid determination of styrene-butadiene-styrene (SBS) content in modified asphalt based on Fourier transform infrared (FTIR) spectrometer and linear regression analysis. Measurement 2020, 151, 107204–107212. [Google Scholar] [CrossRef]
- Wang, R.; Dong, D.; Ye, S.; Jiao, L. Measurement of Volatile Compounds Released from Plastic Using Long-Optical-Path FTIR. Spectrosc. Spectr. Anal. 2021, 41, 3039–3044. [Google Scholar]
- Cui, F.X.; Hao, Y.; Ma, F.X.; Wu, J.; Wang, A.; Li, D.; Li, Y.Y. Optimization of FTIR Passive Remote Sensing Signal-to-Noise Ratio and Its Application in SF6, Leak Detection in Transform Substation. Spectrosc. Spectr. Anal. 2021, 41, 1436–1440. [Google Scholar]
- Pan, M.; Sun, S.; Zhou, Q.; Chen, J. A Simple and Portable Screening Method for Adulterated Olive Oils Using the Hand-Held FTIR Spectrometer and Chemometrics Tools. J. Food Sci. 2018, 83, 1605–1612. [Google Scholar] [CrossRef]
- Cebi, N.; Bekiroglu, H.; Erarslan, A.; Rodriguez-Saona, L. Rapid Sensing: Hand-Held and Portable FTIR Applications for On-Site Food Quality Control from Farm to Fork. Molecules 2023, 28, 3727–3741. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Xu, L.; Sheng, X.; Sun, Y.; Xu, H.; Xu, H.; Wu, H. Vehicle-Mounted Solar Occultation Flux Fourier Transform Infrared Spectrometer and Its Remote Sensing Application. Sensors 2023, 23, 4317–4334. [Google Scholar] [CrossRef]
- Qu, L.; Xu, L.; Liu, J.; Feng, M.; Liu, W.; Xu, H.; Jin, L. Numerical Simulation Analysis of Portable High-Speed FTIR Rotary Interferometers. Acta Opt. Sin. 2021, 41, 0907001. [Google Scholar]
- Zhang, M.; Zhang, J.; Yang, H. Research on speed stability of moving mirror in FTIR spectrometer. Infrared Laser Eng. 2014, 43, 1240–1246. [Google Scholar]
- Qin, Y.; Li, X.; Han, X.; Tong, J.; Gao, M.; Liu, S. Study on the influence of interferometer velocity fluctuation on spectral signal-to-noise ratio. J. Optoelectron. Laser 2022, 33, 0449–0457. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, F.; Wang, E.; Liu, B.; Zeng, W.; Wang, Z. Optimization and simulation of a voice coil motor for fuel injectors of two-stroke aviation piston engine. Adv. Mech. Eng. 2019, 11, 1–17. [Google Scholar] [CrossRef]
- Koerner, L.J.; Secord, T.W. An embedded electrical impedance analyzer based on the AD5933 for the determination of voice coil motor mechanical properties. Sens. Actuators A Phys. 2019, 295, 99–112. [Google Scholar] [CrossRef]
- Rosier, A.; Mabo, P.; Chauvin, M.; Burgun, A. An Ontology-Based Annotation of Cardiac Implantable Electronic Devices to Detect Therapy Changes in a National Registry. IEEE J. Biomed. Health Inform. 2015, 19, 971–978. [Google Scholar] [CrossRef] [PubMed]
- Qu, L. Research on Key Technology and Application of Portable FTIR Spectrometer. Ph.D. Dissertation, University of Science and Technology of China, Anhui, China, 2021. [Google Scholar]
- Shi, L.; Liu, J.; Gao, W.; Zhang, Q.-X.; Wang, W. Design of a Moving Mirror Scanning System in Fourier Transform Infrared Spectrometer. Acta Photonica Sin. 2015, 44, 0430002–0430007. [Google Scholar] [CrossRef]
- Ren, L.; Yang, H.; Wei, H.; Li, Y. Design for multi-gases analyzer based on FTIR principle. Infrared Laser Eng. 2013, 42, 3175–3179. [Google Scholar]
- Wang, W.; Lu, Y.; Lu, F.; Zhang, T.; Fu, Y. Design of moving mirror control system of Fourier transform infrared spectrometer based on DSP. Chin. J. Quantum Electron. 2015, 32, 8. [Google Scholar]
- Liu, R.-L.; Yin, D.-K. Driving Control Technology for Moving Mirror of Fourier Transform Spectrometer. Infrared 2009, 30, 20–25. [Google Scholar]
- Liang, X.-W.; Shi, L. Design of a Moving Mirror Scanning System for Portable Interferometer. Spectrosc. Spectr. Anal. 2017, 37, 3255–3259. [Google Scholar]
- Li, Z.B.; Xu, X.; Le, Y.; Xu, F.Q.; Li, J.-W. Motion Control of Moving Mirror Based on Fixed-Mirror Adjustment in FTIR Spectrometer. Spectrosc. Spectr. Anal. 2012, 32, 2295–2298. [Google Scholar]
- Guo, L.; Ma, W.; Wang, C.; Lin, Z.; Wang, H. Design of translating optical path scanning control system for Fourier spectrometer. Infrared Laser Eng. 2020, 49, 0105002. [Google Scholar]
- Guo, L.; Wang, H.; Wang, C.; Ma, W.; Zhe, L. Optical Path Scanning Control System Based on Modified Repetitive Control. Spacecr. Recovery Remote Sens. 2019, 40, 32–40. [Google Scholar] [CrossRef]
- Li, T.; Hua, J.-W.; Xia, X.; Sheng, H. Simulation of Moving Mirror Control in Fourier Transform Spectrometer. Meas. Control Technol. 2014, 33, 111–114. [Google Scholar]
- Shi, Y.; Zhou, C.; Yin, Q.; Zhou, Y. Simulation on Interference Control System in Fourier Transform Spectrograph. J. Syst. Simul. 2013, 25, 753–759. [Google Scholar] [CrossRef]
- Zhou, X.; Gao, H.; Zhao, B.; Zhao, L. A GA-based parameters tuning method for an ADRC controller of ISP for aerial remote sensing applications. ISA Trans. 2018, 81, 318–328. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, Y.Q.; Wang, C.Y.; Pi, Y.G. Tuning fractional order proportional integral controllers for fractional order systems. J. Process Control 2010, 20, 823–831. [Google Scholar] [CrossRef]
- Yang, J.; Ren, Y. Application of fractional compound control in photoelectric stable platform. Electron. Opt. Control. 2020, 27, 73–78. [Google Scholar]
- Saxena, S.; Hote, Y.V. Design and Validation of Fractional-Order Control Scheme for DC Servomotor via Internal Model Control Approach. IETE Tech. Rev. 2017, 36, 49–60. [Google Scholar] [CrossRef]
- Meng, F.; Liu, S.; Liu, K. Design of an Optimal Fractional Order PID for Constant Tension Control System. IEEE Access 2020, 8, 58933–58939. [Google Scholar] [CrossRef]
- Konstantopoulos, G.C.; Baldivieso-Monasterios, P.R. State-limiting PID controller for a class of nonlinear systems with constant uncertainties. Int. J. Robust Nonlinear Control. 2019, 30, 1770–1787. [Google Scholar] [CrossRef]
- Cheng, M.; Zhai, P.; Zhang, Y.; Li, J.; Feng, K. A Voice Coil Motor-Driven Precision Positioning System Based on Self-Learning Nonlinear PID. Trans. China Electrotech. Soc. 2023, 38, 1519–1570. [Google Scholar] [CrossRef]
- Fonseca, R.R.; Sencio, R.R.; Franco, I.C.; Da Silva, F.V. An Adaptive Fuzzy Feedforward-Feedback Control System Applied to a Saccharification Process. Chem. Prod. Process Model. 2018, 13, 12. [Google Scholar] [CrossRef]
- Cui, J.; Wang, S.; Chu, Z.Y. Feed-forward compensation control of nonlinear friction for high acceleration motion system. Opt. Precis. Eng. 2018, 26, 0077–0085. [Google Scholar]
- Yang, H.; Wu, Q.-Z.; Fan, Y.-K.; Li, Y.-P. Application Research of Acceleration Feedforward in the High Precision Servo Tracking System. Electro-Opt. Technol. Appl. 2007, 22, 0048–0051. [Google Scholar]
- Li, W.; Hou, B.; Gao, J.; Wang, S. Compound Feedforward Control of Velocity Plus Acceleration for Linear Motor. Mach. Tool Hydraul. 2015, 43, 146–149. [Google Scholar]
- Yang, K. Research and Application on a Certain Number of Core Technologies of Fourier Transform Infrared Spectrometer. Ph.D. Dissertation, Wuhan University, Wuhan, China, 2010. [Google Scholar]
- Hsu, C.-F.; Wong, K.-Y. On-line constructive fuzzy sliding-mode control for voice coil motors. Appl. Soft Comput. 2016, 47, 415–423. [Google Scholar] [CrossRef]
- Chen, Q.; Li, L.; Wang, M.; Pei, L. The precise modeling and active disturbance rejection control of voice coil motor in high precision motion control system. Appl. Math. Model. 2015, 39, 5936–5948. [Google Scholar] [CrossRef]
- Li, Z.-h.; Chen, G.; Zhou, L. ADRC Algorithm for Position Control of Voice Coil Motor. J. Nanjing Inst. Technol. (Nat. Sci. Ed.) 2019, 17, 25–30. [Google Scholar]
- Wei, W.; Zhao, X. Fast Steering Mirror Control Based on Improved Active Disturbance Rejection. Infrared Technol. 2018, 40, 1071–1076. [Google Scholar]
- Li, W.-B.; Tian, D. A Three-closed-loop Feedward PID Servo Controller Based on S-curve. Technol. IoT AI 2021, 4, 021–029. [Google Scholar]
- Tan, E.; Shi, T.; Zhang, Z.; Zhang, L. Adaptive Feedforward Control for Reticle Stage of Lithography. Control Eng. China 2021, 28, 1069–1074. [Google Scholar]
- Azizi, M. Atomic orbital search: A novel metaheuristic algorithm. Appl. Math. Model. 2021, 93, 657–683. [Google Scholar] [CrossRef]
- Azizi, M.; Talatahari, S.; Giaralis, A. Optimization of Engineering Design Problems Using Atomic Orbital Search Algorithm. IEEE Access 2021, 9, 102497–102519. [Google Scholar] [CrossRef]
- Li, L.-H.; Zhang, Z.-Q.; Guo, Z.; Luo, Y.-Y.; Zhou, L.-Q.; Yao, J. Optimal order polynomial motion profile for high-precision flexible scanning platform. Opt. Precis. Eng. 2021, 29, 2400–2411. [Google Scholar] [CrossRef]
- Nguyen, K.D.; Ng, T.-C.; Chen, I.-M. On Algorithms for Planning S-Curve Motion Profiles. Int. J. Adv. Robot. Syst. 2008, 5, 99–106. [Google Scholar] [CrossRef]



| Parameter Names and Symbols | Value |
|---|---|
| Resistance of energized coil | |
| Inductance of energized coil | |
| Total mass of moving parts | |
| Damping coefficient | |
| Elastic coefficient |
| Parameter Name | Value |
|---|---|
| Number of electrons | 50 |
| Maximum number of layers | 5 |
| Foton rate | 0.4 |
| Dim | 5 |
| Max number of iterations | 25 |
| Upper limit | {30, 30, 100, 15, 40,000} |
| Lower limit | {1, 1, 1, 1, 10,000} |
| Weight matrix | {3, 10, 5} |
| Parameter | |||||
|---|---|---|---|---|---|
| Value | 16 | 6 | 60 | 11 | 30,000 |
| Error | Maximum Error | Minimum Error | Average Error | STD of Error |
|---|---|---|---|---|
| ) | 6.25 | 0.00 | 1.95 | 1.40 |
| ) | 0.30 | 0.00 | 0.07 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhi, L.; Huang, M.; Wen, Q.; Gao, H.; Han, W. Design of an Optical Path Scanning Control System in a Portable Fourier Transform Spectrometer Based on Adaptive Feedforward–Nonlinear Proportional-Integral Cascade Composite Control. Actuators 2024, 13, 35. https://doi.org/10.3390/act13010035
Zhi L, Huang M, Wen Q, Gao H, Han W. Design of an Optical Path Scanning Control System in a Portable Fourier Transform Spectrometer Based on Adaptive Feedforward–Nonlinear Proportional-Integral Cascade Composite Control. Actuators. 2024; 13(1):35. https://doi.org/10.3390/act13010035
Chicago/Turabian StyleZhi, Liangjie, Min Huang, Qin Wen, Han Gao, and Wei Han. 2024. "Design of an Optical Path Scanning Control System in a Portable Fourier Transform Spectrometer Based on Adaptive Feedforward–Nonlinear Proportional-Integral Cascade Composite Control" Actuators 13, no. 1: 35. https://doi.org/10.3390/act13010035
APA StyleZhi, L., Huang, M., Wen, Q., Gao, H., & Han, W. (2024). Design of an Optical Path Scanning Control System in a Portable Fourier Transform Spectrometer Based on Adaptive Feedforward–Nonlinear Proportional-Integral Cascade Composite Control. Actuators, 13(1), 35. https://doi.org/10.3390/act13010035








