Thrust Model and Trajectory Design of an Interplanetary CubeSat with a Hybrid Propulsion System
Abstract
:1. Introduction
2. Problem Description and Mathematical Model
2.1. HPS Analytical Thrust Model
2.2. Description of the Trajectory Optimization Process
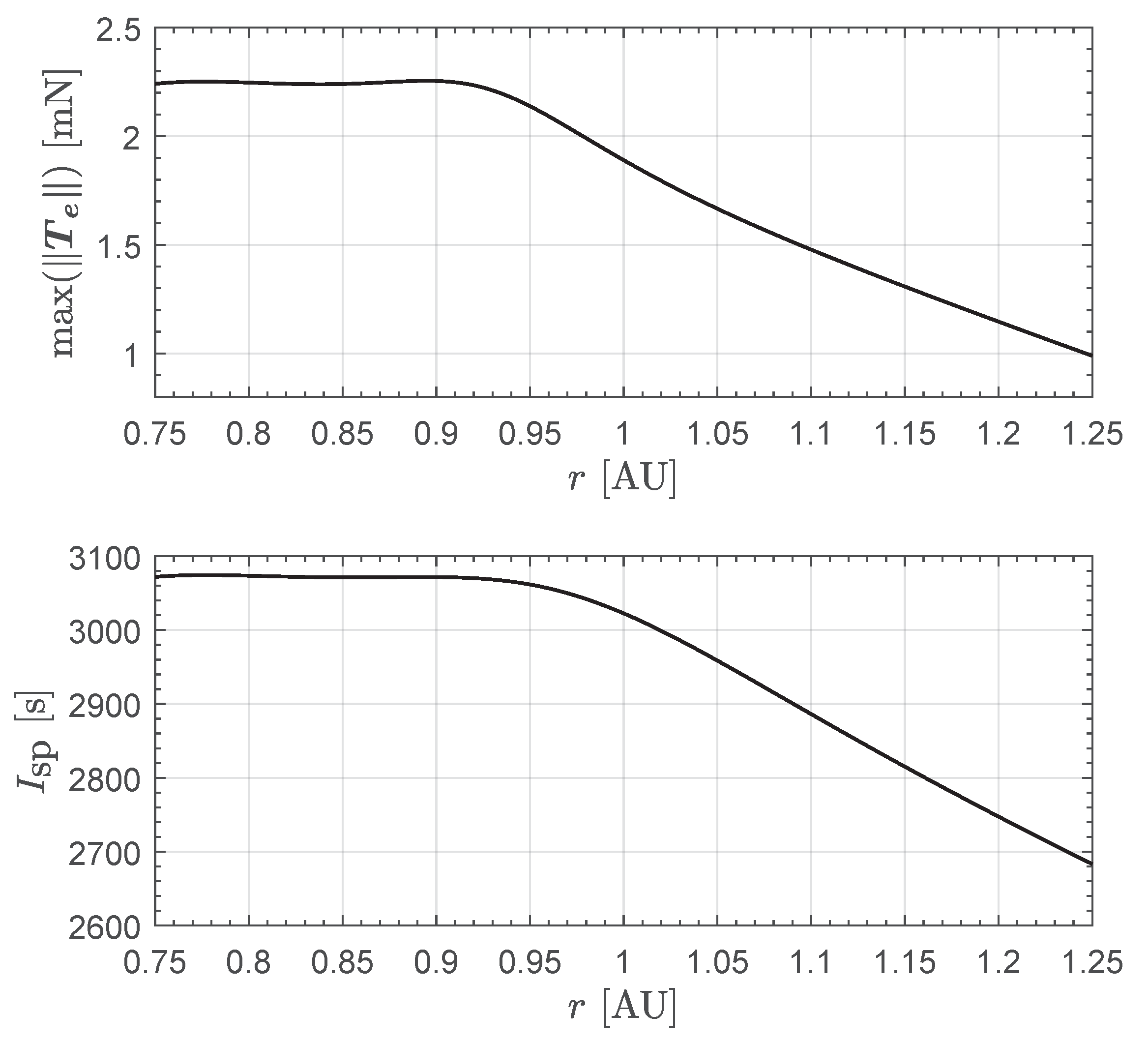
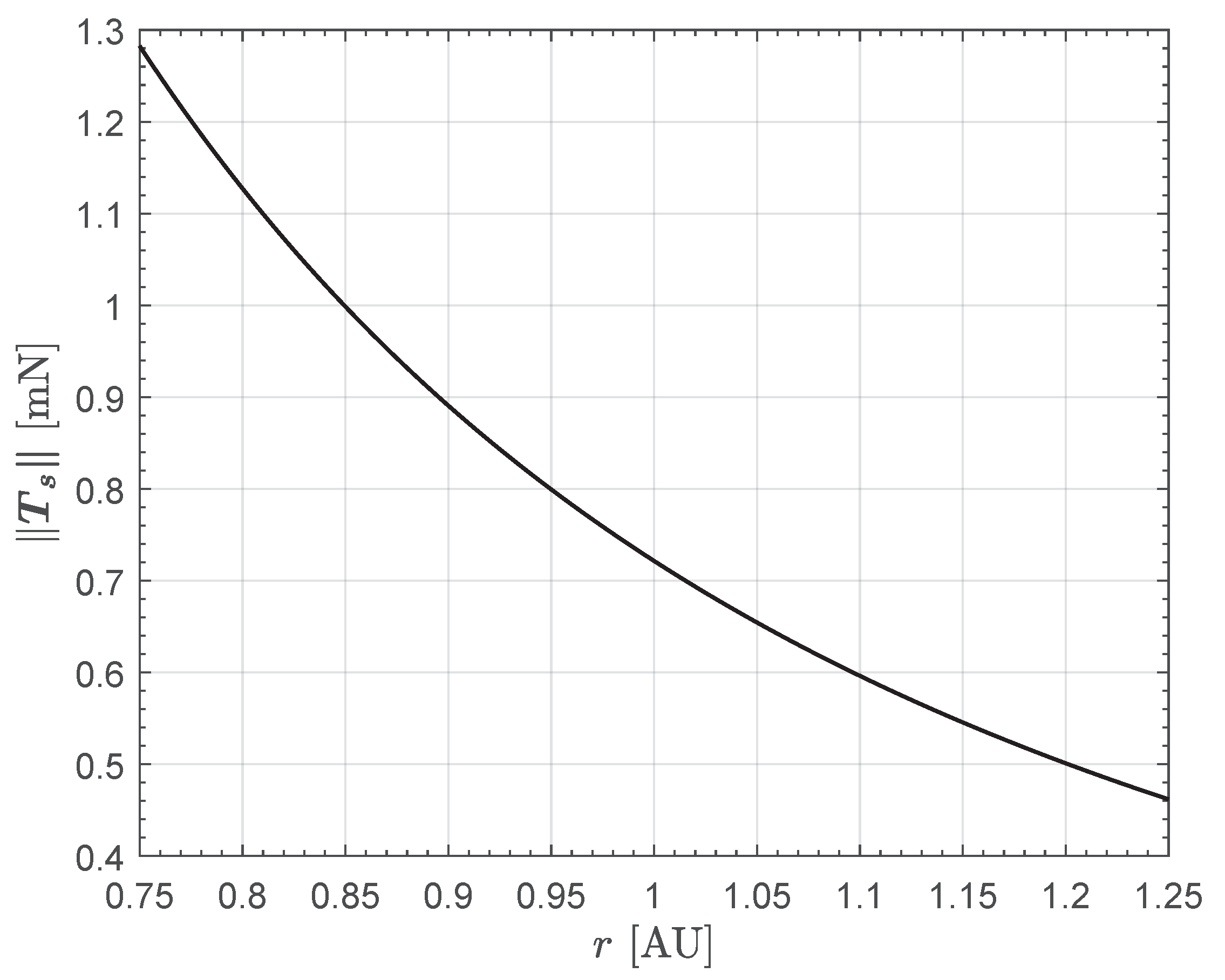
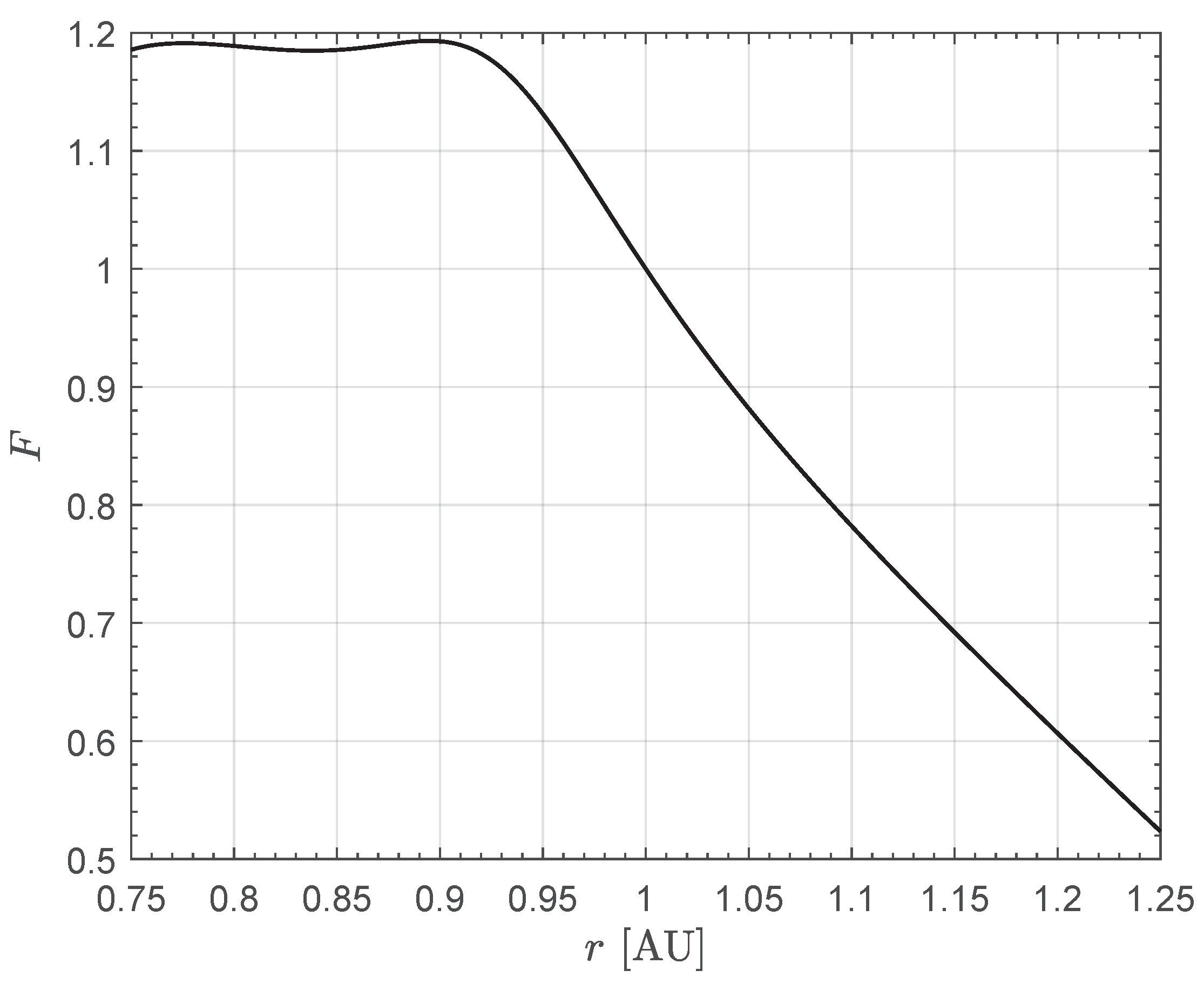
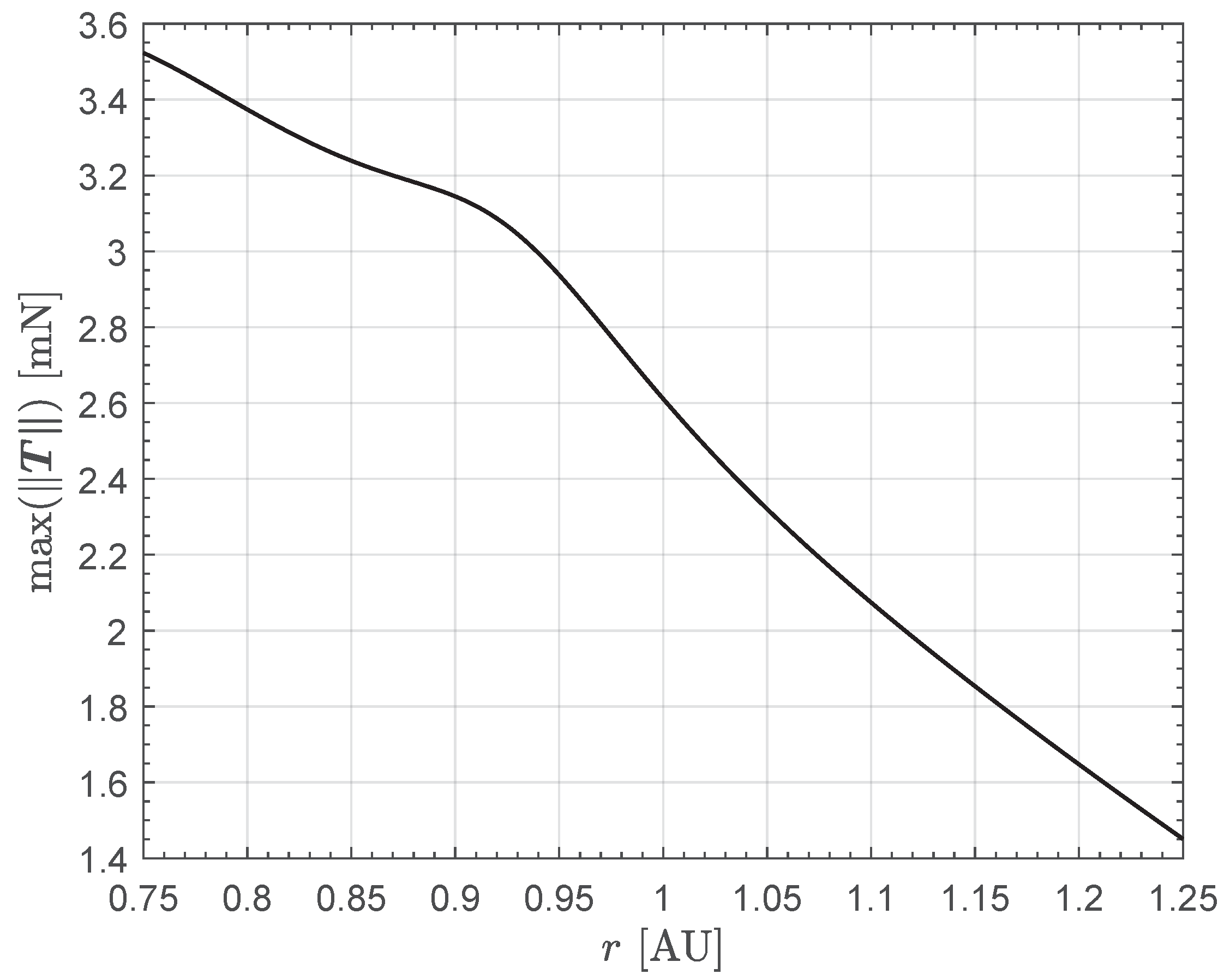
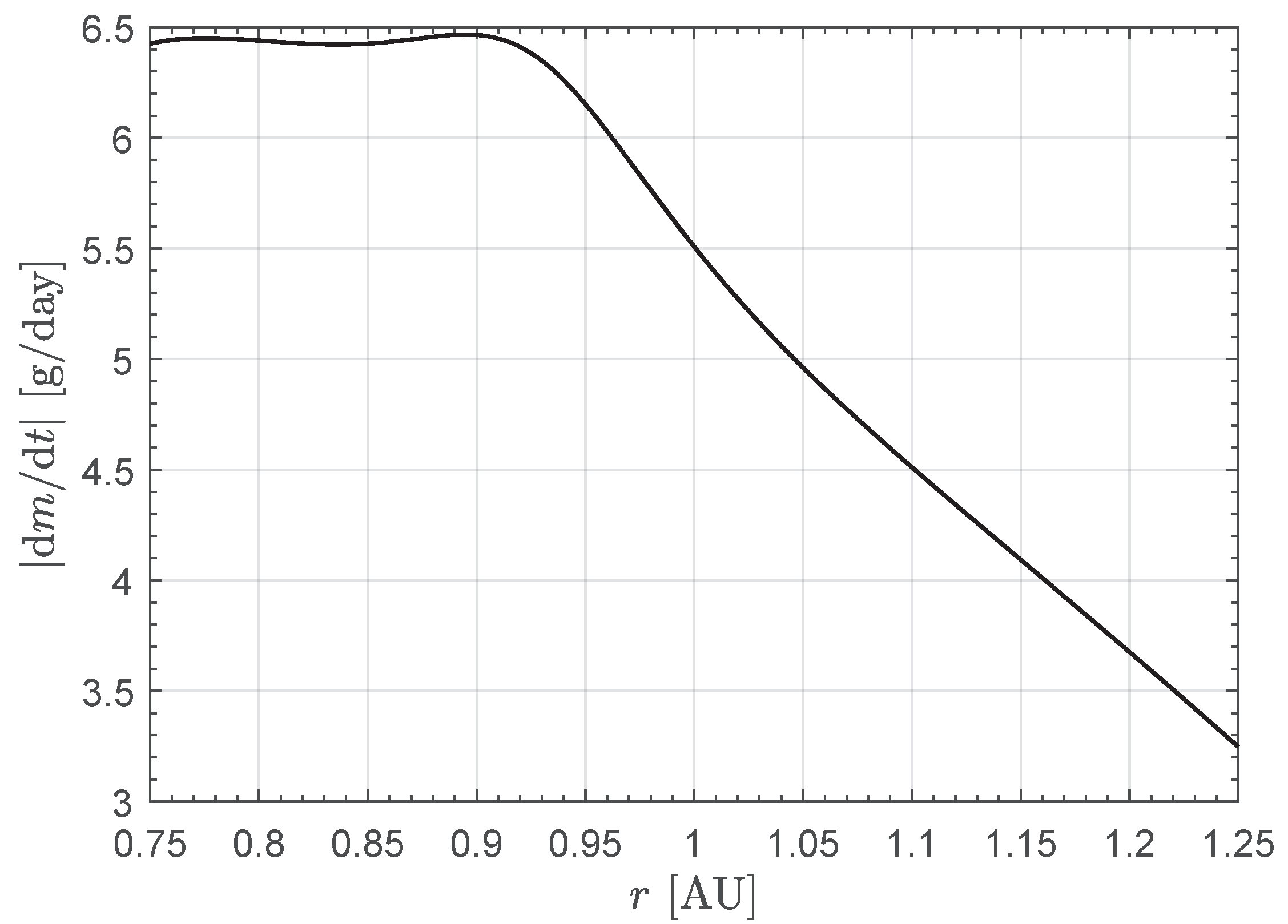
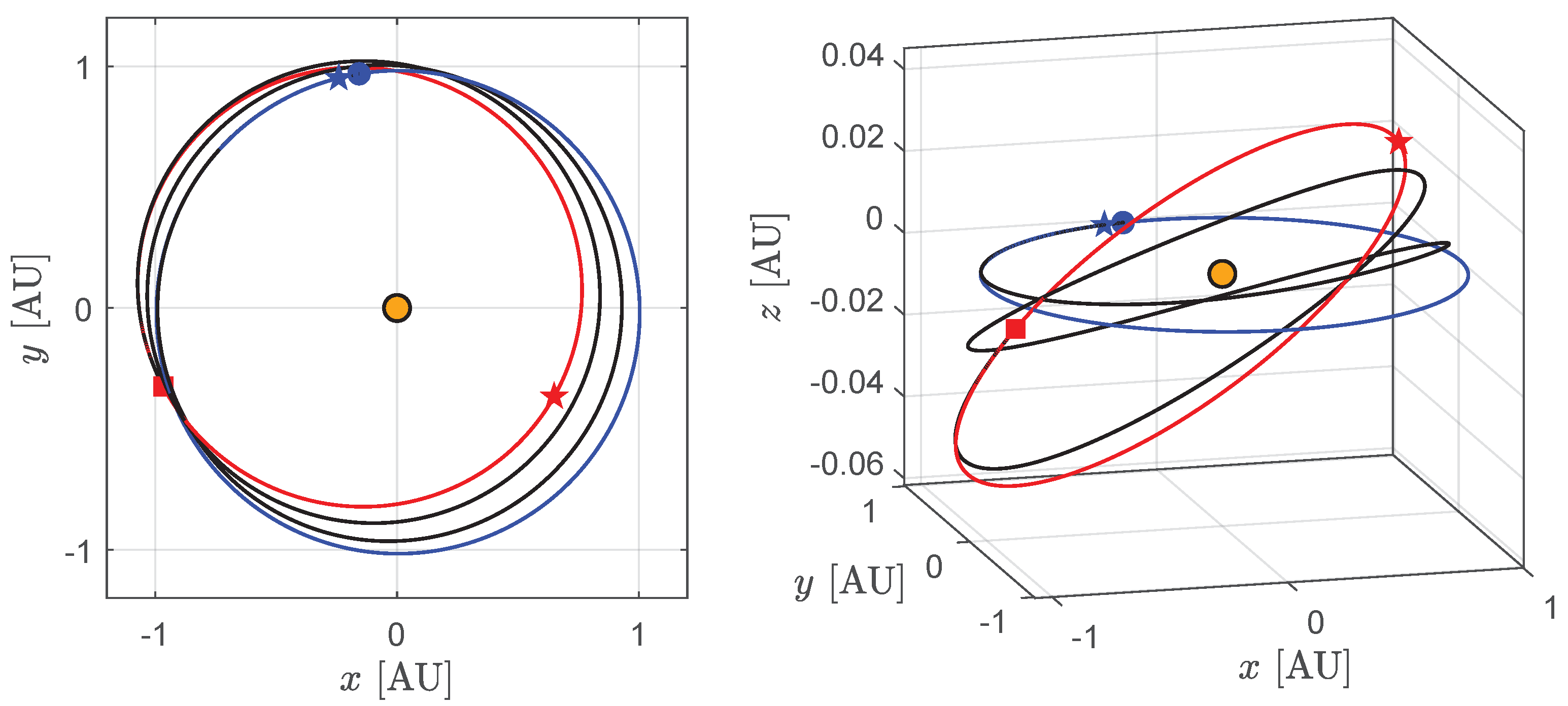
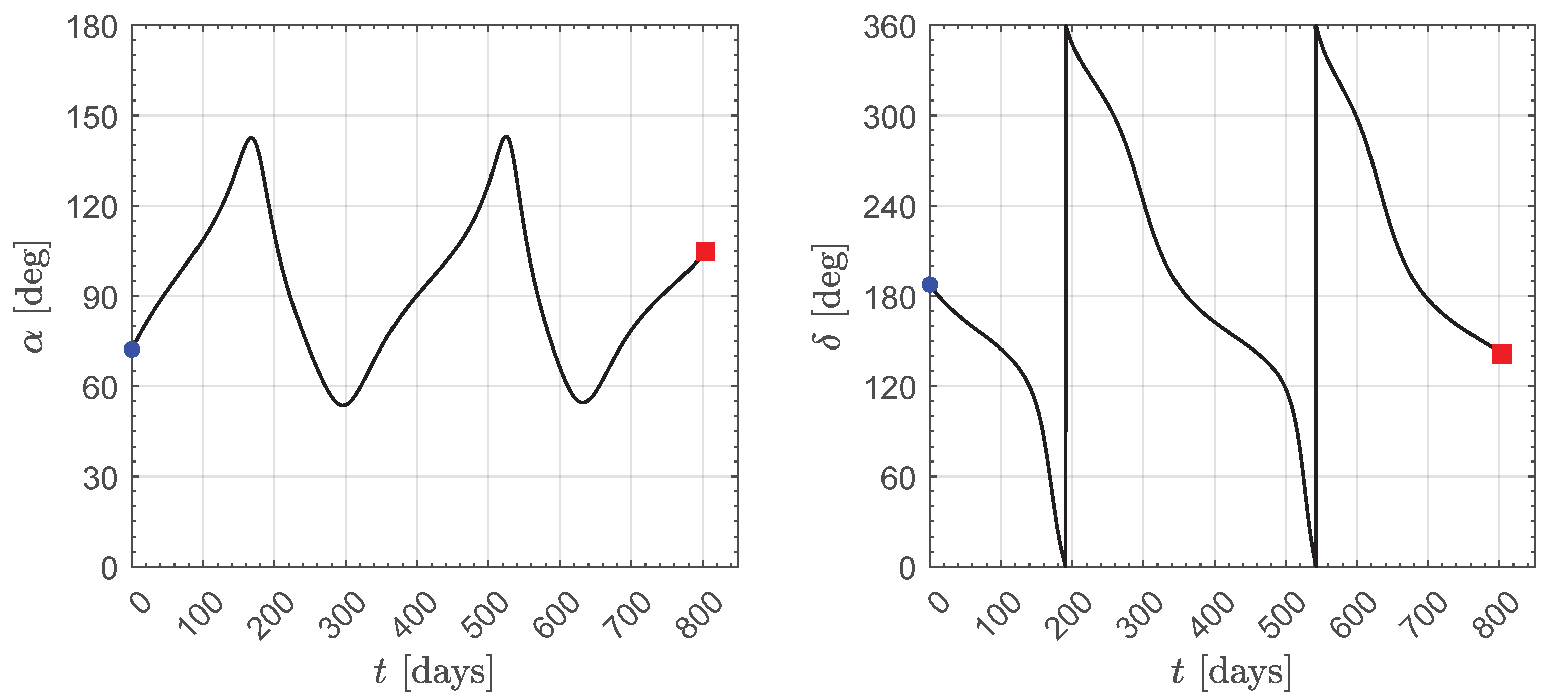
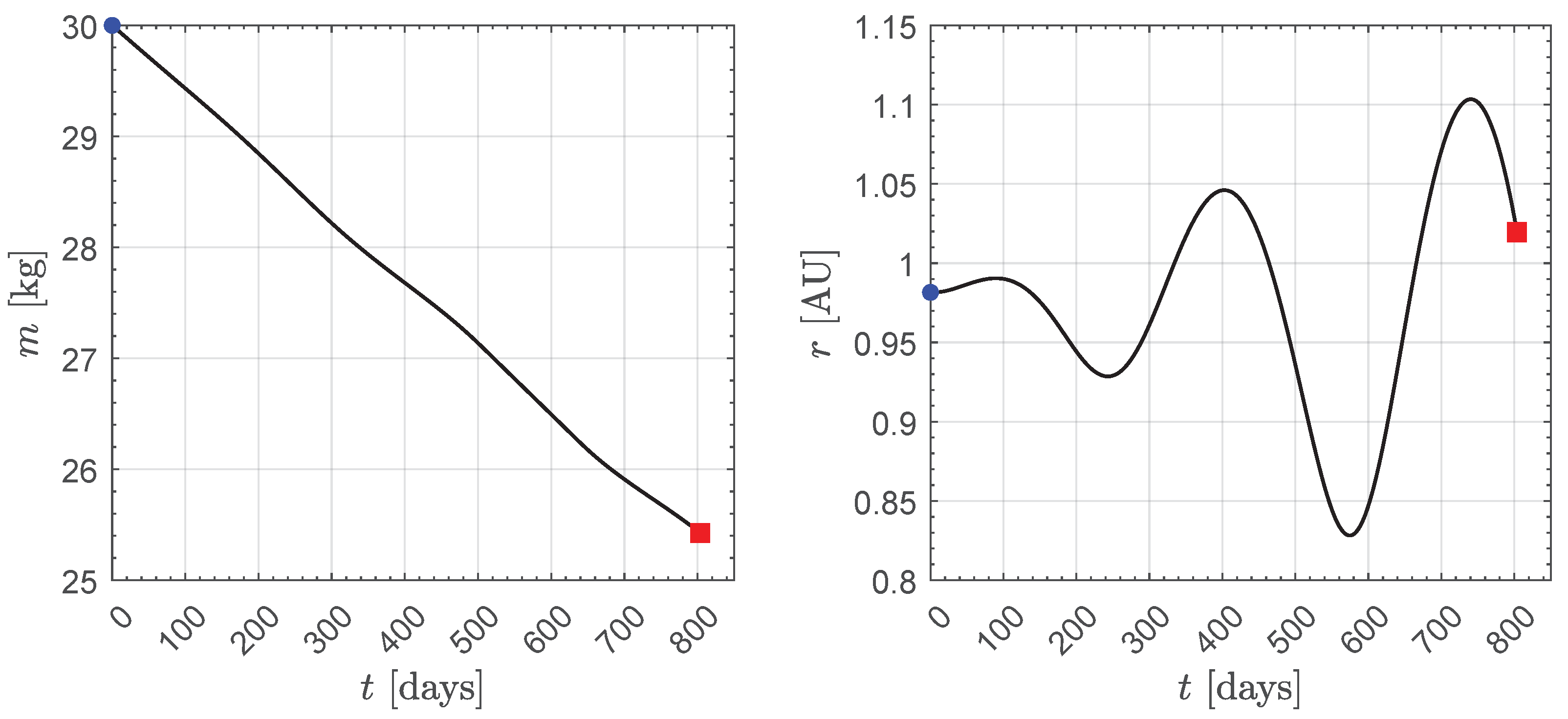
3. Results of Numerical Simulations and Parametric Study
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Mathematical Model of the Electric Thruster-Induced Propulsive Acceleration

Appendix B. Mathematical Model of the Solar Sail-Induced Propulsive Acceleration

References
- Brophy, J.R.; Noca, M. Electric Propulsion for Solar System Exploration. J. Propuls. Power 1998, 14, 700–707. [Google Scholar] [CrossRef]
- Burke, L.M.; Falck, R.D.; McGuire, M.L. Interplanetary Mission Design Handbook: Earth-to-Mars Mission Opportunities 2026 to 2045; techreport NASA/TM—2010-216764; National Aeronautics and Space Administration: Cleveland, OH, USA, 2010. [Google Scholar]
- Urrios, J.; Pacheco-Ramos, G.; Vazquez, R. Optimal planning and guidance for Solar System exploration using Electric Solar Wind Sails. Acta Astronaut. 2024, 217, 116–129. [Google Scholar] [CrossRef]
- Staehle, R.; Blaney, D.; Hemmati, H.; Jones, D.; Klesh, A.; Liewer, P.; Lazio, J.; Wen-Yu Lo, M.; Mouroulis, P.; Murphy, N.; et al. Interplanetary CubeSat Architecture and Missions, In Proceedings of the AIAA SPACE 2012 Conference & Exposition, Pasadena, CA, USA, 11–13 September 2012. [CrossRef]
- Schoolcraft, J.; Klesh, A.; Werne, T. MarCO: Interplanetary Mission Development on a CubeSat Scale. In Space Operations: Contributions from the Global Community; Springer International Publishing: Berlin, Germany, 2017; Chapter 10; pp. 221–231. [Google Scholar] [CrossRef]
- Malphrus, B.K.; Freeman, A.; Staehle, R.; Klesh, A.T.; Walker, R. Interplanetary CubeSat missions. In CubeSat Handbook: From Mission Design to Operations; Cappelletti, C., Battistini, S., Malphrus, B.K., Eds.; Academic Press: London, UK, 2021; Chapter 4; pp. 85–121. [Google Scholar] [CrossRef]
- Freeman, A.; Malphrus, B.K.; Staehle, R. CubeSat science instruments. In CubeSat Handbook: From Mission Design to Operations; Cappelletti, C., Battistini, S., Malphrus, B.K., Eds.; Academic Press: London, UK, 2021; Chapter 3; pp. 67–83. [Google Scholar] [CrossRef]
- Schoolcraft, J.; Klesh, A.T.; Werne, T. MarCO: Interplanetary mission development on a cubesat scale. In Proceedings of the SpaceOps 2016 Conference, Daejeon, Republic of Korea, 16–20 May 2016. [Google Scholar] [CrossRef]
- Klesh, A.T. MARCO: Flight results from the first interplanetary CubeSat mission. In Proceedings of the 70th Annual International Astronautical Congress, Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Gutierrez, G.; Riccobono, D.; Bruno, E.; Bonariol, T.; Vigna, L.; Reverberi, G.; Fazzoletto, E.; Cotugno, B.; Vitiello, A.; Saita, G.; et al. LICIACube: Mission Outcomes of Historic Asteroid Fly-By Performed by a CubeSat. In Proceedings of the 2024 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2024. [Google Scholar] [CrossRef]
- Franzese, V.; Topputo, F. Celestial Bodies Far-Range Detection with Deep-Space CubeSats. Sensors 2023, 23, 4544. [Google Scholar] [CrossRef]
- Cervone, A.; Topputo, F.; Franzese, V.; Pérez-Silva, A.R.; Leon, B.B.; Garcia, B.D.; Minacapilli, P.; Rosa, P.; Bay, G.; Radu, S. The path towards increasing RAMS for novel complex missions based on CubeSat technology. CEAS Space J. 2023, 16, 203–224. [Google Scholar] [CrossRef]
- Mitchell, A.M.; Panicucci, P.; Franzese, V.; Topputo, F.; Linares, R. Improved detection of a Near-Earth Asteroid from an interplanetary CubeSat mission. Acta Astronaut. 2024, 223, 685–692. [Google Scholar] [CrossRef]
- Lemmer, K. Propulsion for CubeSats. Acta Astronaut. 2017, 134, 231–243. [Google Scholar] [CrossRef]
- Alnaqbi, S.; Darfilal, D.; Swei, S.S.M. Propulsion Technologies for CubeSats: Review. Aerospace 2024, 11, 502. [Google Scholar] [CrossRef]
- O’Reilly, D.; Herdrich, G.; Kavanagh, D.F. Electric Propulsion Methods for Small Satellites: A Review. Aerospace 2021, 8, 22. [Google Scholar] [CrossRef]
- Yeo, S.H.; Ogawa, H.; Kahnfeld, D.; Schneider, R. Miniaturization perspectives of electrostatic propulsion for small spacecraft platforms. Prog. Aerosp. Sci. 2021, 126, 100742. [Google Scholar] [CrossRef]
- Grönland, T.A.; Rangsten, P.; Nese, M.; Lang, M. Miniaturization of components and systems for space using MEMS-technology. Acta Astronaut. 2007, 61, 228–233. [Google Scholar] [CrossRef]
- Alvara, A.N.; Lee, L.; Sin, E.; Lambert, N.; Westphal, A.J.; Pister, K.S. BLISS: Interplanetary exploration with swarms of low-cost spacecraft. Acta Astronaut. 2024, 215, 348–361. [Google Scholar] [CrossRef]
- Shukla, H.; Velidi, G. Energetic material characterization and ignition study of MEMS based micro-thruster for multi spacecrafts missions. FirePhysChem 2024, 4, 122–130. [Google Scholar] [CrossRef]
- Kabirov, V.; Semenov, V.; Torgaeva, D.; Otto, A. Miniaturization of spacecraft electrical power systems with solar-hydrogen power supply system. Int. J. Hydrogen Energy 2023, 48, 9057–9070. [Google Scholar] [CrossRef]
- Janhunen, P. Electric sail for spacecraft propulsion. J. Propuls. Power 2004, 20, 763–764. [Google Scholar] [CrossRef]
- Janhunen, P.; Sandroos, A. Simulation study of solar wind push on a charged wire: Basis of solar wind electric sail propulsion. Ann. Geophys. 2007, 25, 755–767. [Google Scholar] [CrossRef]
- Janhunen, P.; Toivanen, P.K.; Polkko, J.; Merikallio, S.; Salminen, P.; Haeggström, E.; Seppänen, H.; Kurppa, R.; Ukkonen, J.; Kiprich, S.; et al. Electric solar wind sail: Toward test missions. Rev. Sci. Instrum. 2010, 81, 111301. [Google Scholar] [CrossRef]
- Bassetto, M.; Niccolai, L.; Quarta, A.A.; Mengali, G. A comprehensive review of Electric Solar Wind Sail concept and its applications. Prog. Aerosp. Sci. 2022, 128, 1–27. [Google Scholar] [CrossRef]
- Gong, S.; Macdonald, M. Review on solar sail technology. Astrodynamics 2019, 3, 93–125. [Google Scholar] [CrossRef]
- Fu, B.; Sperber, E.; Eke, F. Solar sail technology—A state of the art review. Prog. Aerosp. Sci. 2016, 86, 1–19. [Google Scholar] [CrossRef]
- Tsuda, Y.; Mori, O.; Funase, R.; Sawada, H.; Yamamoto, T.; Saiki, T.; Endo, T.; Kawaguchi, J. Flight status of IKAROS deep space solar sail demonstrator. Acta Astronaut. 2011, 69, 833–840. [Google Scholar] [CrossRef]
- Tsuda, Y.; Mori, O.; Funase, R.; Sawada, H.; Yamamoto, T.; Saiki, T.; Endo, T.; Yonekura, K.; Hoshino, H.; Kawaguchi, J. Achievement of IKAROS—Japanese deep space solar sail demonstration mission. Acta Astronaut. 2013, 82, 183–188. [Google Scholar] [CrossRef]
- Mughal, M.R.; Praks, J.; Vainio, R.; Janhunen, P.; Envall, J.; Näsilä, A.; Oleynik, P.; Niemelä, P.; Nyman, S.; Slavinskis, A.; et al. Aalto-1, multi-payload CubeSat: In-orbit results and lessons learned. Acta Astronaut. 2021, 187, 557–568. [Google Scholar] [CrossRef]
- Dalbins, J.; Allaje, K.; Iakubivskyi, I.; Kivastik, J.; Komarovskis, R.O.; Plans, M.; Sünter, I.; Teras, H.; Ehrpais, H.; Ilbis, E.; et al. ESTCube-2: The Experience of Developing a Highly Integrated CubeSat Platform. In Proceedings of the 2022 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022; pp. 1–16. [Google Scholar] [CrossRef]
- Palos, M.F.; Janhunen, P.; Toivanen, P.; Tajmar, M.; Iakubivskyi, I.; Micciani, A.; Orsini, N.; Kütt, J.; Rohtsalu, A.; Dalbins, J.; et al. Electric Sail Mission Expeditor, ESME: Software Architecture and Initial ESTCube Lunar Cubesat E-sail Experiment Design. Aerospace 2023, 10, 694. [Google Scholar] [CrossRef]
- Boni, L.; Bassetto, M.; Niccolai, L.; Mengali, G.; Quarta, A.A.; Circi, C.; Pellegrini, R.C.; Cavallini, E. Structural response of Helianthus solar sail during attitude maneuvers. Aerosp. Sci. Technol. 2023, 133, 1–9. [Google Scholar] [CrossRef]
- Zhao, P.; Wu, C.; Li, Y. Design and application of solar sailing: A review on key technologies. Chin. J. Aeronaut. 2023, 36, 125–144. [Google Scholar] [CrossRef]
- Berg, S.P.; Rovey, J.L. Assessment of Multimode Spacecraft Micropropulsion Systems. J. Spacecr. Rocket. 2017, 54, 592–601. [Google Scholar] [CrossRef]
- Rovey, J.L.; Lyne, C.T.; Mundahl, A.J.; Rasmont, N.; Glascock, M.S.; Wainwright, M.J.; Berg, S.P. Review of multimode space propulsion. Prog. Aerosp. Sci. 2020, 118, 100627. [Google Scholar] [CrossRef]
- Vulpetti, G. Missions to the heliopause and beyond by staged propulsion spacecrafts. In Proceedings of the 43rd International Astronautical Congress, Washington, DC, USA, 28 August–5 September 1992. [Google Scholar]
- Baig, S.; McInnes, C.R. Artificial Three-Body Equilibria for Hybrid Low-Thrust Propulsion. J. Guid. Control. Dyn. 2008, 31, 1644–1655. [Google Scholar] [CrossRef]
- Li, T.; Wang, Z.; Zhang, Y. Multi-objective trajectory optimization for a hybrid propulsion system. Adv. Space Res. 2018, 62, 1102–1113. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Tradeoff performance of hybrid low-thrust propulsion system. J. Spacecr. Rocket. 2007, 44, 1263–1270. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Trajectory design with hybrid low-thrust propulsion system. J. Guid. Control. Dyn. 2007, 30, 419–426. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Trajectory analysis and optimization of Hesperides mission. Universe 2022, 8, 364. [Google Scholar] [CrossRef]
- Ceriotti, M.; McInnes, C.R. Hybrid solar sail and solar electric propulsion for novel Earth observation missions. Acta Astronaut. 2011, 69, 809–821. [Google Scholar] [CrossRef]
- Ceriotti, M.; McInnes, C.R. An Earth pole-sitter using hybrid propulsion. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Toronto, Canada, 2–5 August 2010. [Google Scholar] [CrossRef]
- Ceriotti, M.; McInnes, C.R. Generation of optimal trajectories for Earth hybrid pole sitters. J. Guid. Control. Dyn. 2011, 34, 847–859. [Google Scholar] [CrossRef]
- Matloff, G.L. The solar photon thruster as a terrestrial pole sitter. Ann. N. Y. Acad. Sci. 2004, 1017, 468–474. [Google Scholar] [CrossRef]
- Dachwald, B.; Seboldt, W.; Macdonald, M.; Mengali, G.; Quarta, A.; McInnes, C.; Rios-Reyes, L.; Scheeres, D.; Wie, B.; Görlich, M.; et al. Potential Solar Sail Degradation Effects on Trajectory and Attitude Control. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, CA, USA, 15–18 August, 2005. [Google Scholar] [CrossRef]
- Dachwald, B.; Macdonald, M.; McInnes, C.R.; Mengali, G.; Quarta, A.A. Impact of optical degradation on solar sail mission performance. J. Spacecr. Rocket. 2007, 44, 740–749. [Google Scholar] [CrossRef]
- McInnes, C.R. Orbits in a Generalized Two-Body Problem. J. Guid. Control. Dyn. 2003, 26, 743–749. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Optimal control laws for axially symmetric solar sails. J. Spacecr. Rocket. 2005, 42, 1130–1133. [Google Scholar] [CrossRef]
- Li, Y.; Cheah, K.H. Solar sail as propellant-less micropropulsion. In Space Micropropulsion for Nanosatellites; Cheah, K.H., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; Chapter 10; pp. 273–284. [Google Scholar] [CrossRef]
- Quarta, A.A. Continuous-Thrust Circular Orbit Phasing Optimization of Deep Space CubeSats. Appl. Sci. 2024, 14, 7059. [Google Scholar] [CrossRef]
- Franzese, V.; Topputo, F.; Ankersen, F.; Walker, R. Deep-Space Optical Navigation for M-ARGO Mission. J. Astronaut. Sci. 2021, 68, 1034–1055. [Google Scholar] [CrossRef]
- Topputo, F.; Wang, Y.; Giordano, C.; Franzese, V.; Goldberg, H.; Perez-Lissi, F.; Walker, R. Envelop of reachable asteroids by M-ARGO CubeSat. Adv. Space Res. 2021, 67, 4193–4221. [Google Scholar] [CrossRef]
- Franzese, V.; Giordano, C.; Wang, Y.; Topputo, F.; Goldberg, H.; Gonzalez, A.; Walker, R. Target selection for M-ARGO interplanetary cubesat. In Proceedings of the 71st International Astronautical Congress, Virtual Event, 12–14 October 2020. [Google Scholar]
- McNutt, L.; Johnson, L.; Clardy, D.; Castillo-Rogez, J.; Frick, A.; Jones, L. Near-earth asteroid scout. In Proceedings of the AIAA SPACE 2014 Conference and Exposition, San Diego, CA, USA, 4–7 August 2014. [Google Scholar]
- Johnson, L.; Castillo-Rogez, J.; Lockett, T. Near Earth asteroid Scout: Exploring asteroid 1991VG using a Smallsat. In Proceedings of the 70th International Astronautical Congress, Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Lockett, T.R.; Castillo-Rogez, J.; Johnson, L.; Matus, J.; Lightholder, J.; Marinan, A.; Few, A. Near-Earth Asteroid Scout Flight Mission. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 20–29. [Google Scholar] [CrossRef]
- Heaton, A.; Miller, K.; Ahmad, N. Near earth asteroid Scout solar sail thrust and torque model. In Proceedings of the 4th International Symposium on Solar Sailing (ISSS 2017), Kyoyo, Japan, 17–20 January 2017. [Google Scholar]
- Pezent, J.; Sood, R.; Heaton, A. High-fidelity contingency trajectory design and analysis for NASA’s near-earth asteroid (NEA) Scout solar sail Mission. Acta Astronaut. 2019, 159, 385–396. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G.; Bassetto, M. Rapid orbit-to-orbit transfer to asteroid 4660 Nereus using Solar Electric Propulsion. Universe 2023, 9, 459. [Google Scholar] [CrossRef]
- Fan, Z.; Huo, M.; Quarta, A.A.; Mengali, G.; Qi, N. Improved Monte Carlo Tree Search-based Approach to Low-thrust Multiple Gravity assist Trajectory Design. Aerosp. Sci. Technol. 2022, 130, 1–8. [Google Scholar] [CrossRef]
- Bryson, A.E.; Ho, Y.C. Applied Optimal Control; Hemisphere Publishing Corporation: New York, NY, USA, 1975; Chapter 2; pp. 71–89. ISBN 0-891-16228-3. [Google Scholar]
- Stengel, R.F. Optimal Control and Estimation; Dover Books on Mathematics, Dover Publications, Inc.: New York, NY, USA, 1994; pp. 222–254. [Google Scholar]
- Ross, I.M. A Primer on Pontryagin’s Principle in Optimal Control; Collegiate Publishers: San Francisco, CA, USA, 2015; Chapter 2; pp. 127–129. [Google Scholar]
- Prussing, J.E. Optimal Spacecraft Trajectories; Oxford University press: Oxford, UK, 2018; Chapter 4; pp. 32–40. [Google Scholar]
- Prussing, J.E. Spacecraft Trajectory Optimization; Cambridge University Press: Cambridge, UK, 2010; Chapter 2; pp. 16–36. [Google Scholar] [CrossRef]
- Walker, M.J.H.; Ireland, B.; Owens, J. A set of modified equinoctial orbit elements. Celest. Mech. 1985, 36, 409–419, Erratum in Celest. Mech. 1986, 38, 391–392. [Google Scholar] [CrossRef]
- Quarta, A.A. Initial costate approximation for rapid orbit raising with very low propulsive acceleration. Appl. Sci. 2024, 14, 1124. [Google Scholar] [CrossRef]
- Boni, L.; Bassetto, M.; Quarta, A.A. Characterization of a solar sail membrane for Abaqus-Based Simulations. Aerospace 2024, 11, 151. [Google Scholar] [CrossRef]
- Boni, L.; Mengali, G.; Quarta, A.A. Finite Element Analysis of Solar Sail Force Model with Mission Application. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 1838–1846. [Google Scholar] [CrossRef]
- McInnes, C.R. Solar Sailing: Technology, Dynamics and Mission Applications; Springer-Praxis Series in Space Science and Technology; Springer-Verlag: Berlin, Germany, 1999; pp. 46–54. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Optimal three-dimensional interplanetary rendezvous using nonideal solar sail. J. Guid. Control. Dyn. 2005, 28, 173–177. [Google Scholar] [CrossRef]

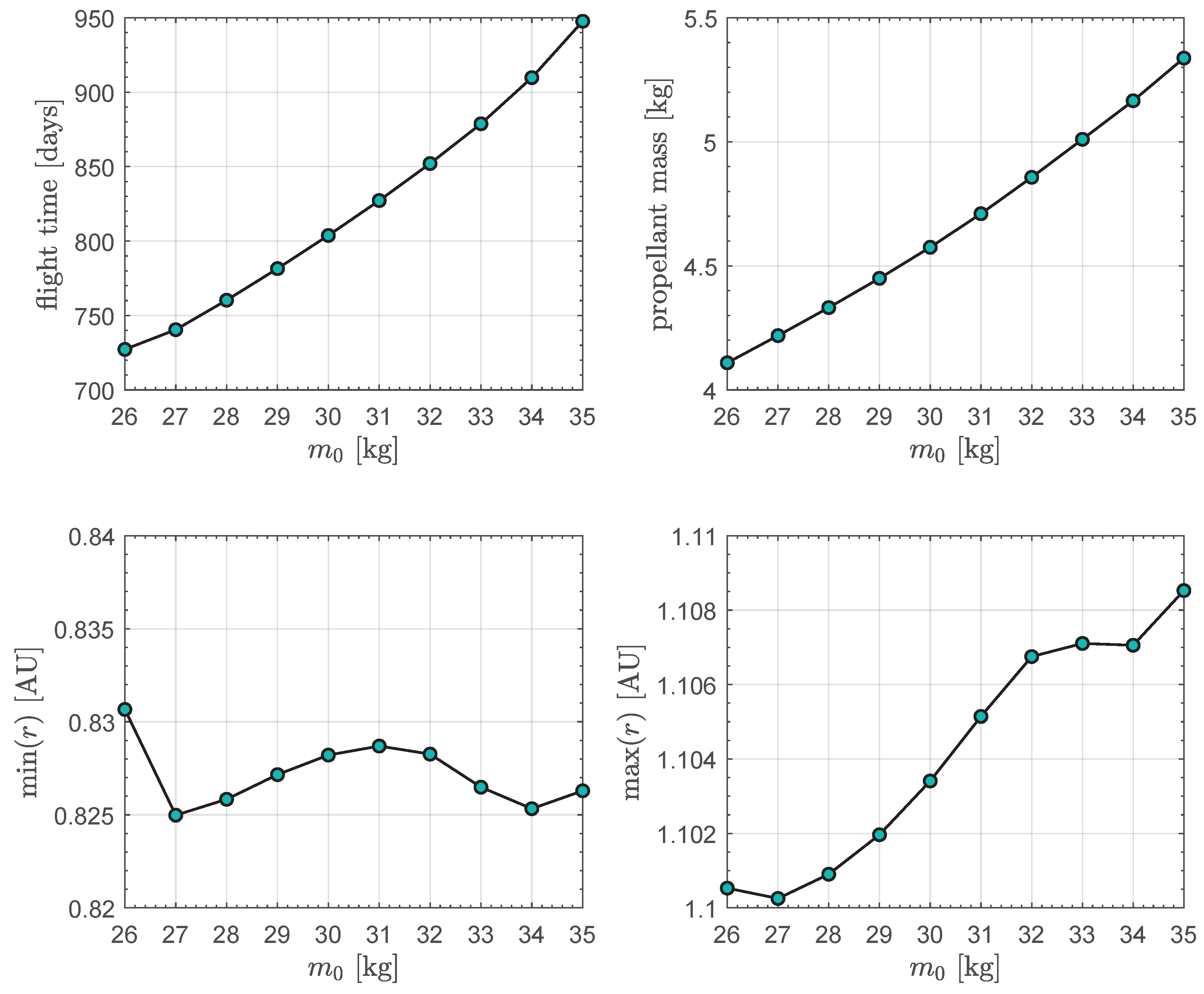
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quarta, A.A. Thrust Model and Trajectory Design of an Interplanetary CubeSat with a Hybrid Propulsion System. Actuators 2024, 13, 384. https://doi.org/10.3390/act13100384
Quarta AA. Thrust Model and Trajectory Design of an Interplanetary CubeSat with a Hybrid Propulsion System. Actuators. 2024; 13(10):384. https://doi.org/10.3390/act13100384
Chicago/Turabian StyleQuarta, Alessandro A. 2024. "Thrust Model and Trajectory Design of an Interplanetary CubeSat with a Hybrid Propulsion System" Actuators 13, no. 10: 384. https://doi.org/10.3390/act13100384
APA StyleQuarta, A. A. (2024). Thrust Model and Trajectory Design of an Interplanetary CubeSat with a Hybrid Propulsion System. Actuators, 13(10), 384. https://doi.org/10.3390/act13100384




