Bionic Walking Control of a Biped Robot Based on CPG Using an Improved Particle Swarm Algorithm
Abstract
1. Introduction
2. Biped Bionic Walking Control Based on CPG
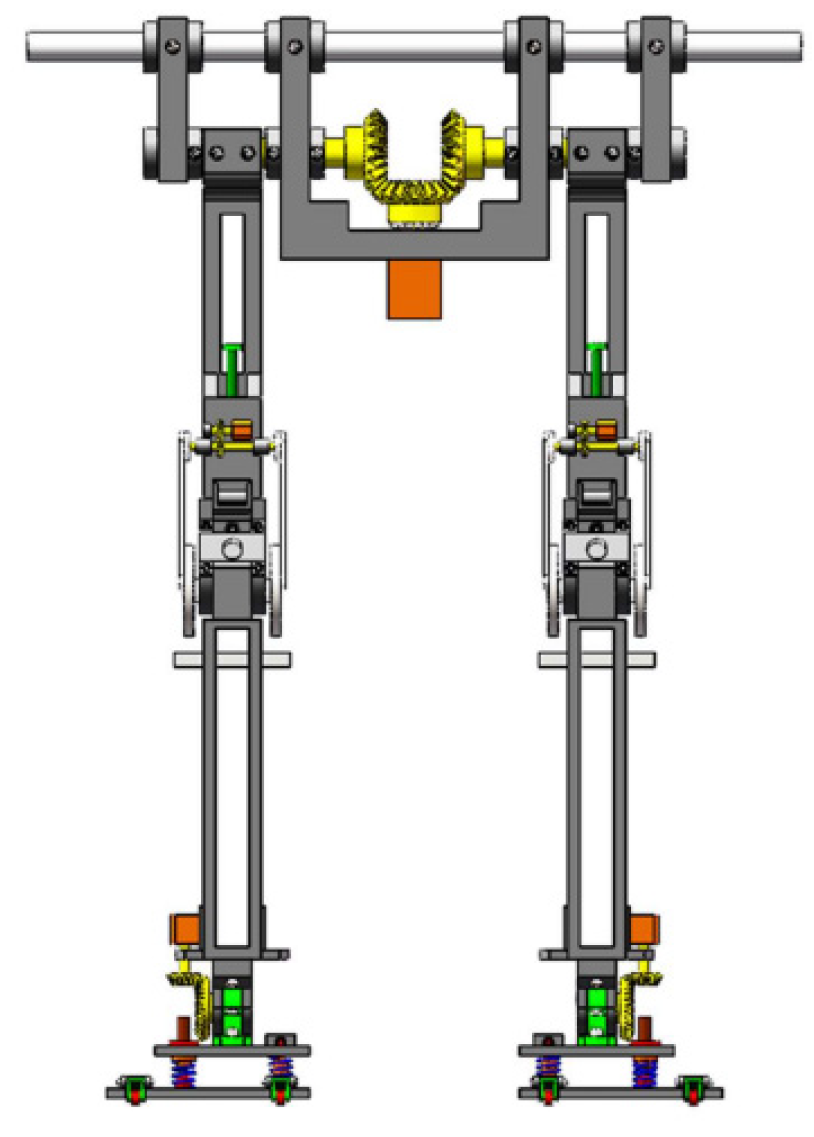
2.1. Structural Design of the Biped Robot
2.2. Design of the Bionic Walking Control of the Biped Based on CPG
3. Improved Design of the Particle Swarm Optimization Algorithm
3.1. Overview of the Traditional Particle Swarm Optimization Algorithm
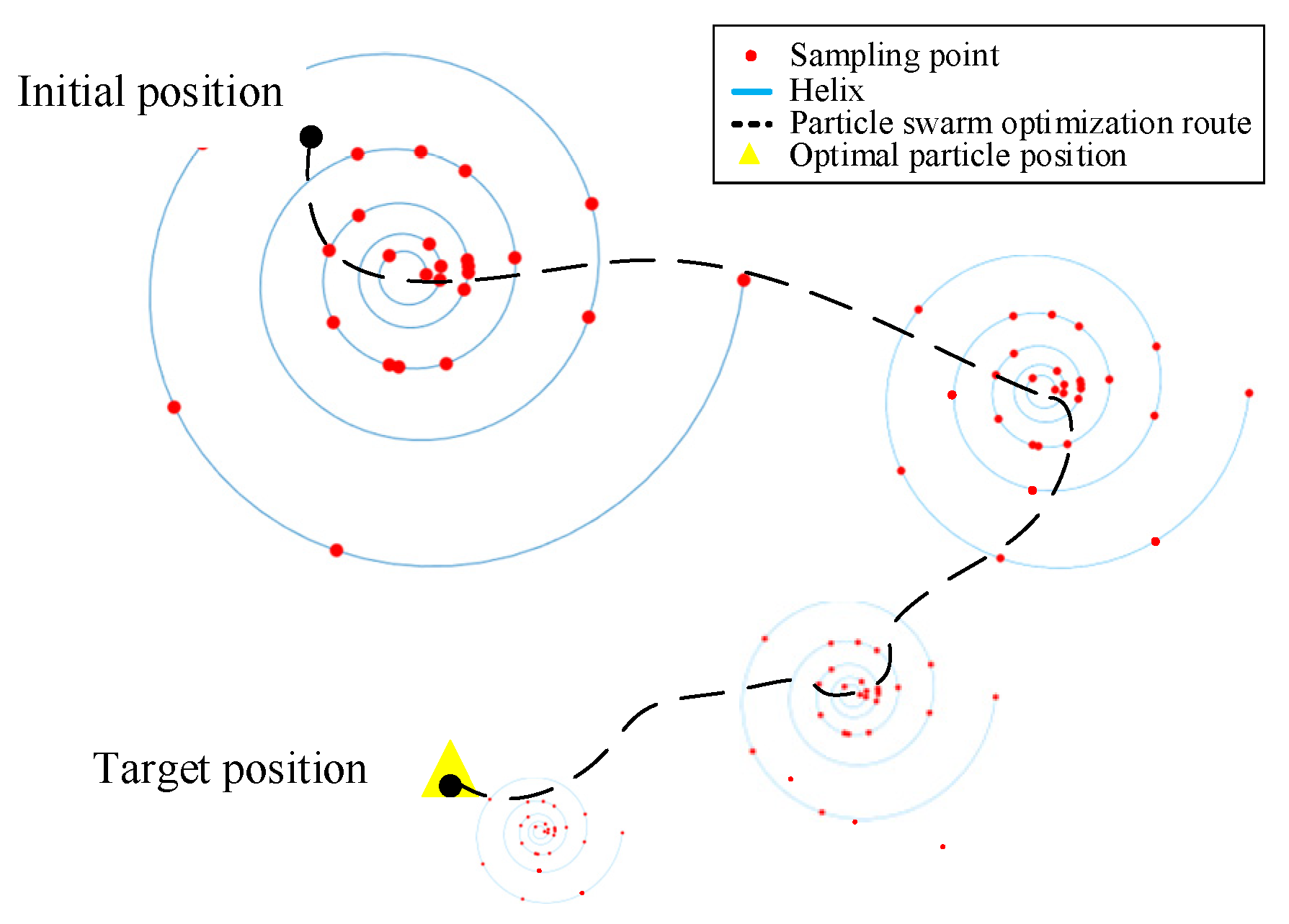
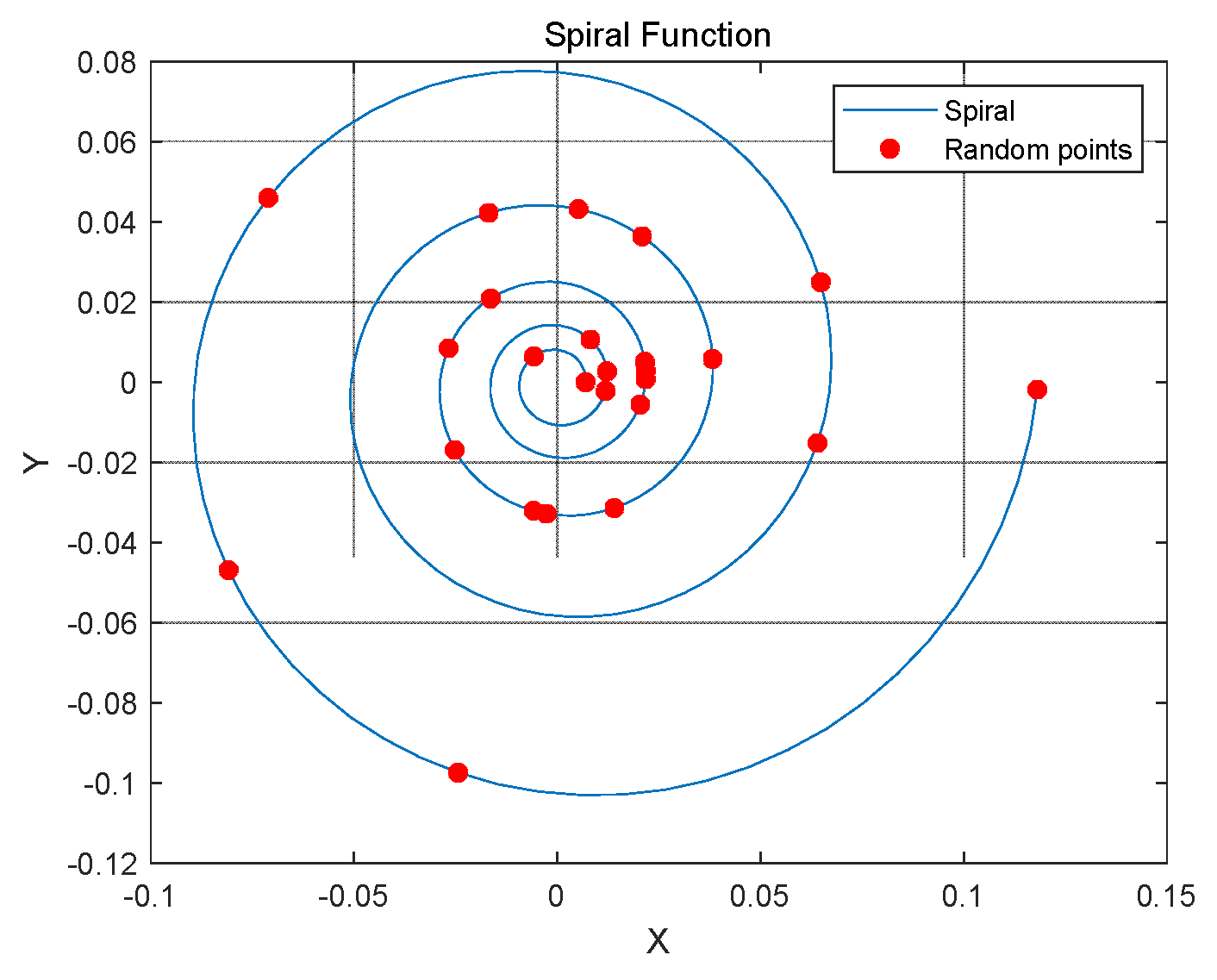
3.2. The Improved PSO Algorithm
| Algorithm 1. The particle swarm optimization algorithm based on the spiral function |
| Input: The optimization space of each CPG network parameter. |
| Output: Optimal CPG network parameters. |
| Step 1: Set the number of particles N, the number of iterations k, and then randomly set the initial position and velocity of the particles within a limited range. |
Step 2: Calculate the fitness value of the current particle.
|
Step 3: Using the spiral function to update the particles.
|
| Step 4: Iterate steps 2 and 3 until the maximum number of iterations k is reached. |
| Return the minimum fitness particle swarm |
4. The Biped Robot Walking Controller Optimization
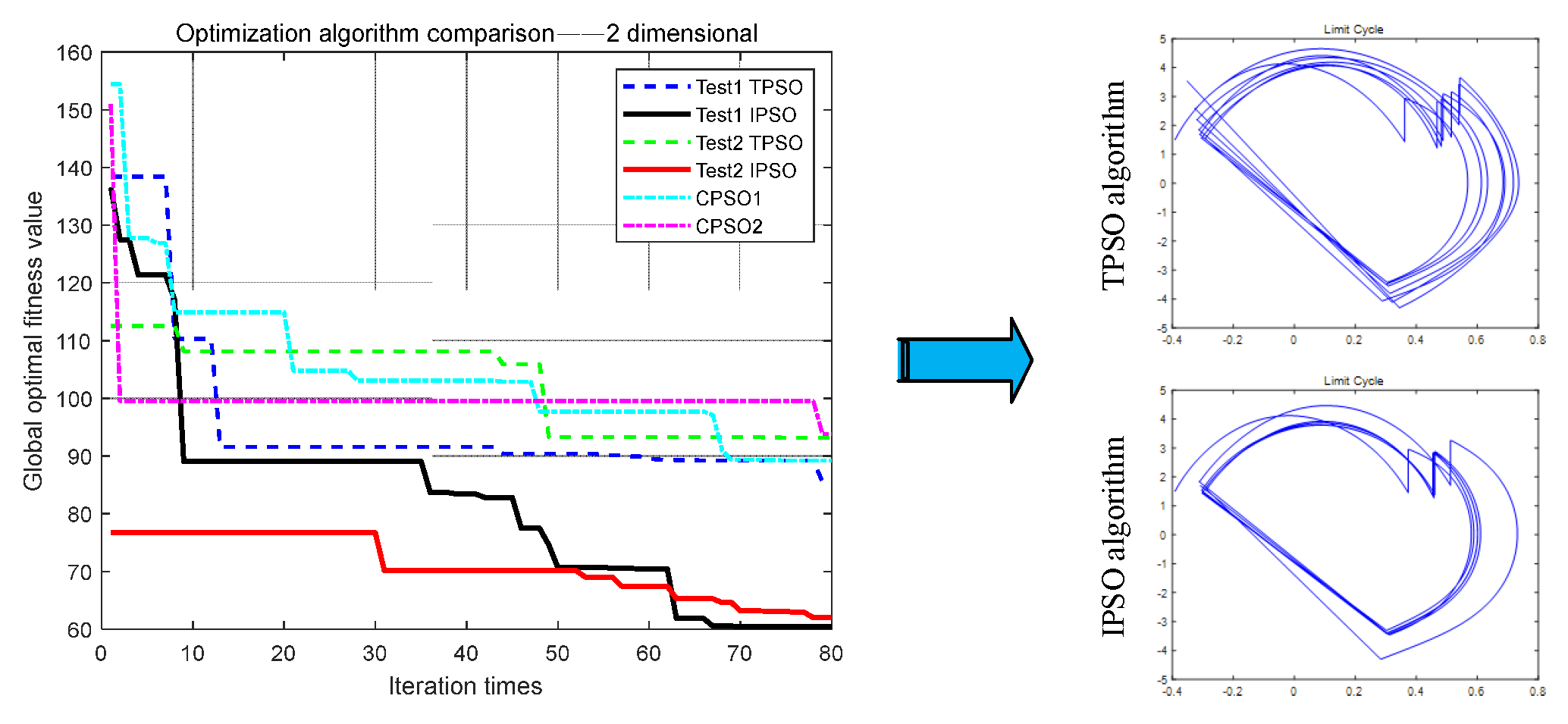
4.1. The Two-Dimensional Comparison Test
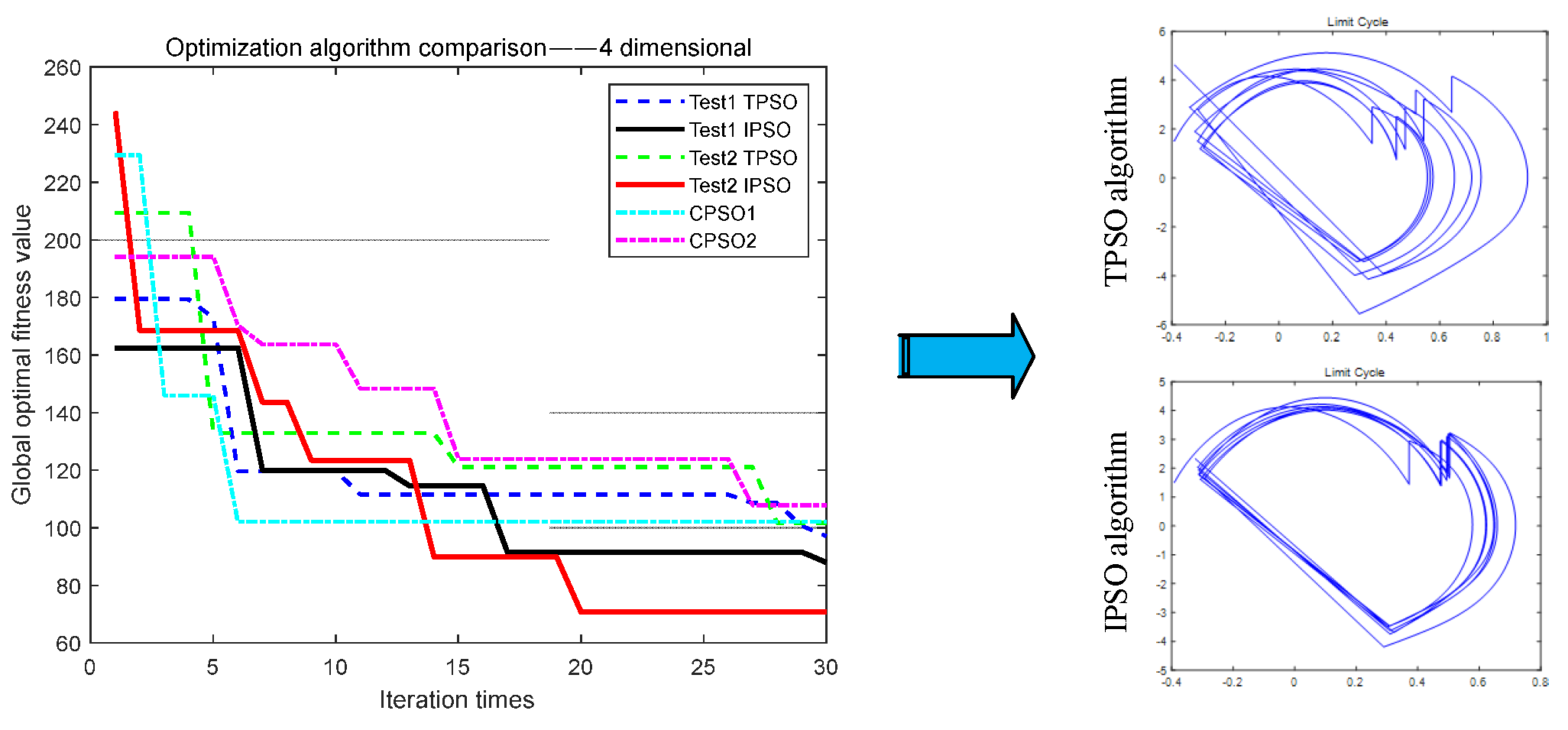
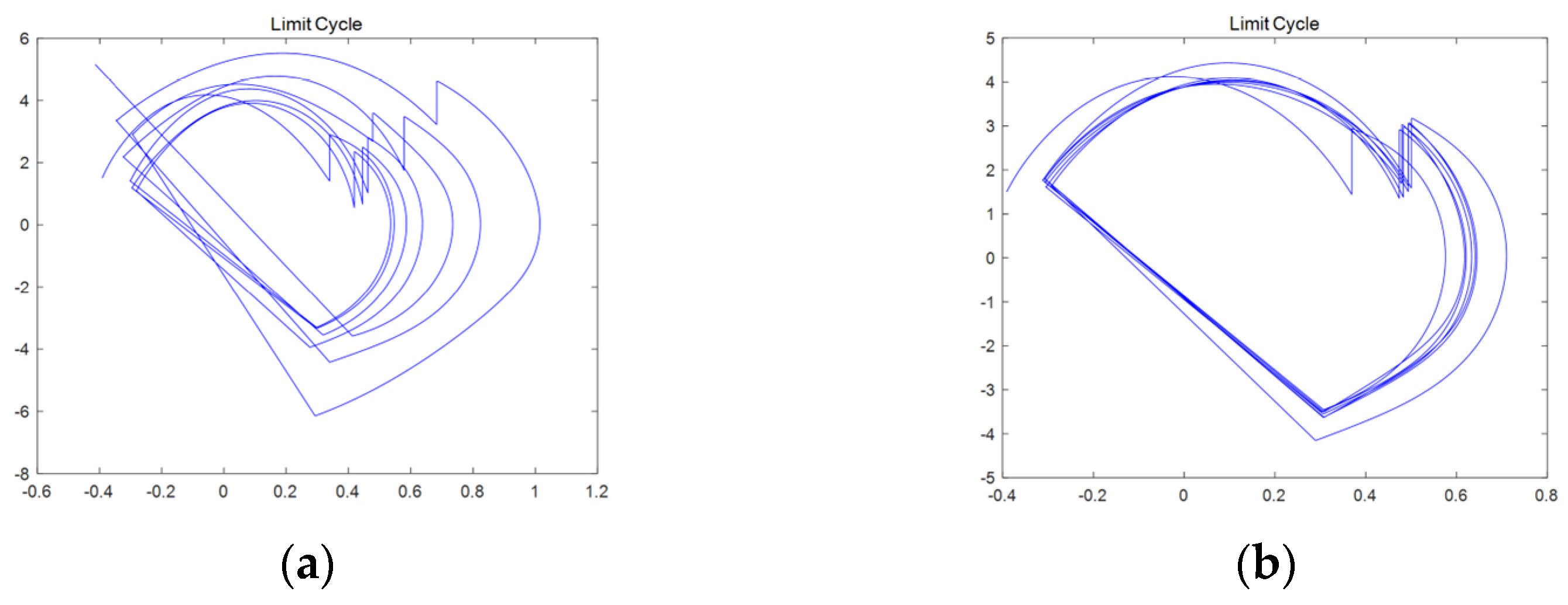
4.2. The Four-Dimensional Comparison Test
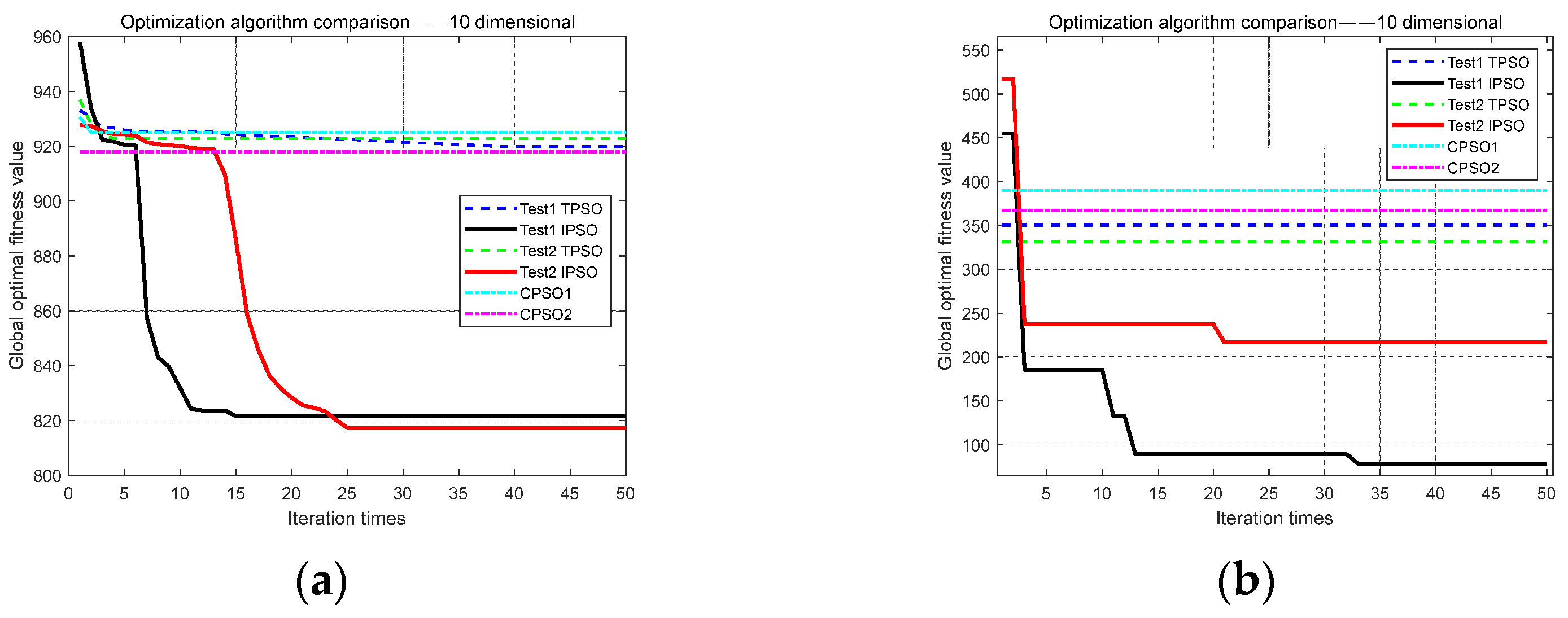
4.3. The Ten-Dimensional Comparison Test
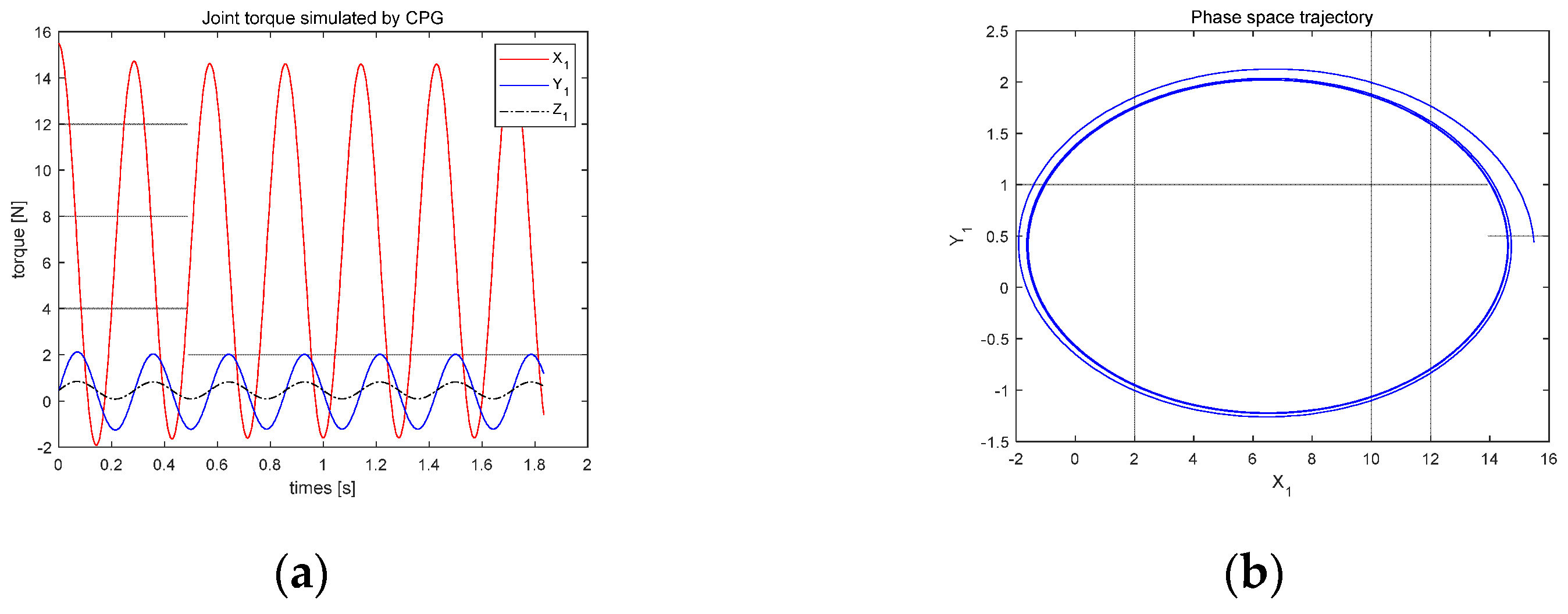
5. Walking Control Results of the Biped Robot
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Katayama, S.; Murooka, M.; Tazaki, Y. Model predictive control of legged and humanoid robots: Models and algorithms. Adv. Robot. 2023, 37, 298–315. [Google Scholar] [CrossRef]
- Wang, J.; Lu, S.; Chen, J. A CPG-based gait planning method for bipedal robots. Artif. Life Robot. 2024, 29, 340–348. [Google Scholar]
- Matsubara, T.; Morimoto, J.; Nakanishi, J.; Sato, M.A.; Doya, K. Learning CPG-based biped locomotion with a policy gradient method. Robot. Auton. Syst. 2006, 54, 911–920. [Google Scholar] [CrossRef]
- Sun, T.; Zhang, S.; Li, R.; Yan, Y. A Bionic Control Method for Human–Exoskeleton Coupling Based on CPG Model. Actuators 2023, 12, 321. [Google Scholar] [CrossRef]
- Li, D.; Wei, W.; Qiu, Z. Combined Reinforcement Learning and CPG Algorithm to Generate Terrain-Adaptive Gait of Hexapod Robots. Actuators 2023, 12, 157. [Google Scholar] [CrossRef]
- Ijspeert, A.J. Central pattern generators for locomotion control in animals and robots: A review. Neural Netw. 2008, 21, 642–653. [Google Scholar] [CrossRef]
- Urraca, R.; Sodupe-Ortega, E.; Antonanzas, J.; Antonanzas-Torres, F.; Martinez-de-Pison, F.J. Evaluation of a novel GA-based methodology for model structure selection: The GA-PARSIMONY. Neurocomputing 2018, 271, 9–17. [Google Scholar] [CrossRef]
- Wu, Y.; Gong, M.; Ma, W.; Wang, S. High-order graph matching based on ant colony optimization. Neurocomputing 2019, 328, 97–104. [Google Scholar] [CrossRef]
- Madani, T.; Daachi, B.; Benallegue, A. Adaptive variable structure controller of redundant robots with mobile/fixed obstacles avoidance. Robot. Auton. Syst. 2013, 61, 555–564. [Google Scholar] [CrossRef]
- Ju, M.Y.; Wang, S.E.; Guo, J.H. Path planning using a hybrid evolutionary algorithm based on tree structure encoding. Sci. World J. 2014, 2014, 746260. [Google Scholar] [CrossRef]
- Son, C. Intelligent rule-based sequence planning algorithm with fuzzy optimization for robot manipulation tasks in partially dynamic environments. Inf. Sci. 2016, 342, 209–221. [Google Scholar] [CrossRef]
- El Ferik, S.; Nasir, M.T.; Baroudi, U. A Behavioral Adaptive Fuzzy controller of multi robots in a cluster space. Appl. Soft Comput. 2016, 44, 117–127. [Google Scholar] [CrossRef]
- Purcaru, C.; Precup, R.E.; Iercan, D.; Fedorovici, L.O.; David, R.C.; Dragan, F. Optimal robot path planning using gravitational search algorithm. Int. J. Artif. Intell. 2013, 10, 1–20. [Google Scholar]
- Liu, E.; Yao, X.; Liu, M.; Jin, H. AGV path planning based on improved grey wolf optimization algorithm and its implementation prototype platform. Comput. Integr. Manuf. Syst. 2018, 24, 2779–2791. [Google Scholar]
- Zaman, H.R.R.; Gharehchopogh, F.S. An improved particle swarm optimization with backtracking search optimization algorithm for solving continuous optimization problems. Eng. Comput. 2022, 38, 2797–2831. [Google Scholar] [CrossRef]
- Das, P.K.; Jena, P.K. Multi-robot path planning using improved particle swarm optimization algorithm through novel evolutionary operators. Appl. Soft Comput. 2020, 92, 106312. [Google Scholar] [CrossRef]
- Yuan, Q.; Sun, R.; Du, X. Path planning of mobile robots based on an improved particle swarm optimization algorithm. Processes 2022, 11, 26. [Google Scholar] [CrossRef]
- Zhao, G.; Jiang, D.; Liu, X.; Tong, X.; Sun, Y.; Tao, B.; Kong, J.; Yun, J.; Liu, Y.; Fang, Z. A tandem robotic arm inverse kinematic solution based on an improved particle swarm algorithm. Front. Bioeng. Biotechnol. 2022, 10, 832829. [Google Scholar] [CrossRef]
- Shao, S.; Peng, Y.; He, C.; Du, Y. Efficient path planning for UAV formation via comprehensively improved particle swarm optimization. ISA Trans. 2020, 97, 415–430. [Google Scholar] [CrossRef]
- Song, B.; Wang, Z.; Zou, L. An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Appl. Soft Comput. 2021, 100, 106960. [Google Scholar] [CrossRef]
- Li, X.; Tian, B.; Hou, S.; Li, X.; Li, Y.; Liu, C.; Li, J. Path planning for mount robot based on improved particle swarm optimization algorithm. Electronics 2023, 12, 3289. [Google Scholar] [CrossRef]
- Tao, C.; Xue, J.; Zhang, Z.; Cao, F.; Li, C.; Gao, H. Gait optimization method for humanoid robots based on parallel comprehensive learning particle swarm optimizer algorithm. Front. Neurorobotics 2021, 14, 600885. [Google Scholar] [CrossRef] [PubMed]
- Sahu, C.; Parhi, D.R. Navigational strategy of a biped robot using regression-adaptive PSO approach. Soft Comput. 2022, 26, 12317–12341. [Google Scholar] [CrossRef]
- Wu, Y.; Qiao, S.; Yao, D. A hybrid chaotic controller integrating hip stiffness modulation and reinforcement learning-based torque control to stabilize passive dynamic walking. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 673–691. [Google Scholar] [CrossRef]
- Wu, Y.; Yao, D.; Xiao, X.; Guo, Z. Intelligent controller for passivity-based biped robot using deep Q network. J. Intell. Fuzzy Syst. 2019, 36, 731–745. [Google Scholar] [CrossRef]
- Wu, Y.; Yao, D.; Xiao, X. Optimal design for flexible passive biped walker based on chaotic particle swarm optimization. J. Electr. Eng. Technol. 2018, 13, 2493–2503. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE Press: Piscataway, NJ, USA, 1995; pp. 1942–1947. [Google Scholar]
- Yang, C.H.; Tsai, S.W.; Chuang, L.Y.; Yang, C.H. An improved particle swarm optimization with double-bottom chaotic maps for numerical optimization. Appl. Math. Comput. 2012, 219, 260–279. [Google Scholar] [CrossRef]
- Meng, H.J.; Zheng, P.; Wu, R.Y.; Hao, X.J.; Xie, Z. A hybrid particle swarm algorithm with embedded chaotic search. In Proceedings of the IEEE Conference on Cybernetics and Intelligent Systems, Singapore, 1–3 December 2004; pp. 367–371. [Google Scholar]
- Ao, T.; Li, M.; Liu, M.; Wang, H. Control Simulation of Dual-Arm Robot Based on Sliding Mode Controller. Process Autom. Instrum. 2019, 40, 34–38. [Google Scholar]


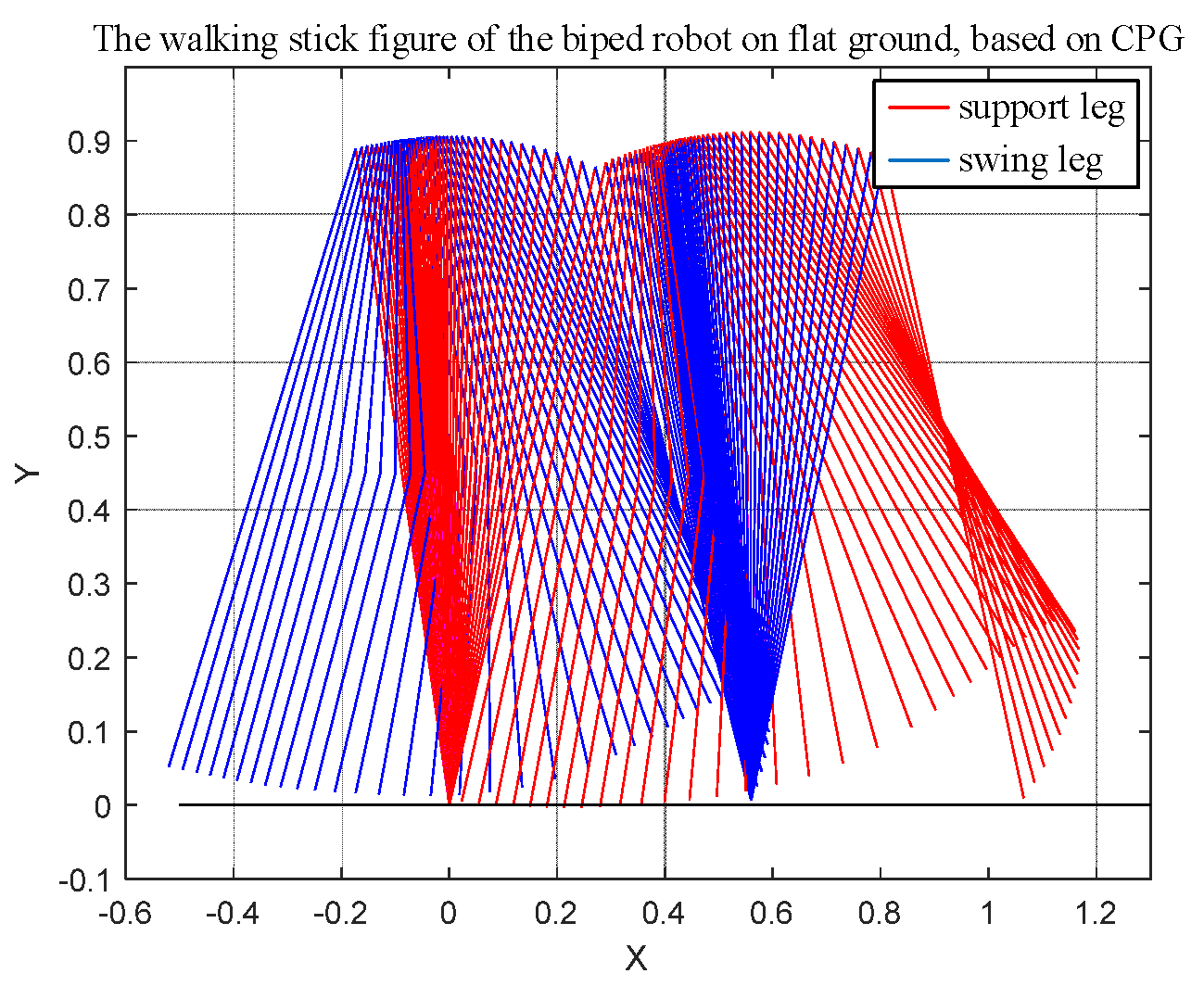
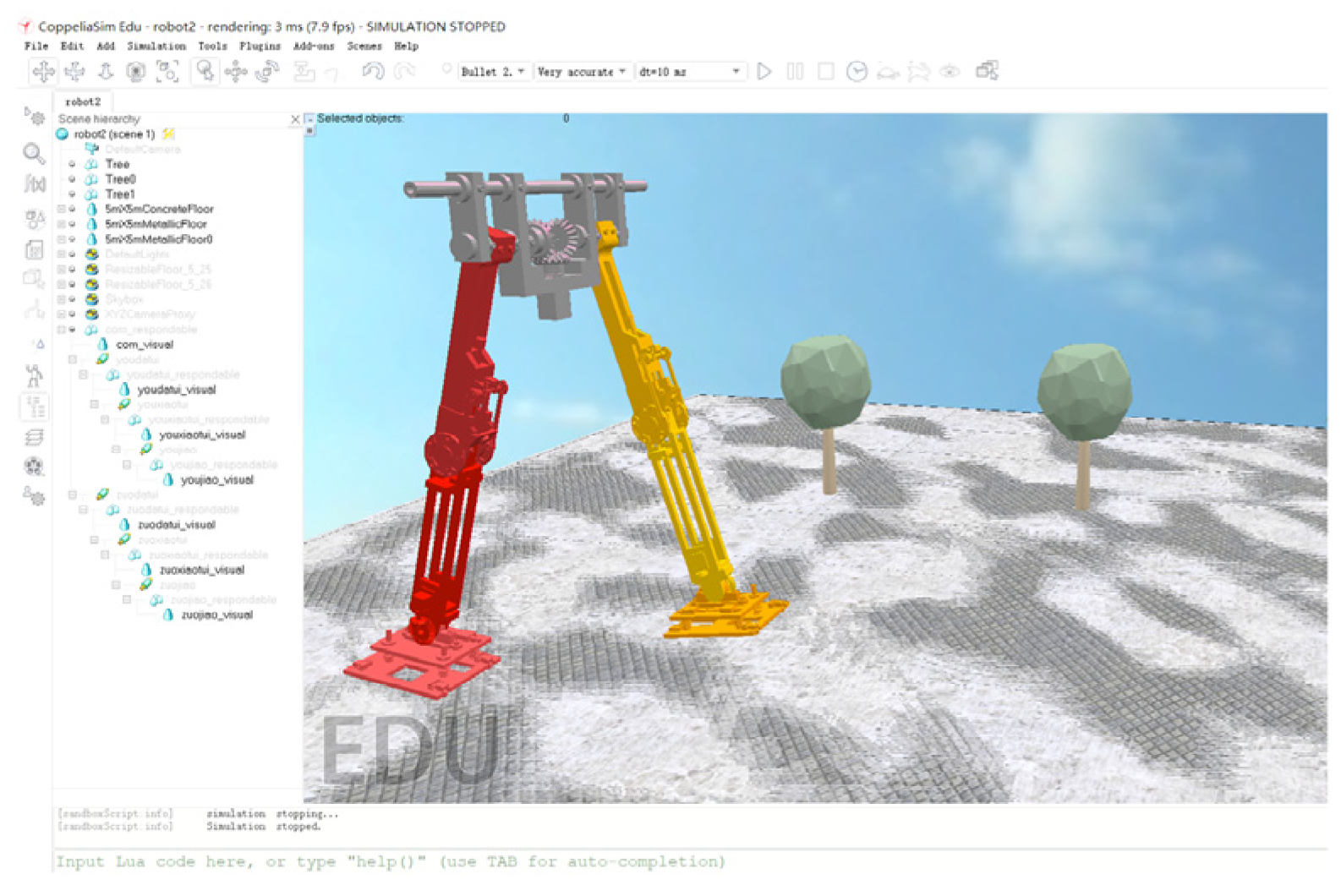


| Parameter Name | Sign | Values [Unit] |
|---|---|---|
| leg length | 0.9062 [m] | |
| waist mass | 11 [kg] | |
| leg mass | 2.2 [kg] | |
| thigh mass | 11 [kg] | |
| centroid position of calf | 0.614 | |
| centroid position of thigh | 0.468 | |
| acceleration of gravity | g | 9.8 [m s−2] |
| Parameter Name | Sign | Values |
|---|---|---|
| velocity inertia weight | ω | 0.3~0.9 |
| particle individual learning factor | 0.95 + 0.1 × rand[0, 1] | |
| particle social learning factor | 0.95 + 0.1 × rand[0, 1] | |
| random number 1 | [0, 1] | |
| random number 2 | [0, 1] | |
| the compression coefficient of spiral line | a | [0.007, 0.18] |
| rotation coefficient of spiral line | b | 0.09 |
| angle range of spiral function | [0, 10π] |
| Dimensional | Iteration Times | Algorithm | SE |
|---|---|---|---|
| 2-dimensions | 80 | TPSO | 66% |
| IPSO | 95.6% | ||
| CPSO1 | 81.5% | ||
| CPSO2 | 71.5% | ||
| 4-dimensions | 30 | TPSO | 275% |
| IPSO | 579.3% | ||
| CPSO1 | 424.3% | ||
| CPSO2 | 287.6% | ||
| 10-dimensions (higher fitness value position) | 50 | TPSO | 28% |
| IPSO | 278.6% | ||
| CPSO1 | 11.2% | ||
| CPSO2 | <1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Tang, B.; Qiao, S.; Pang, X. Bionic Walking Control of a Biped Robot Based on CPG Using an Improved Particle Swarm Algorithm. Actuators 2024, 13, 393. https://doi.org/10.3390/act13100393
Wu Y, Tang B, Qiao S, Pang X. Bionic Walking Control of a Biped Robot Based on CPG Using an Improved Particle Swarm Algorithm. Actuators. 2024; 13(10):393. https://doi.org/10.3390/act13100393
Chicago/Turabian StyleWu, Yao, Biao Tang, Shuo Qiao, and Xiaobing Pang. 2024. "Bionic Walking Control of a Biped Robot Based on CPG Using an Improved Particle Swarm Algorithm" Actuators 13, no. 10: 393. https://doi.org/10.3390/act13100393
APA StyleWu, Y., Tang, B., Qiao, S., & Pang, X. (2024). Bionic Walking Control of a Biped Robot Based on CPG Using an Improved Particle Swarm Algorithm. Actuators, 13(10), 393. https://doi.org/10.3390/act13100393





