Actuators for Large Wind Energy Systems—A Tutorial-Focused Survey
Abstract
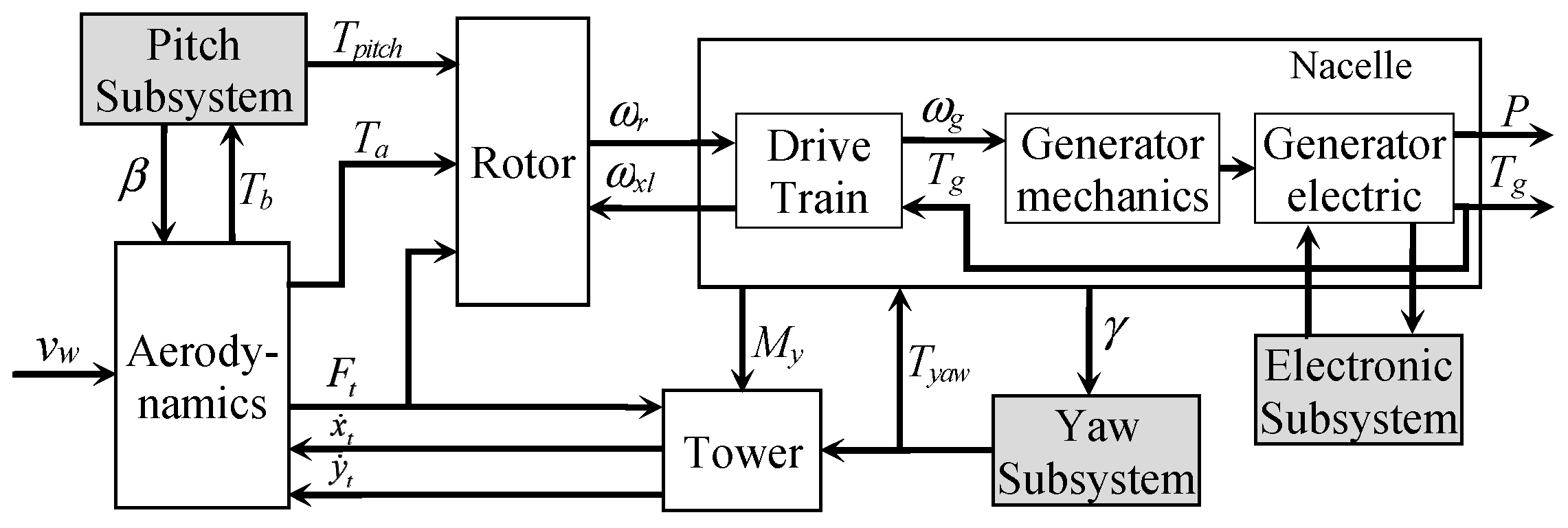
:1. Introduction
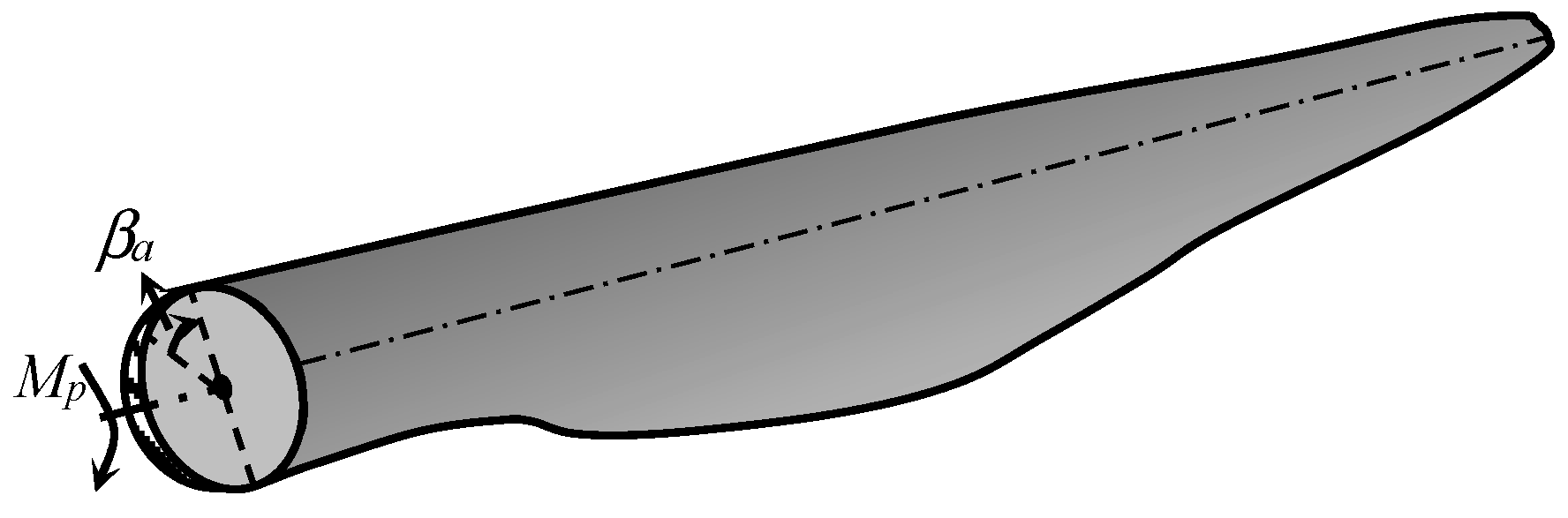
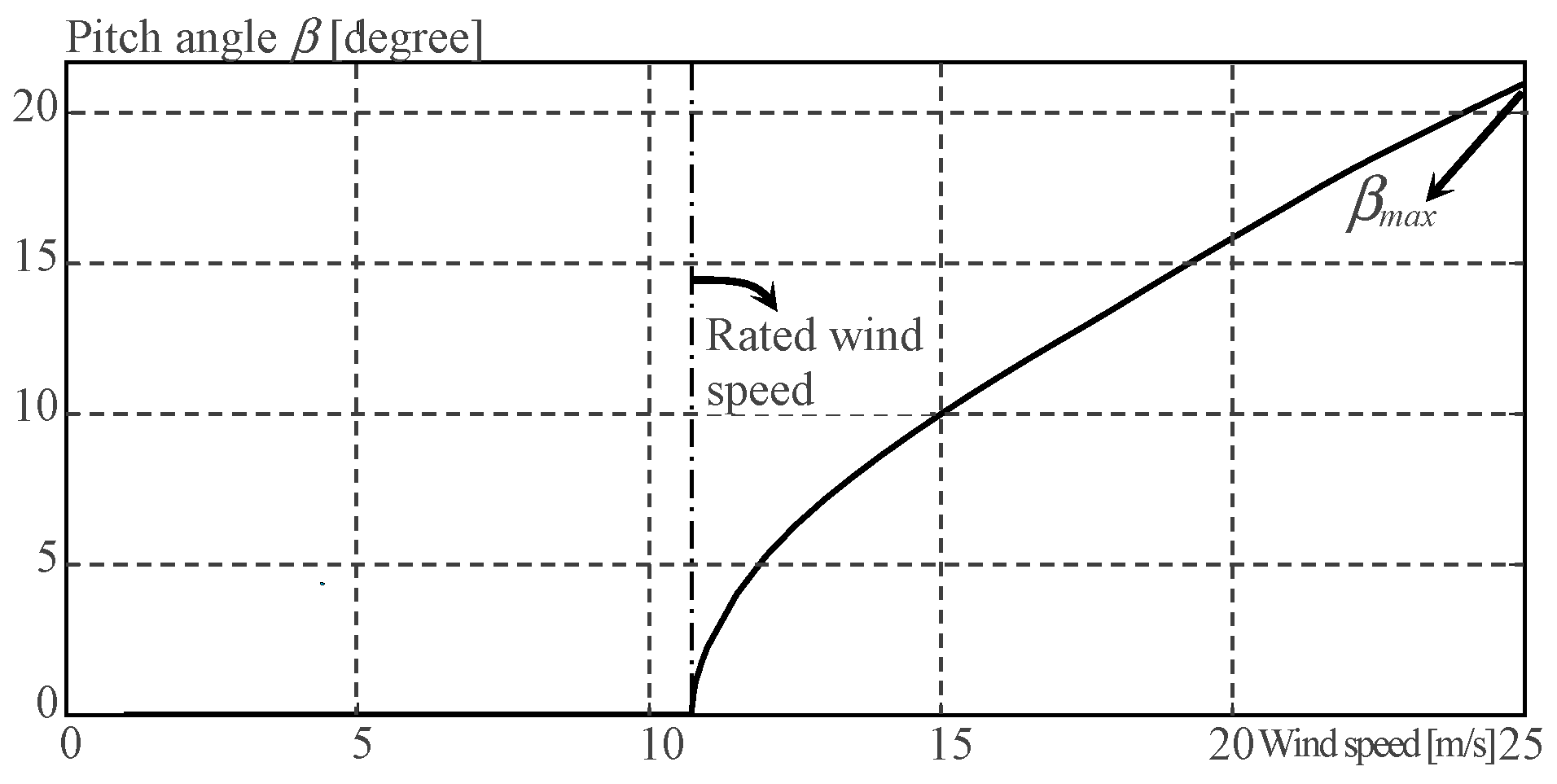
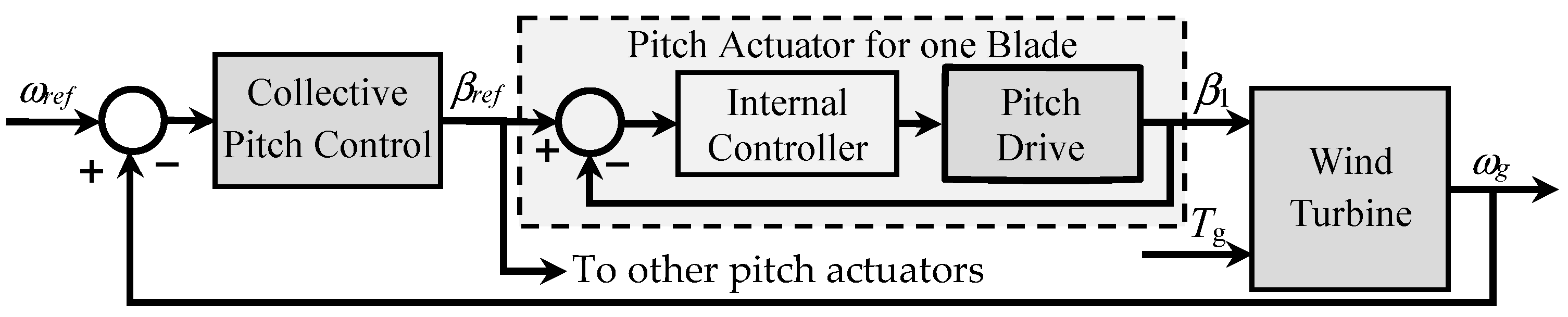
2. Pitch Actuating Systems
2.1. Simple Models of Pitch Actuator
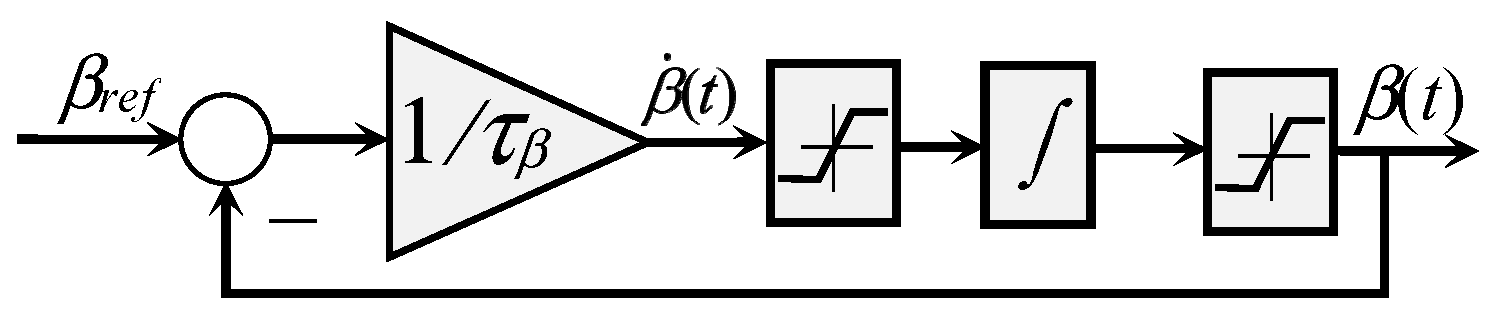
2.1.1. Pitch Actuator as First Order System
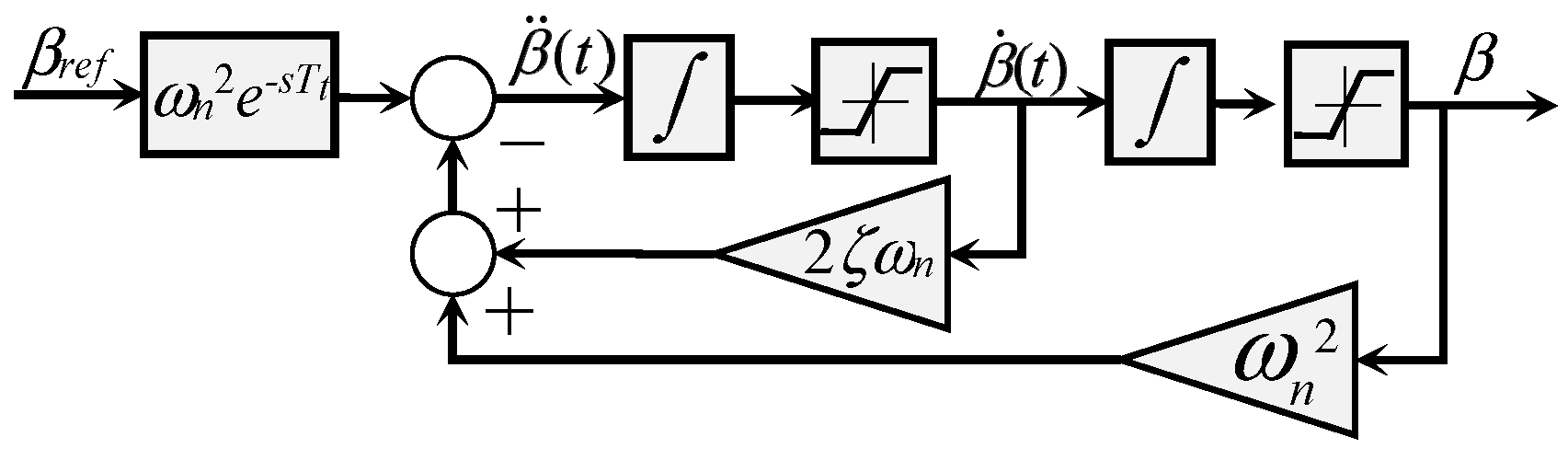
2.1.2. Pitch Actuator as Second Order System
2.1.3. Pitch Actuator with Pitch Rate Reference
2.2. Modelling Pitch Actuators Using Physical Principles
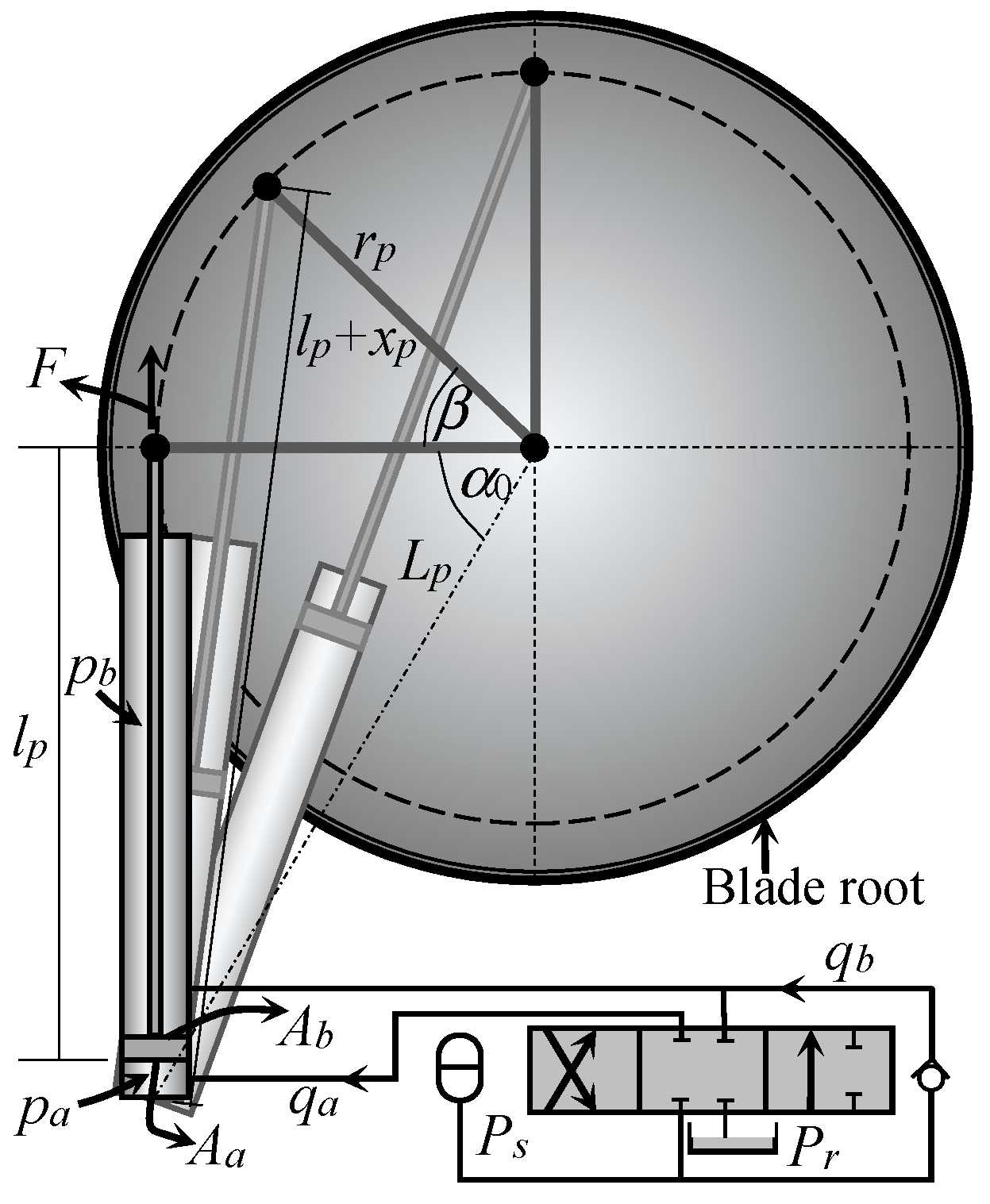
2.2.1. Hydraulically Driven Hydraulic Pitch Actuators
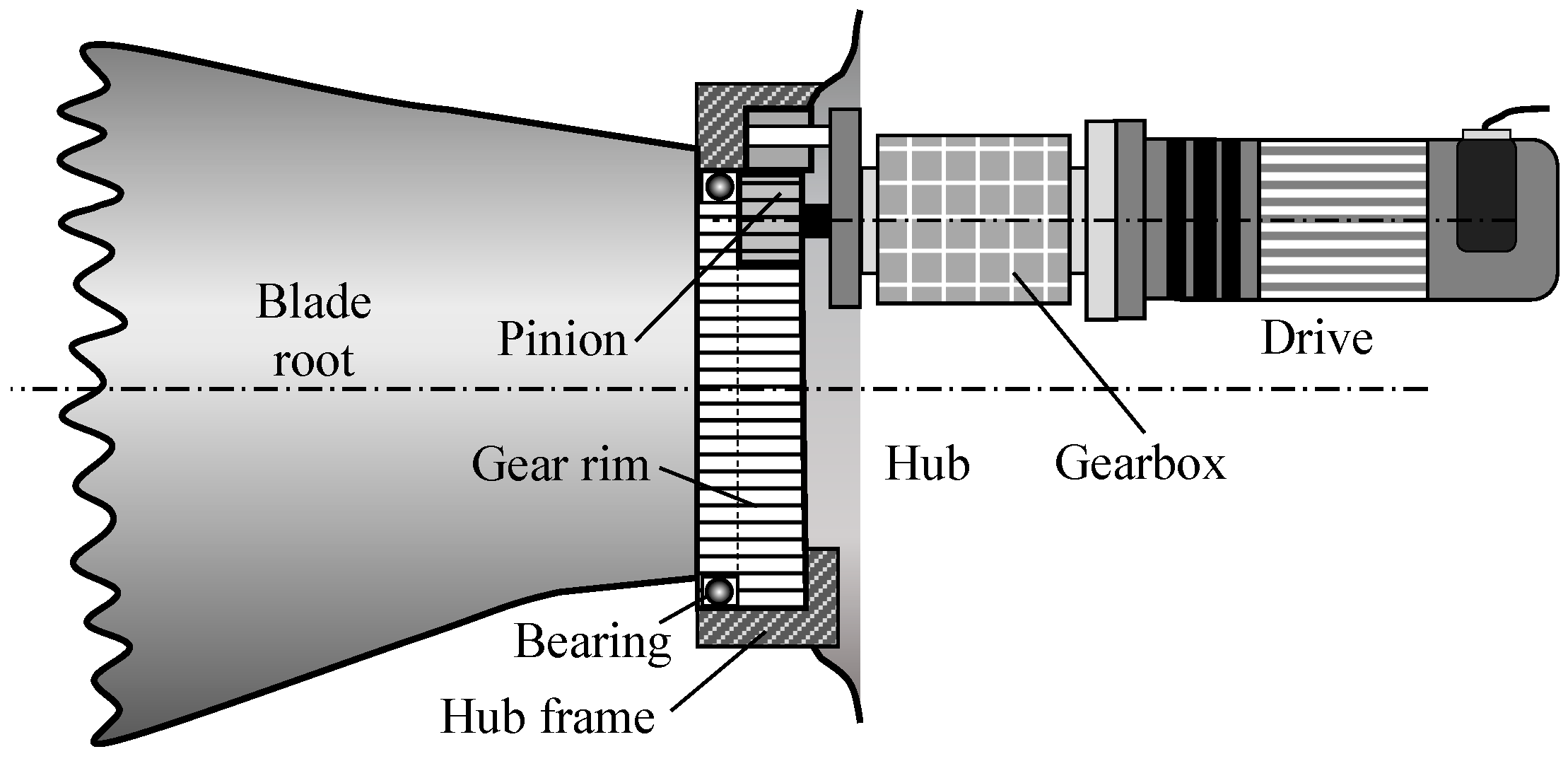
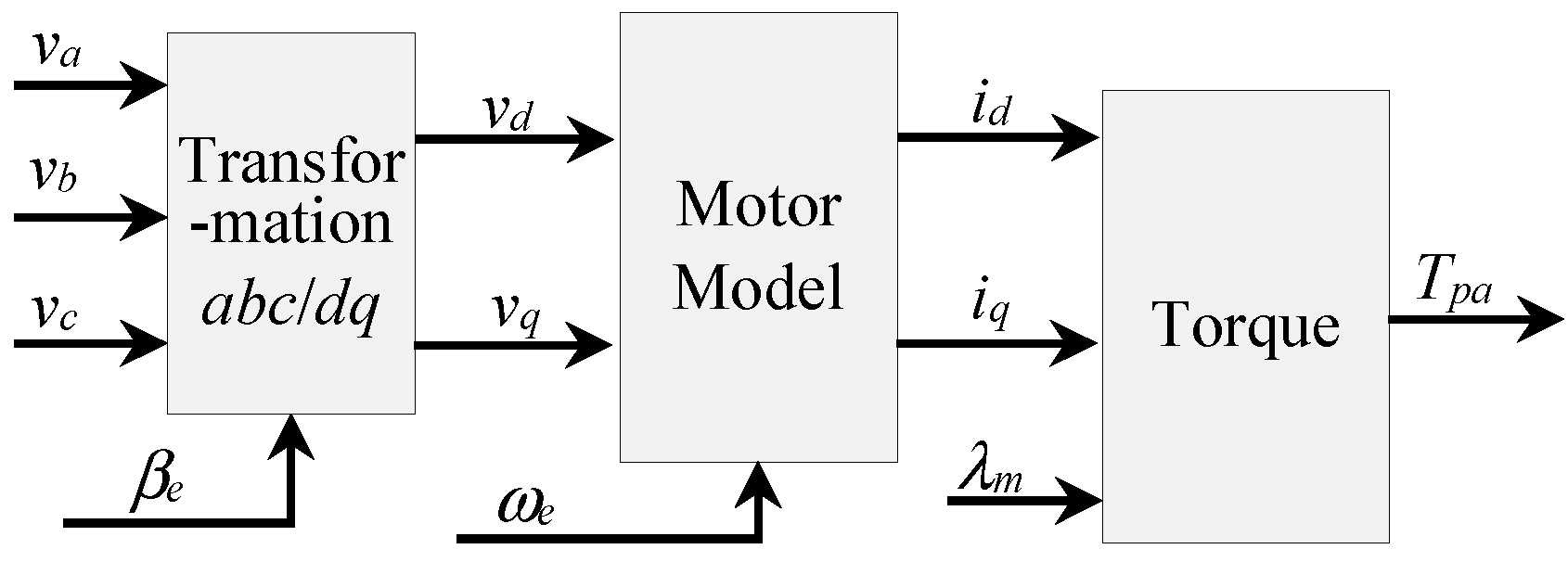
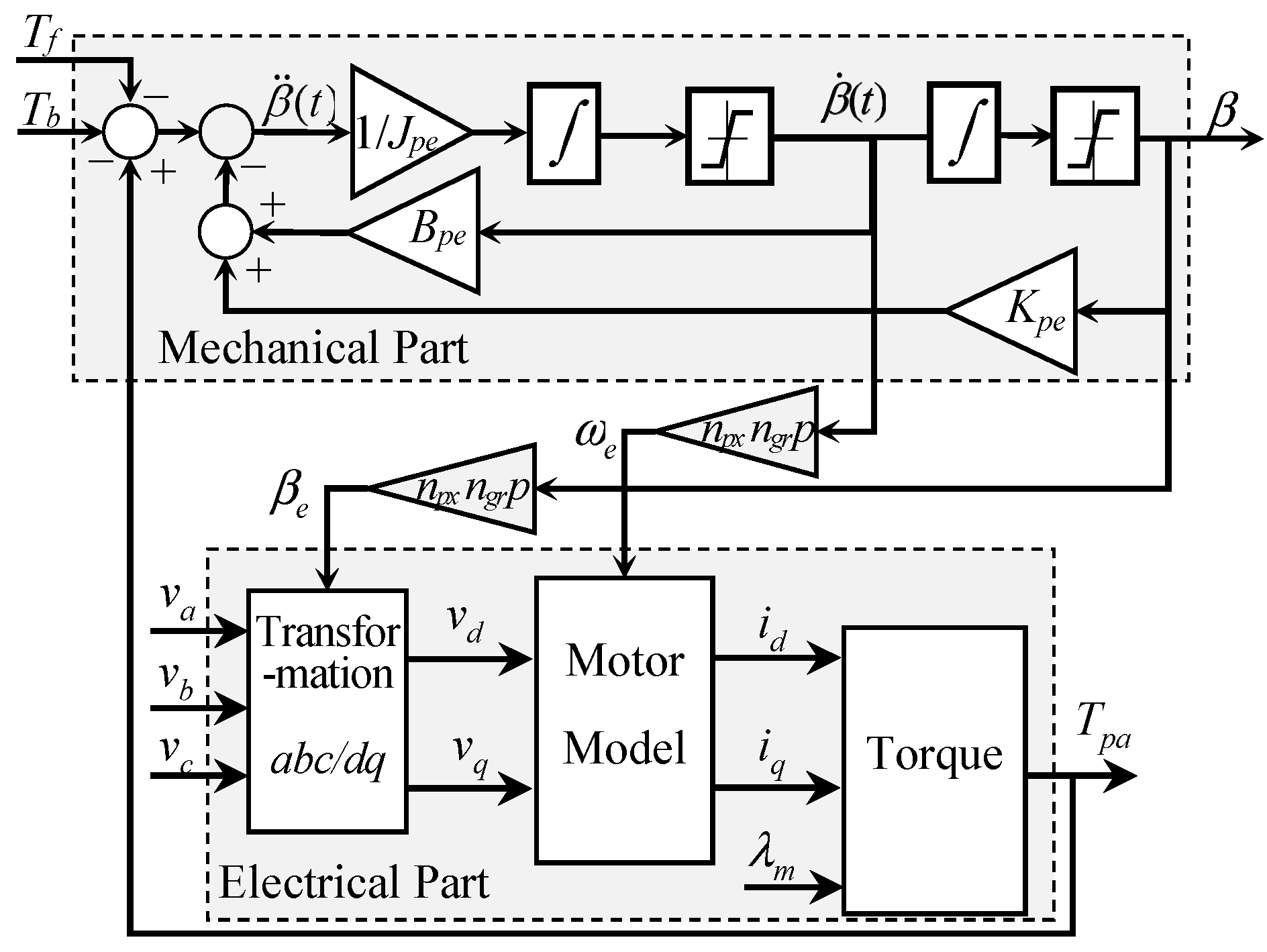
2.2.2. Electrically Driven Pitch Actuators
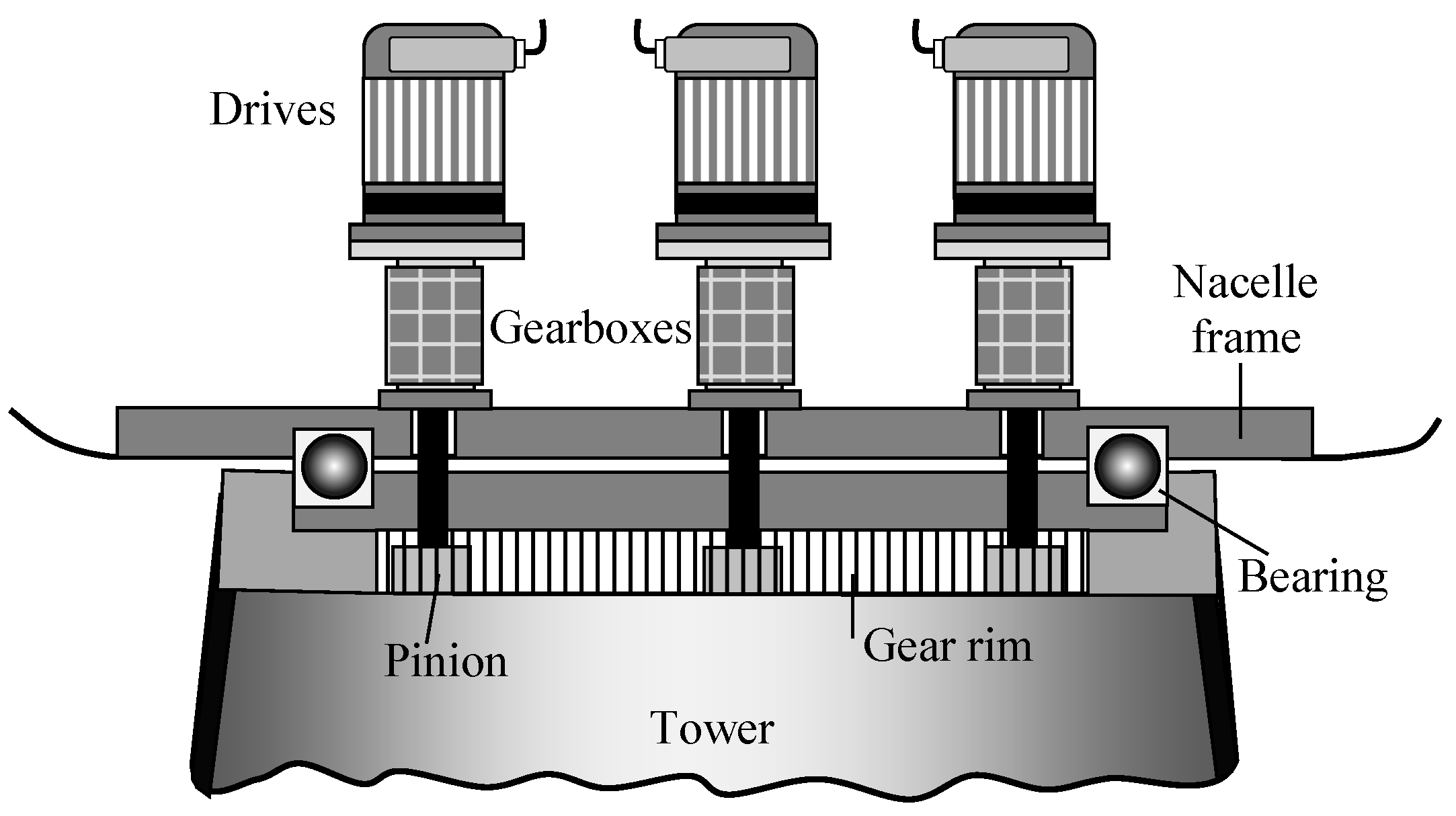
3. Yaw Actuating Systems
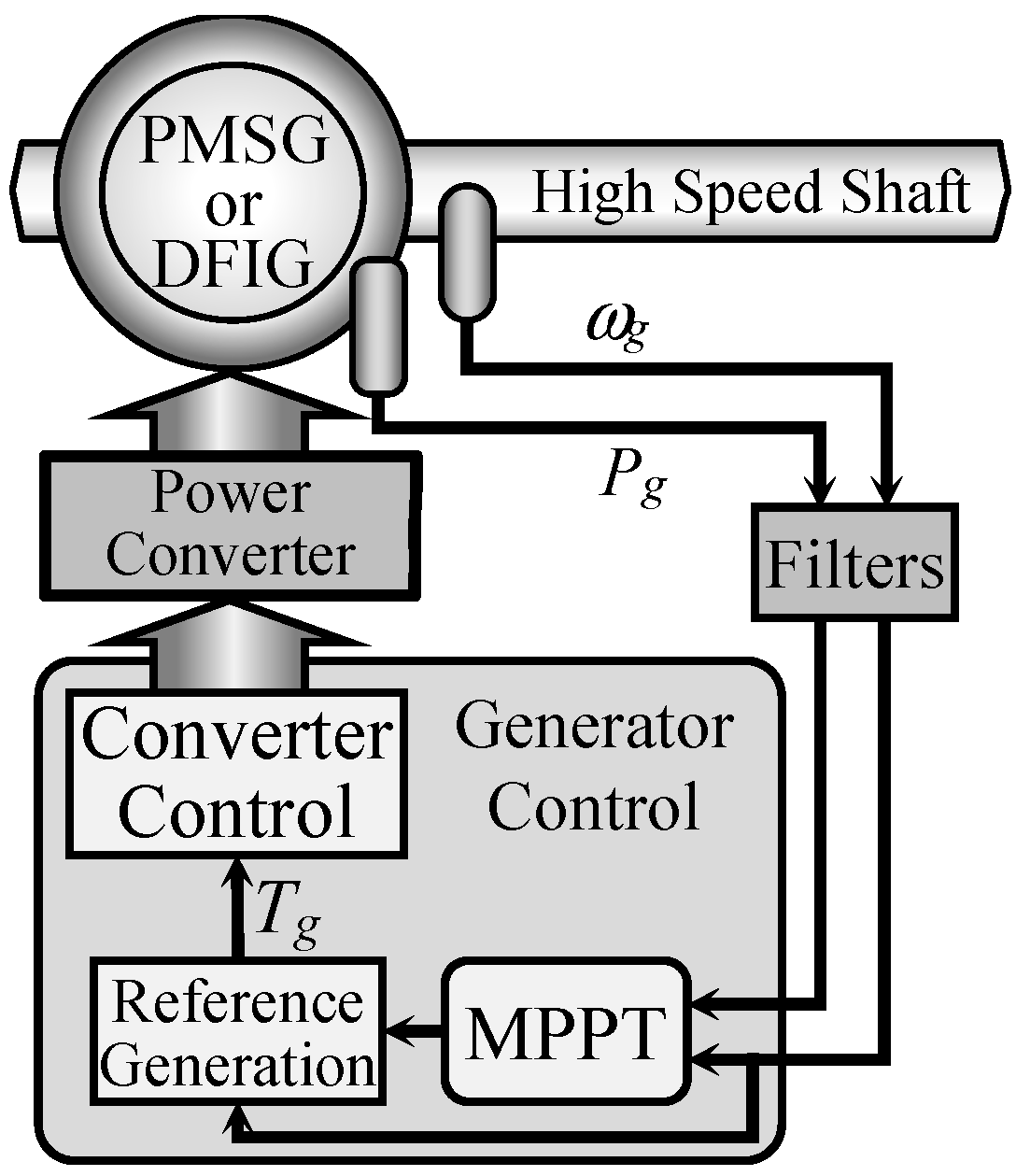
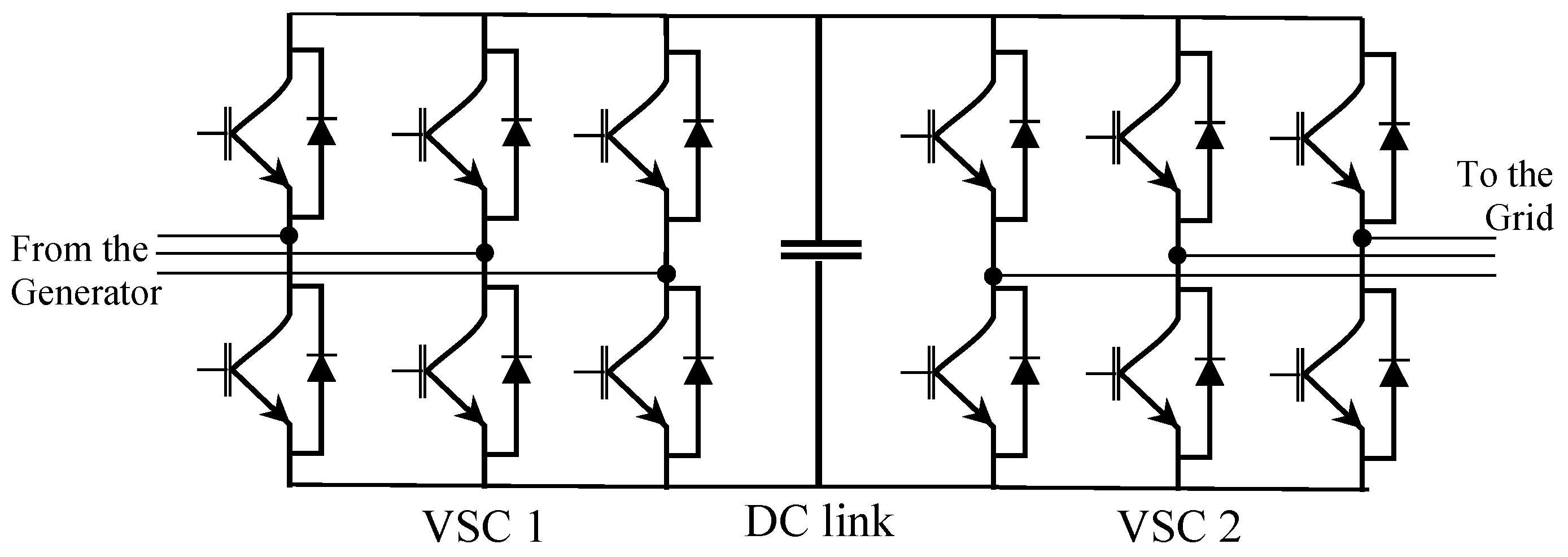
4. Power Converters as Actuators
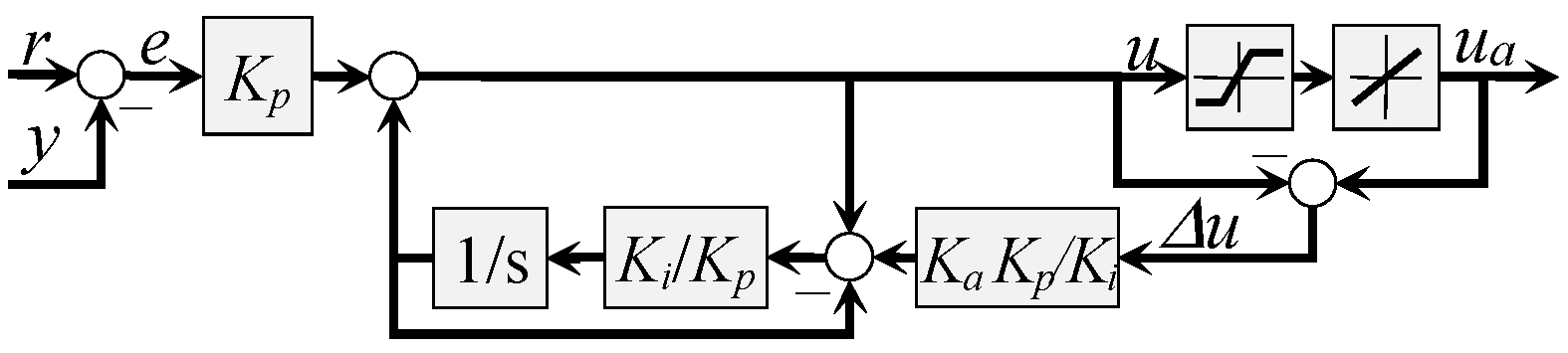
5. Actuator Control
6. Assessment of Performance for Actuator Protection
6.1. The Concept of Actuator Travel
6.2. The Concept of Actuator Duty Cycle
7. Actuators for Smart Blades
8. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CPC | Collective Pitch Control |
| DFIG | Double-Fed Induction Generator |
| DLC | Design Load Cases |
| HPPT | Maximum Power Point Tracking |
| IADE | Integrated Absolute Derivative |
| IFC | Individual Flap Control |
| IPC | Individual Pitch Control |
| PI, PID | Proportional Integral, Proportional Integral Derivative |
| PMSG | Permanent Magnet Synchro Generator |
| PWM | Pulse-Wide Modulation |
| VSC | Voltage Source Converters |
| Nomenclature | |
| Parameters | |
| Aa, Ab | Areas of chambers a and b of a hydraulic piston, m2 |
| Ba, Bb | Effective bulk moduli of chambers a and b of a hydraulic piston |
| bp | The damping coefficient of the piston, Nm s/rad |
| Bpe | Equivalent torsional damping coefficient, Nm s/rad |
| Bpb, Bpm | Torsional damping coefficients of blade and motor, Nm s/rad |
| Bye | Torsional damping coefficients on the yaw axis, Nm s/rad |
| cp | Proportional constant for the piston force |
| Db | Bearing diameter, m |
| g | Gravitational acceleration, m/s2 |
| Jpe | Equivalent second moment of inertia, kg m2 |
| Jpb, Jpm | The second moment of inertia of the blade and motor, kg m2 |
| Jye | The second moment of inertia on the yaw axis, kg m2 |
| Kp | The stiffness coefficient of the piston |
| kv | Valve coefficient |
| Kpe | Equivalent torsional stiffness coefficient |
| Kpb, Kpm | Torsional stiffness coefficients of blade and motor, Nm s/rad |
| Kye | Torsional stiffness coefficients on the yaw axis, Nm s/rad |
| lp | Piston length, m |
| Lp | Pitch-to-centre length, m |
| Ld Lq | Self-inductances, H |
| mp | Piston mass |
| mb | Blade mass, kg |
| my | Number of yaw actuators |
| ny | Yaw actuators multiplied |
| np | Gear ratio including toothing of pinion and blade bearing, -- |
| npx, ngr | Gearbox and gear rim ratios, -- |
| p | Number of pole pairs, -- |
| ps, pr | Pump pressure, ambient pressure, P |
| rp | Actuator torque arm, m |
| rcg | Location of the gravity centre, m |
| R | Rotor radius, m |
| Tt | Dead time, s |
| Va, Vb | Volumes in chambers a and b of a hydraulic piston, m3 |
| Va0, Vb0 | Unusable volumes of chambers a and b of a hydraulic piston, m2 |
| XG | Equivalent generator reactance |
| α0 | The angle between the pitching arm and the pitch-to-centre axis, rad |
| α1, α2 | Fitted coefficients α1 and α2 for a given bearing |
| βmin, βmax, βref | Minimum, maximum, and setpoint values for the pitch angle, rad |
| μ | Bearing friction, N |
| τβ | The time constant, s |
| λm | Flux linkage between the rotor and the stator |
| ζ | Damping ratio |
| ωn | Eigenfrequency, natural frequency |
| Variables | |
| DC | Duty cycle |
| FA, FR | Axial and radial forces on the bearing, N |
| Ft | Thrust force in the wind direction, N |
| Ft,max | Maximum thrust force in the wind direction, N |
| Fp | Piston force |
| id, iq | d and q currents dq reference frame, A |
| JAT | Metric to evaluate the actuator travel |
| JADC | Metric to evaluate the actuator duty cycle after [41] |
| JnADC | Metric to evaluate the cycle after [42,45] |
| Metric to evaluate the cycle after | |
| Mb | Resulting in blade root bending moments, Nm |
| Mx, My | Components of root bending moments, Nm |
| Mt | Tilting moment working on the bearing, Nm |
| pa, pb | Pressures in chambers a and b of a hydraulic piston, P |
| pw | Weibull distribution |
| qa, qb | Flow rates in chambers a and b of a hydraulic piston, m3/s |
| PG | The active power output of a generator, W |
| QG | The reactive power output of a generator, W |
| Tpa | Torque applied to the blade by the actuator, Nm |
| Tb | Whole torsional moment, Nm |
| Tbm | Resulting in blade root bending moment, Nm |
| Tf | Frictional moment, Nm |
| Tpa | Electrical torque of a pitch motor |
| Ty | The torsional moment for all external moments acting in the yaw-axis direction |
| Tyf | Yaw bearing frictional moment |
| Tya | Electrical torque of a yaw motor |
| vG, vC | Voltages in the back-to-back converter |
| vw | Wind speed, m/s |
| Average wind speed, m/s | |
| Vref | The voltage reference for the power conversion |
| u | Control variable |
| xp | Piston rod position, m |
| va, vb, vc | Three-phase input voltages, V |
| vd, vq | d and q voltages, dq reference frame, V |
| β | Pitch angle, rad |
| βe | Electric rotational angle, rad |
| δ | Electric phase angle |
| ϕ | Deflection angle in trailing edge flaps, rad |
| γ | Yaw angle, rad |
| Functions | |
| fp(.) | Relationship between piston force and the pitching moment |
References
- Gambier, A. Control of Large Wind Energy Systems; Springer Nature: Basel, Switzerland, 2022. [Google Scholar]
- Rakoto, L.; Schorsch, J.; Kinnaert, M. Modelling hydraulic pitch actuator for wind turbine simulation under healthy and faulty conditions. IFAC-PapersOnLine 2015, 48, 577–582. [Google Scholar] [CrossRef]
- Tutiven, C.; Vidal, Y.; Acho, L.; Rodellar, J. A fault detection method for pitch actuators faults in wind turbines. In Proceedings of the International Conference on Renewable Energies and Power Quality, La Coruña, Spain, 25–27 March 2015; pp. 698–703. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Y. Power System Optimization: Large-Scale Complex Systems Approaches; John Wiley & Sons: Singapore, 2016. [Google Scholar]
- Kallesøe, B.S. Equations of motion for a rotor blade, including gravity, pitch action and rotor speed variations. Wind Energy 2007, 10, 209–230. [Google Scholar] [CrossRef]
- Erde, R. Slewing Bearings; Catalogue, Rothe Erde, GmbH: Dortmund, Germany, 2009. [Google Scholar]
- Bianchi, F.D.; de Battista, H.; Mantz, R.J. Wind Turbine Control Systems; Springer: London, UK, 2007. [Google Scholar]
- Geng, H.; Yang, G. Output power control for variable-speed variable-pitch wind generation systems. IEEE Trans. Energy Convers. 2010, 25, 494–503. [Google Scholar] [CrossRef]
- Fortmann, J. Modeling of Wind Turbines with Doubly Fed Generator System; Springer Vieweg: Wiesbaden, Germany, 2014. [Google Scholar]
- Georg, S. Fault Diagnosis and Fault-Tolerant Control of Wind Turbines. Ph.D. Thesis, University of Rostock, Rostock, Germany, 2015. [Google Scholar]
- Geng, H.; Yang, G. Linear and nonlinear schemes applied to pitch control of wind turbines. Sci. World J. 2014, 2014, 406382. [Google Scholar] [CrossRef] [PubMed]
- Odgaard, P.F.; Stoustrup, J.; Kinnaert, M. Fault-tolerant control of wind turbines: A benchmark model. IEEE Trans. Control Syst. Technol. 2013, 21, 1168–1182. [Google Scholar] [CrossRef]
- Esbensen, T.; Sloth, C. Fault Diagnosis and Fault-Tolerant Control of Wind Turbines; Aalborg University: Aalborg, Denmark, 2009. [Google Scholar]
- Sloth, C.; Esbensen, T.; Stoustrup, J. Active and passive fault-tolerant LPV control of wind turbines. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 4640–4646. [Google Scholar] [CrossRef]
- Odgaard, P.; Johnson, K. Wind turbine fault detection and fault tolerant control—Anenhanced benchmark challenge. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 4447–4452. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scot, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Research report; NREL: Golden, CO, USA, 2009. [Google Scholar]
- Larsen, A.J.; Mogensen, T.S. Individal Pitch Control of Wind Turbines; Research report; Technical University of Denmark: Kongens Lyngby, Denmark, 2006. [Google Scholar]
- Hansen, M.H.; Kallesøe, B.S. Servo-elastic dynamics of a hydraulic actuator pitching a blade with large deflections. J. Phys. Conf. Ser. 2007, 75, 012077. [Google Scholar] [CrossRef]
- Wu, X.; Li, Y.; Li, F.; Yang, Z.; Teng, W. Adaptive estimation-based leakage detection for a wind turbine hydraulic pitching system. IEEE Trans. Mechatron. 2012, 17, 907–914. [Google Scholar] [CrossRef]
- Merritt, H.E. Hydraulic Control Systems; John Wiley & Sons, Inc.: New York, NY, USA, 1967. [Google Scholar]
- Krishnan, R. Electric Motor Drives: Modeling, Analysis & Control; Prentice Hall: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- van Engelen, T.G.; Markou, H.; Buhl, T.; Marrant, B. Morphological Study of Aeroelastic Control Concepts for Wind Turbines; Research report; Energy Research Centre of the Netherlands (ECN): Petten, The Netherlands, 2002. [Google Scholar]
- Blaabjerg, F. Control of Power Electronic Converters and Systems: Volume 4; Elsevier Inc.: London, UK, 2024. [Google Scholar]
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation for Power Converters: Principles and Practice; John Wiley & Sons, Inc.: Danvers, MA, USA, 2003. [Google Scholar]
- Saccomanno, F. Electric Power Systems—Analysis and Control; Wiley Interscience: Piscataway, NJ, USA, 2003. [Google Scholar]
- Luo, F.L.; Ye, H.; Rashid, M. Digital Power Electronics and Applications; Elsevier Academic Press: San Diego, CA, USA, 2005. [Google Scholar]
- Bacha, S.; Munteanu, I.; Bratcu, A.I. Power Electronic Converters—Modeling and Control; Springer: London, UK, 2014. [Google Scholar]
- Kundur, P. Power System Stability and Control; McGraw-Hill: Palo Alto, CA, USA, 1994. [Google Scholar]
- Rundqwist, L. Anti-Reset Windup for PID Controllers. Ph.D. Thesis, Lund Institute of Technology, Lund, Sweden, 1991. [Google Scholar]
- Bohn, C.; Atherton, D.P. An analysis package comparing PID anti-windup strategies. IEEE Control Syst. Mag. 1995, 15, 34–40. [Google Scholar] [CrossRef]
- Visioli, A. Modified anti-windup scheme for PID controllers. IEE Proc. 2003, 150, 49–54. [Google Scholar] [CrossRef]
- Fertik, H.A.; Ross, C.W. Direct digital control algorithm with anti-windup feature. ISA Trans. 1967, 6, 317–328. [Google Scholar]
- Wang, X.; Gambier, A.; Vinagre, B. Fractional order PID control with rate-limited anti-windup for the pitch system of wind turbines. In Proceedings of the 2020 IEEE Conference on Control Technology and Applications, Montréal, QC, Canada, 24–26 August 2020; pp. 933–938. [Google Scholar] [CrossRef]
- Visioli, A. Practical PID Control; Springer: London, UK, 2006. [Google Scholar]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems, 14th ed.; Pearson Education Ltd.: Harlow, UK, 2021. [Google Scholar]
- Chen, W.; Liu, H.; Lin, Y.; Li, W.; Sun, Y.; Zhang, D. LSTM-NN yaw control of wind turbines based on upstream wind information. Energies 2020, 13, 1482. [Google Scholar] [CrossRef]
- Pawlak, A.M. Sensors and Actuators in Mechatronics: Design and Applications; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Blanding, D.E.; Sexton, M.R.; Segal, M.; Grow, J. The application of confidence interval in the evaluation of electric actuation duty cycle. In Proceedings of the 27th International Conference of the Aeronautical Sciences (ICAS 2010), Nice, France, 19–24 September 2010; pp. 1–6. [Google Scholar]
- Brown, P. Sensors and Actuators: Technology and Applications; Larsen and Keller Education: New York, NY, USA, 2017. [Google Scholar]
- Kendall, L.; Balas, M.J.; Lee, Y.J.; Fingersh, L.J. Application of proportional-integral and disturbance accommodating control to variable speed variable pitch horizontal axis wind turbines. Wind Eng. 1997, 21, 21–38. [Google Scholar]
- Bottasso, C.L.; Campagnolo, F.; Croce, A.; Tibaldi, C. Optimization based study of bend-twist coupled rotor blades for passive and integrated passive/active load alleviation. Wind Energy 2013, 16, 1149–1166. [Google Scholar] [CrossRef]
- Scott, S.; Capuzzi, M.; Langston, D.; Bossany, E.; McCann, G.; Weaver, P.M.; Pirrera, A. Effects of aeroelastic tailoring on performance characteristics of wind turbine systems. Renew. Energy 2017, 114, 887–903. [Google Scholar] [CrossRef]
- Tibaldi, C.; Hansen, M.H.; Henriksen, L.C. Optimal tuning for a classical wind turbine controller. J. Phys. Conf. Ser. 2014, 555, 012099. [Google Scholar] [CrossRef]
- Ungurán, R. Lidar-Assisted Feedback-Feedforward Individual Pitch and Trailing Edge Flaps Control of Variable-Speed Wind Turbines. Ph.D. Thesis, Carl von Ossietzky Universität Oldenburg, Oldenburg, Germany, 2019. [Google Scholar]
- IEC 61400-1; Wind Turbines—Part 1: Design Requirements. International Standard. International Electrotechnical Commission: Geneva, Switzerland, 2005.
- Lobitz, D.W.; Veers, P.S. Load mitigation with bending/twist-coupled blades on rotors using modern control strategies. Wind Energy 2003, 6, 105–117. [Google Scholar] [CrossRef]
- Li, B.; De, T.; Wu, X.; Meng, H.; Su, Y. The impact of bend–twist coupling on structural characteristics and flutter limit of ultra-long flexible wind turbine composite blades. Energies 2023, 16, 5829. [Google Scholar] [CrossRef]
- Wilson, D.G.; Berg, D.E.; Lobitz, D.W.; Zayas, J.R. Optimized active aerodynamic blade control for load alleviation on large wind turbines. In Proceedings of the AWEA WINDPOWER 2008, Huston, TX, USA, 1–4 June 2008; pp. 1–7. [Google Scholar]
- Lackner, M.A.; van Kuik, G. A comparison of smart rotor control approaches using trailing edge flaps and individual pitch control. Wind Energy 2010, 13, 117–134. [Google Scholar] [CrossRef]
- Henriksen, L.; Bergami, L.; Andersen, P.B. A model based control methodology combining blade pitch and adaptive trailing edge flaps in a common framework. In Proceedings of the European Wind Energy Association Conference, Vienna, Austria, 4–7 February 2013. [Google Scholar]
- Bergami, L. Smart Rotor Modeling; Springer: Basel, Switzerland, 2014. [Google Scholar]
- Chetan, M.; Sakib, M.S.; Griffith, D.T.; Gupta, A.; Rotea, M.A. Design of a 3.4-MWwind turbine with integrated plasma. Wind Energy 2022, 25, 517–536. [Google Scholar] [CrossRef]
- Shahrokhi, S.S.; Taeibi Rahni, M.; Akbari, P. Aerodynamic design of a double slotted morphed flap airfoil—A numerical study. Front. Mech. Eng. 2024, 10, 1371479. [Google Scholar] [CrossRef]
- Omidi, J. Advances and opportunities in wind energy harvesting using plasma actuators: A review. Clean Energy 2024, 8, 197–225. [Google Scholar] [CrossRef]
- Pechlivanoglou, G. Passive and Active Flow Control Solutions for Wind Turbine Blades. Ph.D. Thesis, Technical University of Berlin, Berlin, Germany, 2012. [Google Scholar]
- Fu, X.; Li, Y.; Li, B.; Kwok, D.Y. Drag force reduction on an airfoil via glow discharge plasma-based control. Eur. Phys. 2002, 171, 195–204. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gambier, A. Actuators for Large Wind Energy Systems—A Tutorial-Focused Survey. Actuators 2024, 13, 416. https://doi.org/10.3390/act13100416
Gambier A. Actuators for Large Wind Energy Systems—A Tutorial-Focused Survey. Actuators. 2024; 13(10):416. https://doi.org/10.3390/act13100416
Chicago/Turabian StyleGambier, Adrian. 2024. "Actuators for Large Wind Energy Systems—A Tutorial-Focused Survey" Actuators 13, no. 10: 416. https://doi.org/10.3390/act13100416
APA StyleGambier, A. (2024). Actuators for Large Wind Energy Systems—A Tutorial-Focused Survey. Actuators, 13(10), 416. https://doi.org/10.3390/act13100416





