Modeling of Precise Tension with Passive Dancers for Automated Fiber Placement
Abstract
:1. Introduction
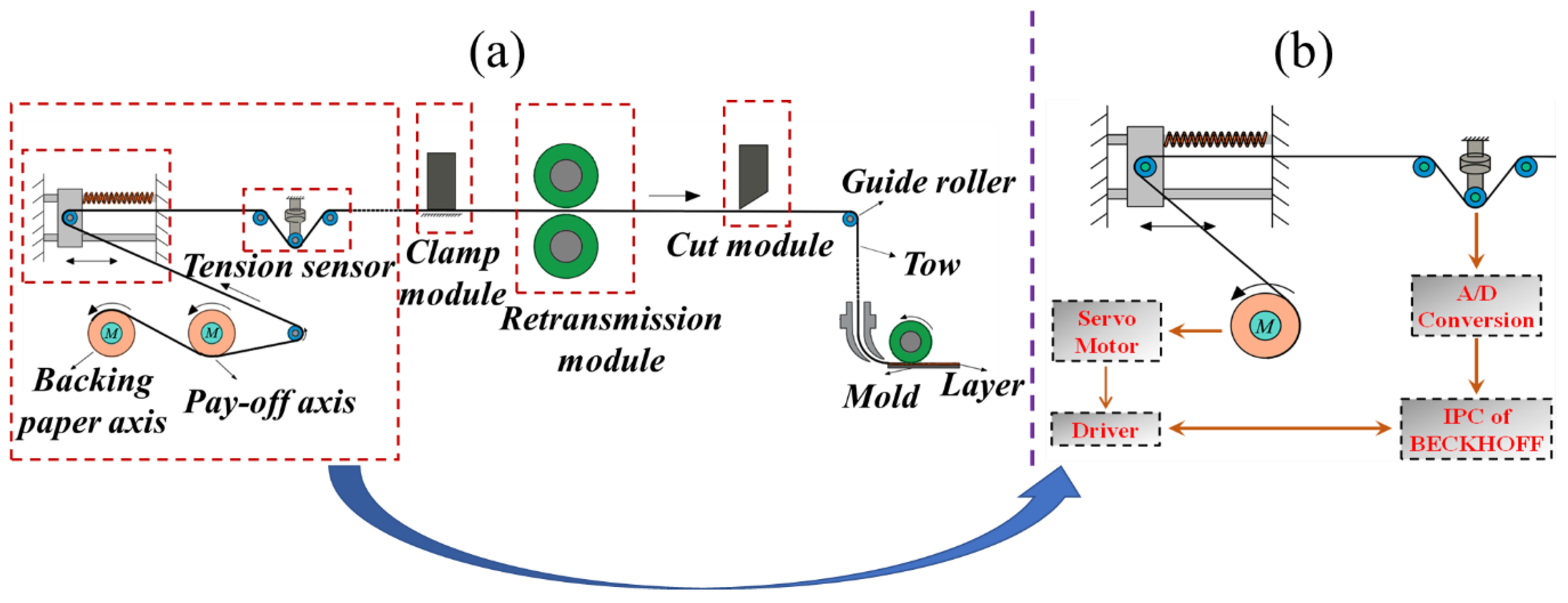
2. Model of the Tension Fluctuation for AFP
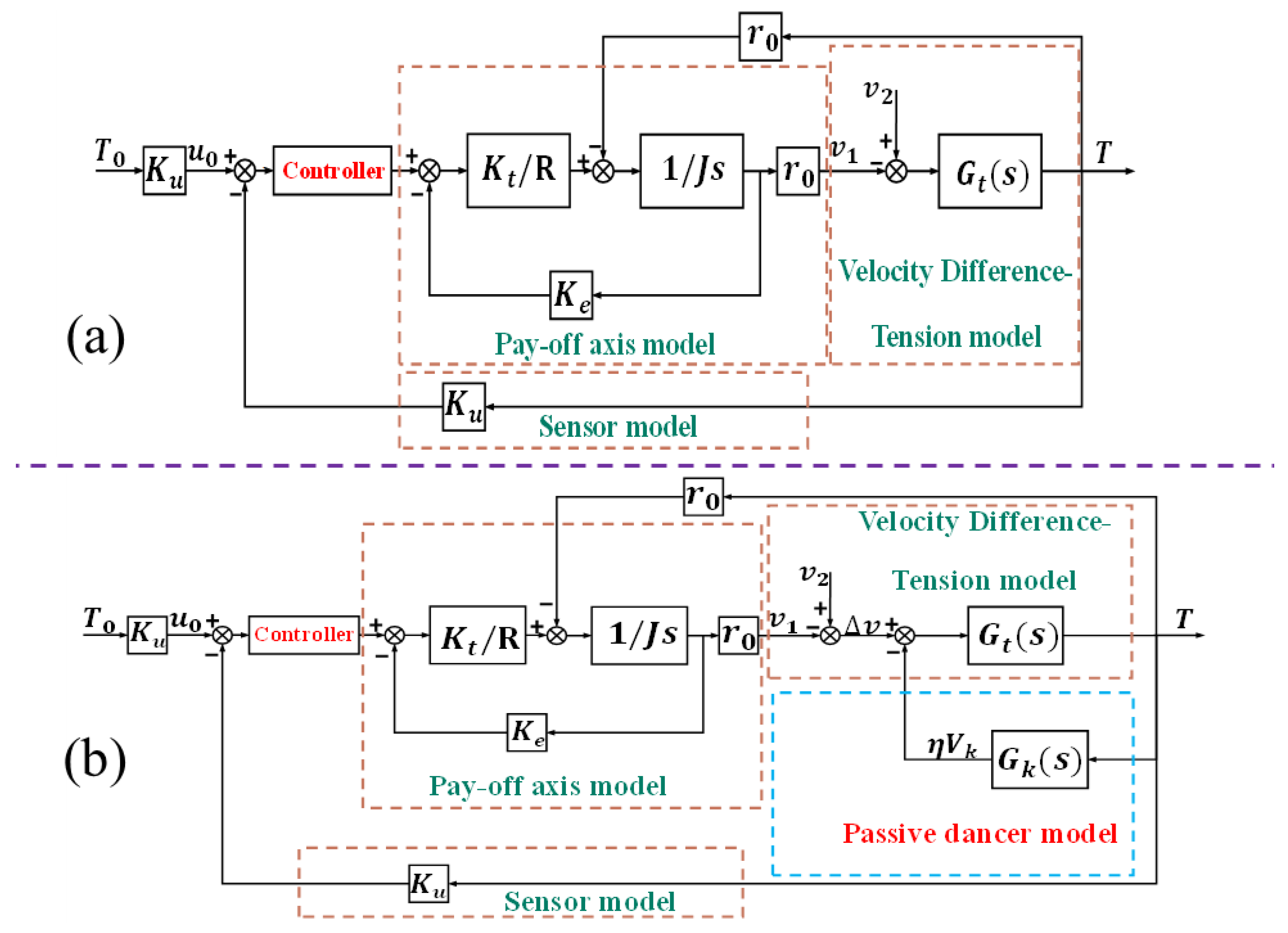
2.1. The Model for the Pay-off Axis
2.2. The Model for Velocity Difference–Tension
2.3. The Model of Passive Dancers
2.4. The Model of the Tension Control with Passive Dancers
3. Analysis of the Precise Tension Control Model
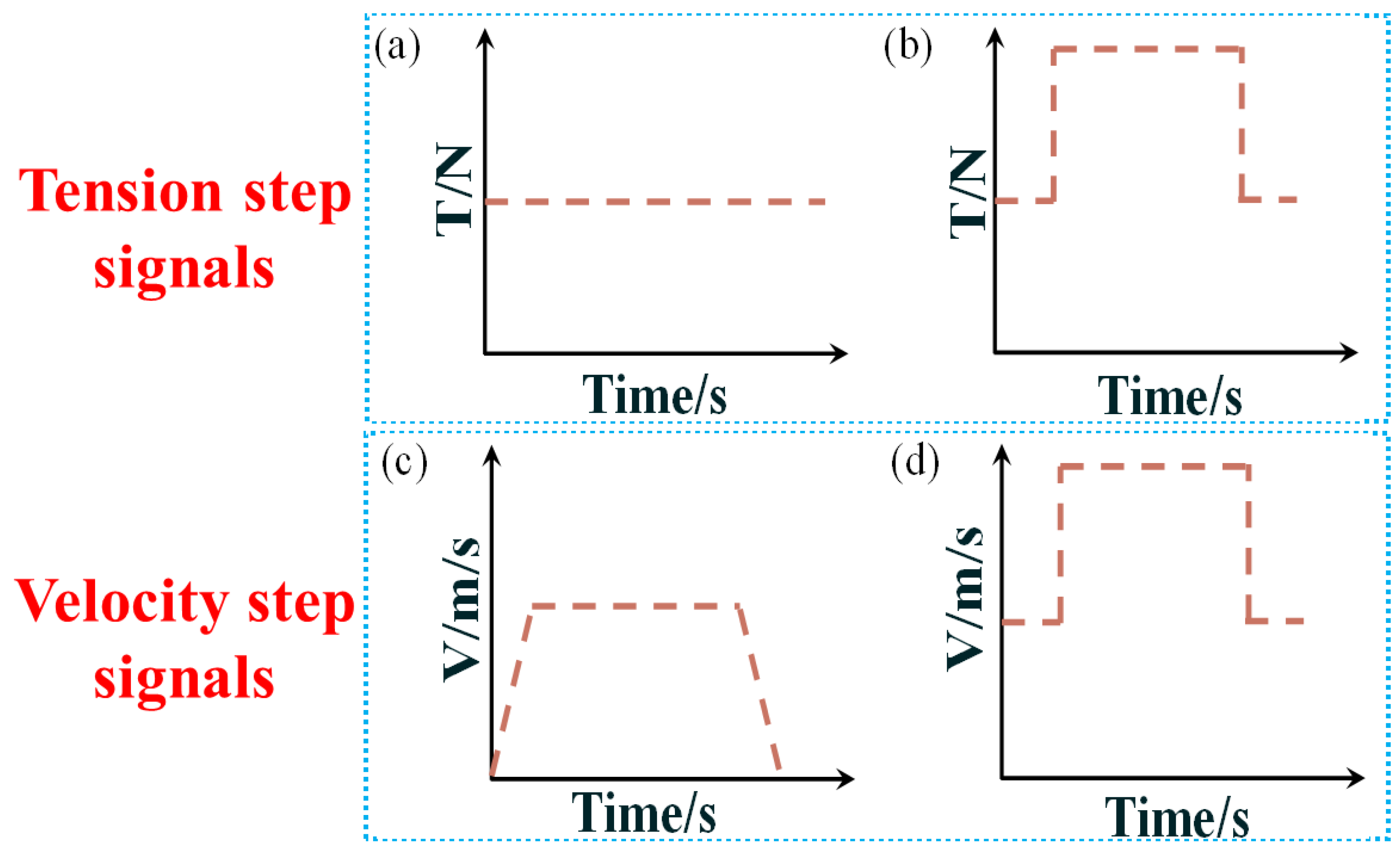
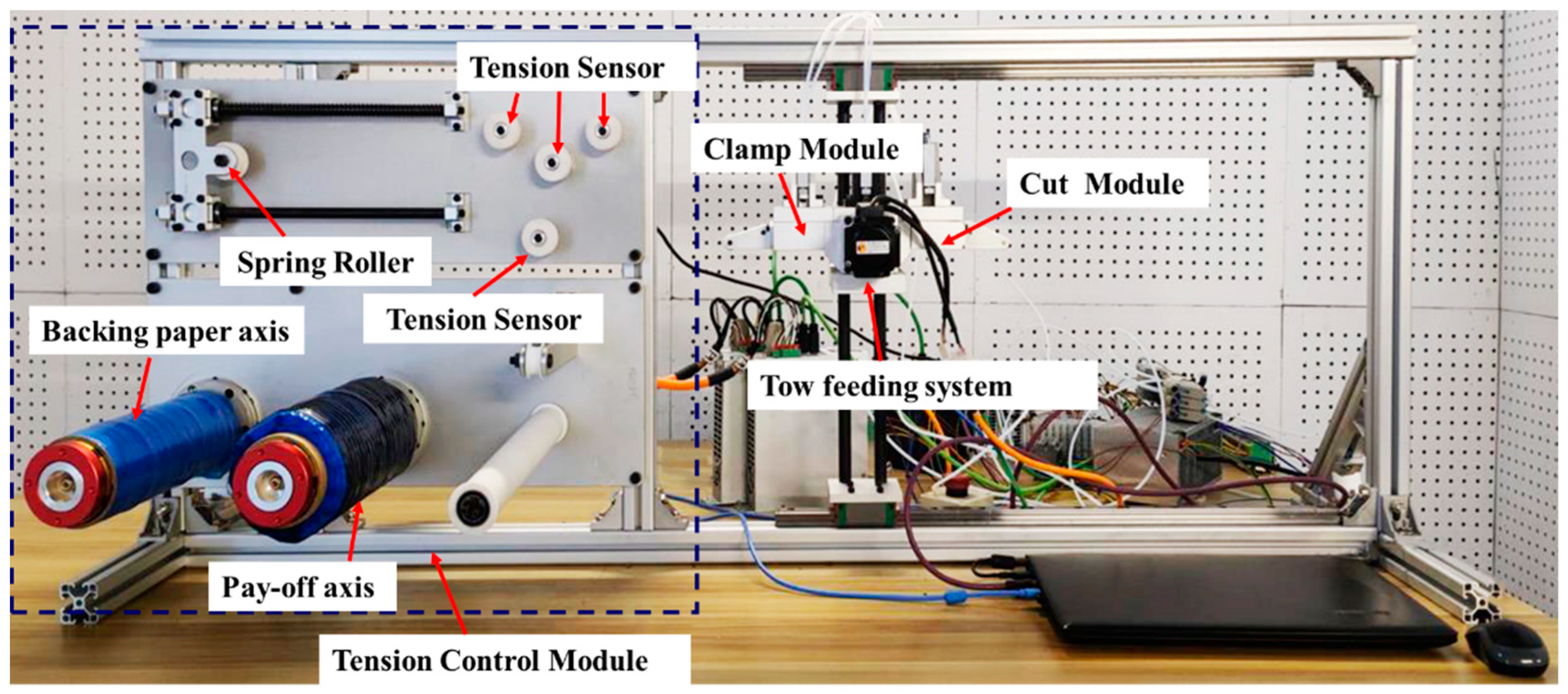
3.1. Model Validation
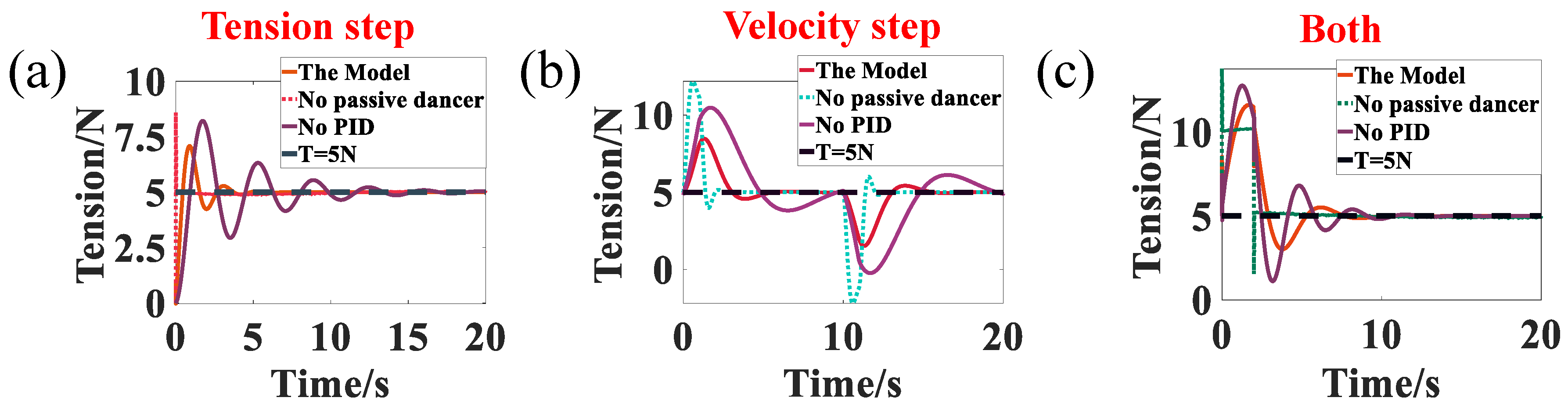
3.2. Analysis of the System Stability and Superiority
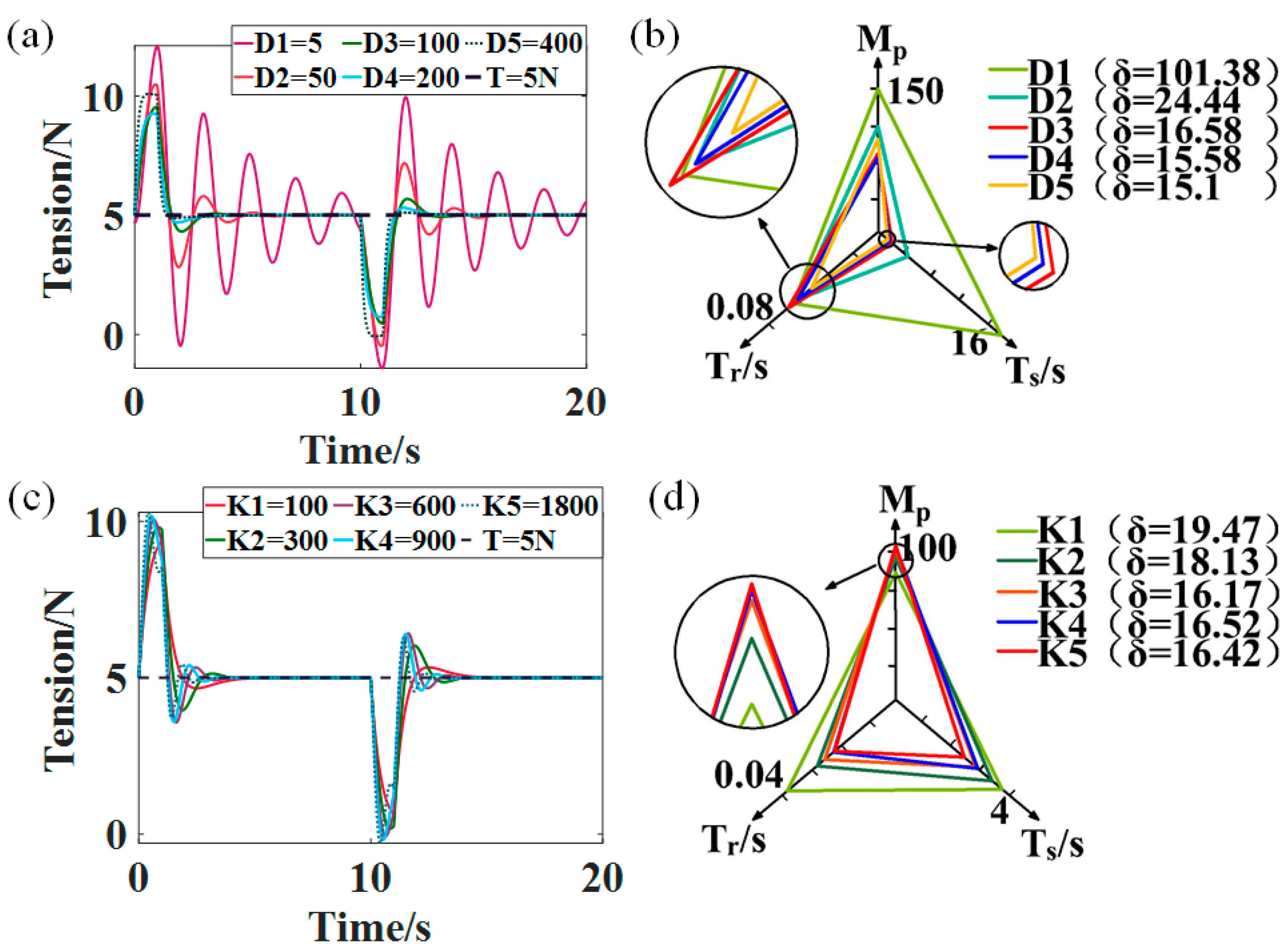
3.3. Selection of the Passive Dancer Parameters during Different Stages
3.4. Layup Experiments
4. Conclusions
- (1)
- The model’s validity was verified by developing wire-feeding and clamping experiments. Also, the stability and superiority of the control system with a passive dancer were illustrated by simulation analysis. The system provides a better buffer for the motor and reduces the maximum overshoot significantly.
- (2)
- The tension fluctuation at each stage of AFP can be derived from the precise tension control model. By analyzing the tension fluctuation with different passive dancer parameters, it can be concluded that the damping has more influence on the tension fluctuation than the elasticity coefficient. Meanwhile, by appropriately increasing the damping and elasticity coefficients, the system performance is improved, and the tension fluctuation is reduced, thus enhancing the layup quality.
- (3)
- By analyzing the tension fluctuations at each stage, the elastic coefficients of the passive dancer in the AFP process were determined to be 600 N/m, 900 N/m, and 1800 N/m, and the damping was 100 N∙s/m, 200 N∙s/m, and 400 N∙s/m. Furthermore, it was demonstrated that using the determined passive dancer parameters for laying could improve the laying quality significantly.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumar, S.; Prasad, L.; Patel, V.K.; Kumar, V.; Kumar, A.; Yadav, A.; Winczek, J. Physical and Mechanical Properties of Natural Leaf Fiber-Reinforced Epoxy Polyester Composites. Polymers 2021, 13, 1369. [Google Scholar] [CrossRef]
- Alonso-Montemayor, F.J.; Tarrés, Q.; Oliver-Ortega, H.; Espinach, F.X.; Narro-Céspedes, R.I.; Castañeda-Facio, A.O.; Delgado-Aguilar, M. Enhancing the Mechanical Performance of Bleached Hemp Fibers Reinforced Polyamide 6 Composites: A Competitive Alternative to Commodity Composites. Polymers 2020, 12, 1041. [Google Scholar] [CrossRef] [PubMed]
- Katouzian, M.; Vlase, S. Creep Response of Carbon-Fiber-Reinforced Composite Using Homogenization Method. Polymers 2021, 13, 867. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; He, B.; Wang, Z.; Qi, S.; Zhang, D.; Tian, G.; Wu, D. Enhanced Impact Properties of Hybrid Composites Reinforced by Carbon Fiber and Polyimide Fiber. Polymers 2021, 13, 2599. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, W.; Shang, J.; Yi, M.; Wang, S.; Ding, X. A Planar Underactuated Compaction Mechanism with Self-Adaptability for Automated Fiber Placement Heads. Aerospace 2022, 9, 586. [Google Scholar] [CrossRef]
- Schmidt, C.; Schultz, C.; Weber, P.; Denkena, B. Evaluation of Eddy Current Testing for Quality Assurance and Process Monitoring of Automated Fiber Placement. Compos. Part B Eng. 2014, 56, 109–116. [Google Scholar] [CrossRef]
- Alshahrani, H.; Hojjati, M. A Theoretical Model with Experimental Verification for Bending Stiffness of Thermosetting Prepreg During Forming Process. Compos. Struct. 2017, 166, 136–145. [Google Scholar] [CrossRef]
- Smith, A.W.; Endruweit, A.; Choong, G.Y.H.; De Focatiis, D.S.A.; Hubert, P. Adaptation of Material Deposition Parameters to Account for Out-Time Effects on Prepreg Tack. Compos. Part A Appl. Sci. Manuf. 2020, 133, 105835. [Google Scholar] [CrossRef]
- Bakhshi, N.; Hojjati, M. An Experimental and Simulative Study on the Defects Appeared During Tow Steering in Automated Fiber Placement. Compos. Part A Appl. Sci. Manuf. 2018, 113, 122–131. [Google Scholar] [CrossRef]
- Bakhshi, N.; Hojjati, M. Effect of Compaction Roller on Layup Quality and Defects Formation in Automated Fiber Placement. J. Reinf. Plast. Comp. 2020, 39, 3–20. [Google Scholar] [CrossRef]
- Lukaszewicz, D.H.J.A.; Ward, C.; Potter, K.D. The Engineering Aspects of Automated Prepreg Layup: History, Present and Future. Compos. Part B Eng. 2012, 43, 997–1009. [Google Scholar] [CrossRef]
- He, R.; Qu, W.; Ke, Y. An Improved Path Discretization Method for Automated Fiber Placement. J. Reinf. Plast. Comp. 2020, 39, 545–559. [Google Scholar] [CrossRef]
- Qu, W.; Pan, H.; Yang, D.; Li, J.; Ke, Y. As-Built Fe Thermal Analysis for Complex Curved Structures in Automated Fiber Placement. Simul. Model. Pract. Theory 2022, 118, 102561. [Google Scholar] [CrossRef]
- Wu, J.; Cheng, L.; Guo, Y.; Li, J.; Ke, Y. Dynamic Modeling and Parameter Identification for a Gantry-Type Automated Fiber Placement Machine. CIRP J. Manuf. Sci. Technol. 2022, 37, 388–400. [Google Scholar] [CrossRef]
- Qureshi, Z.; Swait, T.; Scaife, R.; El-Dessouky, H.M. In Situ Consolidation of Thermoplastic Prepreg Tape Using Automated Tape Placement Technology: Potential and Possibilities. Compos. Part B Eng. 2014, 66, 255–267. [Google Scholar] [CrossRef]
- Liu, Y.; Fang, Q.; Ke, Y. Modeling of Tension Control System with Passive Dancer Roll for Automated Fiber Placement. Math. Probl. Eng. 2020, 2020, 9839341. [Google Scholar] [CrossRef]
- Khan, M.A.; Mitschang, P.; Schledjewski, R. Parametric Study on Processing Parameters and Resulting Part Quality through Thermoplastic Tape Placement Process. J. Compos. Mater. 2013, 47, 485–499. [Google Scholar] [CrossRef]
- He, Y.; Jiang, J.; Qu, W.; Ke, Y. Compaction Pressure Distribution and Pressure Uniformity of Segmented Rollers for Automated Fiber Placement. J. Reinf. Plast. Comp. 2022, 41, 427–443. [Google Scholar] [CrossRef]
- Belhaj, M.; Dodangeh, A.; Hojjati, M. Experimental Investigation of Prepreg Tackiness in Automated Fiber Placement. Compos. Struct. 2021, 262, 113602. [Google Scholar] [CrossRef]
- Pei, J.; Wang, X.; Pei, J.; Yang, Y. Path Planning Based on Ply Orientation Information for Automatic Fiber Placement On Mesh Surface. Appl. Compos. Mater. 2018, 25, 1477–1490. [Google Scholar] [CrossRef]
- Zhao, C.; Xiao, J.; Wang, X. Effects of tows tension on automated fiber placement process. Acta Aeronaut. Astronaut. Sin. 2016, 37, 1384–1392. [Google Scholar]
- Jiang, J.; He, Y.; Wang, H.; Ke, Y. Modeling and Experimental Validation of Compaction Pressure Distribution for Automated Fiber Placement. Compos. Struct. 2021, 256, 113101. [Google Scholar] [CrossRef]
- Budelmann, D.; Detampel, H.; Schmidt, C.; Meiners, D. Interaction of Process Parameters and Material Properties with Regard to Prepreg Tack in Automated Lay-Up and Draping Processes. Compos. Part A Appl. Sci. Manuf. 2019, 117, 308–316. [Google Scholar] [CrossRef]
- Qu, W.; He, R.; Cheng, L.; Yang, D.; Gao, J.; Wang, H.; Yang, Q.; Ke, Y. Placement Suitability Analysis of Automated Fiber Placement on Curved Surfaces Considering the Influence of Prepreg Tow, Roller and Afp Machine. Compos. Struct. 2021, 262, 113608. [Google Scholar] [CrossRef]
- Hirsch, P.; John, M.; Leipold, D.; Henkel, A.; Gipser, S.; Schlimper, R.; Zscheyge, M. Numerical Simulation and Experimental Validation of Hybrid Injection Molded Short and Continuous Fiber-Reinforced Thermoplastic Composites. Polymers 2021, 13, 3846. [Google Scholar] [CrossRef]
- Hu, S.; Li, F.; Zuo, P. Numerical Simulation of Laser Transmission Welding—A Review on Temperature Field, Stress Field, Melt Flow Field, and Thermal Degradation. Polymers 2023, 15, 2125. [Google Scholar] [CrossRef]
- Jiang, F. Servo Control System Study of Permanent Magnet Synchronous Motor. Master’s Thesis, Zhejiang University, Hangzhou, China, 2006. [Google Scholar]
- Wulandari, S.; Iswanto, B.H.; Sugihartono, I. Determination of Springs Constant by Hooke’S Law and Simple Harmonic Motion Experiment. J. Physics. Conf. Ser. 2021, 2019, 12053. [Google Scholar] [CrossRef]
- Kang, H.; Shin, K. Precise Tension Control of a Dancer with a Reduced-Order Observer for Roll-to-Roll Manufacturing Systems. Mech. Mach. Theory 2018, 122, 75–85. [Google Scholar] [CrossRef]
- Lee, C. Infinity and Newton’s Three Laws of Motion. Found. Phys. 2011, 41, 1810–1828. [Google Scholar] [CrossRef]
- Peng, X. Quality Characterization and Regulation of Prepreg Tow Steering Based on Automatic Placement Process. Master’s Thesis, Zhejiang University, Hangzhou, China, 2019. [Google Scholar]






| Parameters | Value | Parameters | Value |
|---|---|---|---|
| 0.8 Nm/A | 0.5 mv/N | ||
| 58 V/Krpm | 52.33 GPa | ||
| 1 m | |||
| 0.075 m | 60 mm/s | ||
| 5 | 60 mm/s, 30 mm/s | ||
| 200 | 5 N | ||
| 0.1 | 0.1 m | ||
| 0.3 kg | |||
| 0.081 m | 0.034 m | ||
| 0.312 m | 0.268 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Che, Z.; Zheng, C.; Li, Z.; Wang, H.; Cheng, L.; Jiang, J. Modeling of Precise Tension with Passive Dancers for Automated Fiber Placement. Actuators 2024, 13, 70. https://doi.org/10.3390/act13020070
Li Y, Che Z, Zheng C, Li Z, Wang H, Cheng L, Jiang J. Modeling of Precise Tension with Passive Dancers for Automated Fiber Placement. Actuators. 2024; 13(2):70. https://doi.org/10.3390/act13020070
Chicago/Turabian StyleLi, Yan, Zhe Che, Chenggan Zheng, Zhi Li, Han Wang, Liang Cheng, and Junxia Jiang. 2024. "Modeling of Precise Tension with Passive Dancers for Automated Fiber Placement" Actuators 13, no. 2: 70. https://doi.org/10.3390/act13020070





