Proxy-Based Sliding Mode Force Control for Compliant Grinding via Diagonal Recurrent Neural Network and Prandtl-Ishlinskii Hysteresis Compensation Model
Abstract
:1. Introduction
- 1.
- This article proposes a rate-dependent hysteresis model that uses a diagonal recurrent neural network and Prandtl–Ishlinskii model (dRNN-PIm) to solve problems related to the rate of air pressure and output force of the cylinder.
- 2.
- The proxy-based mode control (PSMC) method is applied for the first time in controlling the proportional pressure-regulating valve cylinder system. The control method has a fast control response characteristic and can effectively prevent overshoot during the grinding control process, thereby avoiding irreversible damage to the surface of the workpiece, such as scratches and dents.
- 3.
- This article considers the large number of irregular burrs on the workpiece surface that are difficult to model as non-matching disturbances in the system. The stability of the controller is derived and proven, and the anti-interference performance of the controller is verified through experiments to quickly recover and track the desired air pressure under irregular, non-matching disturbances.
2. Problem Statement
3. Calculation of Expected Air Pressure
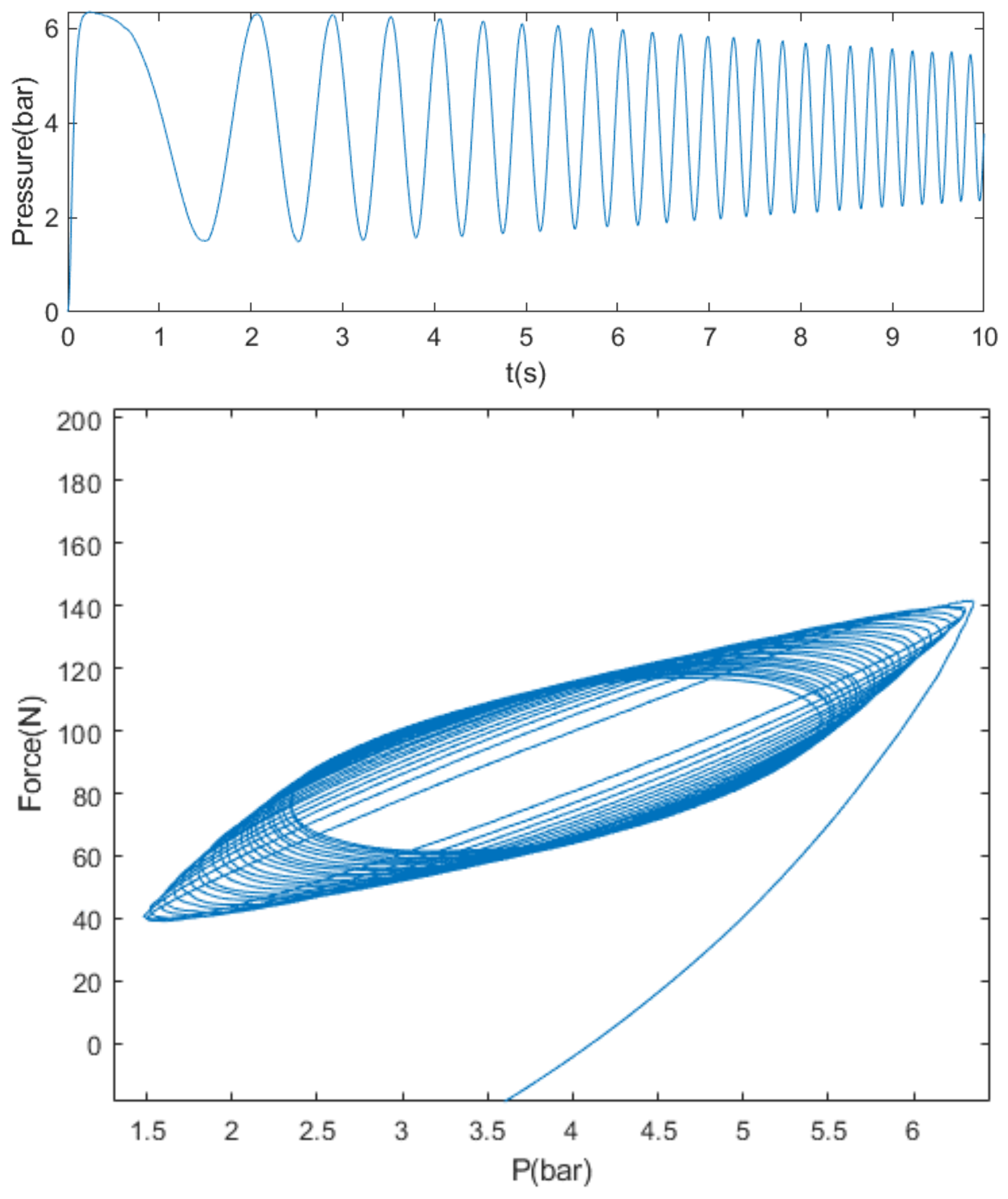
3.1. Rate-Dependent Hysteresis Characteristics of Cylinders
3.2. A Rate-Dependent Hysteresis Model Based on dRNN and PIm Players
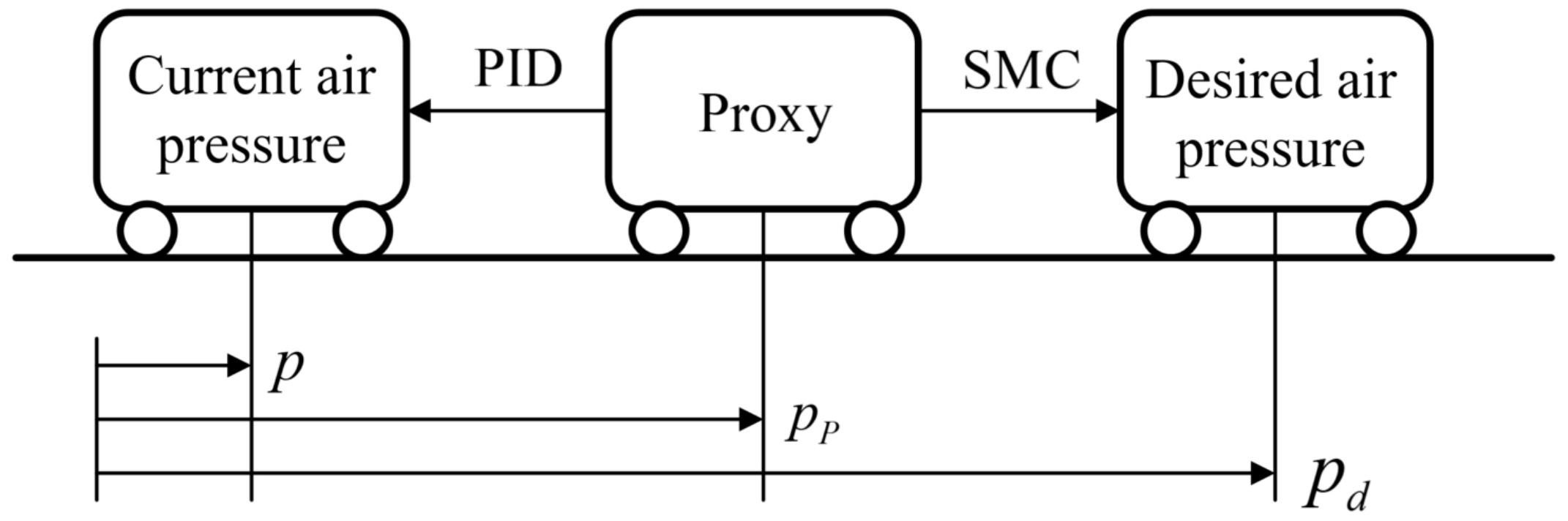
4. Tracking of Planned Air Pressure
4.1. Development of the Control Component
4.2. Stability Proof
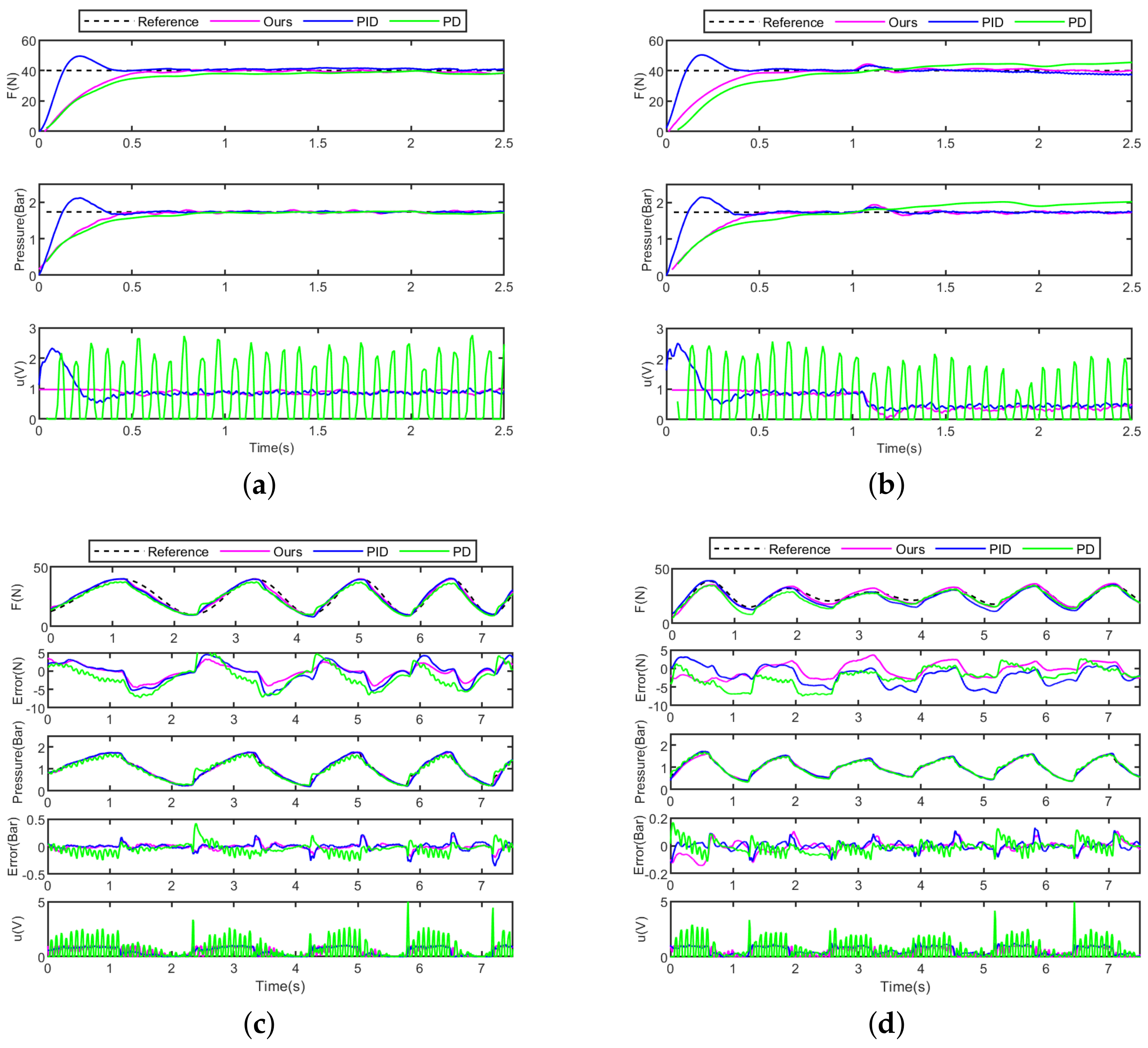
5. Experiments
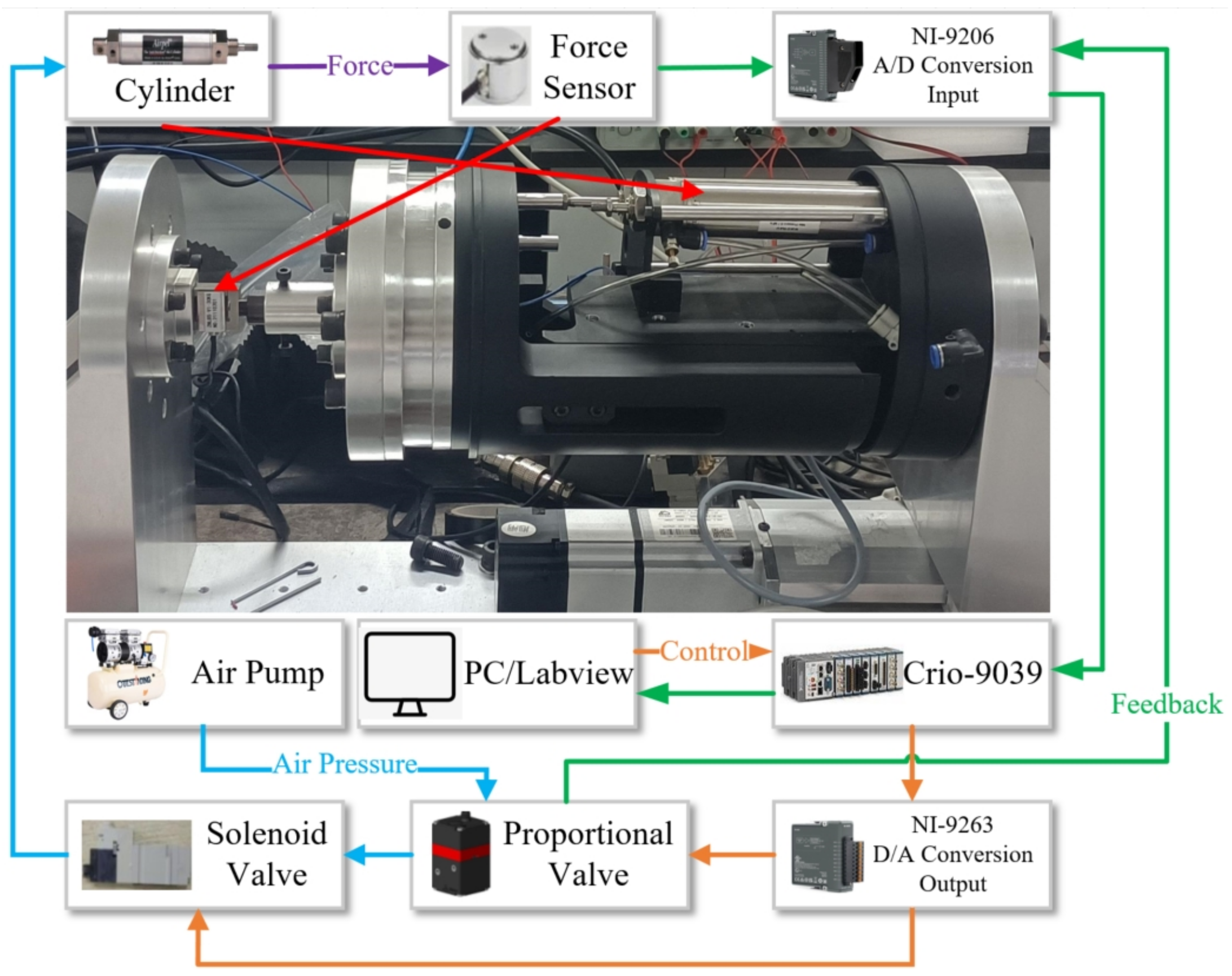
5.1. Self-Built Test Bench
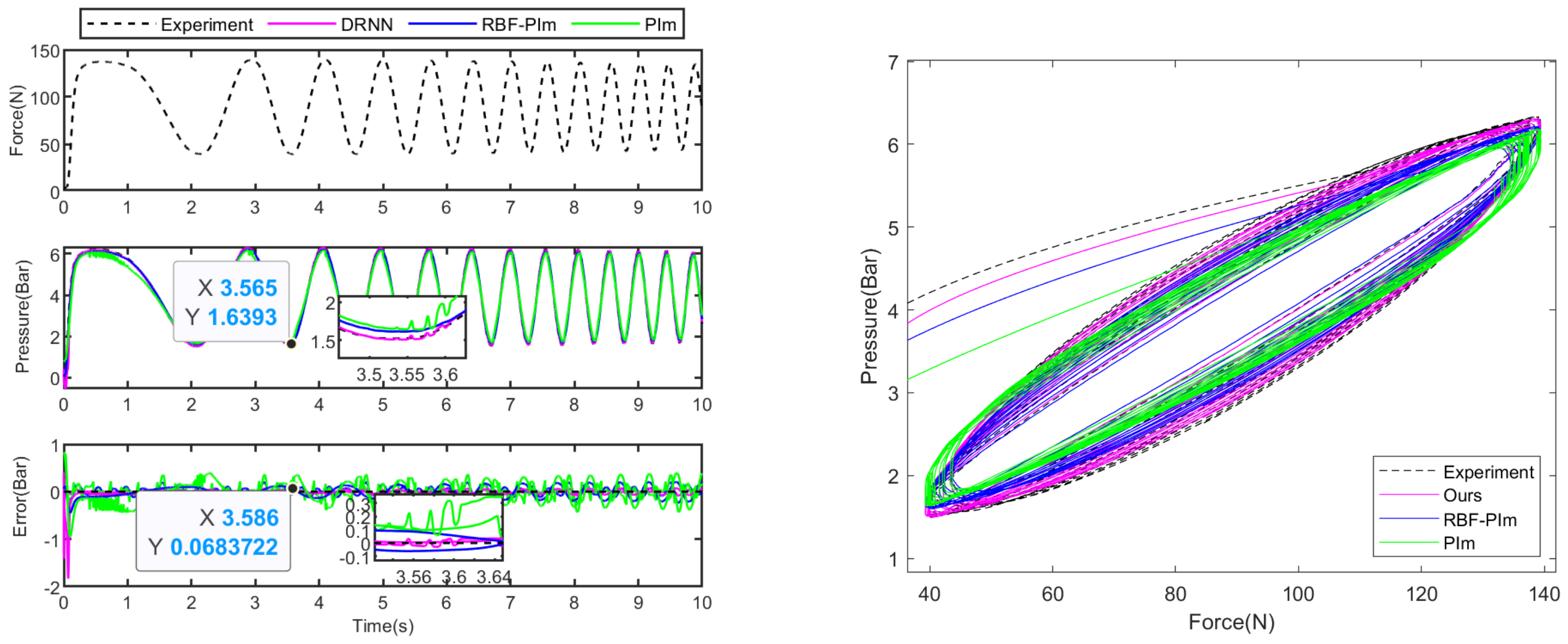
5.2. Experiment Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, X.; Lu, H.; Yu, W.; Tao, B.; Ding, H. Vision-based Mobile Robotic Grinding for Large-scale Workpiece and Its Accuracy Analysis. IEEE/ASME Trans. Mechatron. 2023, 28, 895–906. [Google Scholar] [CrossRef]
- Wu, H.; Wang, Y.; Zhang, H.; Yuan, X.; Zhou, X. Rigid Shape Matching for 3-D Robotic Grinding Measurement with Applications to Blades. IEEE Trans. Instrum. Meas. 2021, 70, 3517309. [Google Scholar] [CrossRef]
- Lu, H.; Zhao, X.; Tao, B.; Yin, Z. Online Process Monitoring Based on Vibration-Surface Quality Map for Robotic Grinding. IEEE/ASME Trans. Mechatron. 2020, 25, 2882–2892. [Google Scholar] [CrossRef]
- Li, W.-L.; Xie, H.; Zhang, G.; Yan, S.-J.; Yin, Z.-P. 3-D Shape Matching of a Blade Surface in Robotic Grinding Applications. IEEE/ASME Trans. Mechatron. 2016, 21, 2294–2306. [Google Scholar] [CrossRef]
- Ramani, S.; Salunke, A.; Ferrao, I.; Noronha, E. Automated Tile Polishing Robot. In Proceedings of the 2019 International Conference on Nascent Technologies in Engineering (ICNTE), Navi Mumbai, India, 4–5 January 2019; pp. 1–5. [Google Scholar]
- Matour, M.E.; Thormann, C.; Winkler, A. Force Controlled Deburring using a Collaborative Robot. In Proceedings of the 2022 26th International Conference on Methods and Models in Automation and Robotics (MMAR), Międzyzdroje, Poland, 22–25 August 2022; pp. 425–429. [Google Scholar]
- Xiong, R.; Lai, Z.; Guan, Y.; Yang, Y.; Cai, C. Local Deformable Template Matching in Robotic Deburring. In Proceedings of the 2018 IEEE International Conference on Robotics and Biomimetics (ROBIO), Kuala Lumpur, Malaysia, 12–15 December 2018; pp. 401–407. [Google Scholar]
- Subhashini, P.; Raju, N.V.S.; Rao, G.V. Studies on robotic deburring of machined components using a SCARA robot. In Proceedings of the 2015 International Conference on Robotics, Automation, Control and Embedded Systems (RACE), Chennai, India, 18–20 February 2015; pp. 1–6. [Google Scholar]
- Song, H.-C.; Kim, B.-S.; Song, J.-B. Tool path generation based on matching between teaching points and CAD model for robotic deburring. In Proceedings of the 2012 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Kaohsiung, Taiwan, 11–14 July 2012; pp. 890–895. [Google Scholar]
- Wu, W.; Kong, L.; Liu, W.; Zhang, C. Laser Sensor Weld Beads Recognition and Reconstruction for Rail Weld Beads Grinding Robot. In Proceedings of the 2017 5th International Conference on Mechanical, Automotive and Materials Engineering (CMAME), Guangzhou, China, 1–3 August 2017; pp. 143–148. [Google Scholar]
- Sterling, T.; Chen, H. Robotic welding parameter optimization based on weld quality evaluation. In Proceedings of the 2016 IEEE International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Chengdu, China, 19–22 June 2016; pp. 216–221. [Google Scholar]
- Saito, K.; Miyoshi, T. Automation of polishing process for a cavity surface on dies and molds by using an expert system. CIRP Ann. 1993, 42, 553–556. [Google Scholar] [CrossRef]
- Li, P.; Li, Y.; Zha, T.; Sun, L. Research on Gridding Robots Based on Compliant Device Force Control. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 3056–3060. [Google Scholar]
- Li, J.; Guan, Y.; Chen, H.; Wang, B.; Zhang, T. Robotic Polishing of Unknown-Model Workpieces with Constant Normal Contact Force Control. IEEE/ASME Trans. Mechatron. 2023, 28, 1093–1103. [Google Scholar] [CrossRef]
- Liu, S.; Xing, D.-P.; Li, Y.-F.; Zhang, J.; Xu, D. Robust Insertion Control for Precision Assembly with Passive Compliance Combining Vision and Force Information. IEEE/ASME Trans. Mechatron. 2019, 24, 1974–1985. [Google Scholar] [CrossRef]
- Shetty, B.R.; Ang, M.H. Active compliance control of a PUMA 560 robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996; Volume 4, pp. 3720–3725. [Google Scholar]
- Yu, Y.; Shi, R.; Lou, Y. Bias Estimation and Gravity Compensation for Wrist-Mounted Force/Torque Sensor. IEEE Sens. J. 2022, 22, 17625–17634. [Google Scholar] [CrossRef]
- Huang, T.; Liu, X.; Qiao, X. Design and dynamics control of a lightweight 6-axis collaborative robot. In Proceedings of the 2023 5th International Conference on Industrial Artificial Intelligence (IAI), Shenyang, China, 21–24 August 2023. [Google Scholar]
- Huang, Q.; Dong, C.; Yu, Z.; Chen, X.; Li, Q.; Chen, H.; Liu, H. Resistant Compliance Control for Biped Robot Inspired by Humanlike Behavior. IEEE/ASME Trans. Mechatron. 2022, 27, 3463–3473. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, H.; Yang, N.; Lin, H.; He, K. A structure and control design of constant force polishing end actuator based on polishing robot. In Proceedings of the 2017 IEEE International Conference on Information and Automation (ICIA), Macao, China, 18–20 July 2017; pp. 764–768. [Google Scholar]
- Li, C.; Wang, Z.; Fan, C.; Chen, G.; Huang, T. Research on Grinding and Polishing Force Control of Compliant Flange. MATEC Web Conf. 2015, 22, 03012. [Google Scholar] [CrossRef]
- Qin, Y.; Wu, H.; Li, Z.; Sun, N.; Sun, L. Design and Analysis of a Compliant End-Effector for Robotic Polishing Using Flexible Beams. Actuators 2022, 11, 284. [Google Scholar] [CrossRef]
- Liu, J.; Li, Z.; Lin, W.; Sun, L. Predefined Performance Torque Control for a Series Elastic Actuator Based on State Observer and Disturbance Observer. In Proceedings of the 2023 42nd Chinese Control Conference (CCC), Tianjin, China, 24–26 July 2023; pp. 50–54. [Google Scholar]
- Arman, N.; Bradley, C.; Ahmadian, A.S. Design, dynamic modeling, control and implementation of hydraulic artificial muscles in an antagonistic pair configuration. Mech. Mach. Theory 2020, 153.5, 104007. [Google Scholar]
- Hassani, V.; Tjahjowidodo, T.; Do, T.N. A survey on hysteresis modeling, identification and control. Mech. Syst. Signal Process. 2014, 49, 209–233. [Google Scholar] [CrossRef]
- Nicoló, V.; Rosati, L. Analytical and differential reformulations of the Vaiana–Rosati model for complex rate-independent mechanical hysteresis phenomena. Mech. Syst. Signal Process. 2023, 199, 110448. [Google Scholar]
- Nicoló, V.; Rosati, L. Classification and Unified Phenomenological Modeling of Complex Uniaxial Rate-Independent Hysteretic Responses. Mech. Syst. Signal Process. 2023, 182, 109539. [Google Scholar]
- Li, Z.; Liu, J.; Lin, W.; Sun, L. Hysteresis Fitting for Grinding Robots Based on Compliant Device Force Control. In Proceedings of the 2023 42nd Chinese Control Conference (CCC), Tianjin, China, 24–26 July 2023; pp. 6993–6997. [Google Scholar]
- Kikuuwe, R.; Yasukouchi, S.; Fujimoto, H.; Yamamoto, M. Proxy-Based Sliding Mode Control: A Safer Extension of PID Position Control. IEEE Trans. Robot. 2010, 26, 670–683. [Google Scholar] [CrossRef]
- Chen, G.; Lou, Y. Recurrent-Neural-Network-Based Rate-Dependent Hysteresis Modeling and Feedforward Torque Control of the Magnetorheological Clutch. IEEE/ASME Trans. Mechatron. 2022, 27, 2875–2886. [Google Scholar] [CrossRef]
- Xu, Y.; Shu, F.; Yang, X.; Su, X.; Hu, B. A New Regressive RBF Neural Network Model for Rate-Dependent Hysteresis in Reluctance Actuators. In Proceedings of the 2021 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 1–3 July 2021. [Google Scholar]
- Edardar, M.M.; Abougarair, A.J. Tracking Control with Hysteresis Compensation Using Neural Networks. In Proceedings of the 2021 IEEE 1st International Maghreb Meeting of the Conference on Sciences and Techniques of Automatic Control and Computer Engineering MI-STA, Tripoli, Libya, 25–27 May 2021. [Google Scholar]


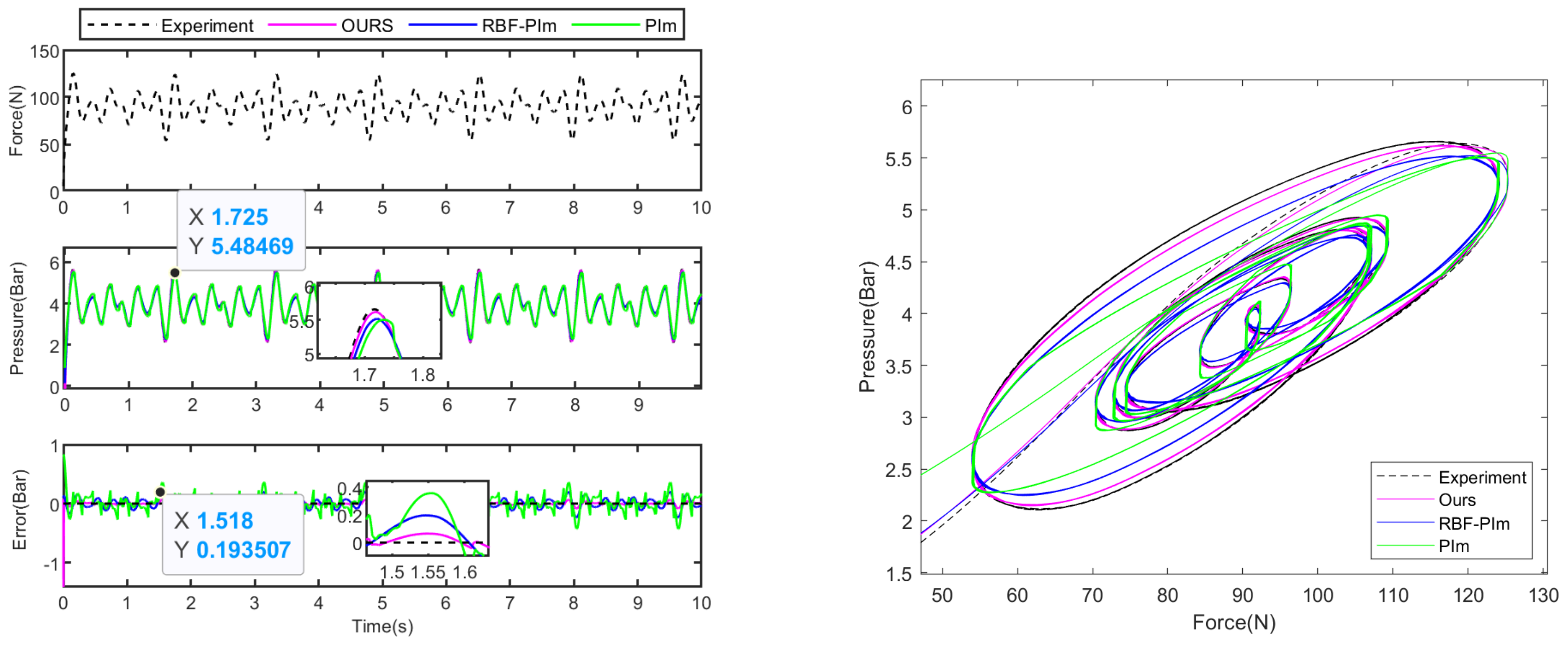
| Ours (Bar) | RBF-PIm (Bar) | PIm (Bar) | |
|---|---|---|---|
| Case 1 | |||
| Case 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Sun, L.; Liu, J.; Qin, Y.; Sun, N.; Zhou, L. Proxy-Based Sliding Mode Force Control for Compliant Grinding via Diagonal Recurrent Neural Network and Prandtl-Ishlinskii Hysteresis Compensation Model. Actuators 2024, 13, 83. https://doi.org/10.3390/act13030083
Li Z, Sun L, Liu J, Qin Y, Sun N, Zhou L. Proxy-Based Sliding Mode Force Control for Compliant Grinding via Diagonal Recurrent Neural Network and Prandtl-Ishlinskii Hysteresis Compensation Model. Actuators. 2024; 13(3):83. https://doi.org/10.3390/act13030083
Chicago/Turabian StyleLi, Zhiyuan, Lei Sun, Jidong Liu, Yanding Qin, Ning Sun, and Lu Zhou. 2024. "Proxy-Based Sliding Mode Force Control for Compliant Grinding via Diagonal Recurrent Neural Network and Prandtl-Ishlinskii Hysteresis Compensation Model" Actuators 13, no. 3: 83. https://doi.org/10.3390/act13030083
APA StyleLi, Z., Sun, L., Liu, J., Qin, Y., Sun, N., & Zhou, L. (2024). Proxy-Based Sliding Mode Force Control for Compliant Grinding via Diagonal Recurrent Neural Network and Prandtl-Ishlinskii Hysteresis Compensation Model. Actuators, 13(3), 83. https://doi.org/10.3390/act13030083







