Grey-Box Modeling and Decoupling Control of a Lab Setup of the Quadruple-Tank System
Abstract
:1. Introduction
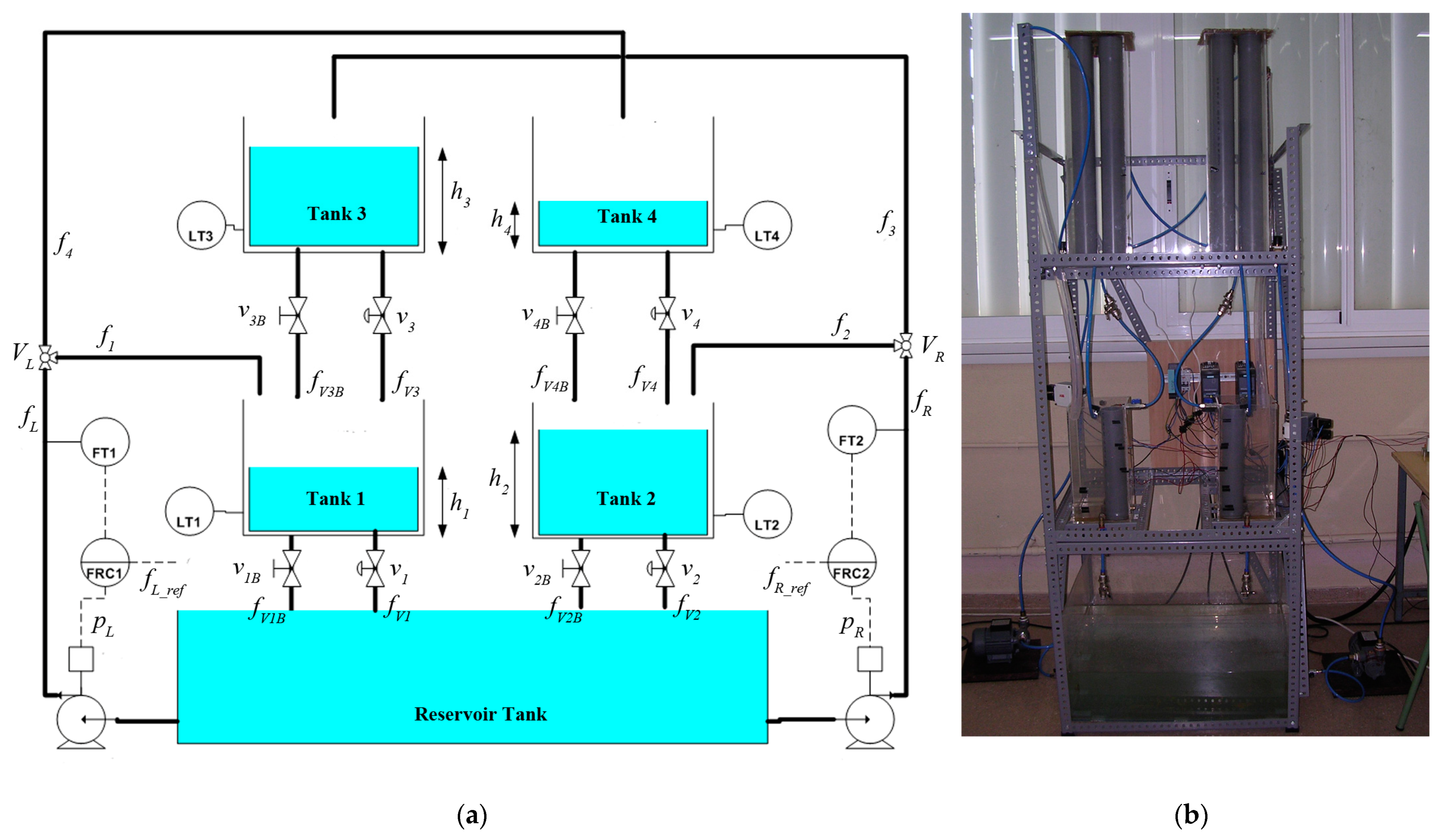
2. Laboratory Setup of the Quadruple-Tank System
- Two 0.30 kW three-phase centrifugal pumps.
- Five methacrylate tanks. The reservoir tank measures 60 × 50 × 40 cm. The other four tanks have a square internal section of 19 × 19 cm2 and a height of 35 cm for the lower tanks and 70 cm for the upper tanks. To improve the response time of the tanks, cylindrical tubes of constant section were introduced, as shown in Figure 3b. The cross-sectional area of the lower tanks, where only one tube is present, is 316.82 cm2. The cross-sectional area of the upper tanks, where four tubes are present, is 184.29 cm2.
- Two manual three-way diverter valves (VL and VR) are used to adjust the proportion of flow going to the lower tank in each branch. When in the 0% position, all the flow goes to the corresponding upper tank, so no water reaches the lower tank of that branch. Conversely, when in the 100% position, all the flow goes to the lower tank.
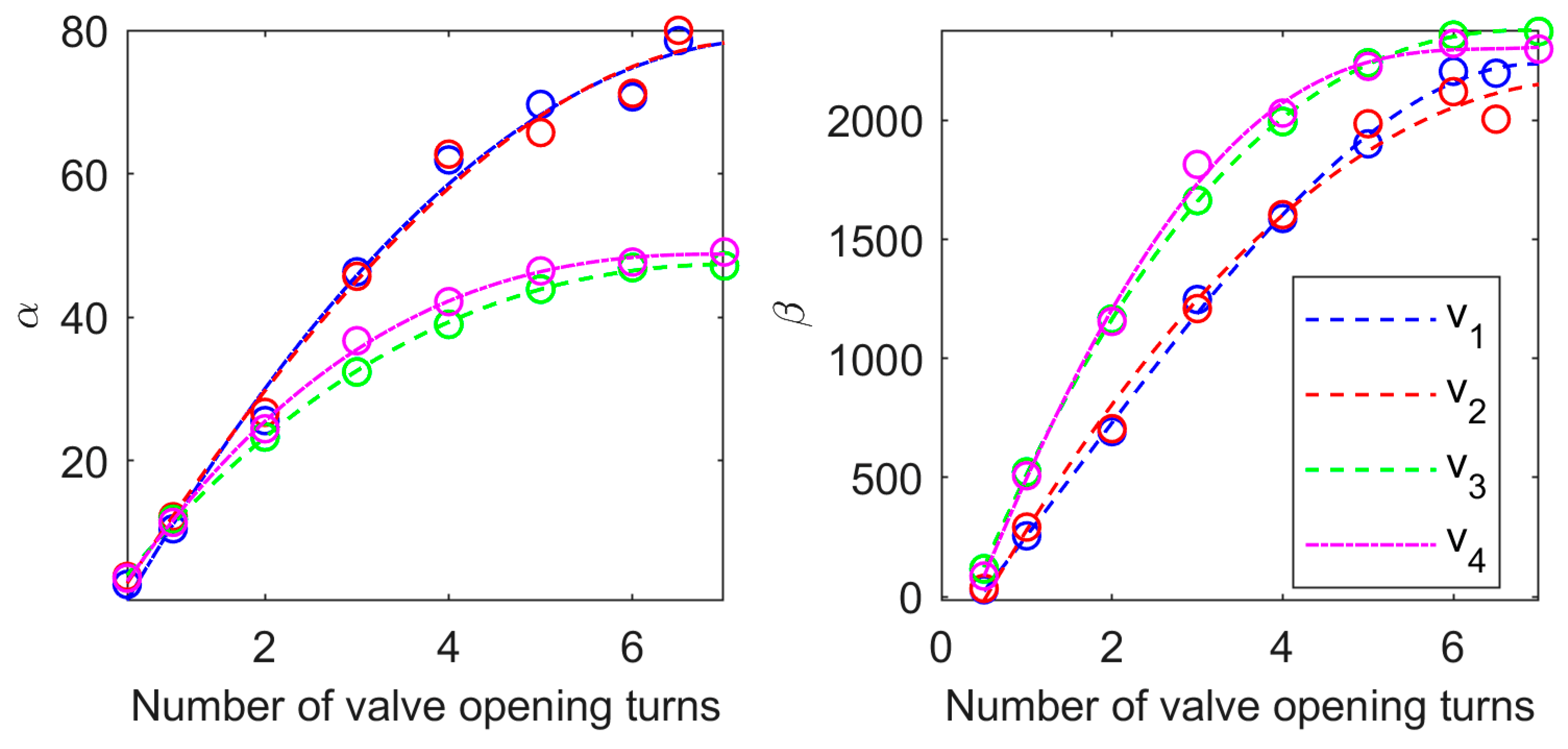
- Eight manual two-way valves are used to adjust the outflows of the four tanks. The multi-turn valves v1, v2, v3, and v4 can vary their opening degree with a total of up to six and a half or seven turns, depending on the valve. In contrast, valves v1B, v2B, v3B, and v4B have only two positions: fully closed or fully open.
- We use 10/8 mm polyurethane pipes and pipe fittings for connecting the different elements of the hydraulic circuit. In addition, two 40/32 mm PVC hoses are used to drain the inlet flows from the three-way valves to the lower tanks. Unlike the schematic shown in Figure 3a, the two outlets from each three-way valve are brought to the same height through 10/8 mm pipes. One branch goes to the corresponding upper tank, whereas the other branch goes to the 44/38 mm pipe so that from the upper height it drains without head loss. This design ensures that the two outlet branches of the three-way valves have similar head loss and that the flow distribution, depending on the position of the valve, is independent of the total inlet flow to the three-way valve.
- Four upwelling diaphragm pressure transmitters for general applications. A measuring range of [0–0.1] bar, which is approximately a [0–100] cm water column. These transmitters were used to measure the water level in the four tanks.
- Two electromagnetic flow meters for measuring the total flow rates of the branches fL and fR. The measurement range is set to [0–200] cm3/s.
- Two frequency inverters to control the flow rate delivered by the pumps through a secondary control loop.
- An NI-DAQ 6035E data acquisition card to connect the process signals to a computer.
- A personal computer contains the acquisition card and the control software, which in this case is MATLAB 7.4 and its Real Time Windows Target toolbox. The configured sampling time is 1 s.
3. Modeling of the Quadruple-Tank System
- Pump dynamics and flow control: they determine the total flow rates of each branch (left and right) that the pumps drive from the reservoir tank to the other tanks.
- Dynamics of the four tanks: They determine the water level of each tank as a function of its corresponding inlet and outlet flow rates. The inlet flow rates depend on the total flow rate of each branch, the position of the three-way valves, and in the case of the lower tanks, the outlet flow rates of the upper tanks. The outflow of each tank depends on its water level and the degree of opening of its outlet valves.
3.1. Dynamics of the Pumps and Secondary Flow Control Loops
3.2. Tank Dynamics
3.3. Complete Nonlinear Model
3.4. Linearization of the Nonlinear Model
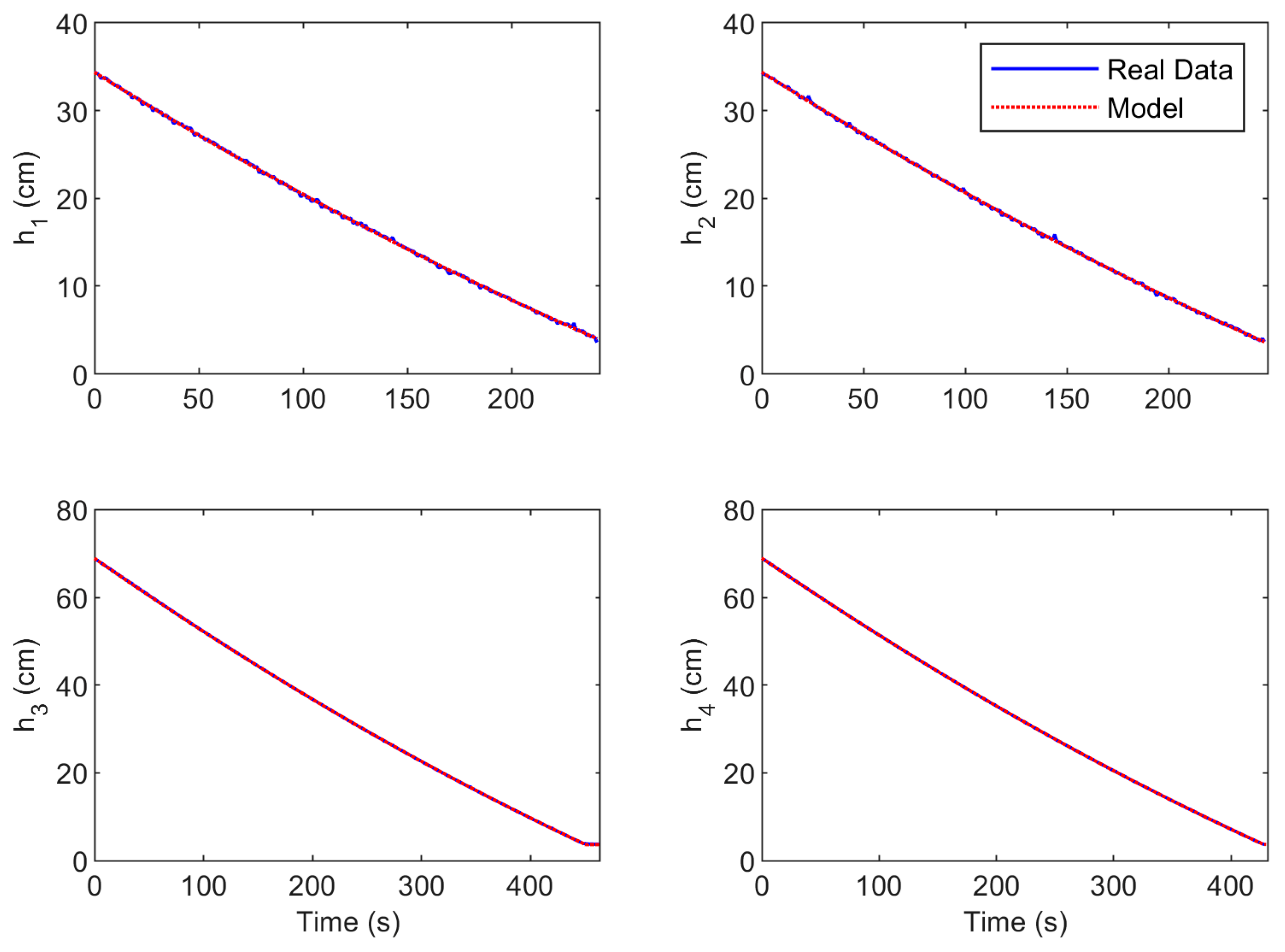
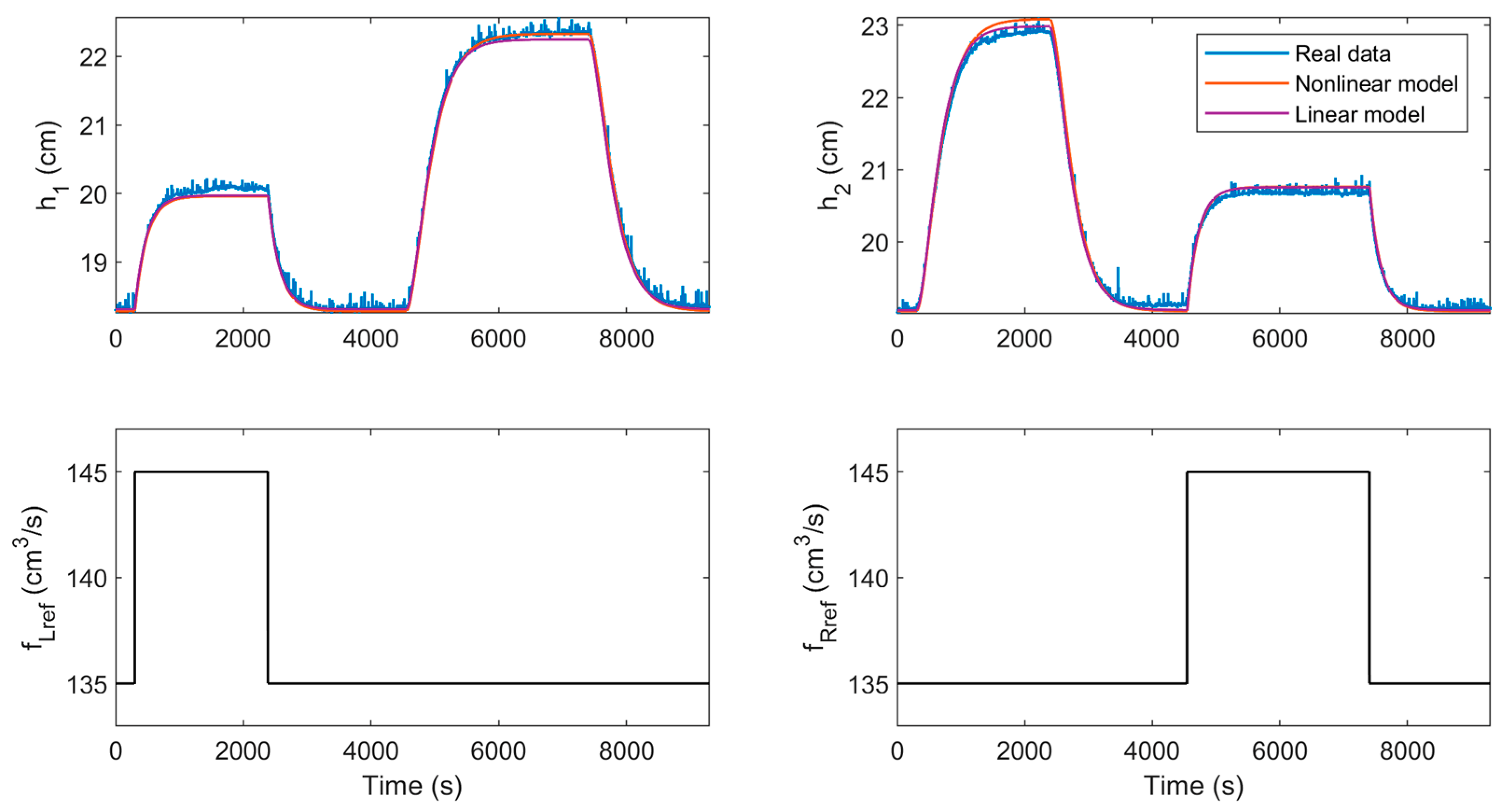
3.5. Validation of the Model
4. Proposed Control Systems Using Decoupling
4.1. Multi-Loop PI Controller
4.2. Static Decoupling
4.3. Simplified Decoupling
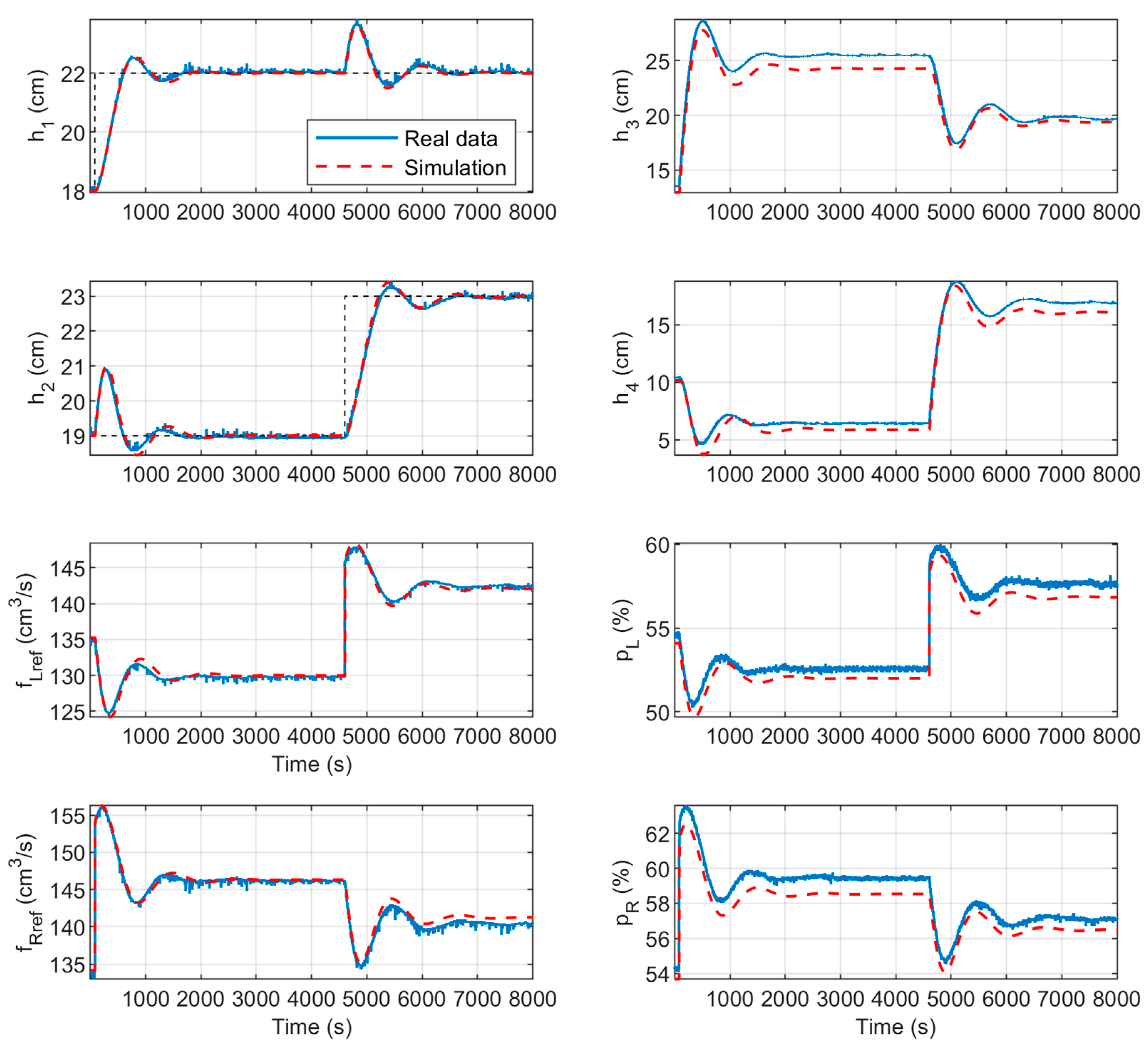
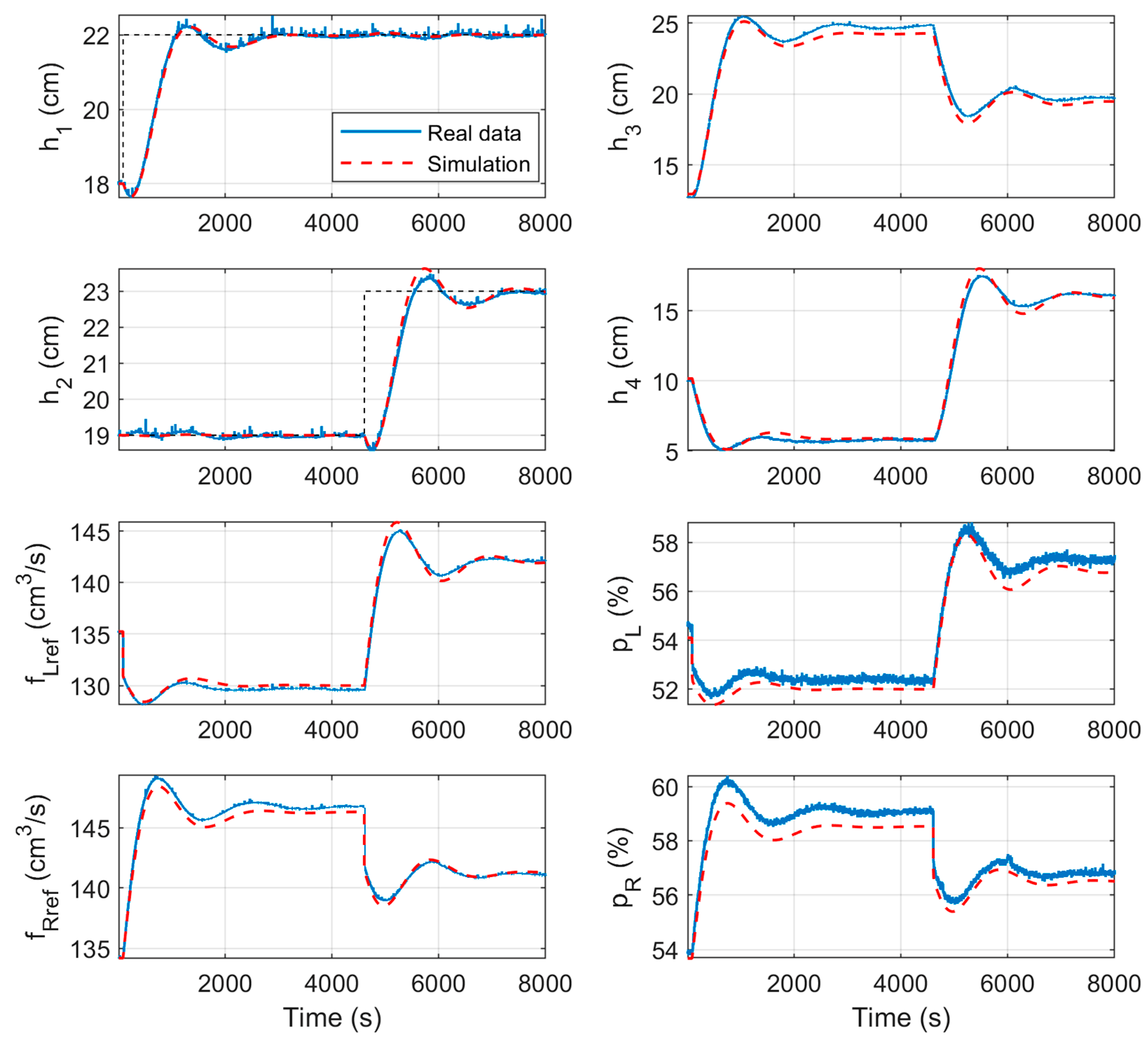
5. Results
6. Conclusions
- Secondary control loops are suggested to regulate the flow rate delivered by each pump, making the new control variables the references for those flow rates. The controllers have integral action, resulting in zero stationary error. In addition, the response of these loops is much faster than the dynamics of the tanks, allowing for the requested changes to the flow rate to be almost instantaneous. This approach helps to avoid pump nonlinearities.
- The proposed method for modeling the outflows of the tanks is based on level data measured during the experience of emptying the tank and is expressed using the Bernoulli equation.
- The percentage of flow diverted to the lower tanks from the three-way valves is modeled using planes as a function of inlet flow and valve position, based on tank filling experiences. To facilitate modeling of these valves, it is useful for the outlet pipes of the three-way valve to have the same length in the construction of the real plant in order to equalize the head losses of both outlet sections. Thus, the distribution of flow is less affected by the total inlet flow, depending on the valve position.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aranda-Cetraro, I.; Pérez-Zúñiga, G.; Rivas-Pérez, R.; Sotomayor-Moriano, J. Nonlinear Robust Control by a Modulating-Function-Based Backstepping Super-Twisting Controller for a Quadruple Tank System. Sensors 2023, 23, 5222. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, J.; Li, D.; Qin, J. Application of Desired Dynamic Equation Method in Simulation of Four-Tank System. In Proceedings of the 2012 International Conference on Systems and Informatics, ICSAI 2012, Yantai, China, 19–20 May 2012; pp. 366–370. [Google Scholar]
- Harsha, S.; Vinod, D.; Saikrishna, P.S. Identification and Multi-Objective H∞ Control Design for a Quadruple Tank System. In Proceedings of the 2019 IEEE 7th Conference on Systems, Process and Control, ICSPC 2019, Melaka, Malaysia, 13–14 December 2019; pp. 70–75. [Google Scholar] [CrossRef]
- Sohlberg, B.; Jacobsen, E.W. Grey Box Modelling—Branches and Experiences; IFAC: New York, NY, USA, 2008; Volume 41, ISBN 9783902661005. [Google Scholar]
- Bohlin, T. Practical Grey-Box Process Identification; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 9781846284021. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; Wiley: Hoboken, NJ, USA, 2007; ISBN 978-0-470-01168-3. [Google Scholar]
- Luyben, W.L. Simple Method for Tuning SISO Controllers in Multivariable Systems. Ind. Eng. Chem. Process Des. Dev. 1986, 25, 654–660. [Google Scholar] [CrossRef]
- Garrido, J.; Ruz, M.L.; Morilla, F.; Vázquez, F. Iterative Method for Tuning Multiloop Pid Controllers Based on Single Loop Robustness Specifications in the Frequency Domain. Processes 2021, 9, 140. [Google Scholar] [CrossRef]
- Bristol, E. On a New Measure of Interaction for Multivariable Process Control. IEEE Trans. Autom. Control 1966, 11, 133–134. [Google Scholar] [CrossRef]
- Shinskey, F.G. Process Control Systems: Application, Design, and Tuning, 4th ed.; McGraw-Hill Inc.: New York, NY, USA, 1996; ISBN 0-07-057101-5. [Google Scholar]
- Skogestad, S. Advanced Control Using Decomposition and Simple Elements. Annu. Rev. Control 2023, 56, 100903. [Google Scholar] [CrossRef]
- Wang, Q.-G. Decoupling Control; Springer: Berlin/Heidelberg, Germany, 2003; ISBN 978-3-540-44128-1. [Google Scholar]
- Liu, L.; Tian, S.; Xue, D.; Zhang, T.; Chen, Y.Q.; Zhang, S. A Review of Industrial MIMO Decoupling Control. Int. J. Control Autom. Syst. 2019, 17, 1246–1254. [Google Scholar] [CrossRef]
- Waller, M.; Waller, J.B.; Waller, K.V. Decoupling Revisited. Ind. Eng. Chem. Res. 2003, 42, 4575–4577. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, R.; Zhang, J. Model-Free Robust Decoupling Control of Nonlinear Nonaffine Dynamic Systems. Int. J. Syst. Sci. 2023, 54, 2590–2607. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, R.; Zhang, J.; Shi, B. Model-Free Robust Decentralised Control of Multi-Input-Multi-Output Nonlinear Interconnected Dynamic Systems. JVC/J. Vib. Control 2023. [Google Scholar] [CrossRef]
- Johansson, K.H.; Nunes, J.L.R. A Multivariable Laboratory Process with an Adjustable Zero. In Proceedings of the American Control Conference, Philadelphia, PA, USA, 26 June 1998; Volume 4, pp. 2045–2049. [Google Scholar] [CrossRef]
- Johanssont, K.H.; Horcht, A.; Wijkt, O.; Hanssont, A. Teaching Multivariable Control Using the Quadruple-Tank Process. In Proceedings of the 38th IEEE Conference on Decision and Control, Phoenix, AZ, USA, 7–10 December 1999. [Google Scholar]
- Johansson, K.H. The Quadruple-Tank Process: A Multivariable Laboratory Process with an Adjustable Zero. IEEE Trans. Control Syst. Technol. 2000, 8, 456–465. [Google Scholar] [CrossRef]
- Meng, X.; Yu, H.; Xu, T.; Wu, H. Disturbance Observer and L2-Gain-Based State Error Feedback Linearization Control for the Quadruple-Tank Liquid-Level System. Energies 2020, 13, 5500. [Google Scholar] [CrossRef]
- Shneiderman, D.; Palmor, Z.J. Properties and Control of the Quadruple-Tank Process with Multivariable Dead-Times. J. Process Control 2010, 20, 18–28. [Google Scholar] [CrossRef]
- Gatzke, E.P.; Meadows, E.S.; Wang, C.; Doyle, F.J. Model Based Control of a Four-Tank System. Comput. Chem. Eng. 2000, 24, 1503–1509. [Google Scholar] [CrossRef]
- Kozáková, A.; Čápková, R.; Kozák, Š. Decentralized QFT Controller Design Based on the Equivalent Subsystems Method. Electronics 2023, 12, 3658. [Google Scholar] [CrossRef]
- Das Neves, G.P.; Barbosa, F.S.; Costa, P.S.; Angelico, B.A. Discrete Time LQG/LTR Applied to a Practical Quadruple Tank System. In Proceedings of the 2016 IEEE Conference on Control Applications, CCA 2016, Buenos Aires, Argentina, 19–22 September 2016; pp. 1232–1237. [Google Scholar] [CrossRef]
- Piñón, A.; Favela-Contreras, A.; Beltran-Carbajal, F.; Lozoya, C.; Dieck-Assad, G. Novel Strategy of Adaptive Predictive Control Based on a MIMO-ARX Model. Actuators 2022, 11, 21. [Google Scholar] [CrossRef]
- Oyehan, I.A.; Osunleke, A.S.; Ajani, O.O. Closed-Loop Stability of a Non-Minimum Phase Quadruple Tank System Using a Nonlinear Model Predictive Controller with EKF. ChemEngineering 2023, 7, 74. [Google Scholar] [CrossRef]
- Alvarado, I.; Limon, D.; Muñoz De La Peña, D.; Maestre, J.M.; Ridao, M.A.; Scheu, H.; Marquardt, W.; Negenborn, R.R.; De Schutter, B.; Valencia, F.; et al. A Comparative Analysis of Distributed MPC Techniques Applied to the HD-MPC Four-Tank Benchmark. J. Process Control 2011, 21, 800–815. [Google Scholar] [CrossRef]
- Gurjar, B.; Chaudhari, V.; Kurode, S. Parameter Estimation Based Robust Liquid Level Control of Quadruple Tank System—Second Order Sliding Mode Approach. J. Process Control 2021, 104, 1–10. [Google Scholar] [CrossRef]
- Biswas, P.P.; Srivastava, R.; Ray, S.; Samanta, A.N. Sliding Mode Control of Quadruple Tank Process. Mechatronics 2009, 19, 548–561. [Google Scholar] [CrossRef]
- Eltantawie, M.A. Decentralized Neuro-Fuzzy Controllers of Nonlinear Quadruple Tank System. SN Appl. Sci. 2019, 1, 39. [Google Scholar] [CrossRef]
- Thamallah, A.; Sakly, A.; M’Sahli, F. A New Constrained PSO for Fuzzy Predictive Control of Quadruple-Tank Process. Measurement 2019, 136, 93–104. [Google Scholar] [CrossRef]
- Son, N.N. Level Control of Quadruple Tank System Based on Adaptive Inverse Evolutionary Neural Controller. Int. J. Control Autom. Syst. 2020, 18, 2386–2397. [Google Scholar] [CrossRef]
- Castelo, G.; Garrido, J.; Vazquez, F. Ajuste, Configuración y Control de Cuatro Tanques Acoplados. In Proceedings of the Jornadas de Automática 2008, Tarragona, Spain, 3–5 September 2008. [Google Scholar]
- Lee, J.; Kim, D.H.; Edgar, T.F. Static Decouplers for Control of Multivariable Processes. AIChE J. 2005, 51, 2712–2720. [Google Scholar] [CrossRef]
- Garrido, J.; Ruz, M.L.; Morilla, F.; Vázquez, F. Interactive Tool for Frequency Domain Tuning of PID Controllers. Processes 2018, 6, 197. [Google Scholar] [CrossRef]


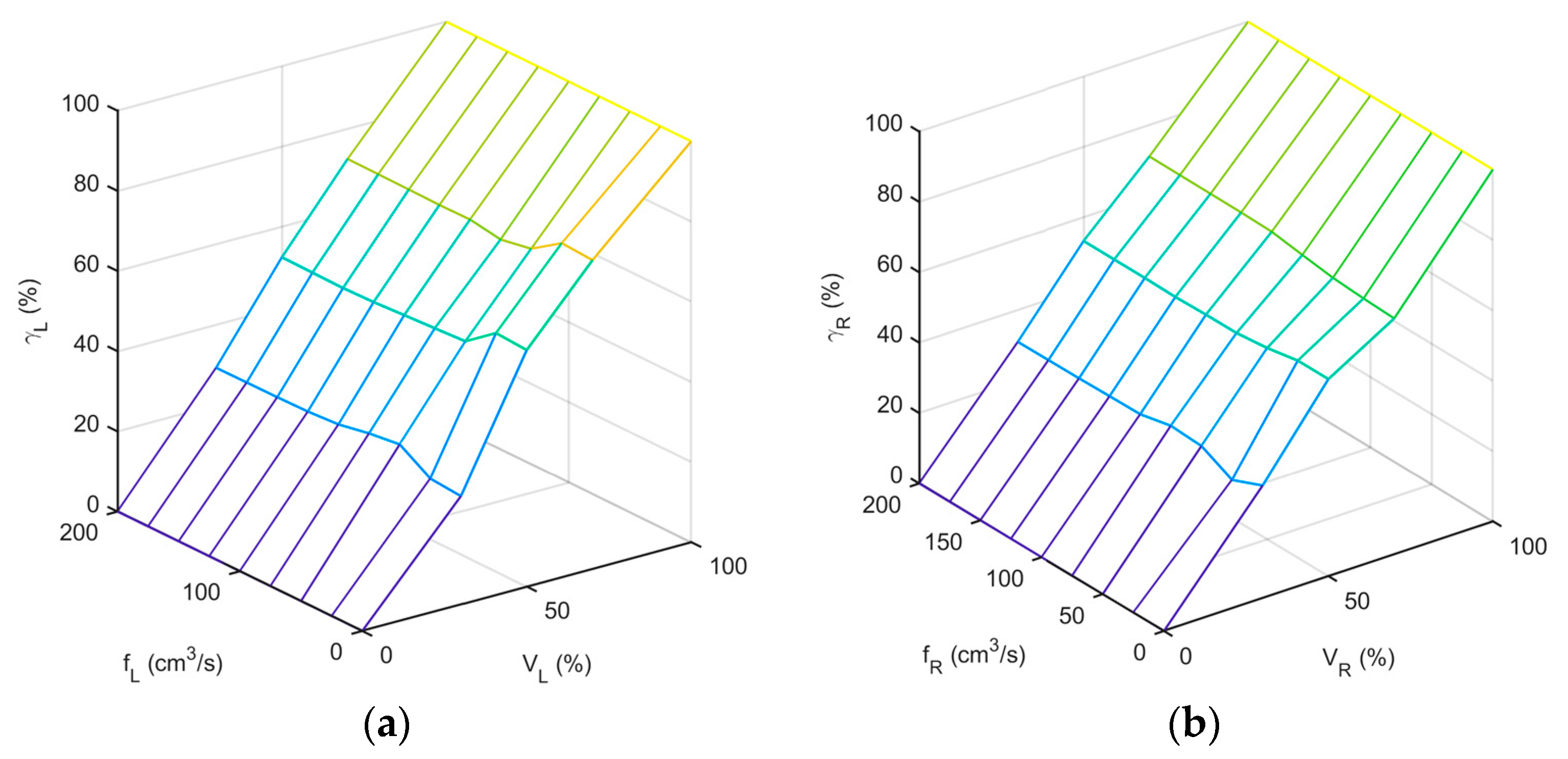

| VL (%) | fL (cm3/s) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 25 | 50 | 75 | 100 | 125 | 150 | 175 | 200 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 30 | 27 | 27.66 | 32.45 | 31.47 | 29.99 | 29.47 | 29.32 | 29.27 | 29.22 |
| 50 | 59 | 59.51 | 53.73 | 53.25 | 52.81 | 52.34 | 52.12 | 52.23 | 52.34 |
| 70 | 77 | 77.50 | 72.38 | 70.97 | 72.22 | 72.13 | 72.26 | 72.35 | 72.44 |
| 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| VR (%) | fR (cm3/s) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 25 | 50 | 75 | 100 | 125 | 150 | 175 | 200 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 30 | 32 | 28.35 | 32.74 | 33.25 | 31.28 | 31.17 | 31 | 30.94 | 30.88 |
| 50 | 56 | 56 | 54.35 | 53.36 | 53.33 | 53.12 | 53.28 | 53.39 | 53.31 |
| 70 | 67 | 67.42 | 68.05 | 69.31 | 70.66 | 70.89 | 70.96 | 71.03 | 71.09 |
| 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| Model | RMSE (h1) (cm) | RMSE (h2) (cm) |
|---|---|---|
| Nonlinear | 0.062 | 0.093 |
| Linear | 0.071 | 0.066 |
| Operation Point | Model Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| fL_ref,0 (cm3/s) | fR_ref,0 (cm3/s) | h1,0 (cm) | h2,0 (cm) | K1_in | K2_in | T1 (s) | T2 (s) | T3 (s) | T4 (s) |
| 135 | 135 | 18.3 | 19 | 0.293 | 0.306 | 179.7 | 176.3 | 238.1 | 218 |
| 150 | 150 | 27.1 | 28 | 0.290 | 0.305 | 199.9 | 196.7 | 264.7 | 242.8 |
| 125 | 125 | 12.9 | 13.6 | 0.295 | 0.306 | 166.2 | 162.7 | 220.5 | 201.5 |
| 125 | 165 | 29.1 | 20.2 | 0.295 | 0.304 | 204.1 | 179.1 | 291.3 | 201.6 |
| 170 | 130 | 22.2 | 33.2 | 0.286 | 0.306 | 188.8 | 207.5 | 229.3 | 276.0 |
| Control System | RMSE | |||||||
|---|---|---|---|---|---|---|---|---|
| h1 (cm) | h2 (cm) | fL (cm3/s) | fR (cm3/s) | h3 (cm) | h4 (cm) | pL (%) | pR (%) | |
| Decentralized | 0.06 | 0.09 | 0.5 | 0.65 | 0.92 | 0.7 | 0.68 | 0.81 |
| Static decoupling | 0.10 | 0.10 | 0.71 | 0.66 | 0.47 | 0.51 | 0.65 | 0.66 |
| Simplified decoupling | 0.06 | 0.11 | 0.44 | 0.46 | 0.41 | 0.30 | 0.45 | 0.53 |
| Control System | IAE (h1) (cms) | IAE (h2) (cms) | TV (fL) (cm3/s) | TV (fR) (cm3/s) | ||||
|---|---|---|---|---|---|---|---|---|
| Total | Tracking | Decoupling | Total | Tracking | Decoupling | |||
| Decentralized | 2322 | 1444 | 878 | 2421 | 1566 | 855 | 535 | 715 |
| Static decoupling | 2682 | 1762 | 920 | 2380 | 1795 | 585 | 500 | 514 |
| Simplified decoupling | 3003 | 2882 | 121 | 3023 | 2818 | 205 | 163 | 168 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garrido, J.; Garrido-Jurado, S.; Vázquez, F. Grey-Box Modeling and Decoupling Control of a Lab Setup of the Quadruple-Tank System. Actuators 2024, 13, 87. https://doi.org/10.3390/act13030087
Garrido J, Garrido-Jurado S, Vázquez F. Grey-Box Modeling and Decoupling Control of a Lab Setup of the Quadruple-Tank System. Actuators. 2024; 13(3):87. https://doi.org/10.3390/act13030087
Chicago/Turabian StyleGarrido, Juan, Sergio Garrido-Jurado, and Francisco Vázquez. 2024. "Grey-Box Modeling and Decoupling Control of a Lab Setup of the Quadruple-Tank System" Actuators 13, no. 3: 87. https://doi.org/10.3390/act13030087
APA StyleGarrido, J., Garrido-Jurado, S., & Vázquez, F. (2024). Grey-Box Modeling and Decoupling Control of a Lab Setup of the Quadruple-Tank System. Actuators, 13(3), 87. https://doi.org/10.3390/act13030087








