Bidirectional Multi-Spectral Vibration Control: Insights from Automotive Engine Mounting Systems in Two-Dimensional Structures with a Damaged Vertical Active Element
Abstract
:1. Introduction
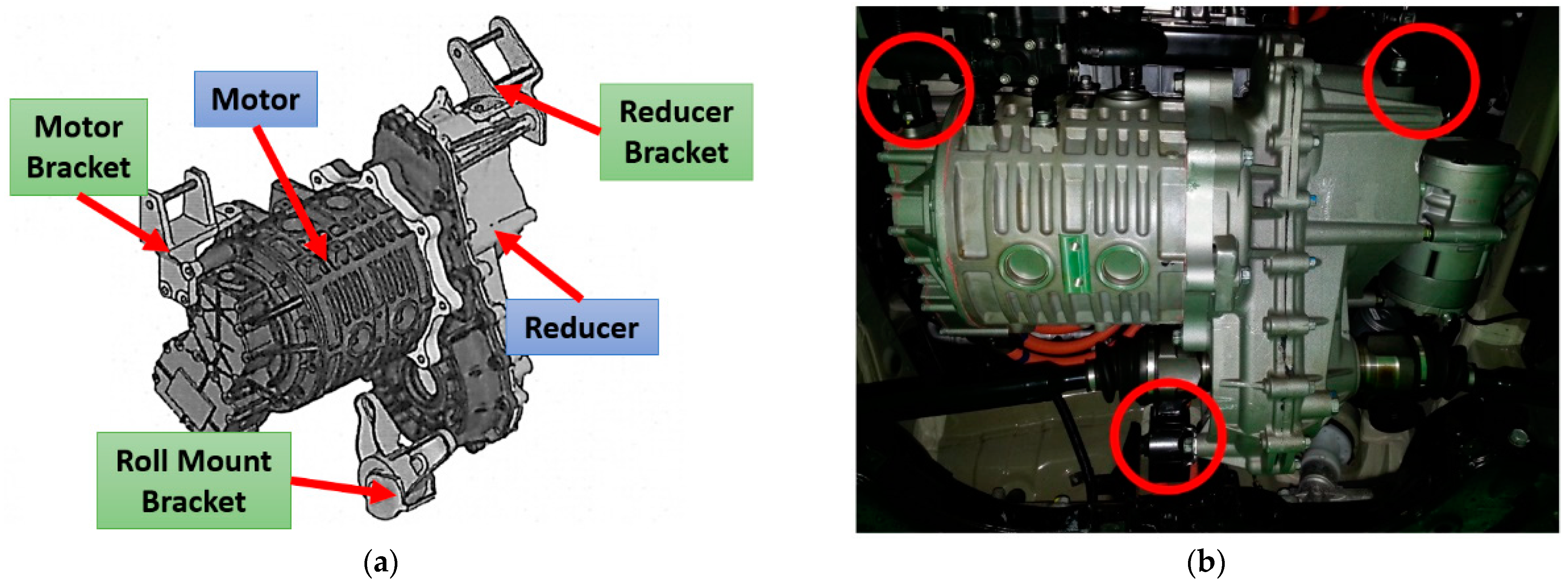
1.1. Research Background
1.2. Literature Search
1.3. Research Purpose
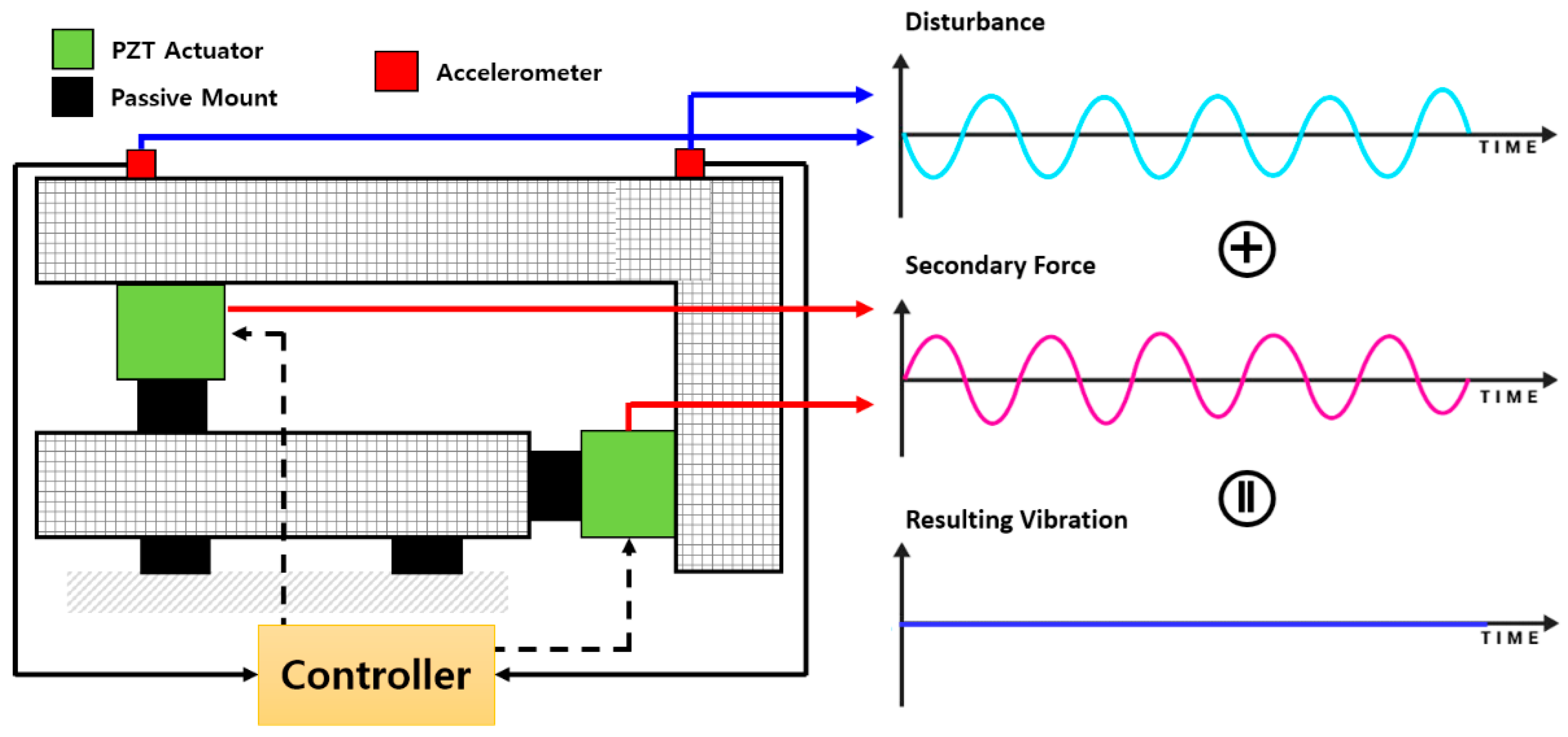
2. Horizontal Active Mounting System for Vibration Reduction
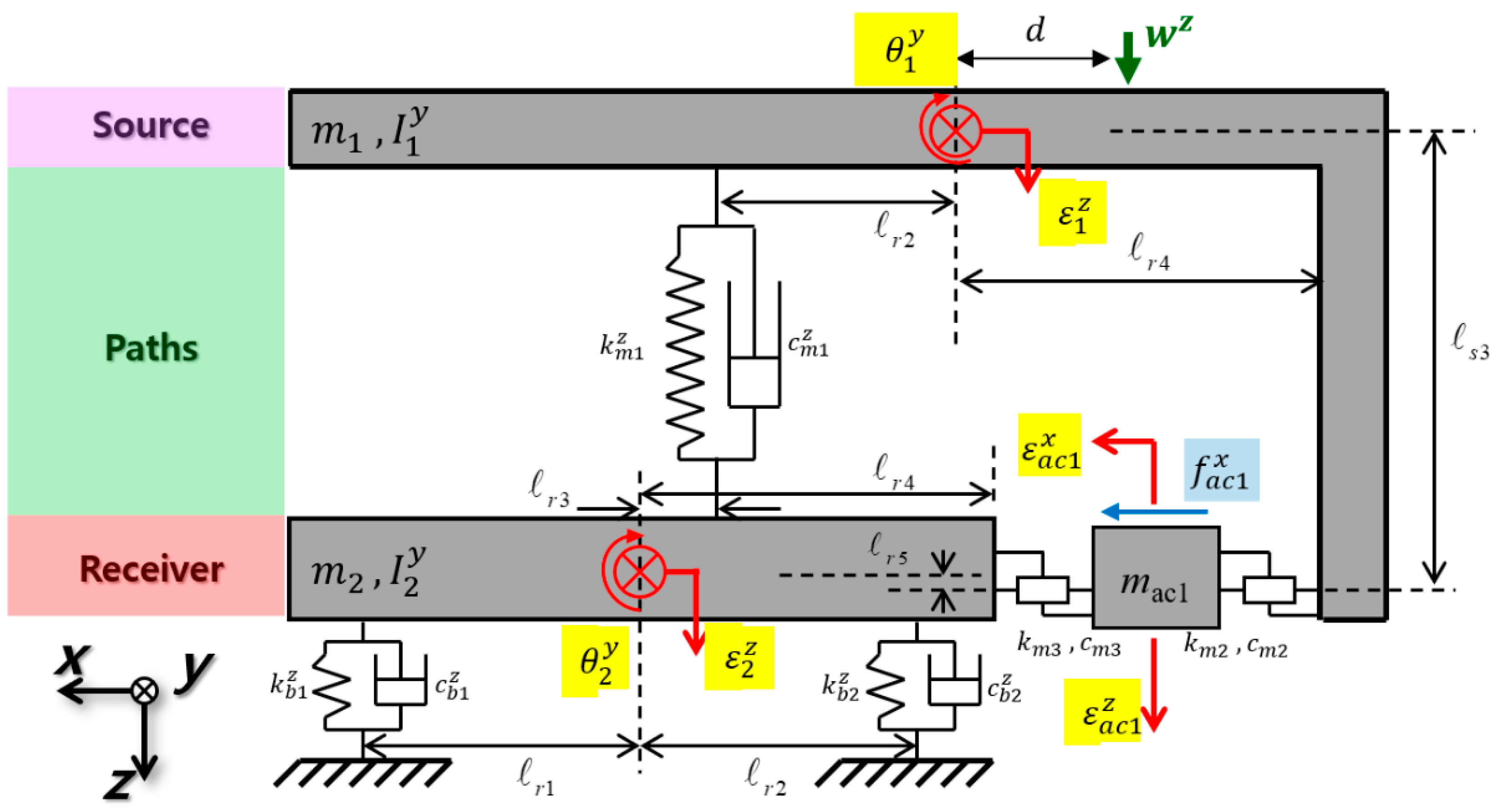
2.1. Six Degrees of Freedom Modeling
2.2. Horizontal Displacement Trend through Dynamic Relations
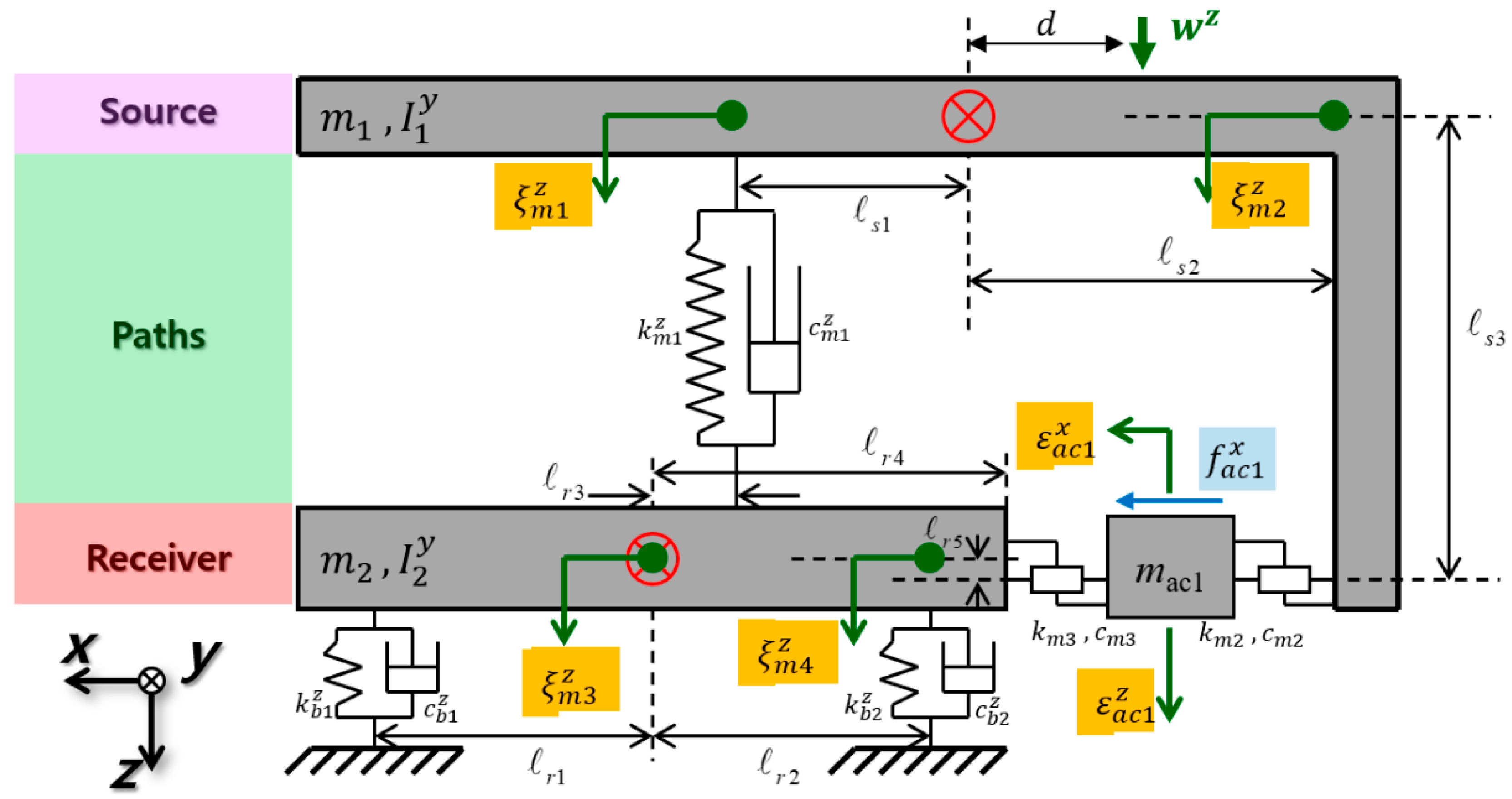
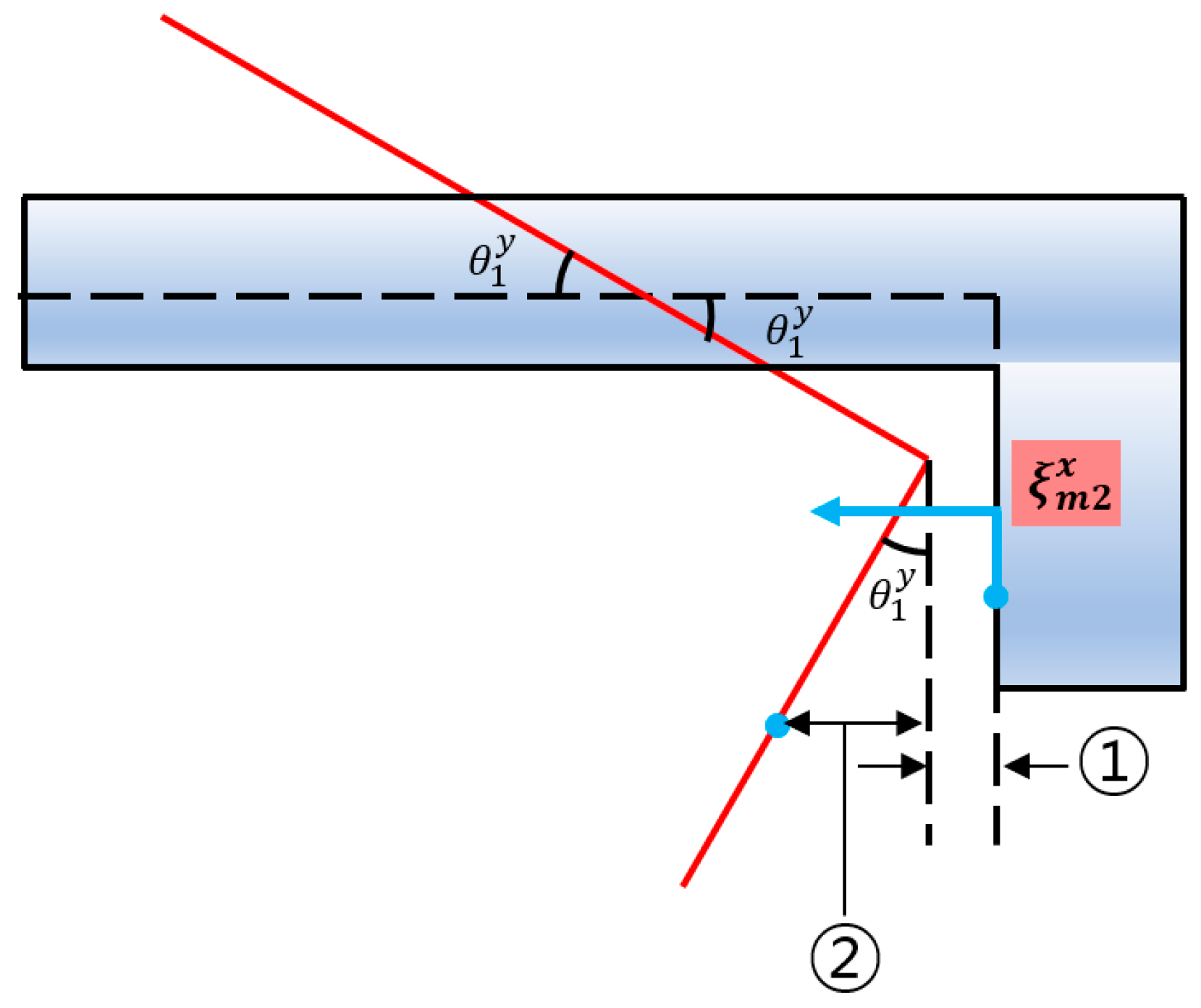
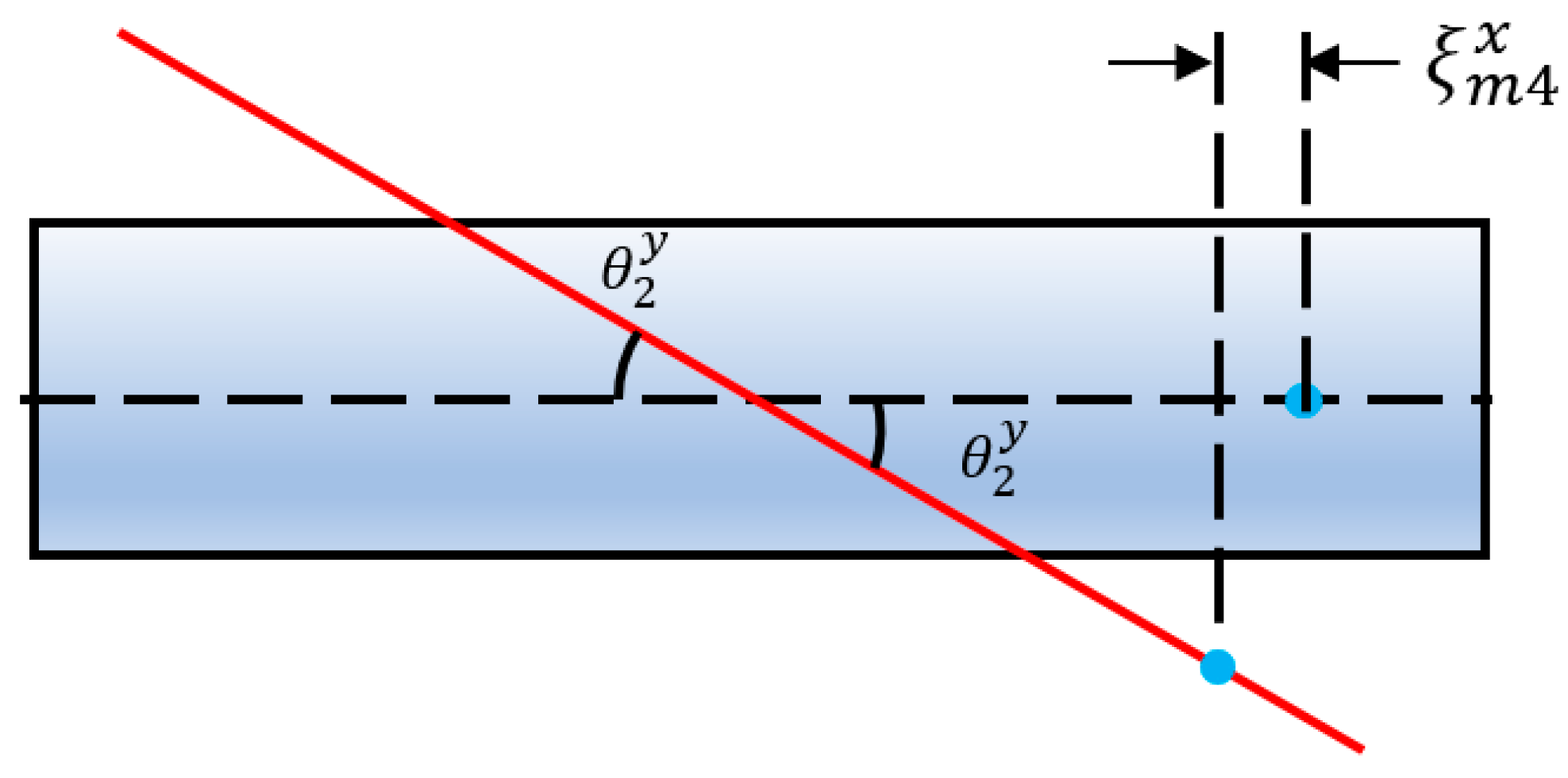
2.3. Secondary Pathway Input Quantification
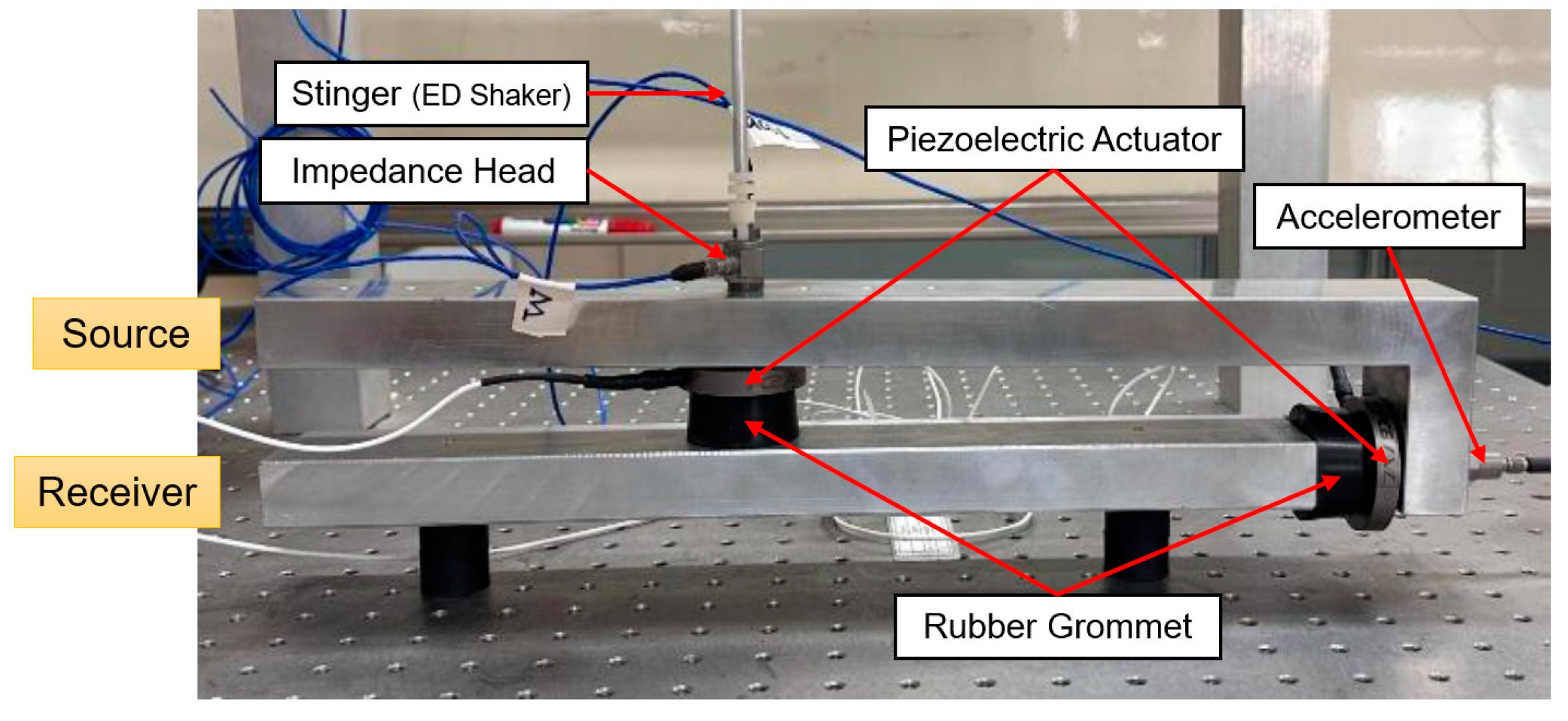
3. Simulation
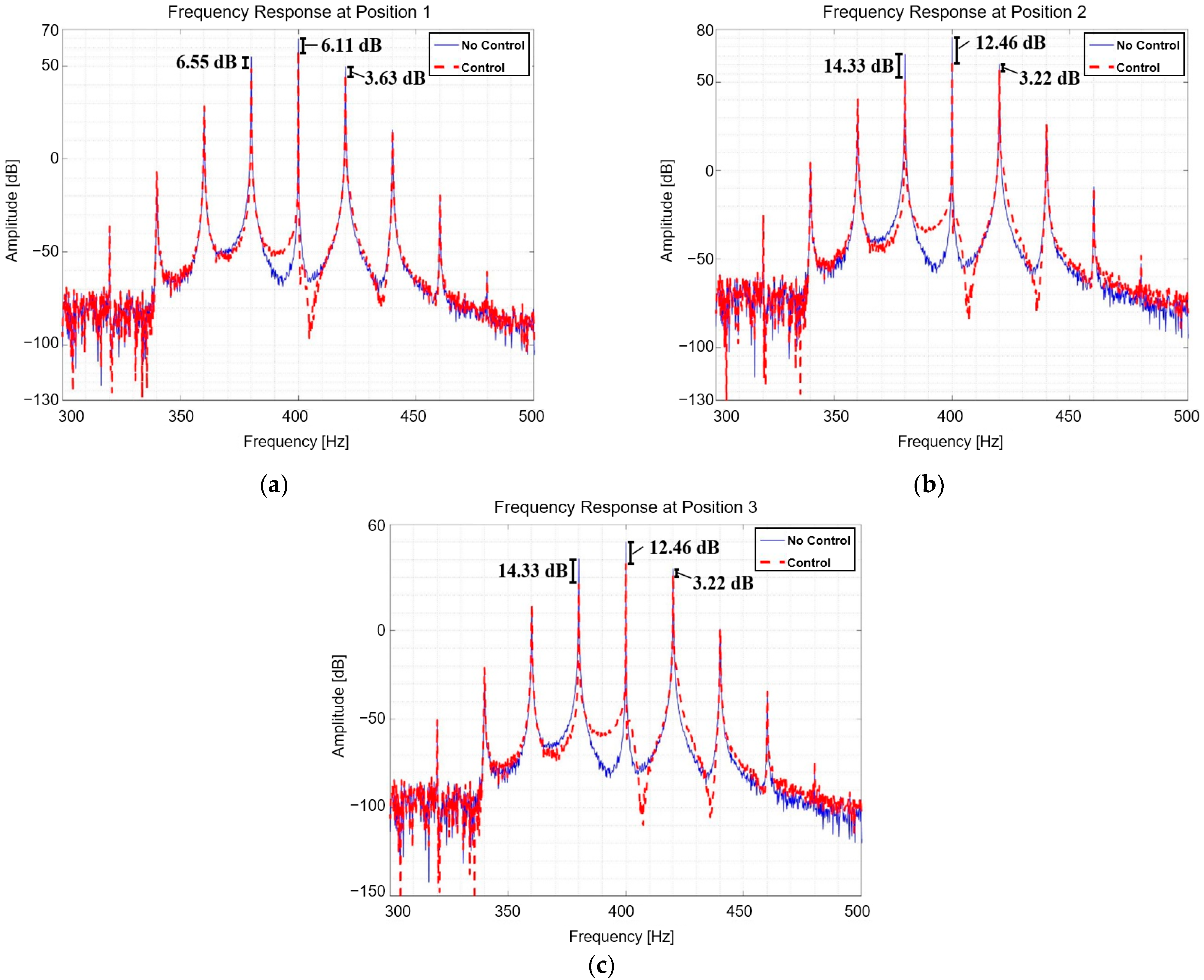
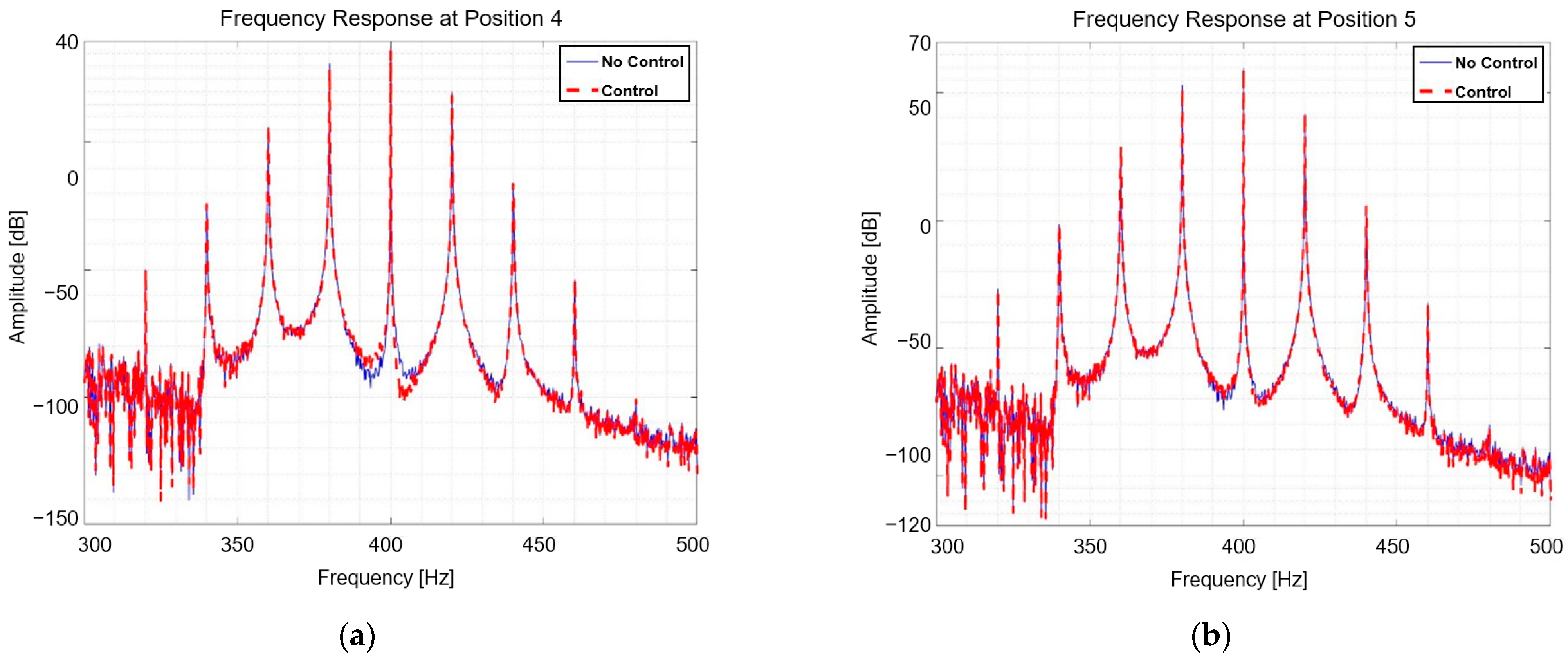
3.1. Control via Quantified Input
3.2. Control through NLMS Algorithm
4. Conclusions
- (1)
- A comprehensive methodology is proposed to analyze the vibrational behavior of mounting structures. This approach incorporates mathematical modeling and quantification of actuator inputs, enabling its applicability and expansion to encompass a wide range of mounting systems.
- (2)
- This study investigates and observes the interactions between vertical and lateral vibration of a structure inspired by an automotive mount. Previous research has predominantly concentrated on the actuation method and vibration attenuation in a single direction. Furthermore, the efficacy of vibration attenuation is evaluated and compared in relation to the specific positions employed to quantify actuator input. This would also contribute to the development of an actuation strategy.
- (3)
- Multi-spectral excitations are applied to the suggested structure to investigate the vibration reduction performance for relatively complicated vibration signals.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, Y.; Naganathan, N.G.; Dukkipati, R.B. A literature review of automotive vehicle engine mounting systems. Mech. Mach. Theory 2001, 36, 123–142. [Google Scholar] [CrossRef]
- Hosseini, M.; Arzanpour, S.; Golnaraghi, F.; Parameswa-ran, A.M. Solenoid actuator design and modeling with application in engine vibration isolators. J. Vib. Control 2012, 19, 1015–1023. [Google Scholar] [CrossRef]
- Kraus, R.; Herold, S.; Millitzer, J.; Jungblut, T. Development of active engine mounts based on piezo actuators. ATZ Peer Rev. 2014, 116, 50–55. [Google Scholar] [CrossRef]
- Chae, H.D.; Choi, S.B. A new vibration isolation bed stage with magneto-rheological dampers for ambulance vehicles. Smart Mater. Struct. 2015, 24, 0964–1726. [Google Scholar] [CrossRef]
- Yang, T.J.; Suai, Z.J.; Sun, Y.; Zhu, M.G.; Xiao, Y.H.; Liu, X.G.; Du, J.T.; Jin, G.Y.; Liu, Z.G. Active vibration isolation system for a diesel engine. Noise Control Engr. J. 2012, 60, 267–282. [Google Scholar] [CrossRef]
- Jeon, J.; Han, Y.M.; Lee, D.Y.; Choi, S.B. Vibration control of the engine body of a vehicle utilizing the magneto-rheological roll mount and the piezostack right-hand mount. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2013, 227, 1562–1577. [Google Scholar] [CrossRef]
- Jiang, J.; Gao, W.; Wang, L.; Teng, Z.; Liu, Y. Active vibration control based on modal controller considering structure actuator interaction. J. Mech. Sci. Technol. 2018, 32, 3515–3521. [Google Scholar] [CrossRef]
- Fakhari, V.; Choi, S.B.; Cho, C.H. A new robust adaptive con-troller for vibration control of active engine mount subjected to large uncertainties. Smart Mater. Struct. 2015, 24, 045044. [Google Scholar] [CrossRef]
- Elahinia, M.; Ciocanel, C.; Nguten, M.; Wang, S. MR and ER based semiactive engine mounts. Smart Mater. Res. 2013, 21, 831017. [Google Scholar] [CrossRef]
- Wu, W.; Chen, X. and Y. Shan. Analysis and experiment of a vibra-tion isolator using a novel magnetic spring with negative stiffness. J. Sound Vib. 2014, 333, 2958–2970. [Google Scholar] [CrossRef]
- Truong, T.Q.; Ahn, K.K. A new type of semi-active hydraulic engine mount using controllable area of inertia track. J. Sound Vib. 2010, 329, 247–260. [Google Scholar] [CrossRef]
- Kamada, T.; Fujita, T.; Hatayama, T.; Arikabe, T.; Murai, N.; Aizawa, S.; Tohyama, K. Active vibration control of frame structures with smart structures using piezoelectric actuators (vibration control by control of bending moments of columns. Smart Mater. Struct. 1997, 6, 448–456. [Google Scholar] [CrossRef]
- Loukil, T.; Bareille, O.; Ichchou, M.N.; Haddar, M. A low power consumption control scheme: Application to a piezostack-based active mount. Front. Mech. Eng. 2013, 8, 383–389. [Google Scholar] [CrossRef]
- Sui, L.; Shi, X.X.G. Piezoelectric actuator design and applica-tion on active vibration control. Phys. Procedia 2012, 25, 1388–1396. [Google Scholar] [CrossRef]
- Choi, S.B.; Choi, Y.T. Sliding mode control of a shear-mode type ER engine mount. KSME Int. J. 1999, 13, 26–33. [Google Scholar] [CrossRef]
- Sarkar, C.; Hirani, H.; Sasane, A. Magneto-rheological Smart Automotive Engine Mount. Int. J. Curr. Eng. Technol. 2015, 5, 419–428. [Google Scholar]
- Chang, Y.; Zhou, J.; Wang, K.; Xu, D. A quasi-zero-stiffness dynamic vibration absorber. J. Sound Vib. 2020, 494, 115859. [Google Scholar] [CrossRef]
- Liette, J.; Dreyer, J.T.; Singh, R. Interaction between two Paths for source mass motion control over mid-frequency range. J. Sound Vib. 2014, 333, 2369–2385. [Google Scholar] [CrossRef]
- Hong, D.; Kim, B. Vibration Reduction for Modulated Excitation Using Lumped Parameter Modeling and Multi-Channel NLMS Algorithm for a Structure with Three Active Paths between Plates. J. Mech. Sci. Technol. 2019, 33, 4673–4680. [Google Scholar] [CrossRef]
- Hong, D.; Kim, B. Quantification of Active Structural Path for Vibration Reduction Control of Plate Structure under Sinusoidal Excitation. Appl. Sci. 2019, 9, 711. [Google Scholar] [CrossRef]
- Qiu, Y.; Hong, D.; Kim, B. Optimal placement criteria of hybrid mounting system for chassis in future mobility based on beam-type continuous smart structures. Sci. Rep. 2023, 13, 2317. [Google Scholar] [CrossRef]
- Hausberg, F.; Scheiblegger, C.; Pfeffer, P.; Plöchl, M.; Hecker, S.; Rupp, M. Experimental and analytical study of secondary path variations in active engine mounts. J. Sound Vib. 2015, 340, 22–38. [Google Scholar] [CrossRef]
- Bartel, T.; Herold, S.; Mayer, D.; Melz, T. Development and Testing of Active Vibration Control Systems with Piezoelectric Ac-tuators. In Proceedings of the 6th ECCOMAS Conference on Smart Structures and Materials, Torino, Italy, 1–4 July 2013; pp. 24–26. [Google Scholar]
- Li, H.; Goodall, R.M. Linear and nonlinear skyhook damping control laws for active railway suspensions. Control Eng. Pract. 1999, 7, 843–850. [Google Scholar] [CrossRef]
- Singal, K.; Rajamani, R. Zero-Energy Active Suspension System for Automobiles with Adaptive Skyhook Damping. J. Vib. Acoust. 2013, 135, 011011. [Google Scholar] [CrossRef]
- Emura, J.; Kakizaki, S.; Yamaoka, F.; Nakamura, M. Development of the Semi-Active Suspension System Based on the Skyhook Damper Theory. SAE Trans. J. Passeng. Cars 1994, 103, 1110–1119. [Google Scholar]
- Chai, Y.; Li, F.; Song, Z.; Zhang, C. Analysis and active control of nonlinear vibration of composite lattice sandwich plates. Nonlinear Dyn. 2020, 102, 2179–2203. [Google Scholar] [CrossRef]
- Hong, D.; Moon, H.; Kim, B. Bidirectional active vibration control of two-dimensional structure inspired by automotive engine mounting system. J. Mech. Sci. Technol. 2024, 38. in press. [Google Scholar]
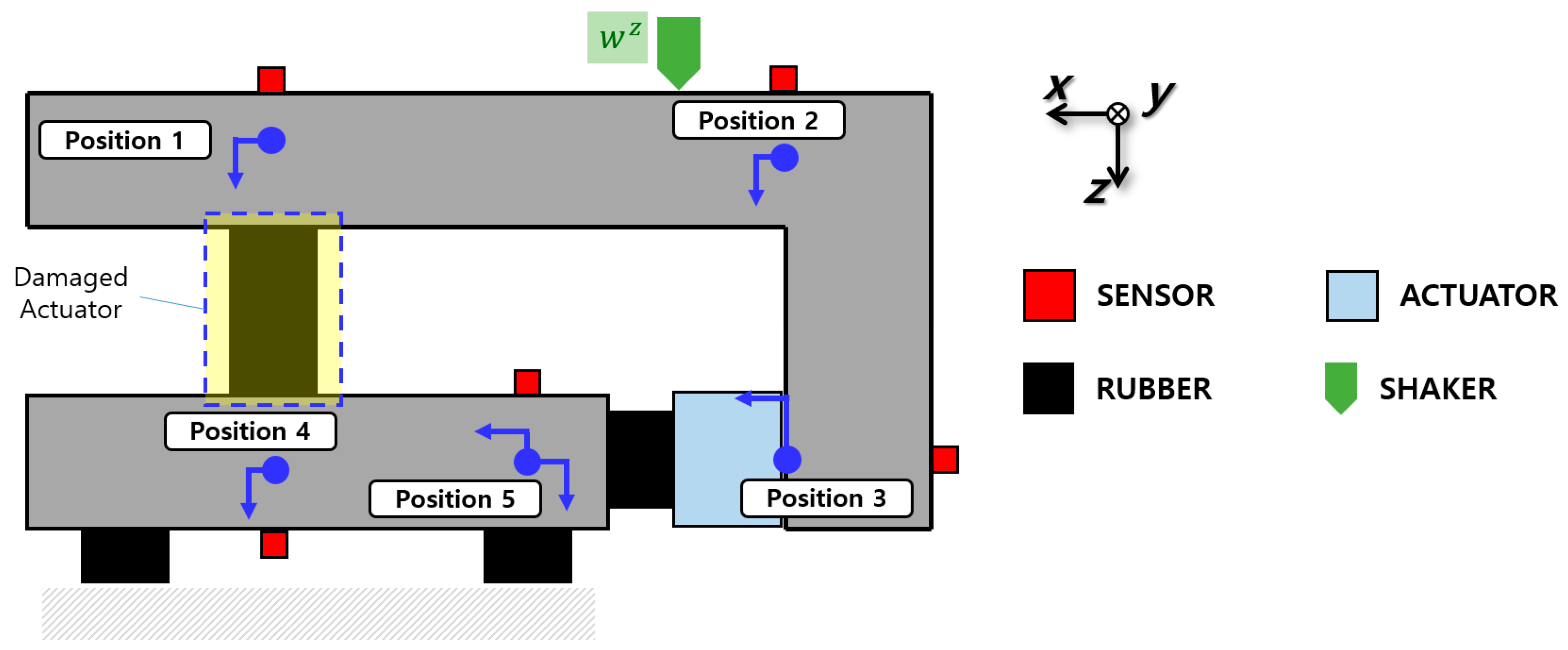
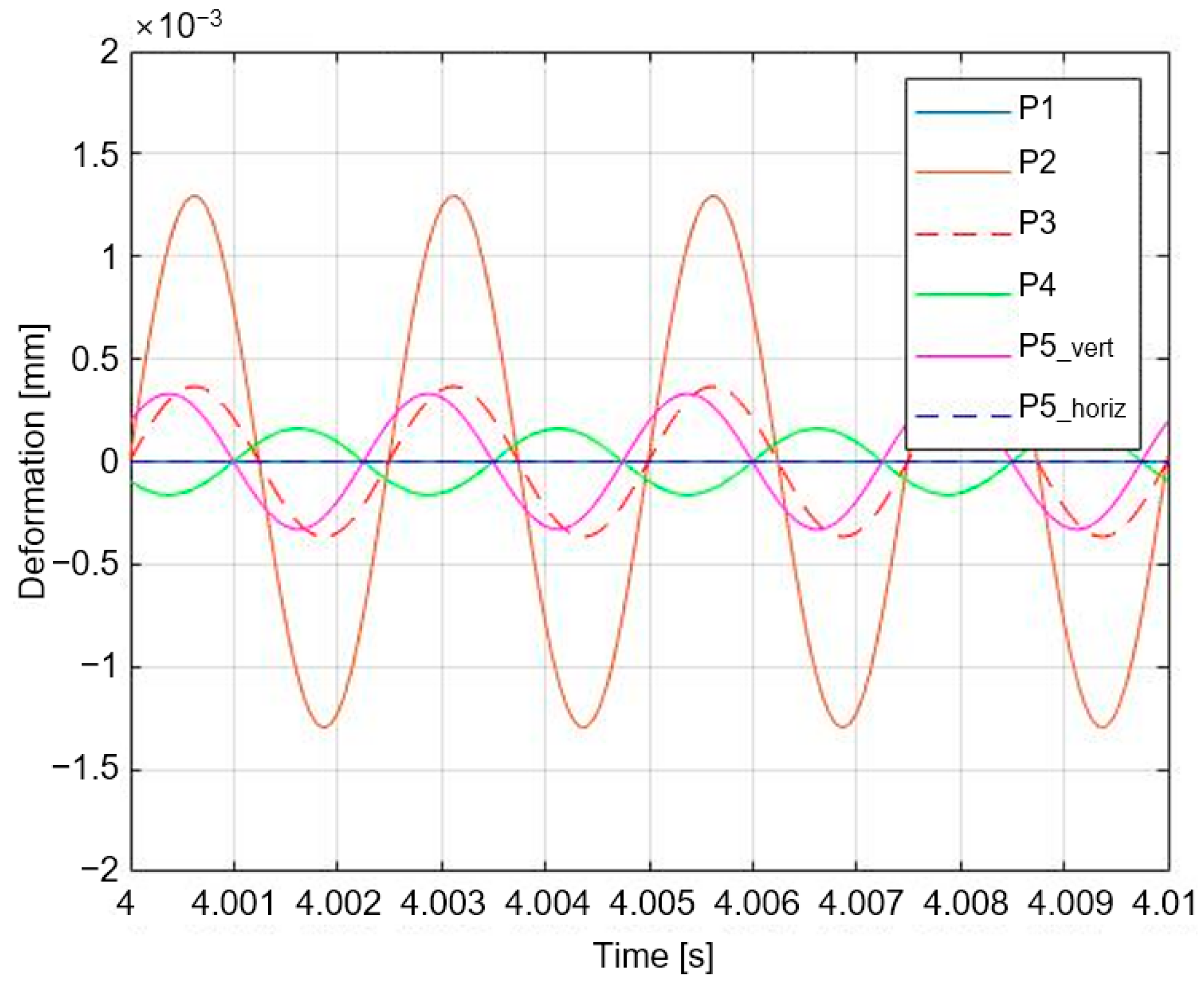
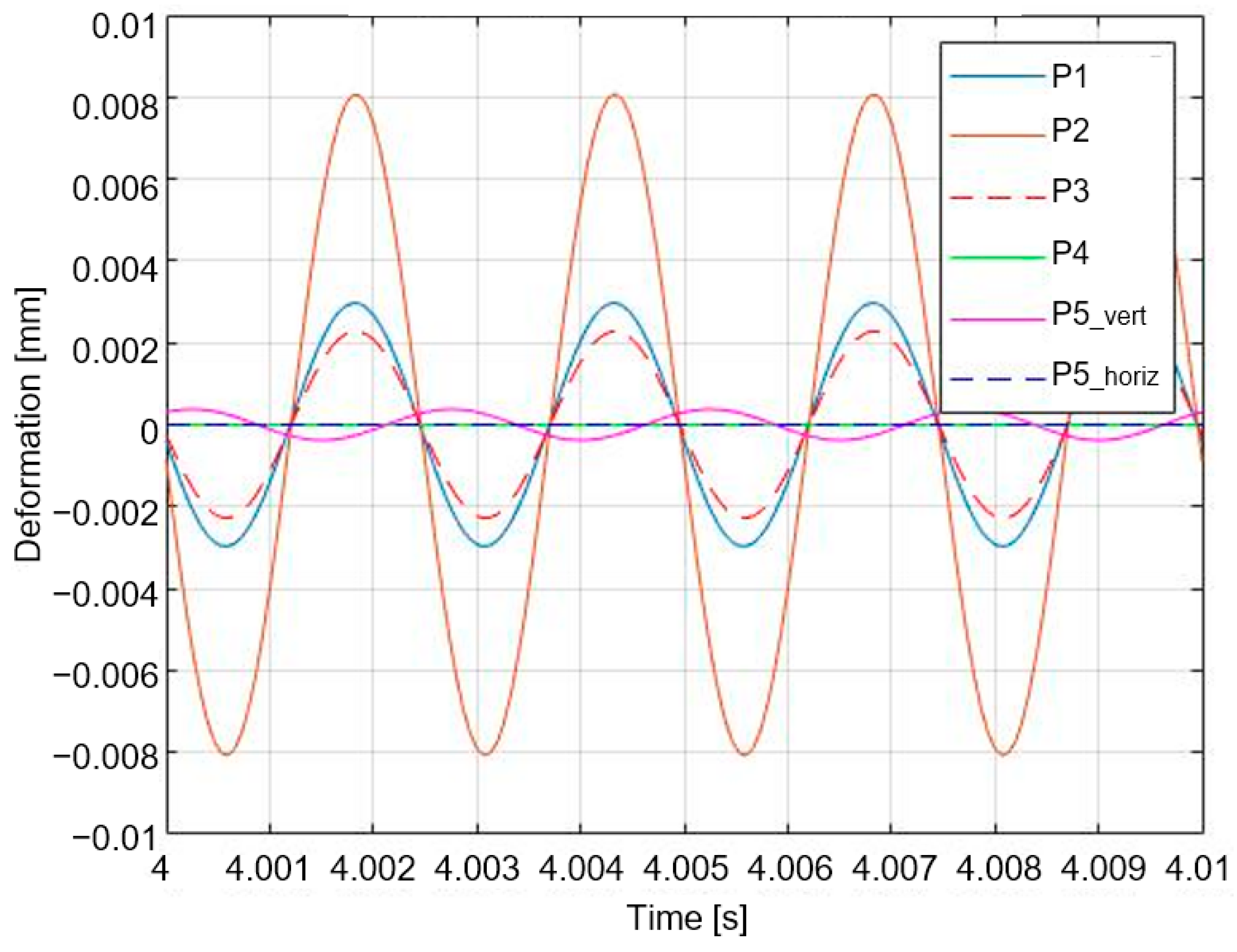
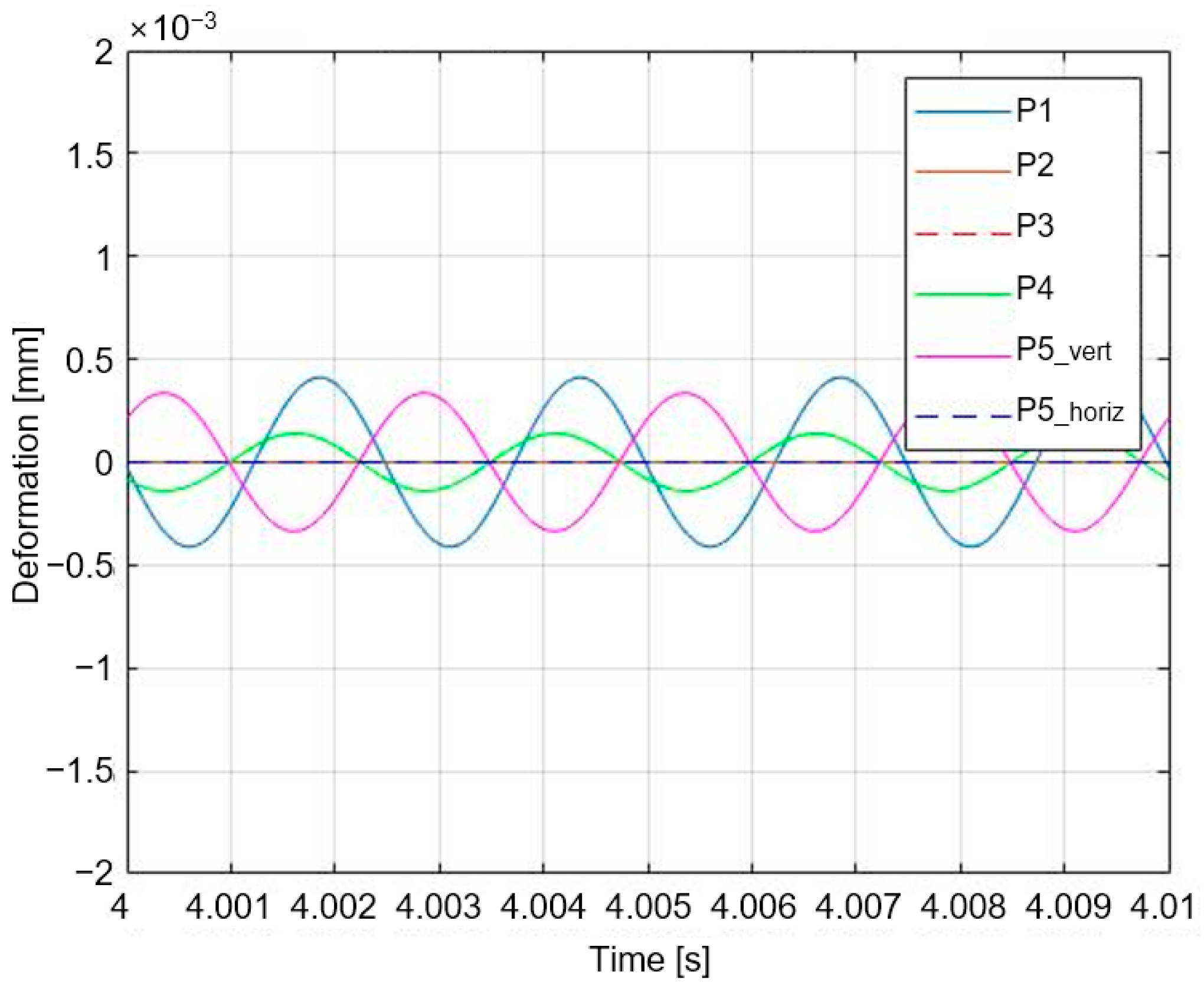
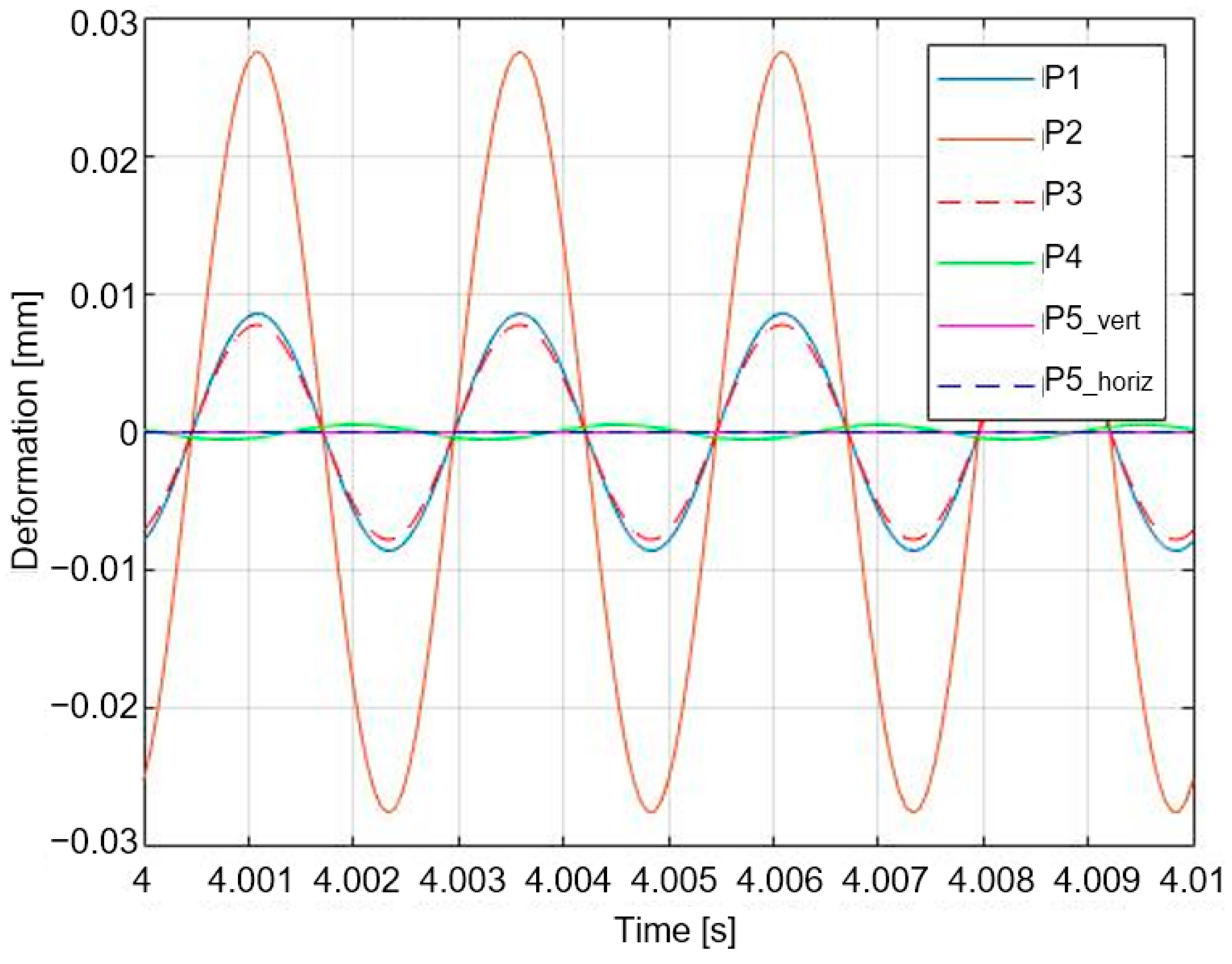
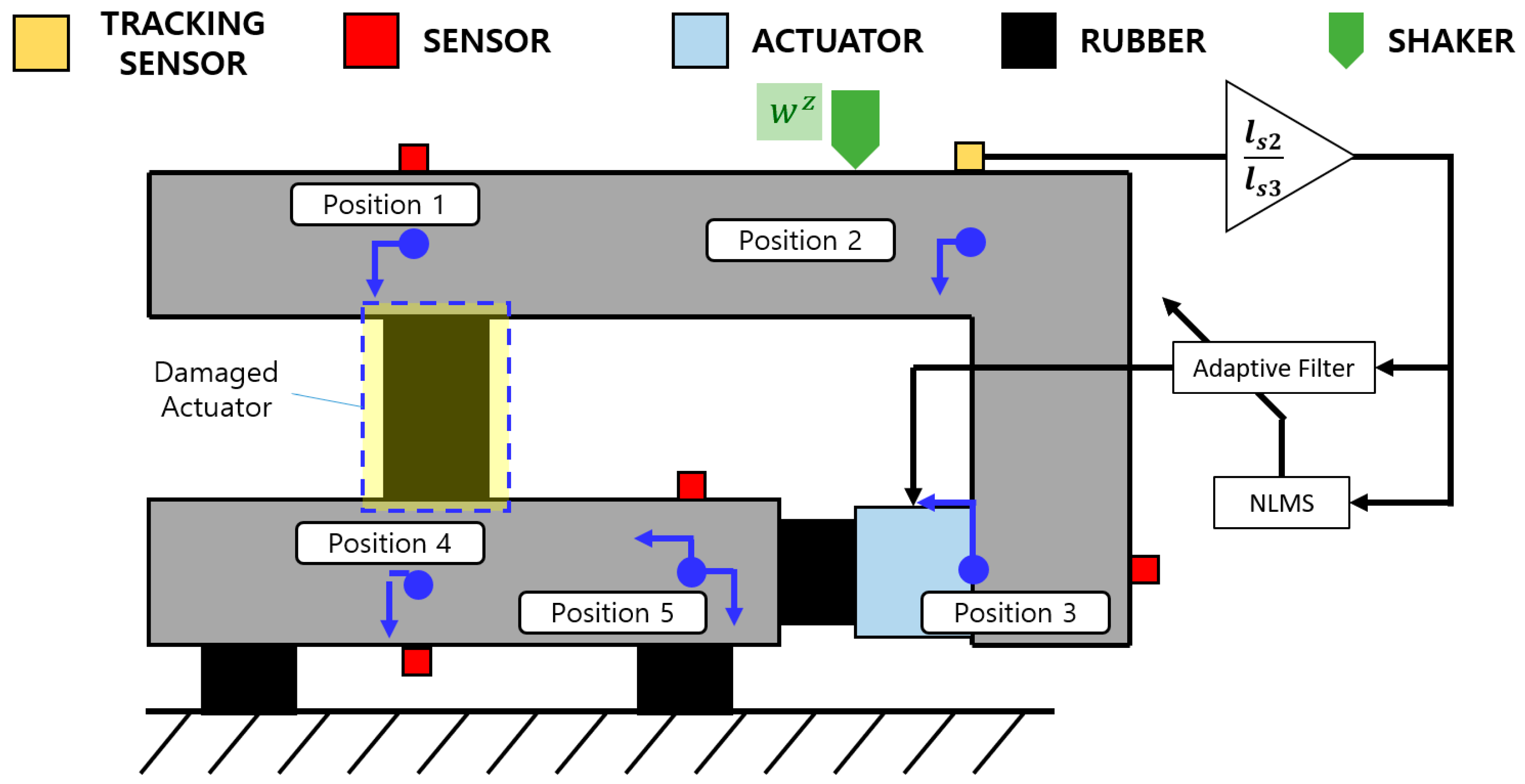
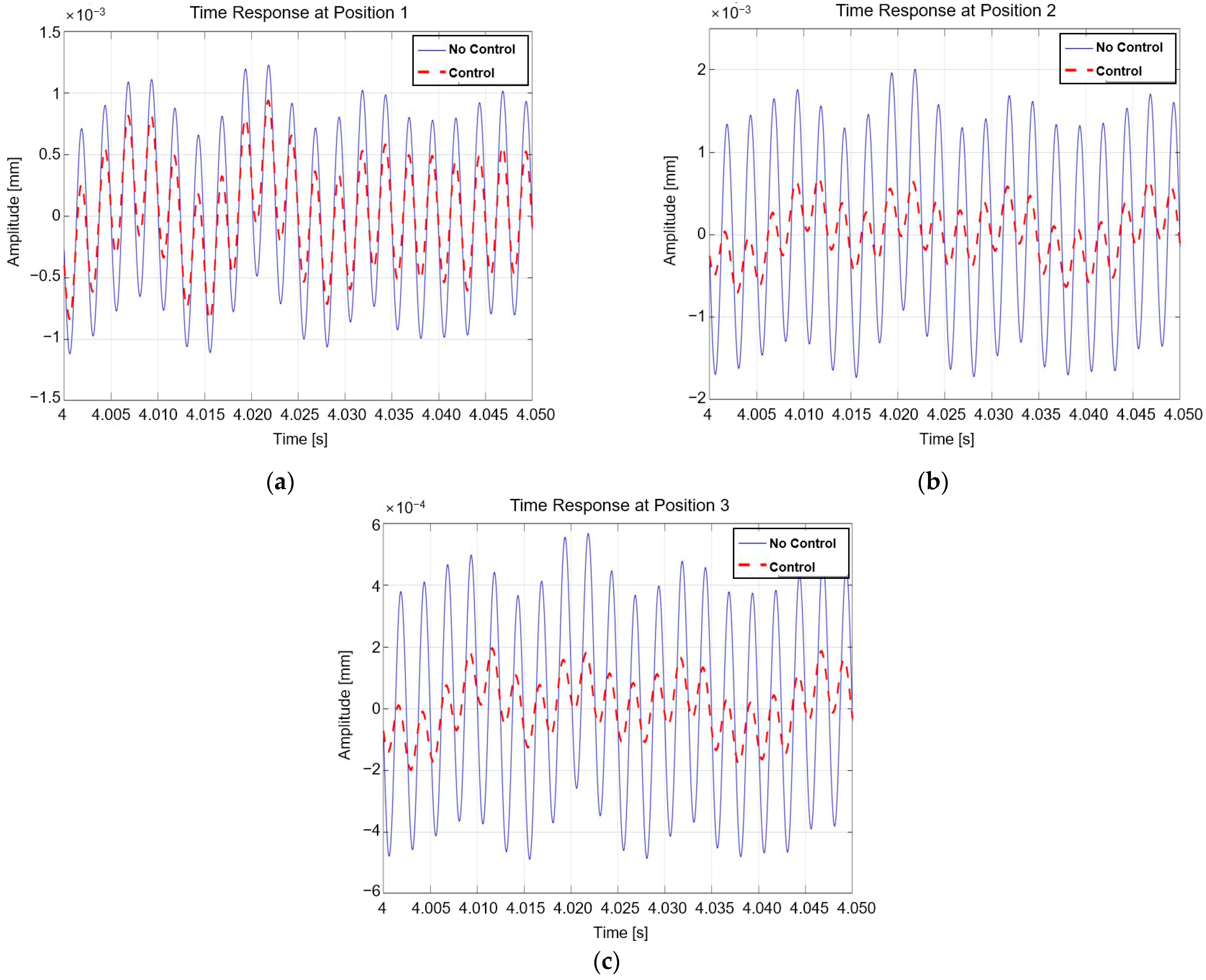
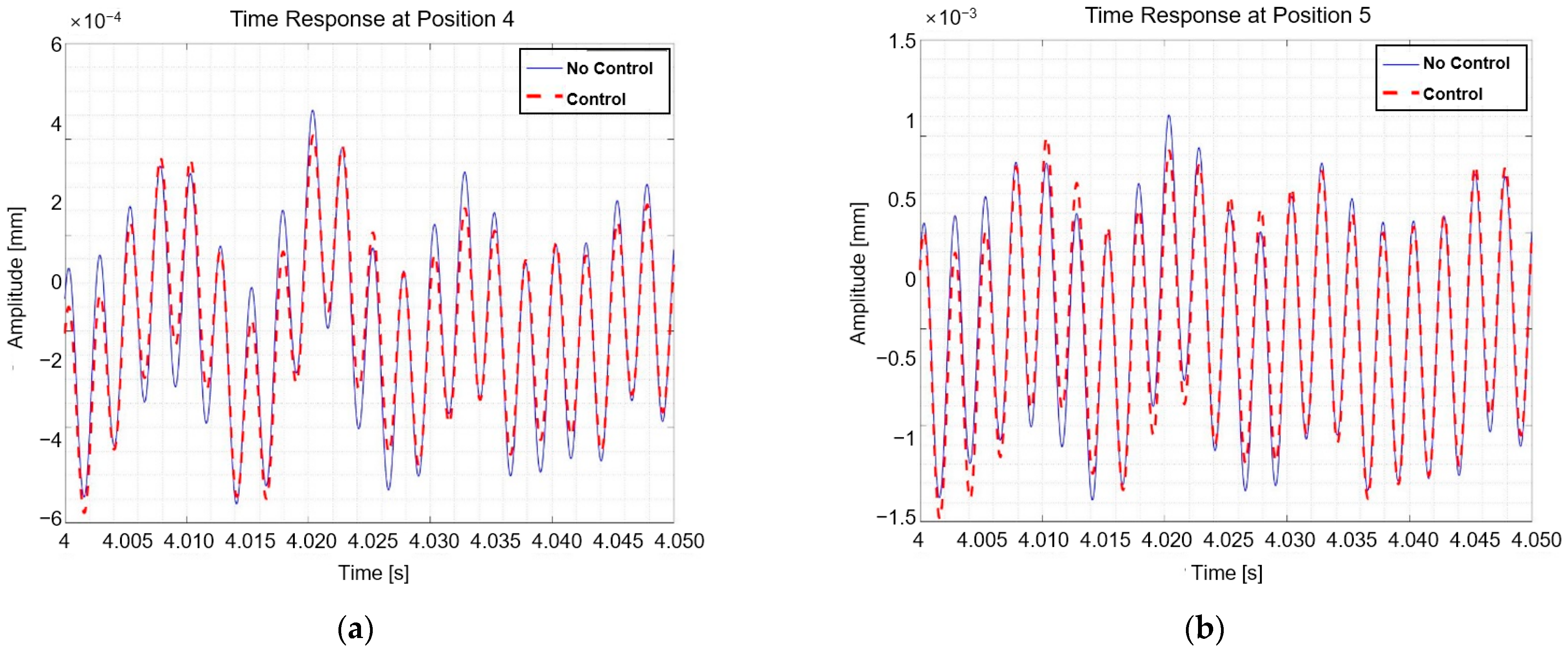
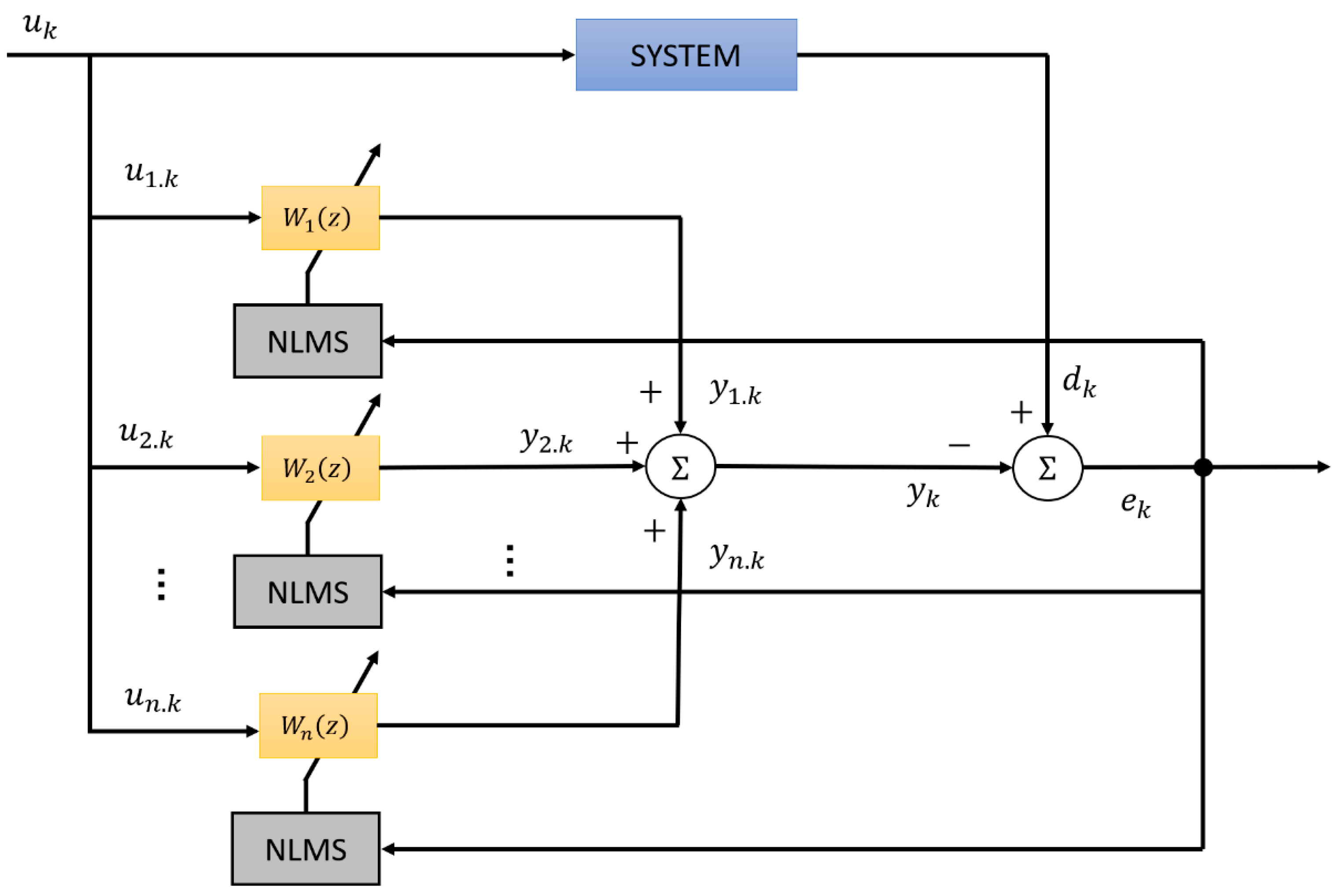
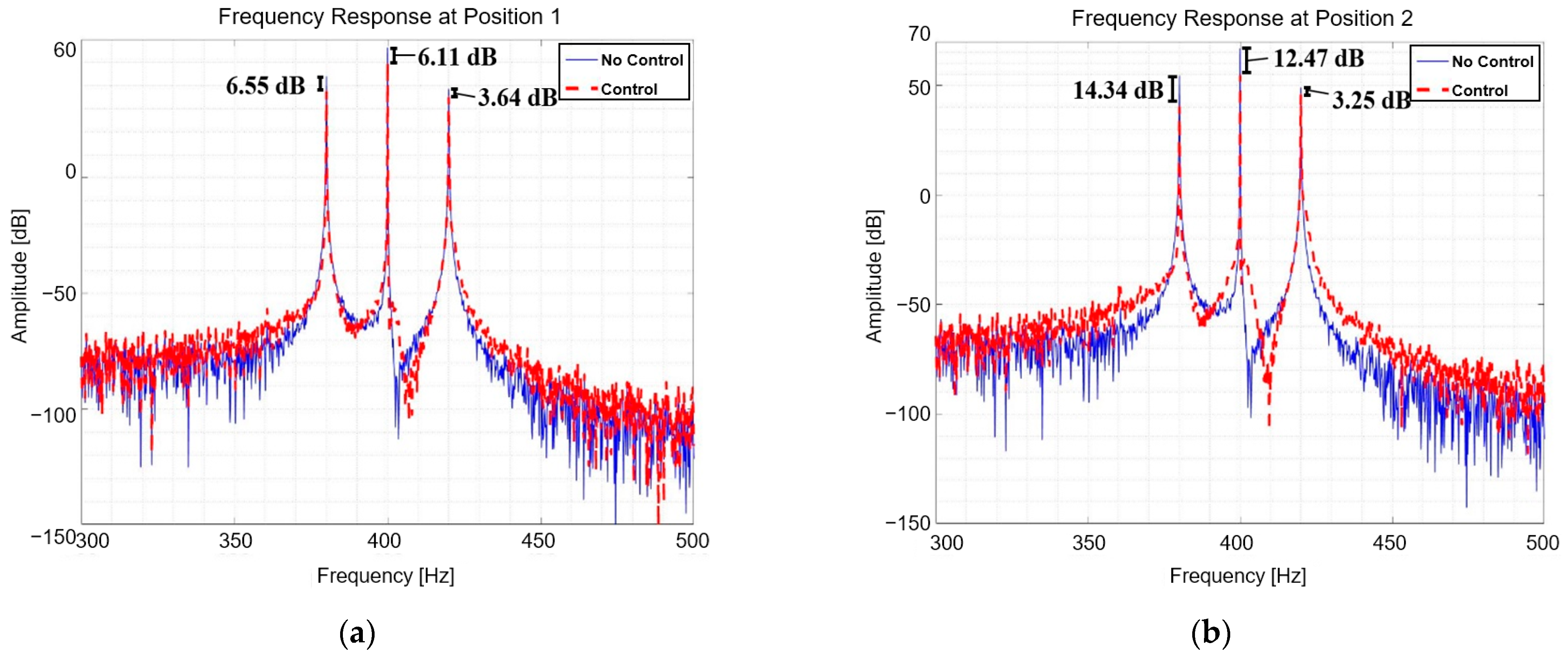
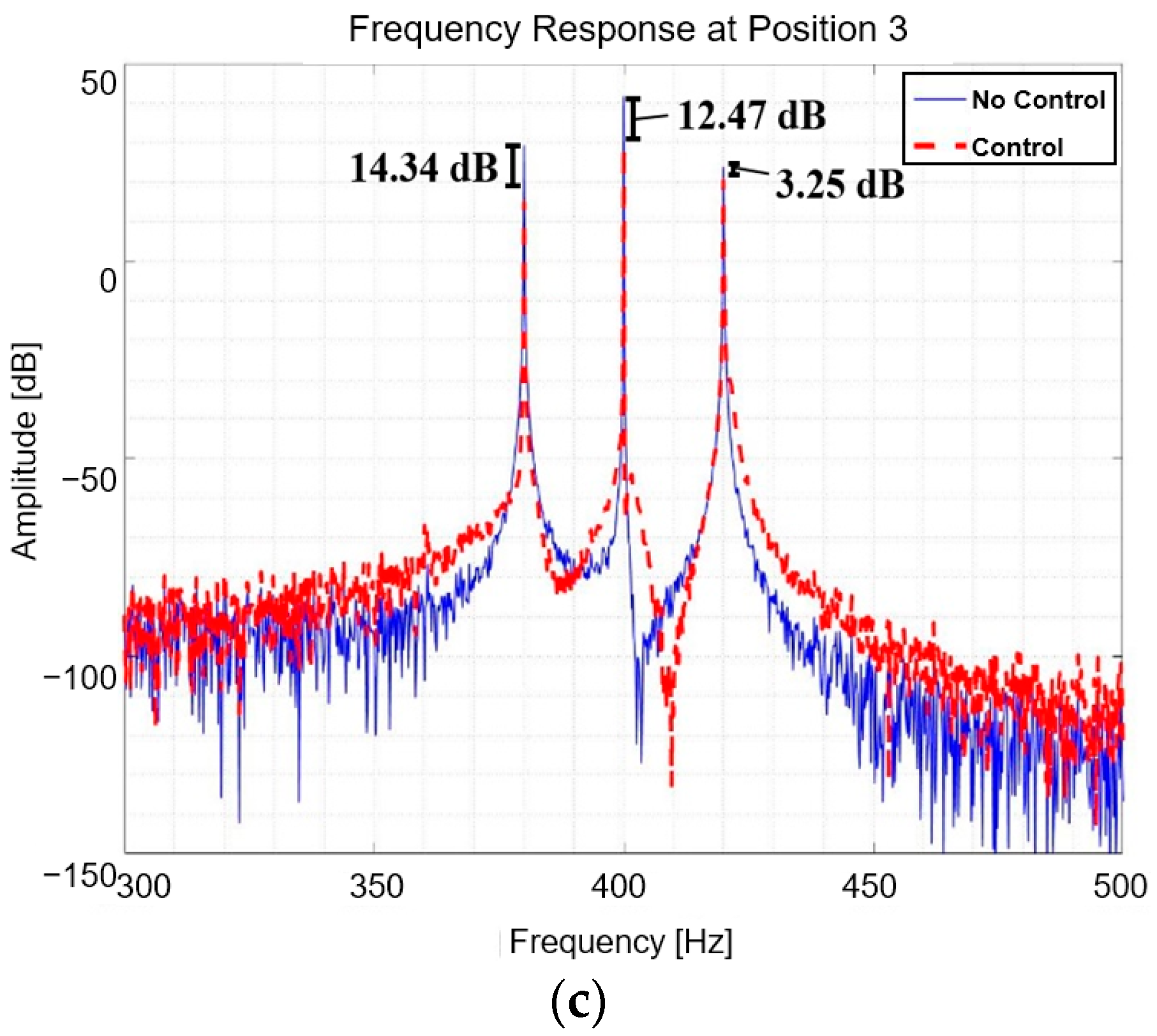
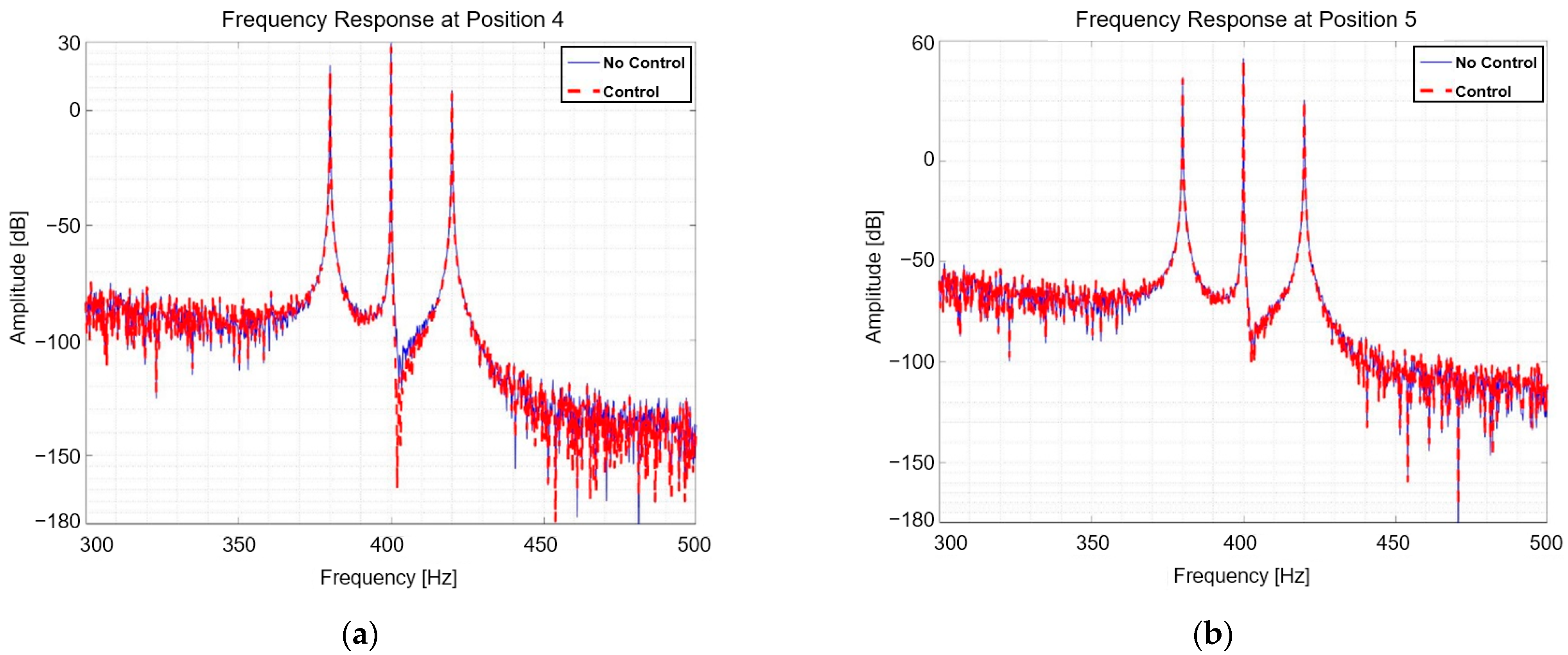
| Variable | Value | Unit | Variable | Value | Unit |
|---|---|---|---|---|---|
| 1.721 | 140 | ||||
| 1.350 | 64 | ||||
| 0.075 | 200 | ||||
| 33.402 | 50.686 | ||||
| 18.070 | 179.314 | ||||
| 5.46 | 136 | ||||
| 0.5 | 0 | ||||
| 0.61 | 200 | ||||
| 0.42 | 50 | ||||
| 22 |
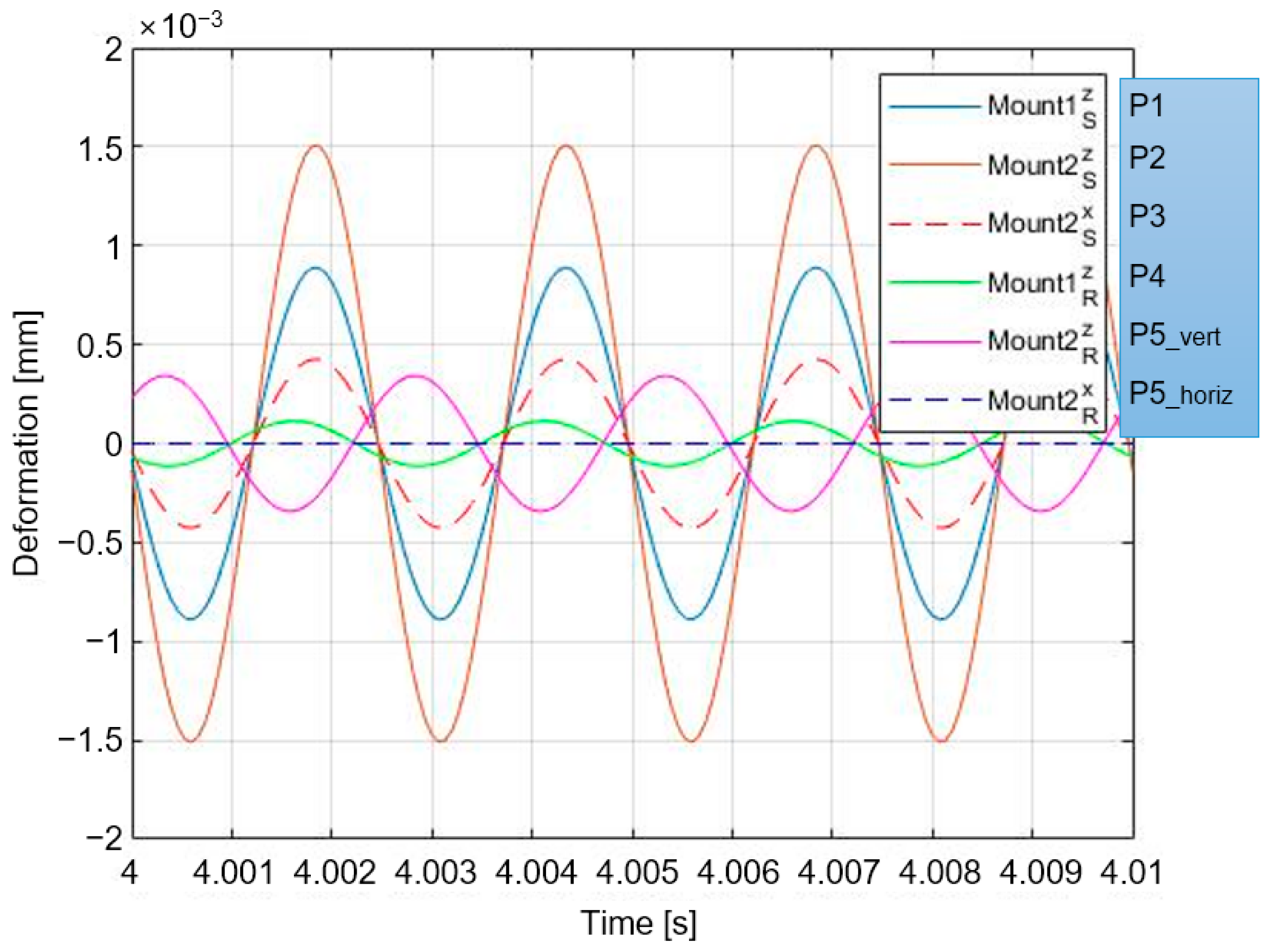
| [Unit: ] | SOURCE | RECEIVER | ||||
|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5_vert | P5_horiz | |
| Before Control | 0.6291 | 1.0668 | 0.3015 | 0.0802 | 0.2425 | |
| After Control | 0 100% | 0.9169 14.04% | 0.2592 14.04% | 0.1144 42.66% | 0.2339 3.54% | 4.22% |
| [Unit: ] | SOURCE | RECEIVER | ||||
|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5_vert | P5_horiz | |
| Before Control | 0.6291 | 1.0668 | 0.3015 | 0.0802 | 0.2425 | |
| After Control | 2.1016 234% | 5.7085 435.2% | 1.6136 435.2% | 0 100% | 0.2676 10.36% | 8.43% |
| [Unit: ] | SOURCE | RECEIVER | ||||
|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5_vert | P5_horiz | |
| Before Control | 0.6291 | 1.0668 | 0.3015 | 0.0802 | 0.2425 | |
| After Control | 0.2910 53.75% | 0 100% | 0 100% | 0.0986 22.97% | 0.238 1.85% | 2.46% |
| [Unit: ] | SOURCE | RECEIVER | ||||
|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5_vert | P5_horiz | |
| Before Control | 0.6291 | 1.0668 | 0.3015 | 0.0802 | 0.2425 | |
| After Control | 6.0759 865.8% | 19.4799 1726% | 5.5063 1726% | 0.3778 371% | 0 100% | 100% |
| [Unit: ] | SOURCE | RECEIVER | ||||
|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5_vert | P5_horiz | |
| Before Control | 0.6536 | 1.0923 | 0.3088 | 0.1882 | 0.5118 | |
| After Control | 0.4133 36.77% | 0.3332 69.5% | 0.0942 69.5% | 0.176 6.5% | 0.5032 1.69% | 3.54% |
| [Unit: ] | SOURCE | RECEIVER | |||
|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5_vert | |
| Before Control | 1.0588 | 1.7953 | 0.5075 | 0.2736 | 0.8159 |
| After Control | 0.5933 43.97% | 0.3942 78.04% | 0.1114 78.04% | 0.2397 12.4% | 0.7989 2.08% |
| [Unit: ] | SOURCE | RECEIVER | ||||
|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5_vert | P5_horiz | |
| Before Control | 0.4245 | 0.6953 | 0.1965 | 0.1391 | 0.3455 | |
| After Control | 0.3495 17.67% | 0.4315 37.95% | 0.122 37.95% | 0.1356 2.55% | 0.3348 3.09% | 4.13% |
| [Unit: ] | SOURCE | RECEIVER | ||||
|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5_vert | P5_horiz | |
| Before Control | 0.6570 | 1.1010 | 0.3112 | 0.1950 | 0.5336 | |
| After Control | 0.5162 21.42% | 0.6813 38.11% | 0.1926 38.11% | 0.1854 4.91% | 0.5196 2.61% | 5.34% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, D.; Moon, H.; Kim, B. Bidirectional Multi-Spectral Vibration Control: Insights from Automotive Engine Mounting Systems in Two-Dimensional Structures with a Damaged Vertical Active Element. Actuators 2024, 13, 171. https://doi.org/10.3390/act13050171
Hong D, Moon H, Kim B. Bidirectional Multi-Spectral Vibration Control: Insights from Automotive Engine Mounting Systems in Two-Dimensional Structures with a Damaged Vertical Active Element. Actuators. 2024; 13(5):171. https://doi.org/10.3390/act13050171
Chicago/Turabian StyleHong, Dongwoo, Hojoon Moon, and Byeongil Kim. 2024. "Bidirectional Multi-Spectral Vibration Control: Insights from Automotive Engine Mounting Systems in Two-Dimensional Structures with a Damaged Vertical Active Element" Actuators 13, no. 5: 171. https://doi.org/10.3390/act13050171
APA StyleHong, D., Moon, H., & Kim, B. (2024). Bidirectional Multi-Spectral Vibration Control: Insights from Automotive Engine Mounting Systems in Two-Dimensional Structures with a Damaged Vertical Active Element. Actuators, 13(5), 171. https://doi.org/10.3390/act13050171







