Light-Weighting and Comparative Simulation Analysis of the Forearm of Welding Robots
Abstract
:1. Introduction
2. Topology Optimization Theory Analysis of the Forearm
3. Lightweight Topology Optimization of the Forearm
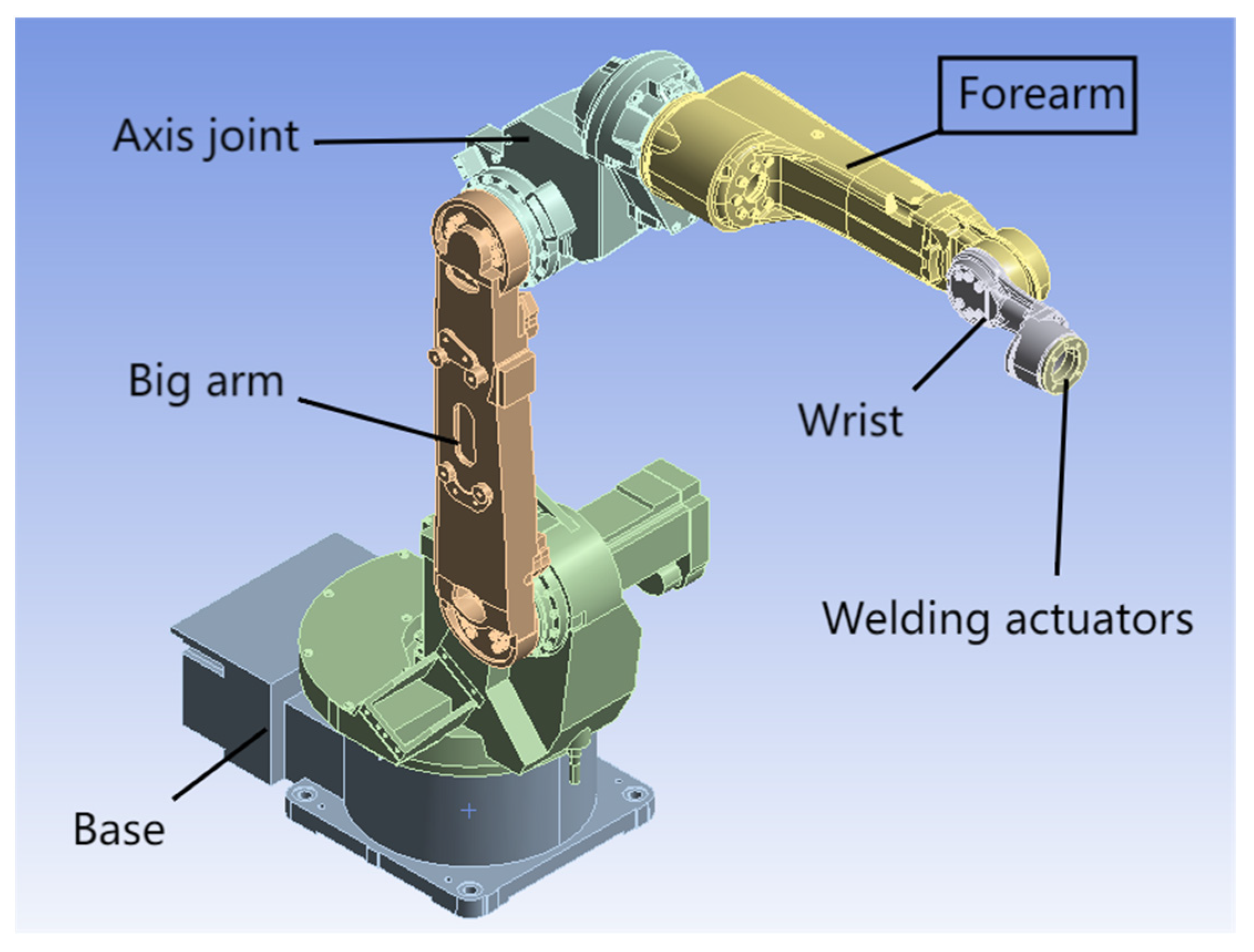
3.1. Geometric Dimensions and Material Characteristics of the Forearm
3.2. Boundary Conditions and Optimization Parameter Settings
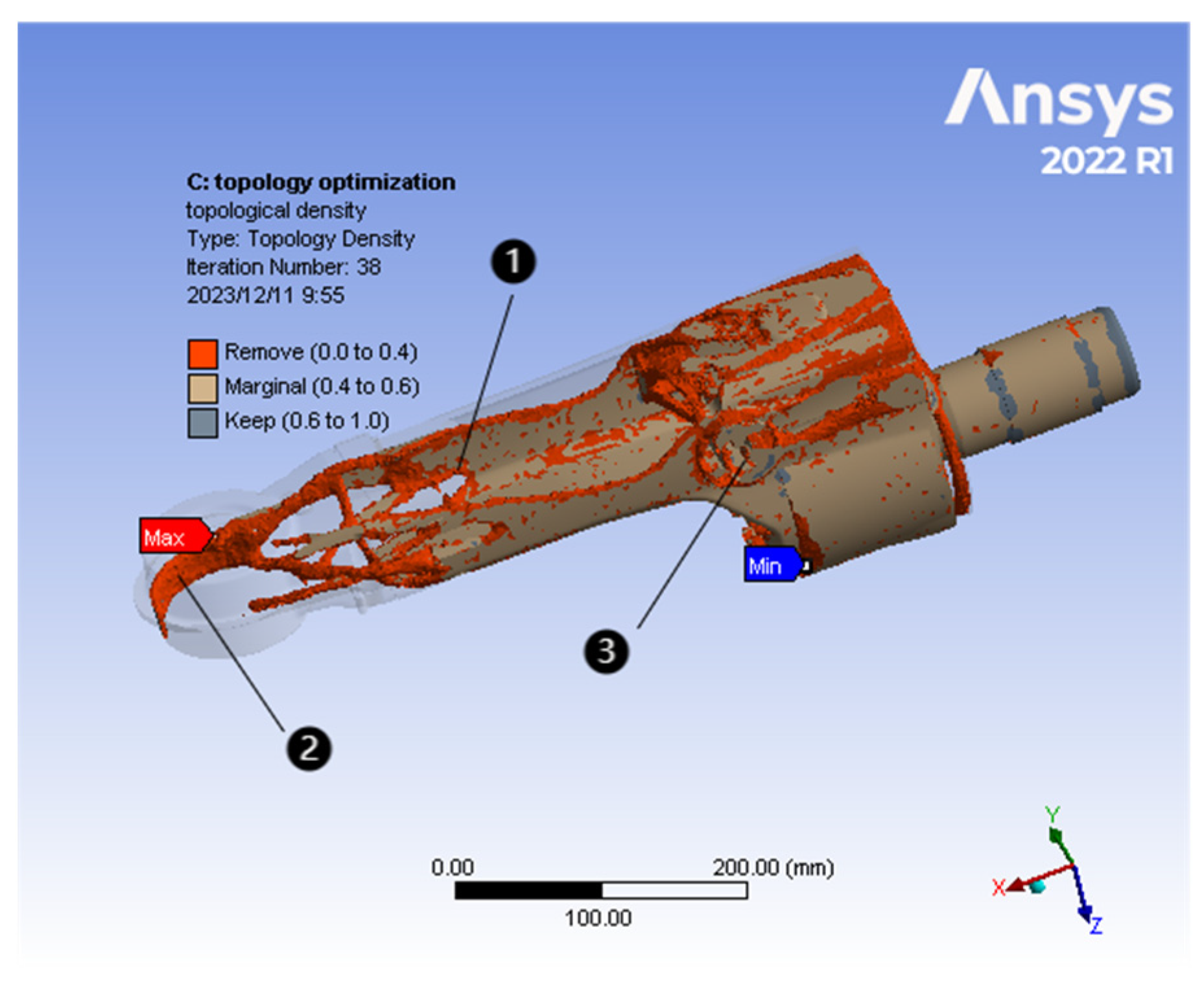
3.3. Topology Optimization Results and Structural Model Reconstruction
4. Simulation Results Analysis
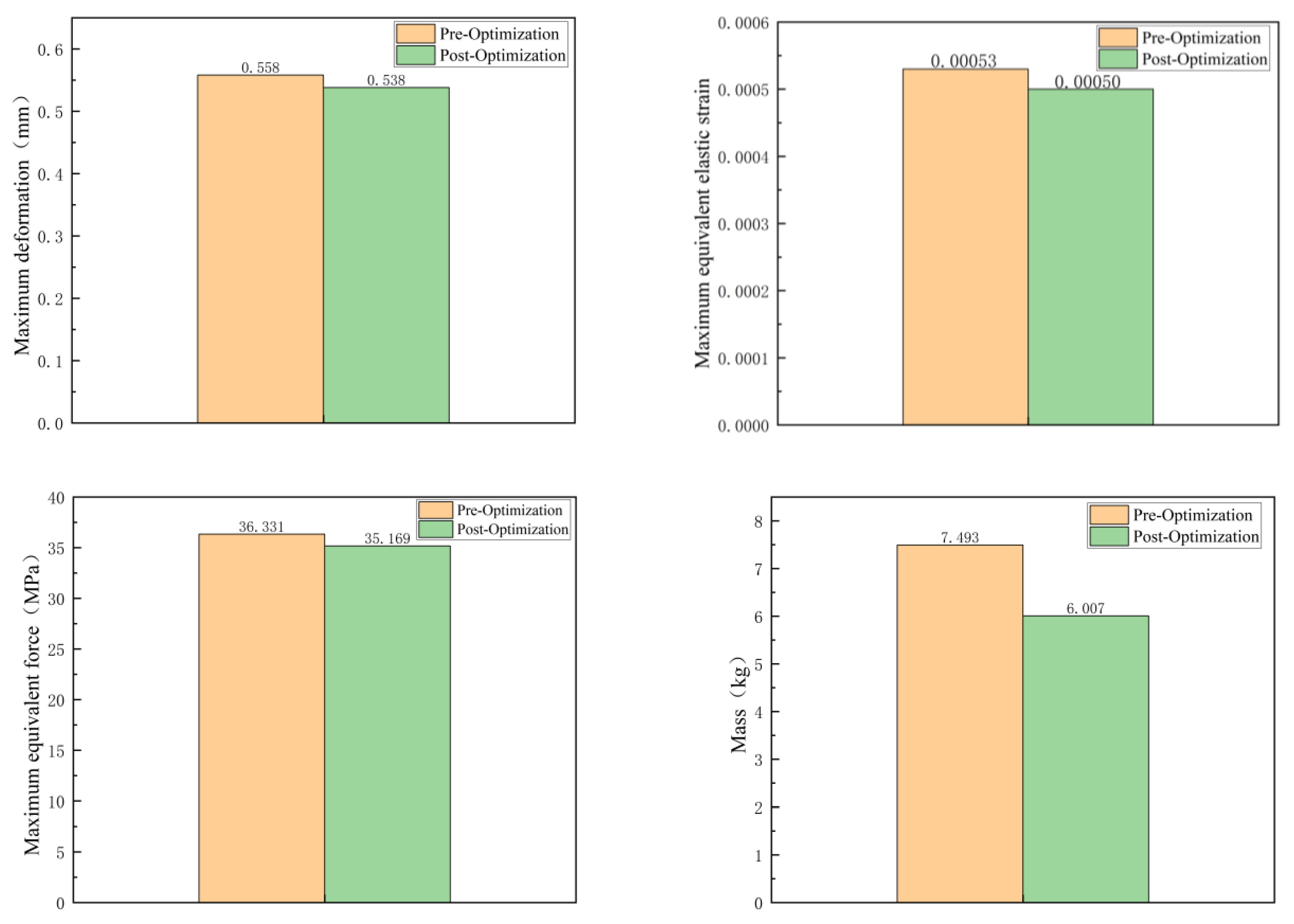
4.1. Static Analysis and Comparison
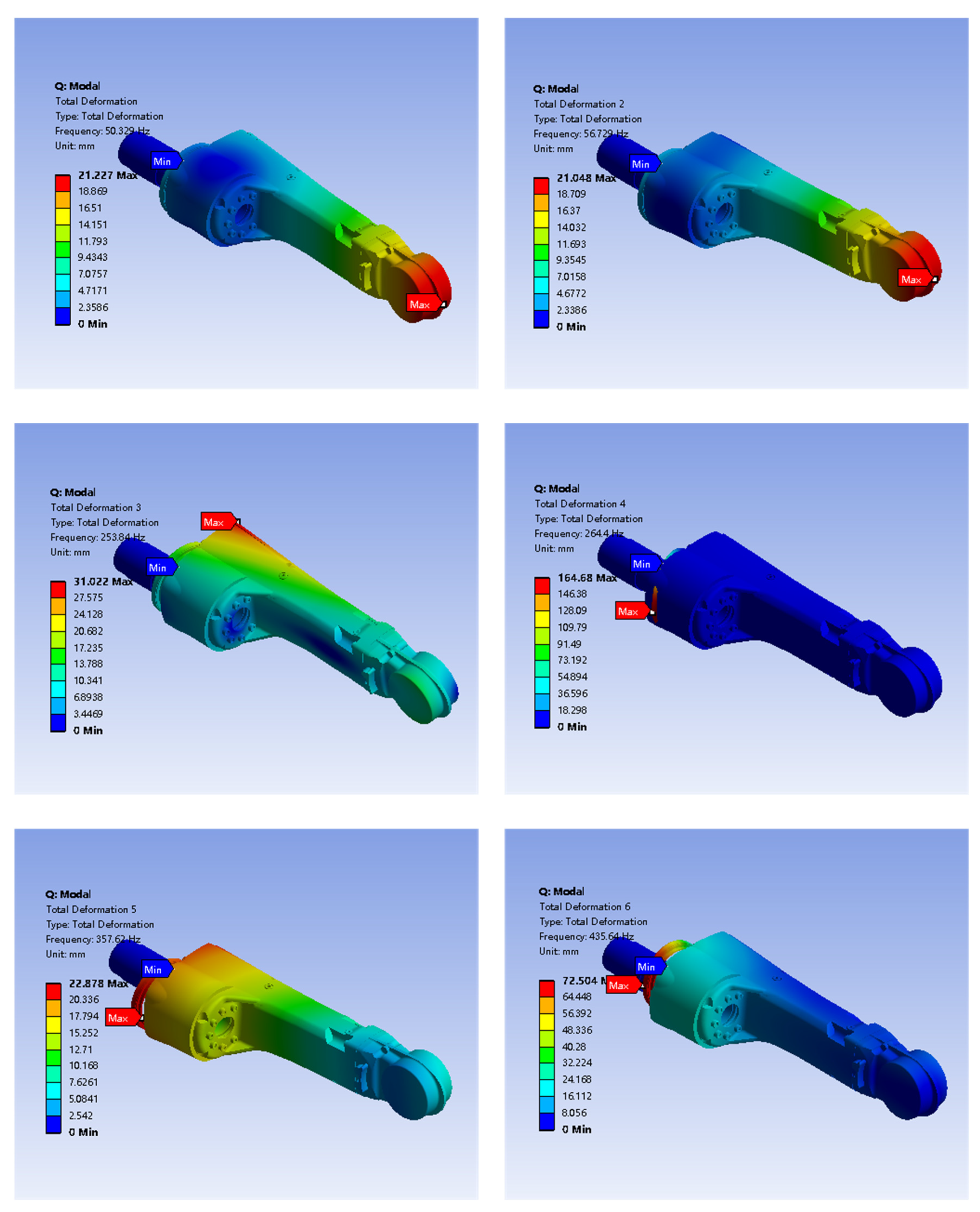
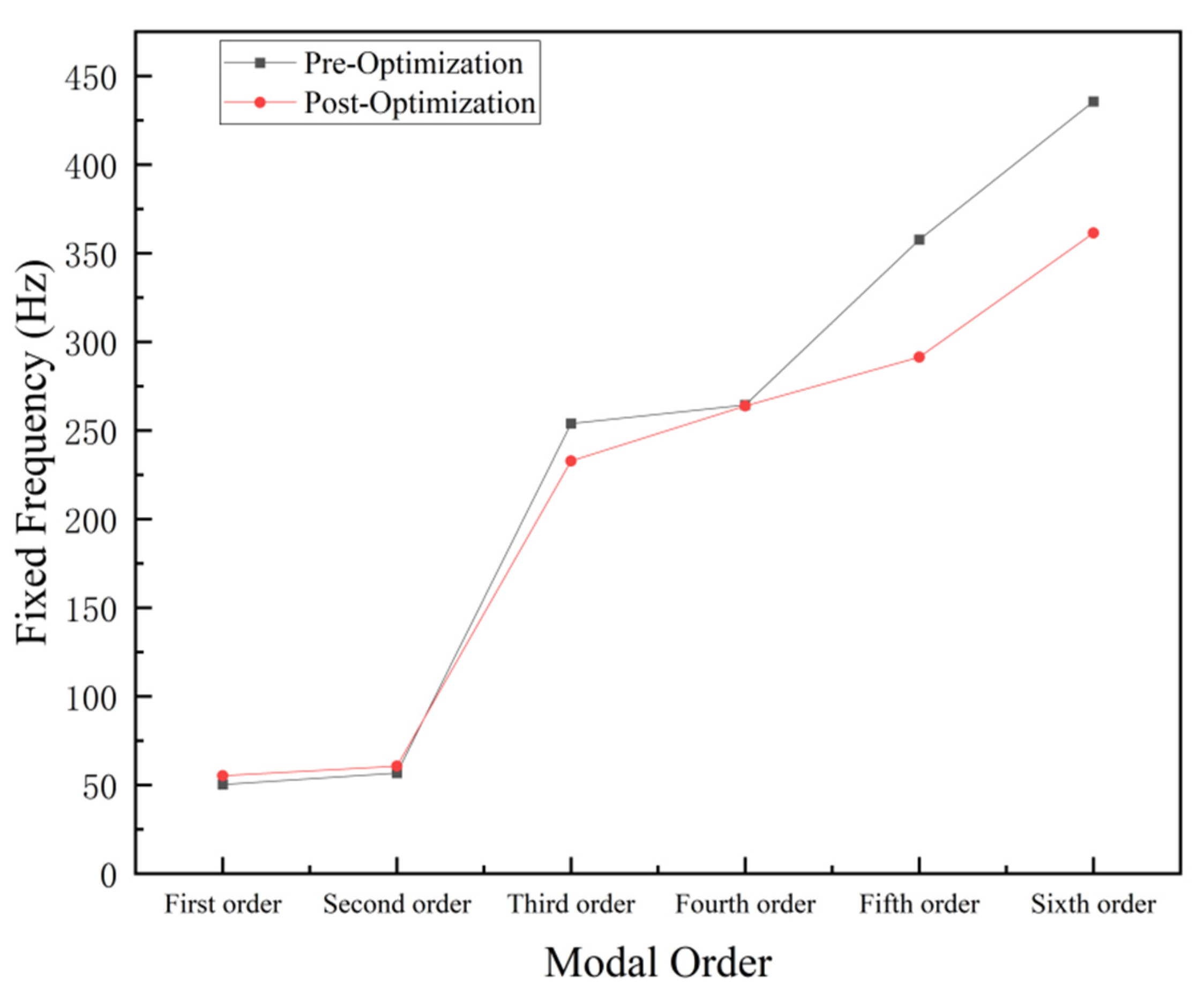
4.2. Modal Analysis Results Analysis
4.3. Transient Simulation Comparative Analysis
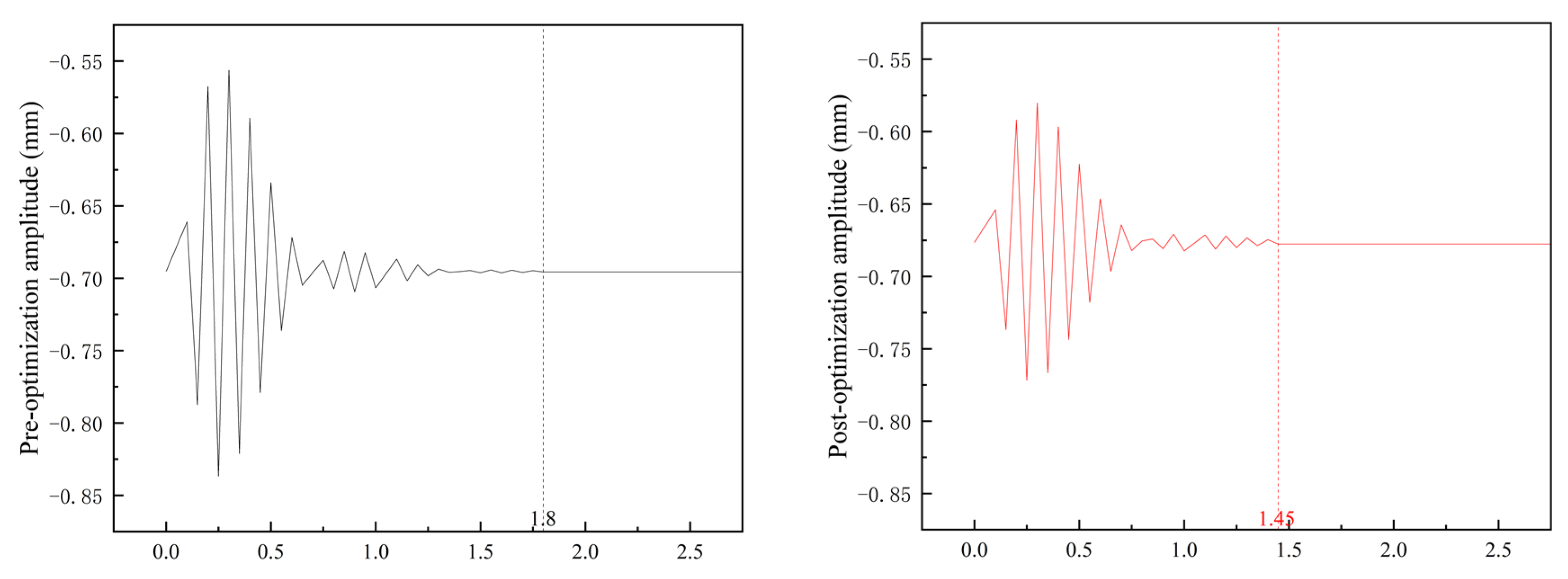
4.3.1. Comparison of Vibration Amplitude and Frequency
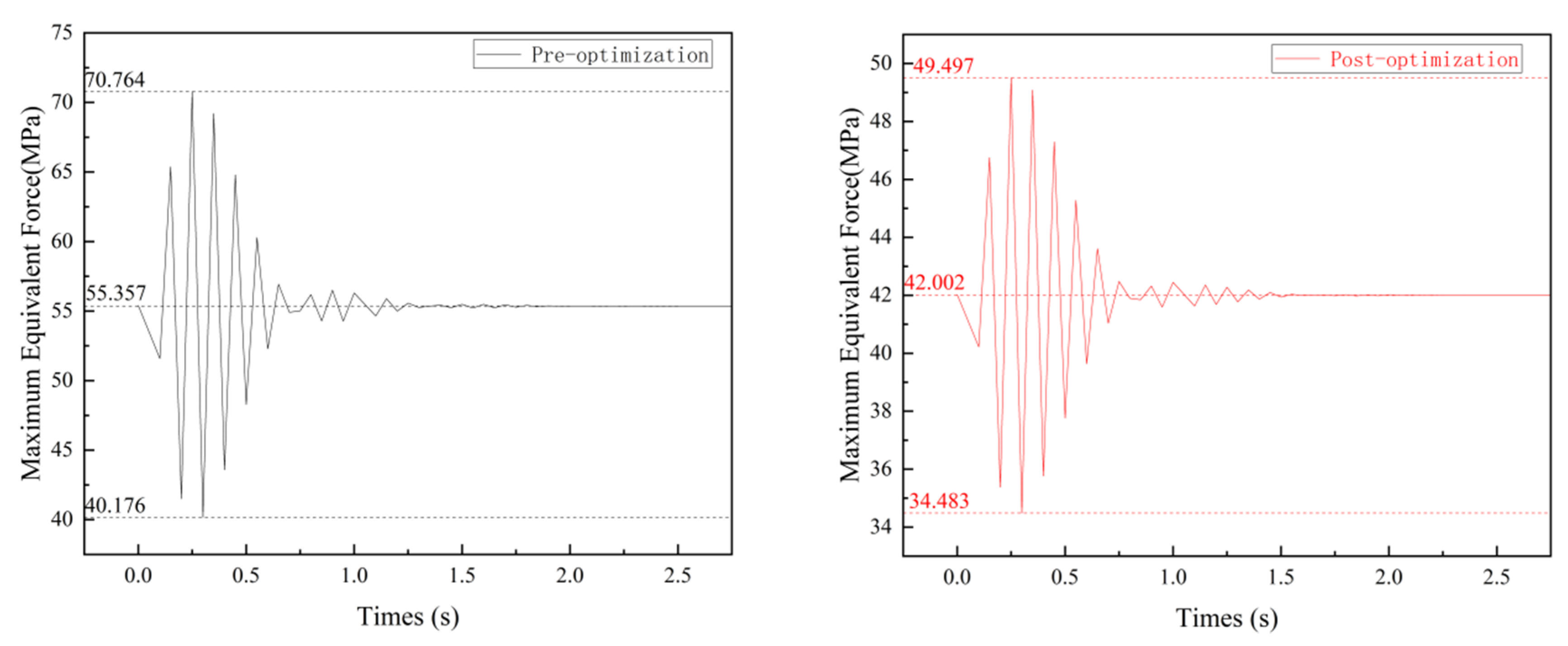
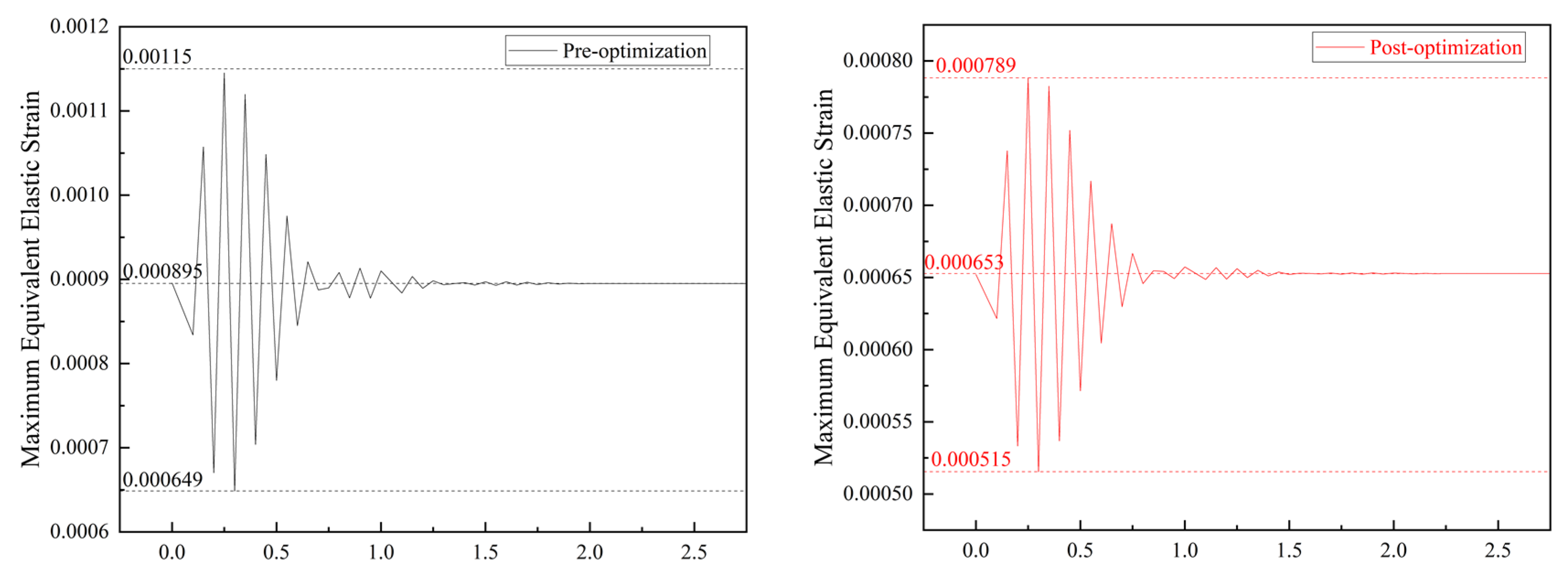
4.3.2. Comparison of Transient Stress and Strain
5. Discussion
6. Conclusions
- (1)
- The lightweight design of the welding robot forearm was achieved, resulting in a 19.8% reduction in mass and material savings, leading to cost reduction.
- (2)
- Through static simulation comparative analysis, it was observed that the mechanical performance of the optimized forearm was improved. The maximum total deformation decreased by 3.6%, the maximum stress decreased by 3.2%, and the maximum strain decreased by 5.7%. The mechanical performance of the optimized forearm exhibited better characteristics.
- (3)
- Modal simulation comparative analysis revealed that the natural frequencies of the optimized forearm increased, especially for the first and second modes, which showed significant improvements of 9.8% and 7.0%, respectively. This further reduced the possibility of resonance occurrence in the forearm.
- (4)
- Transient simulation comparative analysis demonstrated that the optimized forearm exhibited reduced vibration amplitudes and frequencies under maximum operating conditions, with a decrease of 19.4% and 26.9%, respectively. The maximum amplitudes of the equivalent stress and strain curves were reduced by 51.0% and 46%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Albu-Schäffer, A.; Haddadin, S.; Ott, C.; Stemmer, A.; Wimböck, T.; Hirzinger, G. The DLR Lightweight Robot: Design and Control Concepts for Robots in Human Environments. Ind. Robot Int. J. 2007, 34, 376–385. [Google Scholar] [CrossRef]
- Yin, H.; Liu, J.; Yang, F. Hybrid Structure Design of Lightweight Robotic Arms Based on Carbon Fiber Reinforced Plastic and Aluminum Alloy. IEEE Access 2019, 7, 64932–64945. [Google Scholar] [CrossRef]
- Gençer, G.M.; Öztoprak, N.; Akdağ, M.; Şen, H. Investigation of GFRP/AA7075-T6 Scarf Joint as a Robot Arm for High Natural Frequency and Damping Ratio. Arab. J. Sci. Eng. 2024, 49, 2027–2044. [Google Scholar] [CrossRef]
- Vogel, J.; Haddadin, S.; Simeral, J.D.; Stavisky, S.D.; Bacher, D.; Hochberg, L.R.; Donoghue, J.P.; van der Smagt, P. Continuous Control of the DLR Light-Weight Robot III by a Human with Tetraplegia Using the BrainGate2 Neural Interface System. In Experimental Robotics: The 12th International Symposium on Experimental Robotics, New Delhi and Agra, India, 18–21 December 2010; Khatib, O., Kumar, V., Sukhatme, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 125–136. ISBN 978-3-642-28572-1. [Google Scholar]
- Zargham, S.; Ward, T.A.; Ramli, R.; Badruddin, I.A. Topology Optimization: A Review for Structural Designs under Vibration Problems. Struct. Multidisc. Optim. 2016, 53, 1157–1177. [Google Scholar] [CrossRef]
- Jia, J.; Sun, X. Structural Optimization Design of a Six-Degrees-of-Freedom Serial Robot with Integrated Topology and Dimensional Parameters. Sensors 2023, 23, 7183. [Google Scholar] [CrossRef]
- Yin, H.; Huang, S.; He, M.; Li, J. A Unified Design for Lightweight Robotic Arms Based on Unified Description of Structure and Drive Trains. Int. J. Adv. Robot. Syst. 2017, 14, 1729881417716383. [Google Scholar] [CrossRef]
- Liang, M.; Wang, B.; Yan, T. Dynamic Optimization of Robot Arm Based on Flexible Multi-Body Model. J. Mech. Sci. Technol. 2017, 31, 3747–3754. [Google Scholar] [CrossRef]
- Luo, H.; Fu, J.; Wang, P.; Liu, J.; Zhou, W. Design Optimization of the Ram Structure of Friction Stir Welding Robot. Mech. Adv. Mater. Struct. 2020, 27, 108–118. [Google Scholar] [CrossRef]
- Xue, H.; Yu, H.; Zhang, X.; Quan, Q. A Novel Method for Structural Lightweight Design with Topology Optimization. Energies 2021, 14, 4367. [Google Scholar] [CrossRef]
- Duddeck, F.; Hunkeler, S.; Lozano, P.; Wehrle, E.; Zeng, D. Topology Optimization for Crashworthiness of Thin-Walled Structures under Axial Impact Using Hybrid Cellular Automata. Struct. Multidisc. Optim. 2016, 54, 415–428. [Google Scholar] [CrossRef]
- Liu, Q.; Fan, G.; Tan, Z.; Li, Z.; Zhang, D.; Wang, J.; Zhang, H. Precipitation of Al3Zr by Two-Step Homogenization and Its Effect on the Recrystallization and Mechanical Property in 2195 Al–Cu–Li Alloys. Mater. Sci. Eng. A 2021, 821, 141637. [Google Scholar] [CrossRef]
- Xie, L.; Zhang, Y.; Ge, M.; Zhao, Y. Topology Optimization of Heat Sink Based on Variable Density Method. Energy Rep. 2022, 8, 718–726. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, Y.; Zhai, J.; Hou, Z.; Han, Q. Topological Optimization Design on Constrained Layer Damping Treatment for Vibration Suppression of Aircraft Panel via Improved Evolutionary Structural Optimization. Aerosp. Sci. Technol. 2021, 112, 106619. [Google Scholar] [CrossRef]
- Xia, Q.; Shi, T. Generalized Hole Nucleation through BESO for the Level Set Based Topology Optimization of Multi-Material Structures. Comput. Methods Appl. Mech. Eng. 2019, 355, 216–233. [Google Scholar] [CrossRef]
- Xue, R.; Liu, C.; Zhang, W.; Zhu, Y.; Tang, S.; Du, Z.; Guo, X. Explicit Structural Topology Optimization under Finite Deformation via Moving Morphable Void (MMV) Approach. Comput. Methods Appl. Mech. Eng. 2019, 344, 798–818. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Zou, B.; Li, Q.; Ma, Y. Stress Constrained Multi-Material Topology Optimization with the Ordered SIMP Method. Comput. Methods Appl. Mech. Eng. 2021, 373, 113453. [Google Scholar] [CrossRef]
- Rojas-Labanda, S.; Sigmund, O.; Stolpe, M. A Short Numerical Study on the Optimization Methods Influence on Topology Optimization. Struct. Multidisc. Optim. 2017, 56, 1603–1612. [Google Scholar] [CrossRef]
- Wan, C.; Jiao, H.; Lv, L.; Lu, C. Multi-Material Topology Optimization Based on Multiple Simp of Variable Density Method. J. Mech. Sci. Technol. 2024, 38, 749–759. [Google Scholar] [CrossRef]
- Yao, P.; Zhou, K.; Lin, Y.; Tang, Y. Light-Weight Topological Optimization for Upper Arm of an Industrial Welding Robot. Metals 2019, 9, 1020. [Google Scholar] [CrossRef]





| Geometric Dimensions | |
|---|---|
| Length in X direction (mm) | 727.39 |
| Length in Y direction (mm) | 258.69 |
| Length in Z direction (mm) | 274.28 |
| Volume (m3) | 0.0027 |
| Ai5083 Material Characteristics | |
|---|---|
| Density (kg/m3) | 2800 |
| Young’s Modulus (MPa) | 70,300 |
| Poisson’s Ratio | 0.33 |
| Tensile Yield strength (MPa) | 230 |
| Compressive Yield strength (MPa) | 230 |
| Tensile Ultimate strength (MPa) | 320 |
| Mass (kg) | 7.493 |
| Modal Order | Frequency Pre-Optimization (Hz) | Frequency Post-Optimization (Hz) |
|---|---|---|
| First order | 50.329 | 55.267 |
| Second order | 56.729 | 60.678 |
| Third order | 253.84 | 232.86 |
| Fourth order | 264.4 | 263.84 |
| Five order | 357.62 | 291.38 |
| Six order | 435.64 | 361.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, H.; Sun, Z.; Hu, J.; Yang, F. Light-Weighting and Comparative Simulation Analysis of the Forearm of Welding Robots. Actuators 2024, 13, 209. https://doi.org/10.3390/act13060209
Pang H, Sun Z, Hu J, Yang F. Light-Weighting and Comparative Simulation Analysis of the Forearm of Welding Robots. Actuators. 2024; 13(6):209. https://doi.org/10.3390/act13060209
Chicago/Turabian StylePang, Hongchen, Zibin Sun, Jiezhen Hu, and Fang Yang. 2024. "Light-Weighting and Comparative Simulation Analysis of the Forearm of Welding Robots" Actuators 13, no. 6: 209. https://doi.org/10.3390/act13060209
APA StylePang, H., Sun, Z., Hu, J., & Yang, F. (2024). Light-Weighting and Comparative Simulation Analysis of the Forearm of Welding Robots. Actuators, 13(6), 209. https://doi.org/10.3390/act13060209





