Dynamic Output Feedback of Second-Order Systems: An Observer-Based Controller with Linear Matrix Inequality Design
Abstract
:1. Introduction
2. Preliminaries and Problem Formulation
3. Main Result
| Algorithm 1 Controller Design Procedure |
 |
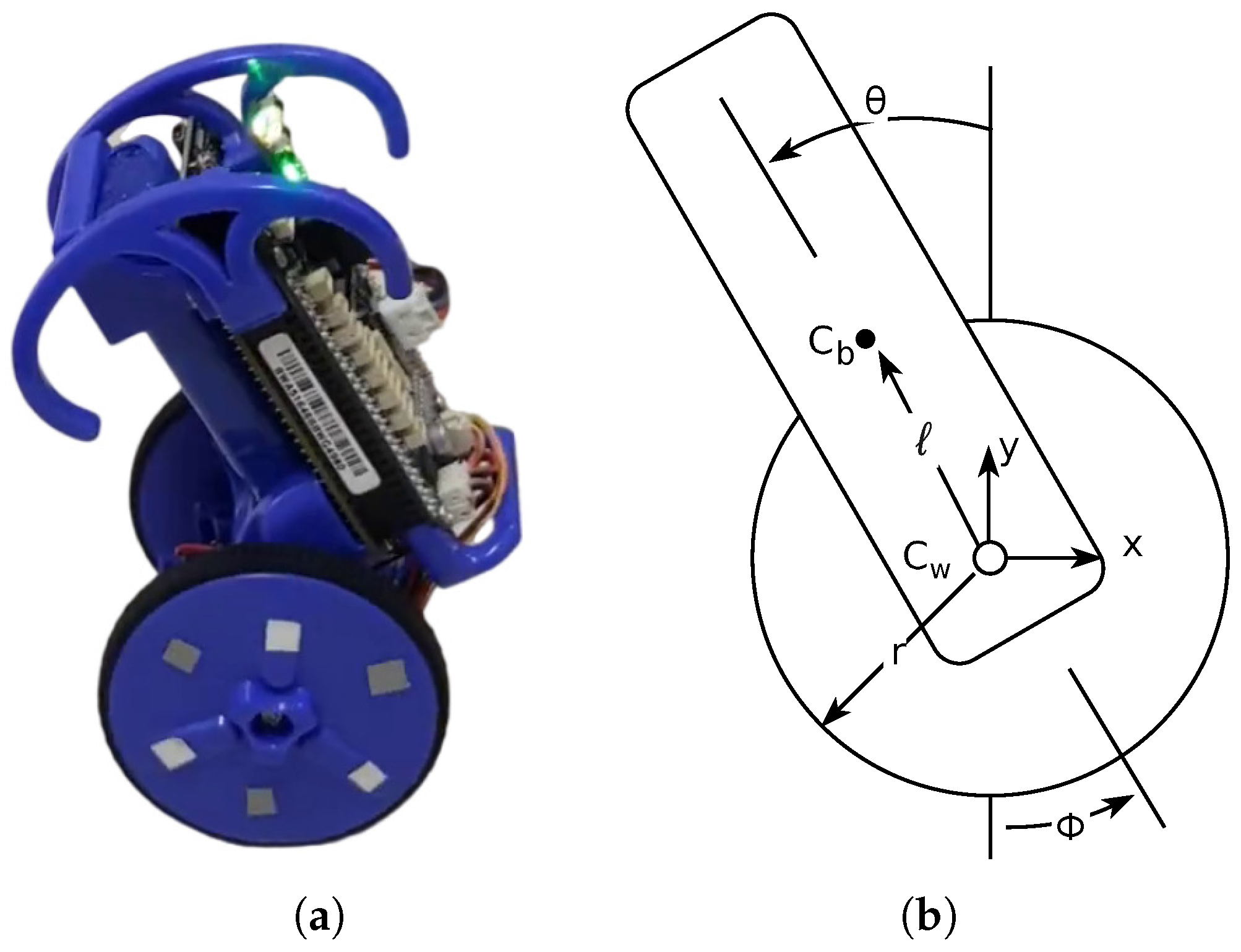
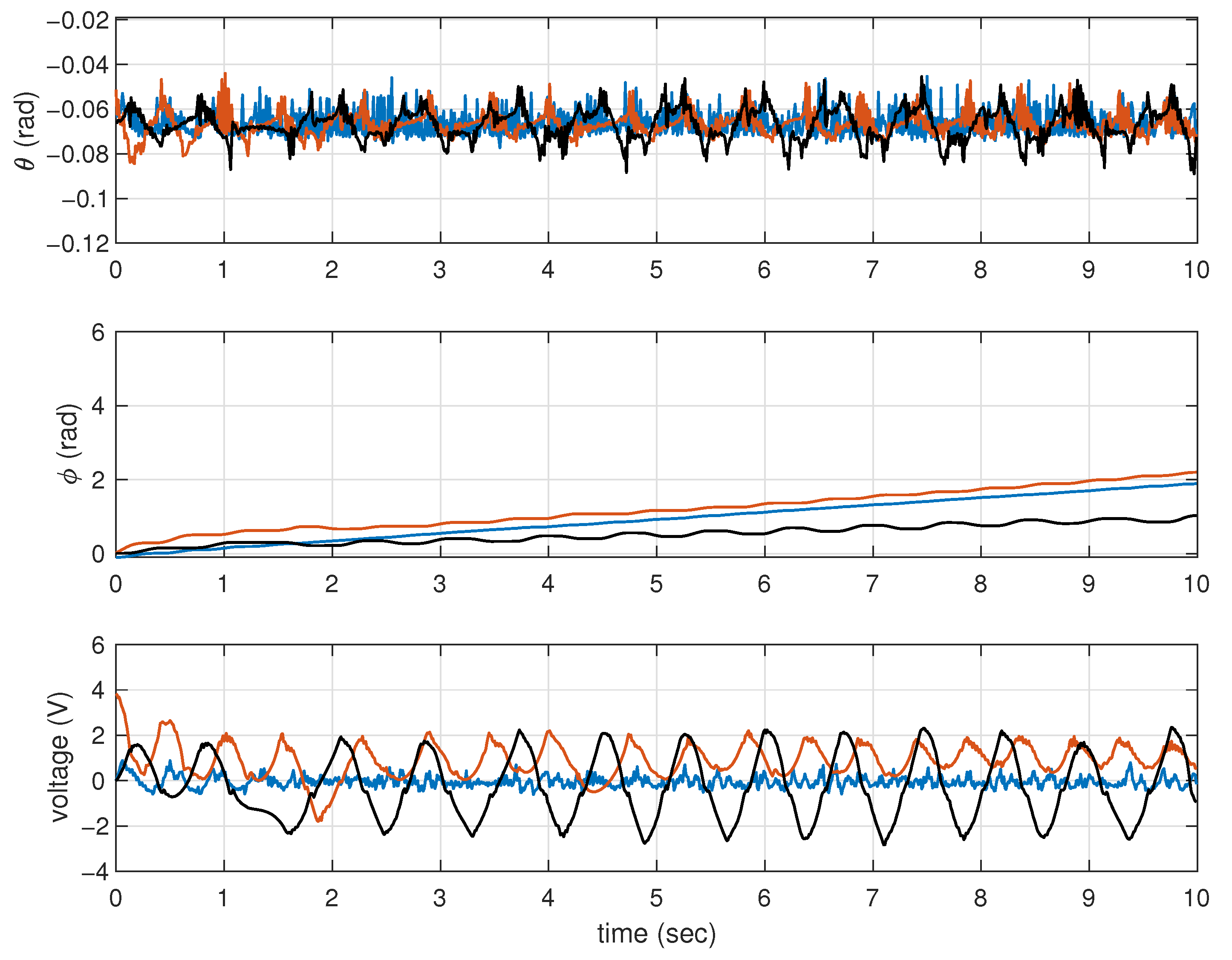
4. Experimental Study
4.1. System Model
4.2. Full State-Feedback Control
4.3. Observer-Based Control
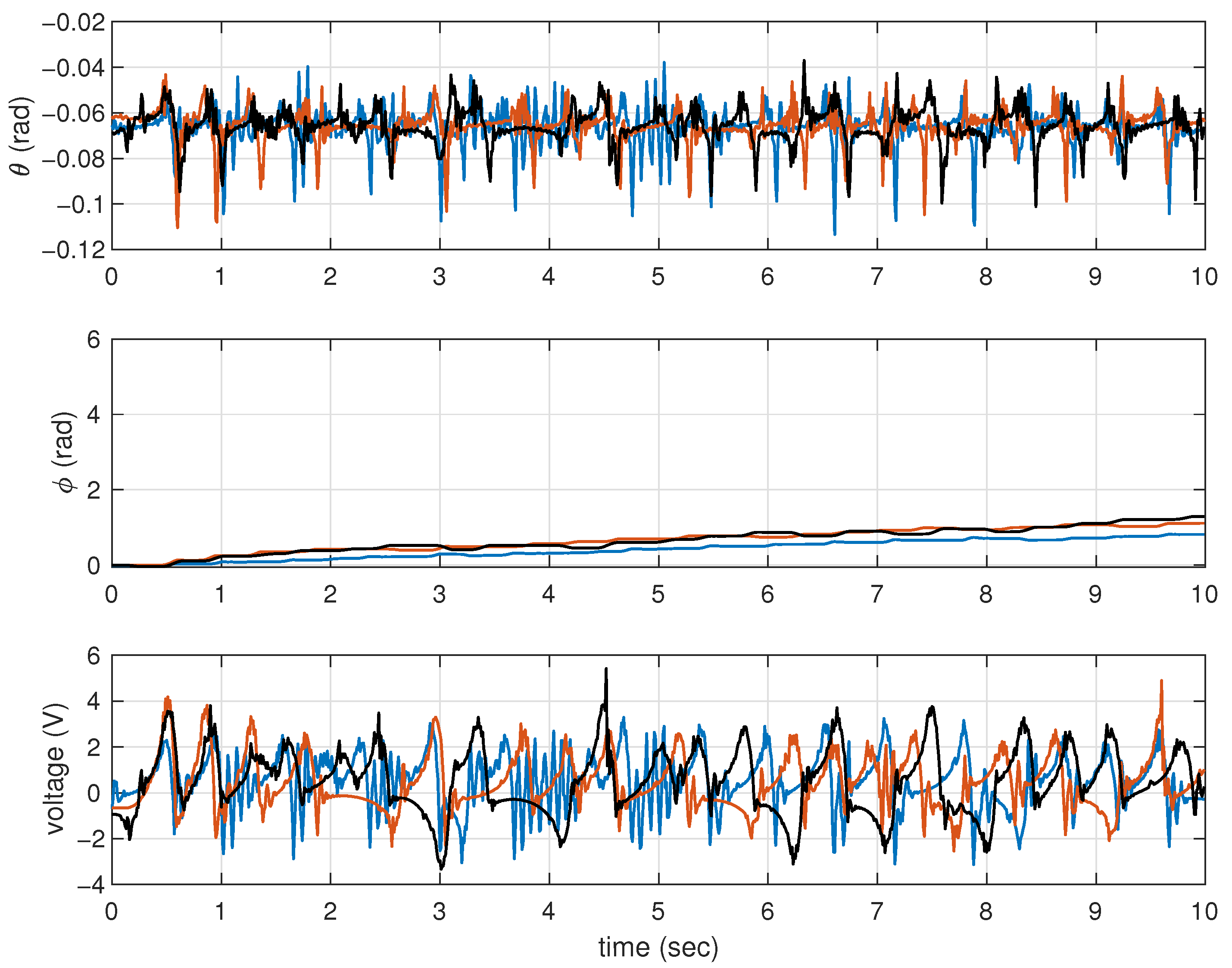
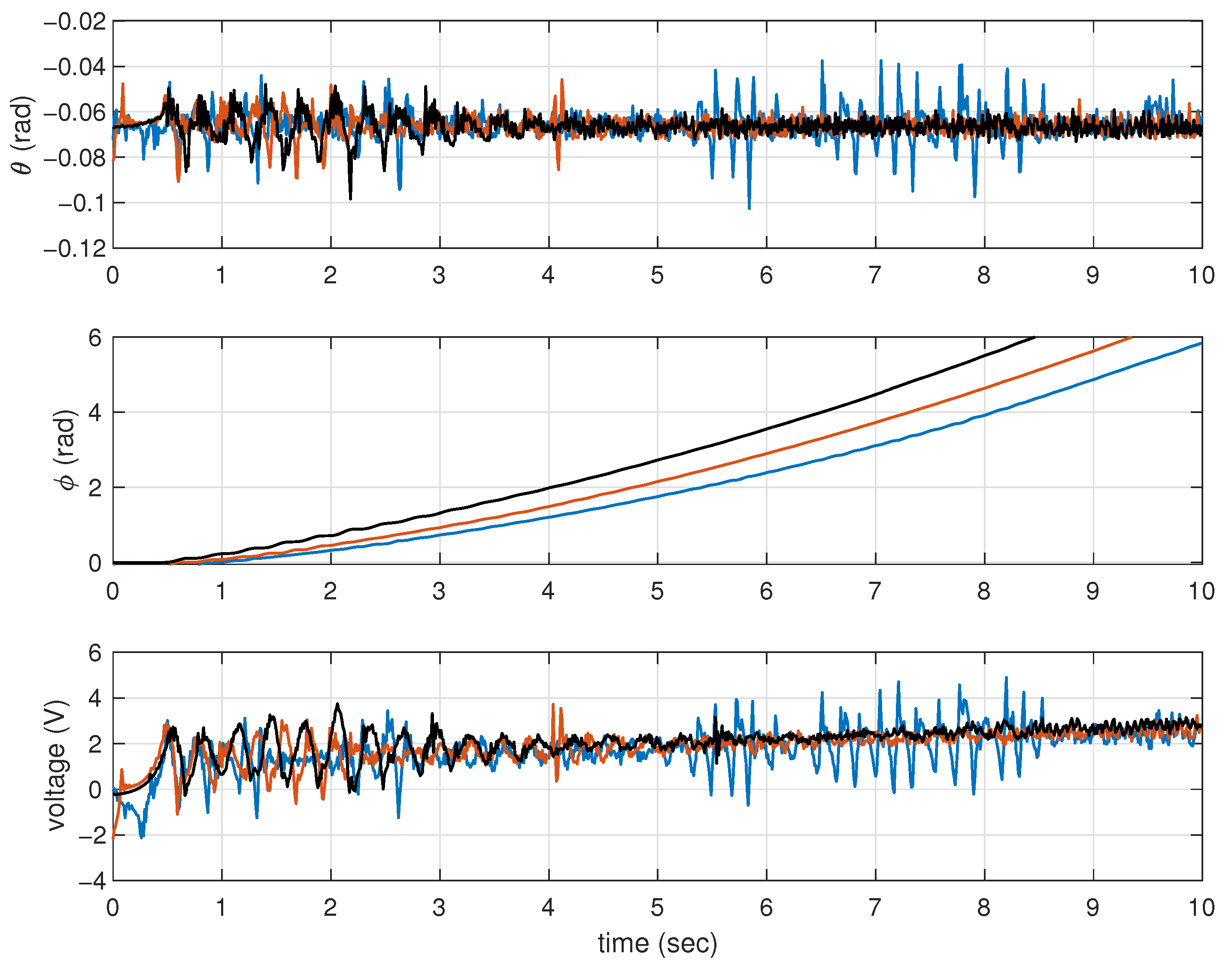
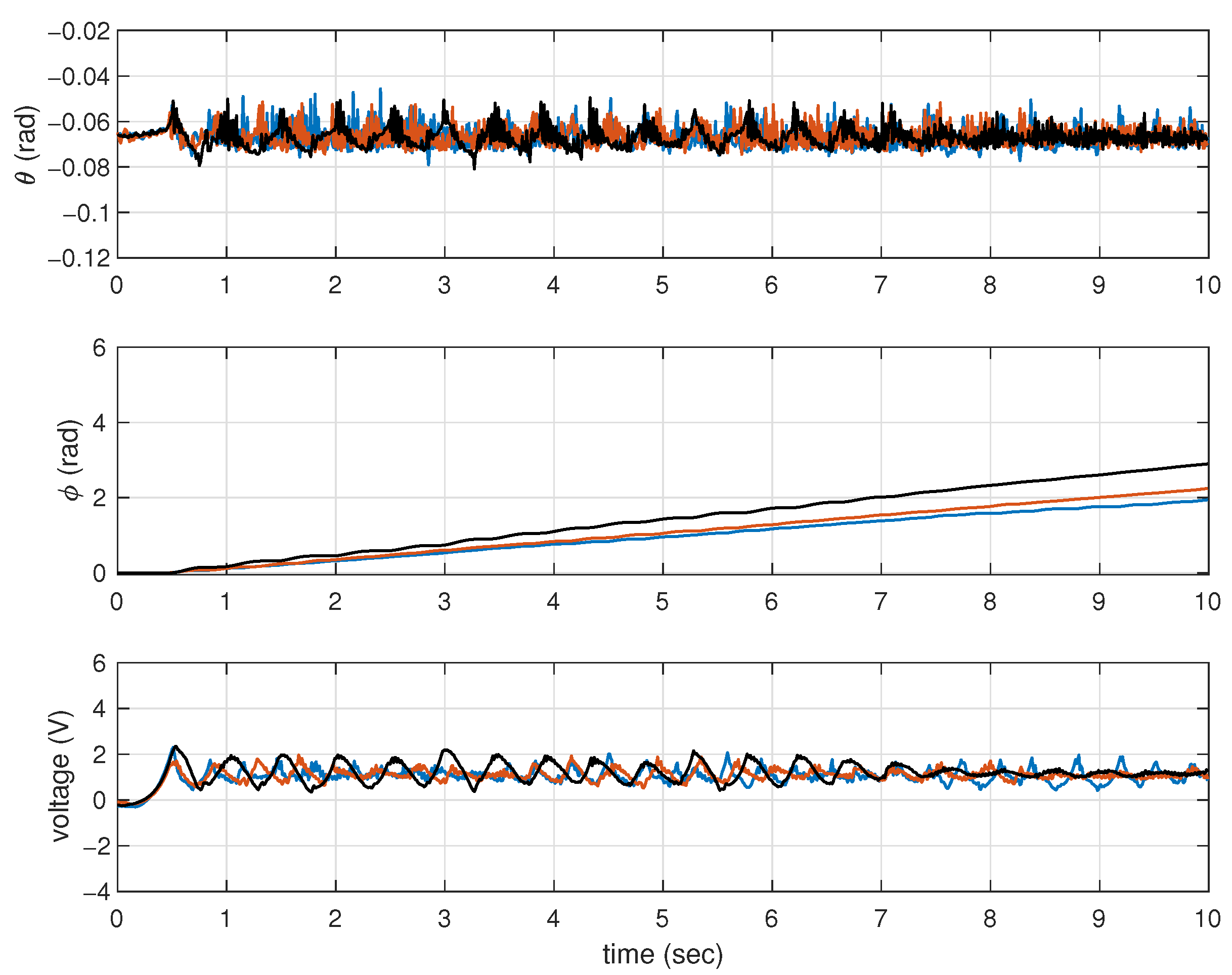
4.4. Experimental Results
4.5. Experimental Performance Comparisons
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ikeda, Y. Active and semi-active vibration control of buildings in Japan—Practical applications and verification. Struct. Control Health Monit. 2009, 16, 703–723. [Google Scholar] [CrossRef]
- Yu, Y.; Guo, J.; Li, L.; Song, G.; Li, P.; Ou, J. Experimental study of wireless structural vibration control considering different time delays. Smart Mater. Struct. 2015, 24, 045005. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, G.; Liu, W. Optimal control of second-order and high-order descriptor systems. Optim. Control Appl. Methods 2019, 40, 791–806. [Google Scholar] [CrossRef]
- Abdelaziz, T.H. Parametric approach for eigenstructure assignment in descriptor second-order systems via velocity-plus-acceleration feedback. J. Dyn. Syst. Meas. Control 2014, 136, 044505. [Google Scholar] [CrossRef]
- Luenberger, D.G. Observing the State of a Linear System. IEEE Trans. Mil. Electron. 1964, 8, 74–80. [Google Scholar] [CrossRef]
- Hayashi, S.; Kanoh, H.; Masubuchi, M. Functional Observers for Some Sort of Linear Systems and Its Application to Unstable Mechanical System. Technol. Rep. Osaka Univ. 1980, 30, 537–544. [Google Scholar]
- Trinh, H. Linear functional state observer for time-delay systems. Int. J. Control 1999, 72, 1642–1658. [Google Scholar] [CrossRef]
- Darouach, M. Existence and design of functional observers for linear systems. IEEE Trans. Autom. Control 2000, 45, 940–943. [Google Scholar] [CrossRef]
- Araujo, J.M.; Barros, P.R.; Dorea, C.E.T. Design of Observers with Error Limitation in Discrete-Time Descriptor Systems: A Case Study of a Hydraulic Tank System. IEEE Trans. Control Syst. Technol. 2012, 20, 1041–1047. [Google Scholar] [CrossRef]
- Trinh, H.; Fernando, T. Functional Observers for Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Darouach, M.; Fernando, T. On the Existence and Design of Functional Observers. IEEE Trans. Autom. Control 2020, 65, 2751–2759. [Google Scholar] [CrossRef]
- Ríos-Ruiz, C.; Osorio Gordillo, G.L.; Darouach, M.; Souley Ali, H.; Astorga-Zaragoza, C.M. Design of finite-time convergent functional observer for descriptor systems: Application to fault estimation. Asian J. Control. 2004. online first. [Google Scholar] [CrossRef]
- Demetriou, M.A. Natural second-order observers for second-order distributed parameter systems. Syst. Control Lett. 2004, 51, 225–234. [Google Scholar] [CrossRef]
- Demetriou, M.A. Unknown input functional observers for vector second order structural systems. Mech. Syst. Signal Process. 2022, 164, 108060. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, H. A survey of underactuated mechanical systems. IET Control Theory Appl. 2013, 7, 921–935. [Google Scholar] [CrossRef]
- Seifried, R. Dynamics of Underactuated Multibody Systems: Modeling, Control and Optimal Design; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Shin, J.H.; Lee, J.J. Fault detection and robust fault recovery control for robot manipulators with actuator failures. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No.99CH36288C), Detroit, MI, USA, 10–15 May 1999. [Google Scholar] [CrossRef]
- Nudehi, S.S.; Mukherjee, R. Enhancing Controllability and Observability in Underactuated and Undersensed Systems Through Switching: Application to Vibration Control. J. Dyn. Syst. Meas. Control 2004, 126, 790–799. [Google Scholar] [CrossRef]
- Venkatraman, A.; Ortega, R.; Sarras, I.; van der Schaft, A. Control of underactuated mechanical systems: Observer design and position feedback stabilization. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008. [Google Scholar] [CrossRef]
- Gesser, R.S.; Lima, D.M.; Normey-Rico, J.E. Robust Model Predictive Control: Implementation Issues with Comparative Analysis. IFAC-PapersOnLine 2018, 51, 478–483. [Google Scholar] [CrossRef]
- Lin, K.J. Sliding Mode Control Design for Uncertain Singular Systems. Appl. Mech. Mater. 2012, 145, 16–20. [Google Scholar] [CrossRef]
- Zhong, Z.; Lam, H.K.; Ying, H.; Xu, G. CMAC-based SMC for uncertain descriptor systems using reachable set learning. IEEE Trans. Syst. Man Cybern. Syst. 2023, 54, 693–703. [Google Scholar] [CrossRef]
- Fairman, F.W. Linear Control Theory: State Space Approach; John Wiley & Sons: Chichester, UK, 1998. [Google Scholar]
- GitHub. Pyctrl: A Python Suite for Systems and Control. 2018. Available online: https://github.com/mcdeoliveira/pyctrl (accessed on 13 July 2023).
- Zhuo, Z. LQG Controller Design of the Mobile Inverted Pendulum. Master’s Thesis, University of California, San Diego, CA, USA, 2017. [Google Scholar]
- Gahinet, P.; Apkarian, P. A linear matrix inequality approach to H∞ control. Int. J. Robust Nonlinear Control 1994, 4, 421–448. [Google Scholar] [CrossRef]


| Parameter | Value | Uncertainty | Parameter | Value | Uncertainty |
|---|---|---|---|---|---|
| r | 34 mm | 0 | kg·m2 | ||
| ℓ | 46 mm | 0 | kg·m2 | ||
| 27 g | 0 | N·m at Vmax | |||
| 263 g | 0 | N·m | |||
| V | 0 | 35.57:1 Gear ratio | 0 |
| R | K | ||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 5 | 2.1554 |
| R | K | ||
|---|---|---|---|
| 1 | 3.7452 | ||
| 2 | 3.9529 | ||
| 5 | } | 4.7545 |
| R | K | L | ||
|---|---|---|---|---|
| 1 | 1.2038 | |||
| 2 | 1.2574 | |||
| 5 | 1.5946 |
| R | K | LQR LQG | ||
|---|---|---|---|---|
| LQR | LQG | |||
| 1 | 7.1513 | 1.3807 | ||
| 2 | 2.5549 | 1.4242 | ||
| 5 | 13.0266 | 2.1356 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gontijo, D.; Araújo, J.M.; Frezzato, L.; Souza, F.d.O. Dynamic Output Feedback of Second-Order Systems: An Observer-Based Controller with Linear Matrix Inequality Design. Actuators 2024, 13, 216. https://doi.org/10.3390/act13060216
Gontijo D, Araújo JM, Frezzato L, Souza FdO. Dynamic Output Feedback of Second-Order Systems: An Observer-Based Controller with Linear Matrix Inequality Design. Actuators. 2024; 13(6):216. https://doi.org/10.3390/act13060216
Chicago/Turabian StyleGontijo, Danielle, José Mário Araújo, Luciano Frezzato, and Fernando de Oliveira Souza. 2024. "Dynamic Output Feedback of Second-Order Systems: An Observer-Based Controller with Linear Matrix Inequality Design" Actuators 13, no. 6: 216. https://doi.org/10.3390/act13060216
APA StyleGontijo, D., Araújo, J. M., Frezzato, L., & Souza, F. d. O. (2024). Dynamic Output Feedback of Second-Order Systems: An Observer-Based Controller with Linear Matrix Inequality Design. Actuators, 13(6), 216. https://doi.org/10.3390/act13060216






