Stiffness Analysis of Cable-Driven Parallel Robot for UAV Aerial Recovery System
Abstract
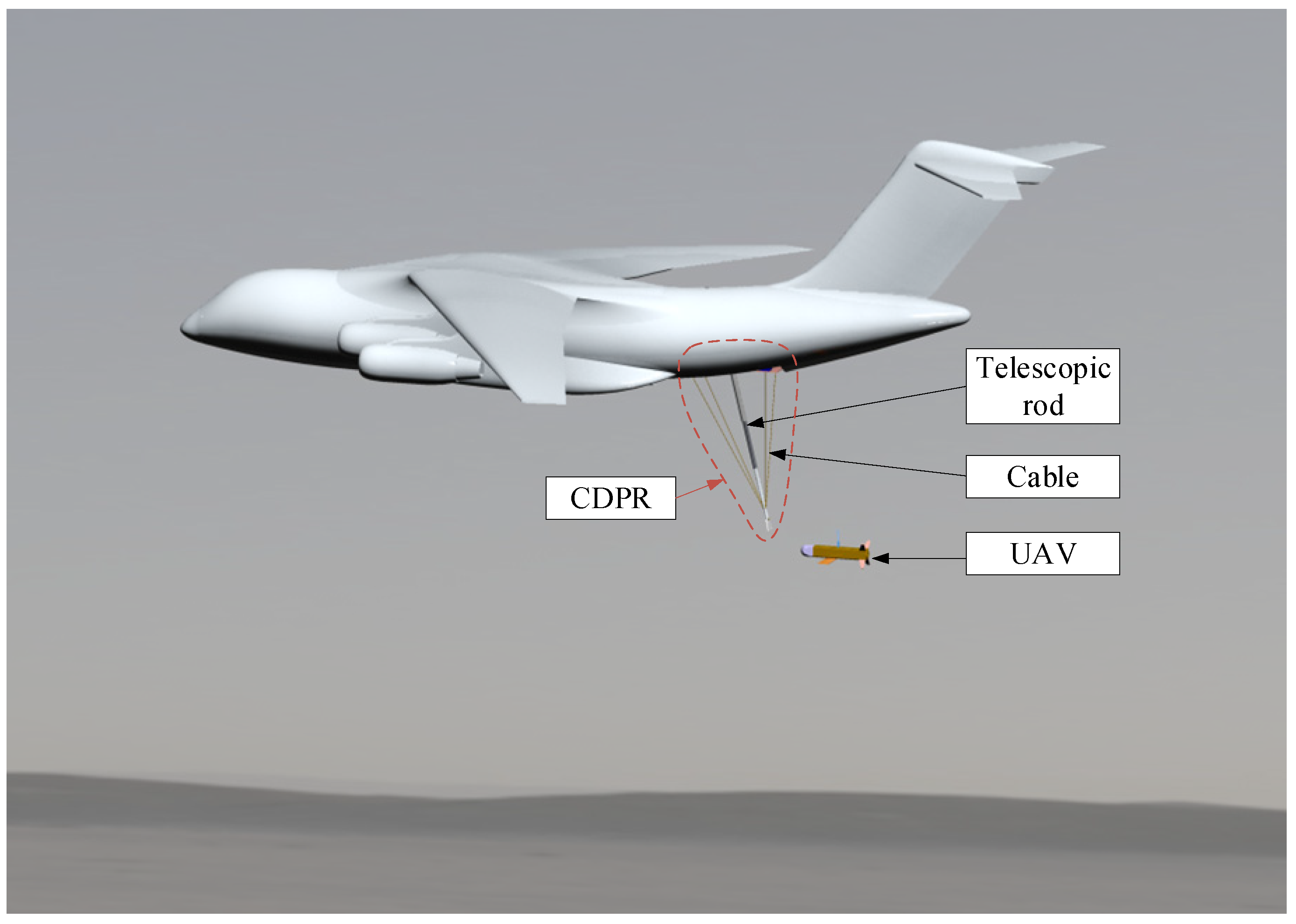
:1. Introduction
2. Stiffness of the Cable Considering Aerodynamic Loads
3. Stiffness Calculation of the CDPR
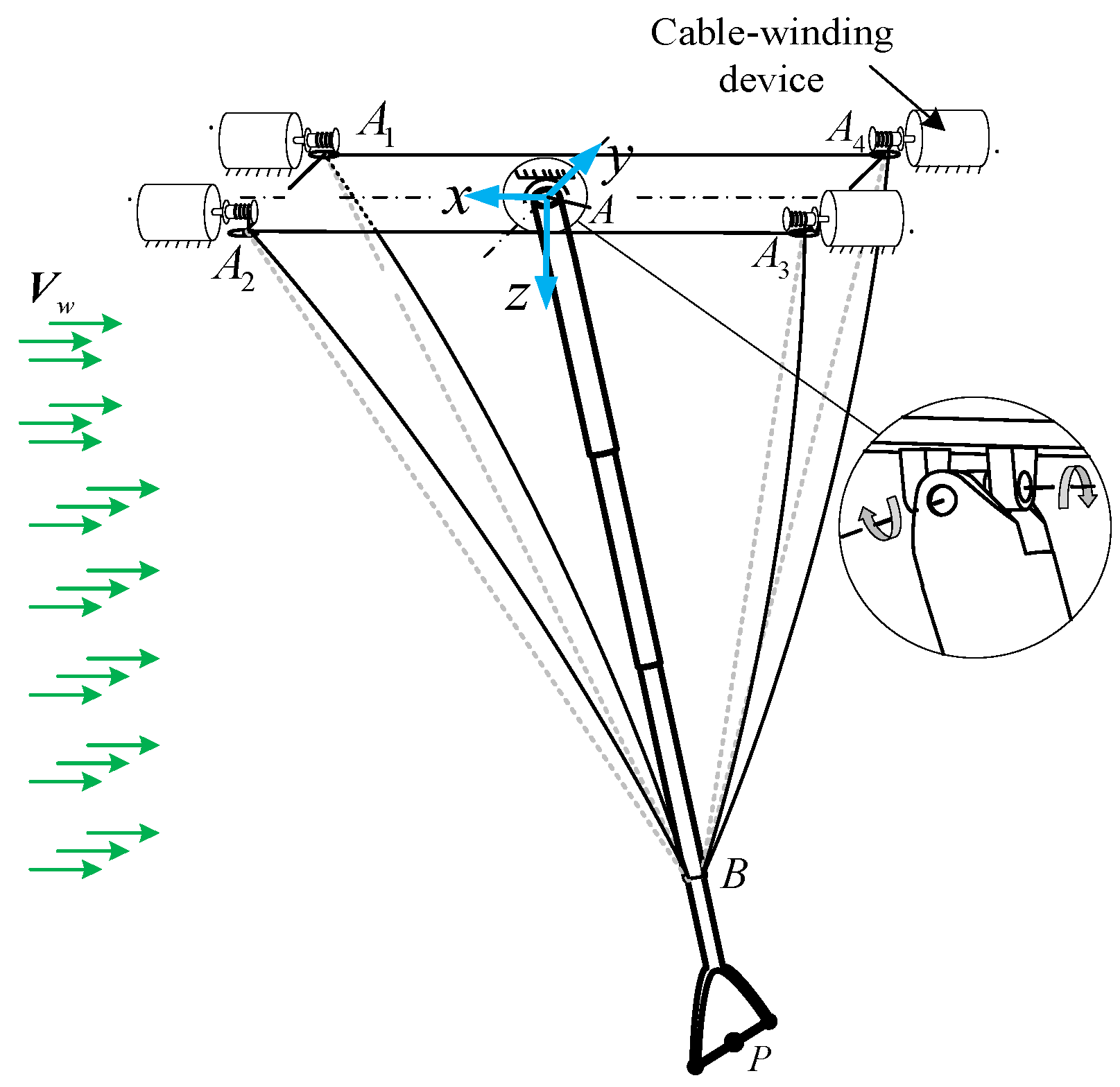
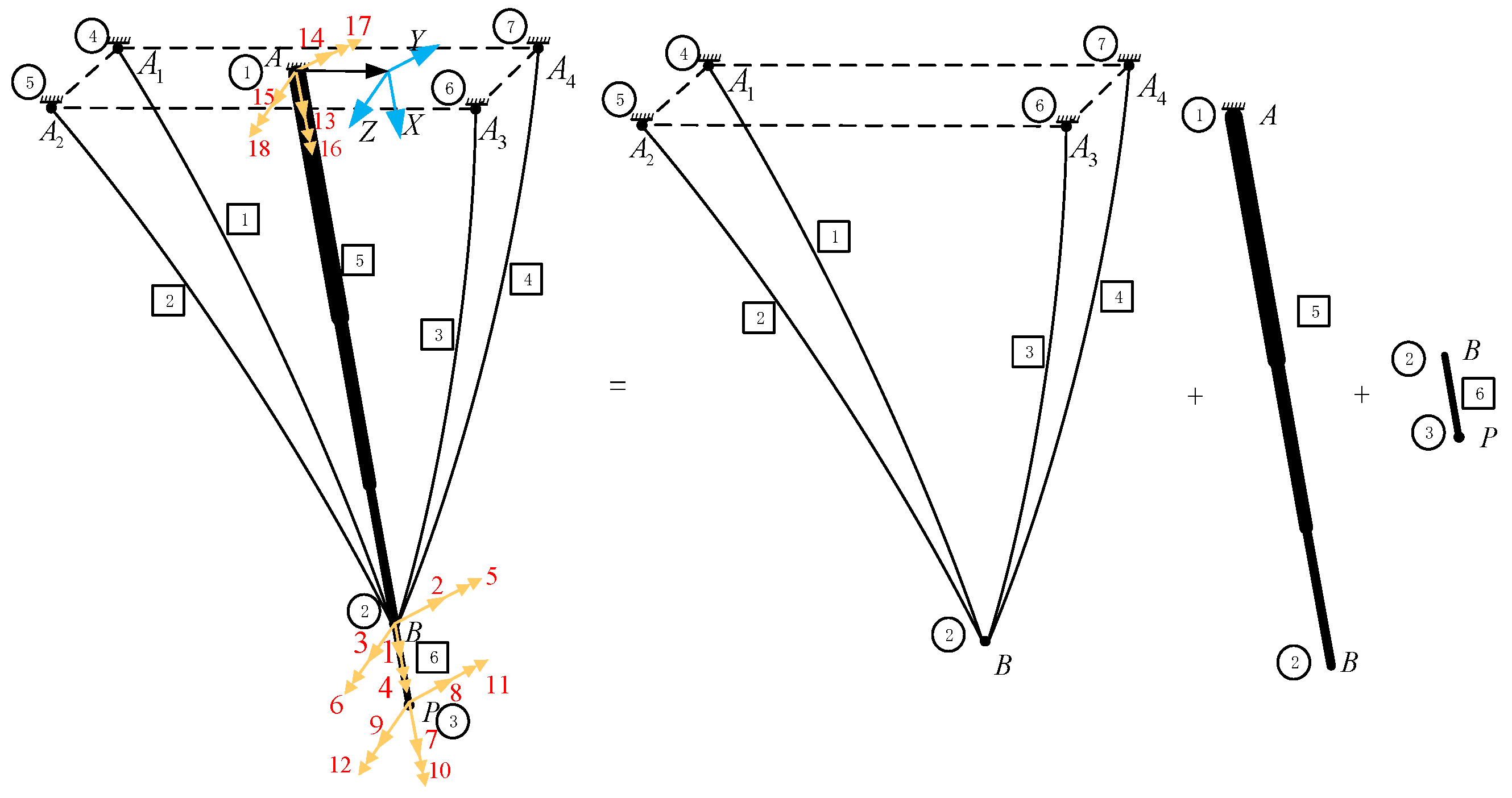
3.1. Global Coordinates and Elements Stiffness of CDPR
3.2. CDPR Stiffness Matrix
4. Stiffness Analysis
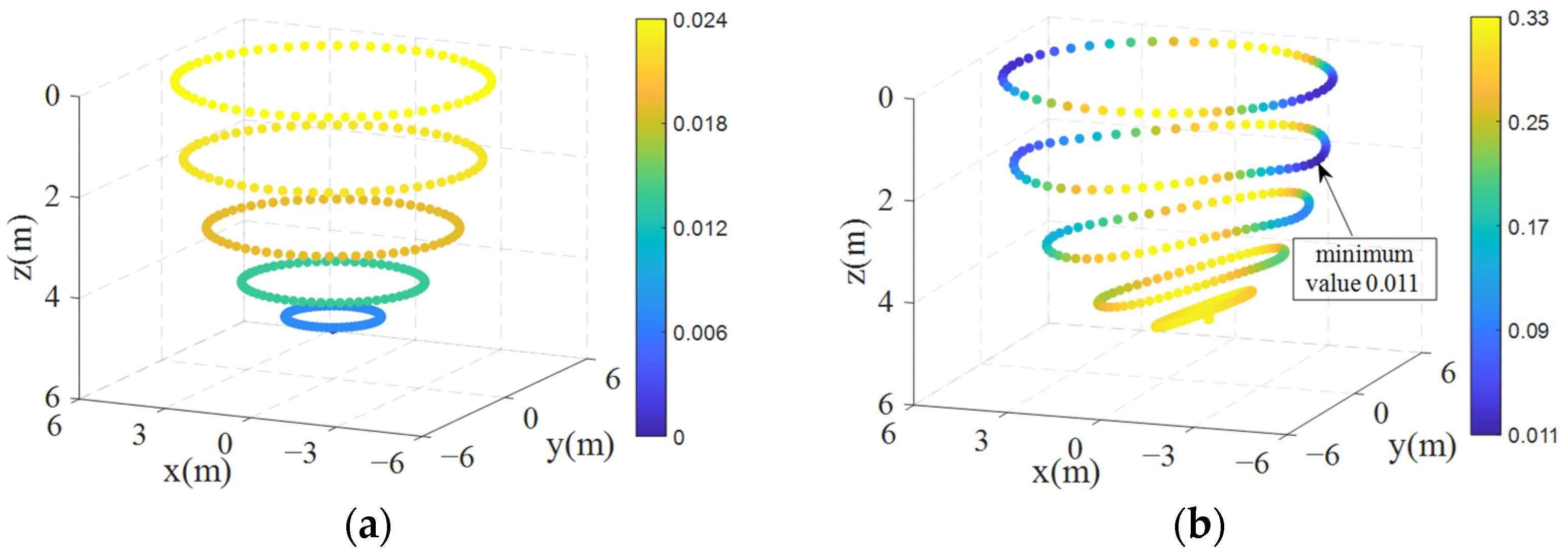
4.1. Analysis of Single Cable Stiffness in Flow Field Environment
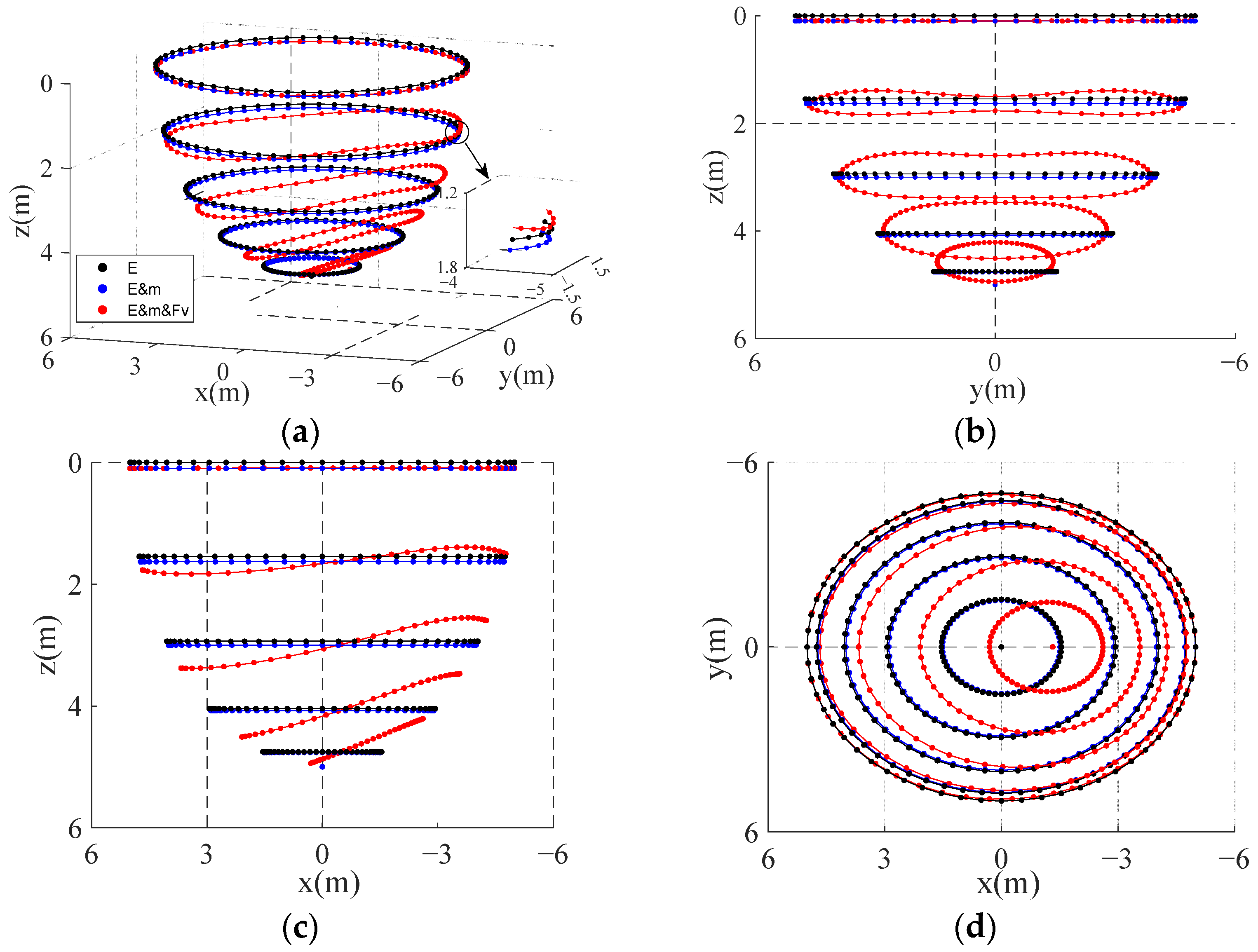
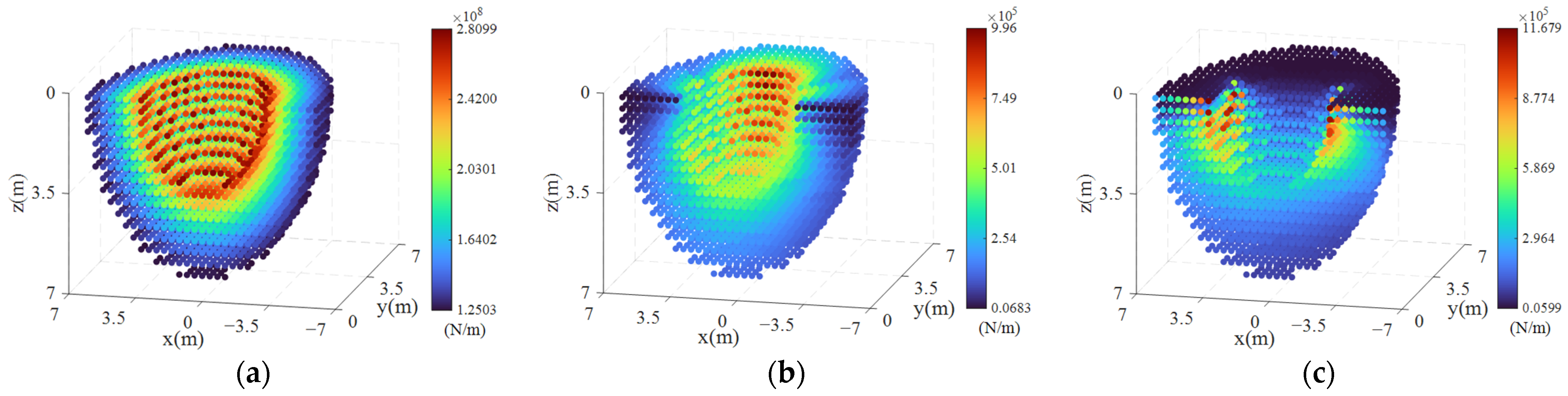
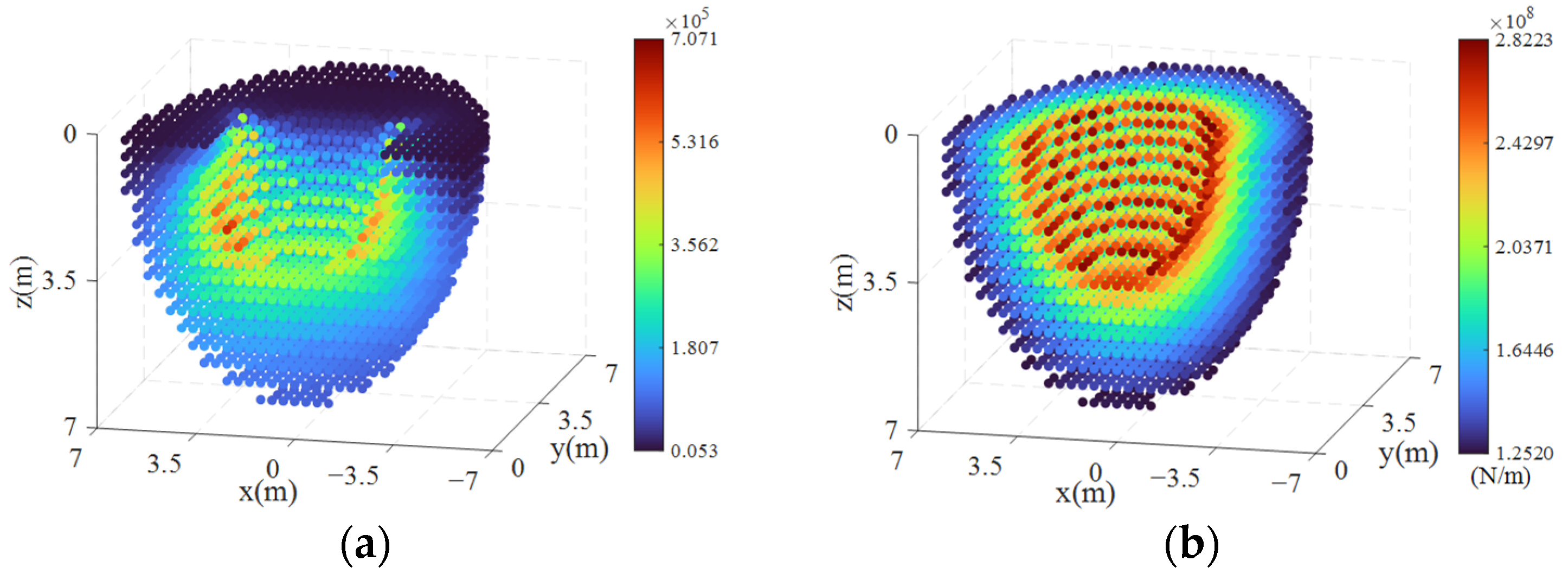
4.2. CDPR Stiffness Analysis
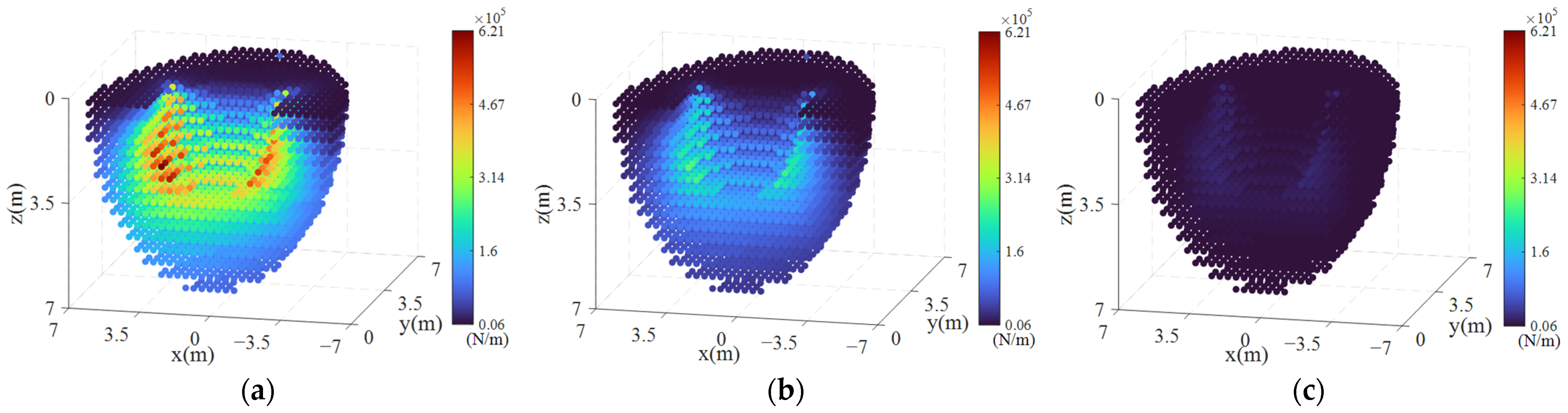
4.2.1. CDPR Stiffness Distribution
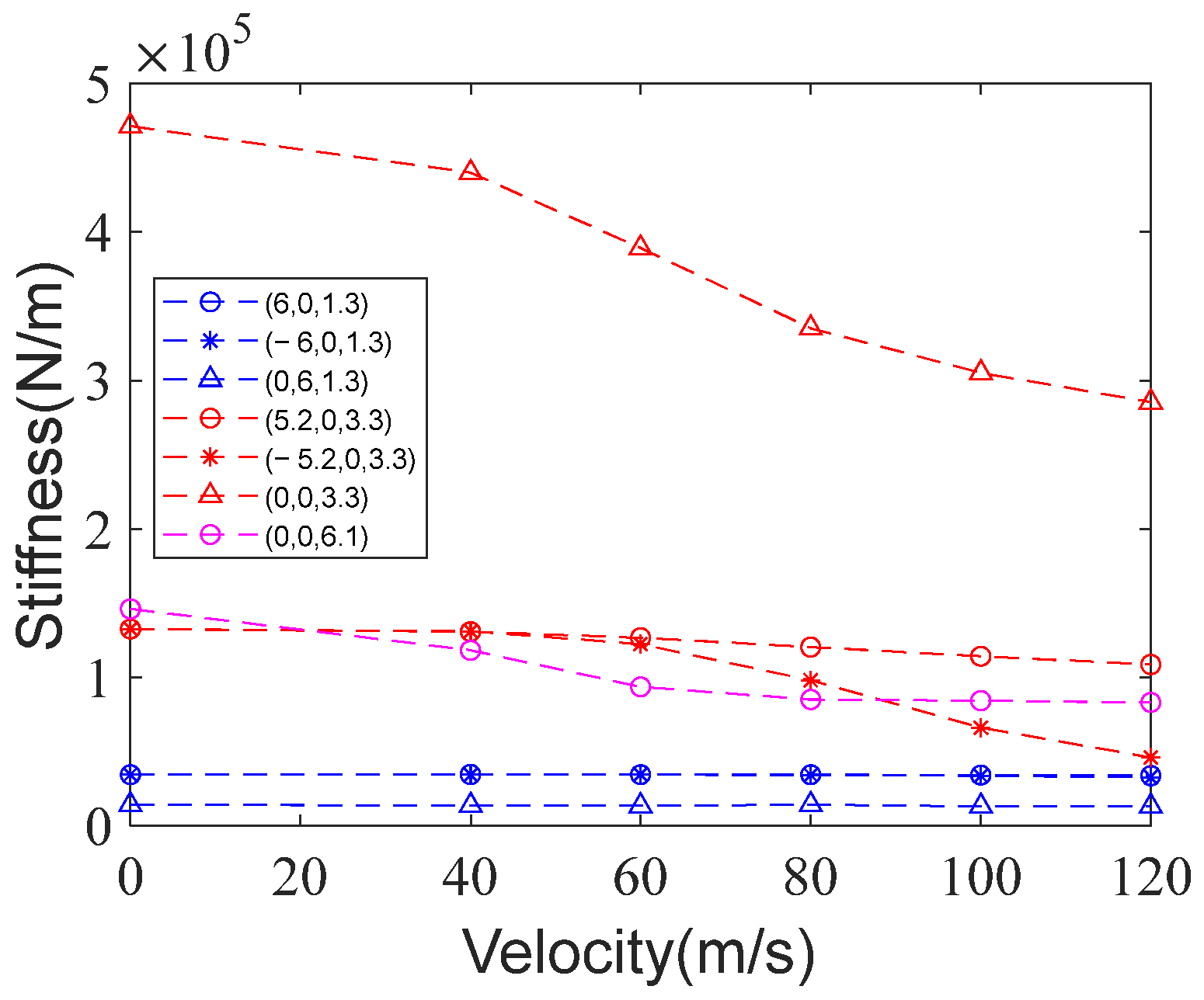
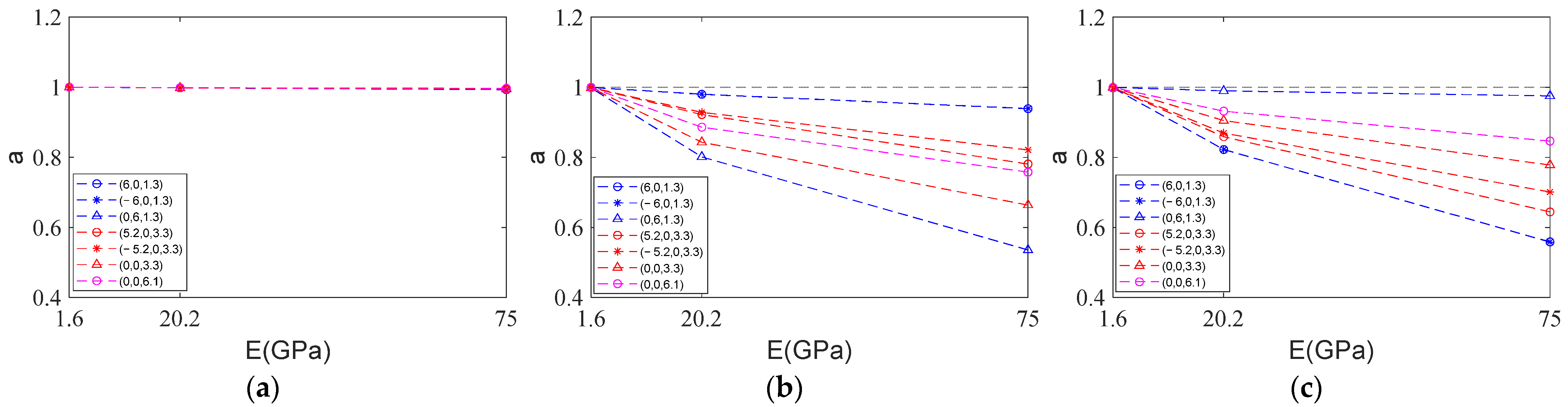
4.2.2. Influence of Flow Velocity on CDPR Stiffness
4.2.3. Influence of Different Cable Materials on CDPR Stiffness
4.3. Design Guidelines for the UAV Recovery System Based on Stiffness Analysis Results
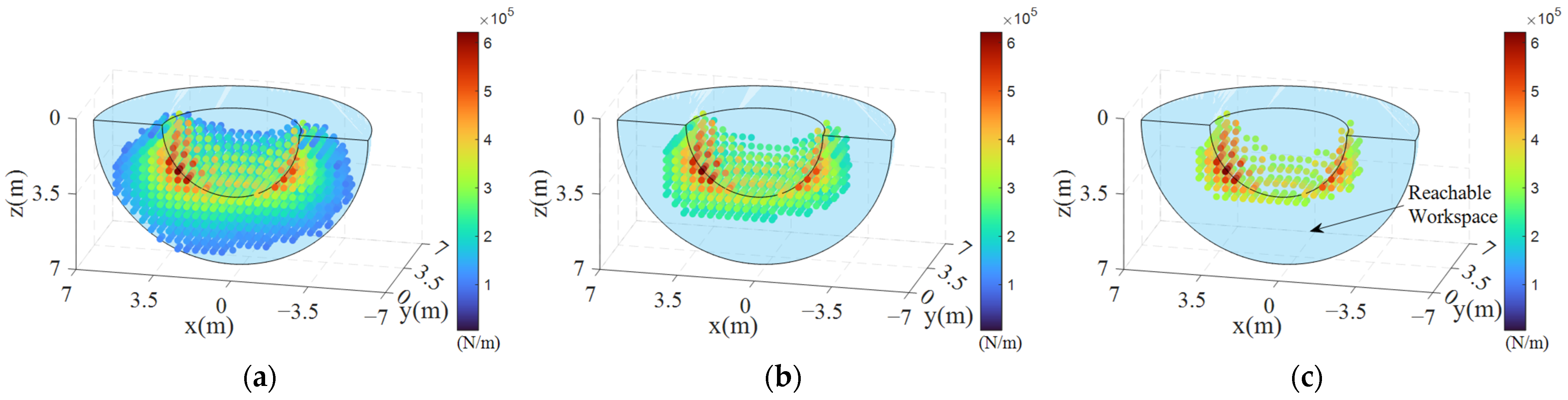
4.3.1. Selection of the UAV Interception Spatial Position
4.3.2. Selection of UAV Recovery Flight Speed
4.3.3. Selection of Cable Material
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.H.; Wang, H.L.; Fan, J.X.; Wang, Y.X.; Wu, J.F. Trajectory stabilization control for aerial recovery of cable-drogue-UAV assembly. Nonlinear Dyn. 2021, 105, 3191–3210. [Google Scholar] [CrossRef]
- Choi, A.J.; Yang, H.H.; Han, J.H. Study on robust aerial docking mechanism with deep learning based drogue detection and docking. Mech. Syst. Signal Process. 2021, 154, 107579. [Google Scholar] [CrossRef]
- Su, Z.K.; Li, C.T.; Liu, Y.H. Anti-disturbance dynamic surface trajectory stabilization for the towed aerial recovery drogue under unknown airflow disturbances. Mech. Syst. Signal Process. 2021, 150, 107342. [Google Scholar] [CrossRef]
- Liu, Y.; Qi, N.; Yao, W.; Zhao, J.; Xu, S. Cooperative Path Planning for Aerial Recovery of a UAV Swarm Using Genetic Algorithm and Homotopic Approach. Appl. Sci. 2020, 10, 4154. [Google Scholar] [CrossRef]
- Voskuijl, M.; Said, M.R.; Pandher, J.; Tooren, M.J.V.; Richards, B. In-flight deployment of morphing UAVs—A method to analyze dynamic stability, controllability and loads. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar]
- Wu, J.; Sun, Y.; Yue, H.; Yang, J.; Yang, F.; Zhao, Y. Design and Optimization of UAV Aerial Recovery System Based on Cable-Driven Parallel Robot. Biomimetics 2024, 9, 111. [Google Scholar] [CrossRef] [PubMed]
- Zarebidoki, M.; Dhupia, J.S.; Xu, W. A Review of Cable-Driven Parallel Robots: Typical Configurations, Analysis Techniques, and Control Methods. IEEE Robot. Autom. Mag. 2022, 29, 89–106. [Google Scholar] [CrossRef]
- Qian, S.; Zi, B.; Shang, W.-W.; Xu, Q.-S. A Review on Cable-driven Parallel Robots. Chin. J. Mech. Eng. 2018, 31, 66. [Google Scholar] [CrossRef]
- Zhang, Z.; Shao, Z.; You, Z.; Tang, X.; Zi, B.; Yang, G.; Gosselin, C.; Caro, S. State-of-the-art on theories and applications of cable-driven parallel robots. Front. Mech. Eng. 2022, 17, 37. [Google Scholar] [CrossRef]
- Kawamura, S.; Kino, H.; Won, C. High-speed manipulation by using parallel wire-driven robots. Robotica 2000, 18, 13–21. [Google Scholar] [CrossRef]
- Cui, Z.; Tang, X. Analysis of stiffness controllability of a redundant cable-driven parallel robot based on its configuration. Mechatronics 2021, 75, 102519. [Google Scholar] [CrossRef]
- Cui, Z.; Tang, X.; Hou, S.; Sun, H. Research on Controllable Stiffness of Redundant Cable-Driven Parallel Robots. IEEE/ASME Trans. Mechatron. 2018, 23, 2390–2401. [Google Scholar] [CrossRef]
- Gueners, D.; Chanal, H.; Bouzgarrou, B.C. Stiffness optimization of a cable driven parallel robot for additive manufacturing. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 843–849. [Google Scholar]
- Max Irvine, H. CABLE Structures; MIT Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Merlet, J.P. A generic numerical continuation scheme for solving the direct kinematics of cable-driven parallel robot with deformable cables. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 4337–4343. [Google Scholar]
- Yuan, H.; Courteille, E.; Deblaise, D. Static and dynamic stiffness analyses of cable-driven parallel robots with non-negligible cable mass and elasticity. Mech. Mach. Theory 2015, 85, 64–81. [Google Scholar] [CrossRef]
- Jung, J. Workspace and Stiffness Analysis of 3D Printing Cable-Driven Parallel Robot with a Retractable Beam-Type End-Effector. Robotics 2020, 9, 65. [Google Scholar] [CrossRef]
- Gao, T.; Wang, Q.; Wang, J.; Su, Y.; Tian, J.; Wu, S. Overall stiffness derivation and enhancement algorithm of a flying cable-driven parallel robot. J. Mech. Sci. Technol. 2024, 38, 873–884. [Google Scholar] [CrossRef]
- Nagarajan, P. Matrix Methods of Structural Analysis, 1st ed.; CRC Press: Boca Raton, FA, USA, 2018; pp. 193–313. [Google Scholar]
- Arsenault, M. Workspace and stiffness analysis of a three-degree-of-freedom spatial cable-suspended parallel mechanism while considering cable mass. Mech. Mach. Theory 2013, 66, 1–13. [Google Scholar] [CrossRef]
- Yuan, H.; Courteille, E.; Deblaise, D. Eastodynamic Analysis of Cable-Driven Parallel Manipulators Considering Dynamic Stiffness of Sagging Cables. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 4055–4060. [Google Scholar]




| Parameter Name | Parameter Symbol |
|---|---|
| Spatial coordinates of endpoint | |
| The tension at endpoint | |
| Cable free length | |
| Young’s modulus of the cable | |
| Cable cross-sectional area | |
| Cable diameter | |
| The aerodynamic forces per unit length | |
| Cable density | |
| Gravity acceleration | |
| Air density at 3 km altitude | |
| Aerodynamic friction coefficient | |
| Aerodynamic drag coefficient | |
| The airflow velocity | |
| Intermediate variables | , , , , , |
| Parameter Name | Parameter Symbol | Value |
|---|---|---|
| Cable diameter | ||
| Cable cross-sectional area | ||
| Young’s modulus | ||
| Cable density | ||
| Span 1 | ||
| Span 2 | ||
| Telescopic rod weight | ||
| Telescopic rod diameter | ||
| Telescopic rod elongation length | ||
| Telescopic rod shortening length | ||
| Telescopic rod elongation length | ||
| Axial stiffness of the telescopic rod | ||
| Air density at 3 km altitude | ||
| Aerodynamic friction coefficient | ||
| Aerodynamic drag coefficient | ||
| Carrier aircraft flight speed | ||
| Gravity acceleration |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Yue, H.; Pan, X.; Wang, Y.; Zhao, Y.; Yang, F. Stiffness Analysis of Cable-Driven Parallel Robot for UAV Aerial Recovery System. Actuators 2024, 13, 343. https://doi.org/10.3390/act13090343
Wu J, Yue H, Pan X, Wang Y, Zhao Y, Yang F. Stiffness Analysis of Cable-Driven Parallel Robot for UAV Aerial Recovery System. Actuators. 2024; 13(9):343. https://doi.org/10.3390/act13090343
Chicago/Turabian StyleWu, Jun, Honghao Yue, Xueting Pan, Yanbing Wang, Yong Zhao, and Fei Yang. 2024. "Stiffness Analysis of Cable-Driven Parallel Robot for UAV Aerial Recovery System" Actuators 13, no. 9: 343. https://doi.org/10.3390/act13090343





