Energy-Based Adaptive Control for Variable-Rope-Length Double-Pendulum Ship-Borne Cranes: A Disturbance Rejection Stabilization Controller Without Overshoot
Abstract
:1. Introduction
2. Dynamic Model Transformation
3. Controller Design
4. Closed-Loop System Stability Analysis
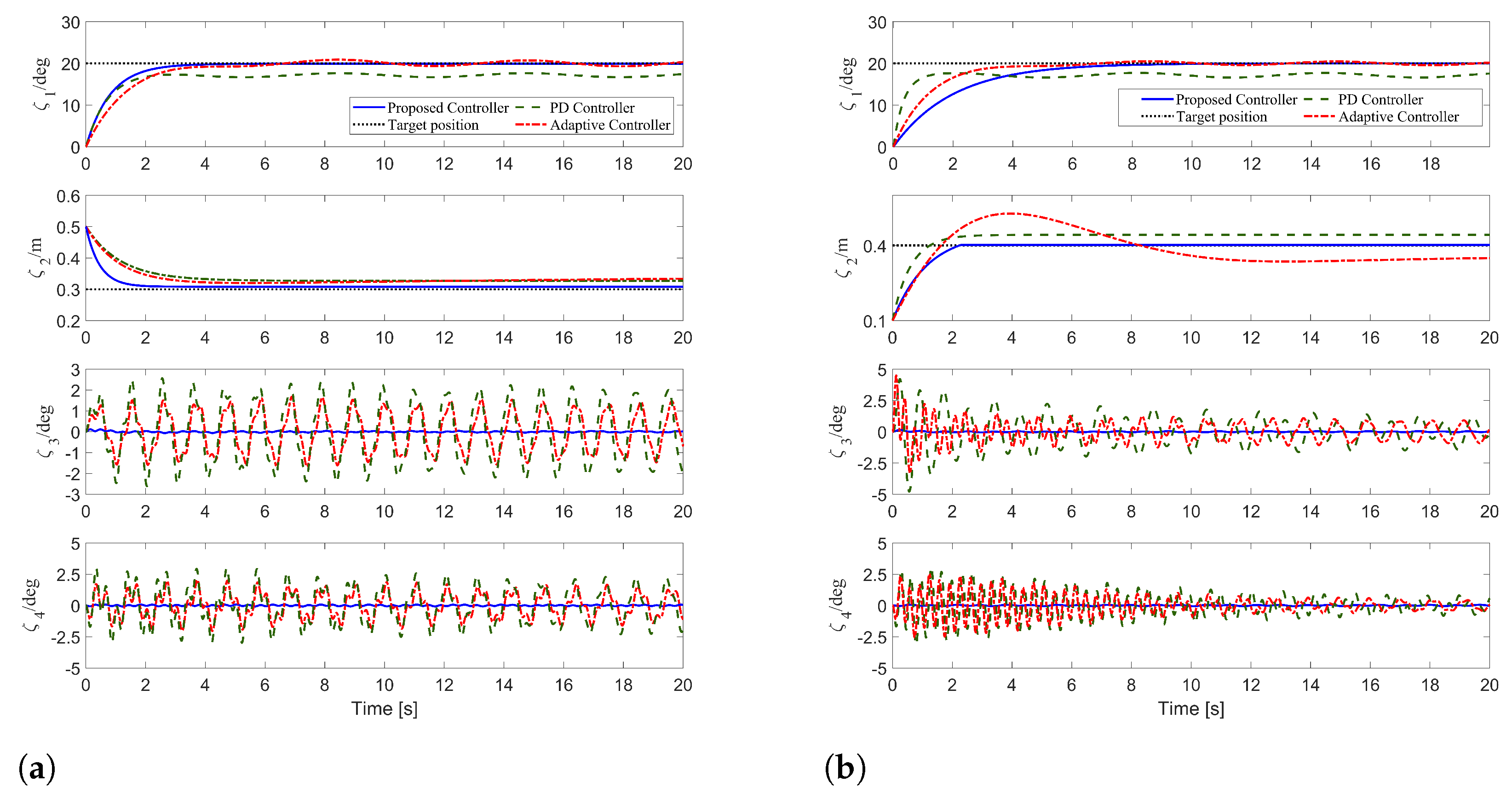
5. Simulation Results and Analysis
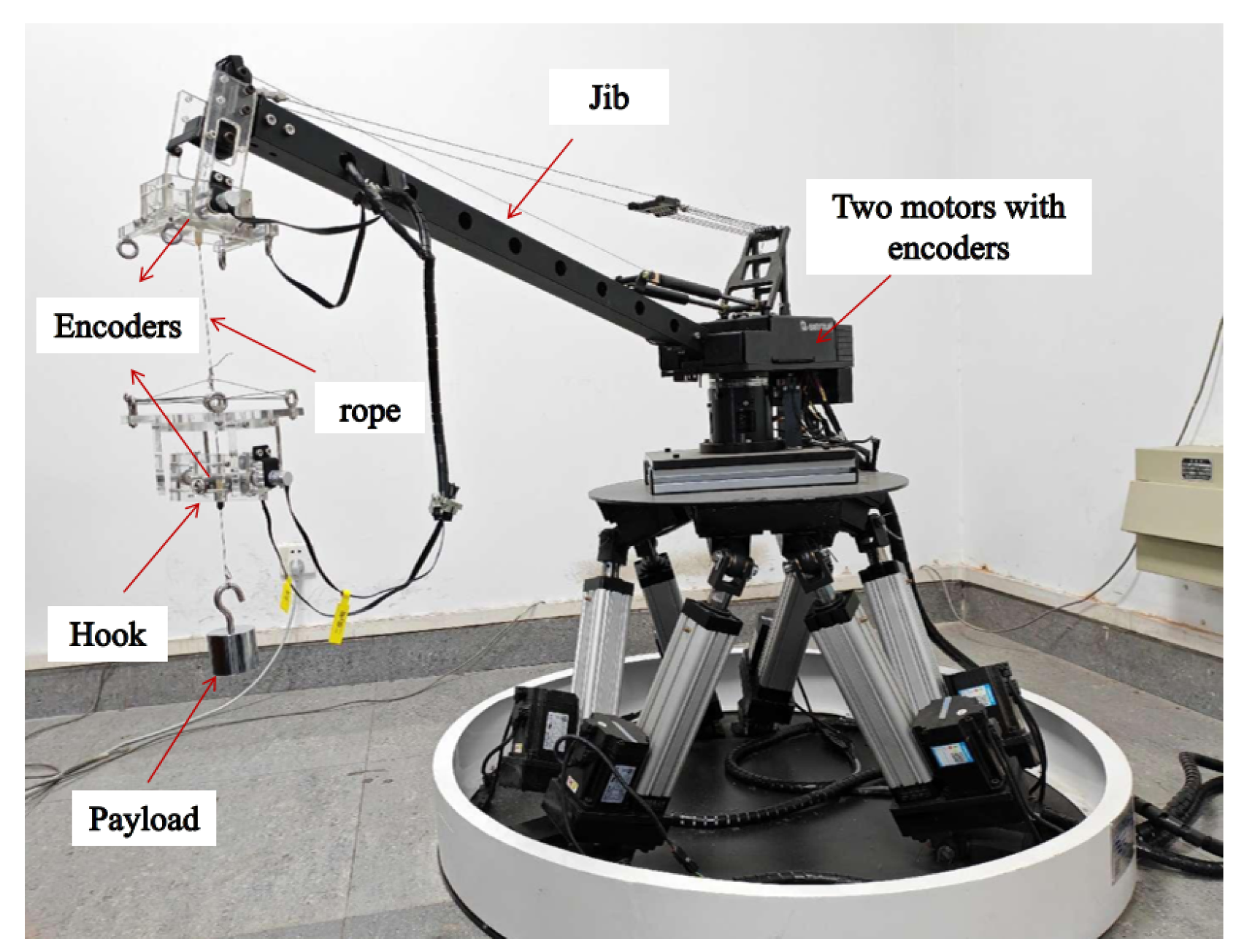
6. Experimental Results and Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, N.; Liang, X. Nonlinear stable transportation control for double-pendulum shipboard cranes with ship-motion-induced disturbances. IEEE Trans. Ind. Electron. 2019, 66, 9467–9479. [Google Scholar] [CrossRef]
- Maghsoudi, M.J.; Mohamed, Z.; Husain, A.R. An optimal performance control scheme for a 3D crane. Mech. Syst. Signal Process. 2016, 66, 756–768. [Google Scholar] [CrossRef]
- Stein, A.; Singh, T. Minimum time control of a gantry crane system with rate constraints. Mech. Syst. Signal Process. 2023, 190, 110120. [Google Scholar] [CrossRef]
- Rigatos, G. Nonlinear optimal control for the underactuated double-pendulum overhead crane. J. Vib. Eng. Technol. 2024, 12, 1203–1223. [Google Scholar] [CrossRef]
- Zhong, K.; Qian, Y. Time-optimal anti-swing trajectory planning of double pendulum crane based on chebyshev pseudo-spectrum method. In Proceedings of the International Conference on Applied Nonlinear Dynamics, Vibration and Control, Hong Kong, China, 4–6 December 2023; Springer Nature: Singapore, 2023; pp. 541–553. [Google Scholar]
- Cong, Y.; Li, G.; Li, J.; Tian, J.; Ma, X. Time-delay-based sliding mode tracking control for cooperative dual marine lifting system subject to sea wave disturbances. Actuators 2024, 13, 491. [Google Scholar] [CrossRef]
- Chen, H.; Tang, S.; Han, J. High-order sliding mode control of a doubly salient permanent magnet machine driving marine current turbine. J. Ocean Eng. Sci. 2021, 6, 12–20. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, H.; Qian, Y. Reinforcement Learning Strategy-Based Adaptive Tracking Control for Underactuated Dual Ship-Mounted Cranes: Theoretical Design and Hardware Experiments. IEEE Trans. Ind. Electron. 2024; Early Access. [Google Scholar] [CrossRef]
- ur Rehman, S.M.F.; Mohamed, Z.; Husain, A.R. Input shaping with an adaptive scheme for swing control of an underactuated tower crane under payload hoisting and mass variations. Mech. Syst. Signal Process. 2022, 175, 109106. [Google Scholar] [CrossRef]
- Zhao, W.; Ebbesen, M.; Hansen, M.; Andersen, T. Experimental verification of a two-motor-two-pump motor-controlled hydraulic cylinder with throttle-free passive load-holding capability in four-quadrant operations. Actuators 2024, 13, 372. [Google Scholar] [CrossRef]
- Wu, Q.; Sun, N.; Wang, X. Equivalent rope length-based trajectory planning for double pendulum bridge cranes with distributed mass payloads. Actuators 2022, 11, 25. [Google Scholar] [CrossRef]
- Zhang, G.; Li, J.; Chang, T. Autonomous navigation and control for a sustainable vessel: A wind-assisted strategy. Sustain. Horizons 2025, 13, 100117. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, G. Prescribed performance fault-tolerant control of nonlinear systems via actuator switching. IEEE Trans. Fuzzy Syst. 2023, 32, 1013–1022. [Google Scholar] [CrossRef]
- Li, L.; Amer, A.; Zhu, X. Numerical analysis of an over-boarding operation for a subsea template. J. Ocean Eng. Sci. 2021, 6, 146–159. [Google Scholar] [CrossRef]
- Zhao, B.; Ouyang, H.; Iwasaki, M. Motion trajectory tracking and sway reduction for double-pendulum overhead cranes using improved adaptive control without velocity feedback. IEEE/ASME Trans. Mechatronics 2021, 27, 3648–3659. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Cabecinhas, D. Prescribed performance path following control of USVs via an output-based threshold rule. IEEE Trans. Veh. Technol. 2023, 73, 6171–6182. [Google Scholar] [CrossRef]
- Ouyang, H.; Xu, X.; Zhang, G. Energy-shaping-based nonlinear controller design for rotary cranes with double-pendulum effect considering actuator saturation. Autom. Constr. 2020, 111, 103054. [Google Scholar] [CrossRef]
- Sun, Z.; Ouyang, H. Adaptive fuzzy tracking control for vibration suppression of tower crane with distributed payload mass. Autom. Constr. 2022, 142, 104521. [Google Scholar] [CrossRef]
- Shi, H.; Huang, J.; Bai, X. Nonlinear anti-swing control of underactuated tower crane based on improved energy function. Int. J. Control Autom. Syst. 2021, 19, 3967–3982. [Google Scholar] [CrossRef]
- Li, G.; Ma, X.; Li, Y. Adaptive anti-swing control for 7-DOF overhead crane with double spherical pendulum and varying cable length. IEEE Trans. Autom. Sci. Eng. 2023, 21, 5240–5251. [Google Scholar] [CrossRef]
- Qiang, H.; Sun, Y.; Lyu, J. Anti-sway and positioning adaptive control of a double-pendulum effect crane system with neural network compensation. Front. Robot. AI 2021, 8, 639734. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Verma, A.; Ataei, B. Model-free anti-swing control of complex-shaped payload with offshore floating cranes and a large number of lift wires. Ocean Eng. 2021, 228, 108868. [Google Scholar] [CrossRef]
- Zhao, T.; Sun, M.; Wang, S. Dynamic analysis and robust control of ship-mounted crane with multi-cable anti-swing system. Ocean Eng. 2024, 291, 116376. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, N.; Chen, H. New adaptive dynamic output feedback control of double-pendulum ship-mounted cranes with accurate gravitational compensation and constrained inputs. IEEE Trans. Ind. Electron. 2021, 69, 9196–9205. [Google Scholar] [CrossRef]
- Qiang, H.; Xie, S.; Xu, Z. An enhanced sliding mode control method for wave compensation system of ship-mounted cranes with roll motions and parametric uncertainties. J. Mar. Sci. Technol. 2020, 28, 6. [Google Scholar]
- Yang, T.; Sun, N.; Chen, H. Neural network-based adaptive antiswing control of an underactuated ship-mounted crane with roll motions and input dead zones. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 901–914. [Google Scholar] [CrossRef]
- Kuchler, S.; Mahl, T.; Neupert, J. Active control for an offshore crane using prediction of the vessel’s motion. IEEE/ASME Trans. Mechatronics 2010, 16, 297–309. [Google Scholar] [CrossRef]
- Guo, B.; Chen, Y. Fuzzy robust fault-tolerant control for offshore ship-mounted crane system. Inf. Sci. 2020, 526, 119–132. [Google Scholar] [CrossRef]
- Li, G.; Ma, X.; Li, Y. Robust Command Shaped Vibration Control for Stacker Crane Subject to Parameter Uncertainties and External Disturbances. IEEE Trans. Ind. Electron. 2024, 71, 14740–14752. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, T.; Zhai, M. Ship-Mounted Cranes Hoisting Underwater Payloads: Transportation Control with Guaranteed Constraints on Overshoots and Swing. IEEE Trans. Ind. Inform. 2023, 19, 9968–9978. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, W.; Long, Z. Active pendulation control of hoisting systems of ship-mounted cranes under ocean wave excitations: Principle and experimental study. Mech. Syst. Signal Process. 2025, 222, 111802. [Google Scholar] [CrossRef]
- Kim, T.; Nguyen, L.; Dinh, X. Adaptive hierarchical sliding mode control design for 3D ship-mounted container crane with saturating actuators. J. Control. Autom. Electr. Syst. 2022, 33, 1643–1658. [Google Scholar] [CrossRef]
- Hu, D.; Qian, Y.; Fang, Y. Modeling and nonlinear energy-based anti-swing control of underactuated dual ship-mounted crane systems. Nonlinear Dyn. 2021, 106, 323–338. [Google Scholar] [CrossRef]
- Wang, F.; Li, G.; Jiang, W. Collaborative heave compensation control of dual ship-mounted lifting arm system based on incremental model predictive control. In Proceedings of the 2024 14th Asian Control Conference (ASCC), Dalian, China, 5–8 July 2024; pp. 1–6. [Google Scholar]
- Li, G.; Ma, X.; Li, Z. Energy Shaping Based Nonlinear Anti-Swing Controller for Double-Pendulum Rotary Crane with Distributed-Mass Beams. In Proceedings of the 2022 IEEE International Conference on Real-time Computing and Robotics (RCAR), Guiyang, China, 17–22 July 2022; pp. 207–212. [Google Scholar]
- Kim, D.; Park, Y. Tracking control in xy plane of an offshore container crane. J. Vib. Control 2017, 23, 469–483. [Google Scholar] [CrossRef]
- Chen, S.; Xie, P.; Liao, J. Cascade NMPC-PID control strategy of active heave compensation system for ship-mounted offshore crane. Ocean Eng. 2024, 302, 117648. [Google Scholar] [CrossRef]
- Bozkurt, B.; Ertogan, M. Heave and horizontal displacement and anti-sway control of payload during ship-to-ship load transfer with an offshore crane on very rough sea conditions. Ocean Eng. 2023, 267, 113309. [Google Scholar] [CrossRef]
- Bae, J.; Cha, J. Heave reduction of payload through crane control based on deep reinforcement learning using dual offshore cranes. J. Comput. Des. Eng. 2023, 10, 414–424. [Google Scholar] [CrossRef]
- Zhang, H.; Qian, Y. Adaptive nonlinear antiswing control for underactuated dual ship-Mounted cranes with sea wave cisturbances. In Proceedings of the IEEE 2023 42nd Chinese Control Conference (CCC), Tianjin, China, 24–26 July 2023; pp. 338–343. [Google Scholar]




| Control Method | s | s | deg |
|---|---|---|---|
| Proposed controller | 10.78 | 2.21 | 0 |
| PD controller | / | / | 0.43 |
| Adaptive controller | 8.84 | / | 0.80 |
| Proposed controller | 0.006 | 0.12 | 0.22 |
| PD controller | 0.030 | 4.11 | 3.04 |
| Adaptive controller | 0.043 | 0.96 | 3.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, K.; Qian, Y.; Chen, H.; Wu, S. Energy-Based Adaptive Control for Variable-Rope-Length Double-Pendulum Ship-Borne Cranes: A Disturbance Rejection Stabilization Controller Without Overshoot. Actuators 2025, 14, 52. https://doi.org/10.3390/act14020052
Zhong K, Qian Y, Chen H, Wu S. Energy-Based Adaptive Control for Variable-Rope-Length Double-Pendulum Ship-Borne Cranes: A Disturbance Rejection Stabilization Controller Without Overshoot. Actuators. 2025; 14(2):52. https://doi.org/10.3390/act14020052
Chicago/Turabian StyleZhong, Ken, Yuzhe Qian, He Chen, and Shujie Wu. 2025. "Energy-Based Adaptive Control for Variable-Rope-Length Double-Pendulum Ship-Borne Cranes: A Disturbance Rejection Stabilization Controller Without Overshoot" Actuators 14, no. 2: 52. https://doi.org/10.3390/act14020052
APA StyleZhong, K., Qian, Y., Chen, H., & Wu, S. (2025). Energy-Based Adaptive Control for Variable-Rope-Length Double-Pendulum Ship-Borne Cranes: A Disturbance Rejection Stabilization Controller Without Overshoot. Actuators, 14(2), 52. https://doi.org/10.3390/act14020052







