The Design and Analysis of a Lightweight Robotic Arm Based on a Load-Adaptive Hoisting Mechanism
Abstract
1. Introduction
2. Design Principles and Characteristics of the Mechanism
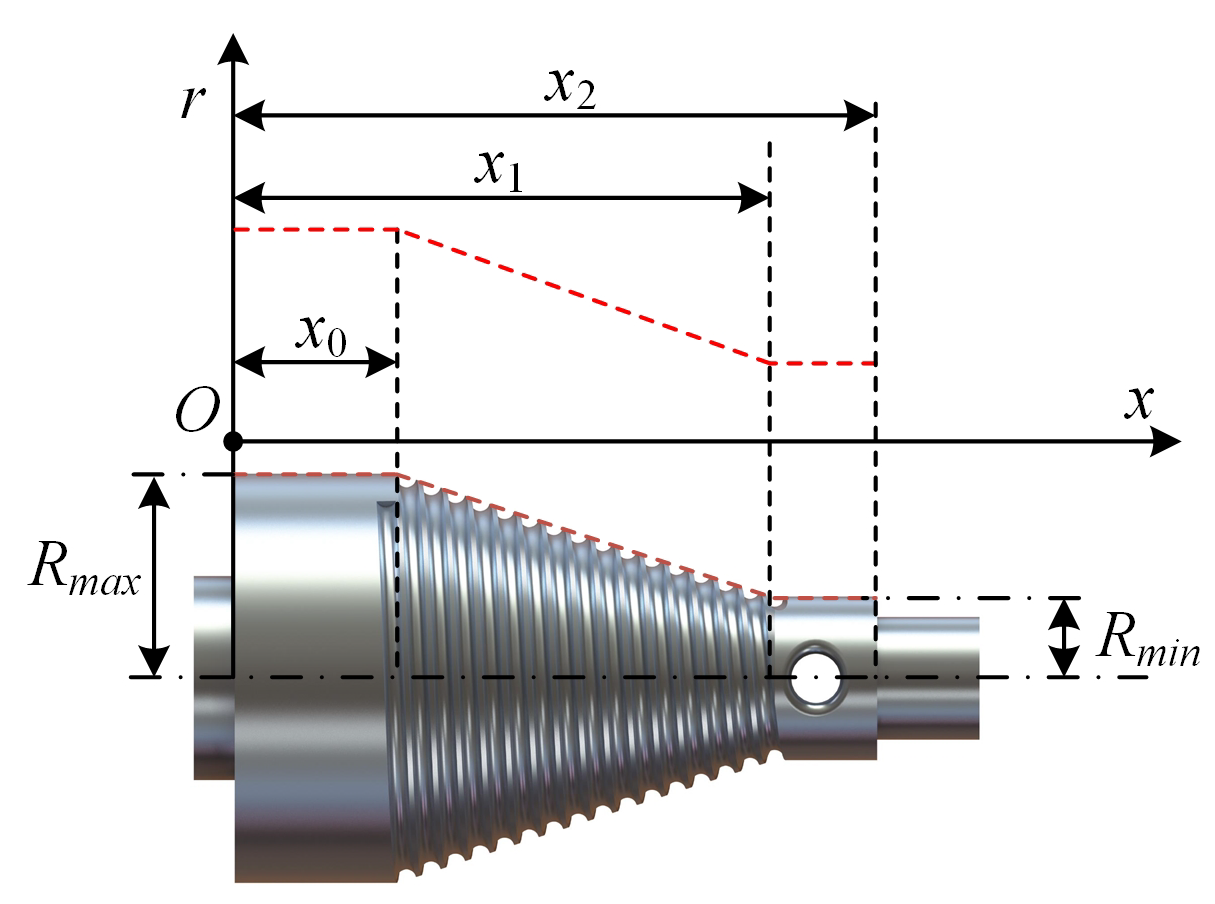
2.1. Improved Load-Adaptive Hoisting Mechanism
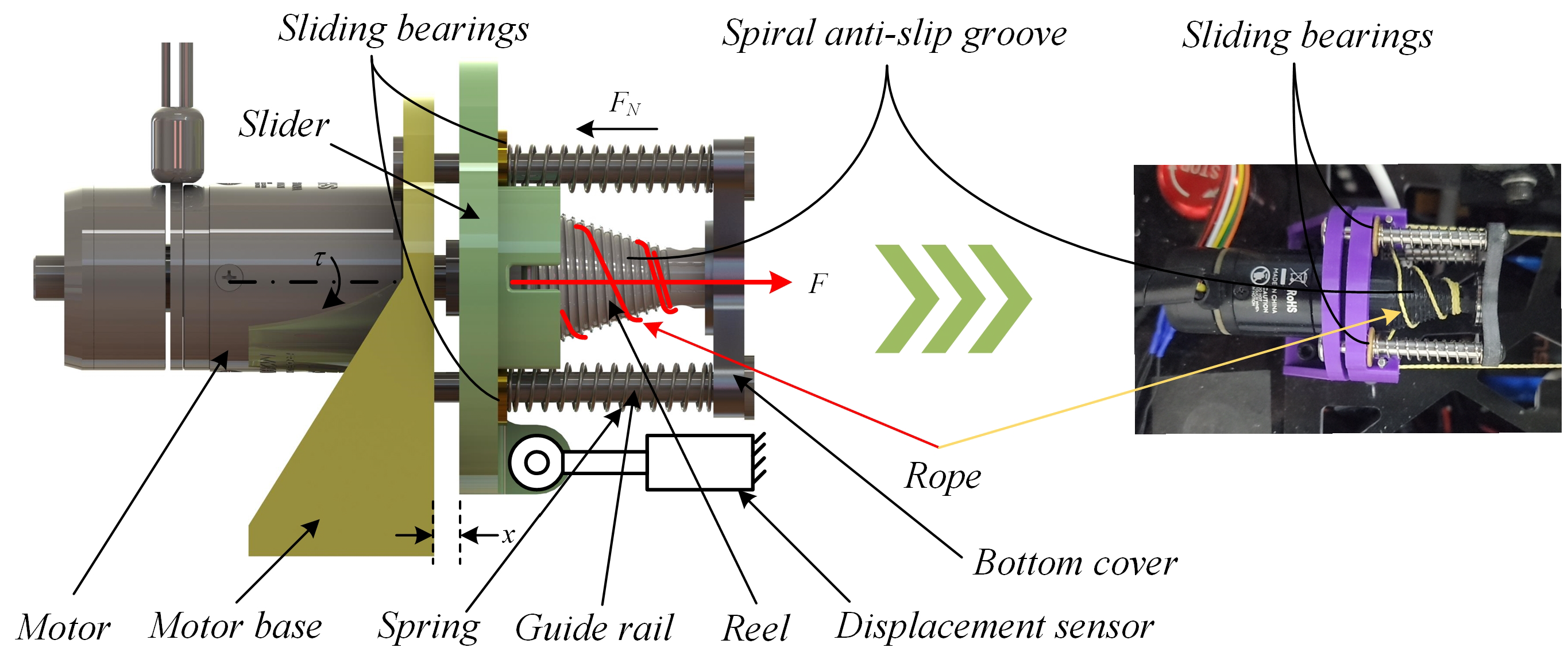
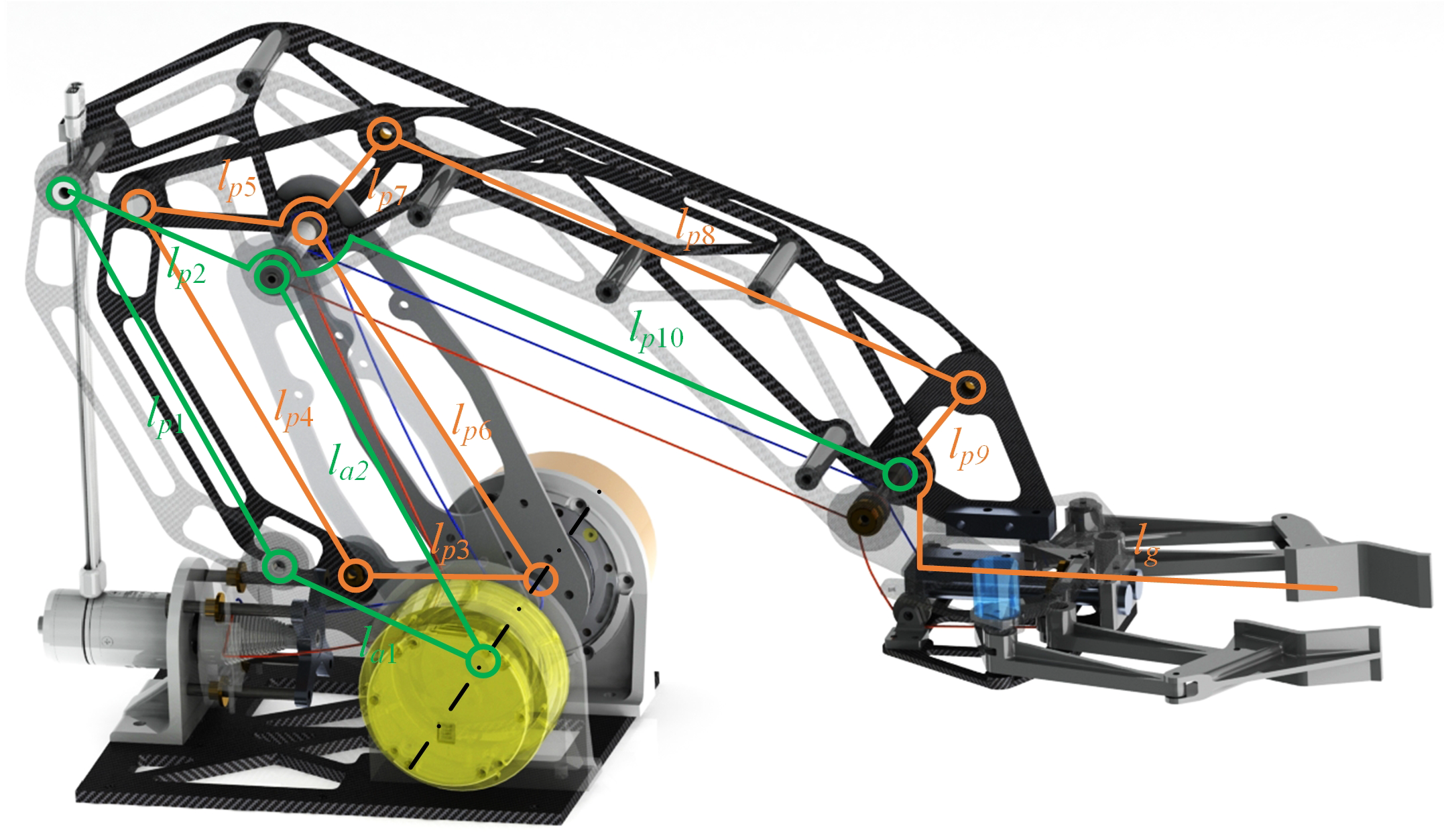
2.2. Robotic Arm Structure
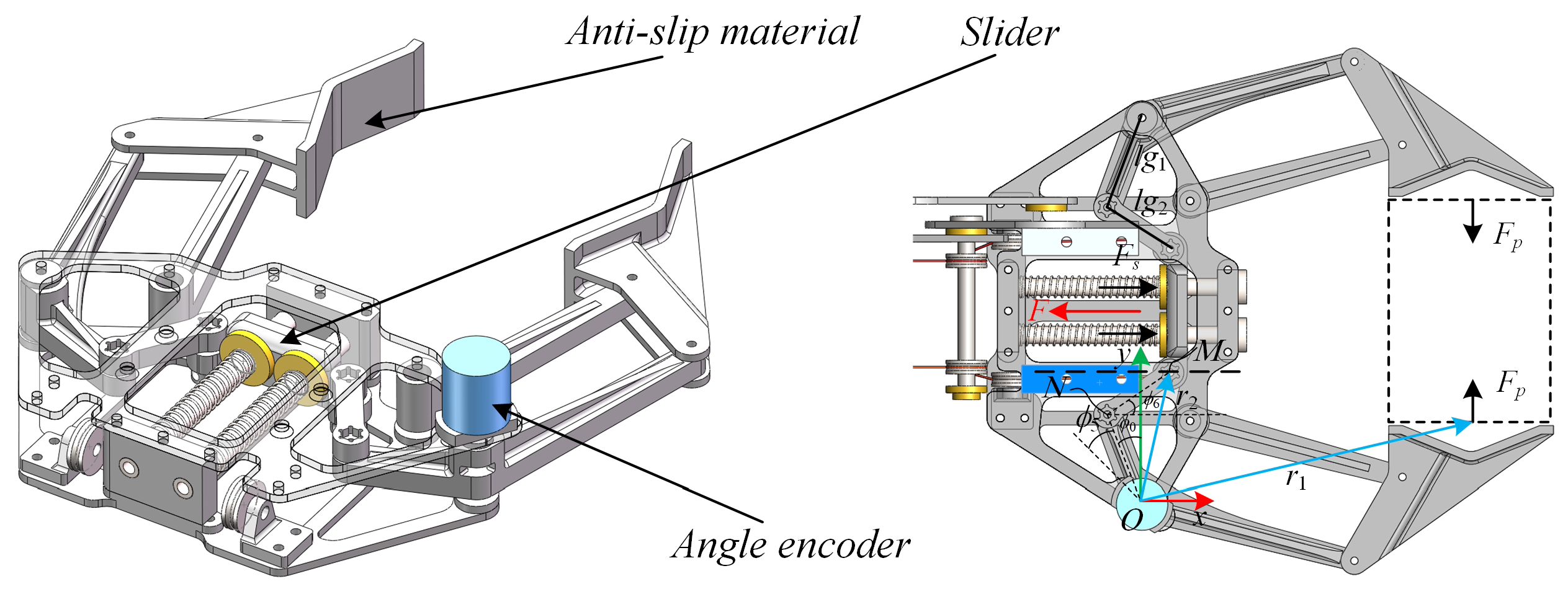
2.3. Gripper Structure
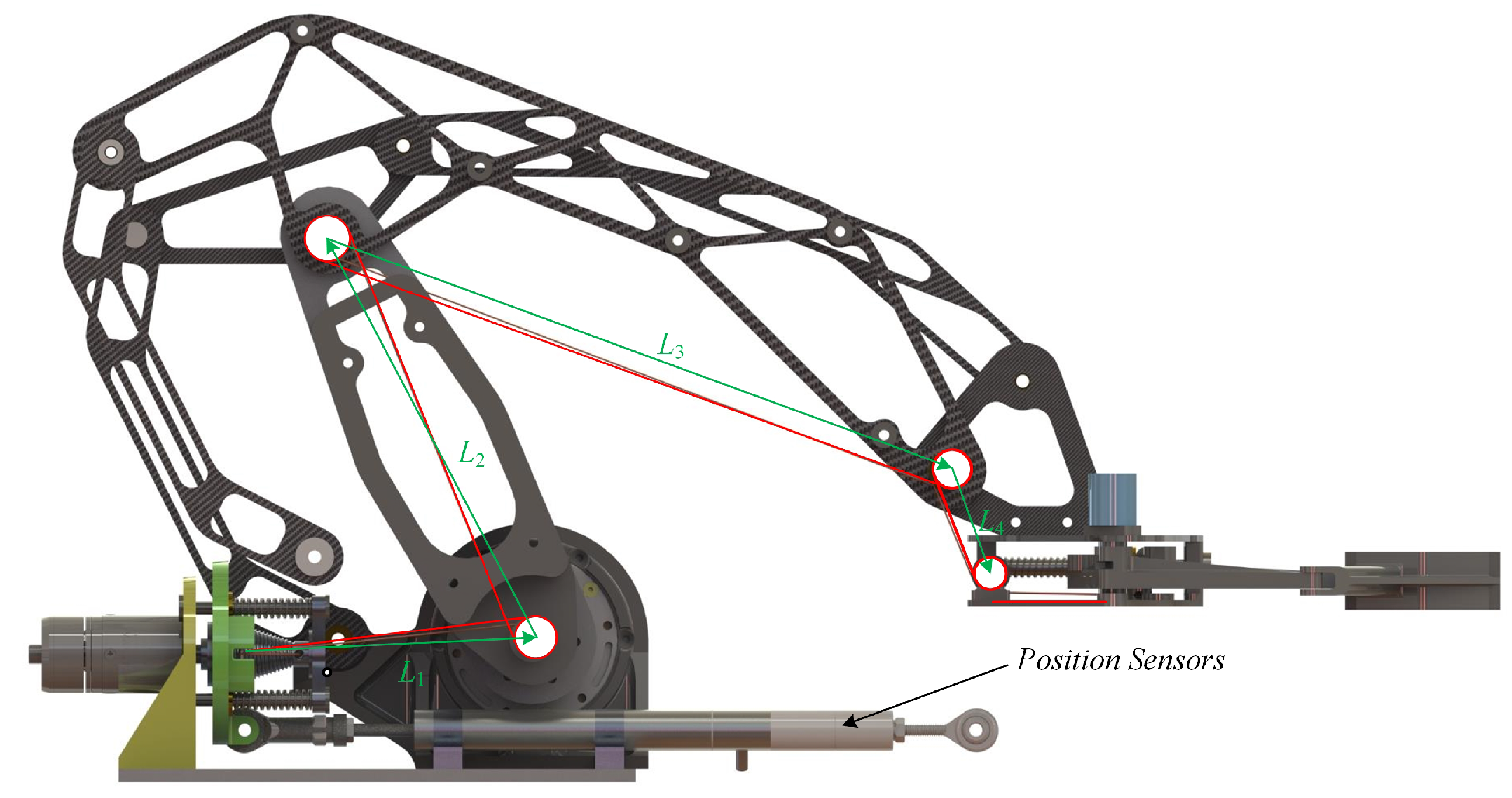
2.4. Constant Line Length
2.5. Sensor Layout
3. Kinematic Analysis of the Robotic Arm
3.1. Motion Characteristics of the Improved Load-Adaptive Hoisting Mechanism
3.2. Analysis of the Robotic Arm’s Motion Characteristics
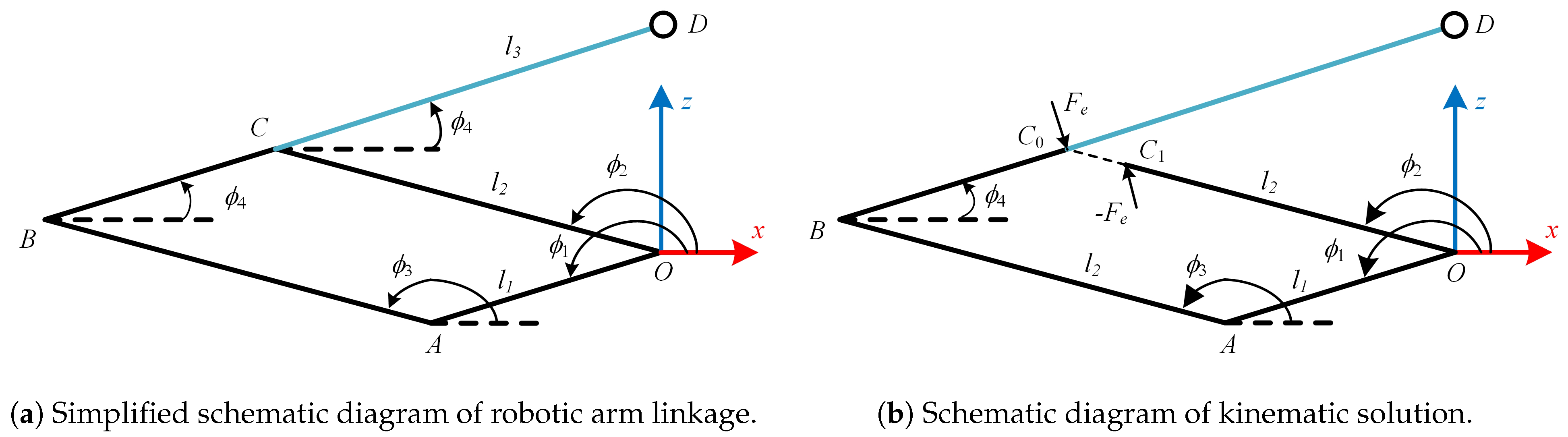
3.2.1. Kinematic Analysis
3.2.2. Dynamics Analysis
3.2.3. Gripper Force Analysis
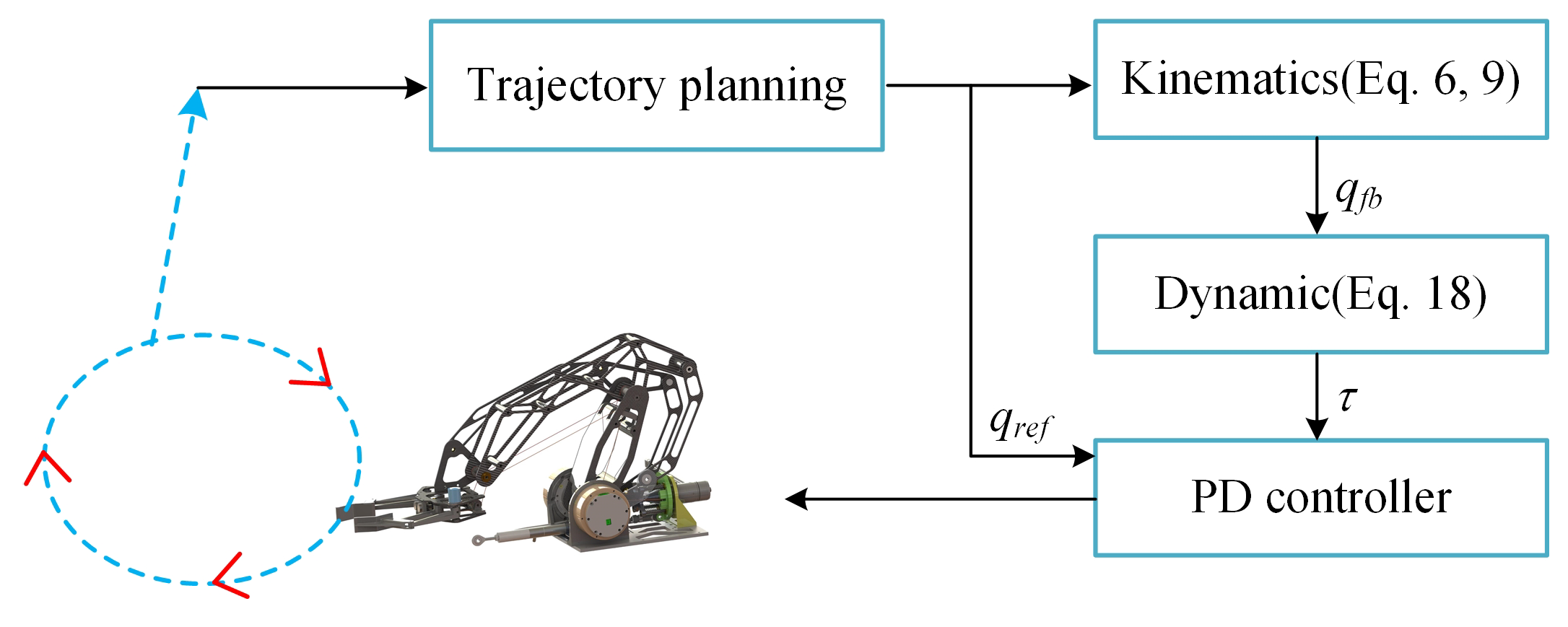
4. Experimental Validation
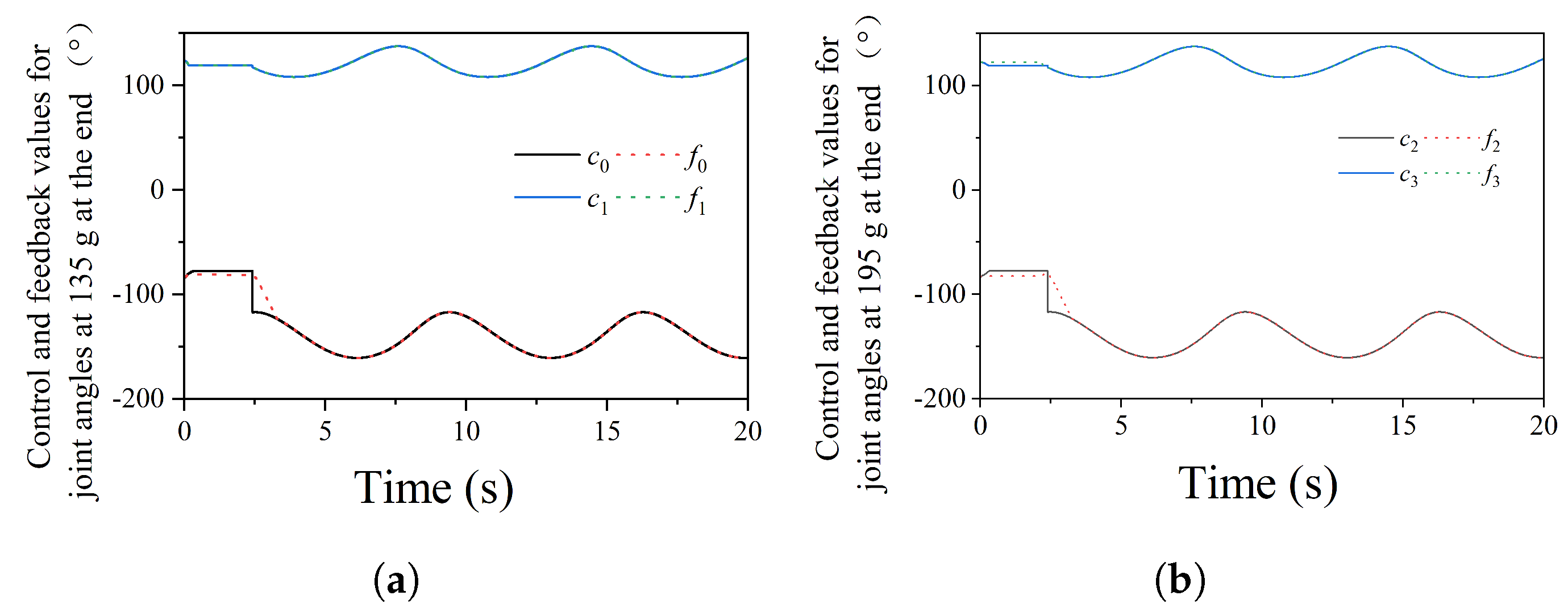
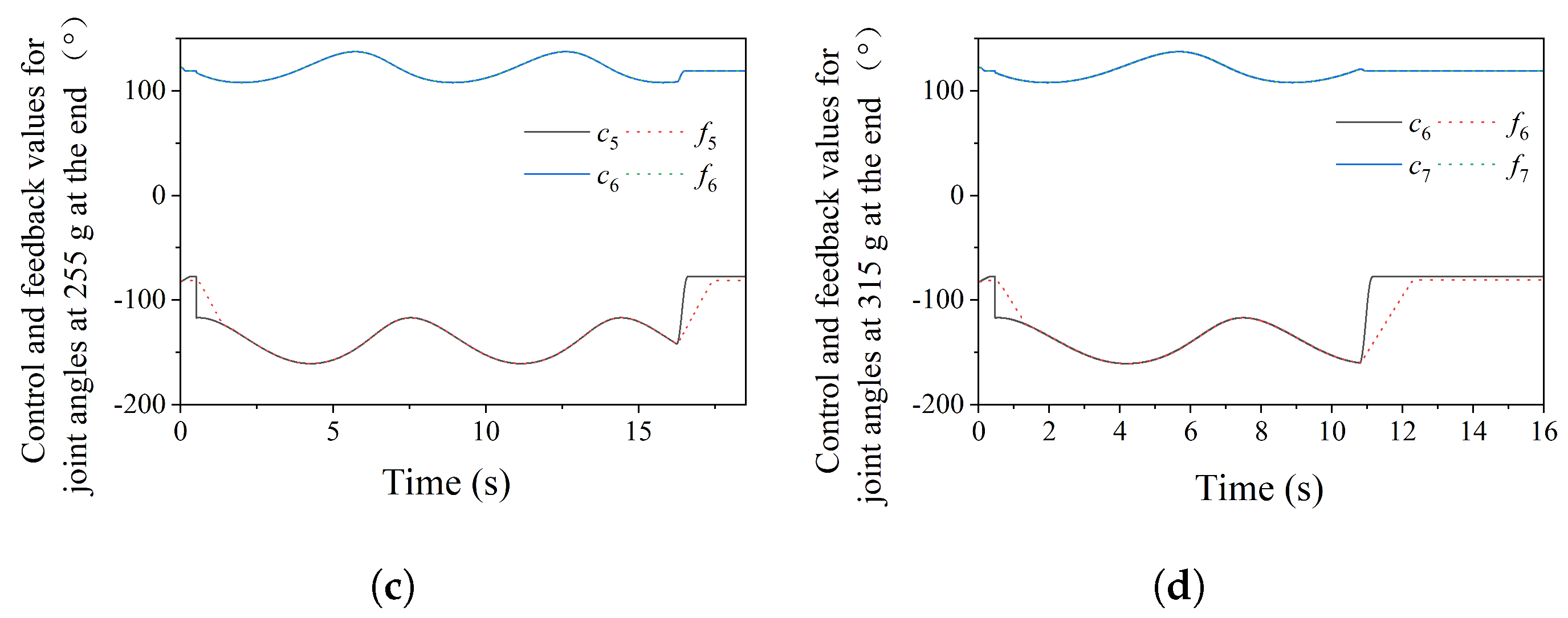
4.1. Motion Tracking of Robotic Arm
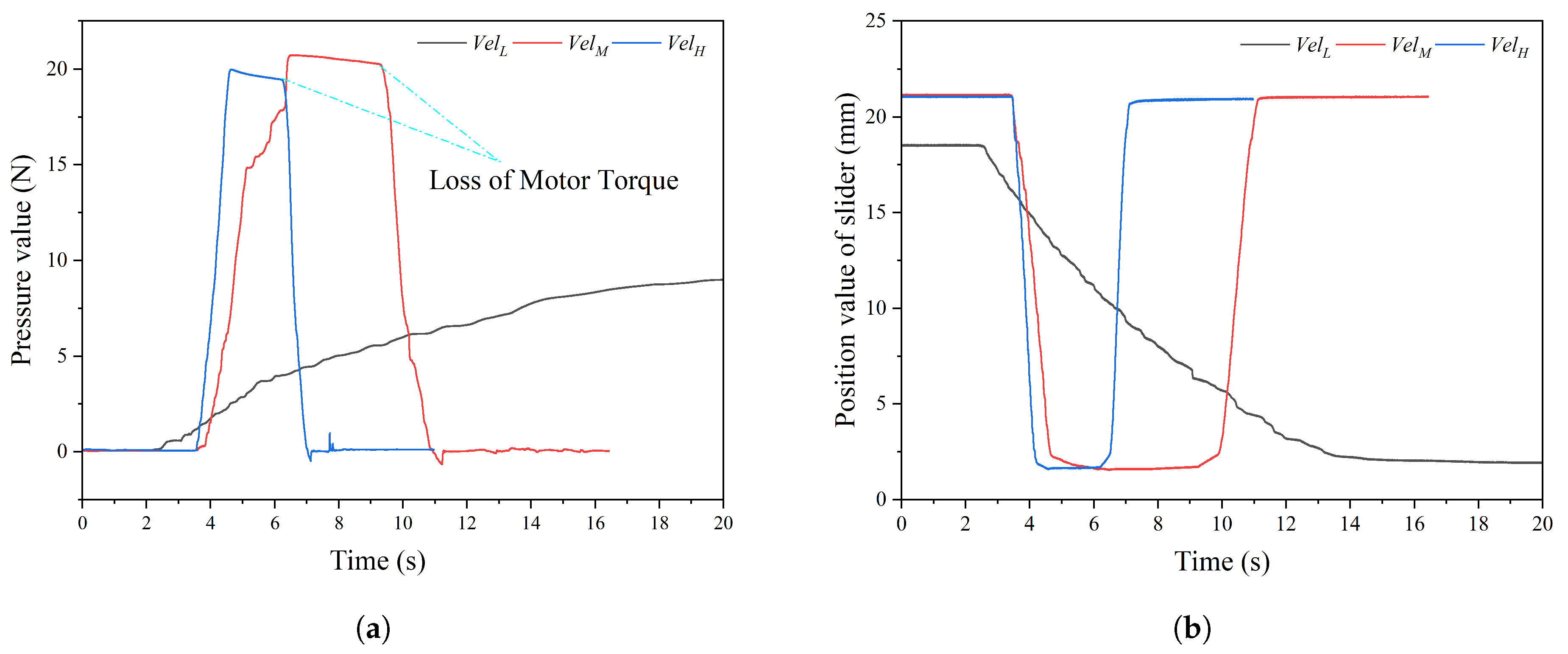
4.2. Slider Position Corresponding to Different Gripper Forces
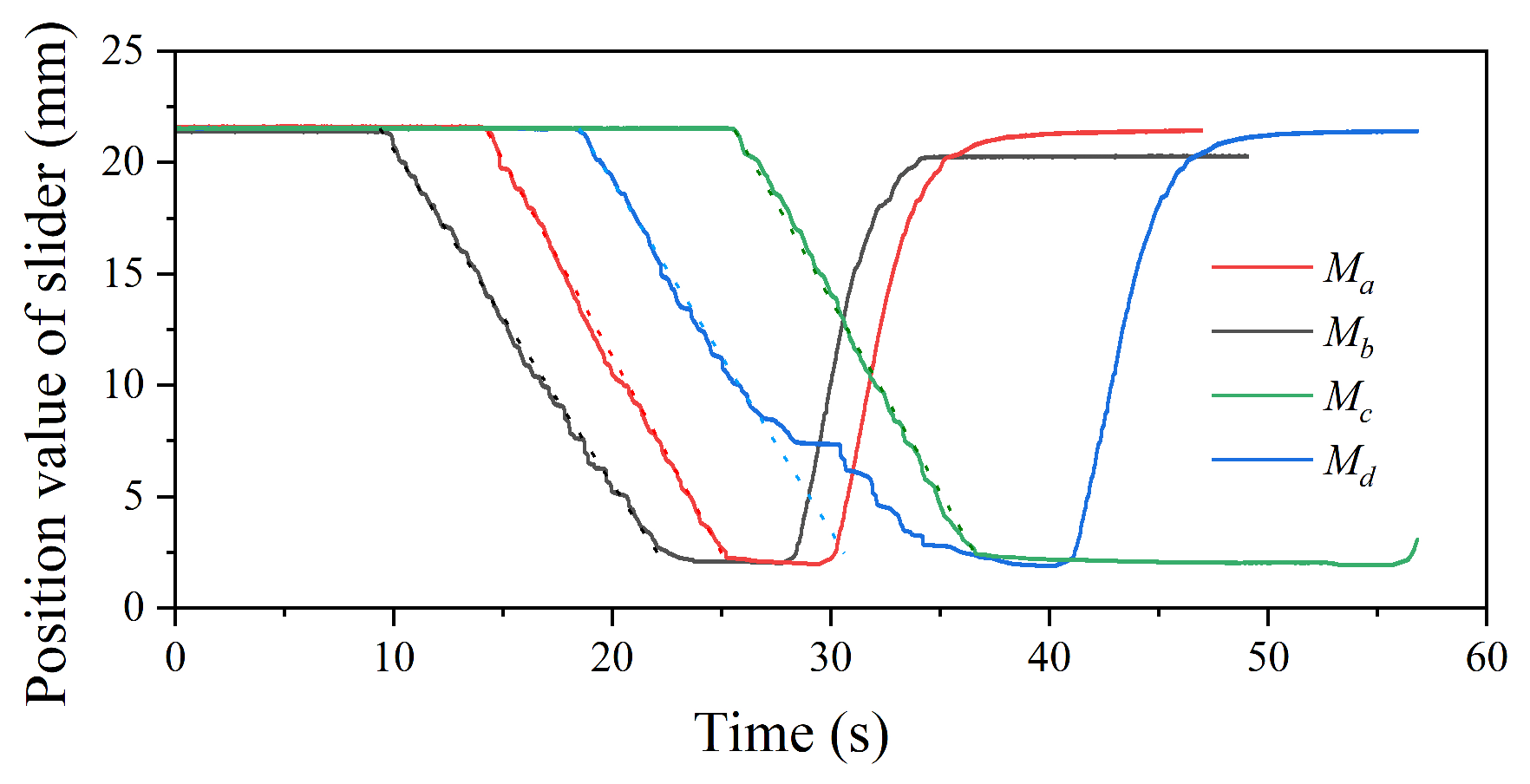
4.3. Motion Characteristics of the Slider When Grasping Objects with Different Stiffness
4.4. Force-Position Mixed Grasping Experiment
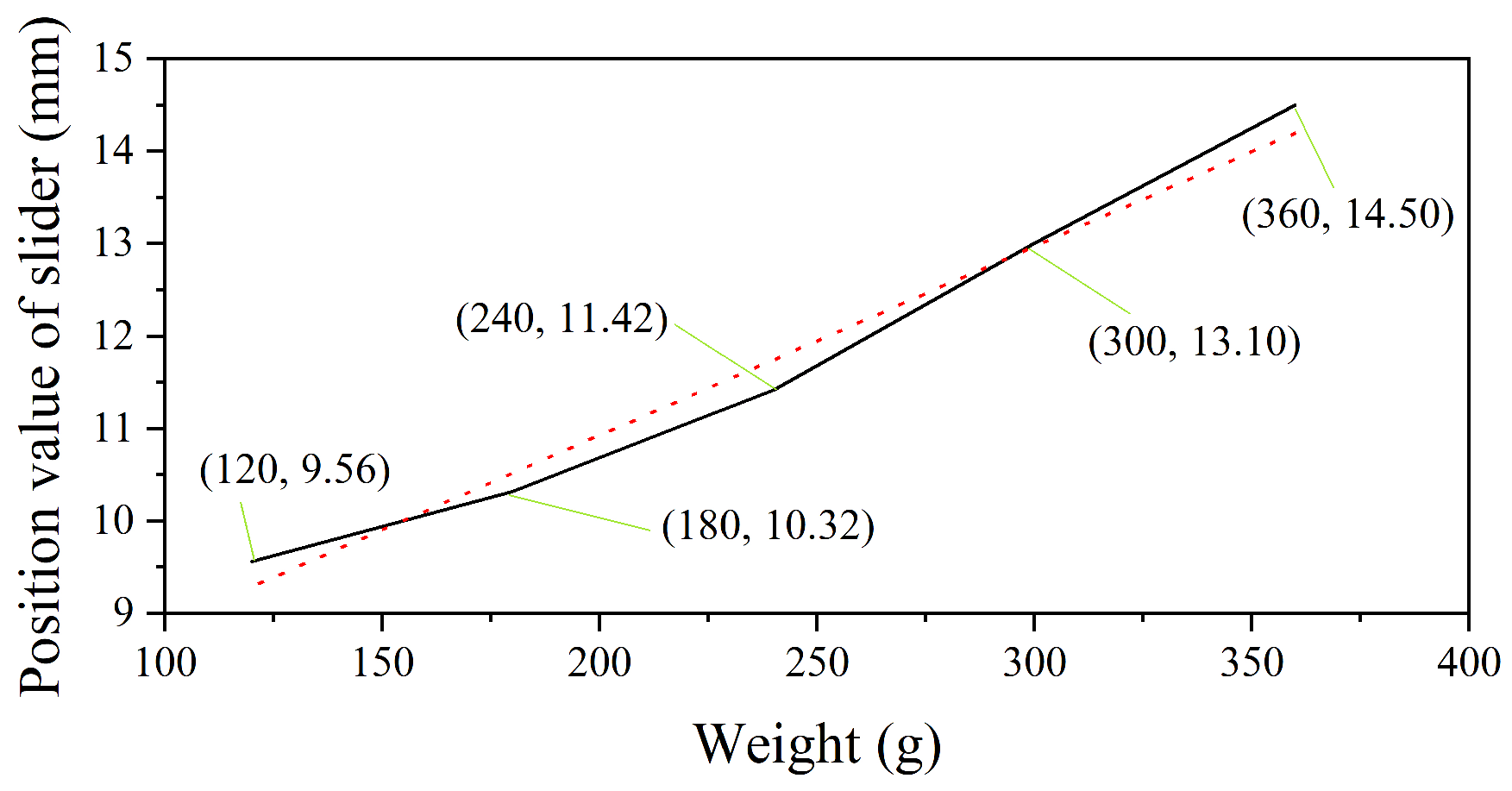
4.5. Slider Position Under Different Load Weights
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, F.; Xu, W.; Zhang, H.; Wang, Y.; Cao, J.; Wang, M.Y.; Ren, H.; Zhu, J.; Zhang, Y. Topology optimized design, fabrication, and characterization of a soft cable-driven gripper. IEEE Robot. Autom. Lett. 2018, 3, 2463–2470. [Google Scholar] [CrossRef]
- Shintake, J.; Cacucciolo, V.; Floreano, D.; Shea, H. Soft robotic grippers. Adv. Mater. 2018, 30, 1707035. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Lu, Z.; Xiao, Y.; Zhao, Y.; Jiang, Q.; Shi, X. Design and Control of a Multi-locomotion Parallel-Legged Bipedal Robot. IEEE Robot. Autom. Lett. 2024, 9, 1993–2000. [Google Scholar] [CrossRef]
- Hubicki, C.; Grimes, J.; Jones, M.; Renjewski, D.; Spröwitz, A.; Abate, A.; Hurst, J. Atrias: Design and validation of a tether-free 3d-capable spring-mass bipedal robot. Int. J. Robot. Res. 2016, 35, 1497–1521. [Google Scholar] [CrossRef]
- Dämmer, G.; Gablenz, S.; Neumann, R.; Major, Z. Design, Topology Optimization, and Additive Manufacturing of a Pneumatically Actuated Lightweight Robot. Actuators 2023, 12, 266. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, R.; Xiao, Y.; Liu, T.; Liu, C.; Zhao, H. A load-adaptive hoisting mechanism based on spring-loaded rope and variable radius reel. Adv. Robot. 2023, 37, 1520–1531. [Google Scholar] [CrossRef]
- Wang, Z.; Torigoe, Y.; Hirai, S. A prestressed soft gripper: Design, modeling, fabrication, and tests for food handling. IEEE Robot. Autom. Lett. 2017, 2, 1909–1916. [Google Scholar] [CrossRef]
- Hernandez, J.; Sunny, M.S.H.; Sanjuan, J.; Rulik, I.; Zarif, M.I.I.; Ahamed, S.I.; Ahmed, H.U.; Rahman, M.H. Current designs of robotic arm grippers: A comprehensive systematic review. Robotics 2023, 12, 5. [Google Scholar] [CrossRef]
- Hu, Q.; Dong, E.; Sun, D. Soft gripper design based on the integration of flat dry adhesive, soft actuator, and microspine. IEEE Trans. Robot. 2021, 37, 1065–1080. [Google Scholar] [CrossRef]
- Yao, P.; Zhou, K.; Lin, Y.; Tang, Y. Light-weight topological optimization for upper arm of an industrial welding robot. Metals 2019, 9, 1020. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Li, L.; Meng, Y.; Tian, Y. Load sharing design of a multi-legged adaptable gripper with Gecko-inspired controllable adhesion. IEEE Robot. Autom. Lett. 2021, 6, 8482–8489. [Google Scholar] [CrossRef]
- Zhakypov, Z.; Heremans, F.; Billard, A.; Paik, J. An origami-inspired reconfigurable suction gripper for picking objects with variable shape and size. IEEE Robot. Autom. Lett. 2018, 3, 2894–2901. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, H.; Yuan, H.; Liang, B. A compliant adaptive gripper and its intrinsic force sensing method. IEEE Trans. Robot. 2021, 37, 1584–1603. [Google Scholar] [CrossRef]
- Jeong, S.H.; Kim, K.S. A 2-speed small transmission mechanism based on twisted string actuation and a dog clutch. IEEE Robot. Autom. Lett. 2018, 3, 1338–1345. [Google Scholar] [CrossRef]
- Jeong, S.H.; Kim, K.S.; Kim, S. Designing anthropomorphic robot hand with active dual-mode twisted string actuation mechanism and tiny tension sensors. IEEE Robot. Autom. Lett. 2017, 2, 1571–1578. [Google Scholar] [CrossRef]
- Tavakoli, M.; Batista, R.; Sgrigna, L. The UC softhand: Light weight adaptive bionic hand with a compact twisted string actuation system. Actuators 2015, 5, 1. [Google Scholar] [CrossRef]
- Park, J.; Park, J.i.; Seo, H.T.; Liu, Y.; Kim, K.S.; Kim, S. Control of tendon-driven (Twisted-string Actuator) robotic joint with adaptive variable-radius pulley. In Proceedings of the 2020 20th International Conference on Control, Automation and Systems (ICCAS), Busan, Republic of Korea, 13–16 October 2020; pp. 1096–1098. [Google Scholar]
- Sugihara, K.; Nozaki, T.; Murakami, T. Continuously variable transmission by high-speed path switching of linear electro-hydrostatic actuator. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 3603–3608. [Google Scholar]
- Gan, Z.; Tang, H.; Treadway, E.; Gillespie, R.B.; Remy, C.D. Modeling and experimental evaluation of a variable hydraulic transmission. IEEE/ASME Trans. Mechatron. 2020, 25, 750–761. [Google Scholar] [CrossRef]
- Shin, W.; Park, S.; Park, G.; Kim, J. A passively adaptable toroidal continuously variable transmission combined with twisted string actuator. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 11409–11415. [Google Scholar]
- Wang, J.x.; Zhao, J.; Zou, H.; Yao, J. Design and simulation of a load-sensitive dual-speed transmission with a wide speed range. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–7. [Google Scholar] [CrossRef]
- Huang, L.; Yu, T.; Jiao, Z.; Li, Y. Research on power matching and energy optimal control of active load-sensitive electro-hydrostatic actuator. IEEE Access 2020, 9, 51121–51133. [Google Scholar] [CrossRef]
- Takaki, T.; Yamasaki, Y.; Ishii, I. Load-sensitive continuously variable transmission using an oblique feed screw for parallel-jaw grippers. In Proceedings of the 2011 International Symposium on Micro-NanoMechatronics and Human Science, Nagoya, Japan, 6–9 November 2011; pp. 507–510. [Google Scholar]
- Ueki, K.; Sato, R.; Ming, A.; Shimojo, M.; Hammadi, M.; Choley, J.Y. Development of knee joint mechanism with variable transmission and joint stop for bipedal robot inspired by human structure. In Proceedings of the 2020 21st International Conference on Research and Education in Mechatronics (REM), Cracow, Poland, 9–11 December 2020; pp. 1–6. [Google Scholar]
- Liu, Y.; Guo, S.; Zhang, S.; Boulardot, L. Modeling and analysis of a variable stiffness actuator for a safe home-based exoskeleton. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018; pp. 2243–2248. [Google Scholar]
- Kernbaum, A.S.; Kitchell, M.; Crittenden, M. An ultra-compact infinitely variable transmission for robotics. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 1800–1807. [Google Scholar]
- Lenzi, T.; Cempini, M.; Hargrove, L.J.; Kuiken, T.A. Actively variable transmission for robotic knee prostheses. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 6665–6671. [Google Scholar]
- Chen, S.; Xu, L.; Xu, H.; Liu, J.; Cheng, G.; Cao, K. Principle, design and simulation of a novel continuously variable transmission for robots. In Proceedings of the 2019 IEEE 8th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 24–26 May 2019; pp. 73–78. [Google Scholar]
- Kim, J.H.; Jang, I.G. Optimization-based investigation of bioinspired variable gearing of the distributed actuation mechanism to maximize velocity and force. IEEE Robot. Autom. Lett. 2020, 5, 6326–6333. [Google Scholar] [CrossRef]
- Lee, E.; Song, H.; Jeong, J.; Jeong, S. Mechanical variable magnetic gear transmission: Concept and preliminary research. IEEE Robot. Autom. Lett. 2022, 7, 3357–3364. [Google Scholar] [CrossRef]
- ABB. 2024. Available online: https://new.abb.com/products/robotics/zh/robots/articulated-robots/irb-460 (accessed on 17 December 2024).






| Parameters | Description | Value |
|---|---|---|
| Weight of base | 146 g | |
| Weight of joint motor | 436 g | |
| Weight of hoist mechanism | 160 g | |
| Weight of upper arm | 140 g | |
| Weight of forearm | 120 g | |
| Weight of gripper | 180 g | |
| Peak torque of joint motor | 7 N.m | |
| Maximum speed of joint motor | 235 rpm | |
| Peak torque of LAHM’s motor | 1 N.m | |
| Maximum speed of LAHM’s motor | 416 rpm | |
| , , | Length coordinates of the reel | 20 mm, 8 mm |
| , | Radius of the reel | 10 mm, 28.4 mm, 33.4 mm |
| , , | Schematic diagram for solving the kinematics of a robotic arm linkage length | 60 mm, 140 mm, 205 mm |
| , , , , | Vector length of rope points | 86 mm, 140 mm, 205 mm, 35 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Lu, Z.; Wang, Y.; Li, Z. The Design and Analysis of a Lightweight Robotic Arm Based on a Load-Adaptive Hoisting Mechanism. Actuators 2025, 14, 71. https://doi.org/10.3390/act14020071
Wang R, Lu Z, Wang Y, Li Z. The Design and Analysis of a Lightweight Robotic Arm Based on a Load-Adaptive Hoisting Mechanism. Actuators. 2025; 14(2):71. https://doi.org/10.3390/act14020071
Chicago/Turabian StyleWang, Ruchao, Zhiguo Lu, Yiru Wang, and Zhongqing Li. 2025. "The Design and Analysis of a Lightweight Robotic Arm Based on a Load-Adaptive Hoisting Mechanism" Actuators 14, no. 2: 71. https://doi.org/10.3390/act14020071
APA StyleWang, R., Lu, Z., Wang, Y., & Li, Z. (2025). The Design and Analysis of a Lightweight Robotic Arm Based on a Load-Adaptive Hoisting Mechanism. Actuators, 14(2), 71. https://doi.org/10.3390/act14020071






