Dynamic Modelling and Experimental Investigation of an Active–Passive Variable Stiffness Actuator
Abstract
:1. Introduction
2. Structural Design and Dynamic Modelling of APVSA
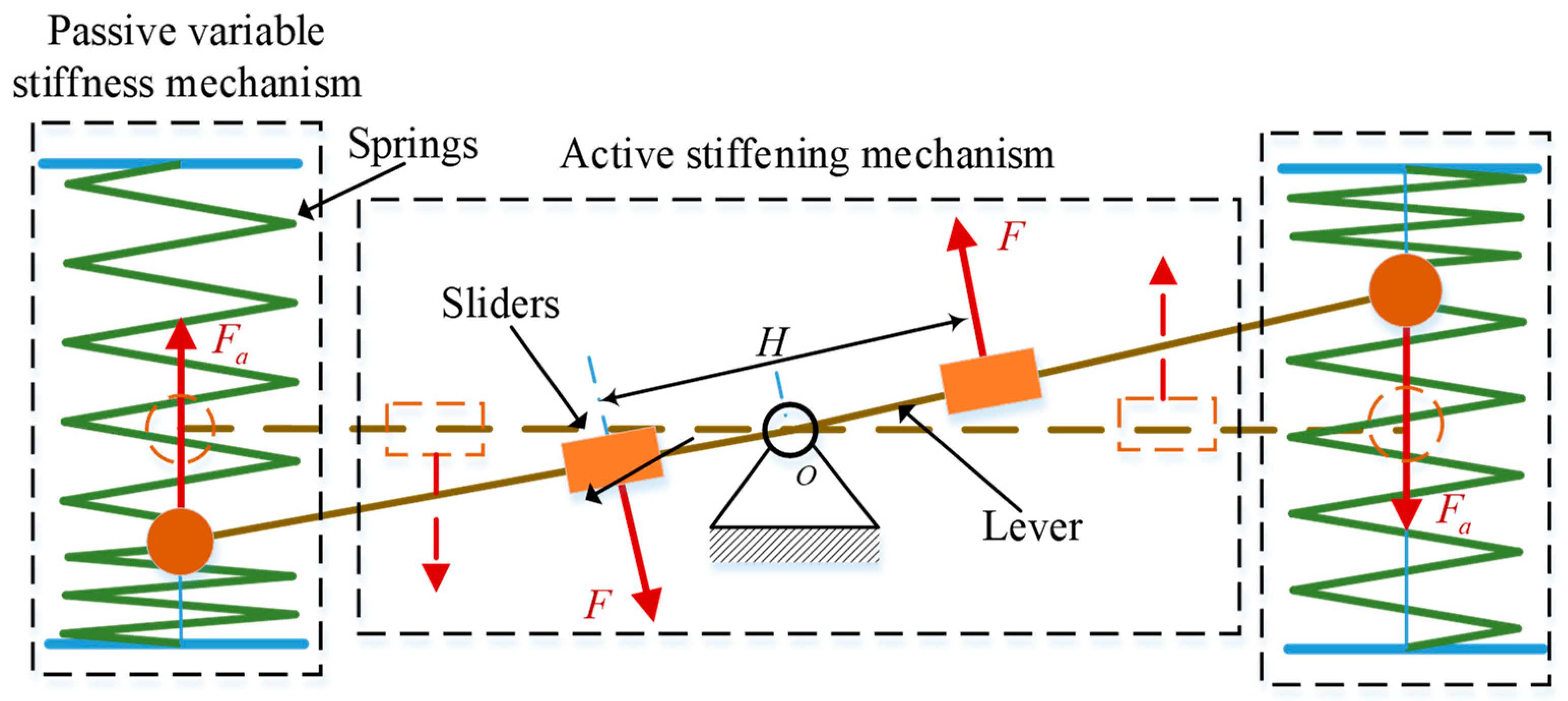
2.1. Working Principle
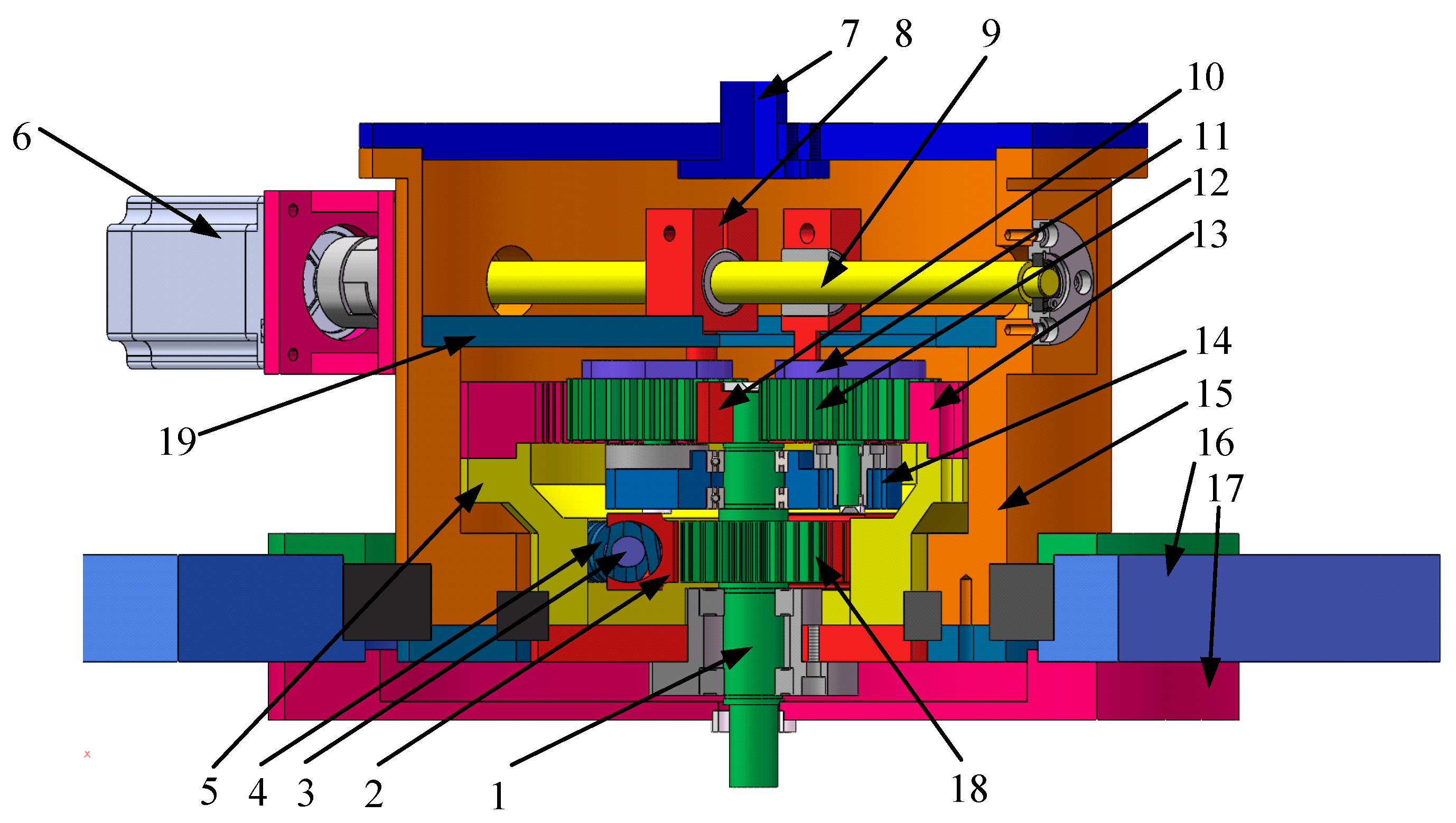
2.2. Structural Design
2.3. Nonlinear Dynamics Modeling
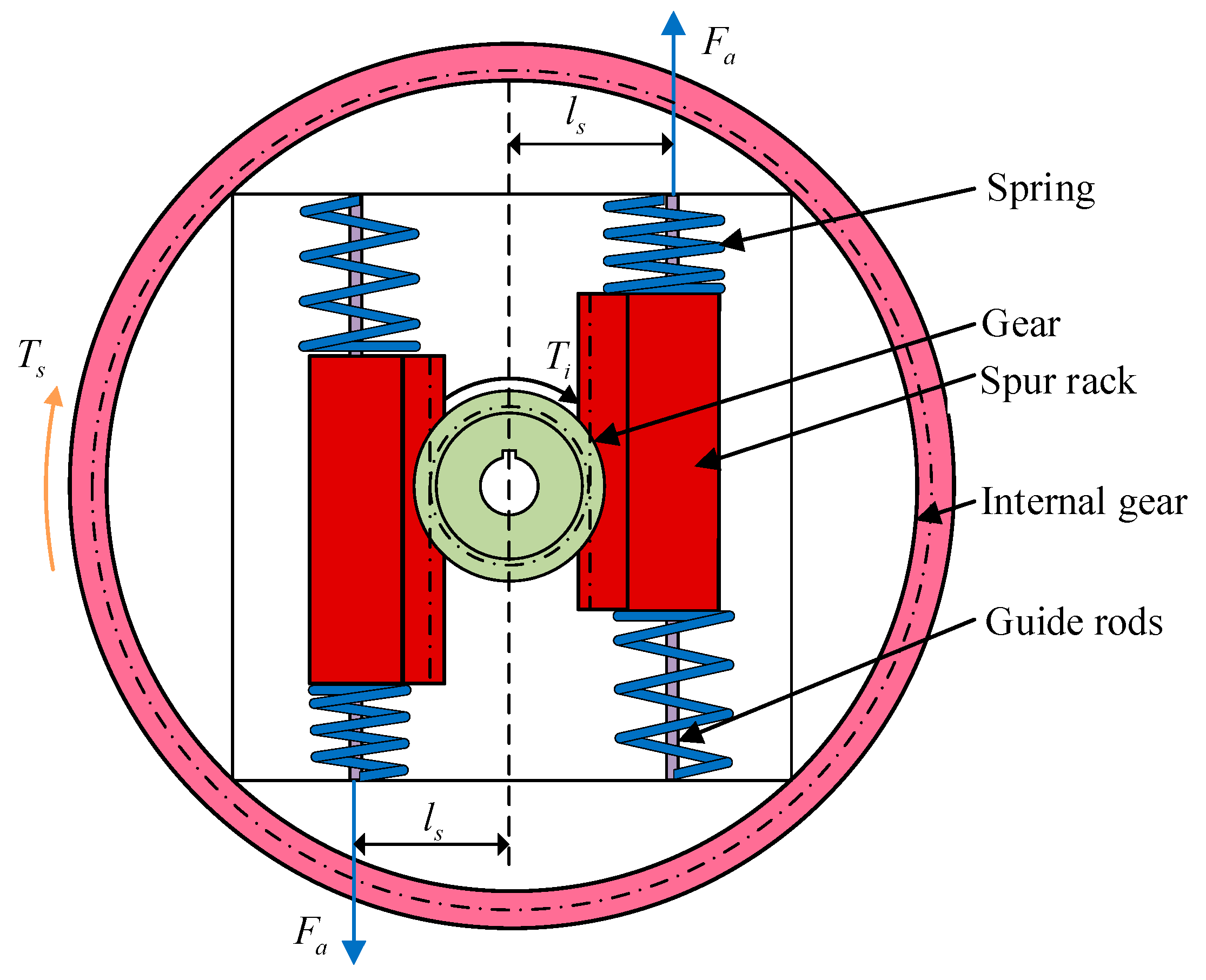
- Passive variable stiffness mechanism
- 2.
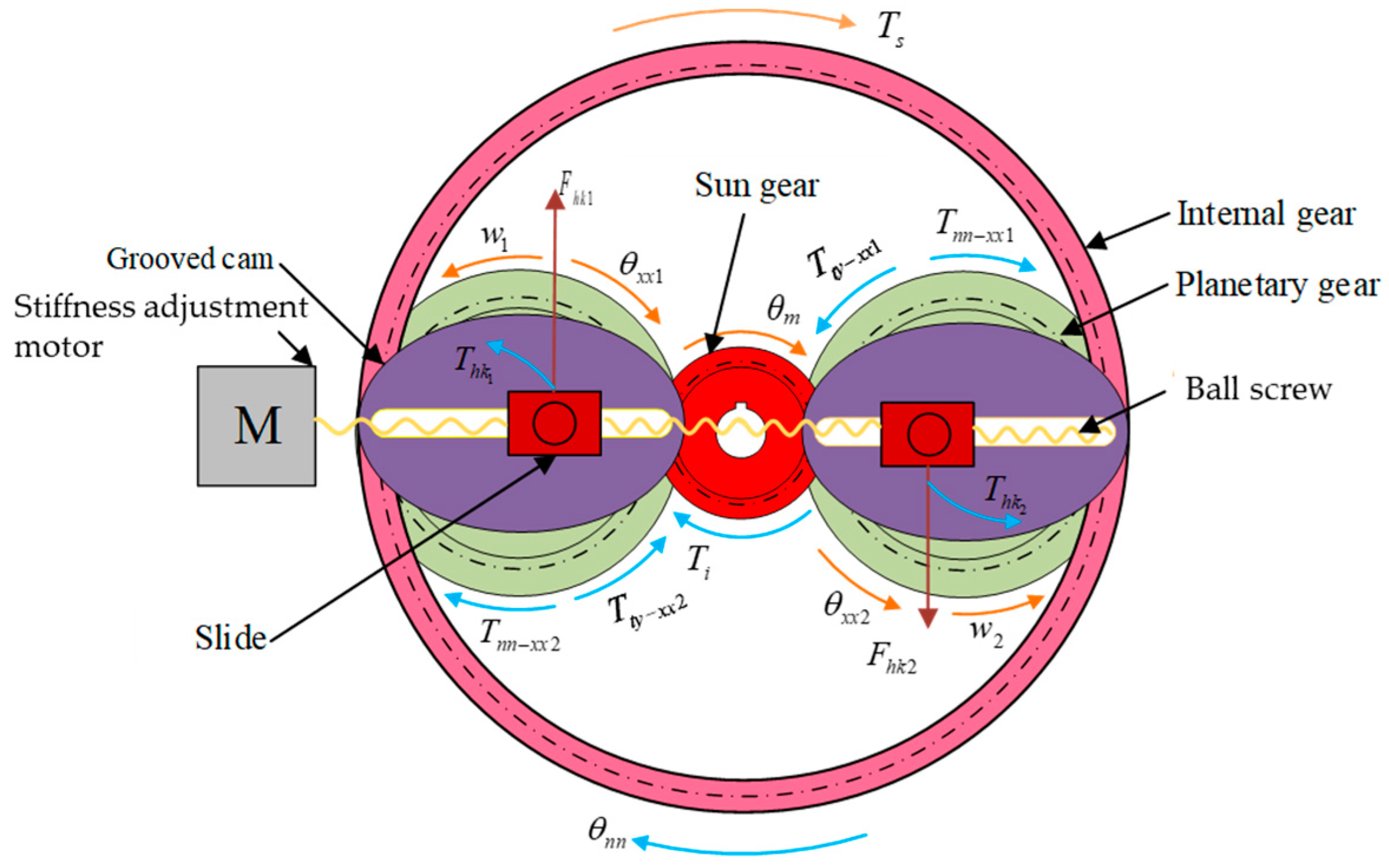
- Active stiffening mechanism
3. APVSA Simulation and Analysis
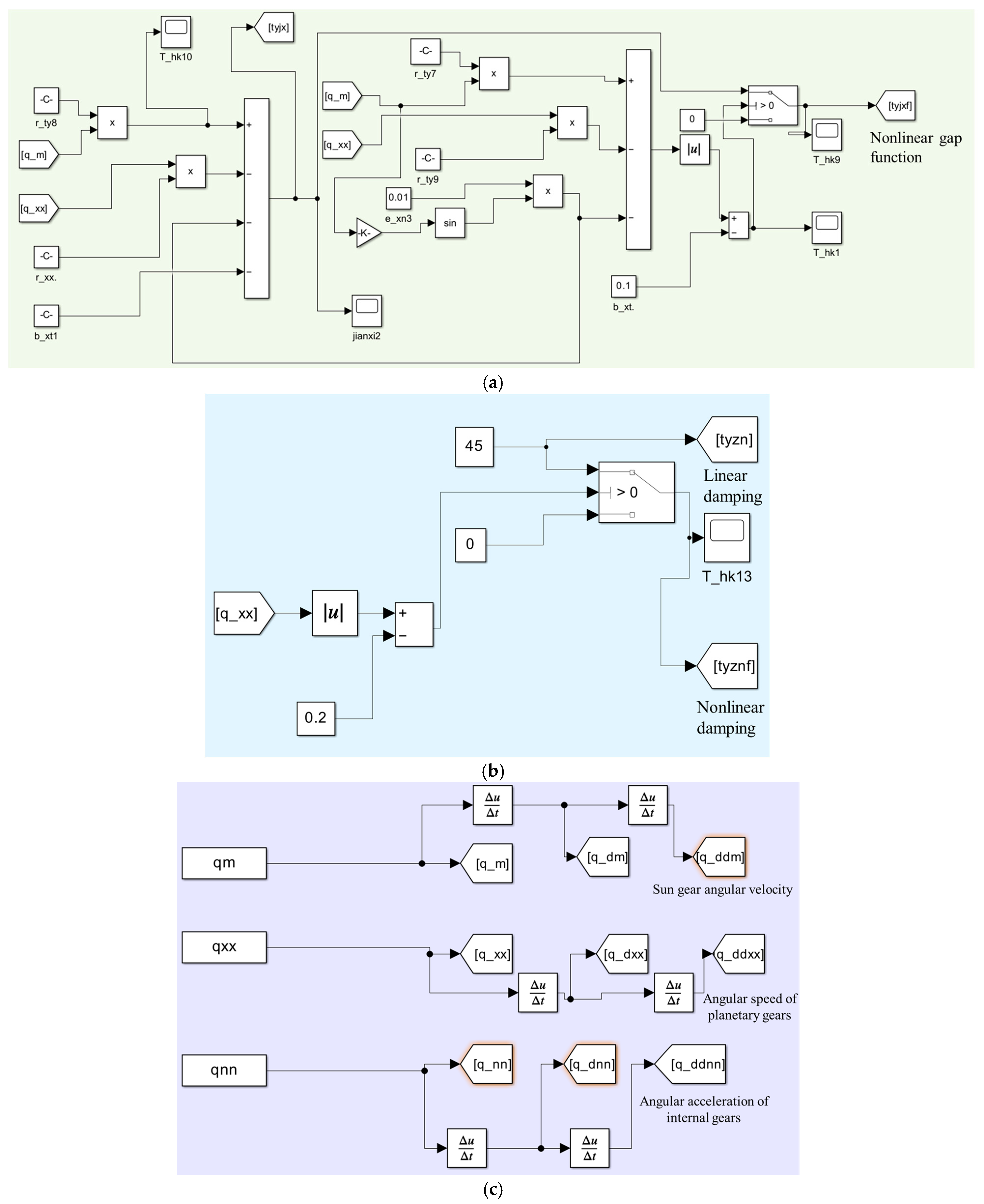
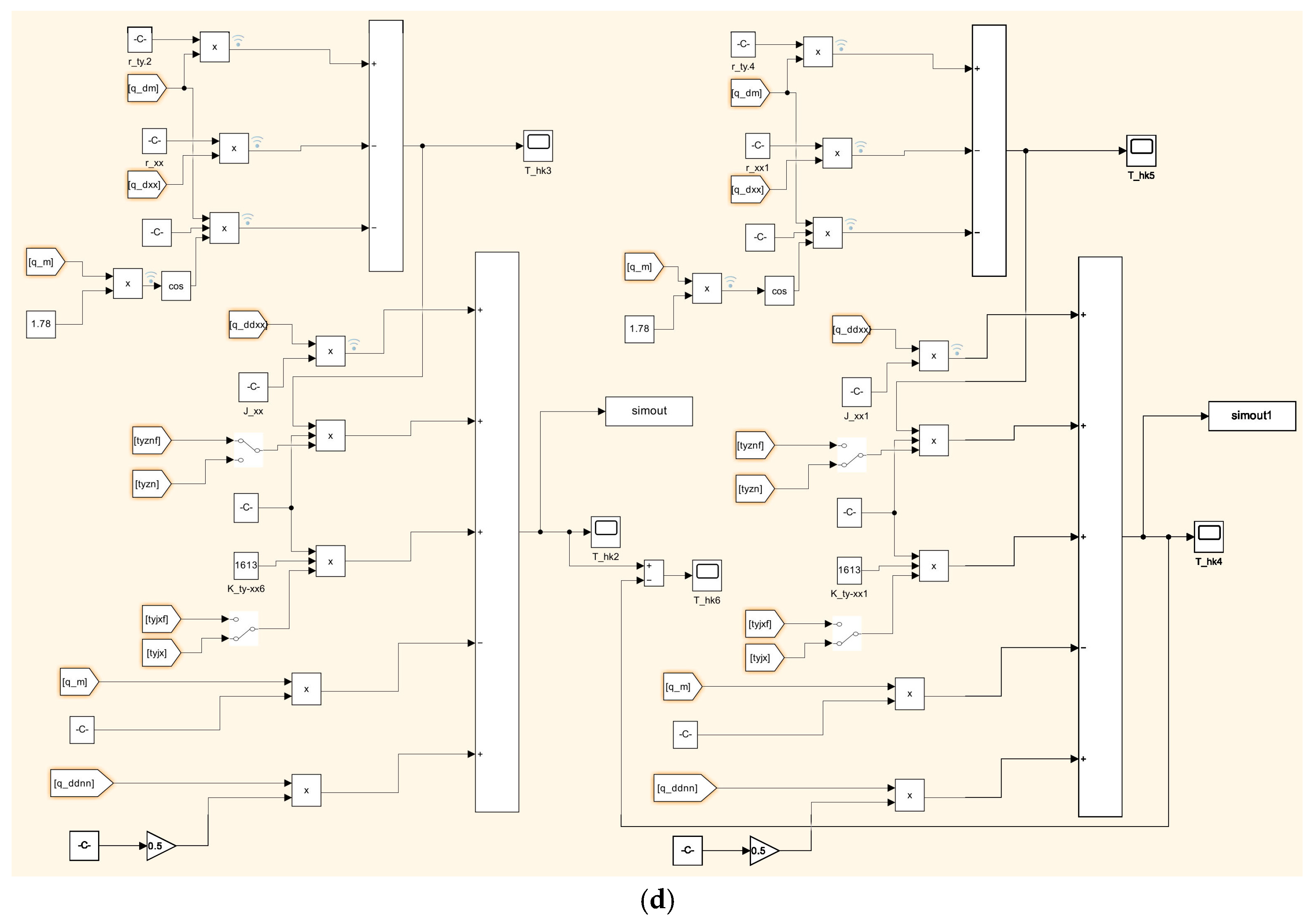
3.1. Discretisation and Expansion of Dynamical Models
- 3.
- The discretisation of the equations for internal gears and planetary gears.
- The discretisation of the equations between the sun and planetary gears.
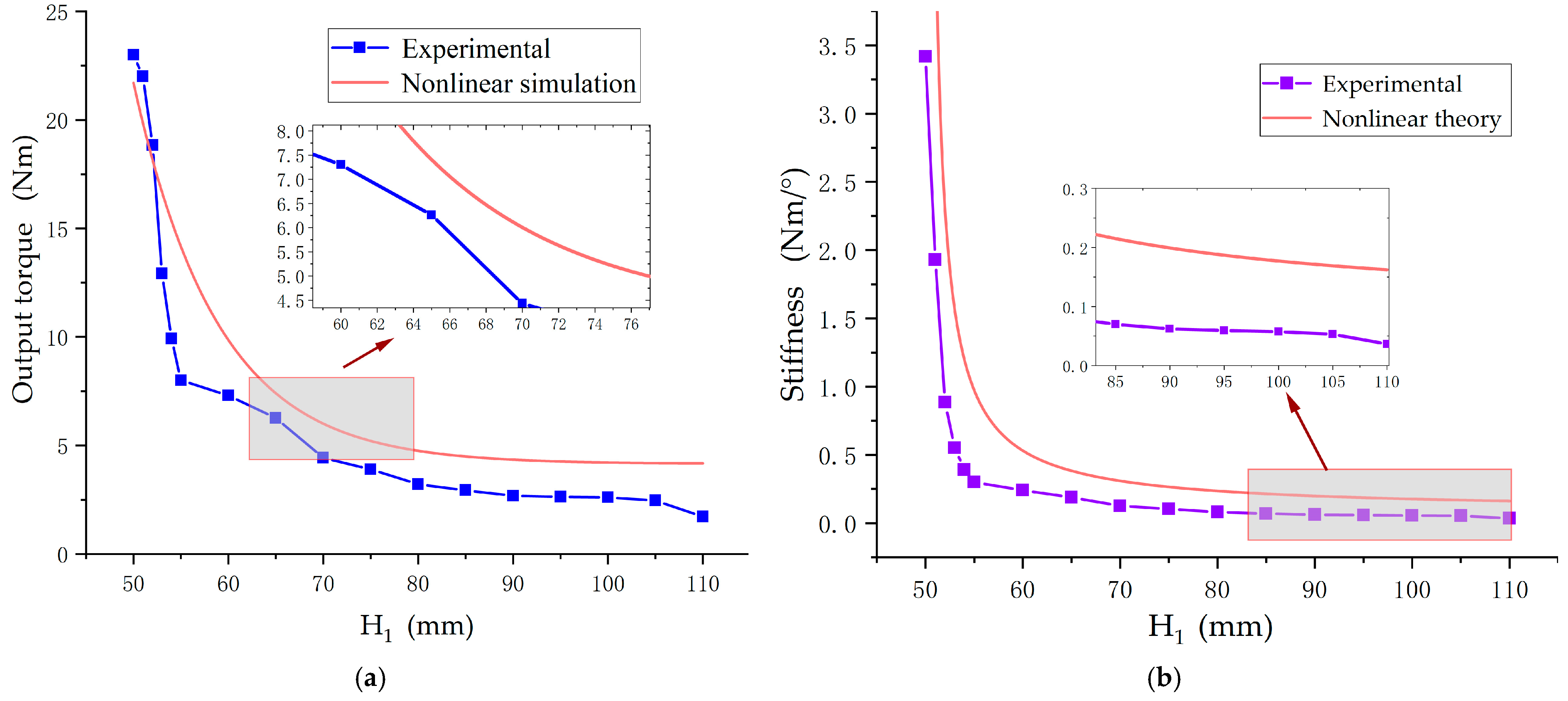
3.2. APVSA Stiffness Simulation Analysis
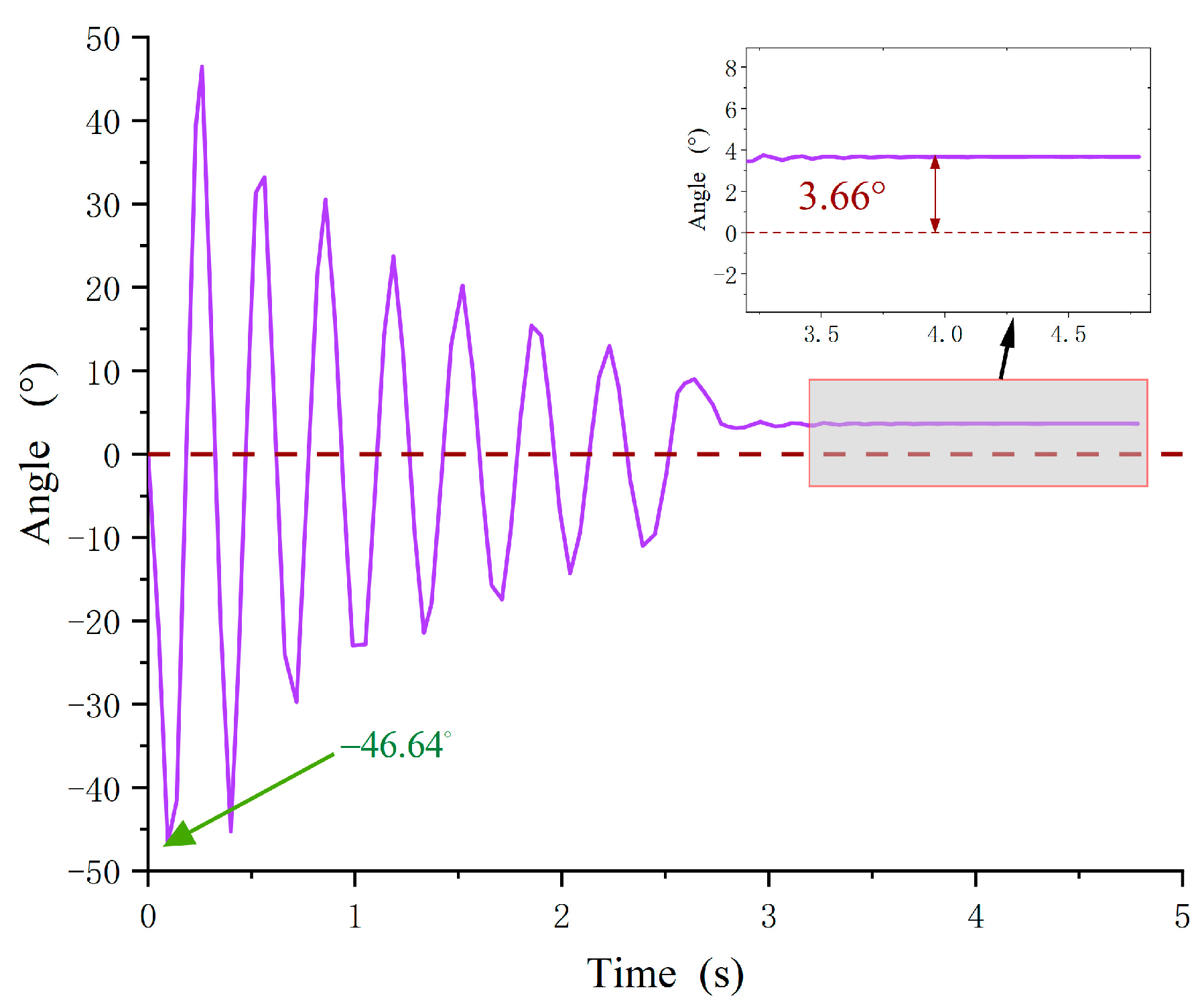
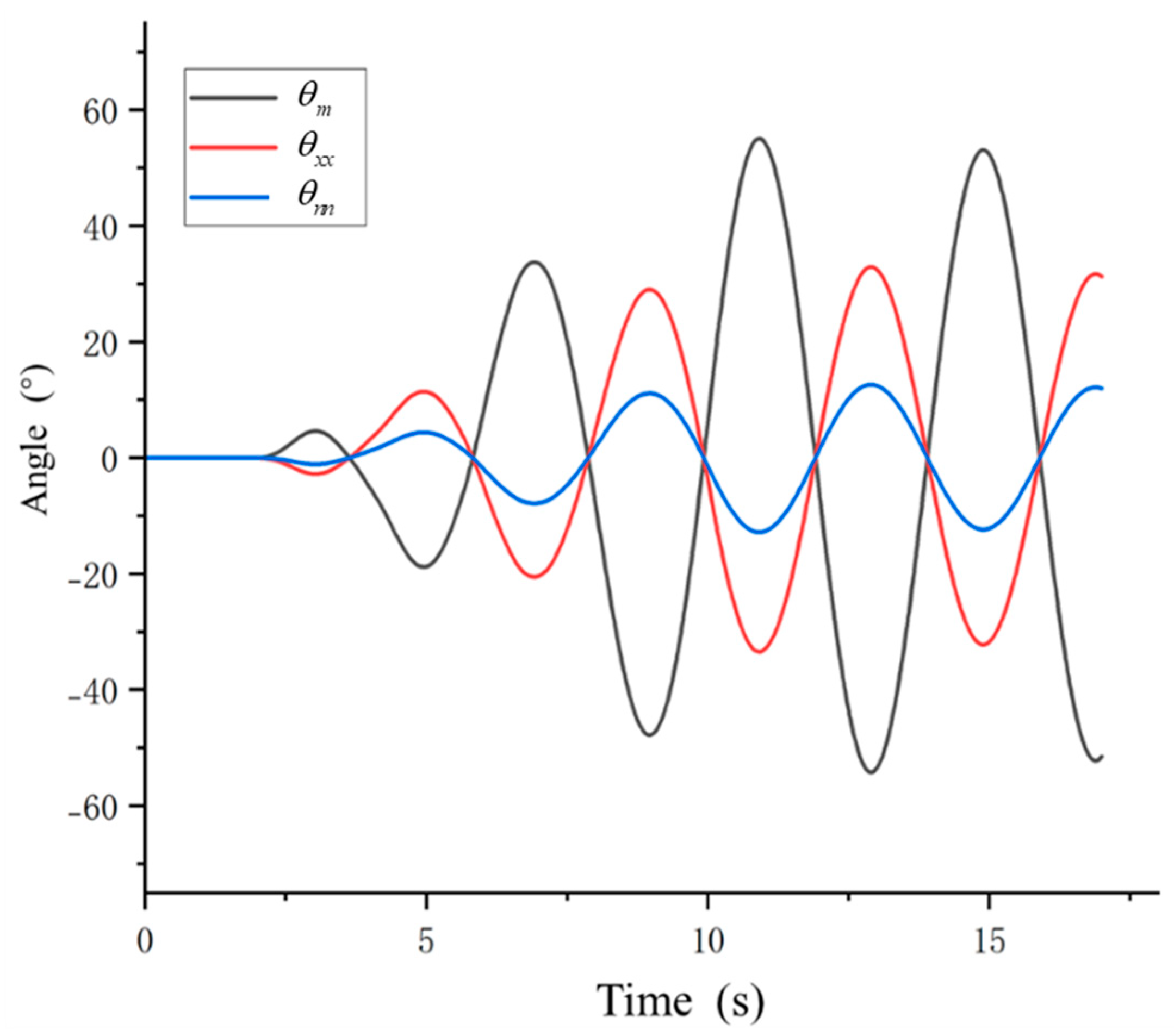
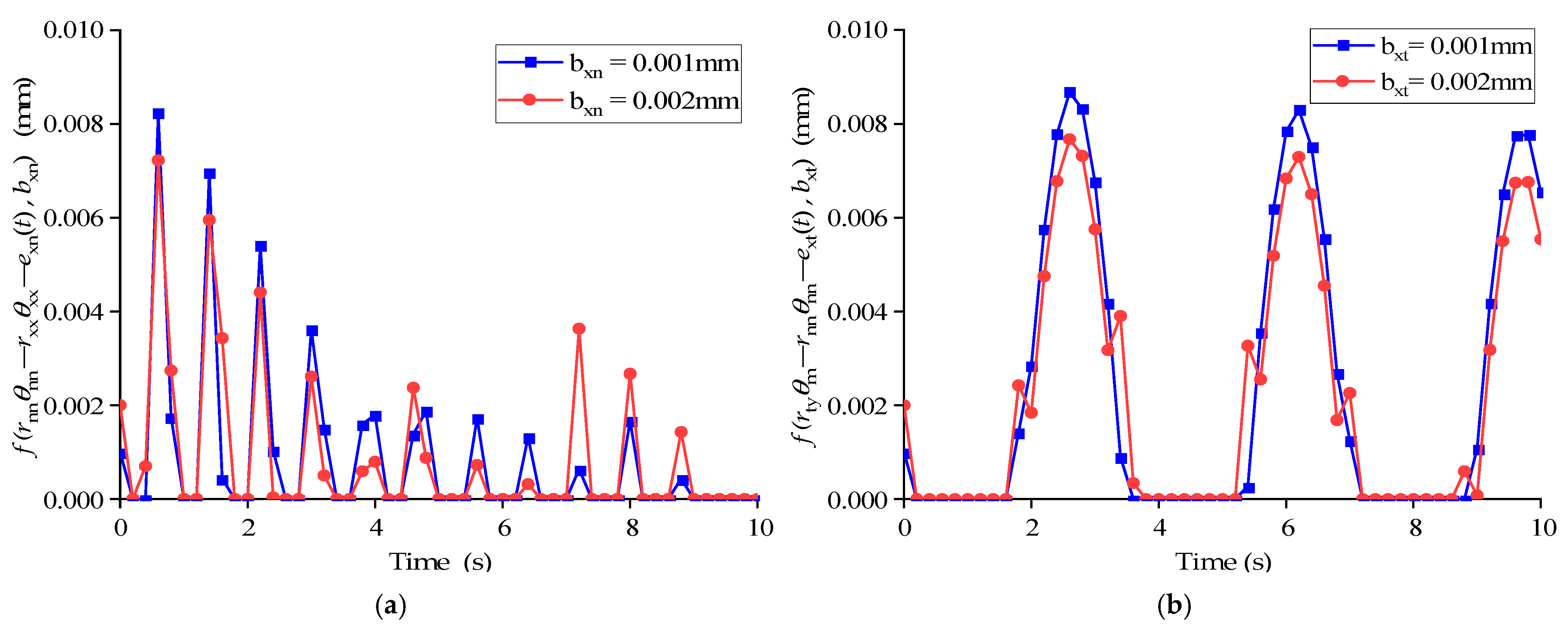
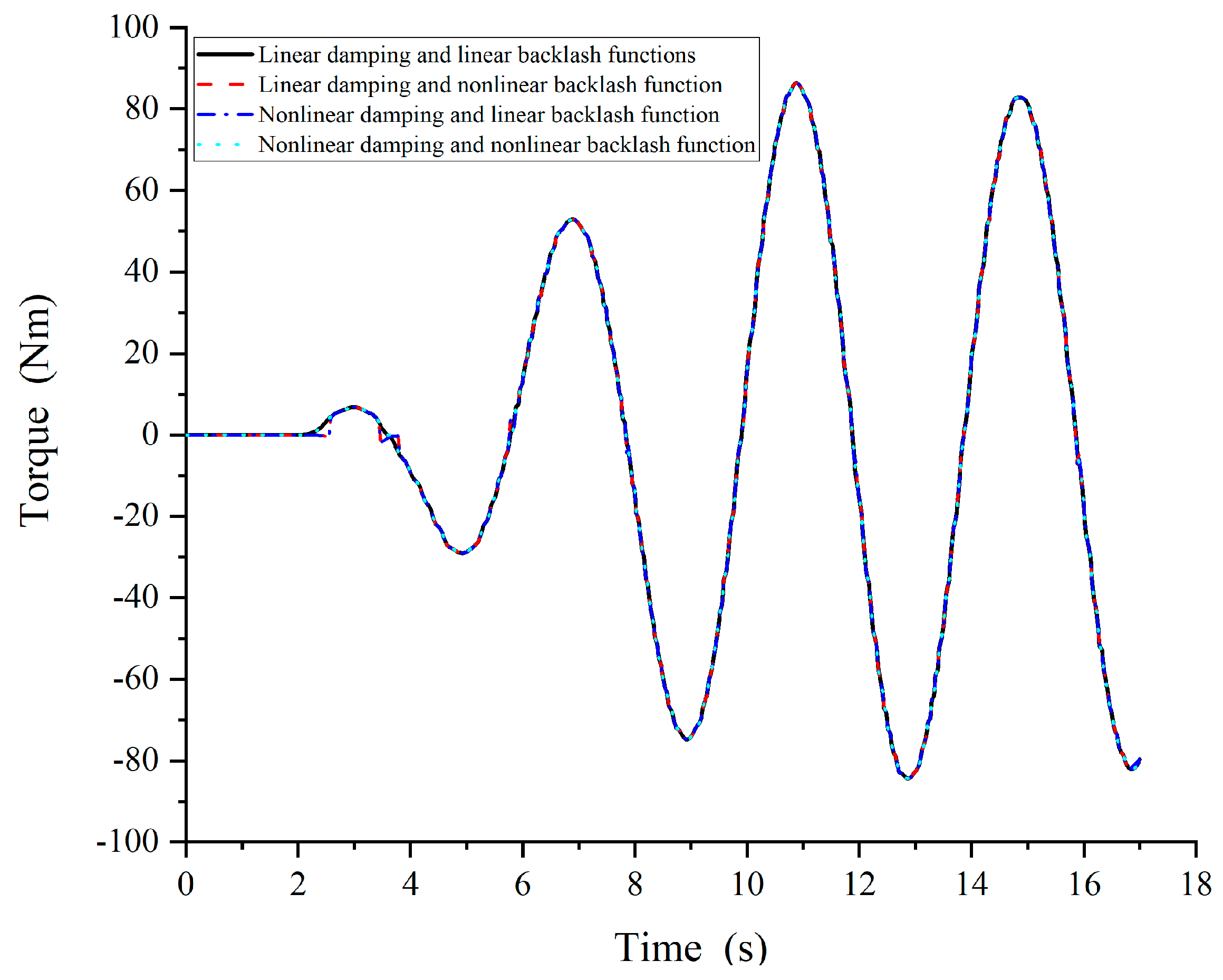
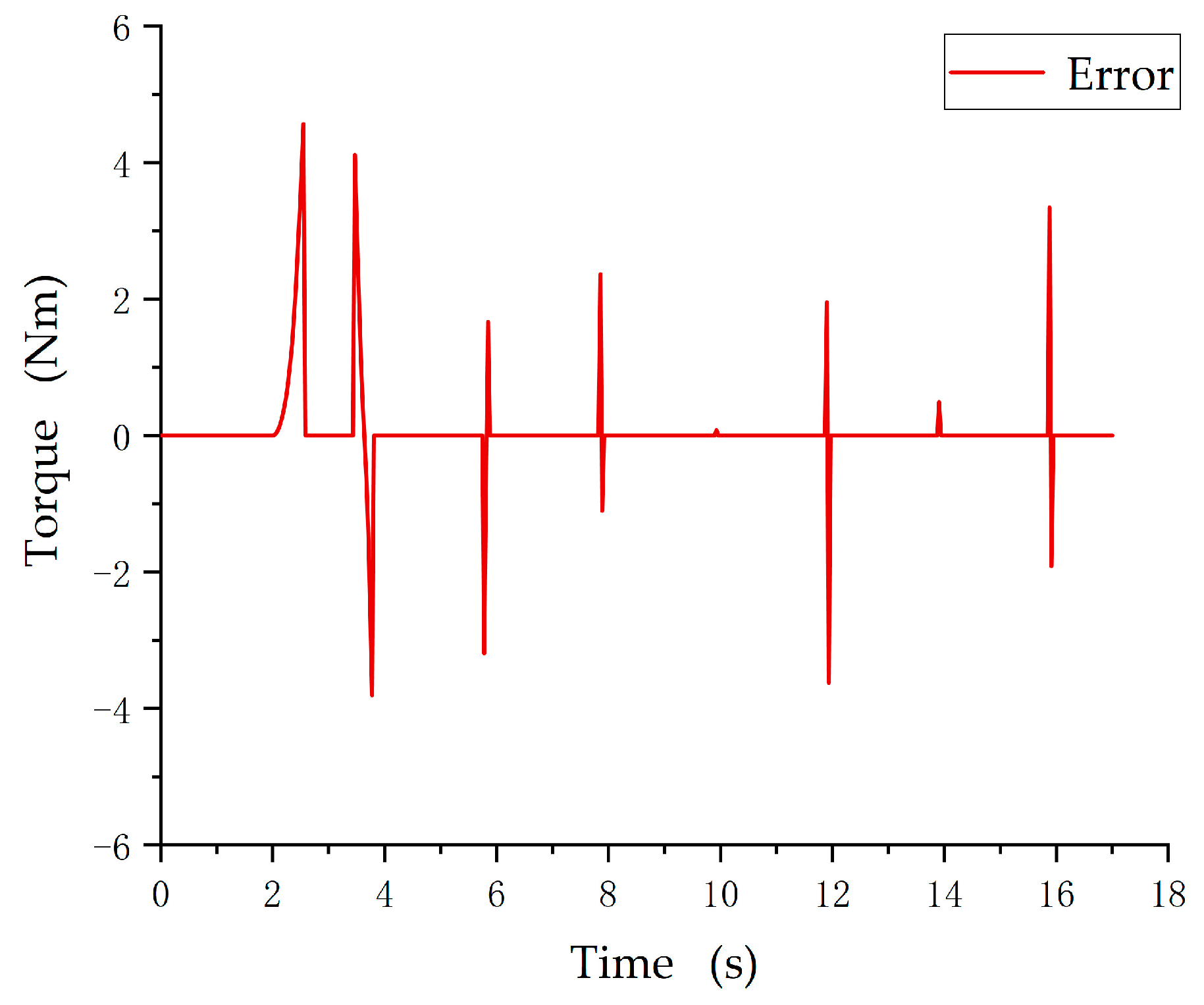
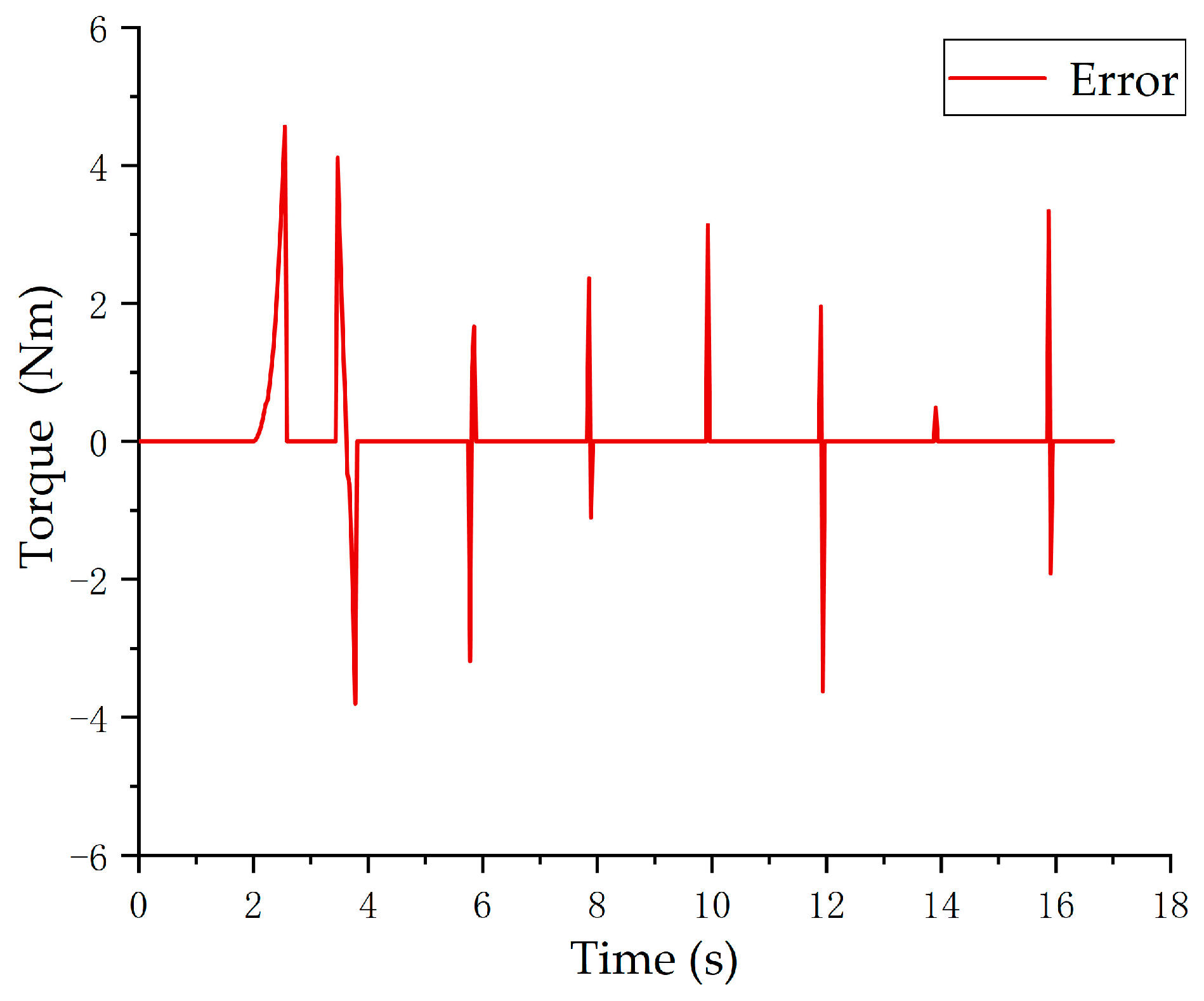
3.3. Simulation and Analysis of APVSA Nonlinear Dynamics Model
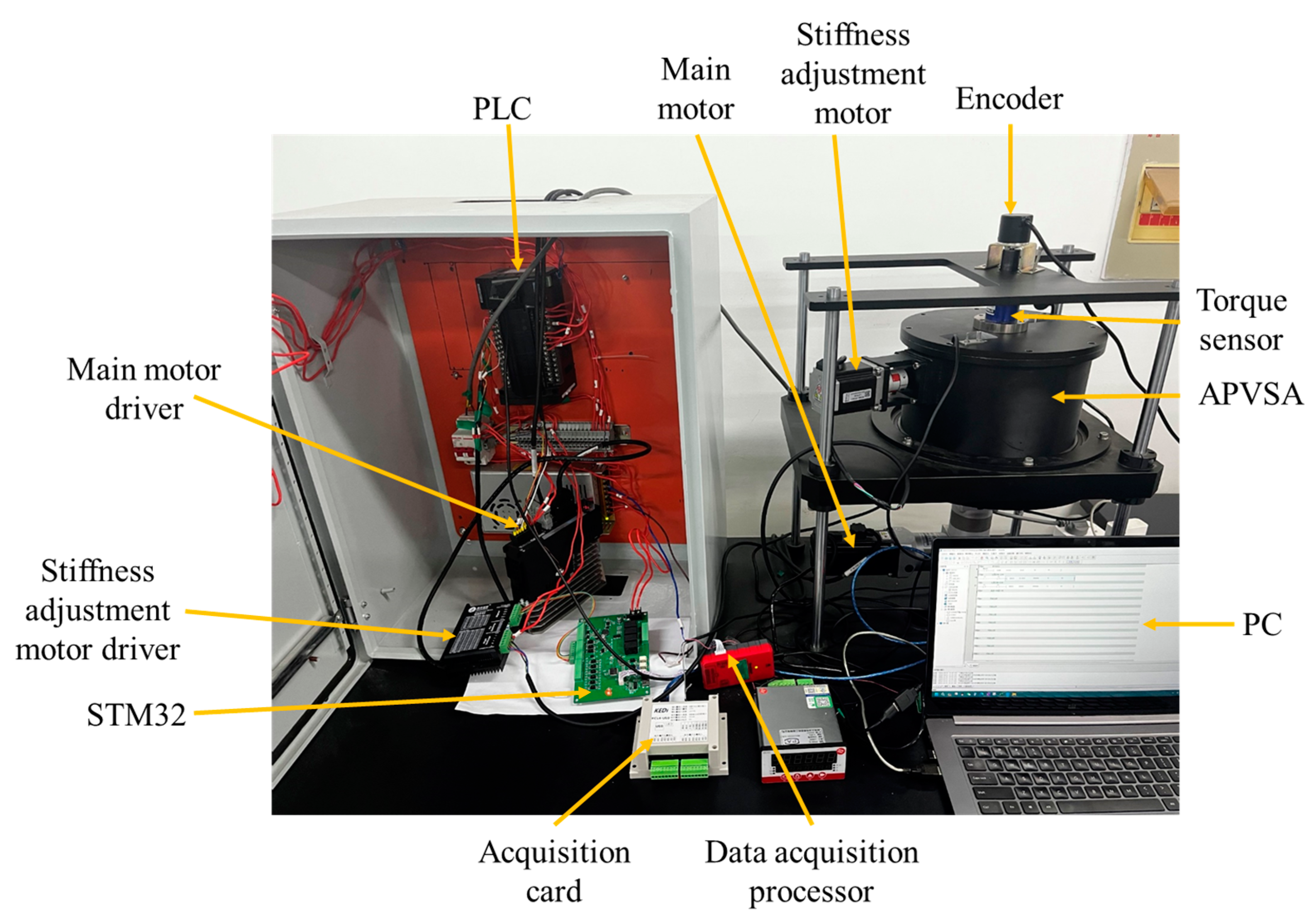
4. Experimental Verification
4.1. Sliders Movement Experiment
4.2. Static Stiffness Test
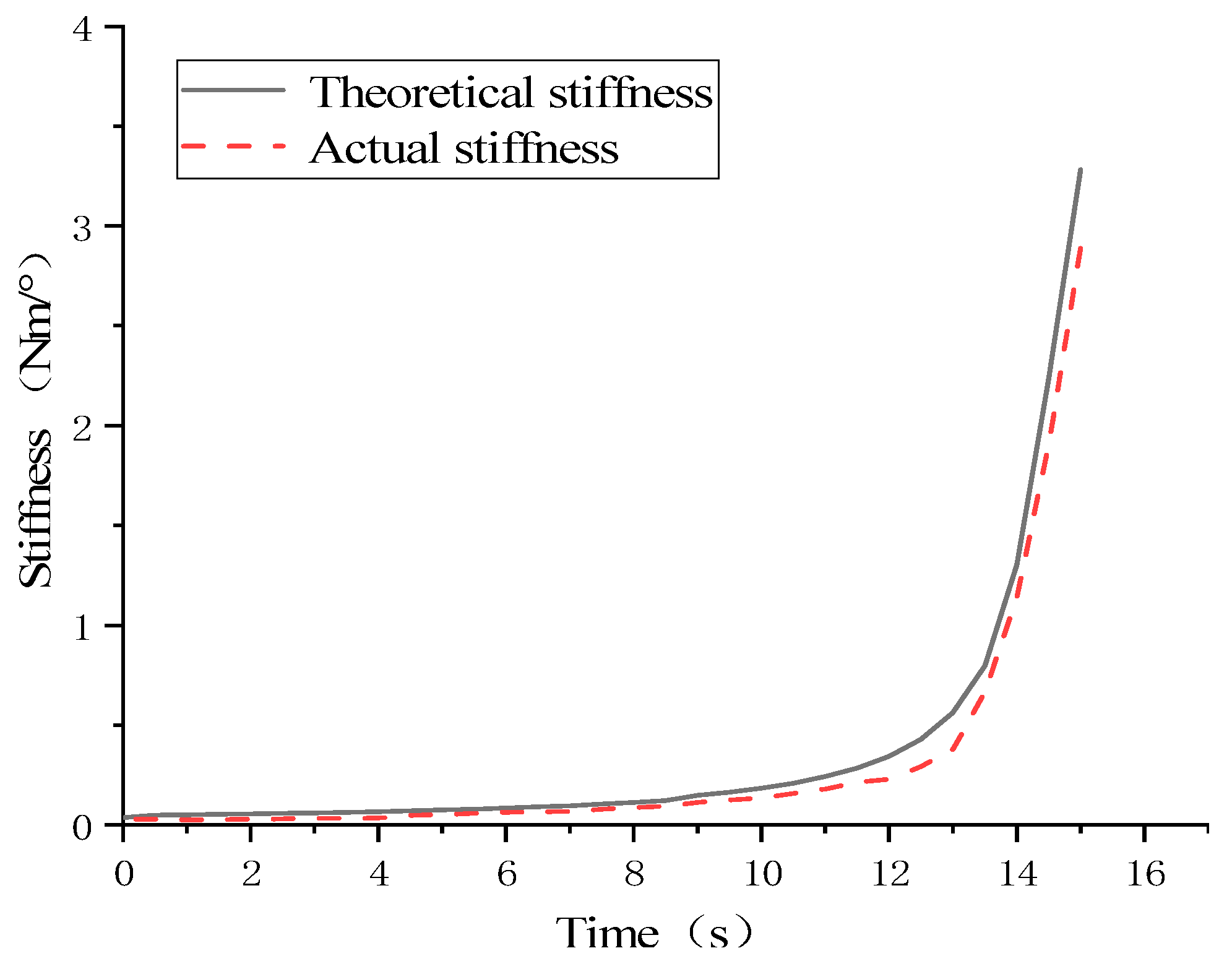
4.3. Dynamic Stiffness Experiment
5. Discussion
6. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | Symbol (Unit) | Parameter | Symbol (Unit) | Parameter | Symbol (Unit) |
|---|---|---|---|---|---|
| Torque between sun gear and planetary gear 1 | (Nm) | Angle of the rigid motor | (°) | Moment of inertia of internal gears | (kg·m2) |
| Torque between sun gear and planetary gear 2 | (Nm) | Output housing rotation angle | (°) | Output housing moment of inertia | (kg·m2) |
| Planetary gear 1 output torque | (Nm) | Gear indexing circle radius | (mm) | Moment of inertia of the sun gear | (kg·m2) |
| Planetary gear 2 output torque | (Nm) | Radius of the base circle of internal gears | (mm) | Slider 1 is pushed by the stopper | (N) |
| Input torque | (Nm) | Radius of the base circle of the sun gear | (mm) | Slider 2 is pushed by the stopper | (N) |
| Torque generated by the internal gear on the planetary gear 2 | (Nm) | Radius of the base circle of the planetary gear 1 | (mm) | The component force in the horizontal direction of the slider | (N) |
| Torque generated by the internal gear on the planetary gear 1 | (Nm) | Radius of the base circle of the planetary gear 2 | (mm) | Horizontal force provided by the stiffness adjustment motor | (N) |
| Internal gear torque | (Nm) | Damping coefficients of gear ratios for internal gears and planetary gears | (s/m) | Combined transmission error of internal gears and planetary gears | (mm) |
| Meshing stiffness of internal gears and planetary gears | (Nm/°) | Damping of the output housing | (s/m) | Combined transmission error of sun gear and planetary gear | (mm) |
| Meshing stiffness of sun gears and planetary gears | (Nm/°) | Damping coefficients of the gear train for sun gears and planetary gears | (s/m) | Distance from the center of the input shaft to the rack | (mm) |
| Torque coefficient of the motor | (Nm/°) | Frequency of meshing of internal gears with planetary gears | (°/s) | Distance between slider and housing | L (mm) |
| Stiffness of the output housing | (Nm/°) | Gear meshing frequency | (°/s) | Electricity | I (A) |
| Actuator stiffness | K (Nm/°) | Mass of the slider | (kg) | Number of internal gear teeth | |
| Equivalent stiffness of a spring | k | Spring viscous damping coefficient | Number of sun gear teeth | ||
| Input shaft angle | (°) | Flexible angle | ρ (°) | Backlash error between internal gears and planetary gears | (mm) |
| Angle of planetary gear i. i = 1,2 | (°) | Moment of inertia of planetary gear 1 | (kg·m2) | Backlash error between sun gear and planetary gears | (mm) |
| Angle of planetary gear 2 | (°) | Moment of inertia of planetary gear 2 | (kg·m2) | Planetary gear 1 speed | (°/s) |
| Acceleration of the slider | (m/s2) | Laser encoder measuring distance | (mm) | Planetary gear 2 speed | (°/s) |
| Screw guide | l (mm) | Motor speed | N (°/s) | Angle of rotation of planetary gear carrier | (°/s) |
References
- Kahnamouei, J.T.; Moallem, M. Advancements in Control Systems and Integration of Artificial Intelligence in Welding Robots: A Review. Ocean Eng. 2024, 312, 119294. [Google Scholar] [CrossRef]
- Chen, T.Y.; Dong, S.J.; Deng, C.M.; Zhang, X.F.; Jiang, J.N.; Deng, L.H.; Cai, Z.H.; Cao, X.Q. Proposition of a Robot-Based Free Diamond Abrasive Grinding Process and Its Influence on the Characteristics of Plasma-Sprayed 8ysz Coatings. J. Mater. Res. Technol.-JMRT 2023, 26, 4423–4435. [Google Scholar] [CrossRef]
- Choi, W.; Suh, J. Design and Evaluation of a Cable-Actuated Palletizing Robot with Geared Rolling Joints. IEEE-ASME Trans. Mechatron. 2024, 29, 3137–3145. [Google Scholar] [CrossRef]
- Li, Z.; Chu, X.Y.; Hu, X.Y.; Zhang, Z.Y.; Li, N.P.; Li, J.F. Variable Stiffness Methods for Robots: A Review. Smart Mater. Struct. 2024, 33, 063002. [Google Scholar] [CrossRef]
- Clark, A.B.; Rojas, N. Malleable Robots: Reconfigurable Robotic Arms with Continuum Links of Variable Stiffness. IEEE Trans. Robot. 2022, 38, 3832–3849. [Google Scholar] [CrossRef]
- Wolf, S.; Grioli, G.; Eiberger, O.; Friedl, W.; Grebenstein, M.; Höppner, H.; Burdet, E.; Caldwell, D.G.; Carloni, R.; Catalano, M.G.; et al. Variable Stiffness Actuators: Review on Design and Components. IEEE-ASME Trans. Mechatron. 2016, 21, 2418–2430. [Google Scholar] [CrossRef]
- Vanderborght, B.; Albu-Schaeffer, A.; Bicchi, A.; Burdet, E.; Caldwell, D.G.; Carloni, R.; Catalano, M.; Eiberger, O.; Friedl, W.; Ganesh, G.; et al. Variable Impedance Actuators: A Review. Robot. Auton. Syst. 2013, 61, 1601–1614. [Google Scholar] [CrossRef]
- Sun, Y.X.; Tang, Y.T.; Zheng, J.; Dong, D.B.; Bai, L. Optimal Variable Stiffness Control and Its Applications in Bionic Robotic Joints: A Review. J. Bionic Eng. 2023, 20, 417–435. [Google Scholar] [CrossRef]
- Ham, R.V.; Sugar, T.G.; Vanderborght, B.; Hollander, K.W.; Lefeber, D. Compliant Actuator Designs. IEEE Robot. Autom. Mag. 2009, 16, 81–94. [Google Scholar] [CrossRef]
- Tung, T.T.; Van Tinh, N.; Phuong Thao, D.T.; Minh, T.V. Development of a Prototype 6 Degree of Freedom Robot Arm. Results Eng. 2023, 18, 101049. [Google Scholar] [CrossRef]
- Rodríguez-Guerra, D.; Sorrosal, G.; Cabanes, I.; Calleja, C. Human-Robot Interaction Review: Challenges and Solutions for Modern Industrial Environments. IEEE Access 2021, 9, 108557–108578. [Google Scholar] [CrossRef]
- Pu, H.Y.; He, L.; Cheng, P.; Sun, M.Y.; Chen, J.M. Security of Industrial Robots: Vulnerabilities, Attacks, and Mitigations. IEEE Netw. 2023, 37, 111–117. [Google Scholar] [CrossRef]
- Li, Y.B.; Guan, X.Y.; Li, Z.B.; Tang, Z.H.; Penzlin, B.; Yang, Z.; Leonhardt, S.; Ji, L.H. Analysis, Design, and Preliminary Evaluation of a Parallel Elastic Actuator for Power-Efficient Walking Assistance. IEEE Access 2020, 8, 88060–88075. [Google Scholar] [CrossRef]
- Oh, S.; Kong, K. High-Precision Robust Force Control of a Series Elastic Actuator. IEEE/ASME Trans. Mechatron. 2017, 22, 71–80. [Google Scholar] [CrossRef]
- Carpino, G.; Accoto, D.; Sergi, F.; Tagliamonte, N.L.; Guglielmelli, E. A Novel Compact Torsional Spring for Series Elastic Actuators for Assistive Wearable Robots. J. Mech. Des. 2012, 134, 10. [Google Scholar] [CrossRef]
- Liu, L.; Leonhardt, S.; Bergmann, L.; Misgeld, B.J.E. Composite Performance of Variable Stiffness Actuator for Exoskeleton Administrated Via Impedance Control and Disturbance Observer. Mech. Mach. Theory 2023, 179, 105096. [Google Scholar] [CrossRef]
- Xiong, J.; Sun, Y.; Zheng, J.; Dong, D.; Bai, L. Design and Experiment of a Sma-Based Continuous-Stiffness-Adjustment Torsional Elastic Component for Variable Stiffness Actuators. Smart Mater. Struct. 2021, 30, 105021. [Google Scholar]
- Albu-Schäffer, A.; Wolf, S.; Eiberger, O.; Haddadin, S.; Petit, F.; Chalon, M. Dynamic Modelling and Control of Variable Stiffness Actuators. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, Alaska, 3–7 May 2010; pp. 2155–2162. [Google Scholar]
- Eiberger, O.; Haddadin, S.; Weis, M.; Albu-Schäffer, A.; Hirzinger, G. On Joint Design with Intrinsic Variable Compliance: Derivation of the Dlr Qa-Joint. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, Alaska, 3–7 May 2010; pp. 1687–1694. [Google Scholar]
- Petit, F.; Friedl, W.; Höppner, H.; Grebenstein, M. Analysis and Synthesis of the Bidirectional Antagonistic Variable Stiffness Mechanism. IEEE/ASME Trans. Mechatron. 2015, 20, 684–695. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Yuan, Z.; Liu, J. Design and Analysis of Spring Parallel Variable Stiffness Actuator Based on Antagonistic Principle. Mech. Mach. Theory 2019, 140, 44–58. [Google Scholar] [CrossRef]
- Li, Z.; Xu, P.; Li, B. A Novel Variable Stiffness Actuator Based on Cable-Pulley-Driven Mechanisms for Robotics. IEEE/ASME Trans. Mechatron. 2024, 29, 4699–4710. [Google Scholar] [CrossRef]
- Ji, C.; Kong, M.; Li, R. Time-Energy Optimal Trajectory Planning for Variable Stiffness Actuated Robot. IEEE Access 2019, 7, 14366–14377. [Google Scholar] [CrossRef]
- Sarani, B.; Ahmadi, H. Mechanical Design and Control of a Novel Variable Impedance Actuator (Via) for Knee Joint of a Rehabilitation Ex-oskeleton. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 81. [Google Scholar] [CrossRef]
- Dežman, M.; Gams, A. Rotatable Cam-Based Variable-Ratio Lever Compliant Actuator for Wearable Devices. Mech. Mach. Theory 2018, 130, 508–522. [Google Scholar] [CrossRef]
- Li, Z.; Xu, P.; Huang, H.; Ning, Y.; Li, B. A Novel Variable Stiffness Actuator Based on a Rocker-Linked Epicyclic Gear Train. Mech. Mach. Theory 2022, 177, 105035. [Google Scholar] [CrossRef]
- Xu, Y.; Guo, K.; Sun, J.; Li, J. Design, Modeling and Control of a Reconfigurable Variable Stiffness Actuator. Mech. Syst. Signal Process. 2021, 160, 107883. [Google Scholar] [CrossRef]
- Zhu, R.; Fei, Q.; Jiang, D.; Marchesiello, S.; Anastasio, D. Identification of Nonlinear Stiffness and Damping Parameters Using a Hybrid Approach. AIAA J. 2021, 59, 4686–4695. [Google Scholar] [CrossRef]
- Hu, B.; Liu, J.; Liu, S.; Li, B.; Lei, X. Simultaneous Multi-Parameter Identification Algorithm for Backlash-Type Nonlinearity. Mech. Syst. Signal Process. 2020, 139, 106423. [Google Scholar] [CrossRef]
- Ting, J.-A.; Mistry, M.N.; Peters, J.; Schaal, S.; Nakanishi, J. A Bayesian Approach to Nonlinear Parameter Identification for Rigid Body Dynamics. In Proceedings of the Robotics: Science and Systems, Philadelphia, PA, USA, 16–19 August 2006. [Google Scholar]
- Zhou, G.; Feng, T.; Lv, X.; Liu, L. Parameter Identification of Electro-Hydrostatic Actuator Based on Particle Swarm Optimization. J. Phys. Conf. Ser. 2020, 1486, 032031. [Google Scholar] [CrossRef]
- Wang, C.; Gao, P.; Wang, X.; Wang, H.; Liu, X.; Zheng, H. Mechanical Design and Experiments of a New Rotational Variable Stiffness Actuator for Hybrid Passive–Active Stiffness Regulation. Actuators 2023, 12, 450. [Google Scholar] [CrossRef]
- Yu, X.B.; Zhang, S.; Sun, L.; Wang, Y.; Xue, C.Q.; Li, B. Cooperative Control of Dual-Arm Robots in Different Human-Robot Collaborative Tasks. Assem. Autom. 2020, 40, 95–104. [Google Scholar] [CrossRef]
- Cherelle, P.; Grosu, V.; Beyl, P.; Mathys, A.; Ham, R.V.; Damme, M.V.; Vanderborght, B.; Lefeber, D. The Maccepa Actuation System as Torque Actuator in the Gait Rehabilitation Robot Altacro. In Proceedings of the 2010 3rd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics, Tokyo, Japan, 26–29 September 2010; pp. 27–32. [Google Scholar]
- Liu, L.; Leonhardt, S.; Misgeld, B.J.E. Design and Control of a Mechanical Rotary Variable Impedance Actuator. Mechatronics 2016, 39, 226–236. [Google Scholar] [CrossRef]
- Wang, W.; Fu, X.; Li, Y.; Yun, C. "Design and Implementation of a Variable Stiffness Actuator Based on Flexible Gear Rack Mechanism. Robot. Int. J. Inf. Educ. Res. Robot. Artif. Intell. 2018, 36, 448–462. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, H.J.; Lee, K.H.; Nam, K.T.; Koo, J.C. A Novel Variable Stiffness Scotch Yoke Series Elastic Actuator for Enhanced Functional Stiffness. Microsyst. Technol. 2020, 26, 3395–3402. [Google Scholar] [CrossRef]
- Karim, A.; Lindner, P.; Verl, A. Control-Based Compensation of Friction and Backlash within Rack-and-Pinion Drives. Prod. Eng. 2018, 12, 589–596. [Google Scholar] [CrossRef]
- Sun, J.; Guo, Z.; Sun, D.; He, S.; Xiao, X. Design, Modeling and Control of a Novel Compact, Energy-Efficient, and Rotational Serial Variable Stiffness Actua-tor (Svsa-Ii). Mech. Mach. Theory 2018, 130, 123–136. [Google Scholar] [CrossRef]
- Chen, G.; Chen, G.; Li, Y.; Zhao, N. Dynamic Analysis of a Face-Gear Drive with Spur Involute Pinion with Backlash Considered. Mech. Sci. Technol. Aerosp. Eng. 2009, 28, 5. [Google Scholar]
- Yu, X.; Sun, Y.; Li, H.; Wu, S. An Improved Meshing Stiffness Calculation Algorithm for Gear Pair Involving Fractal Contact Stiffness Based on Dynamic Contact Force. Eur. J. Mech.-A/Solids 2022, 94, 104595. [Google Scholar] [CrossRef]
- Sánchez, M.B.; Pleguezuelos, M.; Pedrero, J.I. Approximate Equations for the Meshing Stiffness and the Load Sharing Ratio of Spur Gears Including Hertzian Effects. Mech. Mach. Theory 2017, 109, 231–249. [Google Scholar] [CrossRef]
- Liu, S.; Liu, F. Vibration Characteristics of Spur Gear System with Non-Linear Damping under No Lubrication Condition. J. Vibroeng. 2019, 21, 1260–1270. [Google Scholar] [CrossRef]
- Wang, S.; Wang, L.; Im, N.; Zhang, W.; Li, X. Real-Time Parameter Identification of Ship Maneuvering Response Model Based on Nonlinear Gaussian Filter. Ocean Eng. 2022, 247, 110471. [Google Scholar] [CrossRef]
- Hu, J.; Liu, T.Y.; Zeng, H.J.; Chua, M.X.; Katupitiya, J.; Wu, L. Static Modeling of a Class of Stiffness-Adjustable Snake-like Robots with Gravity Compensation. Robotics 2023, 12, 2. [Google Scholar] [CrossRef]
- Sheng, L.C.; Xu, M.C.; Shen, J.W.; Li, W.; Ye, G. Design and Analysis of a Novel Flexible Variable Stiffness Damping Mechanism for Grinding Electric Spindle. J. Vib. Control 2024, 30, 4408–4420. [Google Scholar] [CrossRef]
- Shi, X.J.; Xu, J.; Chen, T.K.; Cong, Q.; Tian, W.J. Novel Low Frequency Bionic Vibration Isolation Structure. J. Vib. Control 2023, 29, 3357–3368. [Google Scholar] [CrossRef]
- Wei, F.; Zhang, L.X.; Zhang, Y.M.; Li, S.P.; Yao, K.; Li, C.J. Design and Analysis of a Novel Variable Stiffness Joints with Robots. Adv. Mech. Eng. 2024, 16, 16878132231219612. [Google Scholar] [CrossRef]
- Zhao, C.L.; Liu, Z.; Zheng, C.S.; Zhu, L.C.; Wang, Y.F. Research on Mechanical Leg Structure Design and Control System of Lower Limb Exoskeleton Rehabilitation Robot Based on Magnetorheological Variable Stiffness and Damping Actuator. Actuators 2024, 13, 132. [Google Scholar] [CrossRef]
- Wang, Y.W.; Wu, J.L.; Zhang, N.; Mo, W.W. Dynamics Modeling and Shift Control of a Novel Spring-Based Synchronizer for Electric Vehicles. Mech. Mach. Theory 2022, 168, 104586. [Google Scholar] [CrossRef]

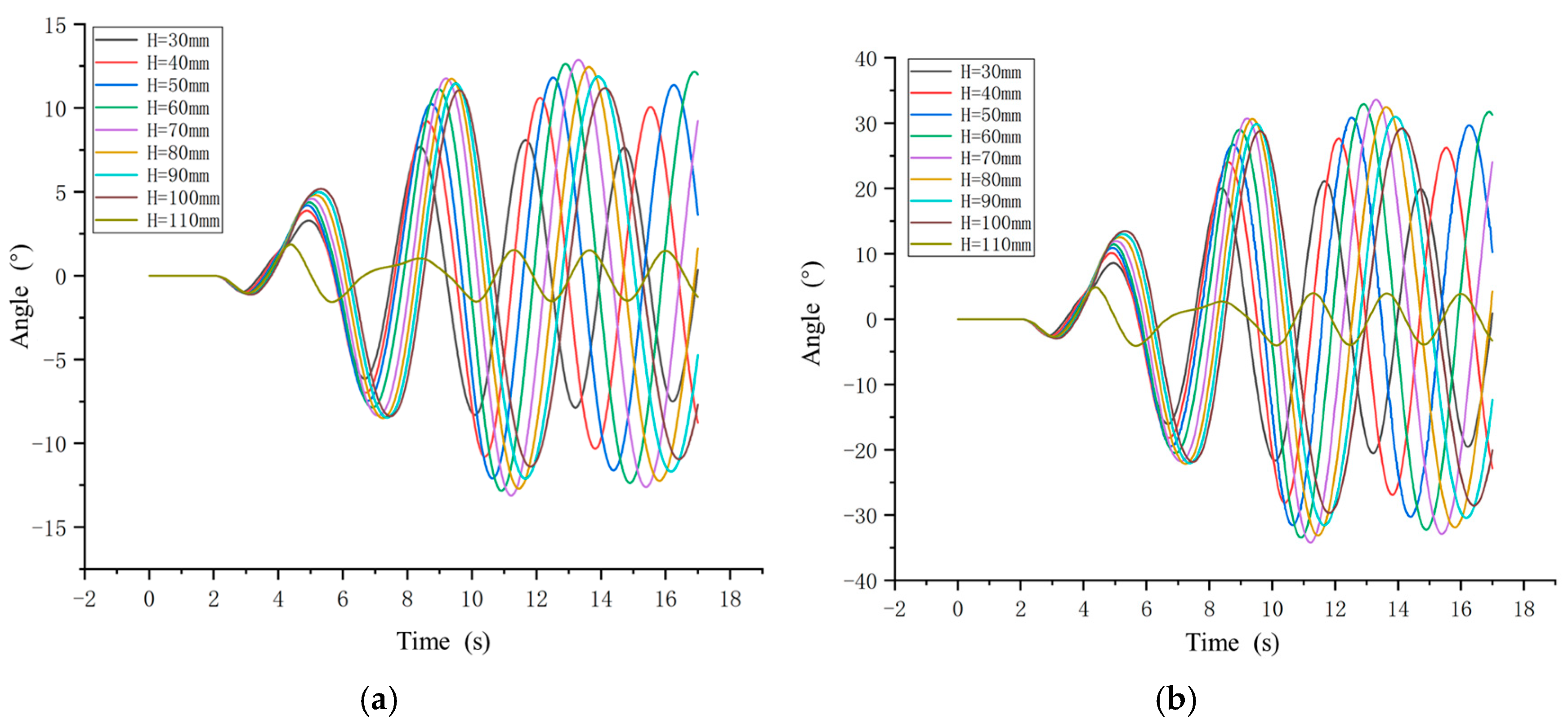
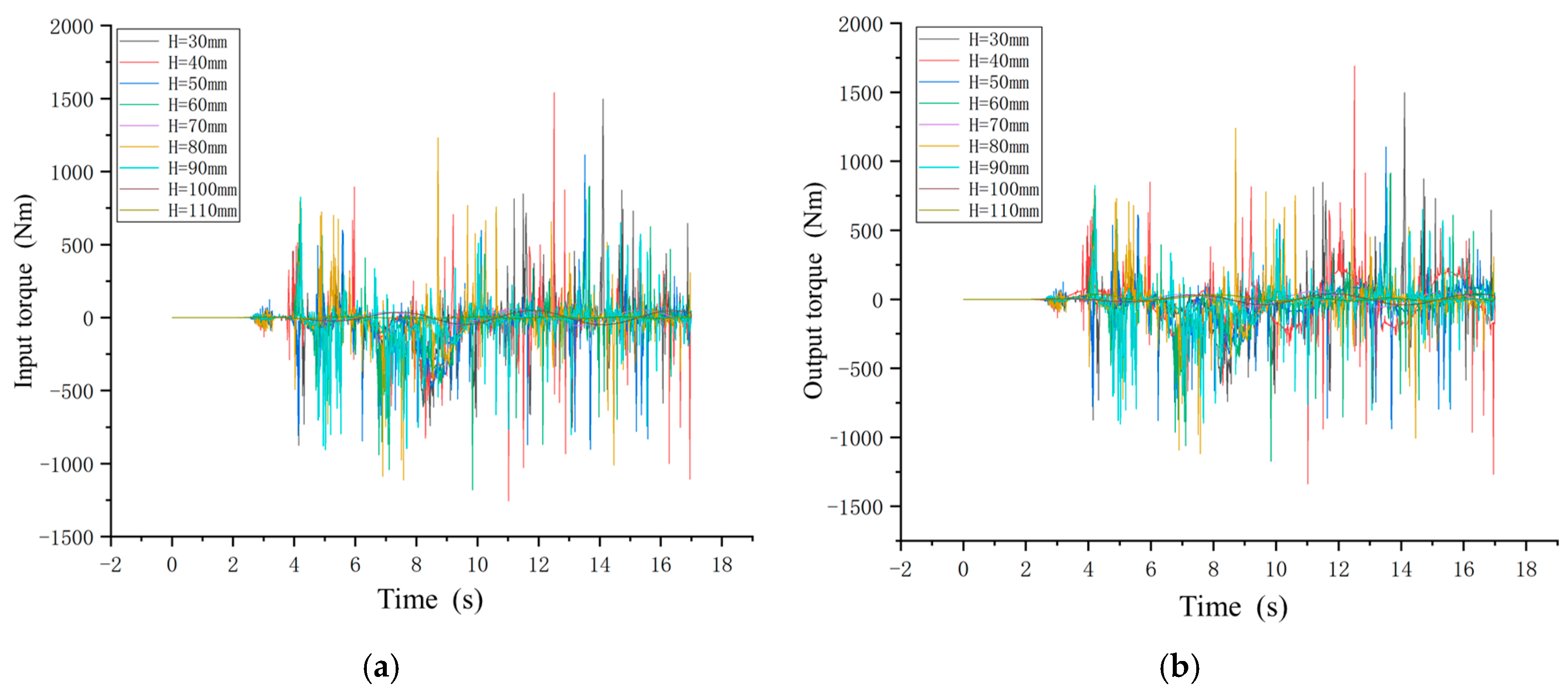
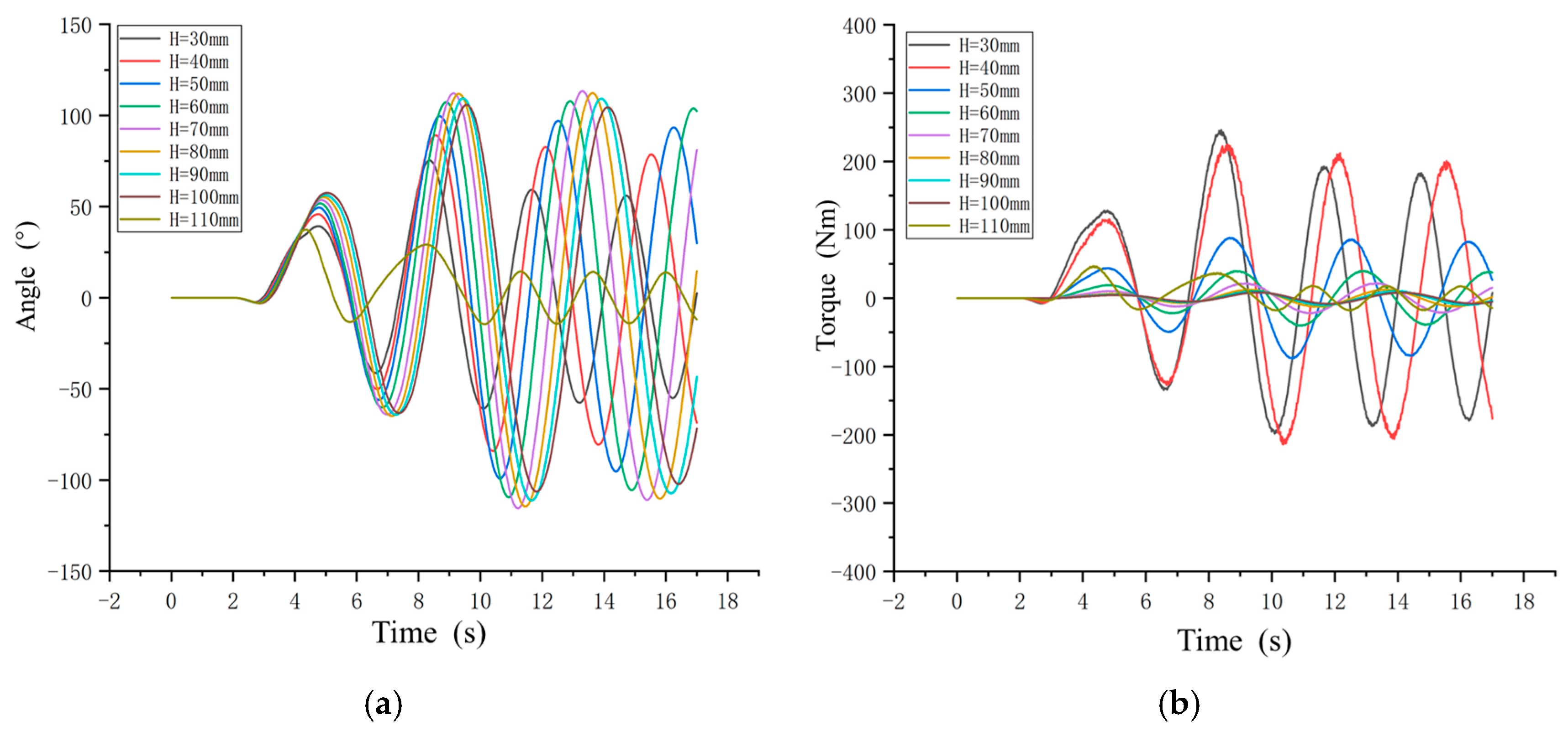
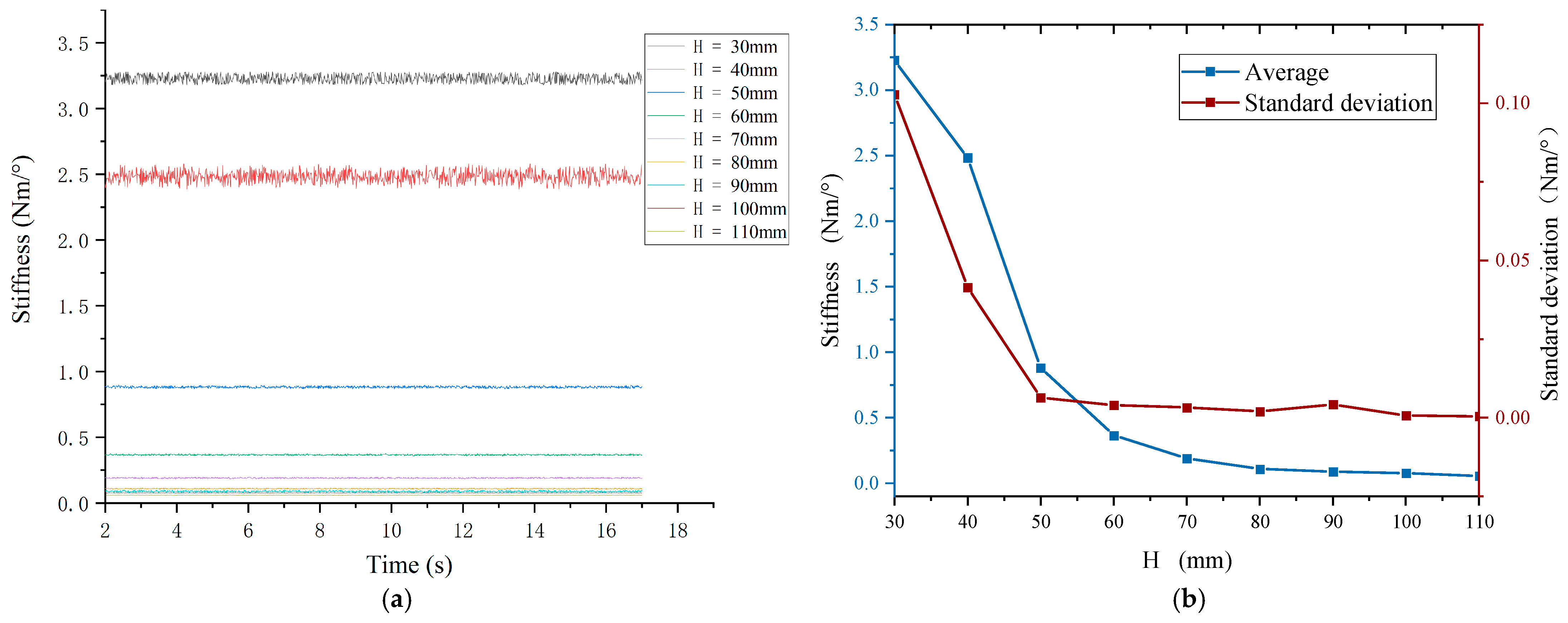





| Name | Type | Stiffness (Nm/rad) | Flexible Angle (°) |
|---|---|---|---|
| Baxter [33] | Traditional robot | inf. | 0 |
| Robot Arm [10] | Traditional robot | inf. | 0 |
| SEA [15] | Passive actuators | 98 | ±4.5 |
| PEA [13] | Passive actuators | 0.00529 | ±24.9 |
| BAVS [20] | VSA (antagonistic) | 3.9–146.6 | ±18.2 |
| SPVSA [21] | VSA (antagonistic) | 0–inf. | ±18.5 |
| MACCEPA [34] | VSA (variable spring-preload) | 5–110 | 60 |
| SDS-VSA [23] | VSA (variable spring-preload) | 0–4680 | - |
| REGT-VSA [26] | VSA (variable lever) | 20–2362 | ±10.31 |
| VSAPLM [24] | VSA (variable lever) | 98–533.6 | ±53 |
| RVSA [27] | VSA (variable spring physical parameter) | 20–inf. | ±8 |
| MERIA [35] | VSA (variable spring physical parameter) | 376–715 | 8 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 8.858 × 10−4 kg·m2 | 28 | ||
| 1.669 × 10−3 kg·m2 | 4 N/mm | ||
| 9.724 × 10−4 kg·m2 | 0.045 m | ||
| 1.613 × 103 kg/m | mm | ||
| 1.774 × 103 N/m | mm | ||
| 0.0255 m | 0.001 mm | ||
| 0.0388 m | 0.001 mm | ||
| 0.1095 m | × 45 kg·s/m | ||
| 17 | × 35 kg·s/m | ||
| 73 | Nonlinear backlash function of sun gear and planetary gear |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Zhang, Z.; Xiao, Y.; Gao, P.; Liu, X. Dynamic Modelling and Experimental Investigation of an Active–Passive Variable Stiffness Actuator. Actuators 2025, 14, 169. https://doi.org/10.3390/act14040169
Wang C, Zhang Z, Xiao Y, Gao P, Liu X. Dynamic Modelling and Experimental Investigation of an Active–Passive Variable Stiffness Actuator. Actuators. 2025; 14(4):169. https://doi.org/10.3390/act14040169
Chicago/Turabian StyleWang, Caidong, Zhou Zhang, Yanqiu Xiao, Pengfei Gao, and Xiaoli Liu. 2025. "Dynamic Modelling and Experimental Investigation of an Active–Passive Variable Stiffness Actuator" Actuators 14, no. 4: 169. https://doi.org/10.3390/act14040169
APA StyleWang, C., Zhang, Z., Xiao, Y., Gao, P., & Liu, X. (2025). Dynamic Modelling and Experimental Investigation of an Active–Passive Variable Stiffness Actuator. Actuators, 14(4), 169. https://doi.org/10.3390/act14040169






