Modeling and Analysis of Transmission Efficiency for 3K Planetary Gearbox with Flexure-Based Carrier for Backdrivable Robot Joints
Abstract
:1. Introduction
- A quasi-static model is established for the anti-backlash 3K planetary gearbox considering the tangential displacements of the planet gears due to the preloaded flexure-based carrier.
- An accurate transmission efficiency model is formulated for the anti-backlash 3K planetary gearbox by correcting the meshing efficiencies of gear pairs, which accounts for the additional power loss caused by the reverse meshing forces in planet gears.
- An anti-backlash 3K planetary gearbox prototype with four different carriers is fabricated and measured to validate the modified efficiency model, and the average errors between the predicted and the experimental results for forward and backward transmission efficiencies are 2.30% and 4.01%, respectively.
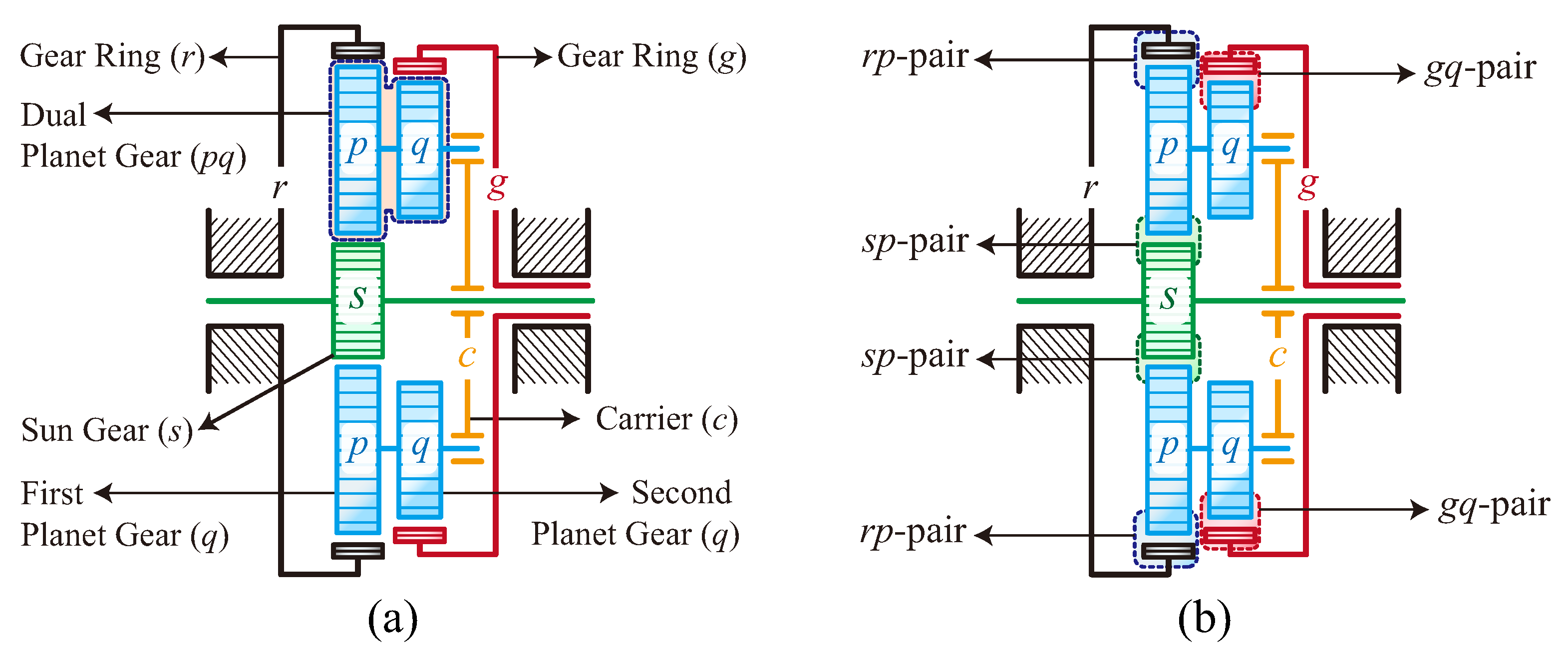
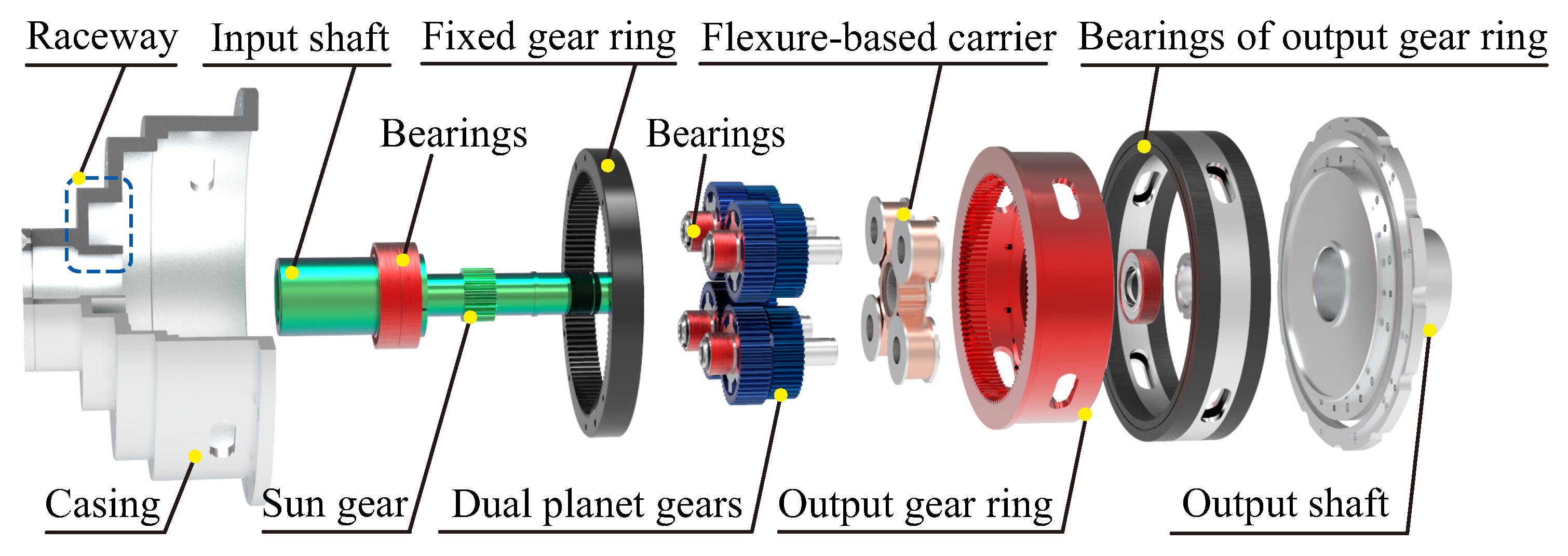
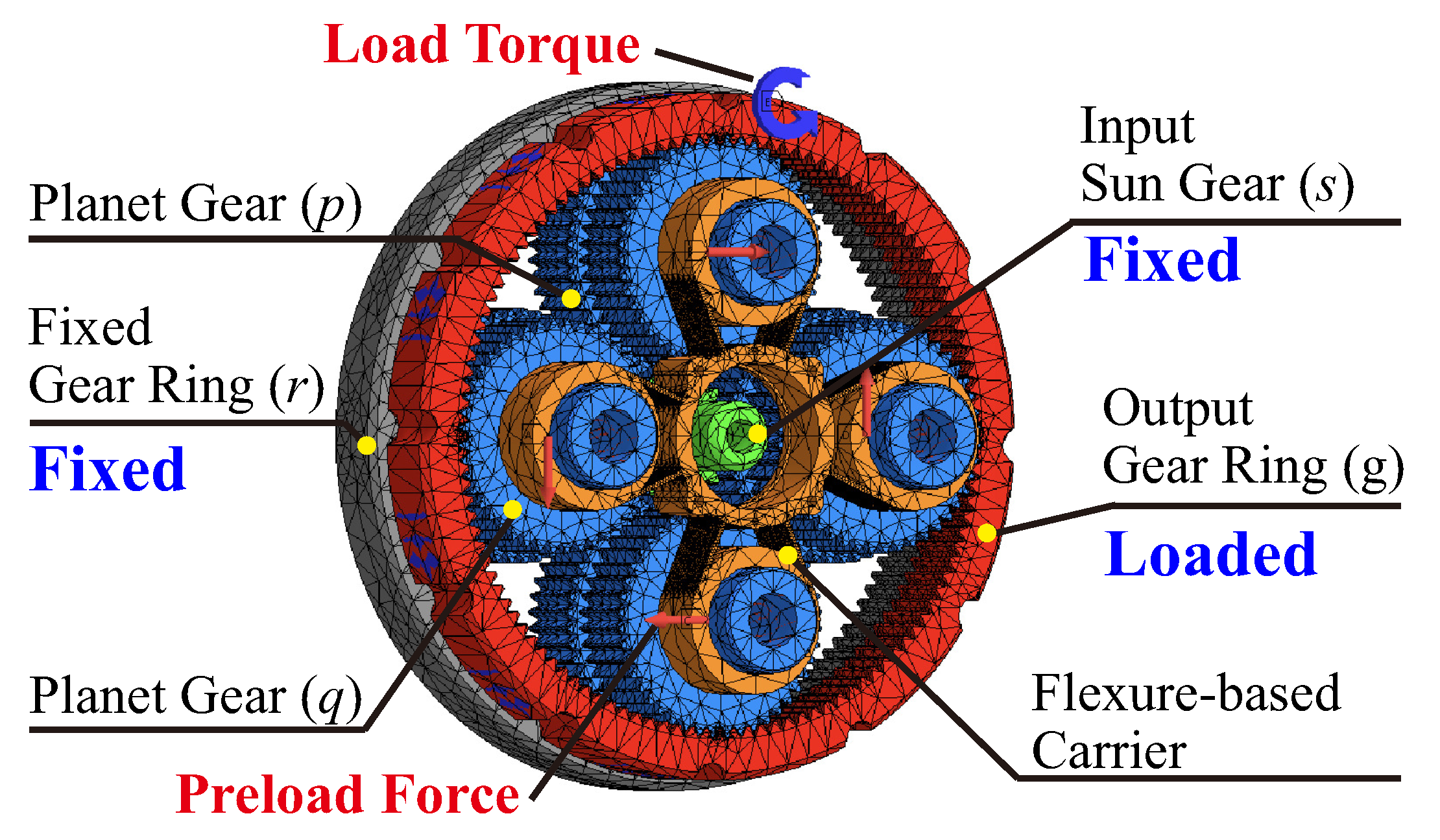
2. Description of Anti-Backlash 3K Planetary Gearbox with Flexure-Based Carrier
2.1. Structure of 3K Planetary Gearbox
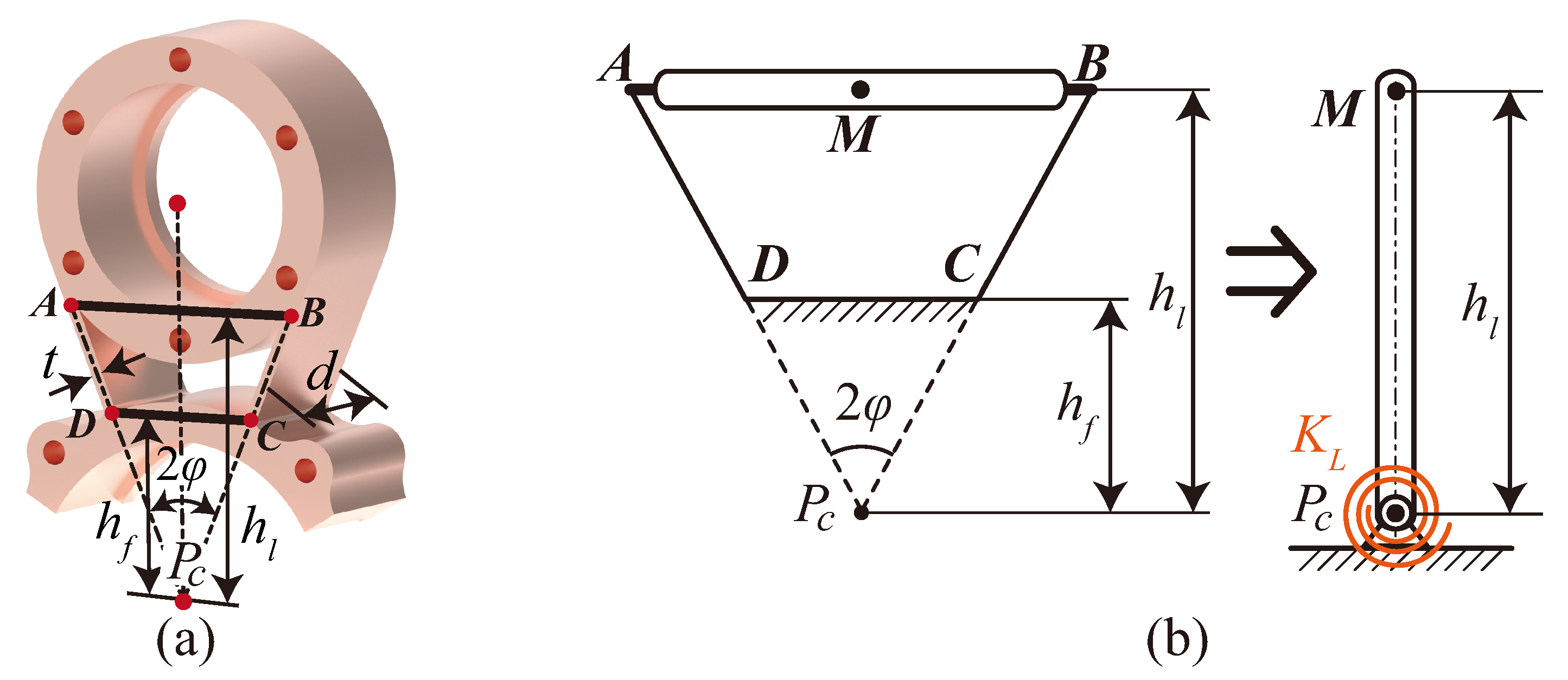
2.2. Structure of Flexure-Based Carrier
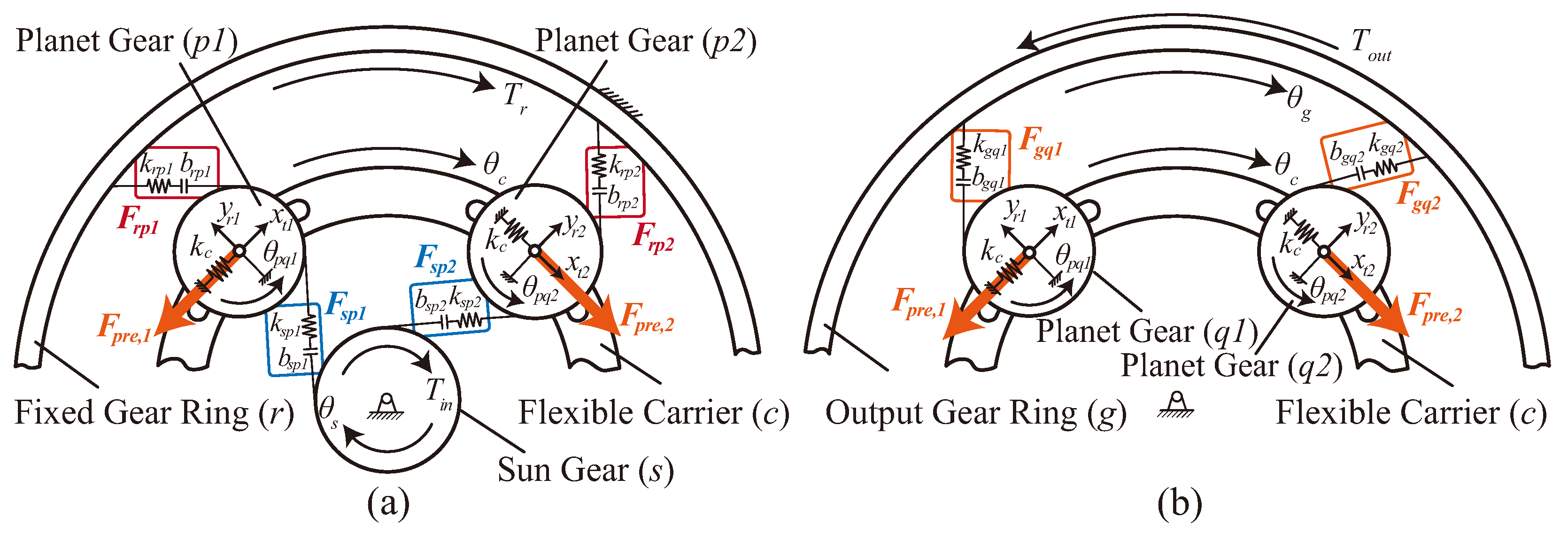
3. Quasi-Static Model of Anti-Backlash 3K Planetary Gearbox
3.1. Force Balance Equations
3.1.1. Meshing Forces
3.1.2. Tangential Supporting Stiffness and Preload of the Flexure-Based Carrier
3.2. Meshing Forces of Anti-Backlash 3K Planetary Gearbox
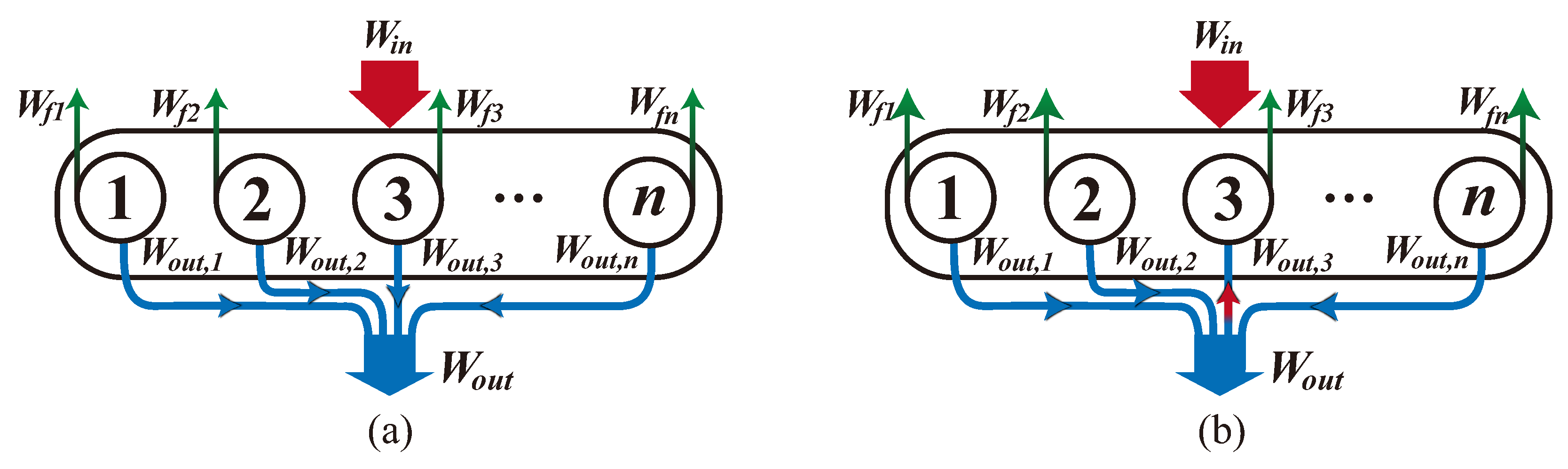
4. Modified Transmission Efficiency Model of the Anti-Backlash 3K Planetary Gearbox
4.1. BTEM of Conventional 3K Planetary Gearbox
4.2. Corrected Meshing Efficiency for Anti-Backlash 3K Planetary Gearbox
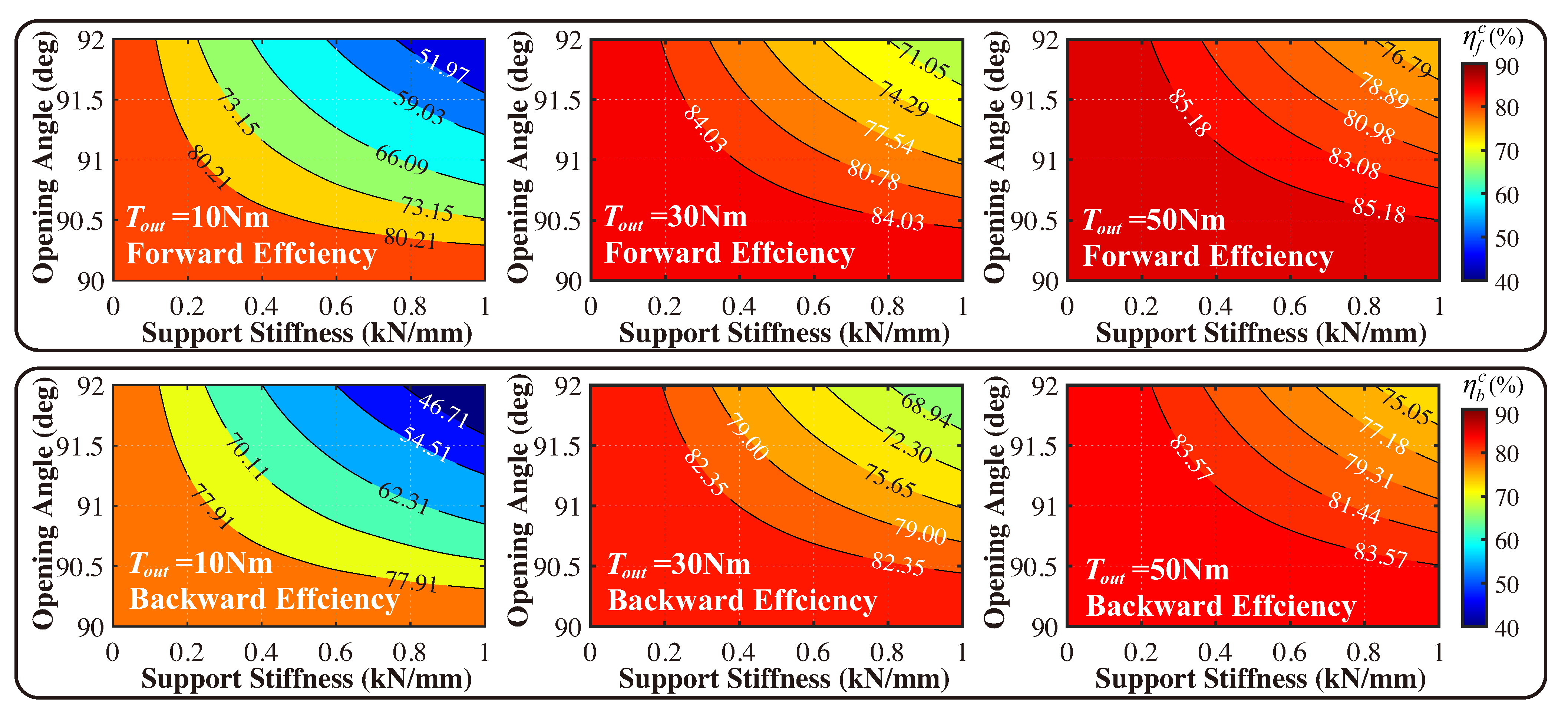
4.3. Effects of Flexure-Based Carrier on Transmission Efficiency
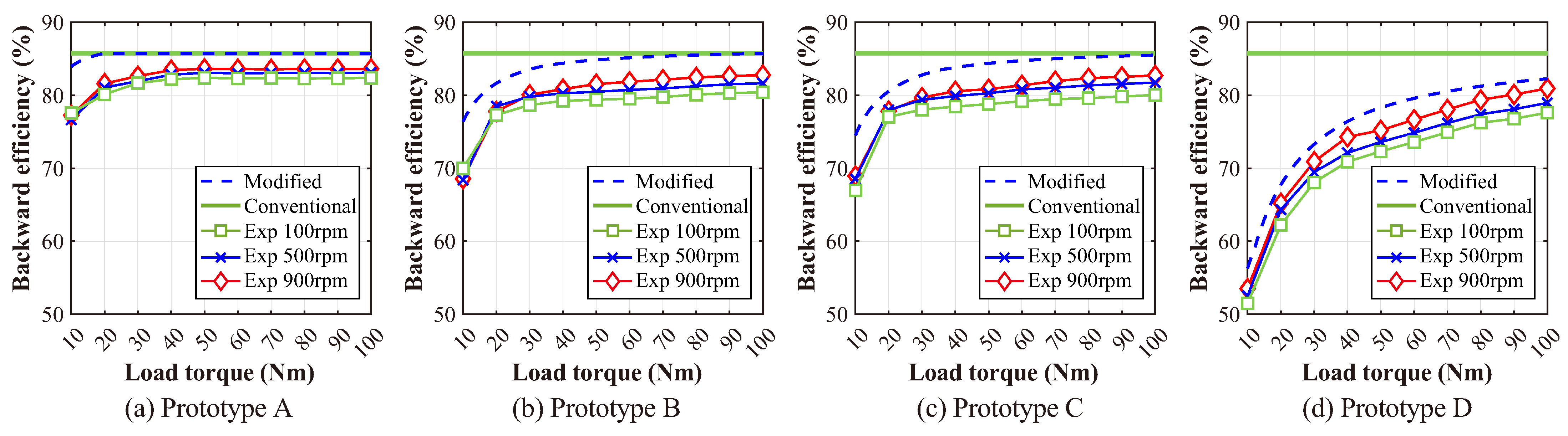
- The bidirectional transmission efficiencies of an anti-backlash 3K planetary gearbox decrease with the increase in the preload of the flexure-based carrier, especially under the light-load condition.
- The efficiencies increase as the load torque increases. It is because that high loads lead to the recovery deflection of the flexure-based carrier due to its compliance, which reduces the opening angle of the carrier and the absolute value of the reverse meshing forces decrease. This phenomenon is consistent with the meshing force analysis in Section 3.2.
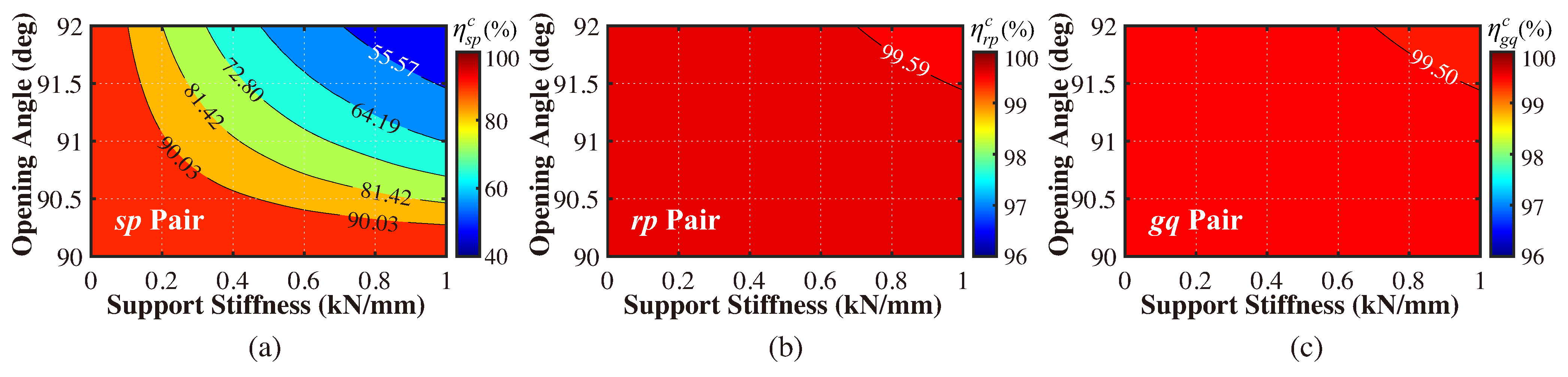
- The backward transmission efficiency is slightly lower than the forward but always higher than 0, which means the flexure-based carrier cannot lead to the self-locking of the 3K planetary gearbox even under the high-preload condition. It is because the reverse meshing forces mainly exist in the sp pair, while the reverse meshing forces in rp and gq pairs vanish rapidly with the increasing of the load torque as shown in Figure 6. It illustrates the preload of a carrier mainly affects the meshing efficiency of the sp pair, rather than rp and gq pairs, as shown in Figure 11. Considering the self-locking of the 3K planetary gearbox only occurs when from Equation (16), the preloaded flexure-based carrier does not affect the self-locking characteristic of the 3K planetary gearbox.
5. Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ishida, T.; Takanishi, A. A Robot Actuator Development with High Backdrivability. In Proceedings of the 2006 IEEE Conference on Robotics, Automation and Mechatronics, Bangkok, Thailand, 1–3 June 2006; pp. 1–6. [Google Scholar]
- Garcia, P.L.; Varadharajan, A.; Crispel, S.; Lefeber, D.; Verstraten, T.; Wikło, M.; Vasileiou, G. On the Potential of High-ratio Planetary Gearboxes for Next-generation Robotics. In Proceedings of the AGMA 2022 Fall Technical Meeting, Rosemont, IL, USA, 17–19 October 2022; pp. 50–63. [Google Scholar]
- Garcia, P.L.; Crispel, S.; Saerens, E.; Verstraten, T.; Lefeber, D. Compact Gearboxes for Modern Robotics: A Review. Front. Robot. 2020, 7, 103. [Google Scholar]
- Matsuki, H.; Nagano, K.; Fujimoto, Y. Bilateral Drive Gear—A Highly Backdrivable Reduction Gearbox for Robotic Actuators. IEEE/ASME Trans. Mechatronics 2019, 24, 2661–2673. [Google Scholar]
- Ling, Z.; Xiao, D.; Zhao, L.; Li, Y.; Ji, Z.; Xi, S.; Xia, X.; Zhou, Y. Self-lock Carrier: Realize Low-backlash Characteristic in 3K Planetary Gearbox. Adv. Mech. Eng. 2024, 16, 16878132241281079. [Google Scholar]
- Shin, W.; Ahn, B.; Kwon, S. A Low Backlash and Highly Efficient Gearbox for Robot Actuator. In Proceedings of the 2024 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 15–18 July 2024; pp. 224–229. [Google Scholar]
- Nandor, M.J.; Heebner, M.; Quinn, R.; Triolo, R.J.; Makowski, N.S. Transmission Comparison for Cooperative Robotic Applications. Actuators 2021, 10, 203. [Google Scholar] [CrossRef]
- Du, Q.; Zhang, T.; Yang, G.; Chen, C.Y.; Wang, W.; Zhang, C. A 3K Planetary Gear Train with a Flexure-based Anti-backlash Carrier for Collaborative Robots. Mech. Mach. Theory 2024, 191, 105495. [Google Scholar]
- Du, Q.; Zhang, T.; Yang, G.; Chen, C.Y.; Wang, W.; Zhang, C. Analytical Backlash Model for 3K-type Planetary Gear Train with Flexure-Based Anti-backlash Carrier. In Proceedings of the International Conference on Intelligent Robotics and Applications, Hangzhou, China, 5–7 July 2023; Springer: Singapore, 2023; pp. 384–397. [Google Scholar]
- Arnaudov, K.; Karaivanov, D.P. Planetary Gear Trains; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Tian, X.; Wang, G.; Jiang, Y. A New Calculation Method for Instantaneous Efficiency and Torque Fluctuation of Spur Gears. Stroj.-Vestn.-J. Mech. Eng. 2024, 70, 55–69. [Google Scholar]
- Yada, T. Review of Gear Efficiency Equation and Force Treatment. JSME Int. J. Ser. Dyn. Control. Robot. Des. Manuf. 1997, 40, 1–8. [Google Scholar] [CrossRef]
- Merritt, H.E. Gears: A Book of Reference for Engineers Concerned with the Design, Manufacture, Application or Maintenance of Gear Drives; Sir Isaac Pitman & Sons, Limited: London, UK, 1946. [Google Scholar]
- Buckingham, E. Analytical Mechanics of Gears; Courier Corporation: North Chelmsford, MA, USA, 1988. [Google Scholar]
- Muneharu, M. A Study of the Efficiency of the Planetary Gear Mechanism Applying the Mechanical Paradox Internal Gear. J. Fac. Eng. Shinshu Univ. 1979, 46, 1–12. [Google Scholar]
- Xu, X.; Chen, J.; Lin, Z.; Qiao, Y.; Chen, X.; Zhang, Y.; Xu, Y.; Li, Y. Optimization Design for the Planetary Gear Train of an Electric Vehicle under Uncertainties. Actuators 2022, 11, 49. [Google Scholar] [CrossRef]
- Li, C.; Qin, D.; Shi, W. Reference efficiency of planetary gear train. J. Chongqing Univ. 2006, 29, 11–14. [Google Scholar]
- Denny, C. Mesh Friction in Gearing; AGMA: Alexandria, VR, USA, 1998. [Google Scholar]
- Michlin, Y.; Myunster, V. Determination of Power Losses in Gear Transmissions with Rolling and Sliding Friction Incorporated. Mech. Mach. Theory 2002, 37, 167–174. [Google Scholar] [CrossRef]
- Xu, H.; Kahraman, A.; Anderson, N.; Maddock, D. Prediction of Mechanical Efficiency of Parallel-axis Gear Pairs. J. Mech. Des. 2007, 129, 58–68. [Google Scholar] [CrossRef]
- Li, S.; Kahraman, A. A Transient Mixed Elastohydrodynamic Lubrication Model for Spur Gear Pairs. J. Tribol. 2010, 132, 011501. [Google Scholar] [CrossRef]
- Li, S.; Kahraman, A. Prediction of Spur Gear Mechanical Power Losses Using a Transient Elastohydrodynamic Lubrication Model. Tribol. Trans. 2010, 53, 554–563. [Google Scholar] [CrossRef]
- Li, S.; Kahraman, A. A Method to Derive Friction and Rolling Power Loss Formulae for Mixed Elastohydrodynamic Lubrication. J. Adv. Mech. Des. Syst. Manuf. 2011, 5, 252–263. [Google Scholar] [CrossRef]
- Fernandes, C.M.; Martins, R.C.; Seabra, J.H. Coefficient of Friction Equation for Gears based on a Modified Hersey Parameter. Tribol. Int. 2016, 101, 204–217. [Google Scholar] [CrossRef]
- Blech, N.; Paschold, C.; Amar, L.; Lohner, T.; Tobie, T.; Stahl, K. Review of Different Calculation Approaches for the Mean Coefficient of Friction in ISO 6336. Forsch. Ingenieurwesen 2023, 87, 1169–1179. [Google Scholar] [CrossRef]
- Duan, Q.; Yang, S. A Fundamental Element Solution to Complicated Epicyclical Gear Trains. Mach. Des. Res. 2001, 17, 55–56+8. [Google Scholar]
- Duan, Q.; Yang, S. A Study on Power Flow and Meshing Efficiency of 3K Type Planetary Gear Train. Mech. Sci. Technol. 2002, 21, 360–362. [Google Scholar]
- Chen, L.F.; Wu, X.L.; Qin, D.T.; Wen, Z.J. Investigation on the Transmission Efficiency of the Planetary Gear Train. Appl. Mech. Mater. 2012, 103, 205–208. [Google Scholar] [CrossRef]
- Laus, L.; Simas, H.; Martins, D. Machine Efficiency Determined Using Graph and Screw Theories with Application in Robotics. Mech. Mach. Theory 2020, 148, 103748. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q. Power Analysis and Efficiency Calculation of the Complex and Closed Planetary Gears Transmission. Energy Procedia 2016, 100, 423–433. [Google Scholar]
- Wang, C. The Effect of Planetary Gear/Star Gear on the Transmission Efficiency of Closed Differential Double Helical Gear Train. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 4215–4223. [Google Scholar]
- Crispel, S.; García, P.L.; Saerens, E.; Varadharajan, A.; Verstraten, T.; Vanderborght, B.; Lefeber, D. A Novel Wolfrom-Based Gearbox for Robotic Actuators. IEEE/ASME Trans. Mechatronics 2021, 26, 1980–1988. [Google Scholar] [CrossRef]
- Shi, J.L.; Ma, X.G.; Xu, C.L.; Zang, S.J. Meshing stiffness analysis of gear using the Ishikawa method. Appl. Mech. Mater. 2013, 401, 203–206. [Google Scholar] [CrossRef]
- Xu, P.; Jingjun, Y.; Guanghua, Z.; Shusheng, B. The Stiffness Model of Leaf-Type Isosceles-Trapezoidal Flexural Pivots. J. Mech. Des. 2008, 130, 082303. [Google Scholar]
- Garcia, P.L.; Saerens, E.; Crispel, S.; Varadharajan, A.; Lefeber, D.; Verstraten, T. Factors influencing actuator’s backdrivability in human-centered robotics. MATEC Web Conf. 2022, 366, 01002. [Google Scholar]
- Varadharajan, A.; Garcia, P.L.; Crispel, S.; Vanderborght, B.; Lefeber, D.; Verstraten, T. Unconventional Gear Profiles in Planetary Gearboxes. In AGMA 2022 Fall Technical Meet; AGMA Foundation: Alexandria, VR, USA, 2022; pp. 40–49. [Google Scholar]
- Talbot, D.; Kahraman, A.; Singh, A. An Experimental Investigation of the Efficiency of Planetary Gear Sets. J. Mech. Des. 2012, 134, 7. [Google Scholar]
- Talbot, D.; Kahraman, A. A Methodology to Predict Power Losses of Planetary Gear Sets. In Proceedings of the International Gear Conference (Lyon-Villeurbanne), Lyon, France, 26–28 August 2014; pp. 26–28. [Google Scholar]
- Wang, A.; Kim, S. Directional Efficiency in Geared Transmissions: Characterization of Backdrivability towards Improved Proprioceptive Control. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 1055–1062. [Google Scholar]



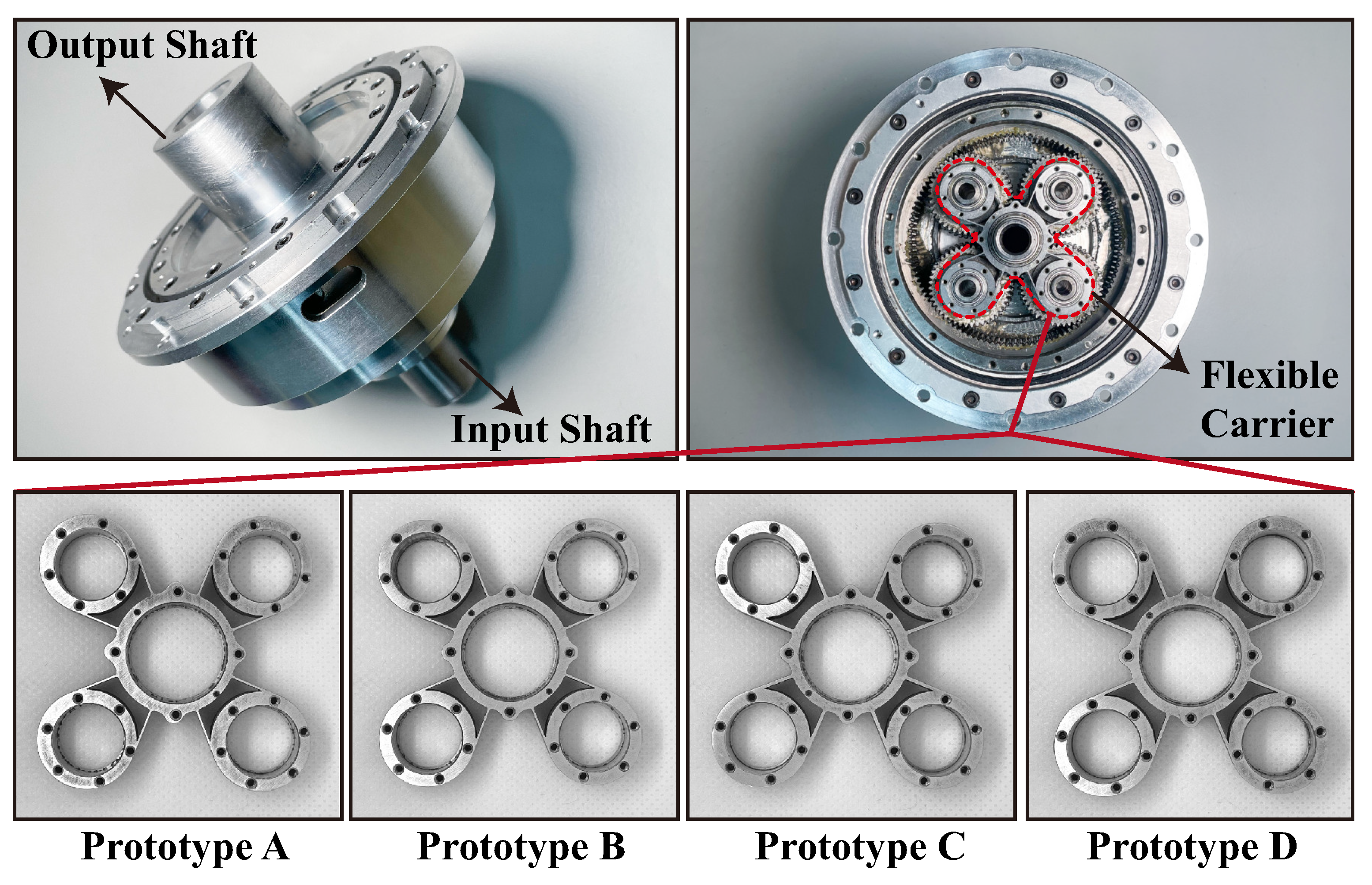


| Parameter | Content | Value |
|---|---|---|
| Tooth number of the sun gear s | 24 | |
| Tooth number of the planet gear p | 48 | |
| Tooth number of the planet gear q | 44 | |
| Tooth number of the gear ring r | 120 | |
| Tooth number of the gear ring g | 116 | |
| n | Number of the dual planet gears | 4 |
| Average stiffness of the -pair | 271 N/m | |
| Average stiffness of the -pair | 317 N/m | |
| Average stiffness of the -pair | 315 N/m | |
| b | Half of the backlash | 30 m |
| Pressure angle | 20 deg | |
| Working pressure angle | 24.31 deg | |
| m | Module | 0.7 mm |
| E | Young’s modulus of the carrier | 71 GPa |
| d | Thickness of the carrier | 9.5 mm |
| Opening angle of the carrier | 91 deg | |
| t | Width of the leaf spring | 0.71 mm |
| Height of LITFP’s long side | 19.39 mm | |
| Height of LITFP’s short side | 12.43 mm | |
| Opening angle of the LITFP | 22.98 deg |
| Case Order | Opening Angle | Tangential Supporting Stiffness |
|---|---|---|
| A | 90.5 deg | 0.2 kN/mm |
| B | 91.5 deg | 0.2 kN/mm |
| C | 90.5 deg | 0.8 kN/mm |
| D | 91.5 deg | 0.8 kN/mm |
| Case Order | Conventional Model (%) | Modified Model (%) | ||
|---|---|---|---|---|
| Forward | Backward | Forward | Backward | |
| A | 1.86 | 3.65 | 1.65 | 3.43 |
| B | 4.86 | 6.45 | 2.94 | 4.52 |
| C | 5.03 | 6.79 | 2.48 | 4.22 |
| D | 11.91 | 13.88 | 2.14 | 3.88 |
| Average | 5.91 | 7.69 | 2.30 | 4.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, Q.; Yang, G.; Wang, W.; Chen, C.-Y.; Fang, Z. Modeling and Analysis of Transmission Efficiency for 3K Planetary Gearbox with Flexure-Based Carrier for Backdrivable Robot Joints. Actuators 2025, 14, 173. https://doi.org/10.3390/act14040173
Du Q, Yang G, Wang W, Chen C-Y, Fang Z. Modeling and Analysis of Transmission Efficiency for 3K Planetary Gearbox with Flexure-Based Carrier for Backdrivable Robot Joints. Actuators. 2025; 14(4):173. https://doi.org/10.3390/act14040173
Chicago/Turabian StyleDu, Qinghao, Guilin Yang, Weijun Wang, Chin-Yin Chen, and Zaojun Fang. 2025. "Modeling and Analysis of Transmission Efficiency for 3K Planetary Gearbox with Flexure-Based Carrier for Backdrivable Robot Joints" Actuators 14, no. 4: 173. https://doi.org/10.3390/act14040173
APA StyleDu, Q., Yang, G., Wang, W., Chen, C.-Y., & Fang, Z. (2025). Modeling and Analysis of Transmission Efficiency for 3K Planetary Gearbox with Flexure-Based Carrier for Backdrivable Robot Joints. Actuators, 14(4), 173. https://doi.org/10.3390/act14040173







