Deep Reinforcement Learning-Based Motion Control Optimization for Defect Detection System
Abstract
:1. Introduction
2. Design and Control Principles of the Defect Detection System
2.1. X-Ray Defect Detection System for Deep-Sea Manned Spherical Shell Welds
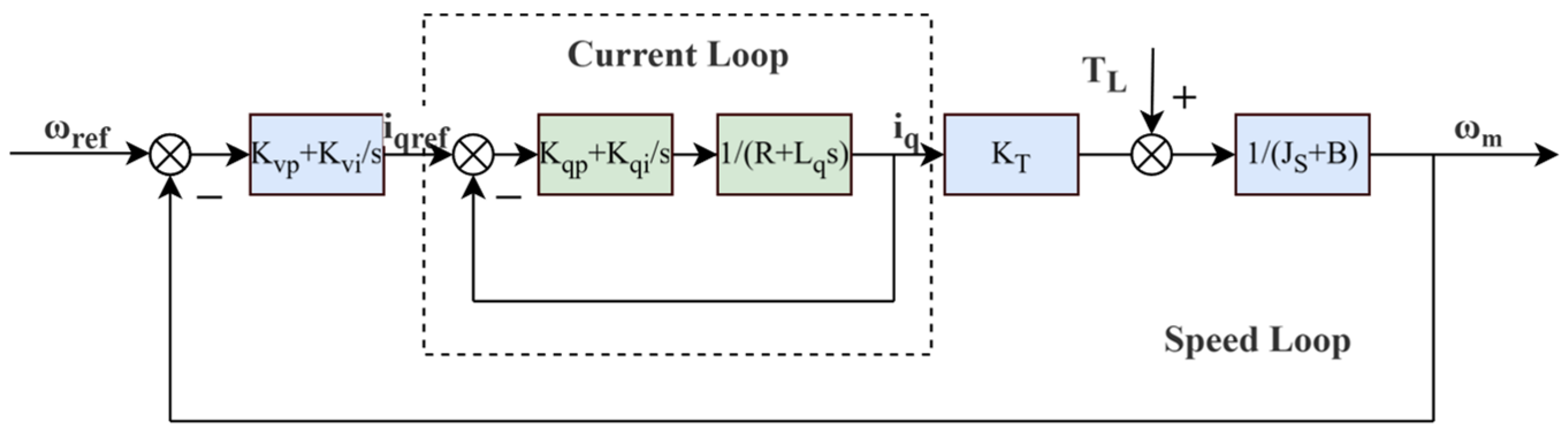
2.2. Drive Motor Control Principle
3. Control Optimization Based on Reinforcement Learning
3.1. TD3 Algorithm
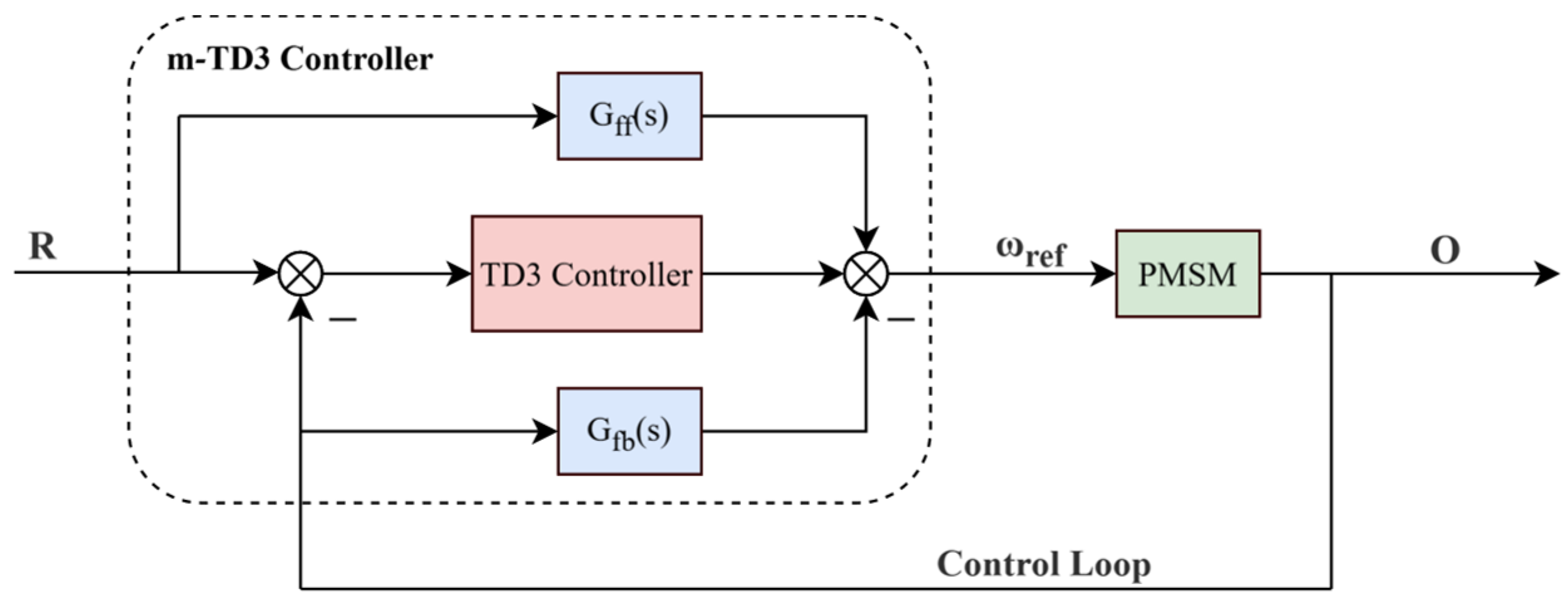
3.2. m-TD3 Composite Controller Based on Reinforcement Learning
3.2.1. Agent Design
- The shallow network will reduce the learning ability of the network, while the deep network will reduce the training speed and increase the computing cost consumption. More importantly, in the actual experiment, we found that the deep network will have a similar change trend in the output result due to the increase in the influence weight of the public part of the front end of the network before output differentiation, which will affect the actual effect. This is obviously not what we want to see, and the double hidden layer can achieve a good balance.
- The application of a tanh activation function in the front end of the actor network can limit the output of the hidden layer and avoid numerical explosion, which solves the instability caused by output oscillation in the actual training process. The additional relu after the output layer aims to limit the gain range of the PID controller.
- The critic network needs to integrate the current state and the output strategy of the actor network, and the output formula of the Q value is .
3.2.2. Improved TD3 Algorithm
- Combination reward mechanism
- b.
- Security constraint mechanism
3.2.3. m-TD3 Composite Controller Based on CP-MPA
- Update formula for the exploration process incorporating Brownian motion:
- Update formula for the exploitation process incorporating Lévy flight:where is the prey matrix, is the predator matrix, is the global step size, is the exploration variable in [0,1), is the Brownian motion variable, is the convergence variable, and is the Levy flight variable. In addition, the MPA applies FAD perturbation to the prey matrix to further improve the exploration ability of the algorithm [32].
- Chaotic initialization: Because the initial population critically affects optimization, random initialization can yield uneven coverage and restricted exploration. Chaotic initialization ensures more uniform coverage and enhances global exploration:where is the chaotic sequence generated by chaotic mapping, and its value is in the range of . An initialization and chaos factor are required, and the chaotic sequence is generated by the formula [33]
- Predator population mechanism: The predator matrix in Reference [32] is repeatedly copied from top predators, and is the same. In the actual natural environment, predator groups should also have individuality; that is, there should be individual differences among predators. At the same time, there is also an apex predator, the leader of the predator population. The individual behavior of the predator should be influenced by the decisions of both the prey and the leader. Therefore, this paper proposes an MPA based on the predator population mechanism. The improved predator population behavior is defined by the formula as follows:
3.2.4. Deployment of the m-TD3 Composite Controller
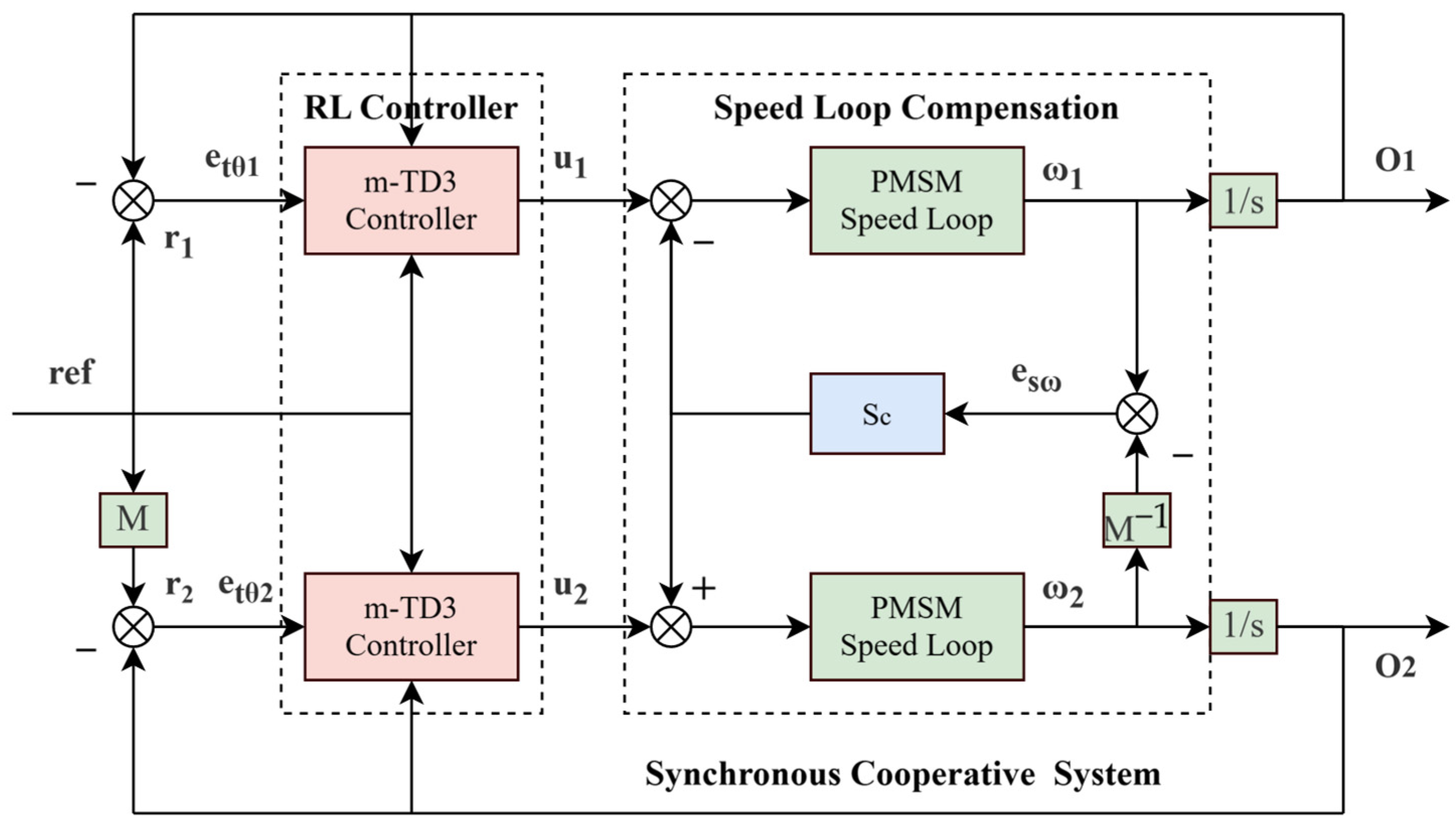
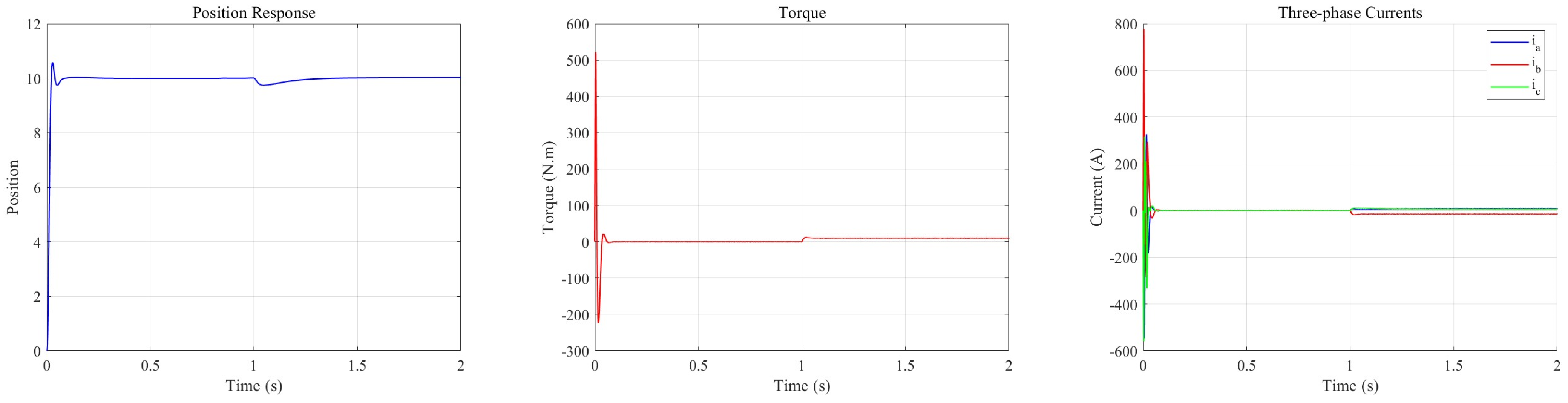
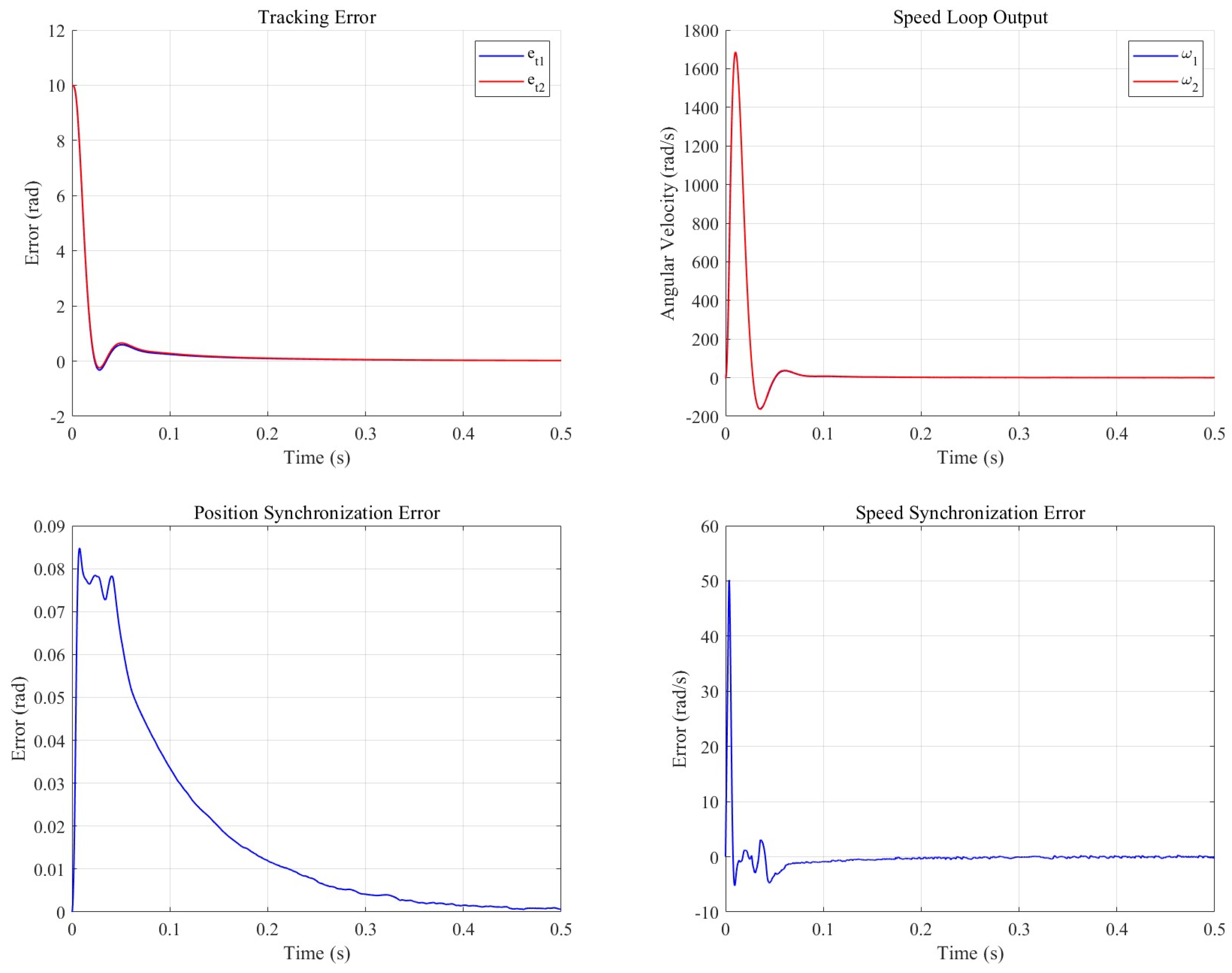
3.3. Synchronous Cooperative Motion Compensator
4. Experiment
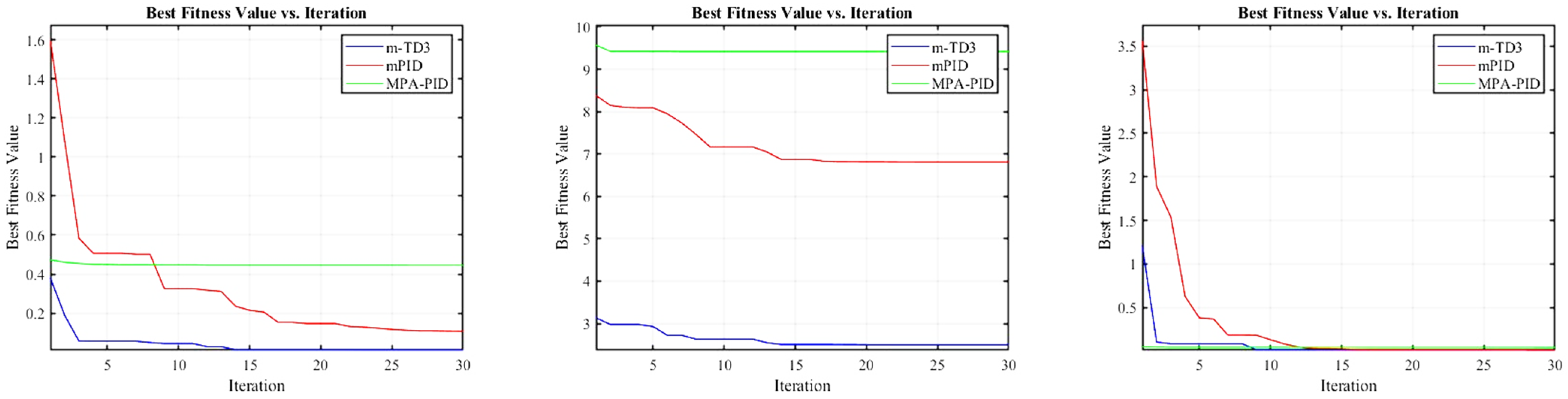
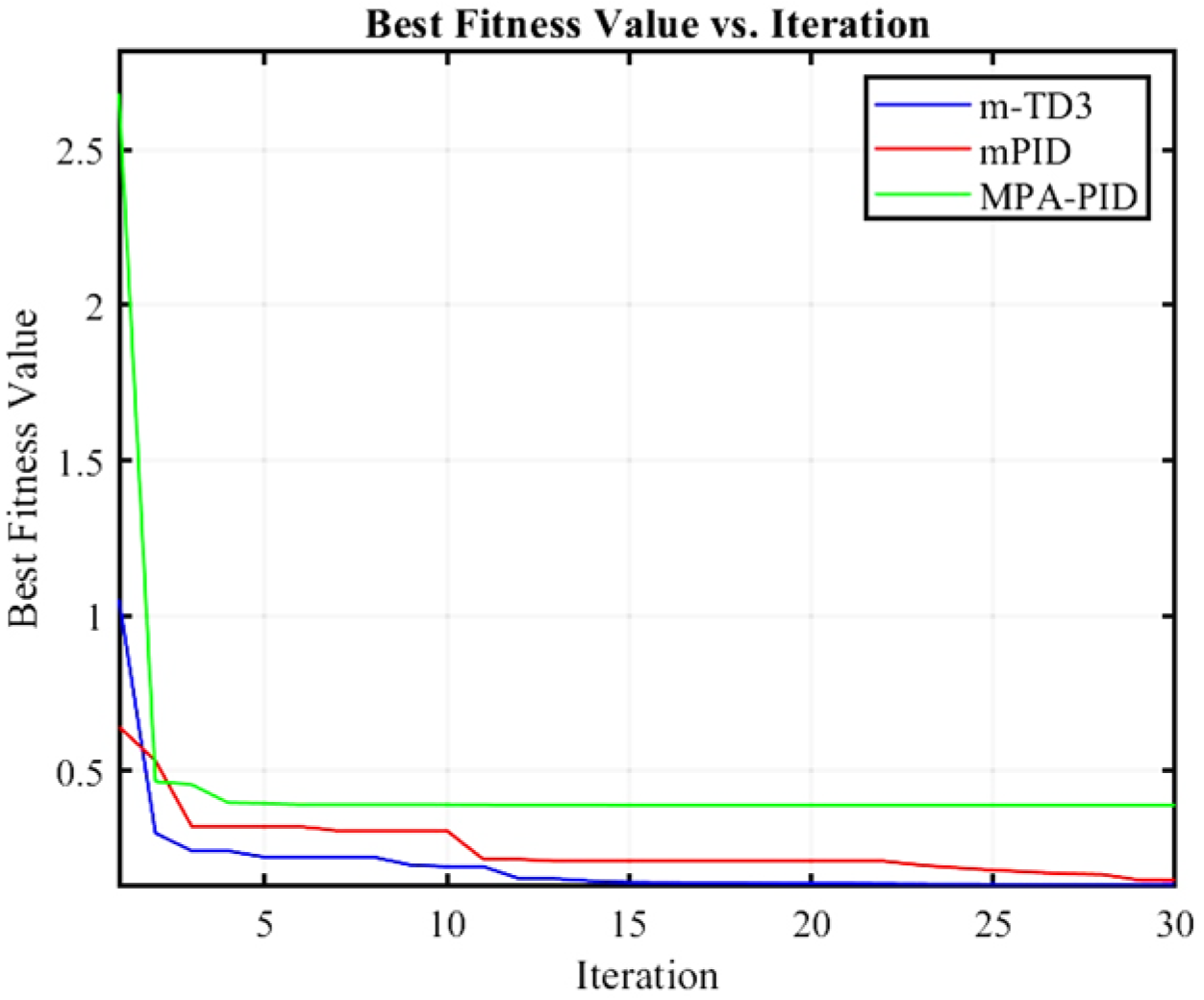
4.1. Linear System Simulation Experiments
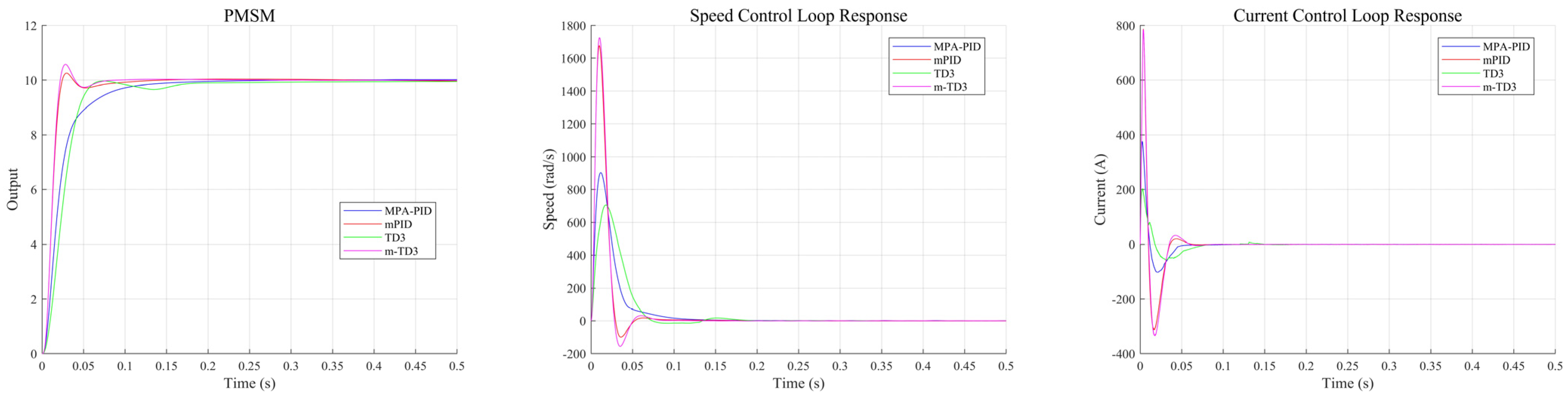
4.2. PMSM Control System Simulation Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miller, T.J.E. Brushless Permanent-Magnet and Reluctance Motor Drives; IEEE Press: New York, NY, USA, 1989. [Google Scholar]
- Li, J.; Yu, J.J.; Chen, Z. A Review of Control Strategies for Permanent Magnet Synchronous Motor Used in Electric Vehicles. Appl. Mech. Mater. 2013, 321–324, 1679–1685. [Google Scholar] [CrossRef]
- Sato, D.; Itoh, J.-I. Open-loop control for permanent magnet synchronous motor driven by square-wave voltage and stabilization control. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Blaschke, F. The principle of field orientation as applied to the new TRANSVECTOR closed loop control system for rotating field machines. Siemens Rev. 1972, 34, 217–220. [Google Scholar]
- Pillay, P.; Krishnan, R. Modeling, simulation, and analysis of permanent-magnet motor drives. I. The permanent-magnet synchronous motor drive. IEEE Trans. Ind. Appl. 1989, 25, 265–273. [Google Scholar] [CrossRef]
- Takahashi, I.; Noguchi, T. A New Quick-Response and High-Efficiency Control Strategy of an Induction Motor. IEEE Trans. Ind. Appl. 1986, IA-22, 820–827. [Google Scholar] [CrossRef]
- Minorsky, N. Directional stability of automatically steered bodies. J. Am. Soc. Nav. Eng. 1922, 34, 280–309. [Google Scholar] [CrossRef]
- Utkin, V. Variable structure systems with sliding modes. IEEE Trans. Autom. Control 1977, 22, 212–222. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A.; Yuan, B.; Klir, G.J. Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems; Selected Papers by Lotfi A. Zadeh; World Scientific Publishing Co., Inc.: Hackensack, NJ, USA, 1996. [Google Scholar]
- Visioli, A. Tuning of PID controllers with fuzzy logic. IEE Proc. Control Theory Appl. 2001, 148, 1–8. [Google Scholar] [CrossRef]
- Mohammed, N.F.; Song, E.; Ma, X.; Hayat, Q. Tuning of PID controller of synchronous generators using genetic algorithm. In Proceedings of the 2014 IEEE International Conference on Mechatronics and Automation, Tianjin, China, 3–6 August 2014; pp. 1544–1548. [Google Scholar] [CrossRef]
- Gaing, Z.-L. A particle swarm optimization approach for optimum design of PID controller in AVR system. IEEE Trans. Energy Convers. 2004, 19, 384–391. [Google Scholar] [CrossRef]
- Bhattacharyya, D.; Ray, A.K. Stepless PWM speed control of AC motors: A neural network approach. Neurocomputing 1994, 6, 523–539. [Google Scholar] [CrossRef]
- Mao, Z.; Kobayashi, R.; Nabae, H.; Suzumori, K. Multimodal Strain Sensing System for Shape Recognition of Tensegrity Structures by Combining Traditional Regression and Deep Learning Approaches. IEEE Robot. Autom. Lett. 2024, 9, 10050–10056. [Google Scholar] [CrossRef]
- Peng, Y.; Yang, X.; Li, D.; Ma, Z.; Liu, Z.; Bai, X.; Mao, Z. Predicting flow status of a flexible rectifier using cognitive computing. Expert Syst. Appl. 2025, 264, 125878. [Google Scholar] [CrossRef]
- Sutton, R.S. Learning to predict by the methods of temporal differences. Mach. Learn. 1988, 3, 9–44. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1928–1937. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Krizhevsky, A.G.; Silver, D.; Salakhutdinov, R. Continuous control with deep reinforcement learning. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Fujimoto, S.; van Hoof, H.; Meger, D. Addressing Function Approximation Error in Actor-Critic Methods. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1582–1590. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Shuprajhaa, T.; Sujit, S.K.; Srinivasan, K. Reinforcement learning based adaptive PID controller design for control of linear/nonlinear unstable processes. Appl. Soft Comput. 2022, 128, 109450. [Google Scholar] [CrossRef]
- Dogru, O.; Velswamy, K.; Ibrahim, F.; Wu, Y.; Sundaramoorthy, A.S.; Huang, B.; Xu, S.; Nixon, M.; Bell, N. Reinforcement Learning Approach to Autonomous PID Tuning. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022; pp. 2691–2696. [Google Scholar] [CrossRef]
- Bloor, M.; Ahmed, A.; Kotecha, N.; Mercangöz, M.; Tsay, C.; del Río-Chanona, E.A. Control-Informed Reinforcement Learning for Chemical Processes. Ind. Eng. Chem. Res. 2024, 64, 4966–4978. [Google Scholar] [CrossRef]
- Zhu, B.; Zhang, Y.; Xu, P.; Song, S.; Jiao, S.; Zheng, X. A dual-motor cross-coupling control strategy for position synchronization. J. Harbin Univ. Sci. Technol. 2022, 27, 114–121. [Google Scholar] [CrossRef]
- Zhang, Y. Research on X-ray Source Optimization and System Control Method for Spherical Shell Weld Inspection. Master’s Thesis, Southeast University, Nanjing, China, 2022. [Google Scholar]
- Yuan, L.; Hu, B.; Wei, K.; Chen, S. Principles of Modern Permanent Magnet Synchronous Motor Control and MATLAB Simulation; Beihang University Press: Beijing, China, 2016. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Shi, R.; Liu, W.; Wang, G.; Lan, C.; Xu, M. Improved voltage regulation strategy for three-phase PWM rectifier based on two-degree-of-freedom PID. Electr. Power Eng. Technol. 2023, 42, 149–156+178. [Google Scholar]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]




| Actor | Critic | |
|---|---|---|
| InputLayer 3 hiddenLayer 128 tanh hiddenLayer 128 tanh ActOutLyr 3 relu | InputLayerS 3 | InputLayerA 3 |
| hiddenLayer 64 tanh | hiddenLayer 64 tanh | |
| ConcatenationLayer | ||
| hiddenLayer 128 tanh | ||
| QvalOutLyr 3 | ||
| Parameter | Value |
|---|---|
| 0.01 | |
| MiniBatchSize | 64 |
| ExperienceBufferLength | |
| LearnRate | |
| GradientThreshold | 5 |
| TargetSmoothing_StandardDeviation | 0.1 |
| MaxEpisodes | |
| MaxStepsPerEpisode | 500 |
| ScoreAveragingWindowLength | 100 |
| DiscountFactor | 0.99 |
| DeferUpdateFrequency | 2 |
| PMSM Parameter | Value |
|---|---|
| H | |
| H | |
| Permanent Magnet Flux Linkage | Wb |
| Moment of Inertia | kg⋅ |
| Friction Coefficient | N⋅m⋅s |
| Number of Pole Pairs | 4 |
| 1.0071 N⋅m/A | |
| Phase | 3 |
| Optimized Parameters | First-Order | Second-Order | Equivalent Approximation | |
|---|---|---|---|---|
| MPA-PID | 67.2921 | 414.6895 | 29.6682 | |
| 64.8467 | 0 | 0 | ||
| 24.9545 | 50 | |||
| 0.44520 | 9.4173 | 0.0446 | ||
| m-PID | 41.8180 | 280.4223 | 7.1142 | |
| 57.0582 | 0.1051 | 0.068071 | ||
| 25.3344 | 50 | 7.9813 | ||
| 0.118036 | 133.8913 | 0 | ||
| 19.8055 | 49.99960 | 0.085011 | ||
| 1.13408 | 144.3892 | 0 | ||
| 18.8222 | 0.010635 | |||
| 0.10560 | 6.811 | 0.01470 | ||
| m-TD3 | 0.26184 | 26.4618 | 0.26436 | |
| 9.85420 | 50 | 0.084062 | ||
| 1.52590 | 34.812 | 0.263970 | ||
| 9.081 | 0.004358 | 0 | ||
| 0.0108 | 2.5002 | 0.0128 |
| EI | |||||
|---|---|---|---|---|---|
| First-order | MPA-PID | 970.34 | |||
| m-PID | 3.5215 × 10−3 | 1969.8 | |||
| TD3 | 127.99 | ||||
| m-TD3 | 1.3095 × 10−9 | 8.7374 × 10−7 | 553.3 | ||
| Second-order | MPA-PID | 9.1091 | 0.26517 | 0.10588 | 0.80199 |
| m-PID | 4.8525 | 0.16675 | 0.056628 | 1.2562 | |
| TD3 | 4.2121 | 0.21615 | 0.025355 | 0.76005 | |
| m-TD3 | 2.428 | 0.072269 | 0.009924 | 1.4451 | |
| Equivalent Approximation | MPA-PID | 0.57269 | 4675.1 | ||
| m-PID | 0.92637 | 26,569 | |||
| TD3 | 0.96858 | 84,416 | |||
| m-TD3 | 5.7279 × 10−3 | 3.963 × 10−5 | 0.97063 | 84,472 | |
| EI | |||||
|---|---|---|---|---|---|
| PMSM0.5s | MPA-PID | 0.26301 | 0.010870 | 0.001707 | 18.681 |
| m-PID | 0.14320 | 0.020315 | 0.025706 | 51.265 | |
| TD3 | 0.29908 | 0.064883 | 0 | 22.279 | |
| m-TD3 | 0.13403 | 0.005963 | 0.058173 | 53.924 | |
| PMSM2.0s | MPA-PID | 0.29464 | 0.021269 | 0.002267 | 18.681 |
| m-PID | 0.31258 | 0.124750 | 0.025706 | 51.265 | |
| TD3 | 0.33170 | 0.014440 | 0 | 22.279 | |
| m-TD3 | 0.15163 | 0.014806 | 0.058173 | 53.924 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.; Zhao, L.; Chen, X.; Li, Z. Deep Reinforcement Learning-Based Motion Control Optimization for Defect Detection System. Actuators 2025, 14, 180. https://doi.org/10.3390/act14040180
Cai Y, Zhao L, Chen X, Li Z. Deep Reinforcement Learning-Based Motion Control Optimization for Defect Detection System. Actuators. 2025; 14(4):180. https://doi.org/10.3390/act14040180
Chicago/Turabian StyleCai, Yuhuan, Liye Zhao, Xingyu Chen, and Zhenjun Li. 2025. "Deep Reinforcement Learning-Based Motion Control Optimization for Defect Detection System" Actuators 14, no. 4: 180. https://doi.org/10.3390/act14040180
APA StyleCai, Y., Zhao, L., Chen, X., & Li, Z. (2025). Deep Reinforcement Learning-Based Motion Control Optimization for Defect Detection System. Actuators, 14(4), 180. https://doi.org/10.3390/act14040180






