A Novel Overlapped Compensation Structure and Its Effectiveness Verification for Expansion Joints in Plate-Type PMEDS Vehicles
Abstract
:1. Introduction
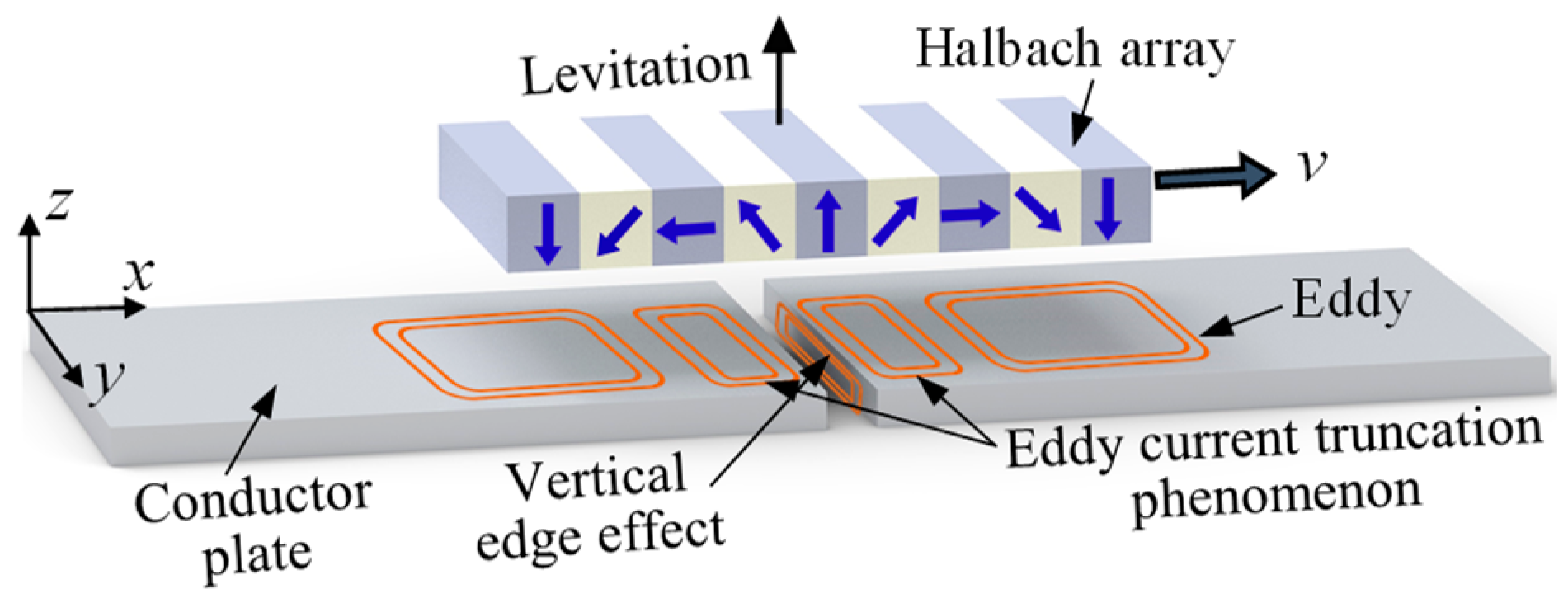
2. Structure and Principle
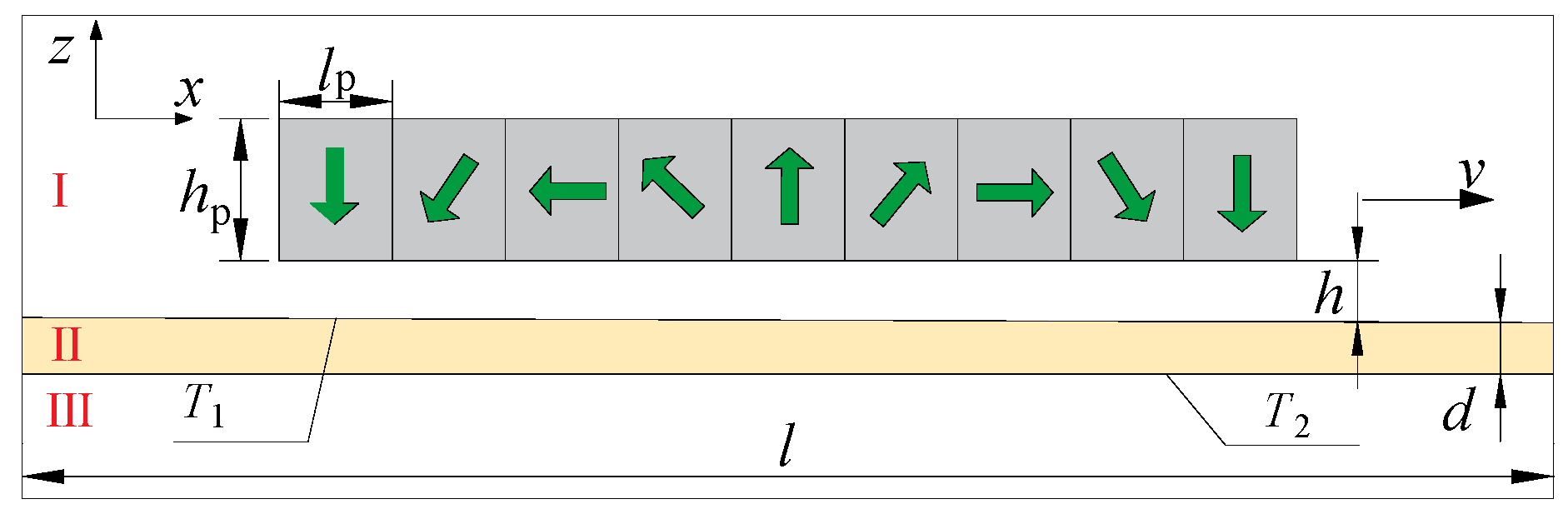
2.1. Structures of Expansion Joints
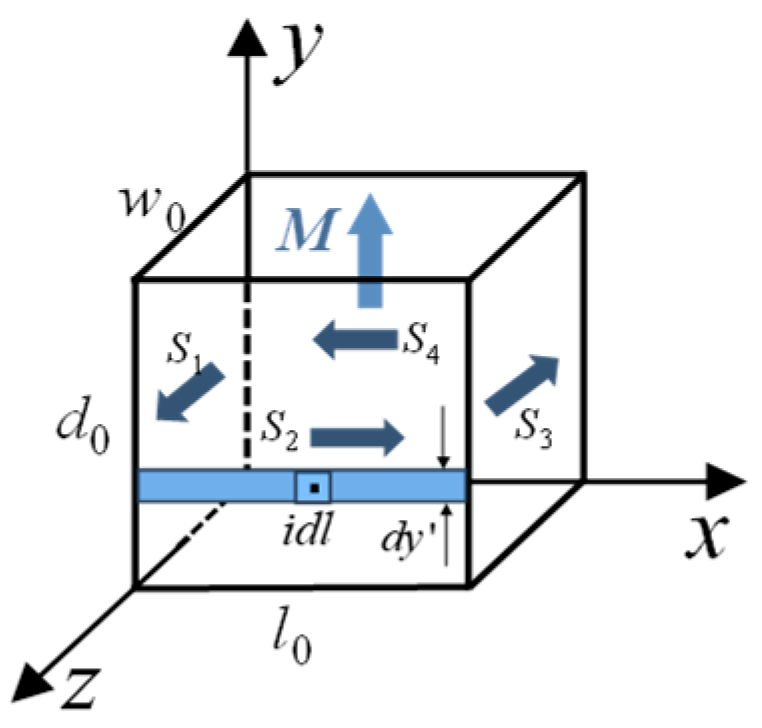
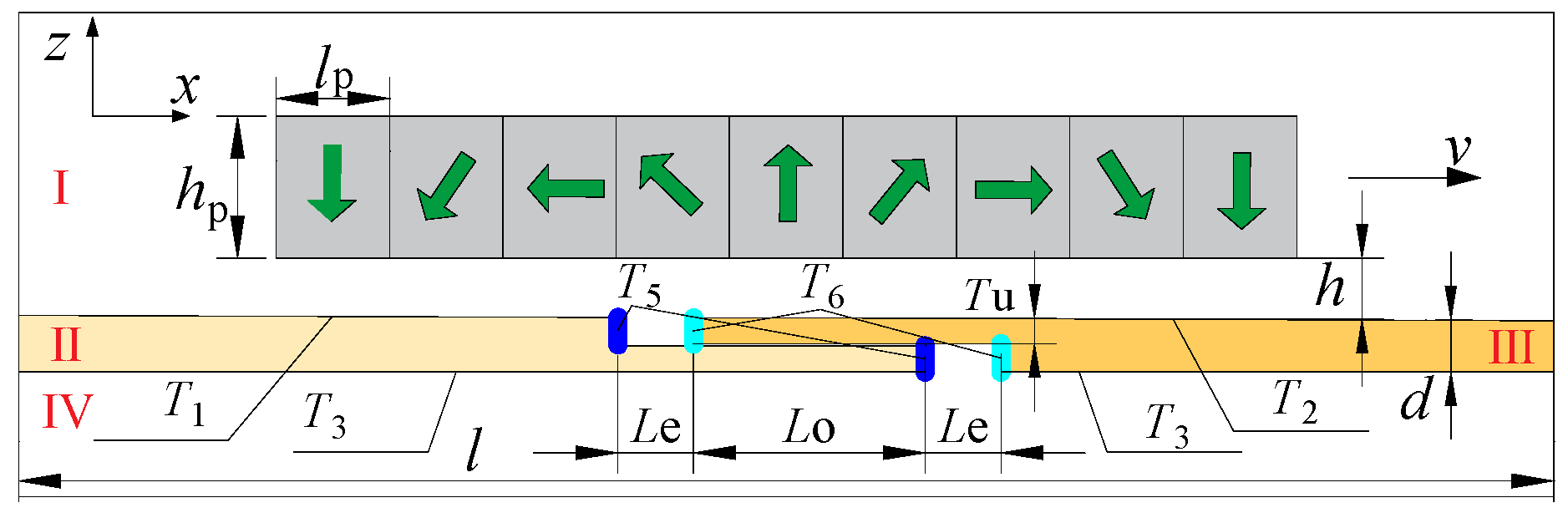
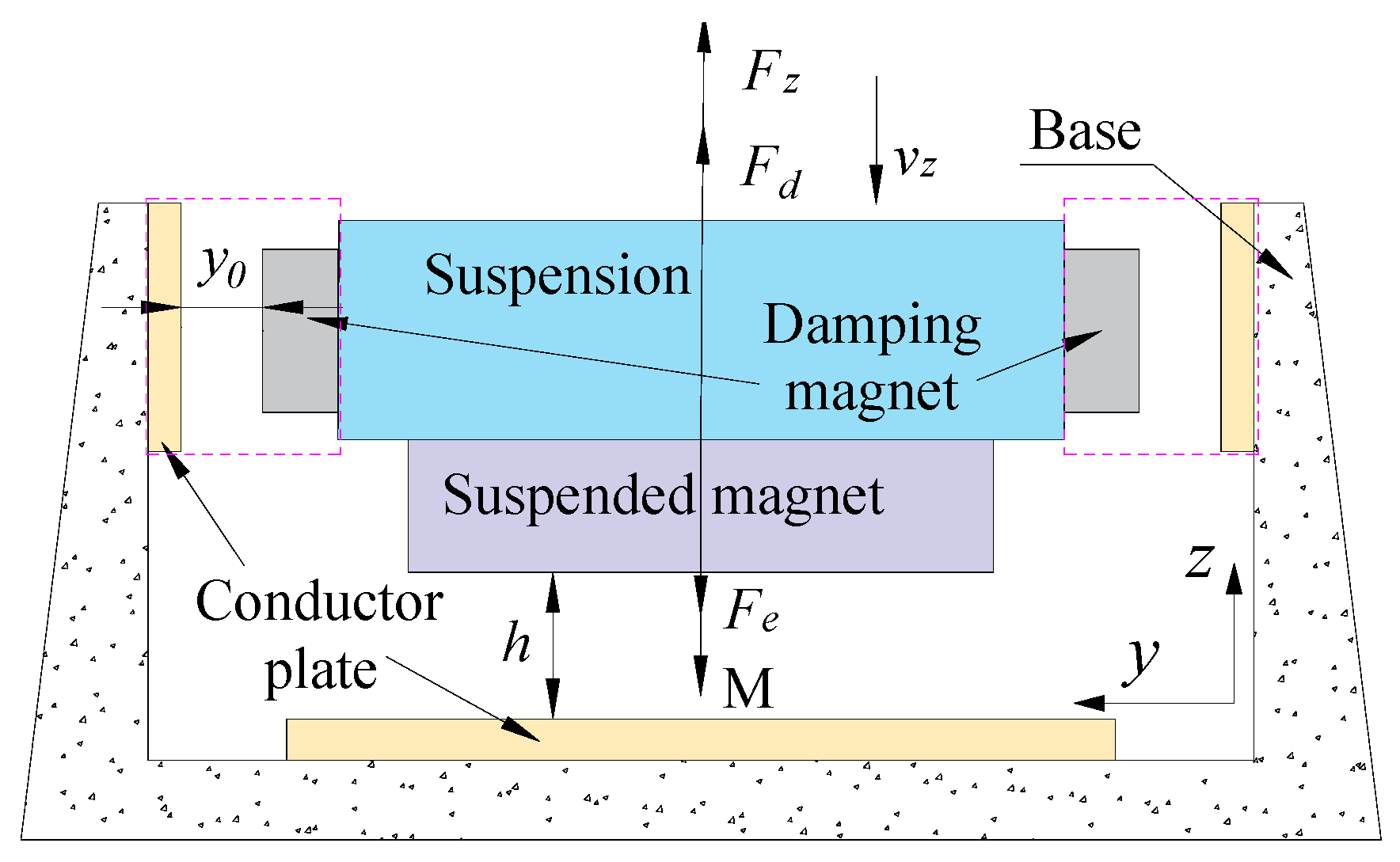
2.2. Analytical Model of PMEDS with Overlapped Compensation Structure
3. Electromagnetic Characteristics and Optimization of Overlapped Compensation
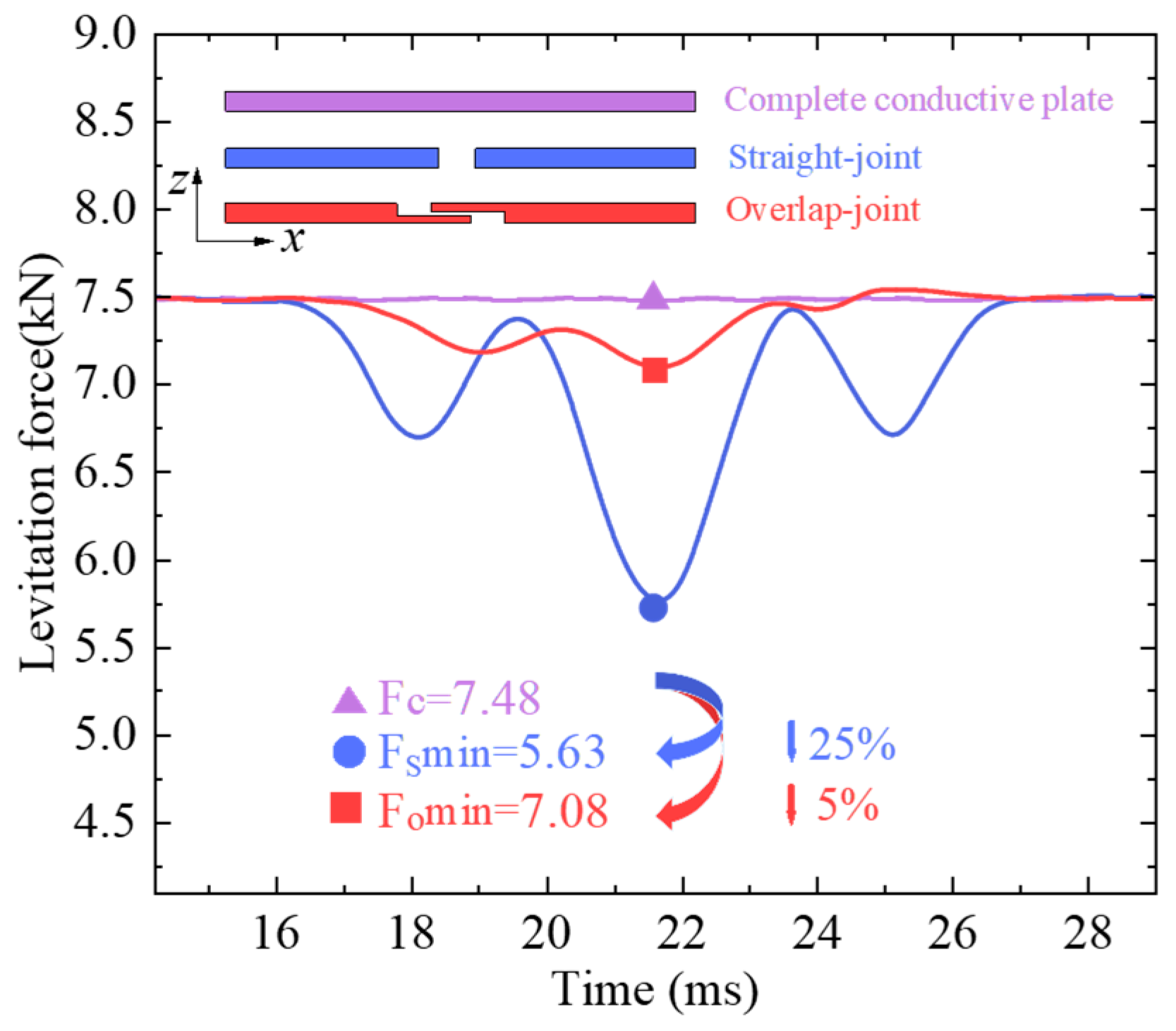
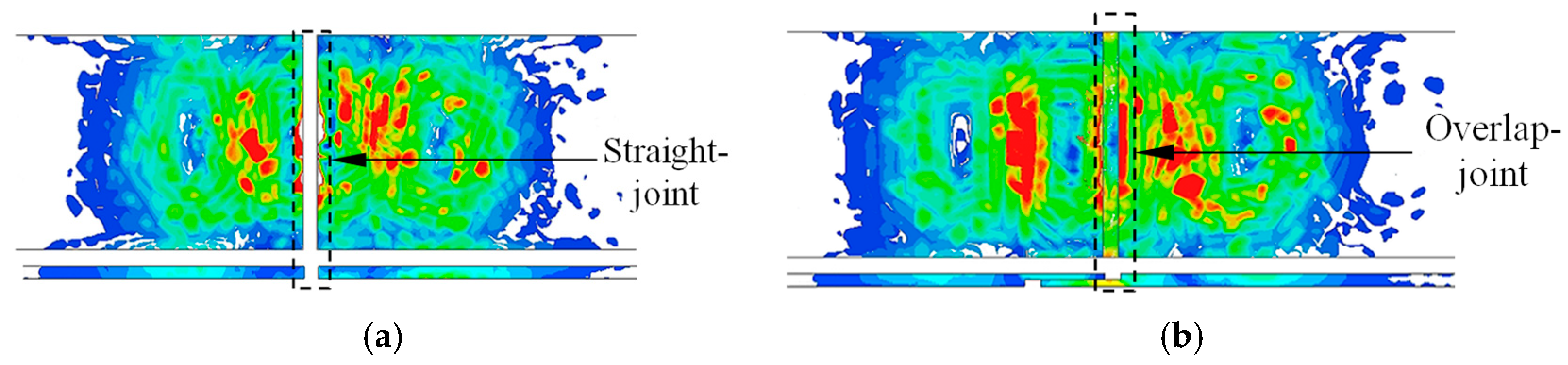
3.1. Effectiveness Analysis of Overlapped Compensation Structure
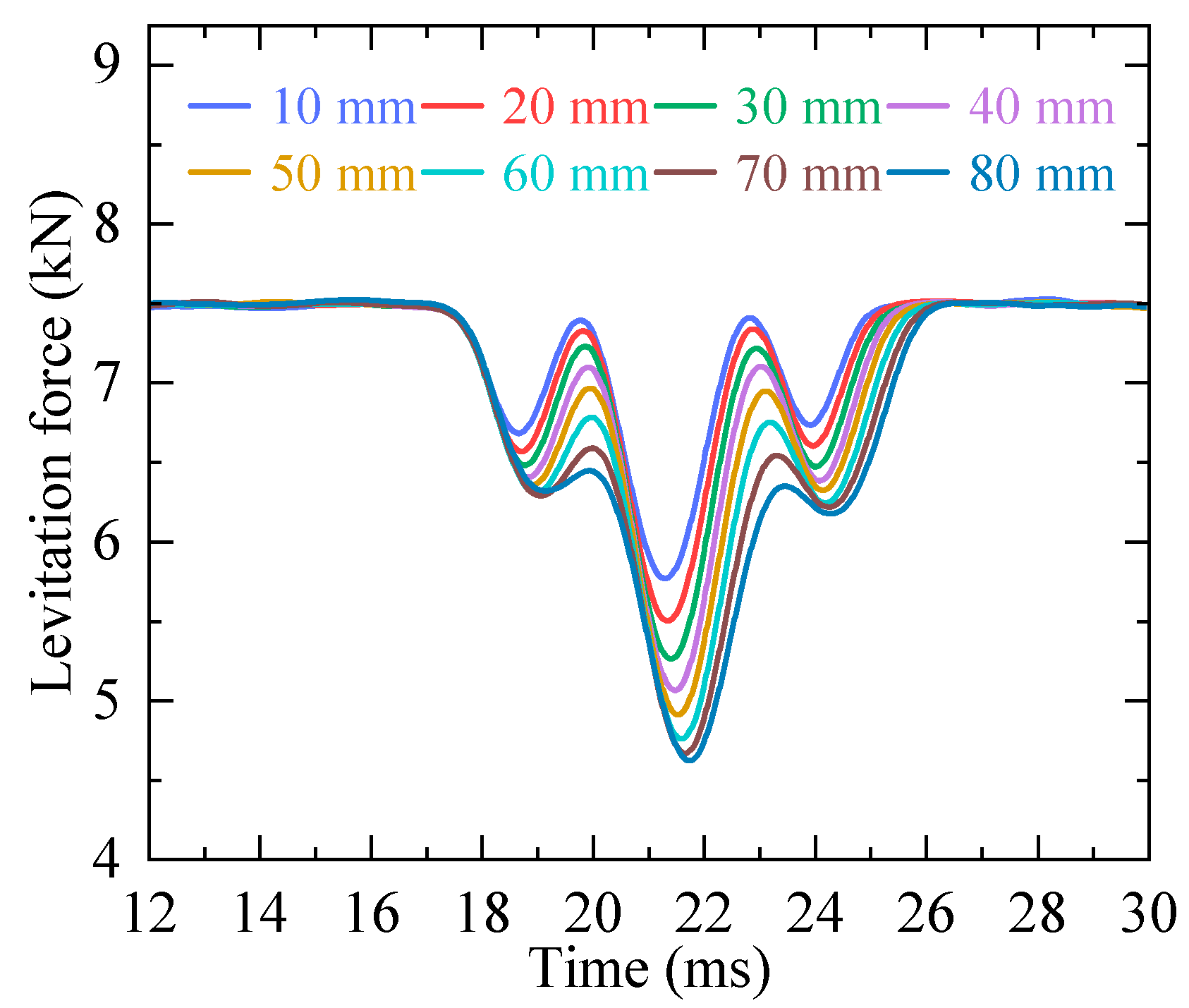
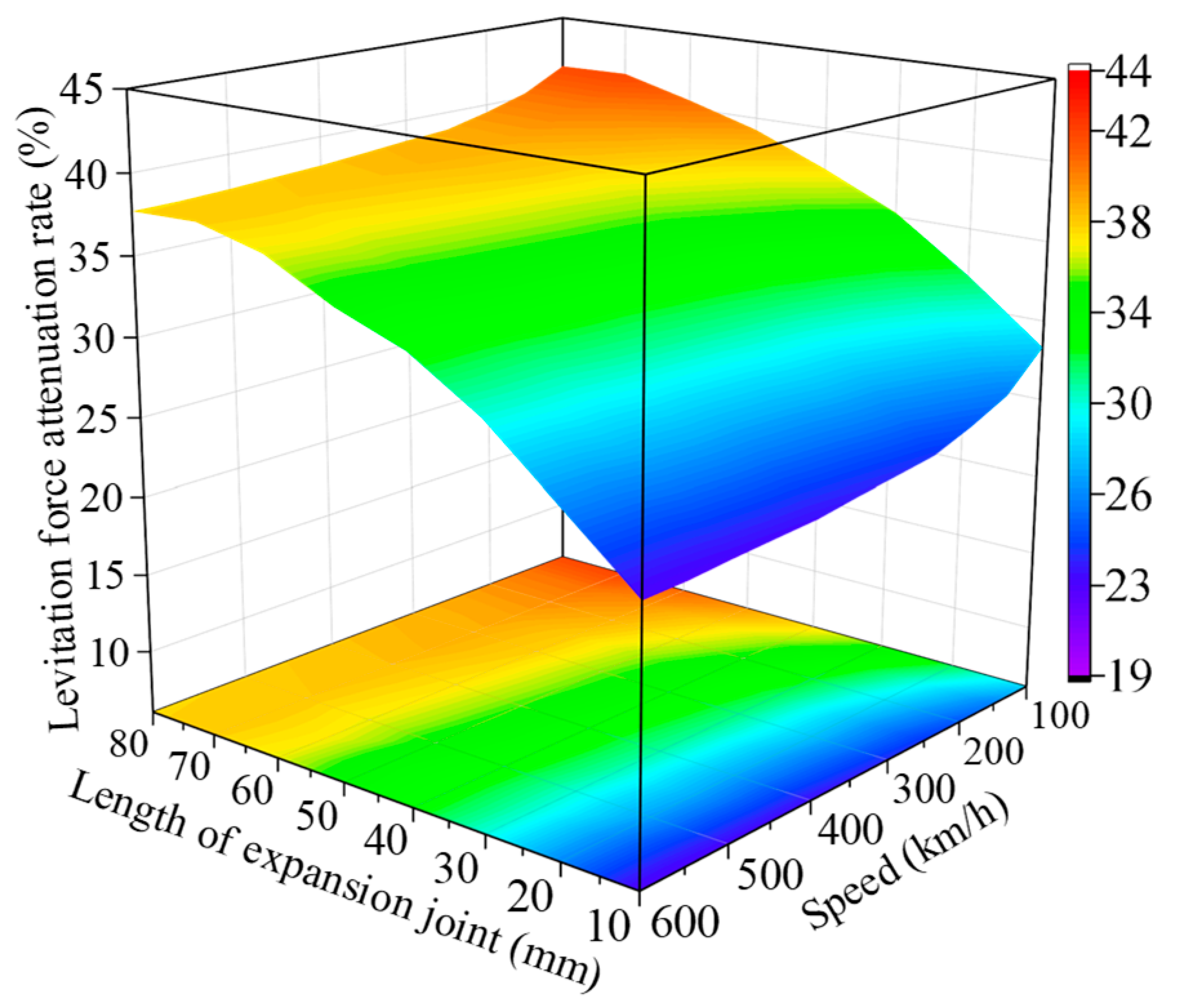
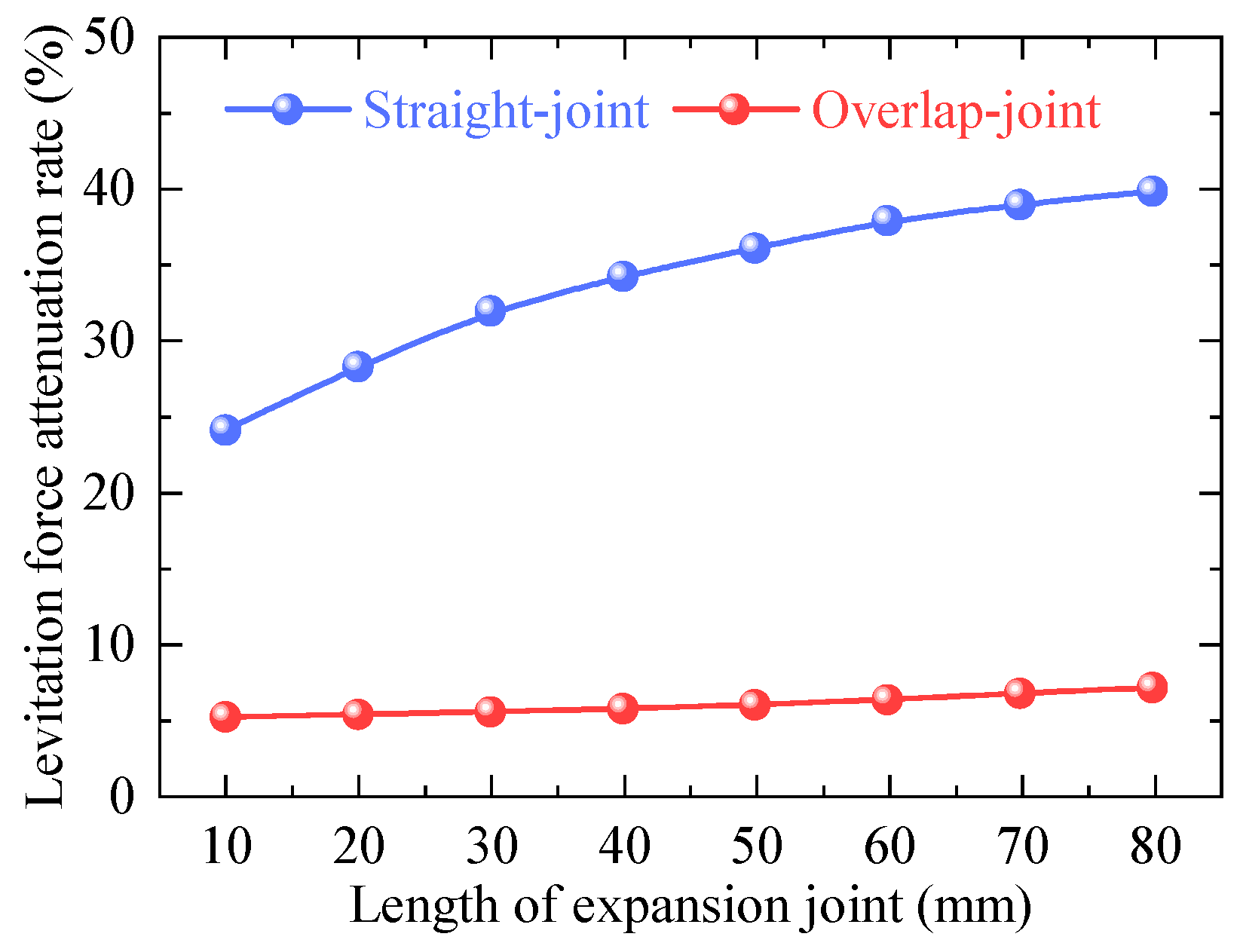
3.2. Analysis and Optimization of Length of Expansion Joint
3.3. Analysis and Optimization of the Length of the Overlap
3.4. Analysis and Optimization of the Thickness of the Upper Overlap Plate
4. Dynamic Comparative Simulation
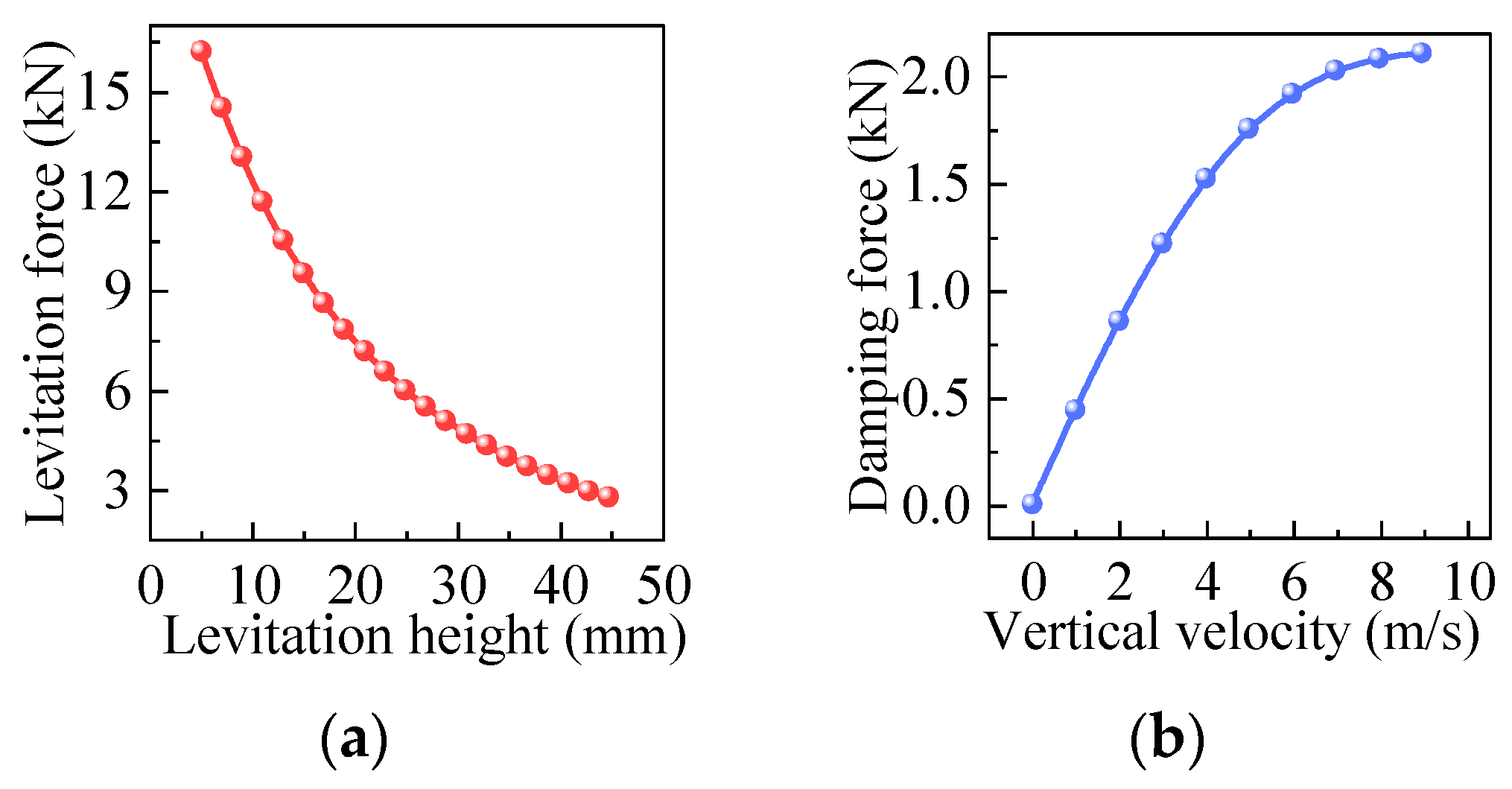
4.1. Vertical Dynamic Analysis of the PMEDS Vehicle
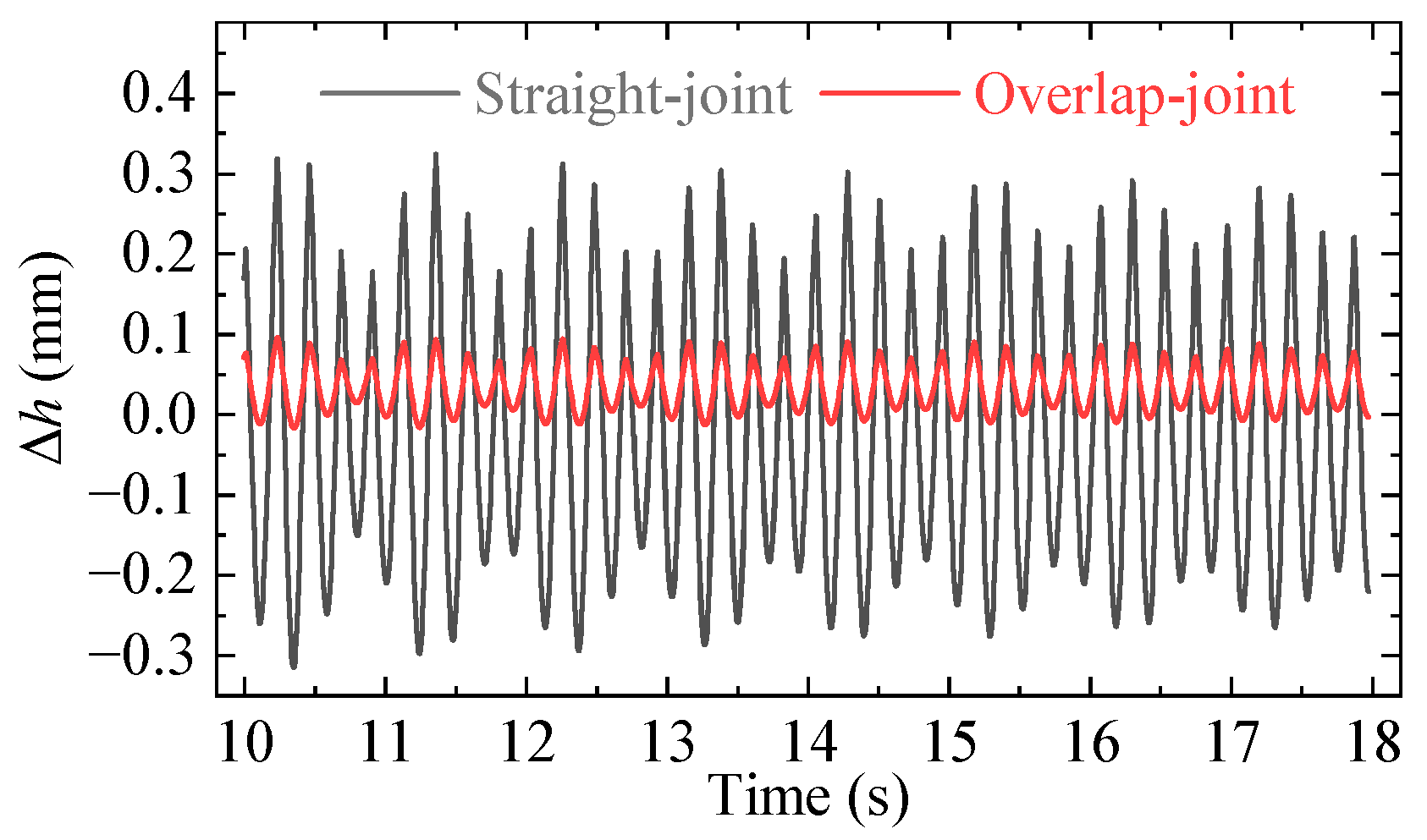
4.2. Comparison of Dynamic Performance
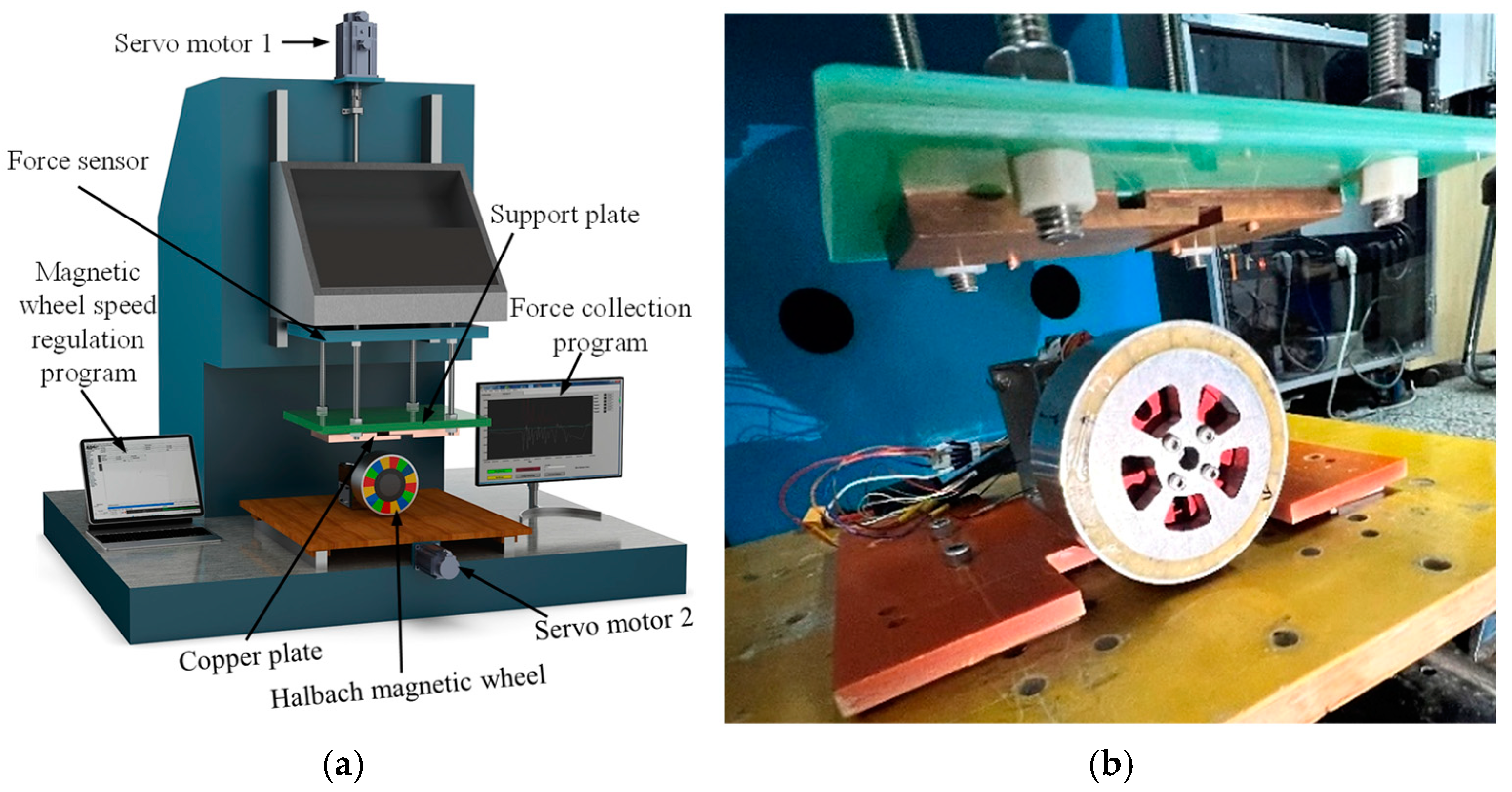
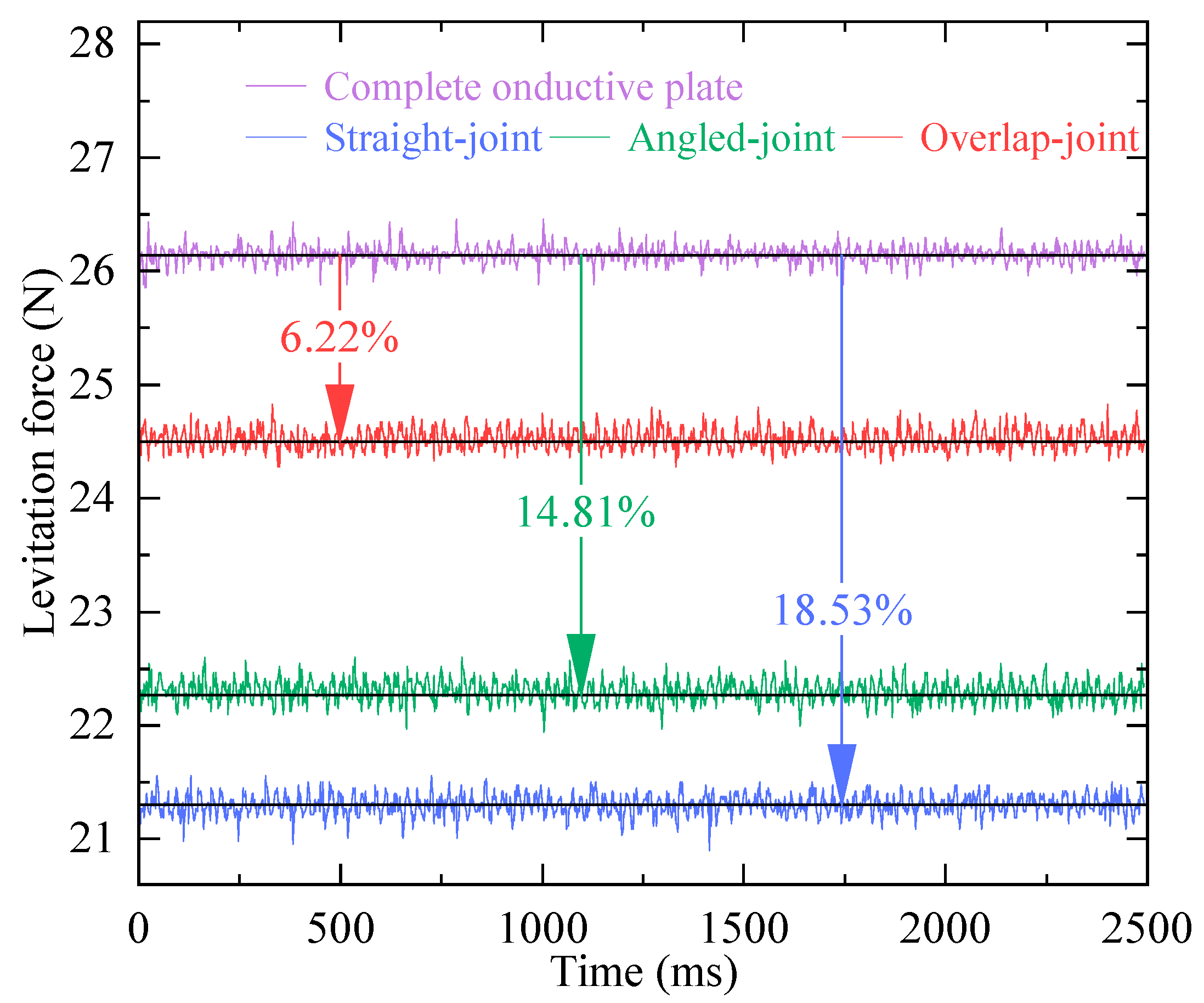
5. Magnetic Wheel Equivalence Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, H.; Kim, K.; Lee, J. Review of maglev train technologies. IEEE Trans. Magn. 2006, 42, 1917–1925. [Google Scholar]
- Tandan; Kumar, G.; Sahu, G.; Sharma, R.; Bohidar, S. A review on development and analysis of maglev train. Int. J. Res. Advent Technol. 2023, 3, 14–17. [Google Scholar]
- Gysen, B.L.J.; Paulides, J.J.H.; Janssen, J.L.G.; Lomonova, E.A. Active Electromagnetic Suspension System for Improved Vehicle Dynamics. IEEE Trans. Veh. Technol. 2010, 59, 1156–1163. [Google Scholar] [CrossRef]
- Li, F.; Sun, Y.; Xu, J.; He, Z.; Lin, G. Control methods for levitation system of EMS-type maglev vehicles: An overview. Energies 2023, 16, 2995–3021. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, W.; Zheng, J.; Wang, B.; Ren, Y.; Zheng, X.; Zhang, J. A High-Temperature Superconducting Maglev-Evacuated Tube Transport (HTS Maglev-ETT) Test System. IEEE Trans. Appl. Supercond. 2017, 27, 3602008. [Google Scholar] [CrossRef]
- Bernstein, P.; Noudem, J. Superconducting magnetic levitation: Principle, materials, physics and models. Supercond. Sci. Technol. 2020, 33, 033001. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, W.; Wang, L.; Wang, Y.; Zhou, W.; Zhao, J.; Lu, K.; Guo, J.; Zhang, W.; Zhou, X.; et al. A High-Speed Running Test Platform for High-Temperature Superconducting Maglev. IEEE Trans. Appl. Supercond. 2022, 32, 3600905. [Google Scholar] [CrossRef]
- Tramacere, E.; Pakštys, M.; Galluzzi, R.; Amati, N.; Tonoli, A.; Lembke, T.A. Modeling and experimental validation of electrodynamic maglev systems. J. Sound Vib. 2024, 568, 117950. [Google Scholar] [CrossRef]
- He, G.; Long, Z.; Cheng, Y. The development and application of permanent-magnet EDS based on Halbach structure. In Proceedings of the 29th Chinese Control Conference, Beijing, China, 29–31 July 2010; pp. 5457–5462. [Google Scholar]
- Beauloye, L.; Dehez, B. Permanent Magnet Electrodynamic Suspensions Applied to MAGLeV Transportation Systems: A Review. IEEE Trans. Transp. Electrif. 2023, 9, 748–758. [Google Scholar] [CrossRef]
- Rezaei, H.; Vaez-Zadeh, S. Modelling and analysis of permanent magnet electrodynamic suspension systems. Prog. Electromagn. Res. M 2014, 36, 77–84. [Google Scholar] [CrossRef]
- Fang, J.; Montgomery, D.B.; Roderick, L. A Novel MagPipe Pipeline Transportation System Using Linear Motor Drives. Proc. IEEE 2009, 97, 1848–1855. [Google Scholar] [CrossRef]
- Post, R.F.; Ryutov, D.D. The Inductrack: A simpler approach to magnetic levitation. IEEE Trans. Appl. Supercond. 2000, 10, 901–904. [Google Scholar] [CrossRef]
- Nøland, J.K. Prospects and Challenges of the Hyperloop Transportation System: A Systematic Technology Review. IEEE Access 2021, 9, 28439–28458. [Google Scholar] [CrossRef]
- Abdelrahman, A.S.; Sayeed, J.; Youssef, M.Z. Hyperloop Transportation System: Analysis, Design, Control, and Implementation. IEEE Trans. Ind. Electron. 2018, 65, 7427–7436. [Google Scholar] [CrossRef]
- Sutar, A.V.; Raut, S.V.; Kulkarni, R.K. Hyperloop System Implementation using Magnetic Levitation Principle. In Proceedings of the 2020 4th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 13–15 May 2020; pp. 979–983. [Google Scholar]
- Rote, D.M.; Cai, Y. Review of dynamic stability of repulsive-force maglev suspension systems. IEEE Trans. Magn. 2002, 38, 1383–1390. [Google Scholar] [CrossRef]
- Circosta, S.; Galluzzi, R.; Amati, N.; Tonoli, A.; Bonfitto, A.; Lembke, T.A.; Kertész, M. Passive multi-degree-of-freedom stabilization of ultra-high-speed maglev vehicles. J. Vib. Acoust. 2021, 143, 061003. [Google Scholar] [CrossRef]
- Ko, W.; Ham, C. A Novel Approach to Analyze the Transient Dynamics of an Electrodynamics Suspension Maglev. IEEE Trans. Magn. 2007, 43, 2603–2605. [Google Scholar] [CrossRef]
- Deng, Z.; Shi, H.; Ke, Z.; Liu, J.; Li, Z.; Zhang, B.; Jiang, Z.; Zhou, J.; Liu, Y. Permanent Magnet Electrodynamic Suspension System Integrated with a Car: Design, Implementation, and Test. IEEE Trans. Transp. Electrif. 2024, 10, 1101–1115. [Google Scholar] [CrossRef]
- Wu, C.; Li, G.; Wang, D.; Xu, J. Dynamic characterization of permanent magnet electrodynamic suspension system with a novel passive damping magnet scheme. J. Sound Vib. 2025, 599, 118849. [Google Scholar] [CrossRef]
- Hu, Y.; Zeng, J.; Long, Z. Analysis of Dynamic Characteristics of Electrodynamic Suspension Train Based on Halbach Permanent Magnet Array. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 3754–3758. [Google Scholar]
- Shi, H.; Yang, W.; Fu, S.; Liu, H.; Yang, J.; Li, K.; Deng, Z. Characteristics Analysis and Dynamic Test of Air-Cored Permanent Magnet Linear Synchronous Motor for Null-Flux PMEDS Vehicle. IEEE Trans. Instrum. Meas. 2024, 73, 3524115. [Google Scholar] [CrossRef]
- Galluzzi, R.; Circosta, S.; Amati, N.; Tonoli, A.; Bonfitto, A.; Lembke, T.A.; Kertész, M. A multi-domain approach to the stabilization of electrodynamic levitation systems. J. Vib. Acoust. 2020, 42, 061004. [Google Scholar] [CrossRef]
- Tan, S.; Lin, C.; Mei, Q. Study on the Operational Status of Rail Expansion Joints in Ballasted Track of High-Speed Railways. J. Railw. Sci. Eng. 2021, 18, 837–843. [Google Scholar]
- Rossing, T.D.; Korte, R.; Hull, J.R. Effect of guideway discontinuities on magnetic levitation and drag forces. J. Appl. Phys. 1991, 70, 6507–6509. [Google Scholar] [CrossRef]
- Choi, J.S.; Yoo, J. Design of a Halbach Magnet Array Based on Optimization Techniques. IEEE Trans. Magn. 2008, 44, 2361–2366. [Google Scholar] [CrossRef]
- Jiao, S.; Liu, X.; Zeng, Z. Intensive Study of Skin Effect in Eddy Current Testing with Pancake Coil. IEEE Trans. Magn. 2017, 53, 6201608. [Google Scholar] [CrossRef]
- Zhou, R.; Li, G.; Wang, Q.; He, J. Torque Calculation of Permanent-Magnet Spherical Motor Based on Permanent-Magnet Surface Current and Lorentz Force. IEEE Trans. Magn. 2020, 56, 8200209. [Google Scholar] [CrossRef]
- Cao, T.; Shi, H.; Liu, J.; Wu, X.; Deng, Z. Investigation of Electromagnetic Force Characteristics of Permanent Magnet Electrodynamic Suspension under Multi-Operation Conditions. Trans. China Electrotech. Soc. 2024, 39, 5262–5277. [Google Scholar]
- Ghosh, M.K.; Gao, Y.; Dozono, H.; Muramatsu, K.; Guan, W.; Yuan, J.; Tian, C.; Chen, B. Proposal of Maxwell Stress Tensor for Local Force Calculation in Magnetic Body. IEEE Trans. Magn. 2018, 54, 7206204. [Google Scholar] [CrossRef]
- Huang, C.; Kou, B.; Zhao, X.; Niu, X. Improved Analytical Model for the Magnetic Drag of a Dual-Conductor Plate Parallel Electric Suspension and Guiding Mechanism. IEEE Trans. Ind. Electron. 2023, 70, 11994–12002. [Google Scholar] [CrossRef]
- Pechenkov, A.N.; Scherbinin, V.E. Eddy currents and conducting and magnetizable spherical inclusions fields in a nonmagnetic medium. Russ. J. Nondestruct. Test. 2016, 52, 226–234. [Google Scholar] [CrossRef]
- Valagiannopoulos, C. Single-Series Solution to the Radiation of Loop Antenna in the Presence of a Conducting Sphere. Prog. Electromagn. Res. 2007, 71, 277–294. [Google Scholar] [CrossRef]
- Yuan, Y.; Deng, Z.; Zhang, S.; Ke, Z.; Shi, H.; Wang, Z.; Zhang, J.; Zheng, J. Working Principle and Primary Electromagnetic Characteristics of a Permanent Magnet Electrodynamic Wheel for Maglev Car Application. IEEE Trans. Appl. Supercond. 2021, 31, 3603905. [Google Scholar] [CrossRef]







| Parameters | Value |
|---|---|
| Magnet material | FeNdB52 |
| Magnetization angle | 45° |
| Magnet remanence | 1.45 T |
| Magnet length (lp) | 50 mm |
| Magnet thickness (hp) | 50 mm |
| Levitation height (h) | 20 mm |
| Conductive plate material | copper |
| Conductive plate thickness (d) | 12 mm |
| Length of expansion joint (Le) | 10–80 mm |
| Length of overlap (Lo) | 50 mm |
| Thickness of the upper overlap plate (Tu) | 6 mm |
| Specifications | Value |
|---|---|
| Magnet wheel outer diameter | 50 mm |
| Magnet wheel inner diameter | 35 mm |
| Thickness of the magnetic wheel | 35 mm |
| Number of magnet wheel modules | 16 |
| Magnetization angle | 90° |
| Magnetizing wheel speed | 3000 rpm |
| Conductive plate material | copper |
| Conductive plate thickness (d) | 10 mm |
| Conductive plate width | 60 mm |
| Length of the expansion joint (Le) | 2–10 mm |
| Length of the overlap (Lo) | 20–28 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Wu, S.; Shi, H.; Li, Z.; Deng, Z. A Novel Overlapped Compensation Structure and Its Effectiveness Verification for Expansion Joints in Plate-Type PMEDS Vehicles. Actuators 2025, 14, 182. https://doi.org/10.3390/act14040182
Zhang S, Wu S, Shi H, Li Z, Deng Z. A Novel Overlapped Compensation Structure and Its Effectiveness Verification for Expansion Joints in Plate-Type PMEDS Vehicles. Actuators. 2025; 14(4):182. https://doi.org/10.3390/act14040182
Chicago/Turabian StyleZhang, Shuqing, Siyi Wu, Hongfu Shi, Zhengyan Li, and Zigang Deng. 2025. "A Novel Overlapped Compensation Structure and Its Effectiveness Verification for Expansion Joints in Plate-Type PMEDS Vehicles" Actuators 14, no. 4: 182. https://doi.org/10.3390/act14040182
APA StyleZhang, S., Wu, S., Shi, H., Li, Z., & Deng, Z. (2025). A Novel Overlapped Compensation Structure and Its Effectiveness Verification for Expansion Joints in Plate-Type PMEDS Vehicles. Actuators, 14(4), 182. https://doi.org/10.3390/act14040182







