Research on Simplified Design of Model Predictive Control
Abstract
:1. Introduction
2. Principle and Simple Design of MPC
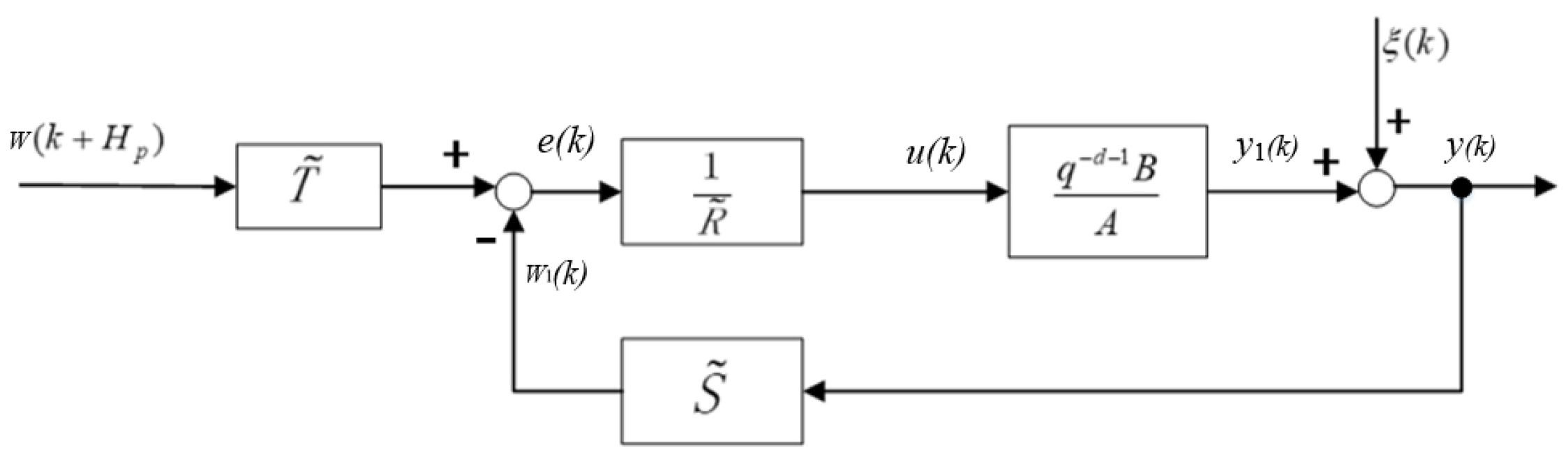
2.1. MPC Principle
2.2. The Simple Design of MPC
2.2.1. Solve
2.2.2. Solve
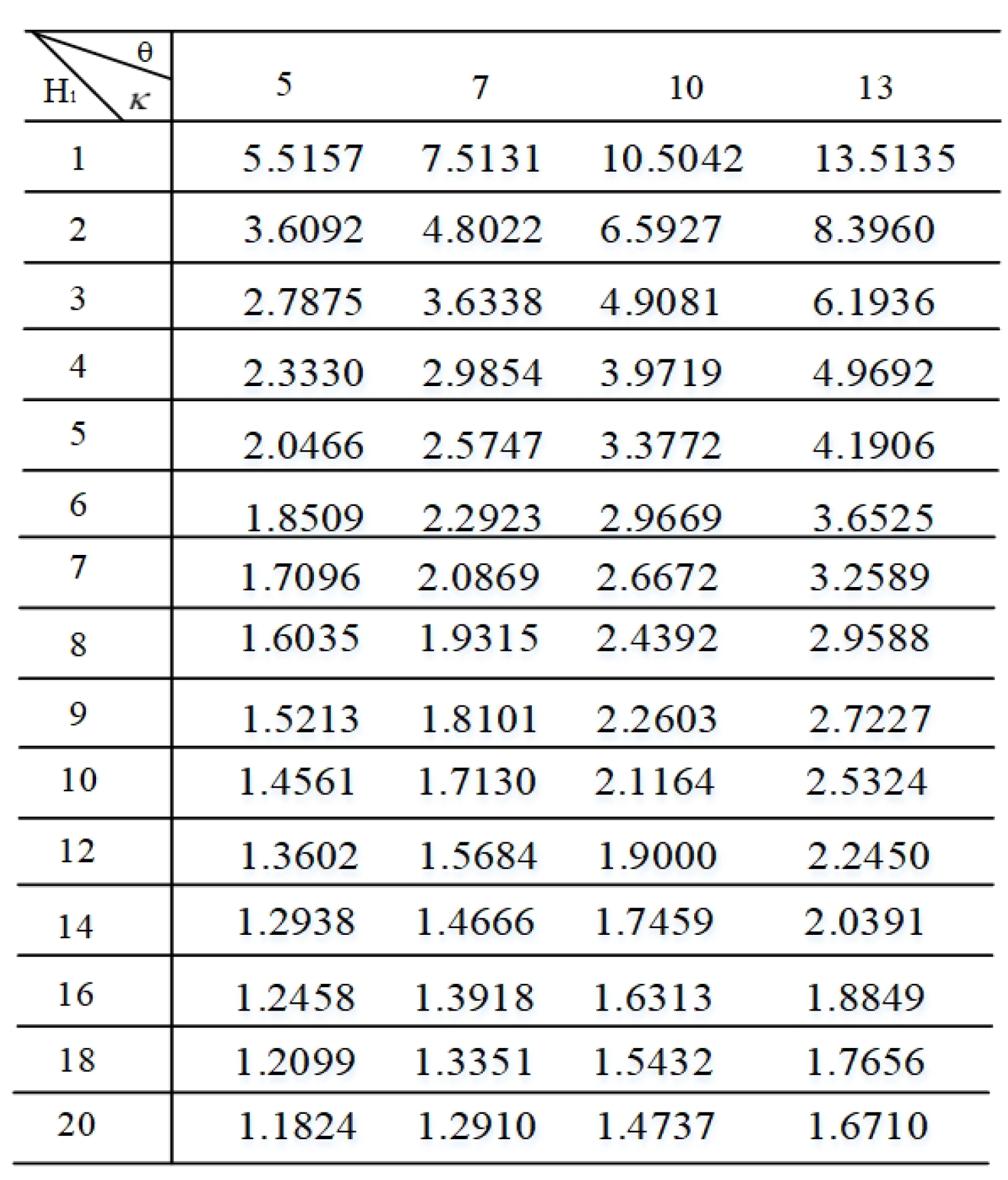
2.2.3. Calculation of κ Value
3. Characteristic Analysis of the Closed-Loop System
3.1. Ideal Dynamic Characteristics
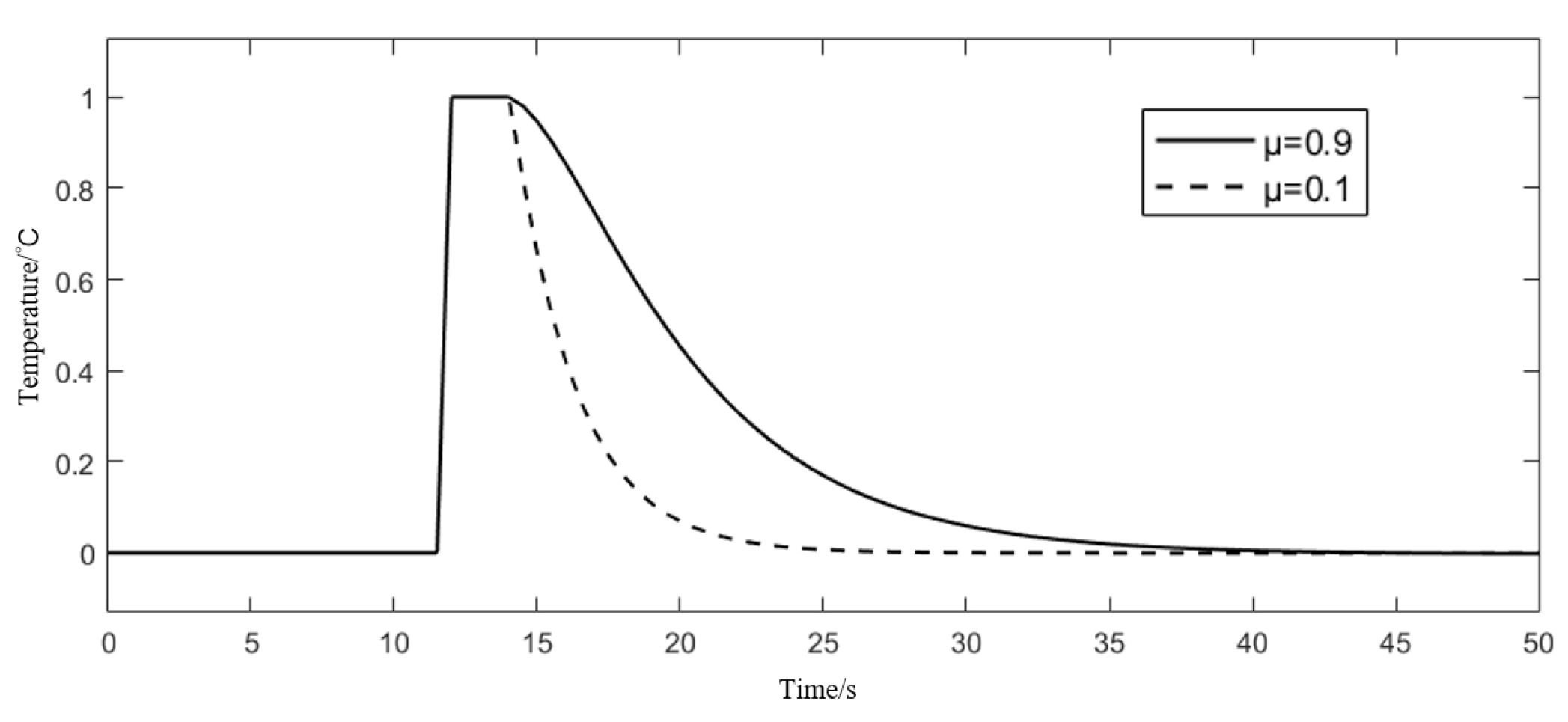
3.2. Interference Channel Characteristics
3.3. Robustness Analysis
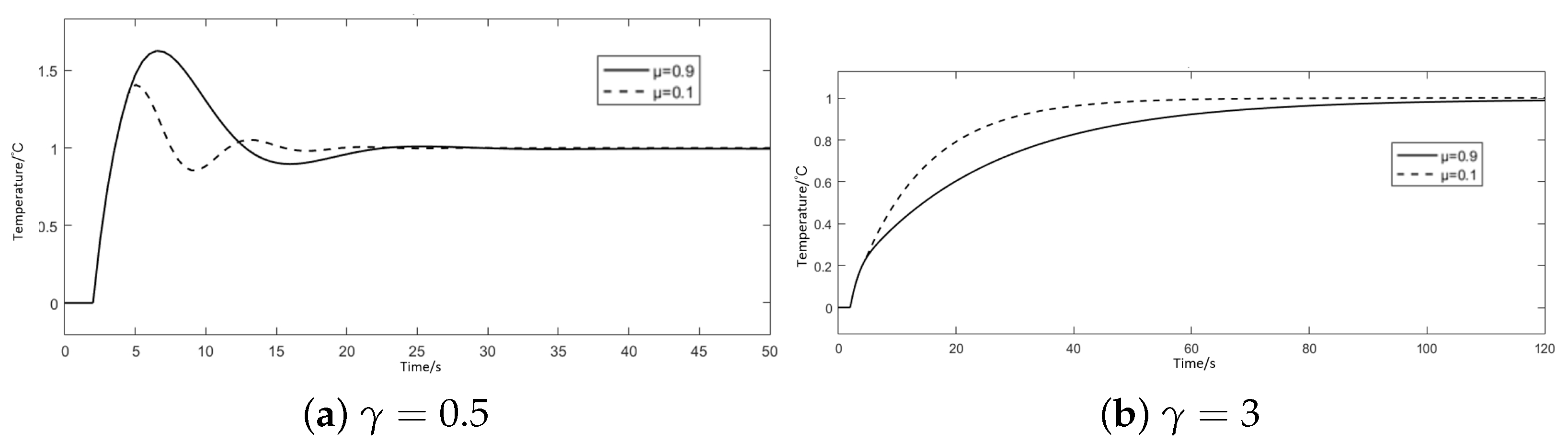
3.3.1. Static Gain Mismatch
3.3.2. Mismatch of Time Constants
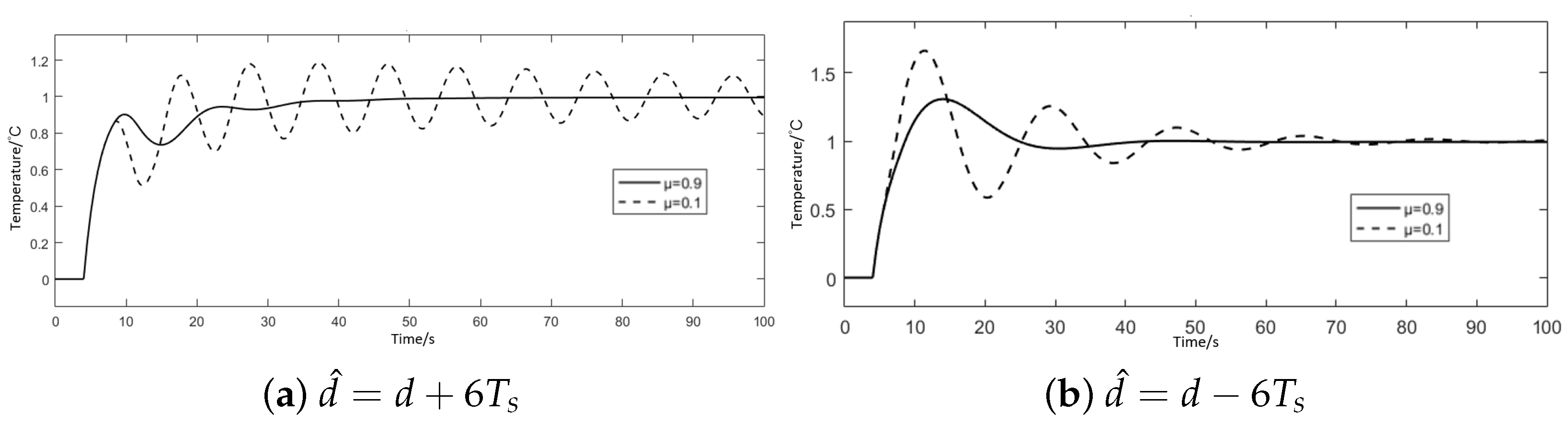
3.3.3. Delay Time Mismatch
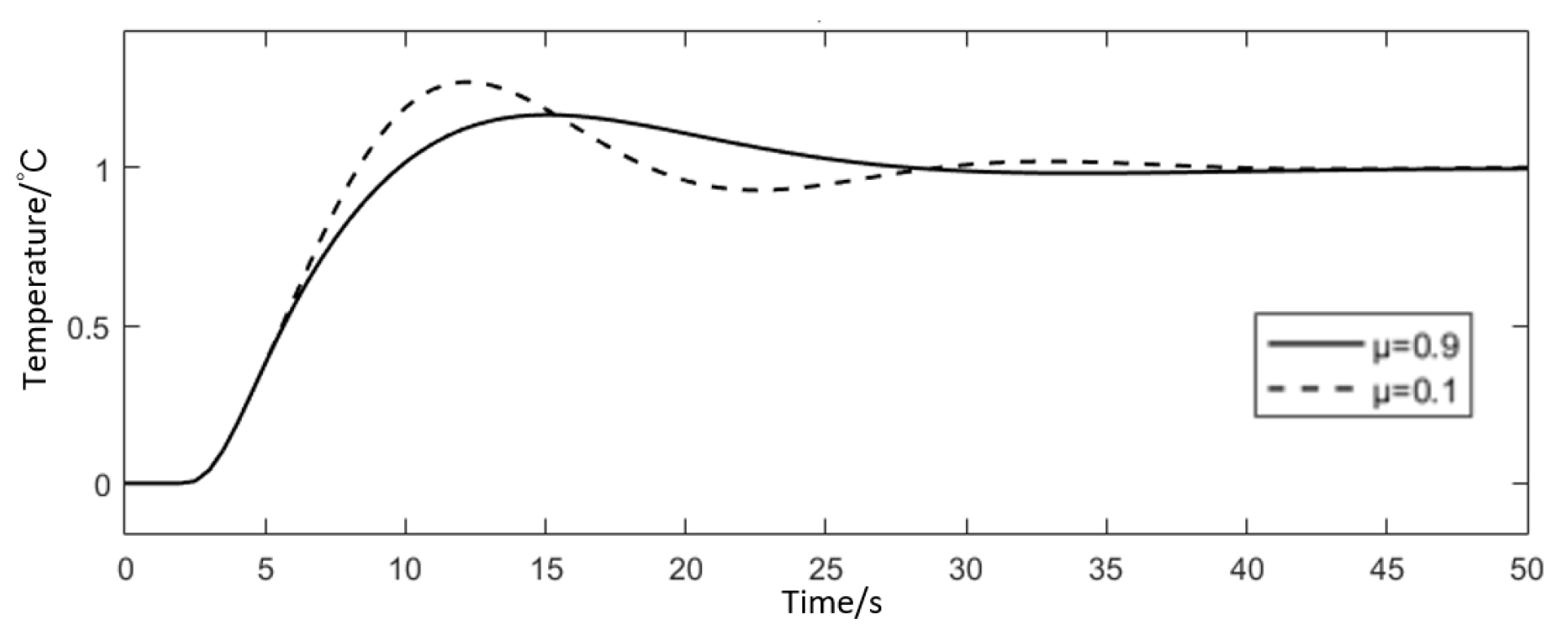
3.3.4. High-Order Object
3.4. Comparison with PID Control
4. Simplify the Field Application of MPC Controller
4.1. Parameter Selection
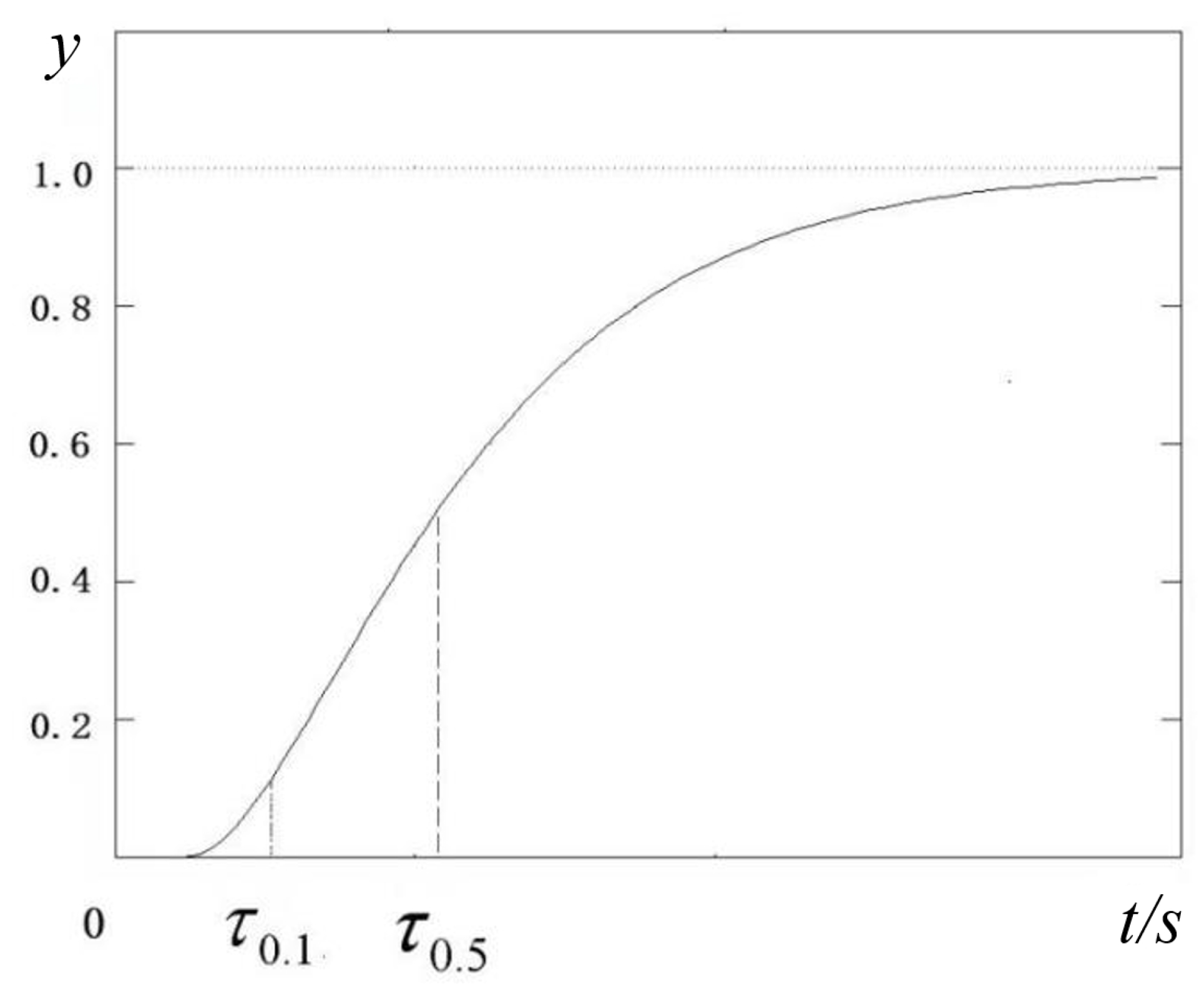
4.2. Parameter Identification
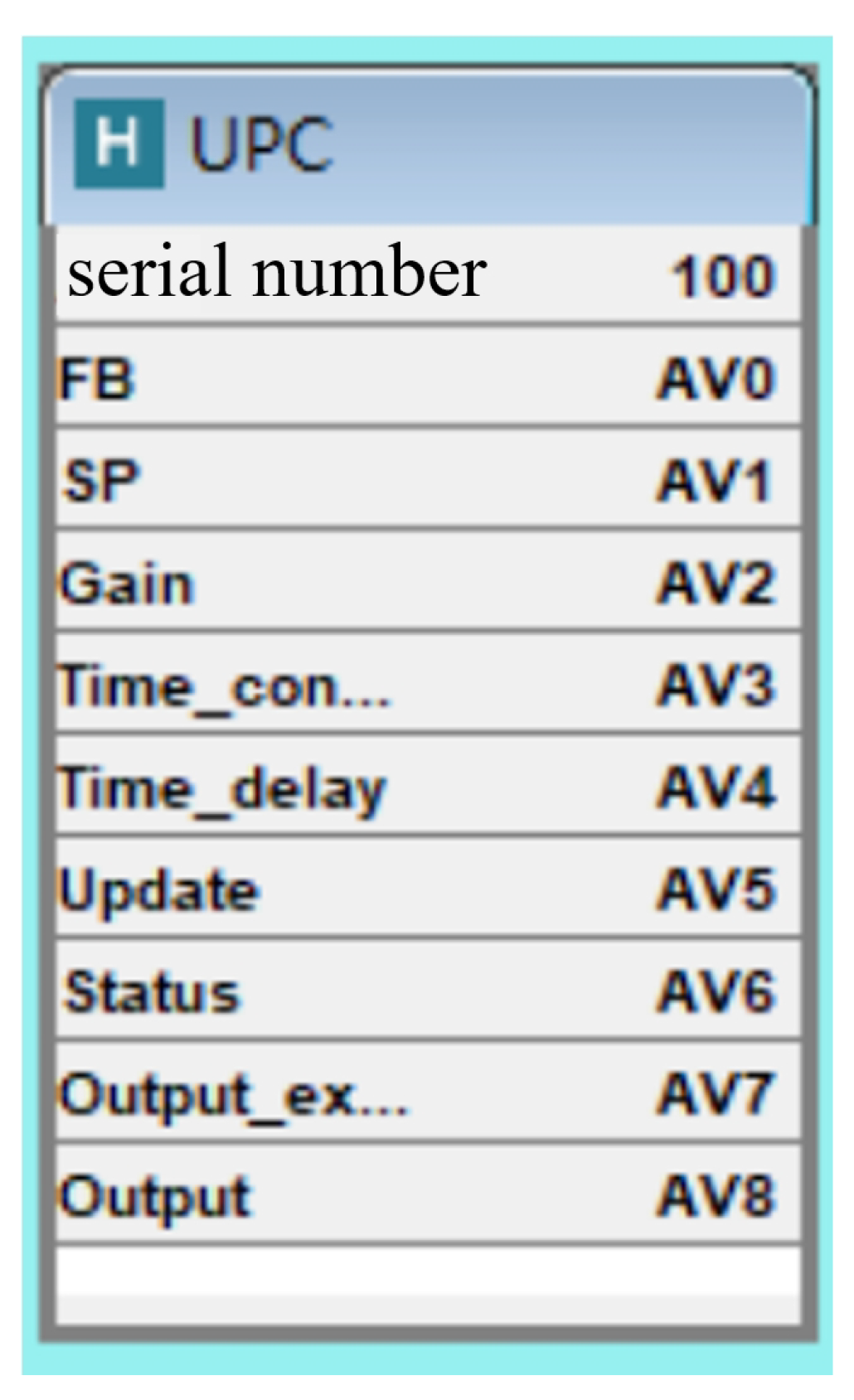
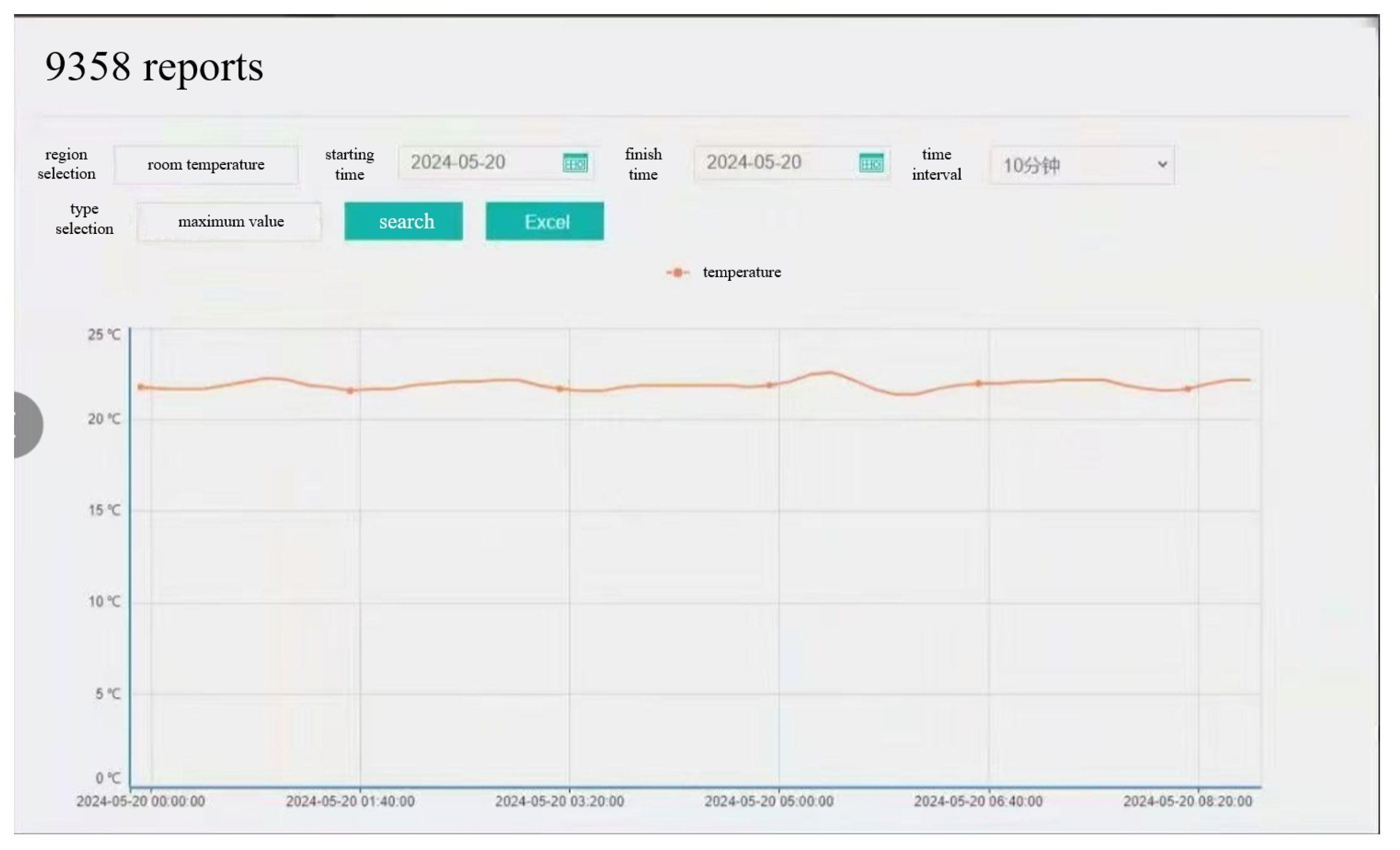
4.3. Design and Field Application of the MPC Function Block
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, L. Feedback and uncertainty: Some basic problems and results. Annu. Rev. Control 2020, 49, 27–36. [Google Scholar] [CrossRef]
- Samad, T. A survey on industry impact and challenges thereof [Technical Activities]. IEEE Control Syst. Mag. 2017, 37, 17–18. [Google Scholar]
- Shukla, M.K.; Rajput, K.; Yadav, A.K.; Prakash, S.A. Classical Techniques for PID Tuning. Int. Res. J. Eng. Technol. 2022, 9, 3440–3444. [Google Scholar]
- Nie, Z.Y.; Li, Z.Y.; Wang, Q.G. A unifying Ziegler-nichols tuning method based on active disturbance rejection. Int. J. Robust Nonlinear 2022, 32, 9525–9541. [Google Scholar] [CrossRef]
- Bazanella, A.S.; Pereira, L.F.A. A new method for PID tuning including plants without ultimate frequency. IEEE Trans. Control Syst. 2017, 25, 637–644. [Google Scholar] [CrossRef]
- Liu, N.; Chai, T.Y.; Parraga, A. An Optimal Tuning Method of PID Controller Parameters. Acta Autom. Sin. 2023, 49, 2272–2285. [Google Scholar]
- Schwenzer, M.; Ay, M.; Bergs, T. Review on model predictive control: An engineering perspective. Int. J. Adv. Manuf. Technol. 2021, 117, 1327–1349. [Google Scholar] [CrossRef]
- Soeterboek, A.R.M. Predictive Control: A unified Approach; Prentice Hall: London, UK, 1992. [Google Scholar]
- Soeterboek, A.; Verbruggen, H.; van den Bosch, P. On the Design of the Unified Predictive Controller. IFAC Proc. Vol. 1991, 24, 351–356. [Google Scholar] [CrossRef]
- Wei, D.; Jiao, H.Y.; Feng, H.D. Nonlinear predictive control of refrigeration station system based on load forecasting. Control Theory Appl. 2021, 38, 1619–1630. [Google Scholar]
- Feng, X.Y.; Wang, B.; Yang, C.L. Anti-disturbance predictive control of superheated steam temperature system for APS. Comput. Simul. 2022, 39, 141–145. [Google Scholar]
- Zhu, Q.G.; Zhen, W.J.; Shi, J.K. Main steam pressure control method of 1000 MW unit based on state feedback-predictive control. Steam Turbine Technol. 2022, 64, 63–66. [Google Scholar]
- Yao, Y.; Shekhar, D. State of the art review on model predictive control (MPC) in Heating Ventilation and Air-conditioning (HVAC) field. Build. Environ. 2021, 200, 107952.1–107952.18. [Google Scholar] [CrossRef]
- Juneja, P.K.; Sunori, S.K.; Sharma, A.; Sharma, A.; Kumar, P.; Joshi, V.; Raizada, R. Comparison of closed loop performance of consistency process dynamics for various PID controller algorithms. J. Phys. Conf. Ser. 2021, 2070, 012113. [Google Scholar] [CrossRef]
- da Silva, L.R.; Flesch, R.C.C.; Normey-Rico, J.E. Controlling industrial dead-time systems: When to use a PID or an advanced controller. ISA Trans. 2020, 99, 339–350. [Google Scholar] [CrossRef] [PubMed]
- Maurya, S.; Peddoju, S.K.; Ahmad, B.; Chihi, I. (Eds.) Cyber Technologies and Emerging Sciences; Lecture Notes in Networks and Systems; Springer: Singapore, 2023; Volume 467. [Google Scholar]
- Muresan, C.I.; Ionescu, C.M. Generalization of the FOPDT Model for Identification and Control Purposes. Processes 2020, 8, 682. [Google Scholar] [CrossRef]
- Bi, J.; Tan, W.; Yu, M. Tuning of PID controllers for unstable first-order plus dead time systems. Chem. Prod. Process Model. 2023, 18, 877–891. [Google Scholar] [CrossRef]
- Sha’aban, Y.A.; Lennox, B.; Laurí, D. PID versus MPC Performance for SISO Dead-time Dominant Processes. IFAC Proc. Vol. 2013, 46, 241–246. [Google Scholar] [CrossRef]
- Ali, E.J.; Feki, E.; Mami, A. Dynamic Matrix Control DMC using the Tuning Procedure based on First Order Plus Dead Time for Infant-Incubator. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 358–367. [Google Scholar] [CrossRef]
- Lin, S.-K.; Lee, A.-C. Adaptive unified predictive control applied to first-order-plus-dead-time processes to eliminate unknown class of deterministic disturbance. Evol. Syst. 2012, 3, 45–56. [Google Scholar] [CrossRef]
- Cordero, R.; Gonzales, J.; Estrabis, T.; Galotto, L.; Padilla, R.; Onofre, J. Variable Frequency Resonant Controller Based on Generalized Predictive Control for Biased-Sinusoidal Reference Tracking and Multi-Layer Perceptron. Energies 2024, 17, 2801. [Google Scholar] [CrossRef]
- Zhang, Q. Research on Unified Predictive Control and Its Application in Thermal Process. Ph.D. Thesis, Tsinghua University, Beijing, China, 1998. [Google Scholar]
- Åström, K.J.; Hägglund, T. Advanced PID Control; ISA: Pittsburgh, PA, USA, 2006. [Google Scholar]




| Parameter | P | T | ||||||
|---|---|---|---|---|---|---|---|---|
| values | 1 | 0 | 0 | 1 |
| Variable Name | Explanation | In/Out |
|---|---|---|
| FB | feedback input | In |
| SP | set value | In |
| Gain | Static gain of controlled object | In/out |
| Time constant | Time constant, unit: seconds, range 10 to 65,535 | In/out |
| Time delay | Delay time, unit: seconds, range 0 to Time constant | In/out |
| Update | Parameter identification command: 0 not identified, 1 identified Gain, 2 identified Time constant and Time delay | In |
| Status | Identify process state markers. When Update = 1 or 2, Status = 5 means waiting to rewrite the SP value to continue the identification process; status = 6 indicates that the identification is over and the parameters have been refreshed. | out |
| Output exec | Actuator actual execution value feedback | In |
| Output | Output of the controller | out |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Zhang, C.; Wang, Q.; Dong, S.; Xiao, A. Research on Simplified Design of Model Predictive Control. Actuators 2025, 14, 191. https://doi.org/10.3390/act14040191
Zhang Q, Zhang C, Wang Q, Dong S, Xiao A. Research on Simplified Design of Model Predictive Control. Actuators. 2025; 14(4):191. https://doi.org/10.3390/act14040191
Chicago/Turabian StyleZhang, Qing, Chi Zhang, Qi Wang, Shiyun Dong, and Aoqi Xiao. 2025. "Research on Simplified Design of Model Predictive Control" Actuators 14, no. 4: 191. https://doi.org/10.3390/act14040191
APA StyleZhang, Q., Zhang, C., Wang, Q., Dong, S., & Xiao, A. (2025). Research on Simplified Design of Model Predictive Control. Actuators, 14(4), 191. https://doi.org/10.3390/act14040191









