Chaos Anticontrol and Switching Frequency Impact on MOSFET Junction Temperature and Lifetime
Abstract
1. Introduction
2. Nonlinear Behavior of a Buck Converter
- The nonlinear feedback method [13] introduces a nonlinear perturbation = + ·, where is a small control gain and is a nonlinear function which introduce chaos. Feedback methods include the nonlinear time delay feedback control method [63], the linear time delay feedback method, and piece-wise linear function feedback.
- The chaotic coupling [64] of a stable system = with a chaotic system = influences x through the coupling function , which introduces chaos. The new system is = + .
- Bifurcation parameter tuning introduces a bifurcation parameter into a system = and pushes it into the chaotic region with a small variation = + .
- A chaotic impulse can destabilize a stable system with discrete spikes = + ·, where is a Dirac impulse and a chaotic input.
- The noise-introduced chaos [22] system = + adding randomness (e.g., stochastic noise).
3. Power Loss Computation and Thermal Model
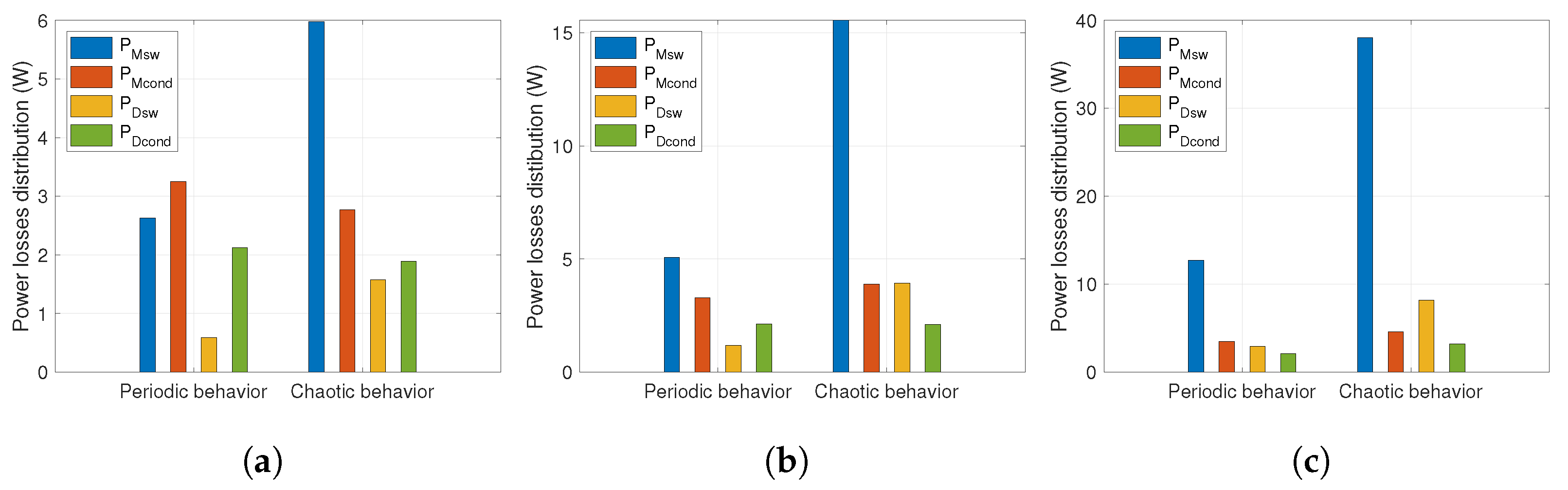
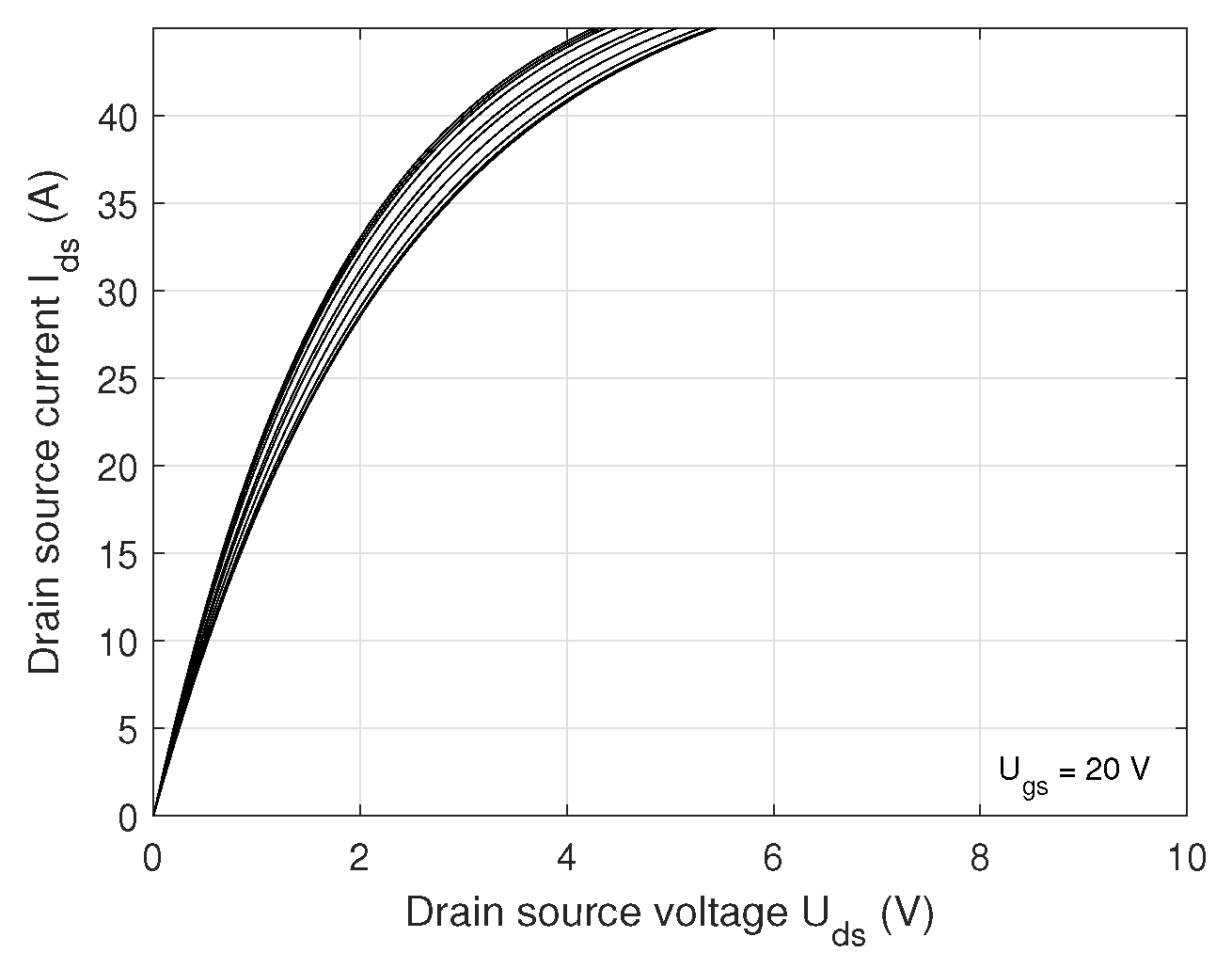
3.1. MOSFET and Diode Power Loss Computation
3.2. Thermal Model
4. Remaining Life Estimation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Minati, L.; Innocenti, G.; Mijatovic, G.; Ito, H.; Frasca, M. Mechanisms of chaos generation in an atypical single-transistor oscillator. Chaos Solitons Fractals 2022, 157, 111878. [Google Scholar] [CrossRef]
- Chen, X.; Long, X.; Hu, W.; Xie, B. Bifurcation and chaos behaviors of Lyapunov function controlled PWM boost converter. Energy Rep. 2021, 7, 163–168. [Google Scholar] [CrossRef]
- Zamani, N.; Ataei, M.; Niroomand, M. Analysis and control of chaotic behavior in boost converter by ramp compensation based on Lyapunov exponents assignment: Theoretical and experimental investigation. Chaos Solitons Fractals 2015, 81, 20–29. [Google Scholar] [CrossRef]
- Dhifaou, R.; Brahmi, H. Fast Simulation and Chaos Investigation of a DC-DC Boost Inverter. Complexity 2021, 9162259. [Google Scholar] [CrossRef]
- Ghosh, A.; Banerjee, S.; Basak, S.; Chakraborty, C. A study of chaos and bifurcation of a current mode controlled flyback converter. In Proceedings of the IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014. [Google Scholar]
- Morel, C.; Akrad, A.; Sehab, R.; Azib, T.; Larouci, C. Open-Circuit Fault-Tolerant Strategy for Interleaved Boost Converters via Filippov Method. Energies 2022, 15, 352. [Google Scholar] [CrossRef]
- Morel, C.; Morel, J.-Y.; Danca, M.F. Generalization of the Filippov method for systems with a large periodic input. Math. Comput. Simul. 2018, 146, 1–13. [Google Scholar] [CrossRef]
- Trujillo, S.C.; Candelo-Becerra, J.E.; Hoyos, F.E. Analysis and Control of Chaos in the Boost Converter with ZAD, FPIC, and TDAS. Symmetry 2022, 14, 13170. [Google Scholar] [CrossRef]
- Morel, C.; Vlad, R.C.; Morel, J.-Y. Similarities between the Lorenz Related Systems. Nonlinear Dyn. Syst. Theory 2022, 22, 66–81. [Google Scholar]
- Wu, J.; Zeng, Y.; Zhou, P.; Li, N. Broadband chaos generation in VCSELs with intensity-modulated optical injection. Opt. Laser Technol. 2023, 159, 108994. [Google Scholar] [CrossRef]
- Gong, X.; Wang, H.; Ji, Y.; Zhang, Y. Optical chaos generation and synchronization in secure communication with electro-optic coupling mutual injection. Opt. Commun. 2022, 521, 128565. [Google Scholar] [CrossRef]
- Yin, T.; Wang, Y. Predicting the price of WTI crude oil futures using artificial intelligence model with chaos. Fuel 2022, 316, 122523. [Google Scholar] [CrossRef]
- He, J.; Yu, S.; Cai, J. Topological horseshoe analysis for a three-dimensional anti-control system and its application. Optik 2016, 127, 9444–9456. [Google Scholar] [CrossRef]
- Erkan, E.; Ogras, H.; Fidan, S. Application of a secure data transmission with an effective timing algorithm based on LoRa modulation and chaos. Microprocess. Microsyst. 2023, 99, 104829. [Google Scholar] [CrossRef]
- Wen, H.; Lin, Y.; Yang, L.; Chen, R. Cryptanalysis of an image encryption scheme using variant Hill cipher and chaos. Expert Syst. Appl. 2024, 250, 123748. [Google Scholar] [CrossRef]
- Raiesdana, S.; Mohammad Hashemi Goplayegani, S. Study on chaos anti-control for hippocampal models of epilepsy. Neurocomputing 2013, 111, 54–69. [Google Scholar] [CrossRef]
- Borah, M.; Das, D.; Gayan, A.; Fenton, F.; Cherry, E. Control and anticontrol of chaos in fractional-order models of Diabetes, HIV, Dengue, Migraine, Parkinson’s and Ebola virus diseases. Chaos Solitons Fractals 2021, 153, 111419. [Google Scholar] [CrossRef]
- Dong, Y.; Yang, S.; Liang, Y.; Wang, G. Neuromorphic dynamics near the edge of chaos in memristive neurons. Chaos Solitons Fractals 2022, 160, 112241. [Google Scholar] [CrossRef]
- Choudhary, D.; Foster, K.R.; Uphoff, S. Chaos in a bacterial stress response. Curr. Biol. 2023, 33, 5404–5414. [Google Scholar] [CrossRef]
- Luo, S.; Li, S.; Tajaddodianfar, F.; Hu, J. Anti-oscillation and chaos control of the fractional-order brushless DC motor system via adaptive echo state networks. J. Frankl. Inst. 2018, 355, 6435–6453. [Google Scholar] [CrossRef]
- Yan, Z.; Li, Y.; Eslami, M. Maximizing micro-grid energy output with modified chaos grasshopper algorithms. Heliyon 2024, 10, e23980. [Google Scholar] [CrossRef]
- Ru, X. Parameter extraction of photovoltaic model based on butterfly optimization algorithm with chaos learning strategy. Sol. Energy 2024, 269, 112353. [Google Scholar] [CrossRef]
- Elmasry, Y.; Chaturvedi, R.; Solomin, E.; Smaisim, G.F.; Hadrawi, S.K. The numerical analysis to assess the second-law features of a solar water heater equipped with a dual-twisted tape turbulator; Developing a predictive model for useful thermal exergy based on the nonlinear calibration using the Chaos Control Method (CCM). Eng. Anal. Bound. Elem. 2024, 159, 37–383. [Google Scholar] [CrossRef]
- Lin, F.L.; Chen, D.Y. Reduction of Power Supply EMI Emission by Switching Frequency Modulation. IEEE Trans. Power Electron. 1994, 9, 132–137. [Google Scholar]
- Stankovic, A.M.; Verghese, G.C.; Perreault, D.J. Analysis and Synthesis of Randomized Modulation Schemes for Power Converters. IEEE Trans. Power Electron. 1995, 10, 680–693. [Google Scholar] [CrossRef]
- Deane, J.H.B.; Ashwin, P.; Hamill, D.C.; Jefferies, D.J. Calculation of the Periodic Spectral Components in a Chaotic DC-DC Converter. IEEE Trans. Circuits Syst.-I Fundam. Theory Appl. 1999, 46, 1313–1319. [Google Scholar] [CrossRef]
- Woywode, O.; Guldner, H.; Baranovski, A.L.; Schwarz, W. Bifurcation and Statistical Analysis of DC-DC Converters. IEEE Trans. Circuits Syst.-I Fundam. Theory Appl. 2003, 50, 1072–1080. [Google Scholar] [CrossRef]
- Morel, C.; Bourcerie, M.; Chapeau-Blondeau, F. Generating independent chaotic attractors by chaos anticontrol in nonlinear circuits. Chaos Solitons Fractals 2005, 26, 541. [Google Scholar] [CrossRef][Green Version]
- Morel, C.; Vlad, R.; Morel, J.-Y. Anticontrol of Chaos Reduces Spectral Emissions. J. Comput. Nonlinear Dyn. 2008, 3, 041009. [Google Scholar] [CrossRef]
- Li, H.; Zhang, B.; Li, Z.; Halang, W.A.; Chen, G. Controlling DC–DC converters by chaos-based pulse width modulation to reduce EMI. Chaos Solitons Fractals 2009, 42, 1378–1387. [Google Scholar] [CrossRef]
- Vidya, P.M.; Sudha, S. A fully integrated VLSI architecture using chaotic PWM for RF transmitter design with electromagnetic interference reduction. Integration 2022, 83, 33–45. [Google Scholar] [CrossRef]
- Chen, Y.; Xing, B.; He, G.; Jiang, W.; Wang, Z. Research on EMI suppression of high frequency isolate quasi-Z-source inverter based on chaotic frequency modulation. Energy Rep. 2022, 8, 10363–10371. [Google Scholar] [CrossRef]
- Morel, C.; Rizoug, N. Electro-Thermal Modeling, Aging and Lifetime Estimation of Power Electronic MOSFETs. Civ. Eng. Res. J. 2022, 14, 555879. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, W.; Wu, J. An Improved Electro-Thermal Model to Estimate the Junction Temperature of IGBT Module. Electronics 2019, 8, 1066. [Google Scholar] [CrossRef]
- Zheng, J.; Zheng, Z.; Xu, H.; Liu, W.; Zeng, Y. Accurate Time-segmented Loss Model for SiC MOSFETs in Electro-thermal Multi-Rate Simulation. arXiv 2023, arXiv:2311.07029. [Google Scholar]
- Jahdi, S.; Alatise, O.; Ran, L.; Mawby, P. Accurate analytical modeling for switching energy of PiN diodes reverse recovery. IEEE Trans. Ind. Electron. 2015, 62, 1461–1470. [Google Scholar] [CrossRef]
- Zhaksylyk, A.; Rauf, A.-M.; Chakraborty, S.; El Baghdadi, M.; Geury, T.; Ciglaric, S.; Hegazy, O. Evaluation of Model Predictive Control for IPMSM Using High-Fidelity Electro-Thermal Model of Inverter for Electric Vehicle Applications. Proc. SAE WCX Digit. 2021, 37, 290–295. [Google Scholar]
- Ma, K.; Bahman, A.S.; Beczkowski, S.; Blaabjerg, F. Complete Loss and Thermal Model of Power Semiconductors Including Device Rating Information. IEEE Trans. Power Electron. 2015, 30, 290–295. [Google Scholar] [CrossRef]
- Górecki, K.; Zarębski, J.; Górecki, P. Influence of Thermal Phenomena on the Characteristics of Selected Electronics Networks. Energies 2021, 14, 4750. [Google Scholar] [CrossRef]
- Zhou, Z.; Kanniche, M.S.; Butcup, S.G.; Igic, P. High-speed electrothermal simulation model of inverter power modules for hybrid vehicles. IEEE Trans. Ind. Electron. 2011, 5, 636–643. [Google Scholar]
- Górecki, P.; Wojciechowski, D. Accurate Electrothermal Modeling of High Frequency DC–DC Converters with Discrete IGBTs in PLECS Software. IEEE Trans. Ind. Electron. 2023, 70, 5739–5746. [Google Scholar] [CrossRef]
- Górecki, P.; d’Alessandro, V. A Datasheet-Driven Electrothermal Averaged Model of a Diode–MOSFET Switch for Fast Simulations of DC–DC Converters. Electronics 2024, 13, 154. [Google Scholar] [CrossRef]
- Karami, M.; Li, T.; Tallam, R.; Cuzner, R. Thermal Characterization of SiC Modules for Variable Frequency Drives. IEEE Open J. Power Electron. 2021, 2, 336–345. [Google Scholar] [CrossRef]
- Chen, H.; Lin, S.; Liu, Y. Transient electro-thermal coupled modeling of three-phase power MOSFET inverter during load cycles. Materials 2021, 14, 5427. [Google Scholar] [CrossRef]
- Nayak, D.P.; Pramanick, S.K. Implementation of an Electro-Thermal Model for Junction Temperature Estimation in a SiC MOSFET Based DC/DC Converter. CPSS Trans. Power Electron. Appl. 2023, 8, 42–53. [Google Scholar] [CrossRef]
- Urkizu, J.; Mazura, M.; Alacano, A.; Aizpuru, I.; Chakraborty, S. Electric vehicle inverter electro-thermal models oriented to simulation speed and accuracy multi-objective targets. Energies 2019, 12, 3608. [Google Scholar] [CrossRef]
- Cao, R. A Thermal Modeling of Power Semiconductor Devices with Heat Sink Considering Ambient Temperature Dynamic. In Proceedings of the IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November 2020–2 December 2020; Volume 37, pp. 290–295. [Google Scholar]
- Kishor, Y.; Patel, R. Thermal modeling and reliability analysis of recently introduced high gain converters for PV application. Clean. Energy Syst. 2022, 3, 100016. [Google Scholar] [CrossRef]
- Sangwongwanich, A.; Yang, Y.; Sera, D.; Blaabjerg, F. Lifetime Evaluation of Grid-Connected PV Inverters Considering Panel Degradation Rates and Installation Sites. IEEE Trans. Power Electron. 2018, 33, 1225–1236. [Google Scholar] [CrossRef]
- Shen, Y.; Chub, A.; Wang, H.; Vinnikov, D.; Liivik, E.; Blaabjerg, F. Wear-Out Failure Analysis of an Impedance-Source PV Microinverter Based on System-Level Electrothermal Modeling. IEEE Trans. Ind. Power Electron. 2019, 66, 3914–3927. [Google Scholar] [CrossRef]
- Shipurkar, U.; Lyrakis, E.; Ma, K.; Polinder, H.; Ferreira, J.A. Lifetime Comparison of Power Semiconductors in Three-Level Converters for 10-MW Wind Turbine Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1366–1377. [Google Scholar] [CrossRef]
- Morel, C.; Morel, J.-Y. Impact of Chaos on MOSFET Thermal Stress and Lifetime. Electronics 2024, 13, 1649. [Google Scholar] [CrossRef]
- Stella, F.; Pellegrino, G.; Member, S.; Armando, E.; Dapr, D. Online junction temperature estimation of SiC power MOSFETS through onstate voltage mapping. IEEE Trans. Ind. Appl. 2018, 54, 3453–3462. [Google Scholar] [CrossRef]
- Baker, N.; Munk-Nielsen, S.; Iannuzzo, F.; Liserre, M. IGBT junction temperature measurement via peak gate current. IEEE Trans. Power Electron. 2016, 31, 3784–3793. [Google Scholar] [CrossRef]
- Barlini, D.; Ciappa, M.; Castellazzi, A.; Mermet-Guyennet, M.; Fichtner, W. New technique for the measurement of the static and of the transient junction temperature in IGBT devices under operating conditions. Microelectron. Reliab. 2006, 46, 1772–1777. [Google Scholar] [CrossRef]
- Bryant, A.; Yang, S.; Mawby, P.; Xiang, D.; Ran, L.; Tavner, P.; Palmer, P.R. Investigation into IGBT dv/dt during turn-off and its temperature dependence. IEEE Trans. Power Electron. 2011, 26, 3019–3031. [Google Scholar] [CrossRef]
- Luo, H.; Li, W.; Iannuzzo, F.; He, X.; Blaabjerg, F. Enabling junction temperature estimation via collector-side thermo-sensitive electrical parameters through emitter stray inductance in high-power igbt modules. IEEE Trans. Ind. Electron. 2018, 65, 4724–4738. [Google Scholar] [CrossRef]
- Yang, F.; Pu, S.; Xu, C.; Akin, B. Turn-on delay based real-time junction temperature measurement for SiC MOSFETs with aging compensation. IEEE Trans. Power Electron. 2021, 36, 1280–1294. [Google Scholar] [CrossRef]
- Zhang, Z.; Dyer, J.; Wu, X.; Wang, F.; Costinett, D.; Tolbert, L.M.; Blalock, B.J. Online junction temperature monitoring using intelligent gate drive for SiC power devices. IEEE Trans. Power Electron. 2019, 34, 7922–7932. [Google Scholar] [CrossRef]
- Dini, P.; Ariaudo, G.; Botto, G.; La Greca, F.; Saponara, S. Real-time electro-thermal modelling and predictive control design of resonant power converter in full electric vehicle applications. IET Power Electron. 2023, 16, 2045–2064. [Google Scholar] [CrossRef]
- Dini, P.; Basso, G.; Saponara, S.; Romano, C. Real-time monitoring and ageing detection algorithm design with application on SiC-based automotive power drive system. IET Power Electron. 2024, 17, 690–710. [Google Scholar] [CrossRef]
- Wolfspeed. C2M0080120D Silicon Carbide Power MOSFET C2M MOSFET Technology; Product datasheet. Datasheet, Rev. 5; Wolfspeed: Durham, NC, USA, 2023; pp. 1–11. [Google Scholar]
- Peng, M. Symmetry breaking, bifurcations, periodicity and chaos in the Euler method for a class of delay differential equations. Chaos Solitons Fractals 2005, 24, 1287–1297. [Google Scholar] [CrossRef]
- Morel, C.; Vlad, R.; Morel, J.-Y.; Petreus, D. Generating chaotic attractors on a surface. Math. Comput. Simul. 2011, 81, 2549–2563. [Google Scholar] [CrossRef][Green Version]

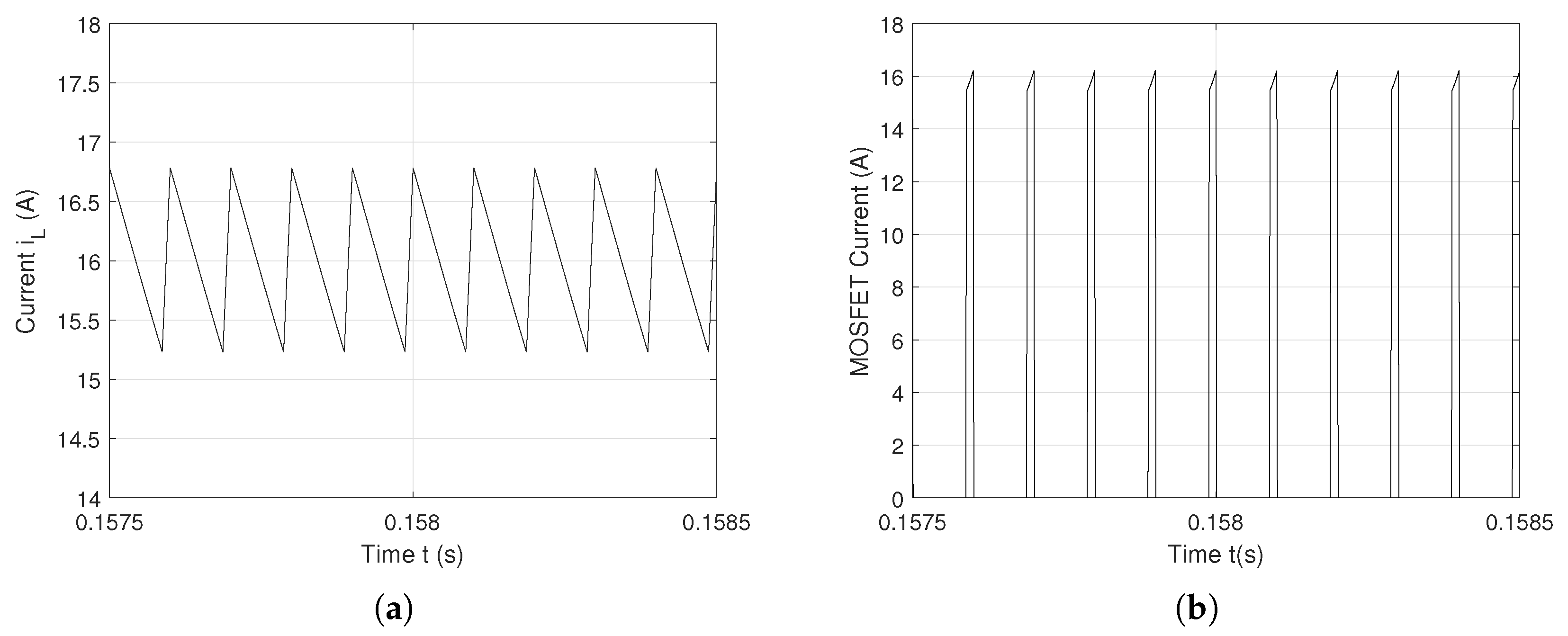

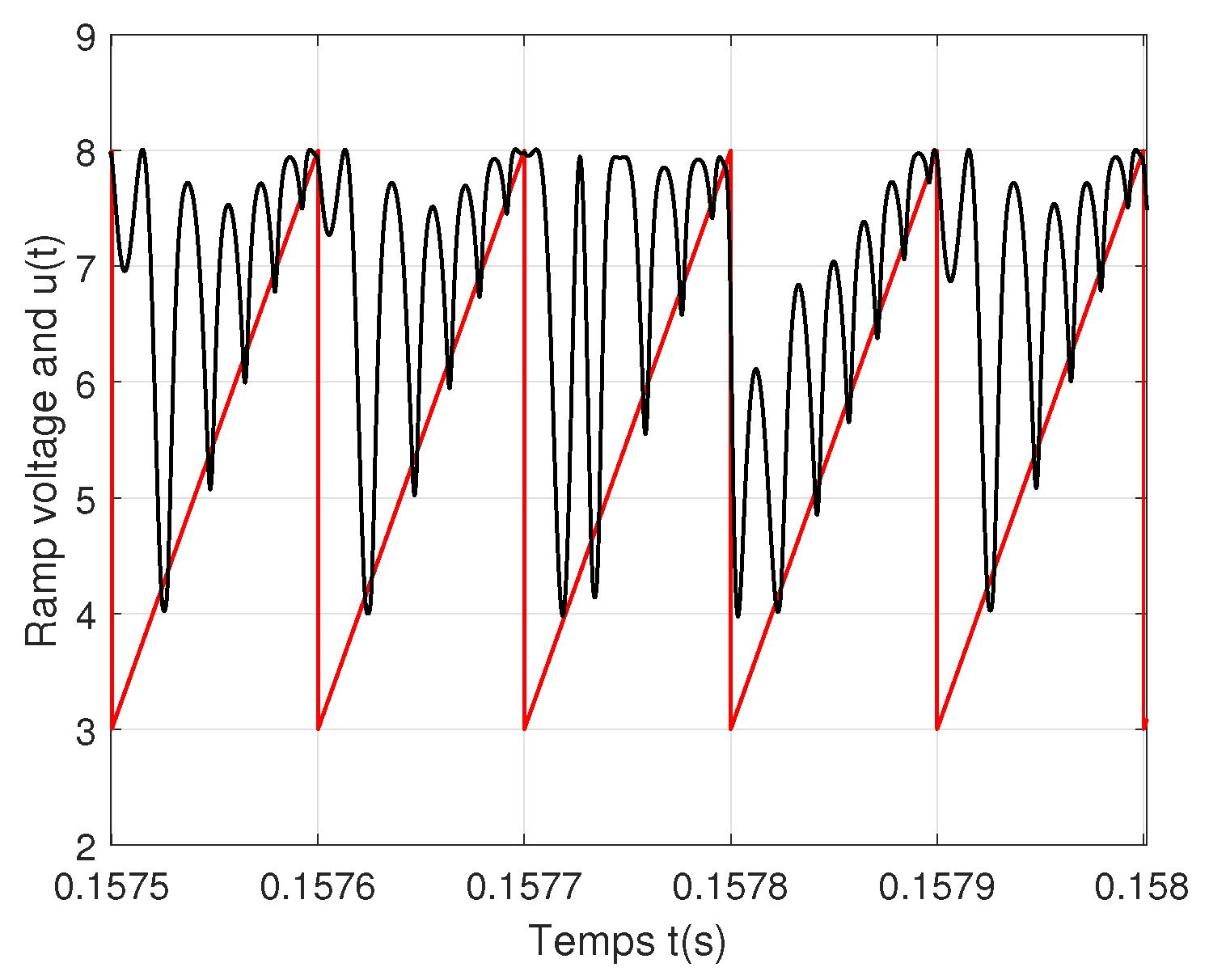
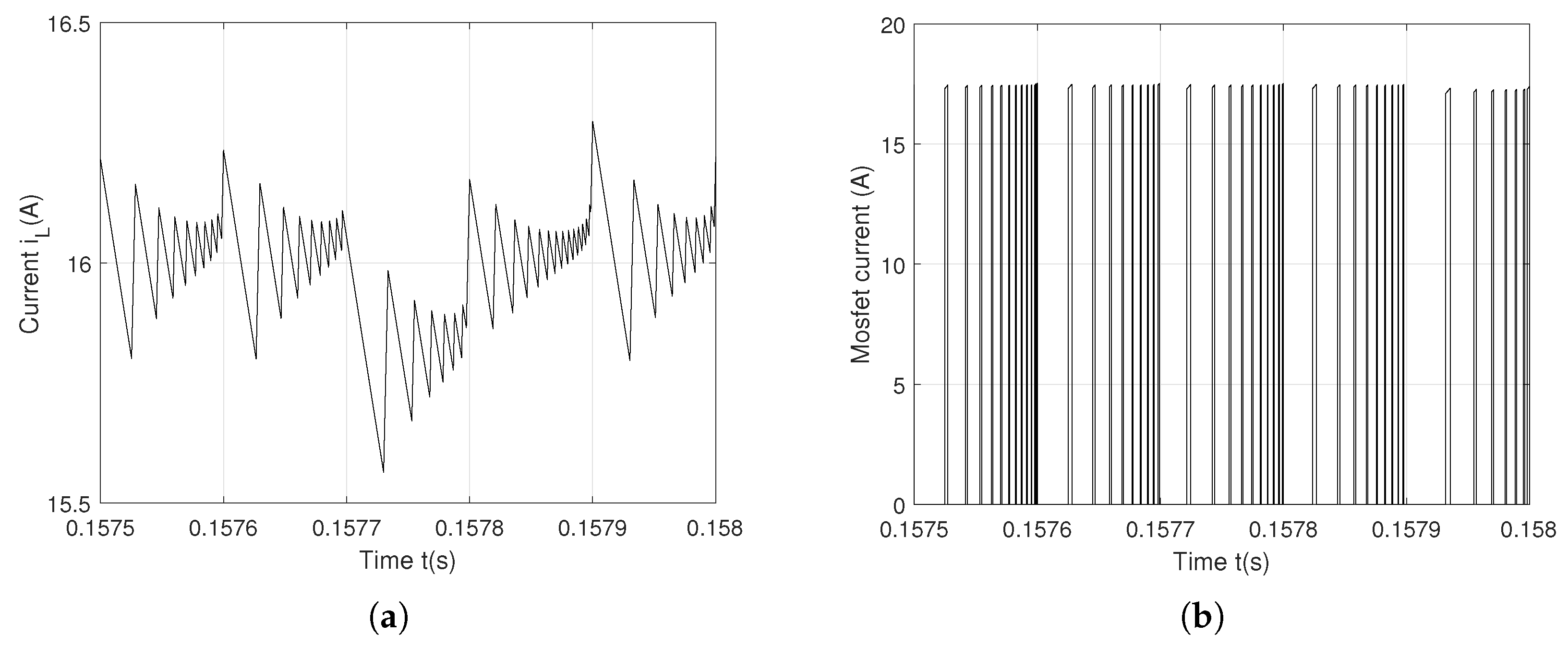
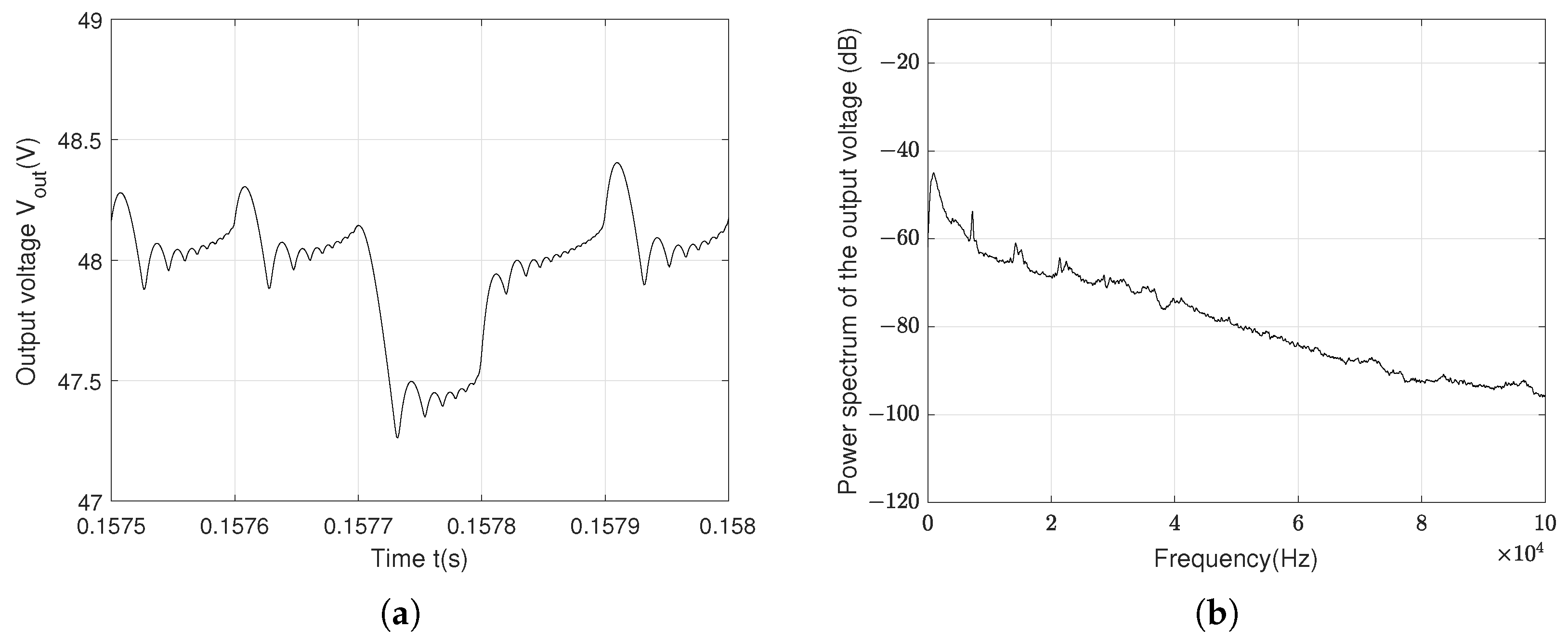

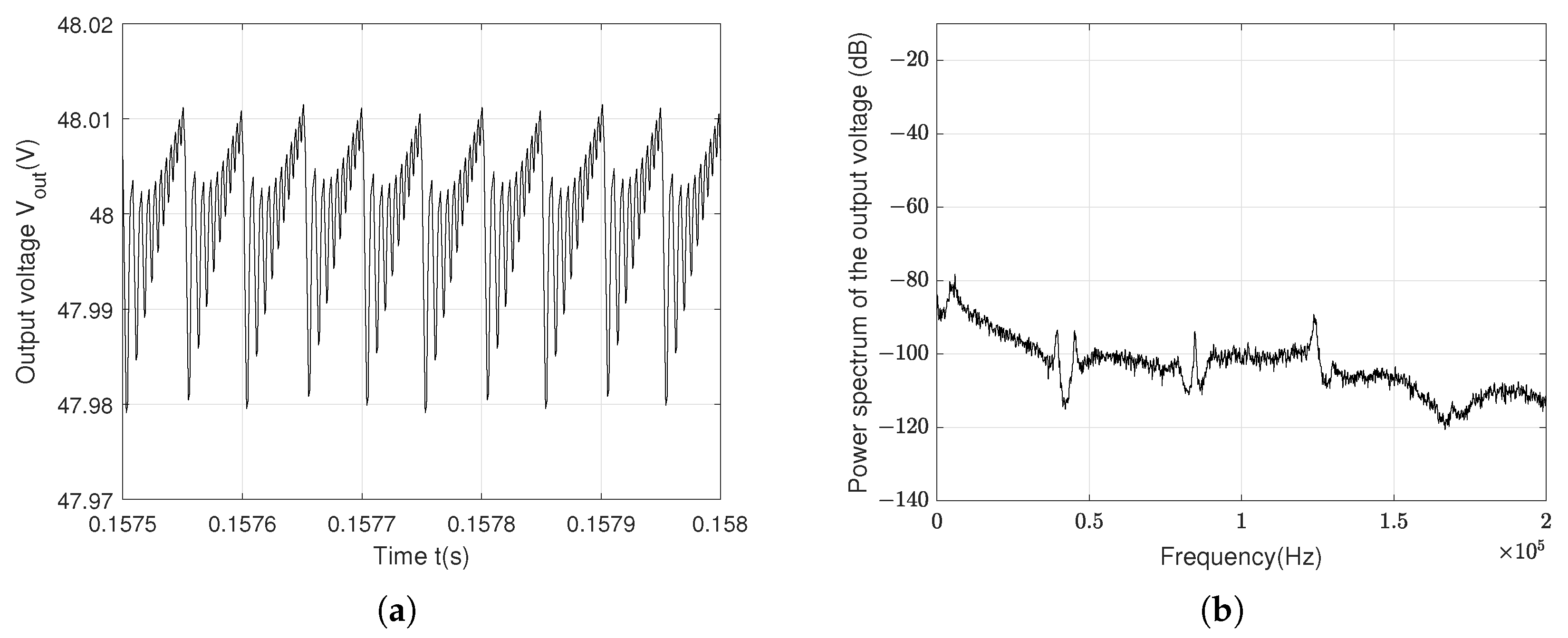
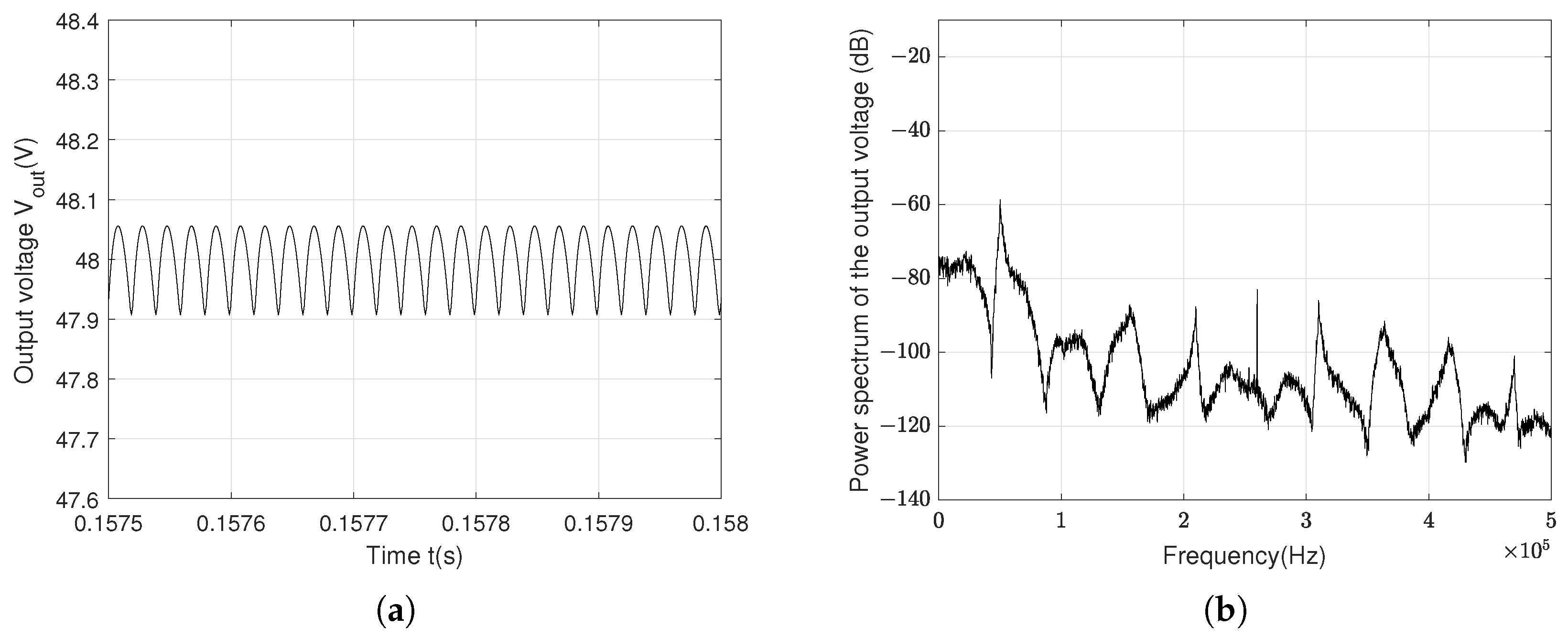
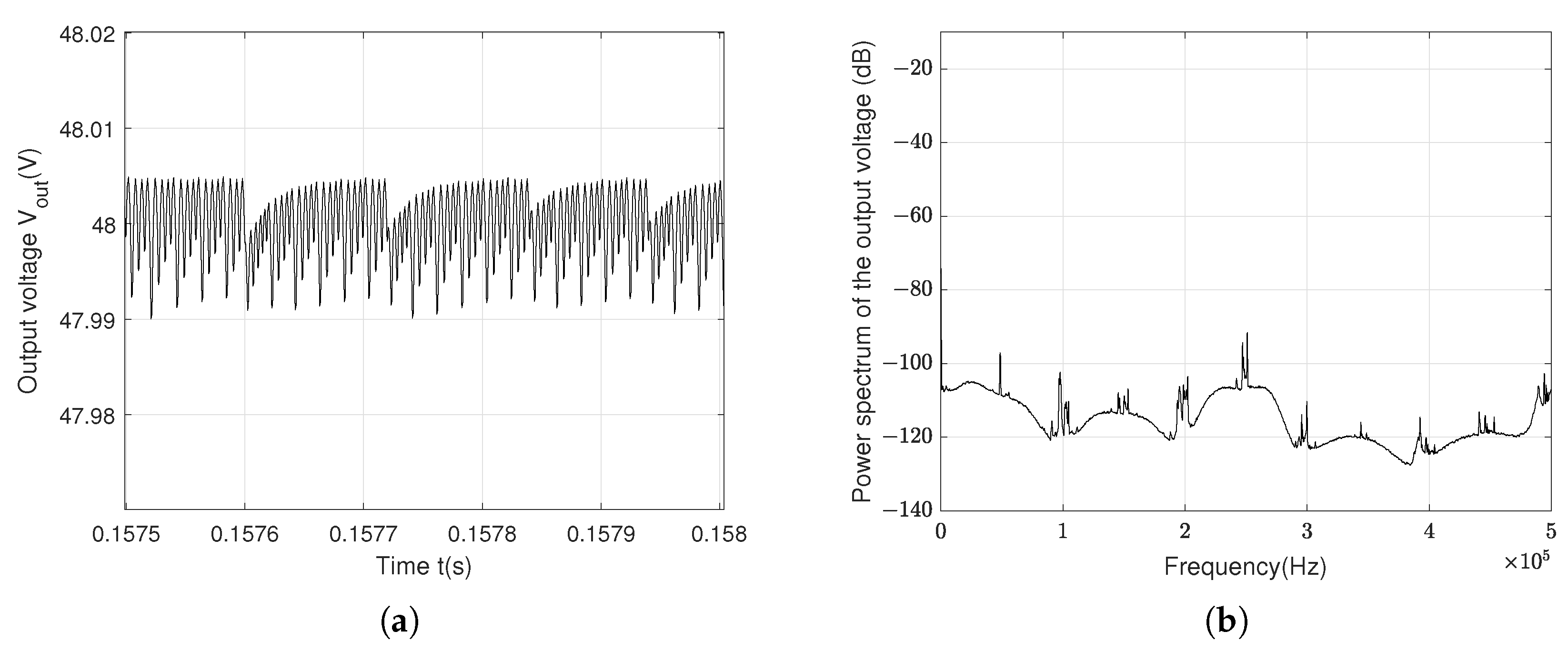
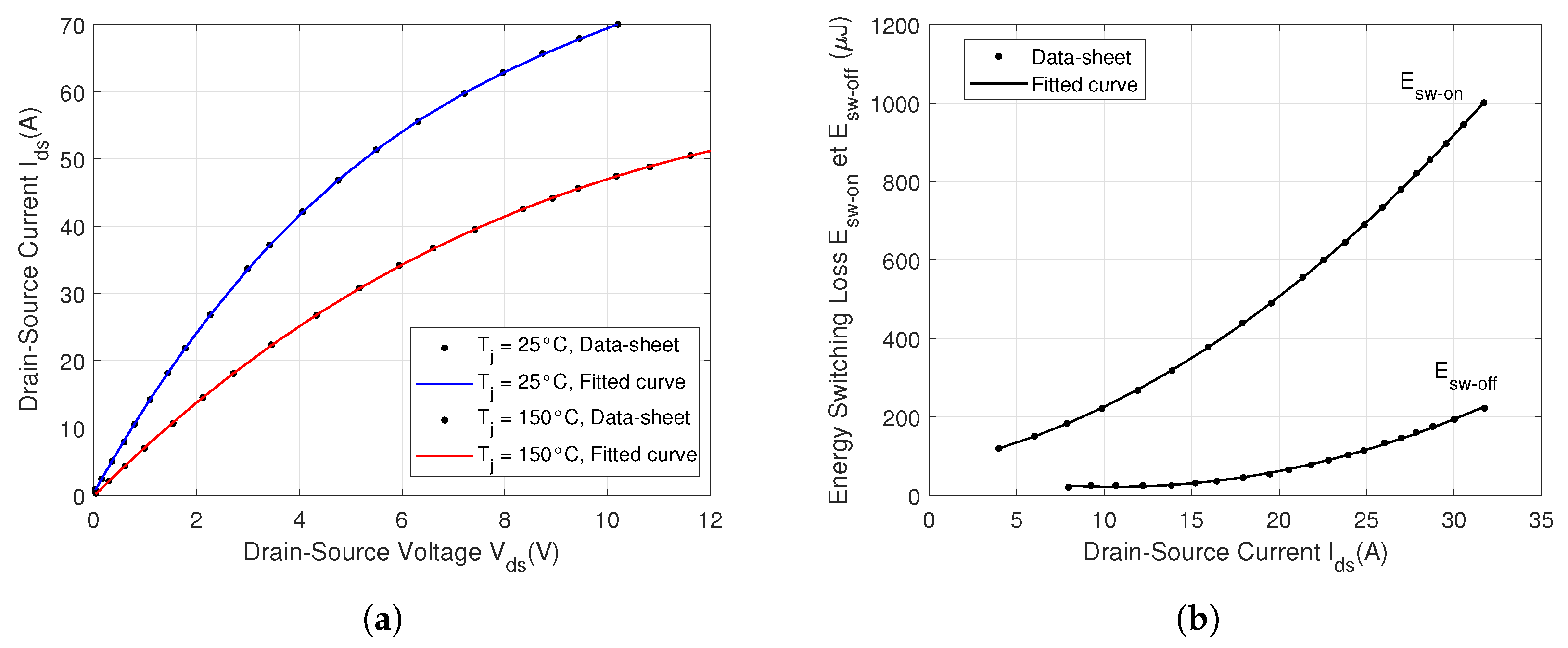
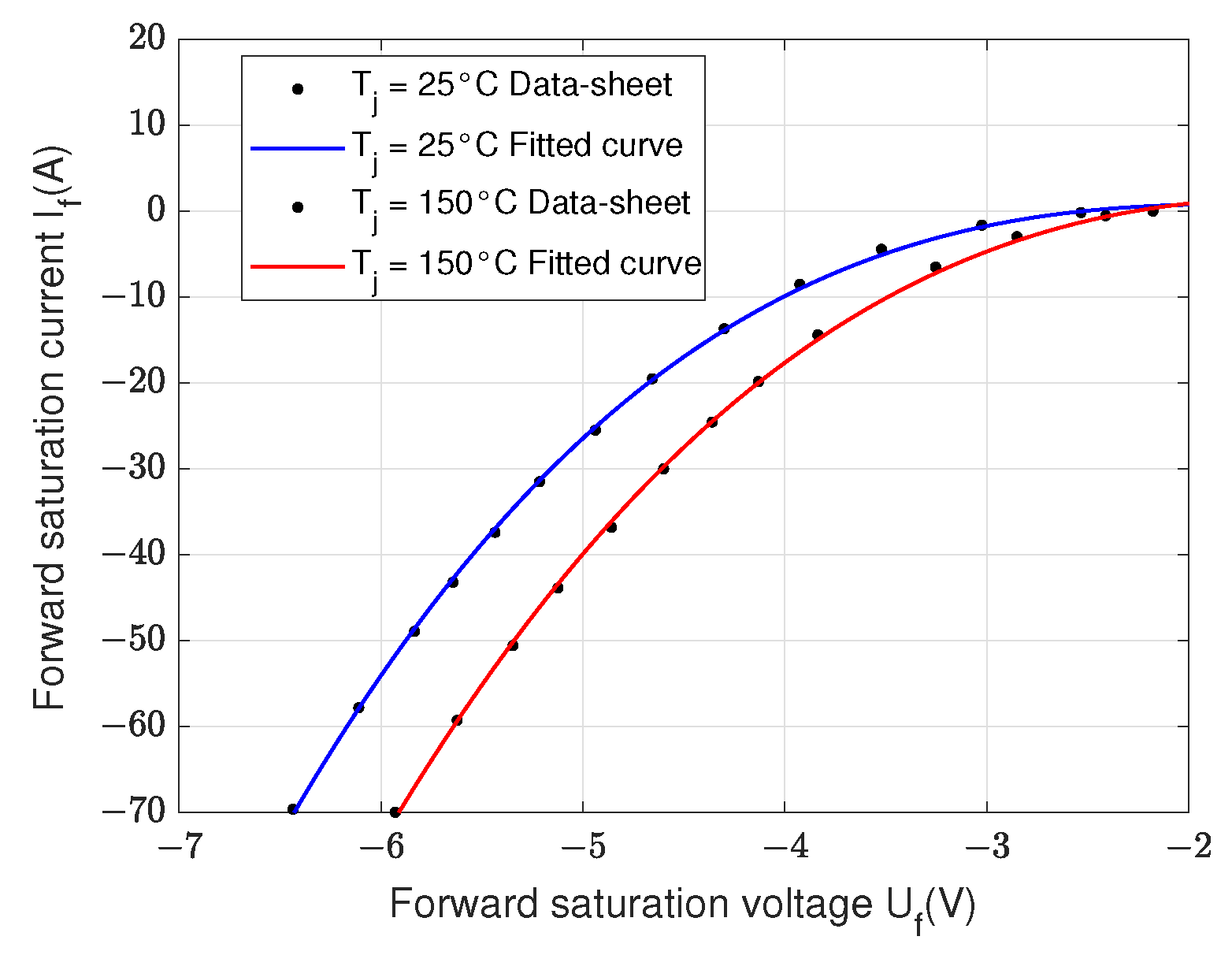



| Specification | Parameter | Symbol | Value | Unit |
|---|---|---|---|---|
| Buck converter | Input voltage | 400 | V | |
| Reference voltage | 48 | V | ||
| Inductance | L | 3 | mH | |
| Capacitance | C | 4.7 | F | |
| Load | R | 3 | ||
| Ramp Input | Upper voltage | 8 | V | |
| Low voltage | 3 | V | ||
| Period | T | 100 | s | |
| controller | Proportional coefficient | P | 0.1 | |
| Integral coefficient | I | 1200 | s−1 | |
| Derivative coefficient | D | 0 | s | |
| Anticontrol of chaos controller | Amplitude of the rectified sinusoidal wave | c | 10 | V |
| Pulsation of the rectified sinusoidal wave | 50 | rad/V |
| Behavior | Controller | Switching Frequency | Ripple | Maximum of Power Spectrum |
|---|---|---|---|---|
| Stable 1T-period | PID | 10 kHz | 2.5 V | −25 dB |
| 20 kHz | 0.8 V | −44 dB | ||
| 50 kHz | 0.15 V | −60 dB | ||
| Chaotic behavior | Anticontrol of chaos + PID | 10 kHz | 1.8 V | −45 dB |
| 20 kHz | 0.025 V | −79 dB | ||
| 50 kHz | 0.015 V | −98 dB |
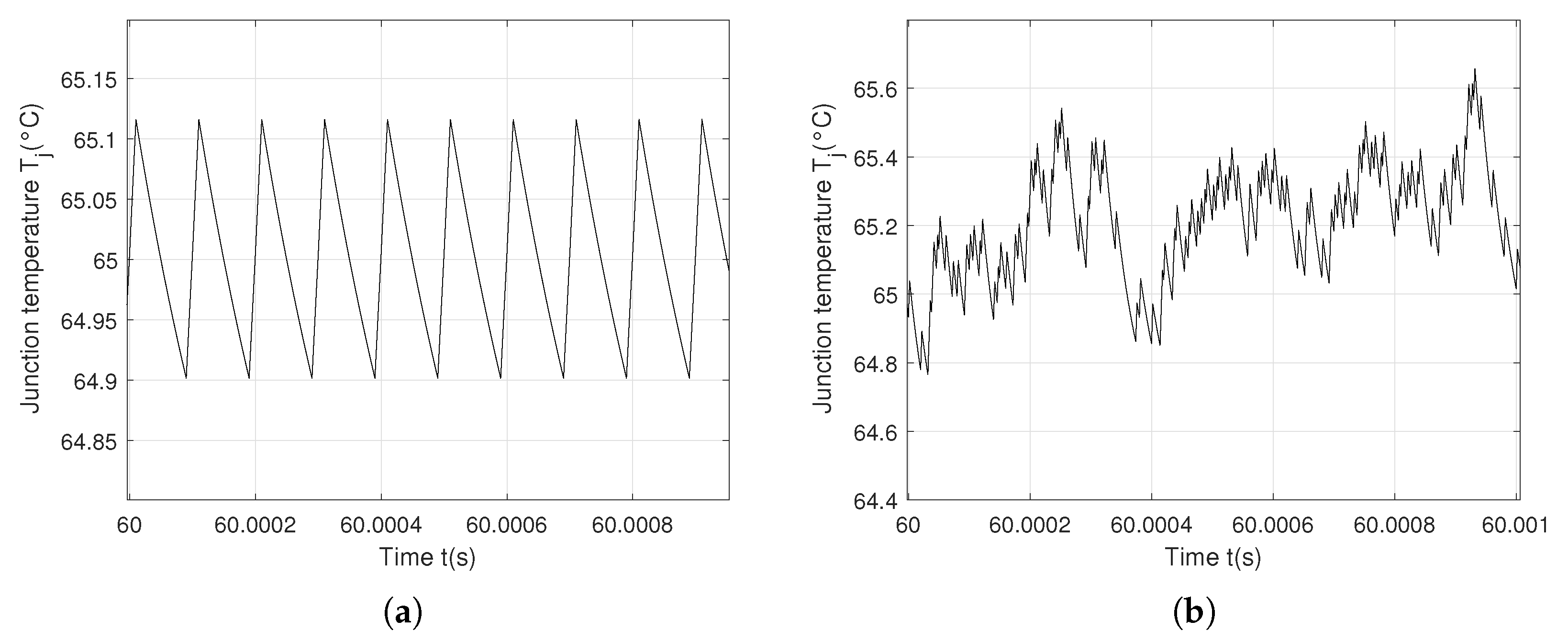
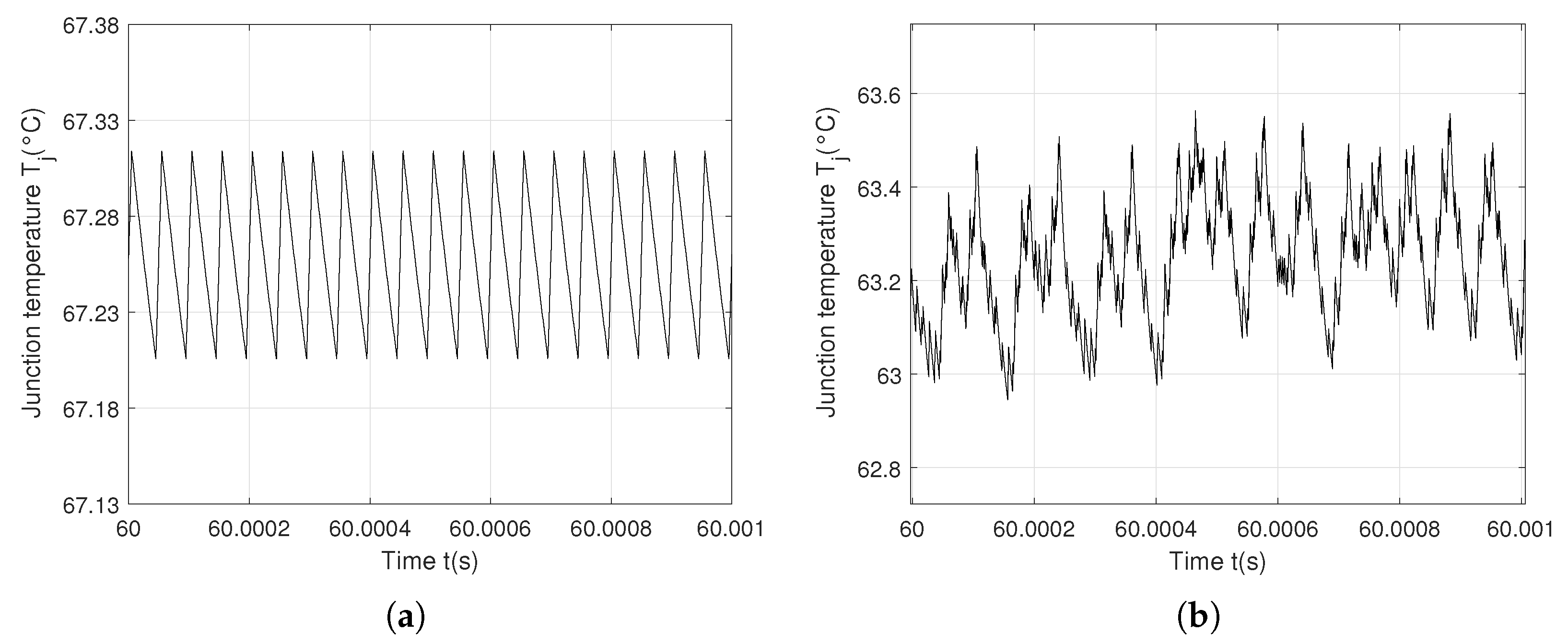
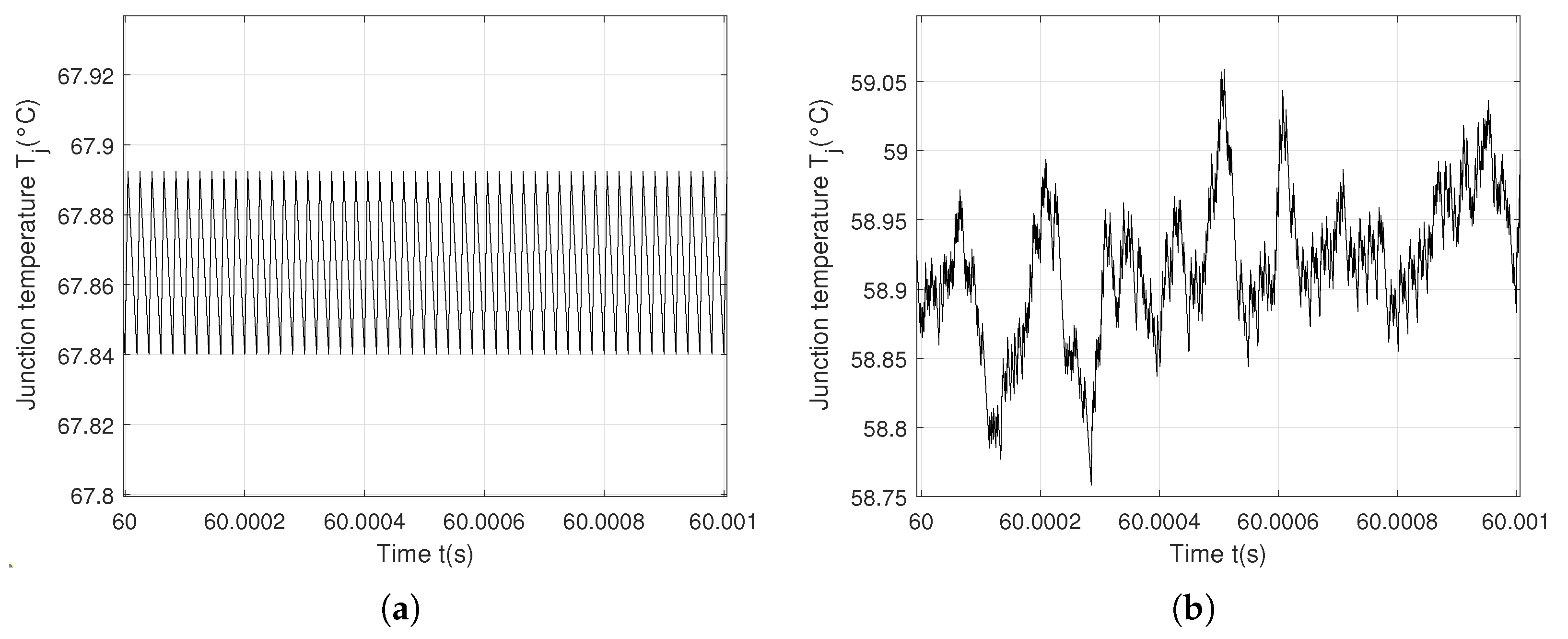
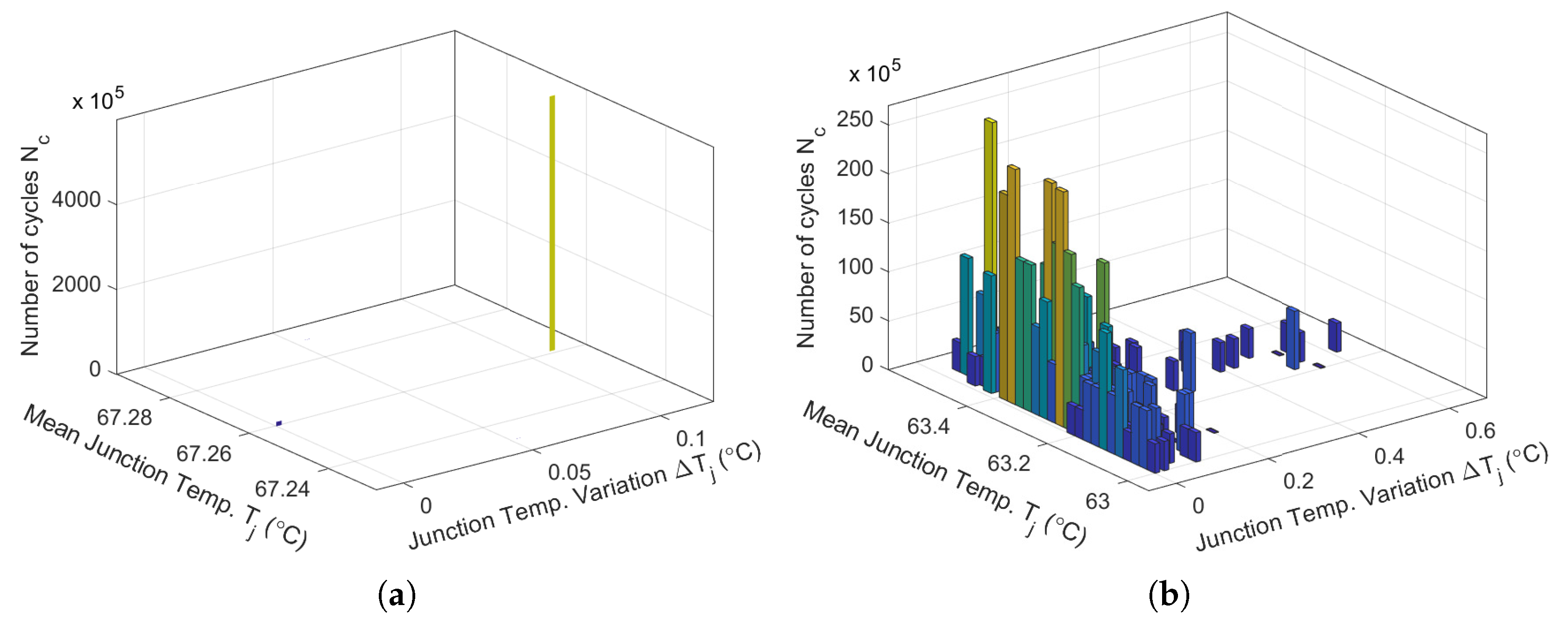
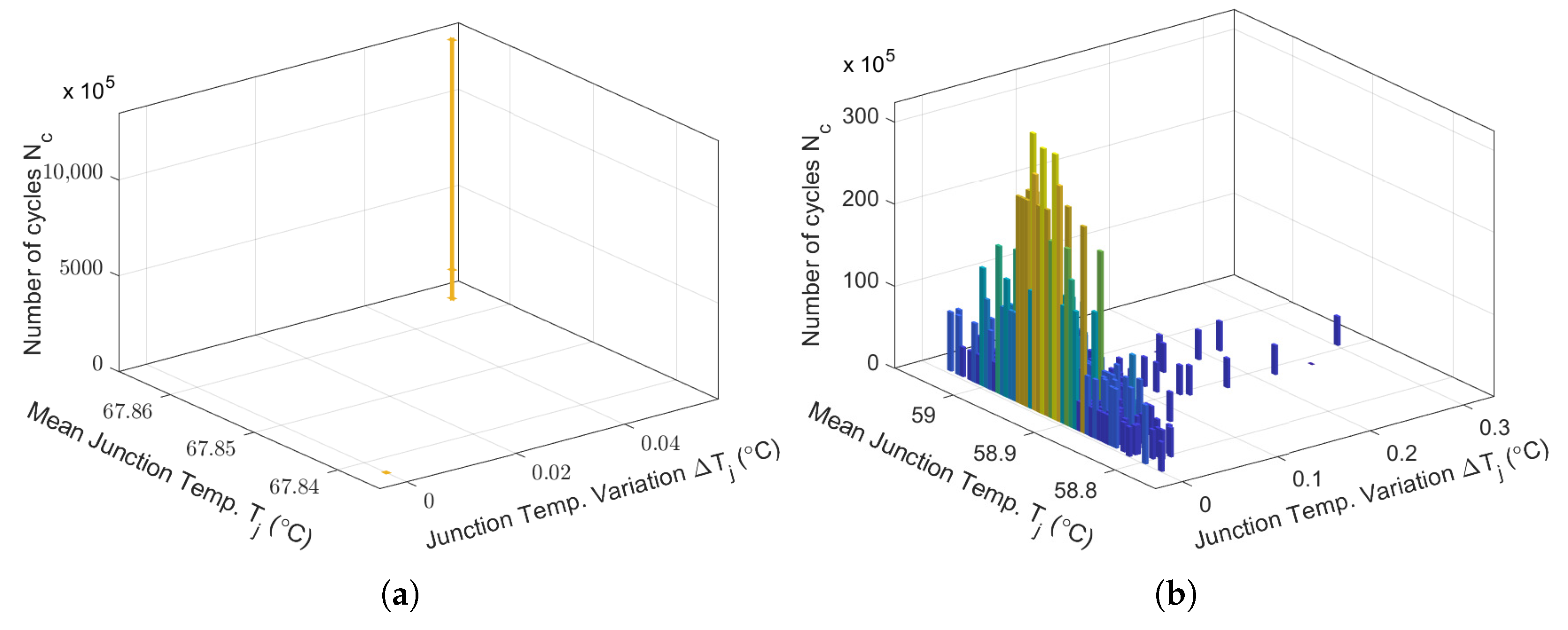
| Behavior | Switching Frequency | Mean of | Variation | Number of Cycles | Accumulated Fatigue |
|---|---|---|---|---|---|
| Periodic behavior | 10 kHz | 65.005 °C | 0.21 °C | 3.9064 × 1012 | 7.68 × 10−3% |
| 20 kHz | 67.26 °C | 0.115 °C | 1.3996 × 1013 | 4.28 × 10−3% | |
| 50 kHz | 67.865 °C | 0.05 °C | 1.9315 × 1015 | 6.99 × 10−5% | |
| Chaotic behavior | 10 kHz | 65.21 °C | 0.87 °C | 1.2548 × 109 | 4.78 × 10−1% |
| 20 kHz | 63.25 °C | 0.6 °C | 2.8520 × 1010 | 4.2 × % | |
| 50 kHz | 58.91 °C | 0.3 °C | 6.6014 × | 2.18 × % |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morel, C.; Morel, J.-Y. Chaos Anticontrol and Switching Frequency Impact on MOSFET Junction Temperature and Lifetime. Actuators 2025, 14, 203. https://doi.org/10.3390/act14050203
Morel C, Morel J-Y. Chaos Anticontrol and Switching Frequency Impact on MOSFET Junction Temperature and Lifetime. Actuators. 2025; 14(5):203. https://doi.org/10.3390/act14050203
Chicago/Turabian StyleMorel, Cristina, and Jean-Yves Morel. 2025. "Chaos Anticontrol and Switching Frequency Impact on MOSFET Junction Temperature and Lifetime" Actuators 14, no. 5: 203. https://doi.org/10.3390/act14050203
APA StyleMorel, C., & Morel, J.-Y. (2025). Chaos Anticontrol and Switching Frequency Impact on MOSFET Junction Temperature and Lifetime. Actuators, 14(5), 203. https://doi.org/10.3390/act14050203






