A Spatiotemporal Domain-Coupled Clustering Method for Performance Prediction of Cluster Systems
Abstract
:1. Introduction
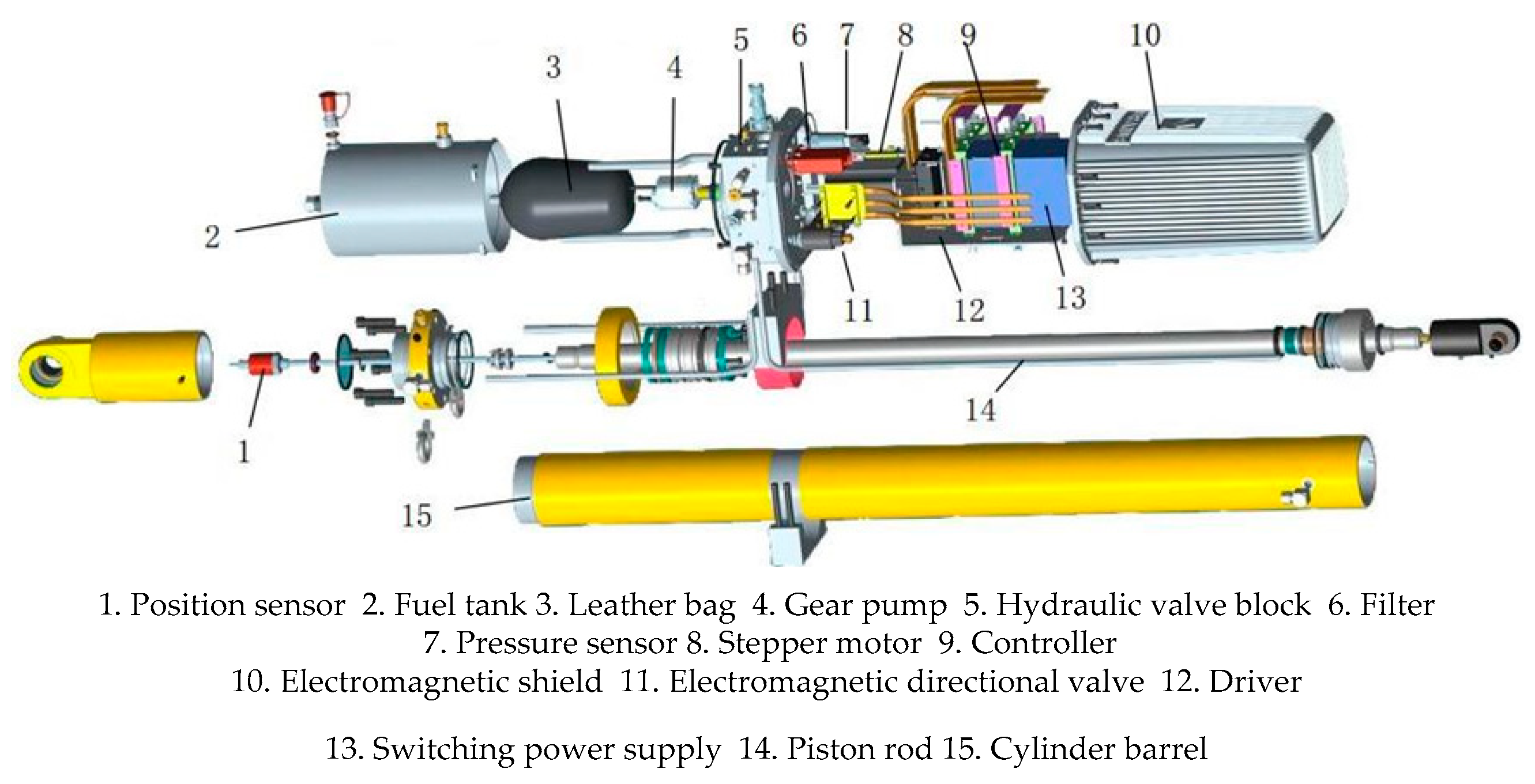
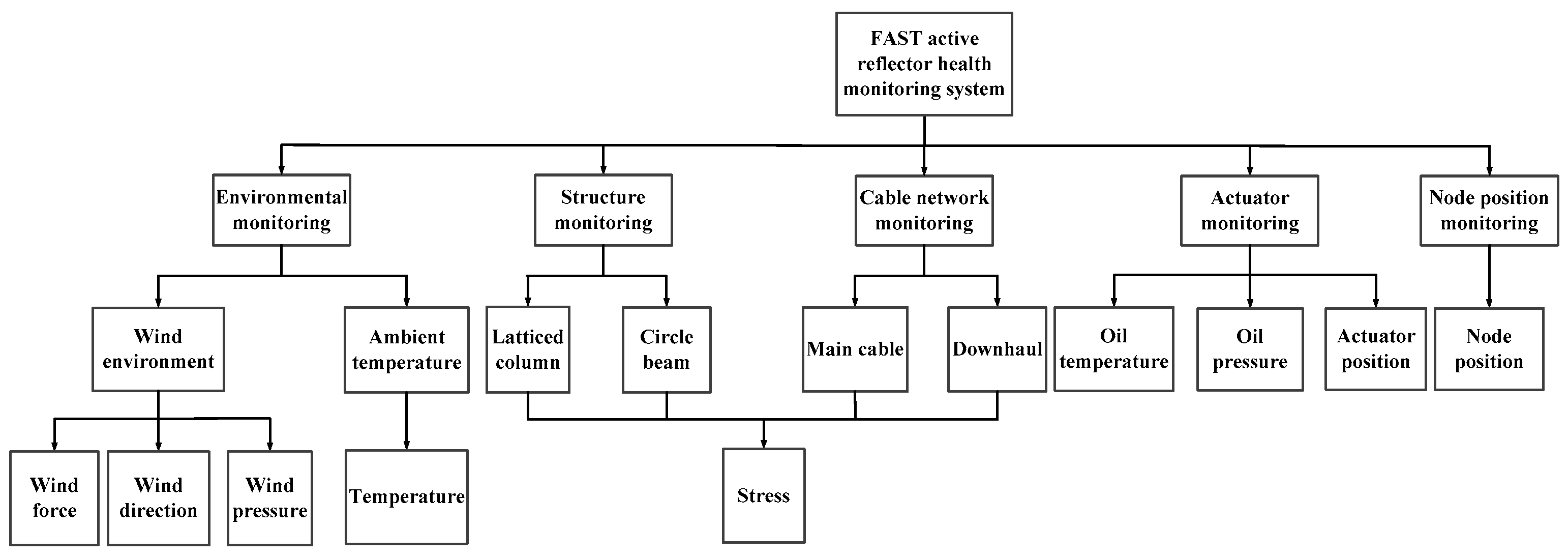
2. Data Preprocessing of the FAST Health Monitoring System
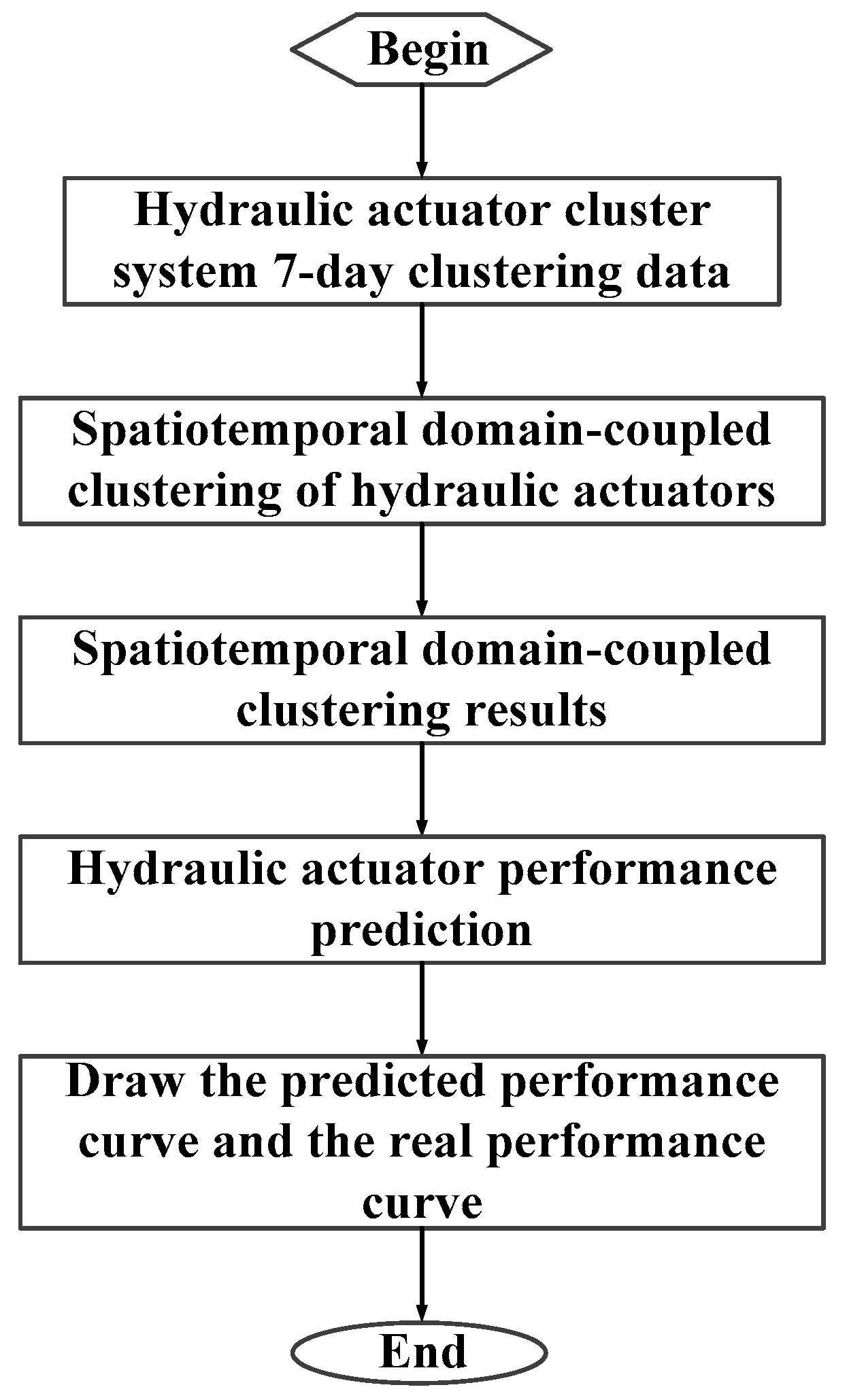
3. Spatiotemporal Domain-Coupled Clustering Method
3.1. Spatial-Domain BIRCH Clustering Method for Hydraulic Actuator
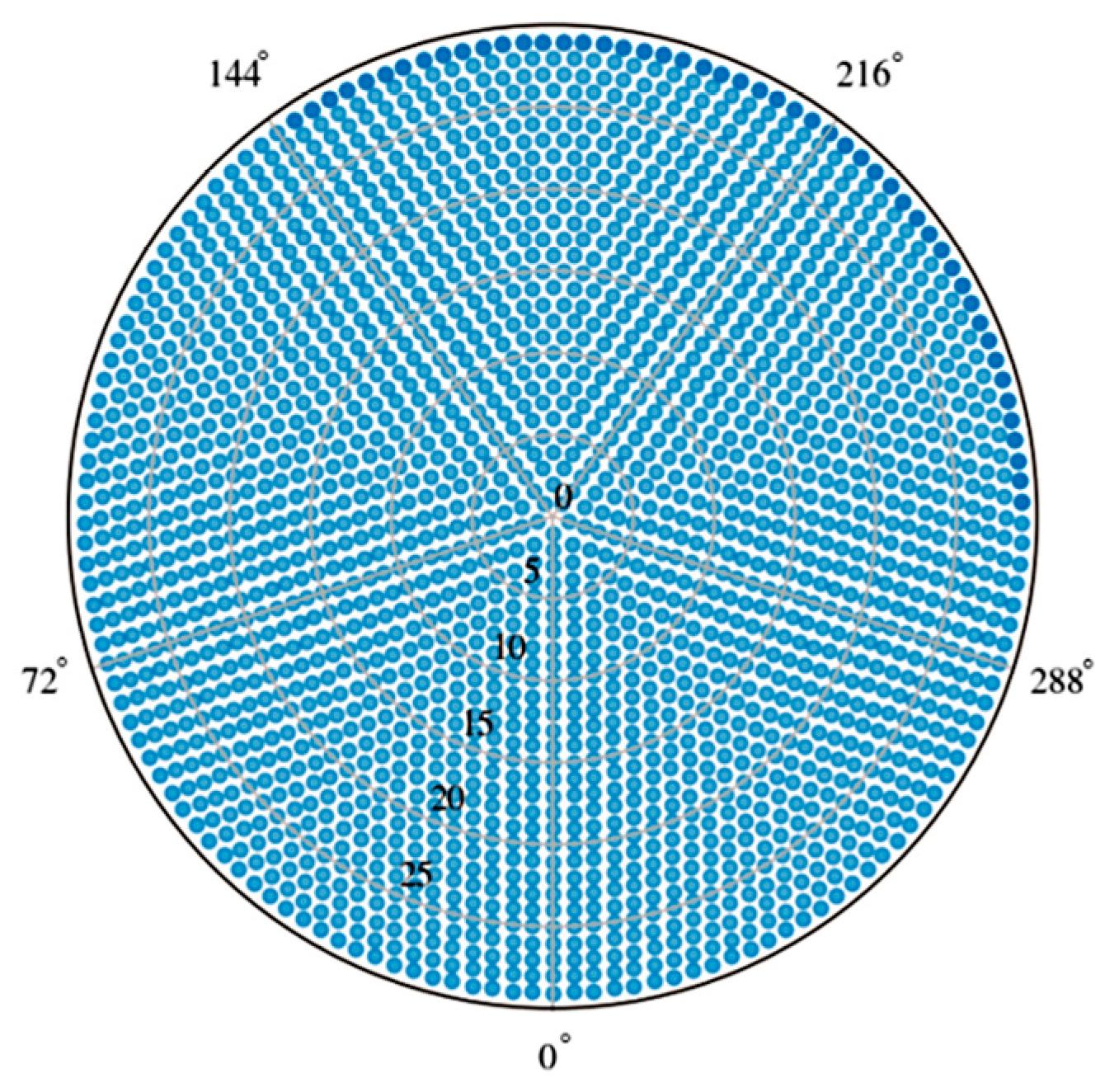
3.1.1. Polar Coordinate of the Spatial Position of the Hydraulic Actuator
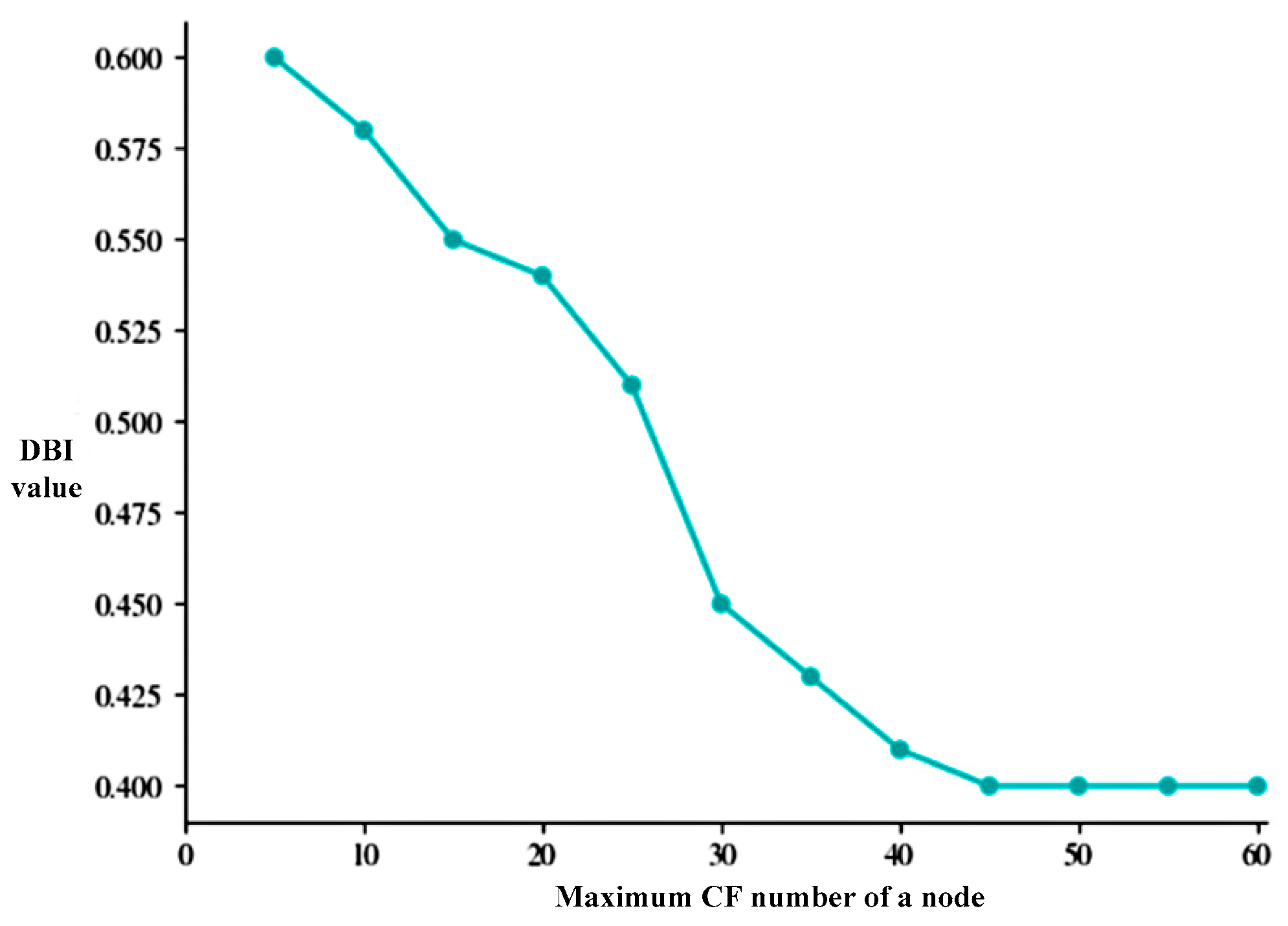
3.1.2. Spatial Clustering Feature Selection
3.1.3. The Main Process of Spatial-Domain BIRCH Clustering
- (1)
- Initialize, set the maximum number of data items B allowed in the leaf node and the maximum number of nodes L that can be accommodated in the memory;
- (2)
- Establish a CF tree, calculate their centroid and radius by scanning the data set, take B data as the unit, and insert operations in the CF tree until all data in the data set are processed;
- (3)
- Cluster, traverse the CF tree, and process each node as follows.
- (4)
- Compress the CF tree, traverse the CF tree, and perform the following processing for each node.
- (5)
- Repeat steps (3) and (4) until there is only one family left in the compressed CF tree, or compression cannot continue.
3.2. Temporal-Domain K-Means Clustering Method for Hydraulic Actuator
3.2.1. Temporal-Domain K-Means Clustering Algorithm Principle
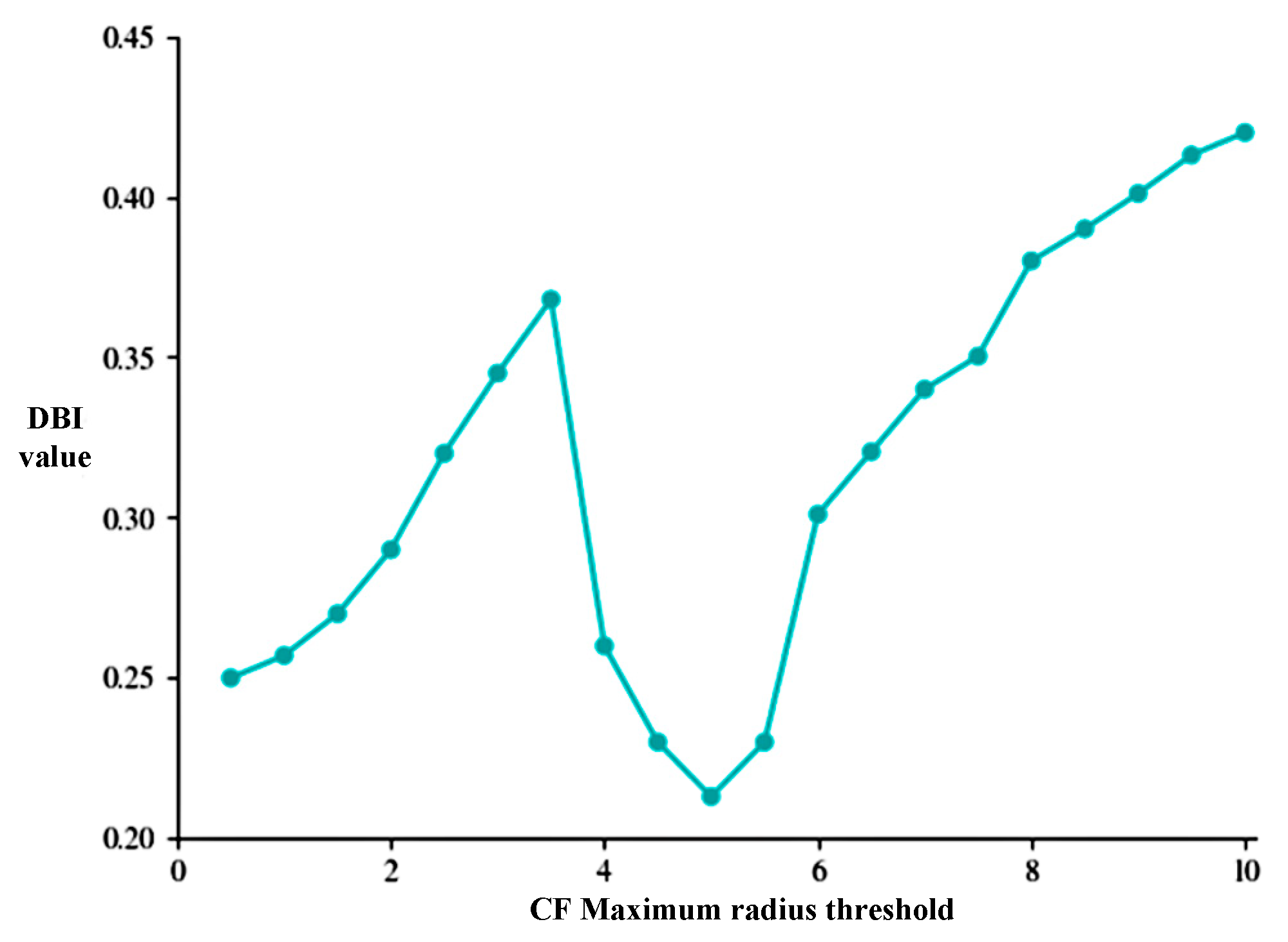
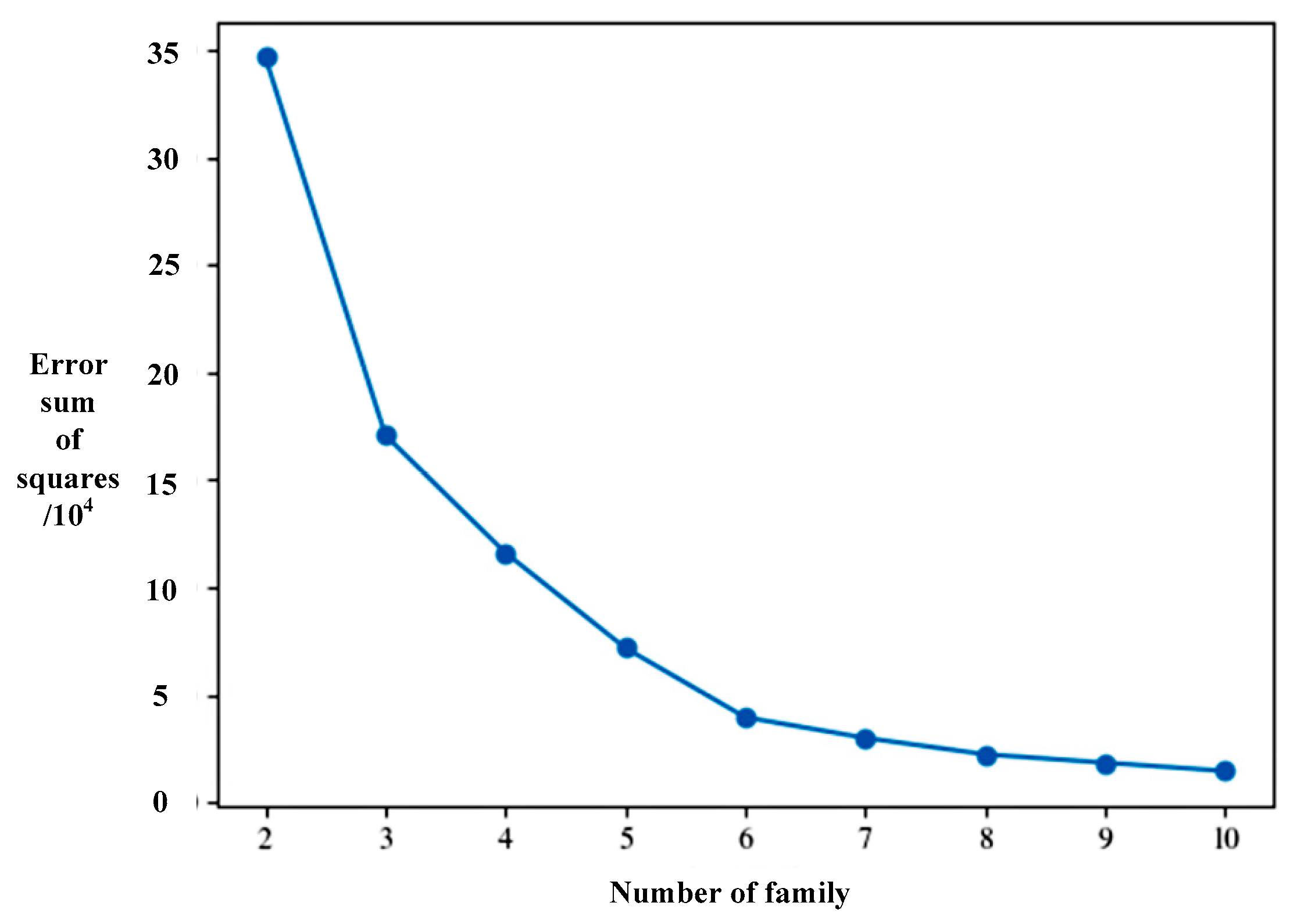
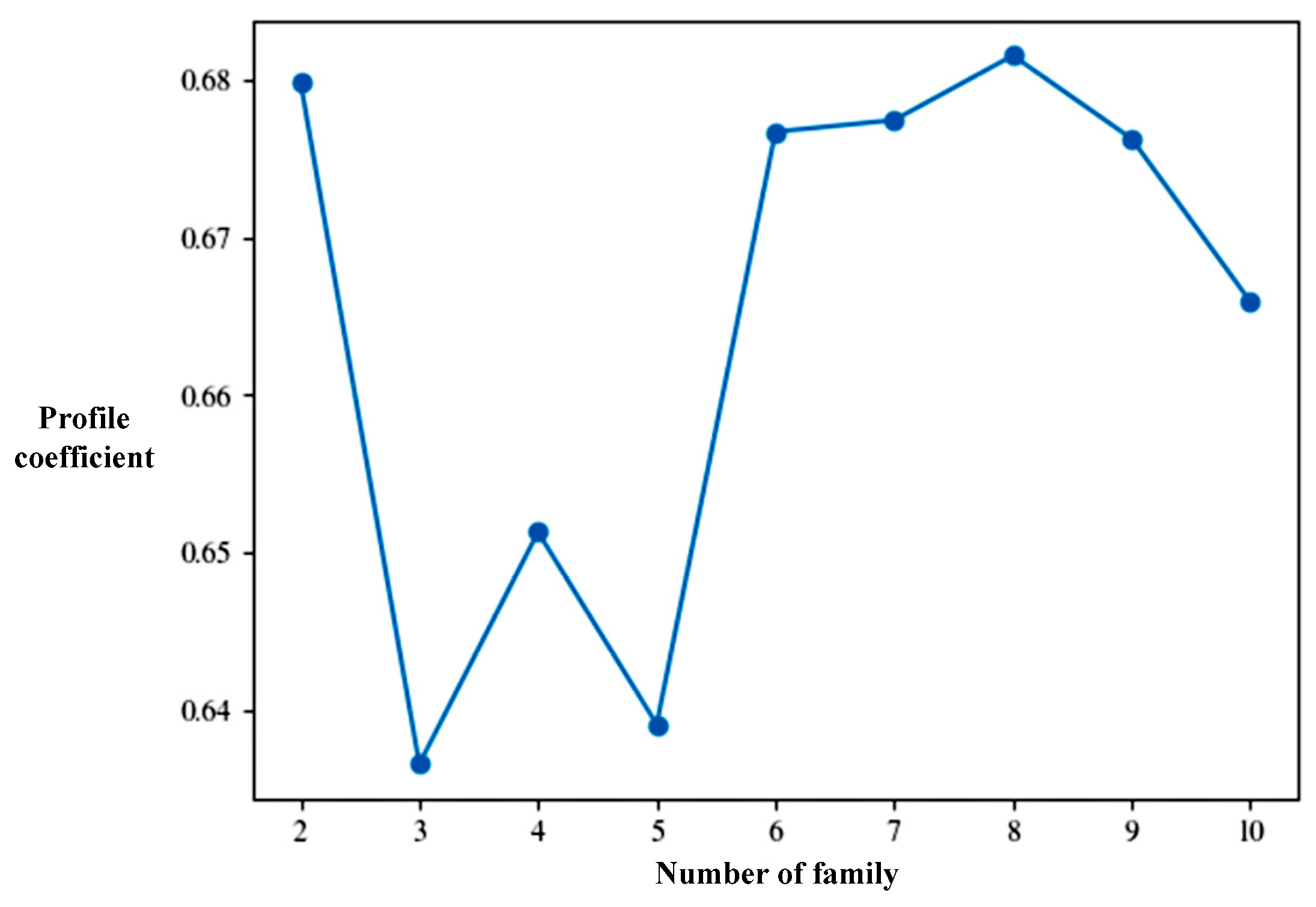
3.2.2. Determination of the Optimal Value
4. Analysis of Spatiotemporal Domain-Coupled Clustering Result
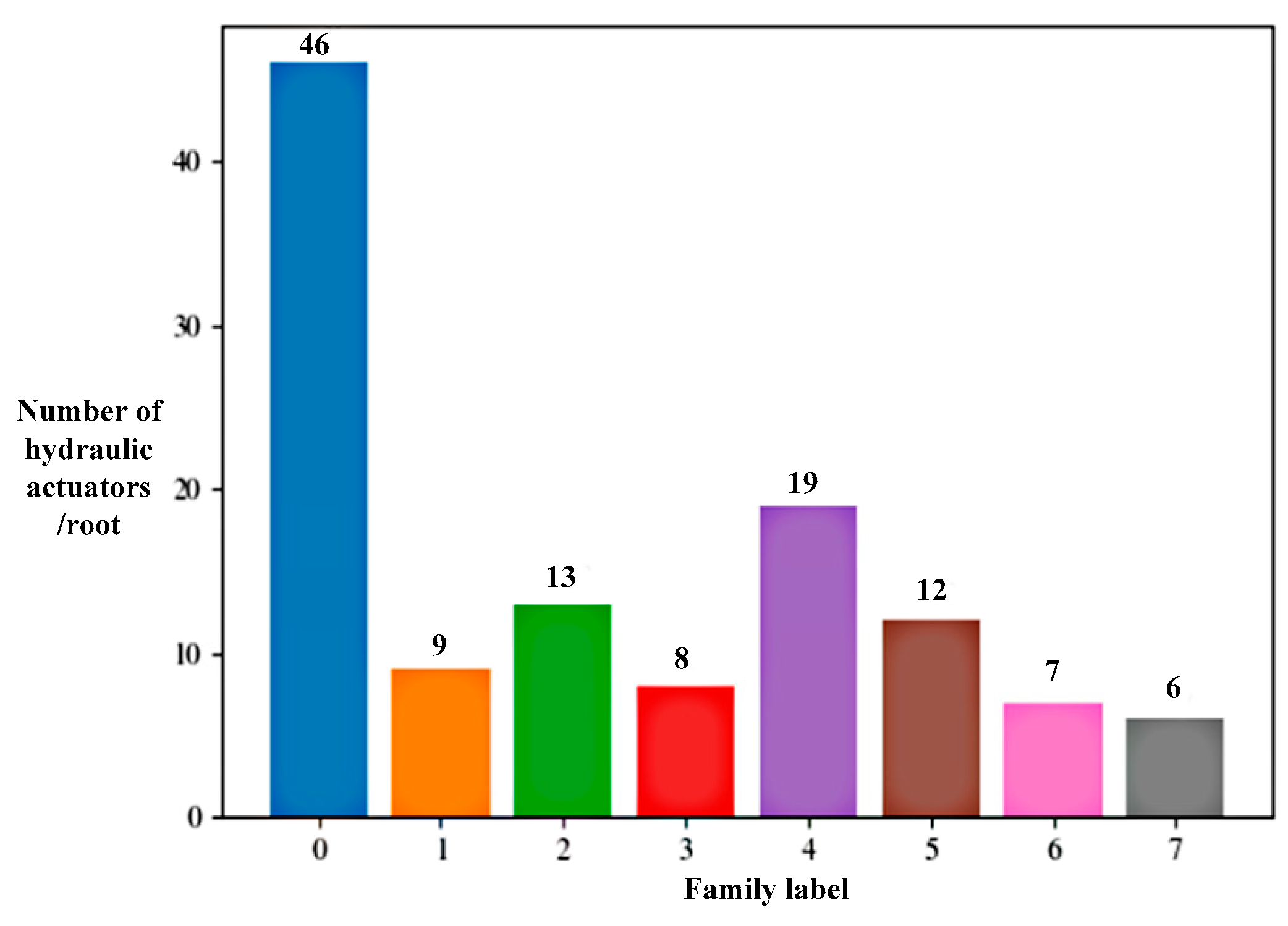
4.1. Analysis of Spatial-Domain BIRCH Clustering Result
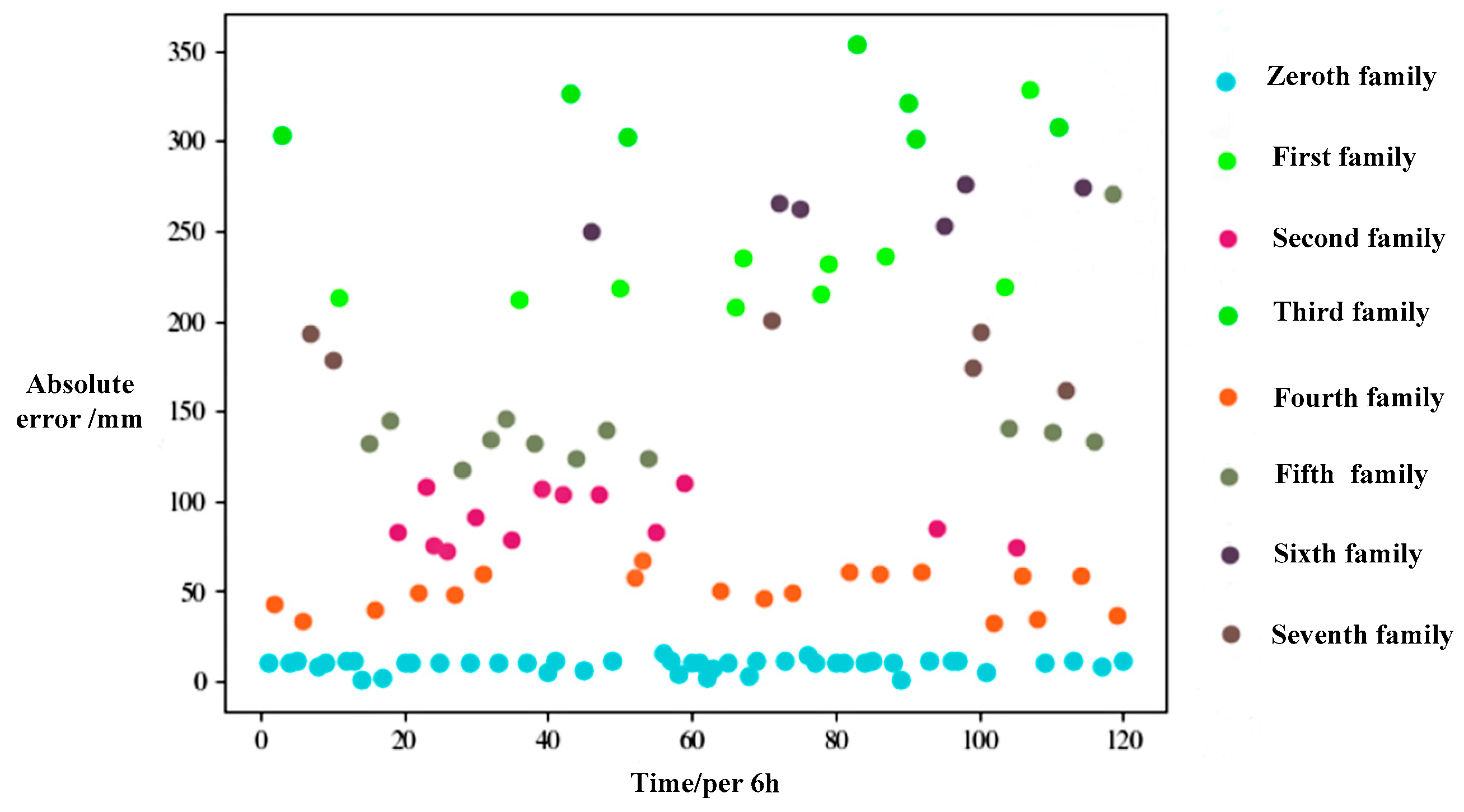
4.2. Analysis of Temporal-Domain K-Means Clustering Result
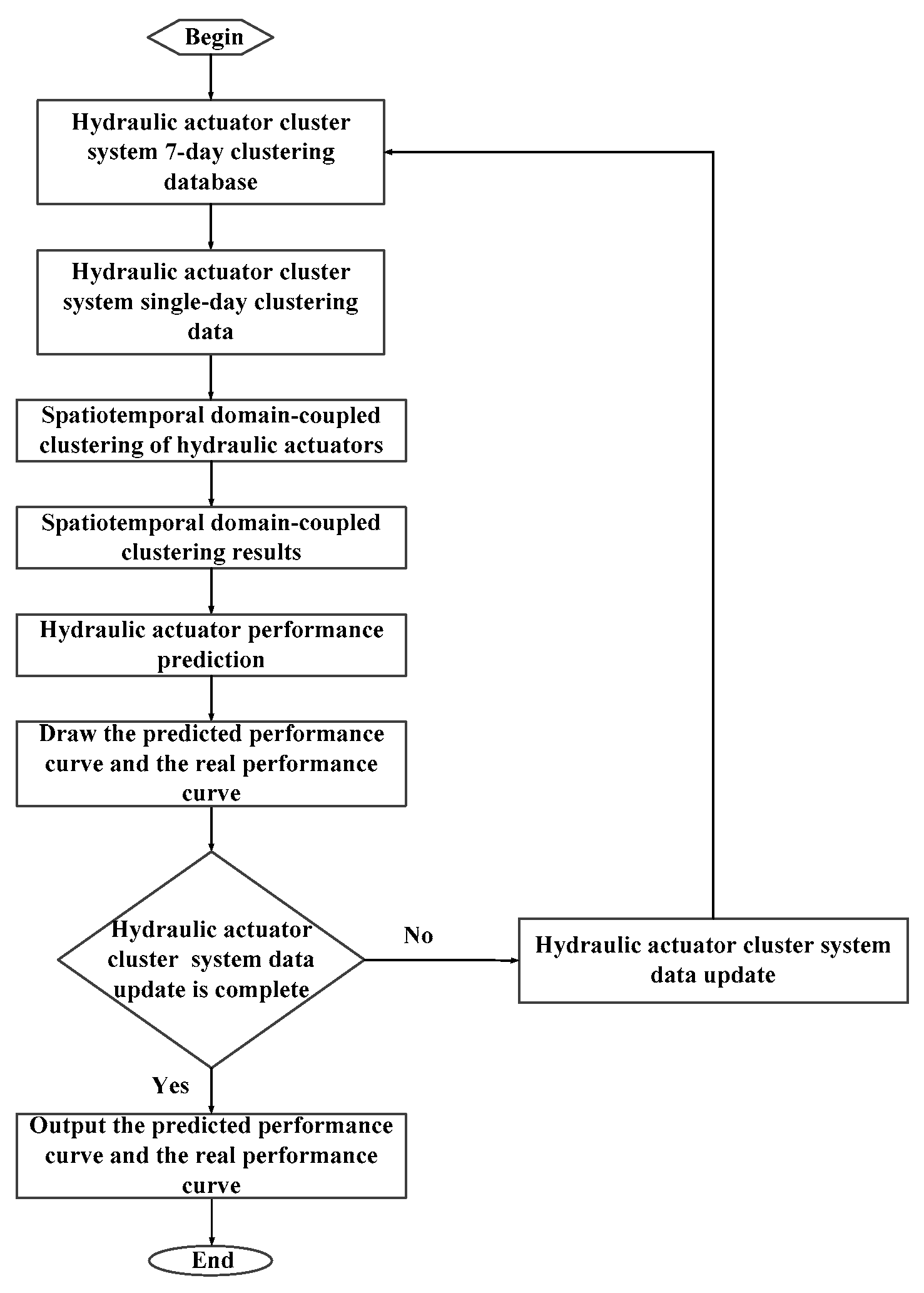
5. Validation and Optimization of Spatiotemporal Domain-Coupled Clustering Prediction Algorithm
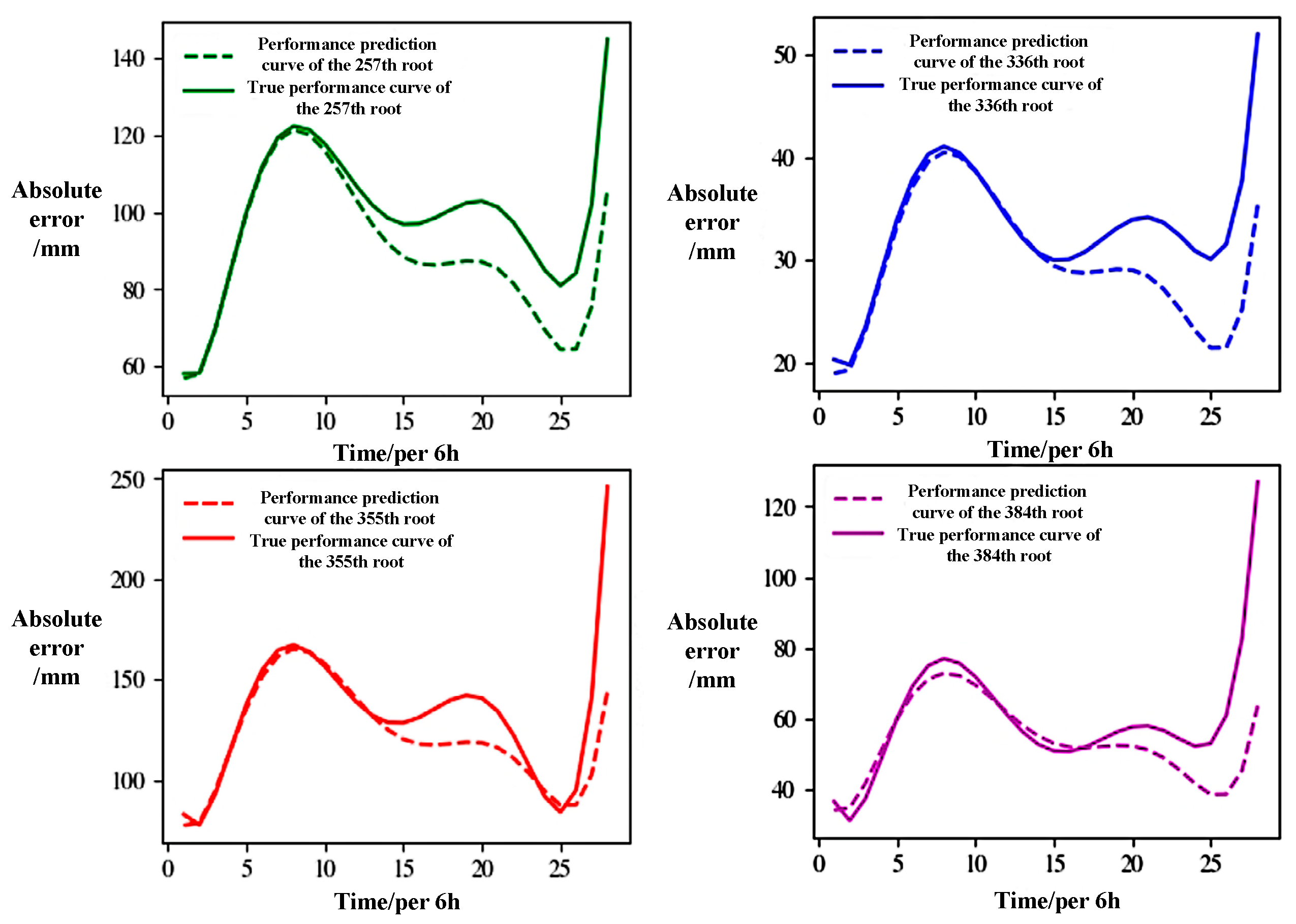
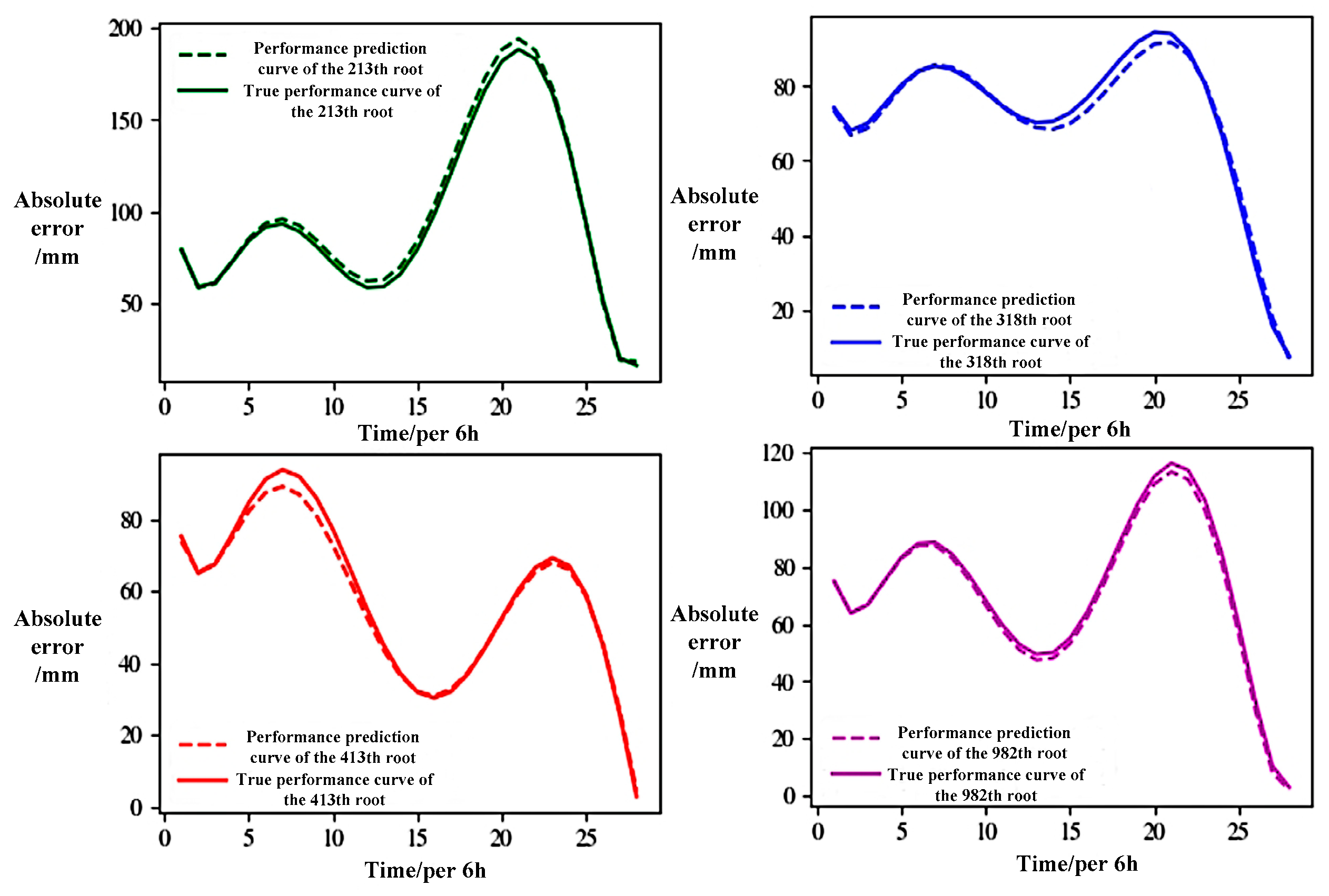
5.1. Performance Prediction and Result Analysis of Hydraulic Actuator
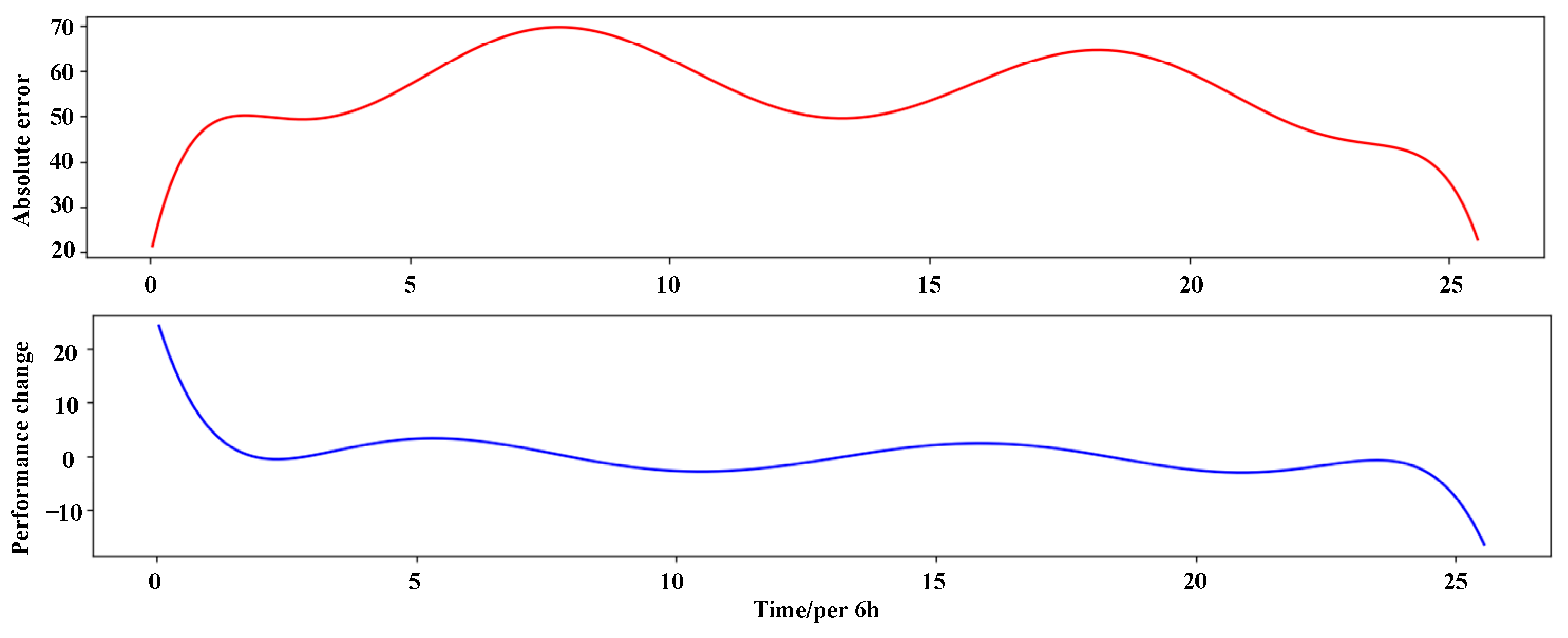
5.2. Error Analysis and Algorithm Optimization of Hydraulic Actuator Performance Prediction
5.3. Hydraulic Actuator Performance Prediction Optimization Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nan, R. Five-hundred-meter aperture spherical radio telescope. Sci. China Ser. G Phys. Mech. Astron. 2006, 49, 129–148. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, Y.; Xue, J.; Zhu, M.; Wang, Y. Key performance analysis of five-hundred-meter aperture spherical radio telescope reflective surface hydraulic actuator. J. Mech. Eng. 2017, 53, 183–191. [Google Scholar] [CrossRef]
- Zhu, M.; Zhao, J.; Wang, Q. Reliability evaluation of key hydraulic components for actuators of FAST based on small sample test. Int. J. Precis. Eng. Manuf. 2017, 18, 1561–1566. [Google Scholar] [CrossRef]
- Jiang, P.; Gan, H.; Yao, R.; Sun, J.; Lu, J.; Yu, D.; Li, H.; Yu, J.; Dong, B.; Chai, X.; et al. FAST: The Five-Hundred-Meter Aperture Spherical Radio Telescope. Engineering 2023, 28, 21–25. [Google Scholar] [CrossRef]
- Peng, C. Research on the reliability of coal mining machines based on fault tree analysis and Bayesian networks. Coal Mine Mach. 2023, 44, 181–183. [Google Scholar]
- Han, X.; Zhan, J.; Zhang, F.; Hu, J.; Wu, X. Robust topological superconductivity in spin–orbit coupled systems at higher-order van Hove filling. Sci. Bull. 2024, 69, 319–324. [Google Scholar] [CrossRef]
- Hasan, M.; Mia, B.; Ahmed, U.; Karim, M.A.; Islam, A.A.; Mohi-Ud-Din, M. Heat stress tolerance in wheat seedling: Clustering genotypes and identifying key traits using multivariate analysis. Heliyon 2024, 10, 38623. [Google Scholar] [CrossRef]
- Martinez-Martin, P.; Rojo-Abuín, J.M.; Weintraub, D.; Chaudhuri, K.R.; Rodriguez-Blázquez, C.; Rizos, A.; Schrag, A. Factor Analysis and Clustering of the Movement Disorder Society-non-motor Rating Scale. Mov. Disord. 2020, 35, 969–975. [Google Scholar] [CrossRef]
- Abdolmajid, D.; Ali, D.; Alireza, A. Modeling and Forecasting Nonstationary Voltage Fluctuation Based on Grey System Theory. IEEE Trans. Power Deliv. 2017, 32, 1212–1219. [Google Scholar]
- Zheng, D.; Wang, H.; An, J.; Chen, J.; Pan, H.; Chen, L. Real-Time Estimation of Battery State of Charge with Metabolic Grey Model and LabVIEW Platform. IEEE Access 2018, 6, 13170–13180. [Google Scholar] [CrossRef]
- Chen, L.; Wang, H.; Chen, J.; An, J.; Ji, B.; Lyu, Z.; Cao, W.; Pan, H. A Novel Remaining Useful Life Prediction Framework for Lithium-ion Battery Using Grey Model and Particle Filtering. Int. J. Energy Res. 2020, 44, 7435–7449. [Google Scholar] [CrossRef]
- Tomasz, K.; Kazimierz, O. Forecasting the Number of Failures of the Steering System Components with the Use of the Grey System Theory Method. Sci. J. Silesian Univ. Technol. 2021, 112, 85–97. [Google Scholar]
- Yang, J.; Qiu, X.; Chen, Z. The Reliability Evaluation of Antiskid Valve of CRH2 EMUs Based on Bayes Method. Period. Polytech. Transp. Eng. 2018, 47, 268–276. [Google Scholar] [CrossRef]
- Rodrigues, A.; Pereira, C.; Polpo, A. Estimation of Component Reliability in Coherent Systems with Masked Data. IEEE Access 2019, 7, 57476–57487. [Google Scholar] [CrossRef]
- Fan, X.; Guo, W.; Sun, J. Reliability of High-Voltage GaN-Based Light-Emitting Diodes. IEEE Trans. Device Mater. Reliab. 2019, 19, 402–408. [Google Scholar] [CrossRef]
- Ali, S.; Shah, I.; Siddiqui, G.F.; Saba, T.; Rehman, A. Reliability Analysis for Electronic Devices Using Generalized Exponential Distribution. IEEE Access 2020, 8, 108629–108644. [Google Scholar] [CrossRef]
- Zhou, K.; Cruise, J.; Dent, C.; Dobson, I.; Wang, Z.; Wilson, A.; Wehenkel, L. Bayesian Estimates of Transmission Line Outage Rates that Consider Line Dependencies. IEEE Trans. Power Syst. 2021, 360, 1095–1106. [Google Scholar] [CrossRef]
- Loutas, T.; Roulias, D.; Georgoulas, G. Remaining Useful Life Estimation in Rolling Bearings Utilizing Data-Driven Probabilistic E-Support Vectors Regression. IEEE Trans. Reliab. 2013, 62, 821–832. [Google Scholar] [CrossRef]
- Aikhuele, D.; Periola, A.; Ighravwe, D. Wind Turbine Systems Operational State and Reliability Evaluation: An Artificial Neural Network Approach. Int. J. Data Netw. Sci. 2019, 3, 323–330. [Google Scholar] [CrossRef]
- Koley, E.; Shukla, S.; Ghosh, S.; Mohanta, D.K. Protection Scheme for Power Transmission Lines Based on SVM and ANN Considering the Presence of Non-Linear Loads. IET Gener. Transm. Distrib. 2017, 11, 2333–2334. [Google Scholar] [CrossRef]
- Picheny, V.; Kim, N.; Haftka, R. Application of Bootstrap Method in Conservative Estimation of Reliability with Limited Samples. Struct. Multidiscip. Optim. 2010, 41, 205–217. [Google Scholar] [CrossRef]
- Lee, S.; Bolic, M.; Groza, V.; Dajani, H.R.; Rajan, S. Confidence Interval Estimation for Oscillometric Blood Pressure Measurements Using Bootstrap Approaches. IEEE Trans. Instrum. Meas. 2011, 60, 3405–3415. [Google Scholar] [CrossRef]
- Rodrigues, A.; Silva, M. Confidence Intervals Estimation for Reliability Data of Power Distribution Equipments Using Bootstrap. IEEE Trans. Power Syst. Publ. Power Eng. Soc. 2013, 28, 3283–3291. [Google Scholar] [CrossRef]
- Li, H.; Xie, L.; Li, M.; Ren, J.; Zhao, B.; Zhang, S. Reliability Assessment of High- Quality and Long-Life Products Based on Zero-Failure Data. Qual. Reliab. Eng. Int. 2019, 35, 470–482. [Google Scholar] [CrossRef]
- Zhai, Q.; Ye, Z. Robust Degradation Analysis with Non-Gaussian Measurement Errors. IEEE Trans. Instrum. Meas. 2017, 66, 2803–2812. [Google Scholar] [CrossRef]
- Liu, F.; Guo, W.; Liu, R.; Liu, J. Improved Load Forecasting Model Based on Two-Stage Optimization of Gray Model with Fractional Order Accumulation and Markov Chain. Commun. Stat.-Theory Methods 2019, 50, 2659–2673. [Google Scholar] [CrossRef]
- Fan, M.; Zeng, Z.; Zio, E.; Kang, R.; Chen, Y. A Sequential Bayesian Approach for Remaining Useful Life Prediction of Dependent Competing Failure Processes. IEEE Trans. Reliab. 2019, 68, 317–329. [Google Scholar] [CrossRef]
- Zhao, W.; Cao, K.; Tao, Y.; Zhang, J.; Tu, X.; Wang, J.; Dong, H. Performance Reliability Evaluation of Explosive Initiator Based on Bayes-Bootstrap Method. In Proceedings of the 2021 Global Reliability and Prognostics and Health Management, Nanjing, China, 15–17 October 2021; pp. 1–6. [Google Scholar]
- Li, Y.; Wang, H.; Fu, Q. Aeroengine Performance Degradation Evaluation Method Based on Hierarchical Bayes Integrated with DNN Fusion Decision. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 1, p. 1910. [Google Scholar]
- Cai, W.; Zhao, J.; Zhu, M. A real time methodology of cluster-system theory-based reliability estimation using k-means clustering. Reliab. Eng. Syst. Saf. 2020, 202, 107045. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X.; Chai, J.; Wang, Y.; Jin, X.; He, Z.; Cai, W.; Guo, R. Numerical and experimental investigation on active hydraulic tensioner system for a TLP under tether fails condition. Mar. Struct. 2025, 99, 103693. [Google Scholar] [CrossRef]
- Xie, W. Stability and dynamic responses of a top-tensioned riser under two different parametric excitations. Mar. Struct. 2024, 97, 103653. [Google Scholar] [CrossRef]
- Wang, L.; Xiong, C.; Yang, Y. A novel methodology of reliability-based multidisciplinary design optimization under hybrid interval and fuzzy uncertainties. Comput. Methods Appl. Mech. Eng. 2018, 337, 439–457. [Google Scholar] [CrossRef]
- Cai, W.; Li, Z.; Zhu, M.; Guo, R.; Wang, J.; Zhao, J. A Performance Prediction Method Utilizing Time-Dependent Subsystem Transfers between Family Systems. Appl. Sci. 2024, 14, 2448. [Google Scholar] [CrossRef]
- Li, R.; Bao, L.; Chen, L.; Zha, C.; Dong, J.; Qi, N.; Tang, R.; Lu, Y.; Wang, M.; Huang, R.; et al. Accelerated aging of lithium-ion batteries: Bridging battery aging analysis and operational lifetime prediction. Sci. Bull. 2023, 68, 3055–3079. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Yuan, H.; Li, P. Estimation Method for Extremely Small Sample Accelerated Degradation Test Data. In Proceedings of the 2015 First International Conference on Reliability Systems Engineering, Hangzhou, China, 21–23 October 2015; pp. 1–5. [Google Scholar]



| Device ID | Control Theory | Control Actual | Control Temperature | Control Pressure |
|---|---|---|---|---|
| 1 | 1,070,000 | 1,070,000 | 26.17 | 2777 |
| 2 | 961,943 | 962,634 | 25.48 | 2293 |
| 3 | 1,000,000 | 1,000,000 | 25.98 | 2383 |
| … | … | … | … | … |
| 2223 | 445,522 | 445,620 | 26.05 | 3700 |
| 2224 | 389,577 | 389,675 | 26.2 | 5125 |
| 2225 | 395,675 | 395,731 | 25.14 | 4397 |
| Device ID | Performance Index | Clustering Result | Device ID | Performance Index | Clustering Result |
|---|---|---|---|---|---|
| 1050 | −1.5961 | 26 | 1253 | 103.9906 | 27 |
| 1060 | −1.6547 | 26 | 1277 | 103.2148 | 27 |
| 1061 | −1.6256 | 26 | 1062 | 104.1170 | 27 |
| 257 | −1.5767 | 26 | 580 | 104.1656 | 27 |
| 336 | −1.5394 | 26 | 213 | 103.9227 | 27 |
| 355 | −1.6139 | 26 | 318 | 104.8158 | 27 |
| 384 | −1.5911 | 26 | 413 | 104.1684 | 27 |
| - | - | - | 982 | 103.8739 | 27 |
| Device ID | Fitting Coefficient of the First Three Days | Fitting Coefficient of the After Four Days | Fitting Coefficient for One Week |
|---|---|---|---|
| 257 | 0.9989 | 0.7461 | 0.8757 |
| 336 | 0.9797 | 0.7784 | 0.8799 |
| 355 | 0.9917 | 0.7687 | 0.8835 |
| 384 | 0.9793 | 0.7748 | 0.8793 |
| Actuator Fitting Coefficient R2 | Number of Actuators/(Roots) | Proportion of the Total Number of Hydraulic Actuators |
|---|---|---|
| R2 < 0.80 | 0 | 0% |
| 0.80 ≤ R2 < 0.85 | 102 | 4.6% |
| 0.85 ≤ R2 < 0.90 | 334 | 15.0% |
| 0.90 ≤ R2 < 0.95 | 852 | 38.8% |
| 0.95 ≤ R2 < 0.99 | 919 | 41.3% |
| R2 > 0.99 | 18 | 0.8% |
| Device ID | Fitting Coefficient of the First Three Days | Fitting Coefficient of the After Four Days | Fitting Coefficient for One Week |
|---|---|---|---|
| 213 | 0.9977 | 0.9980 | 0.9981 |
| 318 | 0.9997 | 0.9952 | 0.9971 |
| 413 | 0.9983 | 0.9932 | 0.9969 |
| 982 | 0.9995 | 0.9978 | 0.9985 |
| Actuator Fitting Coefficient R2 | Number of Actuators/(Roots) | Proportion of the Total Number of Hydraulic Actuators |
|---|---|---|
| R2 < 0.80 | 0 | 0% |
| 0.80 ≤ R2 < 0.85 | 0 | 0% |
| 0.85 ≤ R2 < 0.90 | 3 | 0.1% |
| 0.90 ≤ R2 < 0.95 | 17 | 0.8% |
| 0.95 ≤ R2 < 0.99 | 52 | 2.3% |
| R2 > 0.99 | 2153 | 96.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Cai, W.; Zhang, J.; Zhu, M.; Wang, H. A Spatiotemporal Domain-Coupled Clustering Method for Performance Prediction of Cluster Systems. Actuators 2025, 14, 208. https://doi.org/10.3390/act14050208
Zhang Y, Cai W, Zhang J, Zhu M, Wang H. A Spatiotemporal Domain-Coupled Clustering Method for Performance Prediction of Cluster Systems. Actuators. 2025; 14(5):208. https://doi.org/10.3390/act14050208
Chicago/Turabian StyleZhang, Yirui, Wei Cai, Jianxin Zhang, Ming Zhu, and He Wang. 2025. "A Spatiotemporal Domain-Coupled Clustering Method for Performance Prediction of Cluster Systems" Actuators 14, no. 5: 208. https://doi.org/10.3390/act14050208
APA StyleZhang, Y., Cai, W., Zhang, J., Zhu, M., & Wang, H. (2025). A Spatiotemporal Domain-Coupled Clustering Method for Performance Prediction of Cluster Systems. Actuators, 14(5), 208. https://doi.org/10.3390/act14050208






