Shape Memory Polymer Composite Actuator: Modeling Approach for Preliminary Design and Validation
Abstract
:1. Introduction
2. Materials and Manufacturing Methodology
3. Actuator Prototype Modeling
- although large displacements are admitted and modeled, the stress–strain curve of the materials, at fixed temperature, is linear; a consequence of the large displacement assumption is a different load distribution, depending on the current deformed shape of the sample
- no sliding among the laminas is considered during the entire process; this leads to a classical modality of absorption of the loads, described by the laminate constitutive laws
- the specific state points of the process refer to temperature far enough to the transition range; this means that the present scheme does not describe temperature intermediate situations (during phase change) but provides estimates in fully activated and non-activated conditions
3.1. Modeling Approach
3.2. Simulation Results
4. Prototype Instrumentation and Validation Test
4.1. Actuator Instrumentation
4.2. Results and Validation
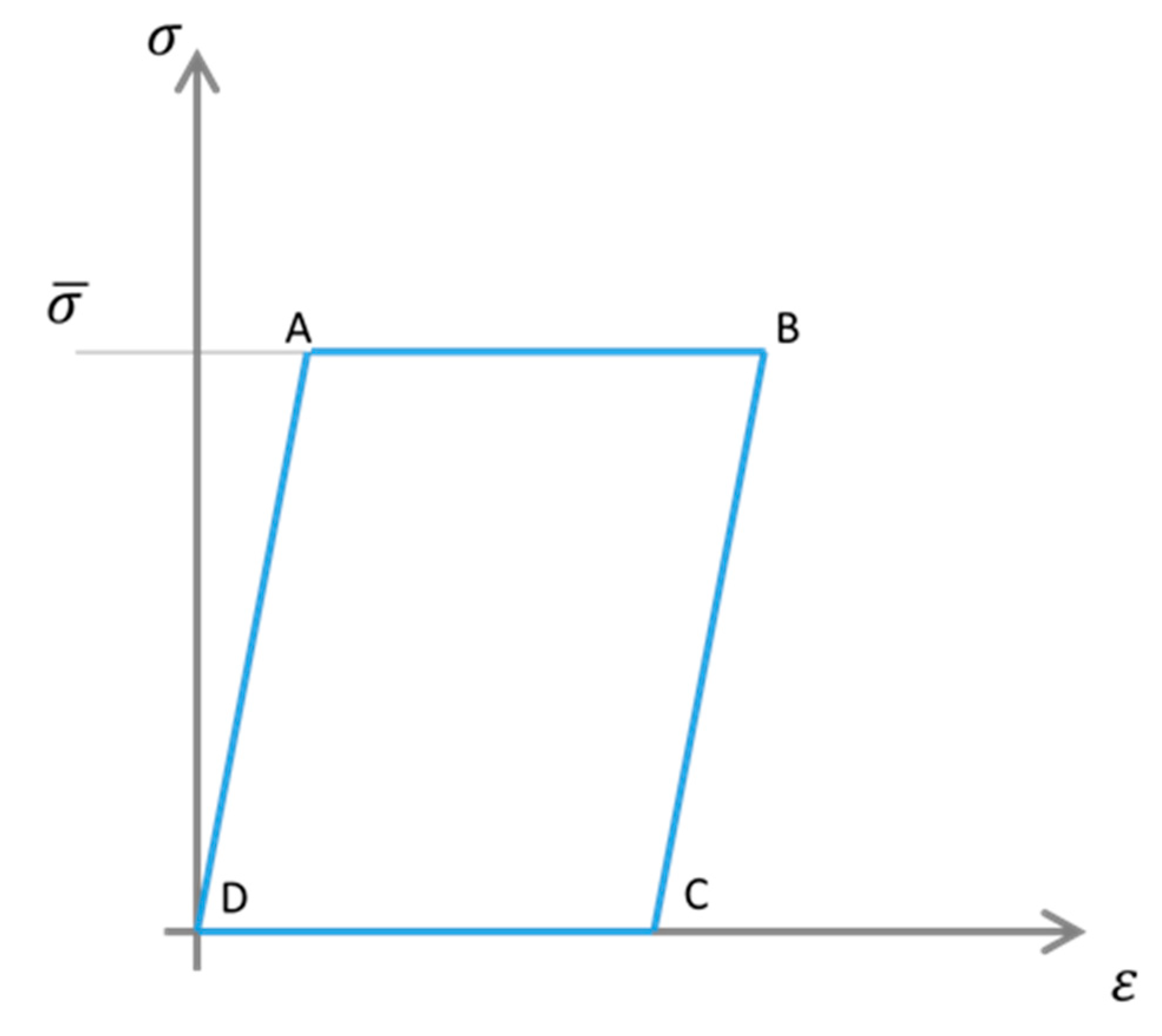
- Step 1: a weighted mass was hung to the tip of the sample at room temperature, waiting for the stabilization of the configuration; the achieved deflection corresponds to the point A of the processStep 2: the sample was heated by a thermo-gun up to arrive at a temperature of 120 °C; a large displacement was registered when the test condition was stabilized (no further vertical displacement were observed); this condition correspond to the point B of the process
- Step 3: the system was left cooling up to coming back to the environmental temperature; in this phase of the process, strain is stored for the forthcoming shape memory recovery. The geometric configuration is still represented by the point B, even as temperature and mechanical properties got back to the values at the beginning of the process
- Step 4: the mass is removed to allow the elastic recovery and arrive at condition C. A residual deformation is clearly present and corresponds to the strain stored in the previous step
- Step 5: the sample is heated again, up to recover the original shape (condition D)
5. Conclusions and Further Steps
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Ameduri, S.; Concilio, A.; Pecora, R.; Karagiannis, D. A single slotted morphing flap based on SMA technology. Smart Struct. Syst. 2016, 17, 819–835. [Google Scholar] [CrossRef]
- Dayananda, G.N.; Varughese, B.; Rao, M.S. Shape Memory Alloy Based Smart Landing Gear for an Airship. J. Aircr. 2007, 44, 1469–1477. [Google Scholar] [CrossRef] [Green Version]
- Ameduri, S.; Concilio, A.; Favaloro, N.; Pellone, L. A Shape Memory Alloy Application for Compact Unmanned Aerial Vehicles. Aerospace 2016, 3, 16. [Google Scholar] [CrossRef]
- Singh, A.; Raj Singh, J.; Kumar Verma, P. Automotive application of shape memory alloys. In Proceedings of the 15th International Conference on Recent Trends in Engineering, Applied Science and Management, Rajasthan, India, 1 April 2018. [Google Scholar]
- Petrini, L.; Migliavacca, F. Biomedical Applications of Shape Memory Alloys. J. Metall. 2011, 2011. [Google Scholar] [CrossRef]
- Ozbulut, O.E.; Hurlebaus, S.; Desroches, R. Seismic Response Control Using Shape Memory Alloys: A Review. J. Intell. Mater. Syst. Struct. 2011, 22, 1531–1549. [Google Scholar] [CrossRef]
- Hager, M.D.; Bode, S.; Weber, C.; Schubert, U.S. Shape memory polymers: Past, present and future developments. Prog. Polym. Sci. 2015, 49, 3–33. [Google Scholar] [CrossRef]
- An, Y.; Kim, J.; Goo, N.S.; Kim, Y.; Park, J.K.; Yu, W.-R. Quantitative evaluation of the three-dimensional deployment behavior of a shape memory polymer antenna. Smart Mater. Struct. 2018, 27, 105007. [Google Scholar] [CrossRef]
- Alexander, P.W.; Luntz, J.E.; Moyer, A.W.; Brei, D.; Ranga, S.; Johnson, N.L. Adjustable Panel Closure Bumpers Incorporating Shape Memory Polymers. U.S. Patent 9,290,979,B1, 22 March 2016. [Google Scholar]
- Wong, Y.; Kong, J.; Widjaja, L.K.; Venkatraman, S.S.; Venkatraman, S. Biomedical applications of shape-memory polymers: how practically useful are they? Sci. China Ser. B Chem. 2014, 57, 476–489. [Google Scholar] [CrossRef]
- Quadrini, F.; Santo, L.; Ciminello, M.; Concilio, A.; Volponi, R.; Spena, P. Shape memory polymeric composites sensing by optic fibre Bragg gratings: A very first approach. AIP Conf. Proc. 2016, 1736, 020090. [Google Scholar] [CrossRef]
- Quadrini, F.; Tedde, G.M.; Santo, L. Shape memory composite hands for space applications. In Proceedings of the ASME 2015 International Manufacturing Science and Engineering Conference, Charlotte, NC, USA, 8–12 June 2015; Volume 1. [Google Scholar]
- Santo, L.; Quadrini, F.; Squeo, E.A.; Dolce, F.; Mascetti, G.; Berolotto, D.; Villadei, W.; Ganga, P.L.; Zolesi, V. Behavior of shape memory epoxy foams in microgravity: Experimental results of STS-134 mission, Micrograv. Microgravity Sci. Technol. 2012, 24, 287–296. [Google Scholar] [CrossRef]
- Ayranci, C.; Carey, J.P. Handbook of Advances in Braided Composite Materials; Carey, J.P., Ed.; Woodhead Publishing: Sawston, Cambridge, UK, 2017. [Google Scholar]
- Díaz Lantada, A.; Lafont Morgado, P.; Lorenzo Yustos, H.; Lorenzo Esteban, V.; Muñoz-García, J.; Muñoz Sanz, J.L.; Echavarri Otero, J.; Muñoz Guijosa, J.M. Biodevices based on shape-memory polymers: Current capabilities and challenges. In Proceedings of the Biodevices 2009—International Conference on Biomedical Electronics and Devices, Porto, Portugal, 14–17 January 2009. [Google Scholar]
- Chen, Y.J.; Sun, J.; Liu, Y.J.; Leng, J.S. Variable stiffness property study on shape memory polymer composite tube. Smart Mater. Struct. 2012, 21, 094021. [Google Scholar] [CrossRef]
- Lan, X.; Liu, Y.; Lv, H.; Wang, X.; Leng, J.; Du, S. Fiber reinforced shape-memory polymer composite and its application in a deployable hinge. Smart Mater. Struct. 2009, 18, 024002. [Google Scholar] [CrossRef]
- Liu, Y.; Du, H.; Liu, L.; Leng, J. Shape memory polymers and their composites in aerospace applications: A review. Smart Mater. Struct. 2014, 23, 023001. [Google Scholar] [CrossRef]
- Yu, K.; Yin, W.L.; Sun, S.H.; Liu, Y.J.; Leng, J.S. Design and analysis of morphing wing based on SMP composite. SPIE 2009, 7290, 72900S. [Google Scholar]
- Yin, W.L.; Fu, T.; Liu, J.C.; Leng, J.S. Structural shape sensing for variable camber wing using FBG sensors. SPIE 2009, 7292, 72921H. [Google Scholar]
- Tobushi, H.; Hashimoto, T.; Hayashi, S.; Yamada, E. Thermomechanical Constitutive Modeling in Shape Memory Polymer of Polyurethane Series. J. Intell. Mater. Syst. Struct. 1997, 8, 711–718. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Tobushi, H. Analysis of the isothermal mechanical response of a shape memory polymer rheological model. Polym. Eng. Sci. 2000, 40, 2498–2510. [Google Scholar] [CrossRef]
- Tobushi, H.; Okumura, K.; Hayashi, S.; Ito, N. Thermomechanical constitutive model of shape memory polymer. Mech. Mater. 2001, 33, 545–554. [Google Scholar] [CrossRef]
- Lin, J.R.; Chen, L.W. Shape-memorized crosslinked ester-type polyurethane and its mechanical viscoelastic model. J. Appl. Polym. Sci. 1999, 73, 1305–1319. [Google Scholar] [CrossRef]
- Liu, Y.; Gall, K.; Dunn, M.L.; Greenberg, A.R.; Diani, J. Thermomechanics of shape memory polymers: Uniaxial experiments and constitutive modeling. Int. J. Plast. 2006, 22, 279–313. [Google Scholar] [CrossRef]
- Gilormini, P.; Diani, J. On modeling shape memory polymers as thermoelastic two-phase composite materials. Comptes Rendus Mécanique 2012, 340, 338–348. [Google Scholar] [CrossRef] [Green Version]
- Diani, J.; Liu, Y.; Gall, K. Finite strain 3D thermoviscoelastic constitutive model for shape memory polymers. Polym. Eng. Sci. 2006, 46, 486–492. [Google Scholar] [CrossRef]
- Chen, Y.-C.; Lagoudas, D.C. A constitutive theory for shape memory polymers. Part I: Large deformations. J. Mech. Phys. Solids 2008, 56, 1766–1778. [Google Scholar] [CrossRef]
- Reese, S.; Böl, M.; Christ, D. Finite element-based multi-phase modelling of shape memory polymer stents. Comput. Methods Appl. Mech. Eng. 2010, 199, 1276–1286. [Google Scholar] [CrossRef]
- Belmonte, A.; Lama, G.C.; Gentile, G.; Cerruti, P.; Ambrogi, V.; Fernández-Francos, X.; De la Flor, S. Thermally-triggered free-standing shape-memory actuators. Eur. Polym. J. 2017, 97, 241–252. [Google Scholar] [CrossRef]
- Belmonte, A.; Lama, G.C.; Cerruti, P.; Ambrogi, V.; Fernández-Francos, X.; De la Flor, S. Motion control in free-standing shape-memory actuators. Smart Mater. Struct. 2018, 27, 075013. [Google Scholar] [CrossRef] [Green Version]
- Ciminello, M.; Bettini, P.; Ameduri, S.; Sala, G.; Concilio, A. Monito-Ring: An original fiber optic system for morphing applications. J. Intell. Mater. Syst. Struct. 2015, 26, 2463–2476. [Google Scholar] [CrossRef]
- Ciminello, M.; Concilio, A.; Galasso, B.; Richiello, C.; Fabbi, G.; Mataloni, A.; Perugini, P. Sensitivity analysis of OFDR-based distributed sensing for flaws detection in representative coupon from filament wound motor vessel. In Proceedings of the SPIE Commercial + Scientific Sensing and Imaging + Fiber Optic Sensors and Applications XV, Orlando, FL, USA, 14 May 2018. [Google Scholar]









| Parameter | Description | Value |
|---|---|---|
| (GPa) | Young modulus of carbon fabric ply along 1 direction in the ply reference coordinate frame, at low temperature (25 °C) | 52 |
| (GPa) | Young modulus of carbon fabric ply along 2 direction in the ply reference coordinate frame, at low temperature (25 °C) | 52 |
| (GPa) | Young modulus of carbon fabric ply along 1 direction in the ply reference coordinate frame, at high temperature (120 °C) | 3.64 |
| (GPa) | Young modulus of carbon fabric ply along 2 direction in the ply reference coordinate frame, at high temperature (120 °C) | 3.64 |
| Poisson ration referred to directions 1 and 2 | 0.33 | |
| (GPa) | Young modulus of the SMP, at low temperature (25 °C) | 3.64 |
| (GPa) | Young modulus of the SMP, at high temperature (120 °C) | 0.080 |
| (mm) | Thickness of the carbon fibre plies | 0.33 |
| (mm) | Thickness of the SMP ply | 0.10 |
| and (µε/C°) | Thermal expansion coefficients of the carbon fabric ply in the local reference frame | 0.5 |
| (1/C°) | Thermal expansion coefficient of the SMP | 36 |
| b (mm) | Laminate width | 40 |
| L (mm) | Laminate length | 80 |
| F (N) | Applied force at the tip | 1.267 |
| Tip Displacement | Curvature at the Root | |||||
|---|---|---|---|---|---|---|
| condition | Linear (mm) | Non-linear (mm) | Delta (mm) | Linear (1/m) | Non-linear (1/m) | Delta (1/m) |
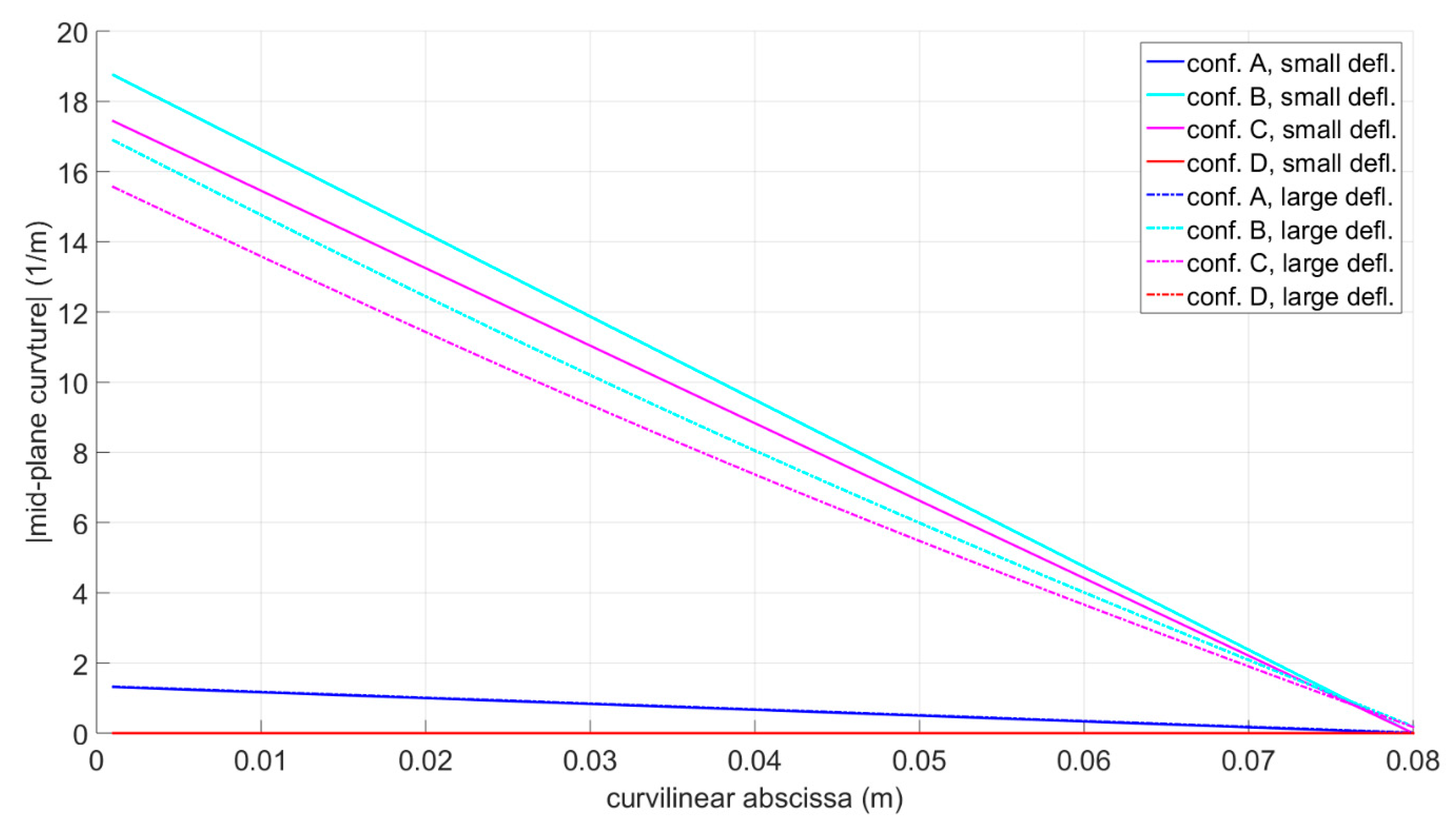
| A | 2.83 | 2.88 | 0.05 | 1.31 | 1.33 | 0.02 |
| B | 37.9 | 33.7 | −4.2 | 18.7 | 16.9 | −1.8 |
| C | 35.5 | 31.2 | −4.3 | 17.4 | 15.5 | −1.9 |
| D | 0 | 0 | 0 | 0 | 0 | 0 |
| Tip Displacement | Strain Closed to the Root | |||||
|---|---|---|---|---|---|---|
| condition | Numerical (mm) | Experimental (mm) | Delta (mm) | Numerical (µ-strain) | Experimental (µ-strain) | Delta (µ-strain) |
| A | 2.88 | 2.94 | 0.06 | −524.4 | −573 | −48.6 |
| B | 33.7 | 29.2 | −4.5 | −6422 | −6133 | 289 |
| C | 31.2 | 27.7 | −3.5 | −5890 | −5227 | 663 |
| D | 0 | 0.69 | 0.69 | 0 | 64 | 64 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ameduri, S.; Ciminello, M.; Concilio, A.; Quadrini, F.; Santo, L. Shape Memory Polymer Composite Actuator: Modeling Approach for Preliminary Design and Validation. Actuators 2019, 8, 51. https://doi.org/10.3390/act8030051
Ameduri S, Ciminello M, Concilio A, Quadrini F, Santo L. Shape Memory Polymer Composite Actuator: Modeling Approach for Preliminary Design and Validation. Actuators. 2019; 8(3):51. https://doi.org/10.3390/act8030051
Chicago/Turabian StyleAmeduri, Salvatore, Monica Ciminello, Antonio Concilio, Fabrizio Quadrini, and Loredana Santo. 2019. "Shape Memory Polymer Composite Actuator: Modeling Approach for Preliminary Design and Validation" Actuators 8, no. 3: 51. https://doi.org/10.3390/act8030051
APA StyleAmeduri, S., Ciminello, M., Concilio, A., Quadrini, F., & Santo, L. (2019). Shape Memory Polymer Composite Actuator: Modeling Approach for Preliminary Design and Validation. Actuators, 8(3), 51. https://doi.org/10.3390/act8030051









