Analysis and Control of Slotless Self-Bearing Motor
Abstract
:1. Introduction
2. Design of the Control System for the SSBM
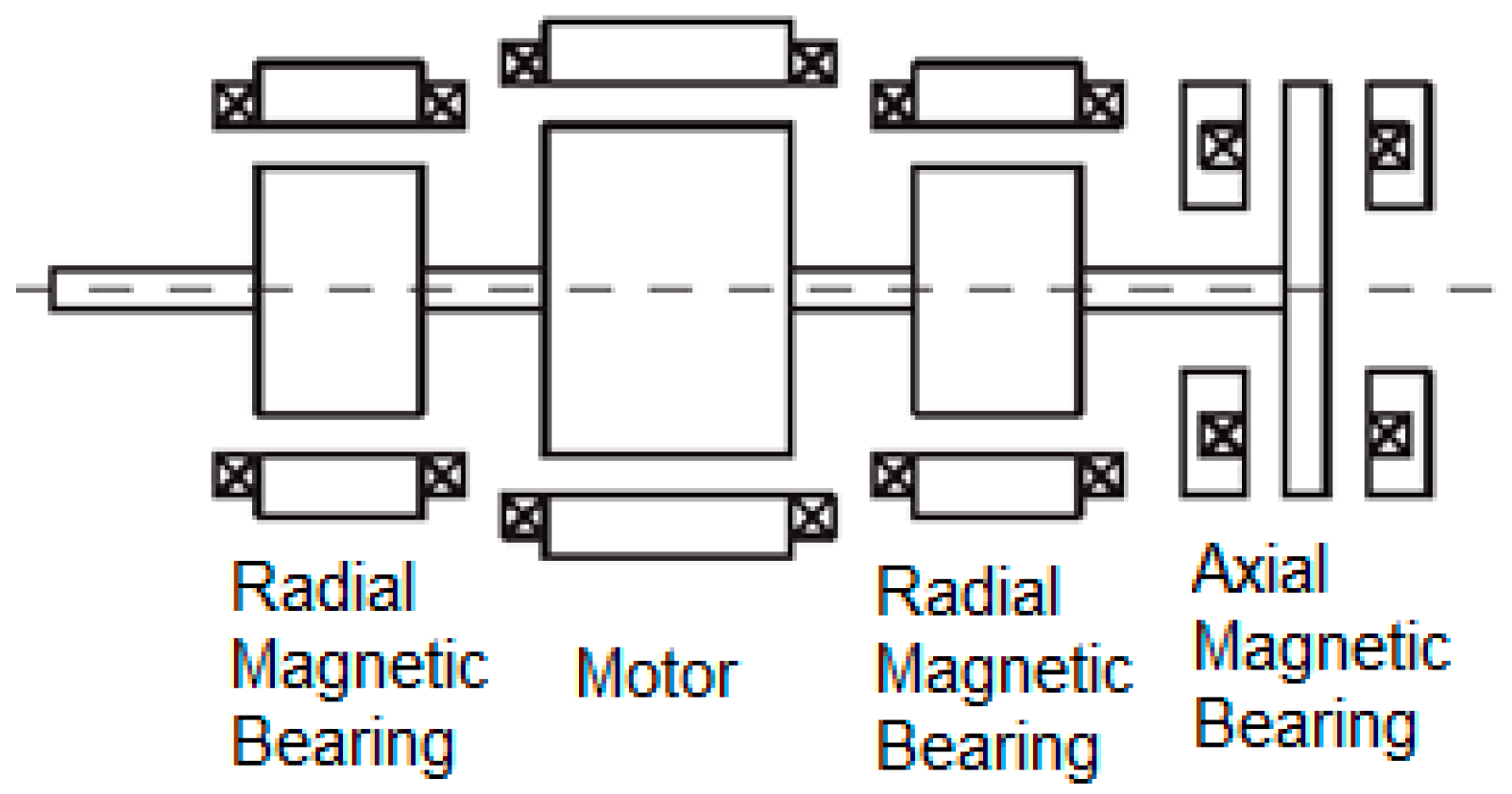
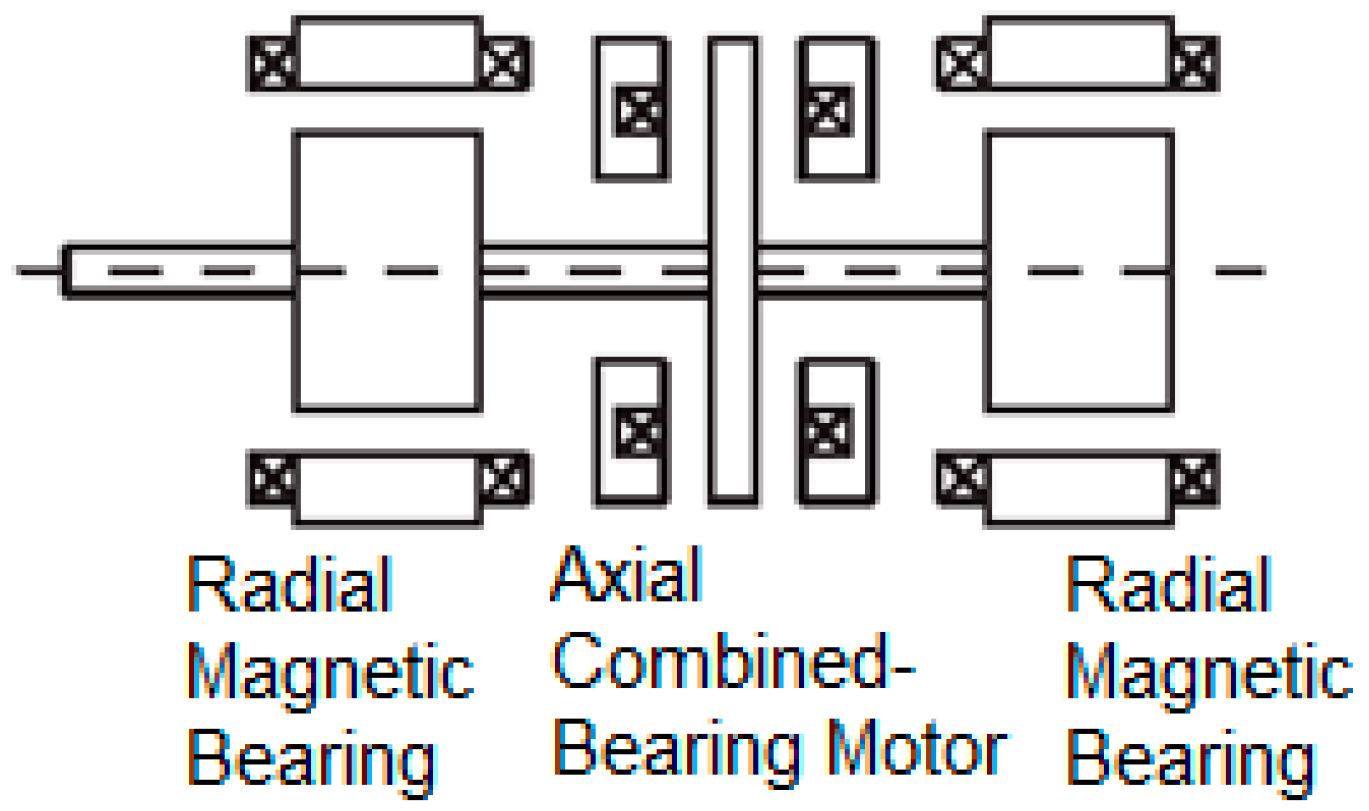
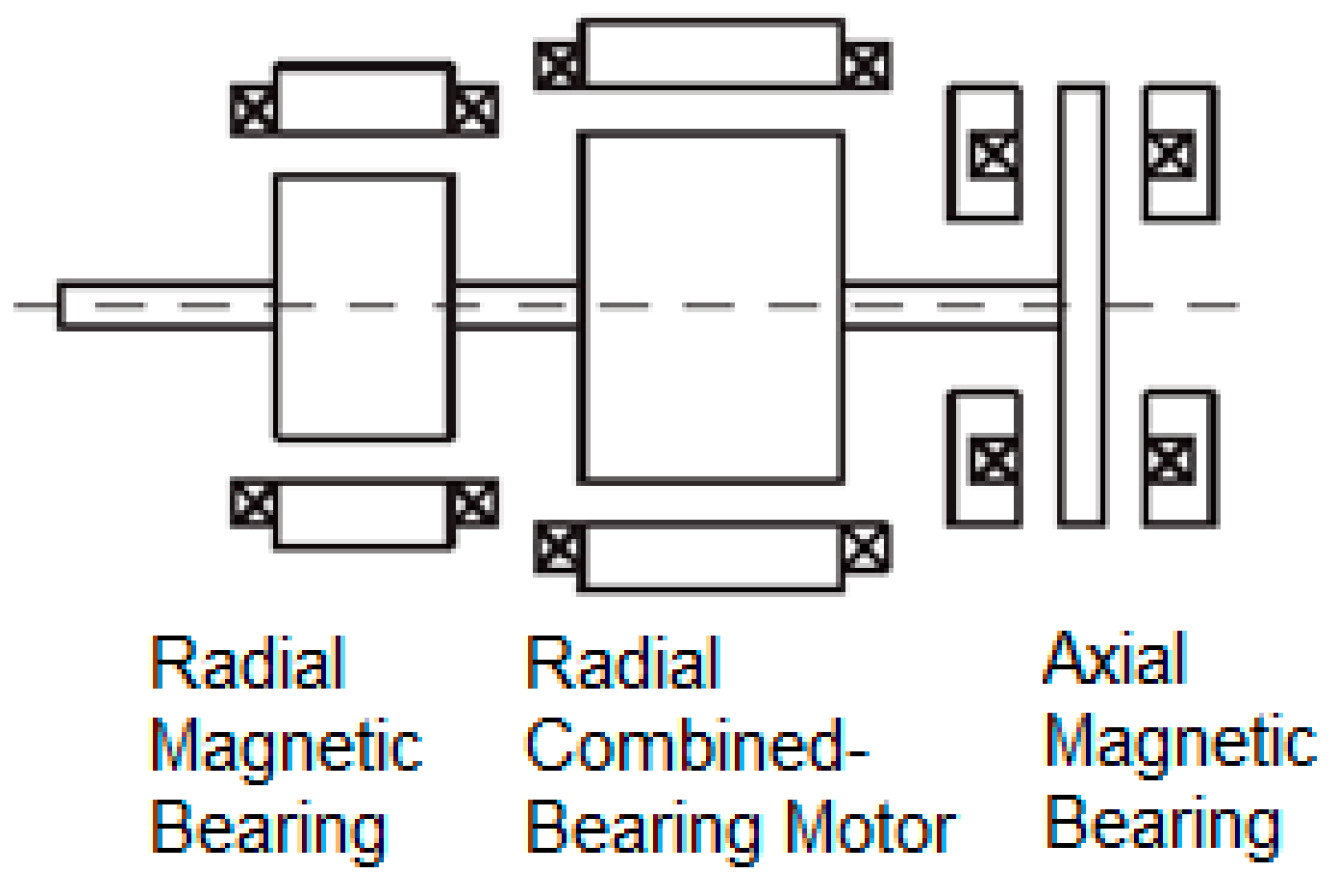
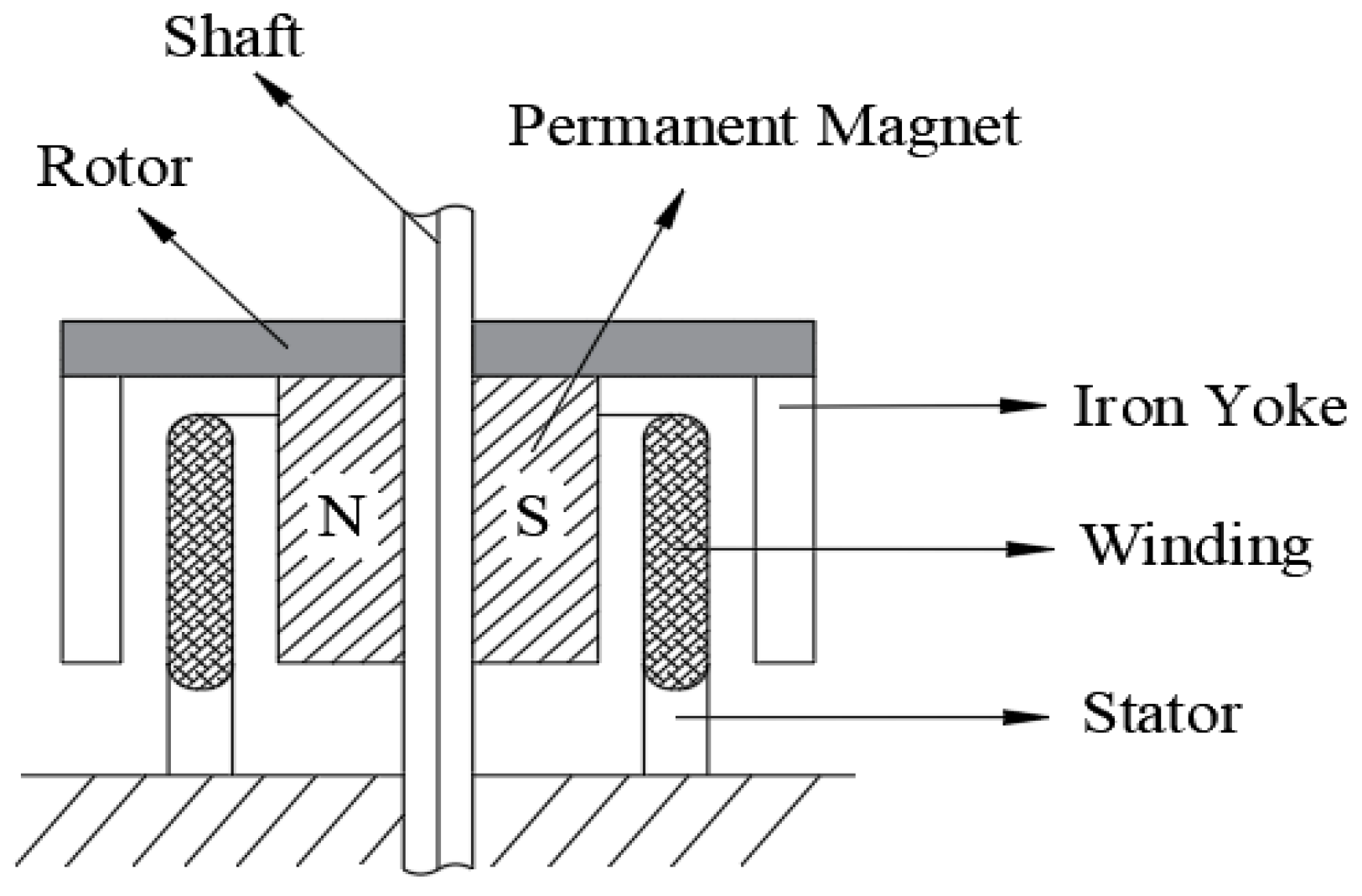
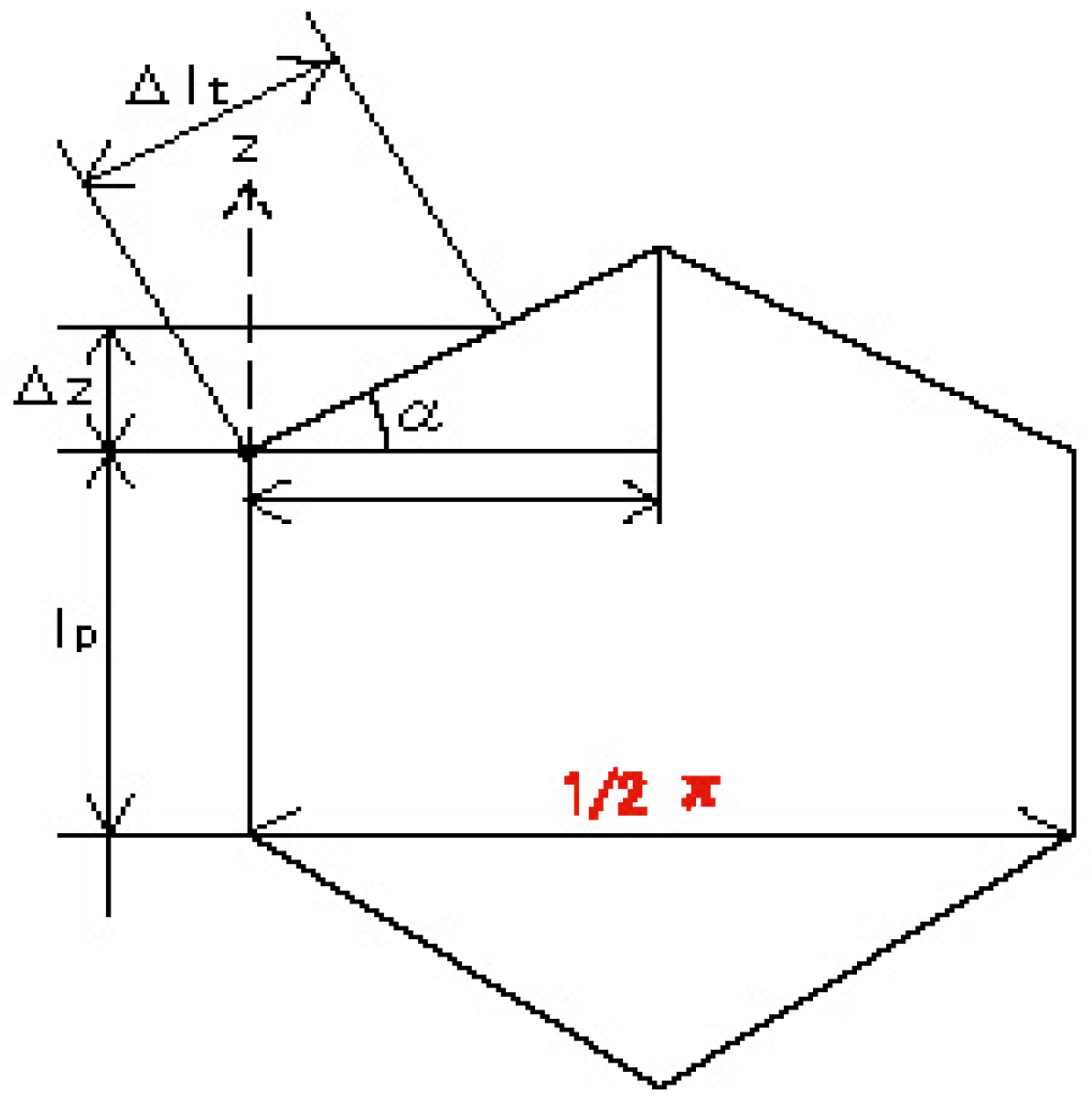
2.1. Introduction of the SSBM
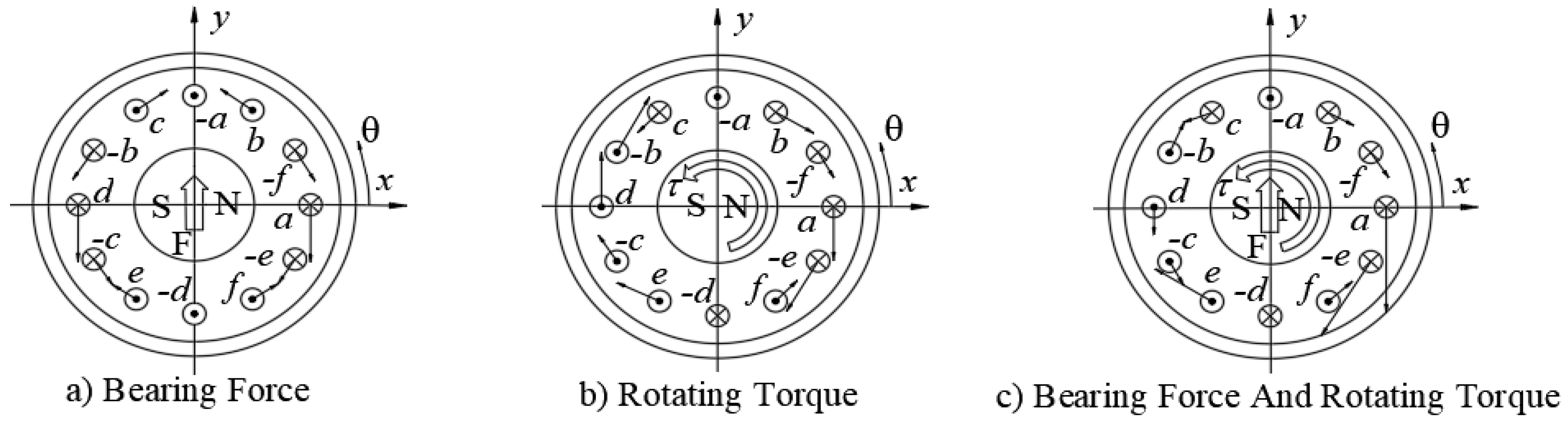
2.2. Calculation of Bearing Force and Torque
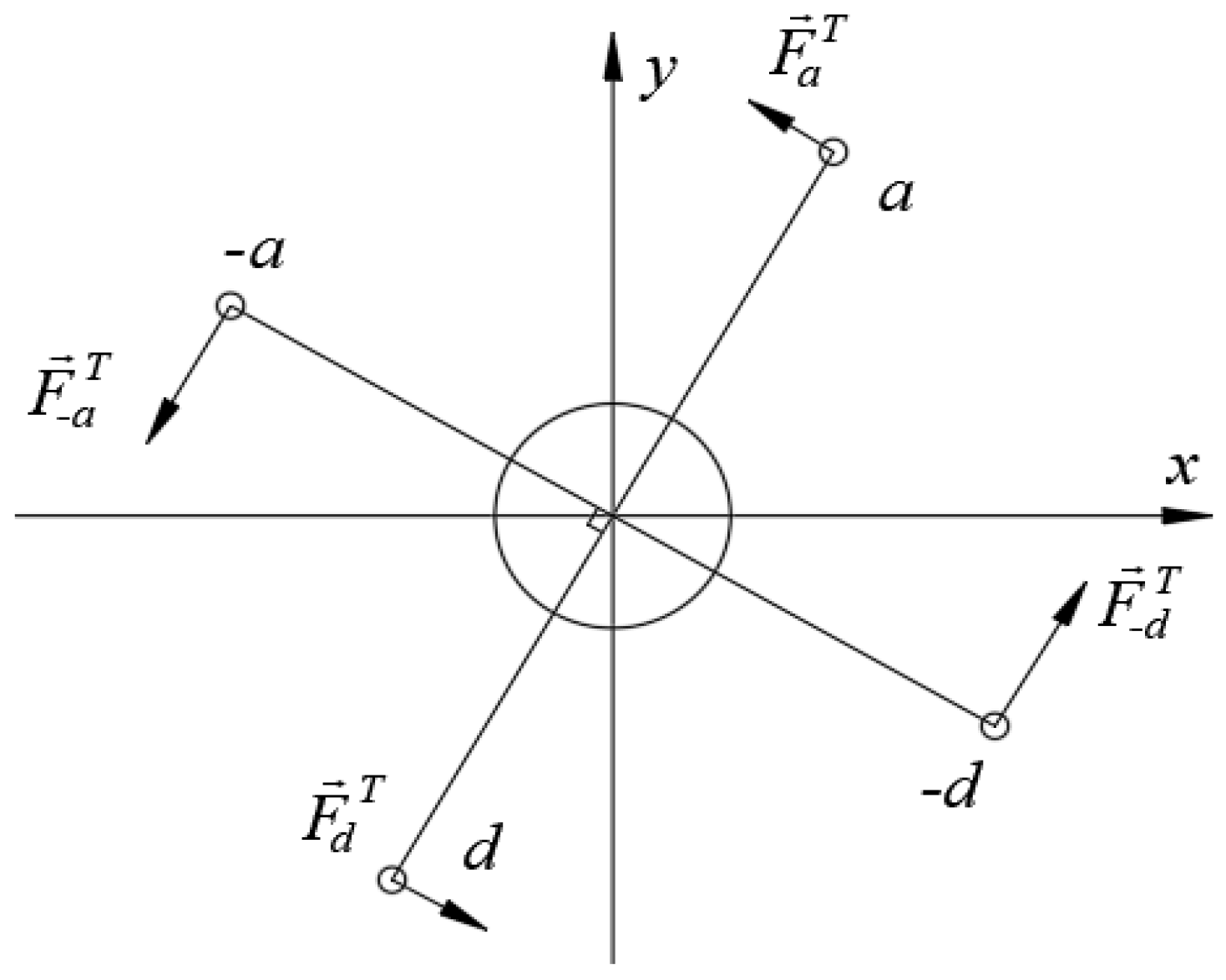
2.2.1. Bearing Force
2.2.2. Torque
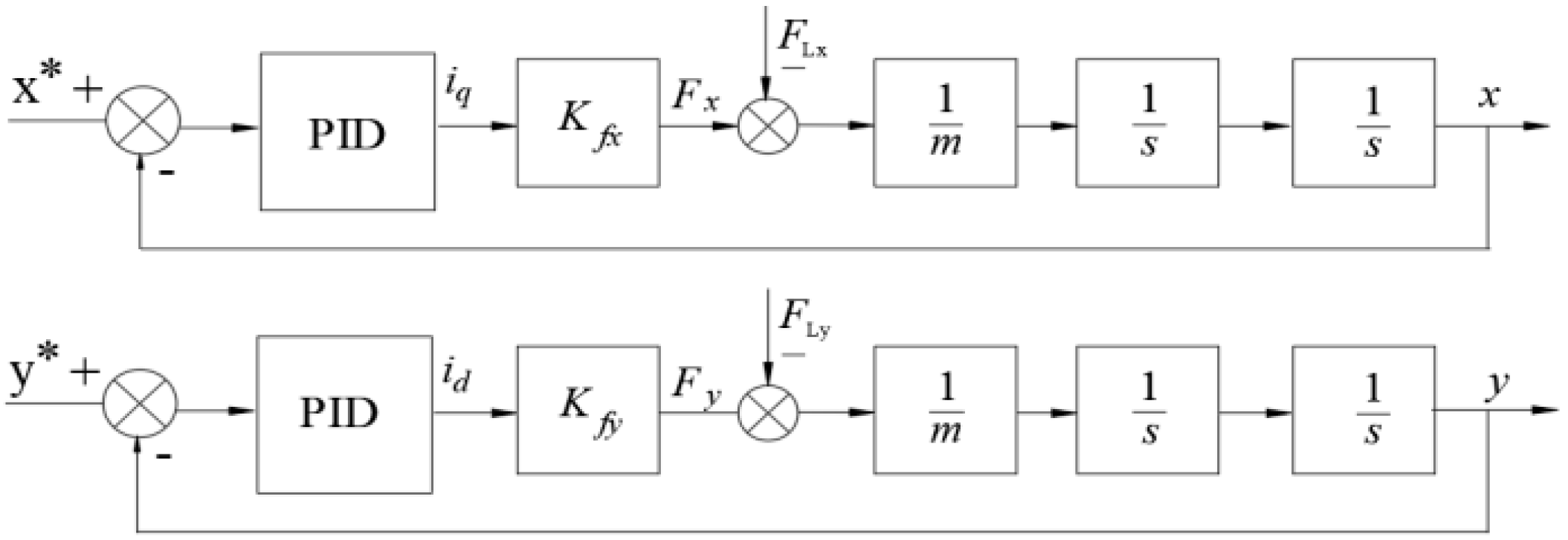
2.3. Designing the Control System
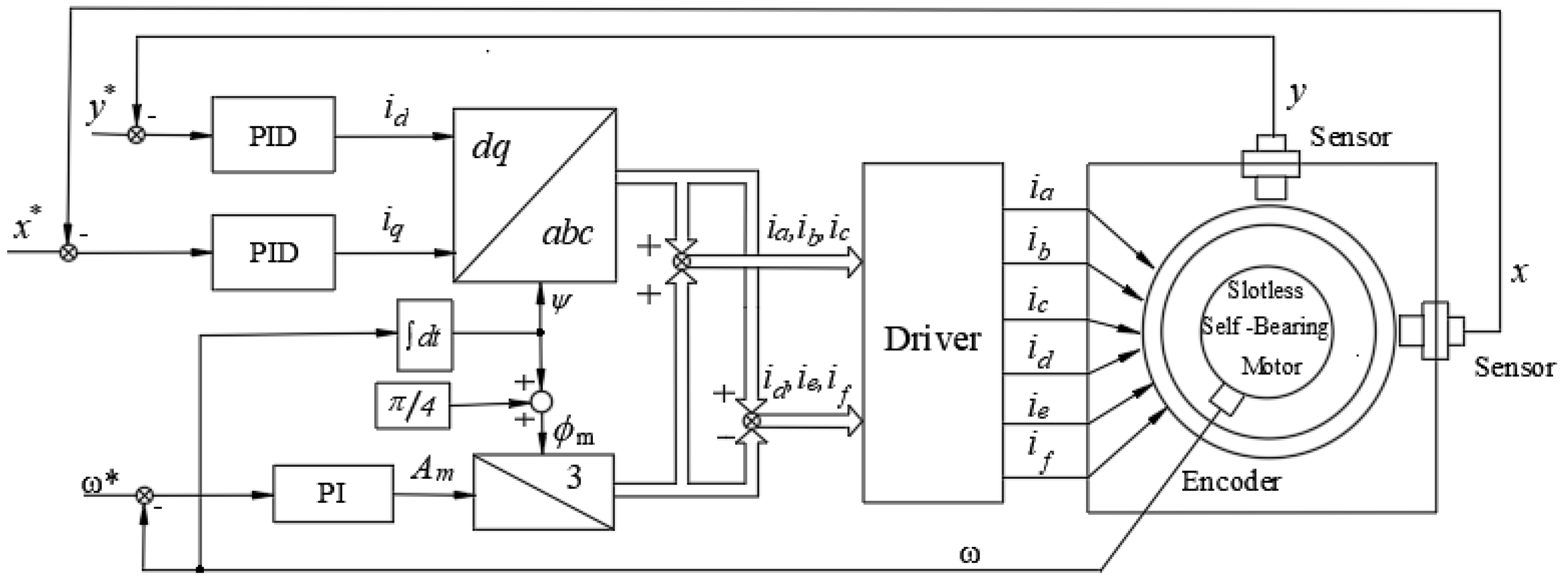
2.3.1. Control Structure
2.3.2. Designing Speed and Position Controller
3. Simulation and Experimental Results
3.1. Control Hardware
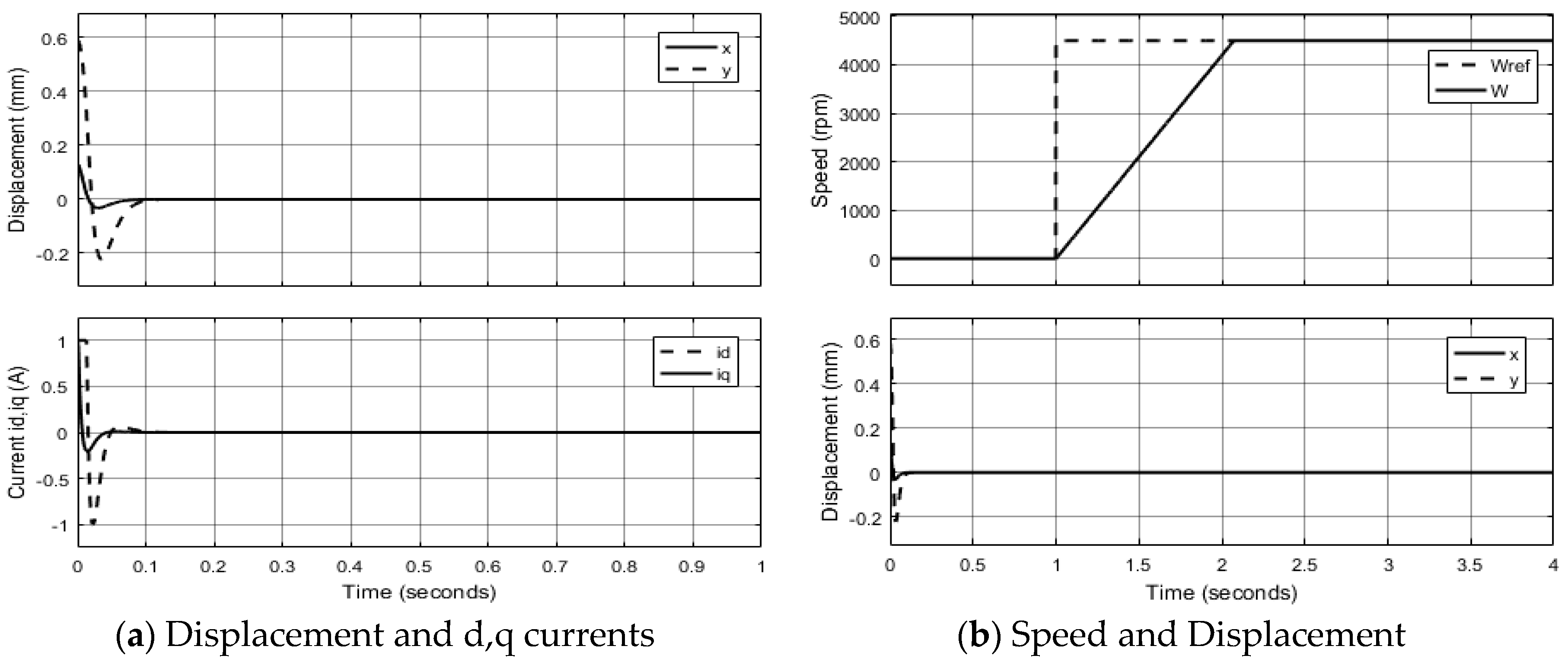
3.2. Simulation Results
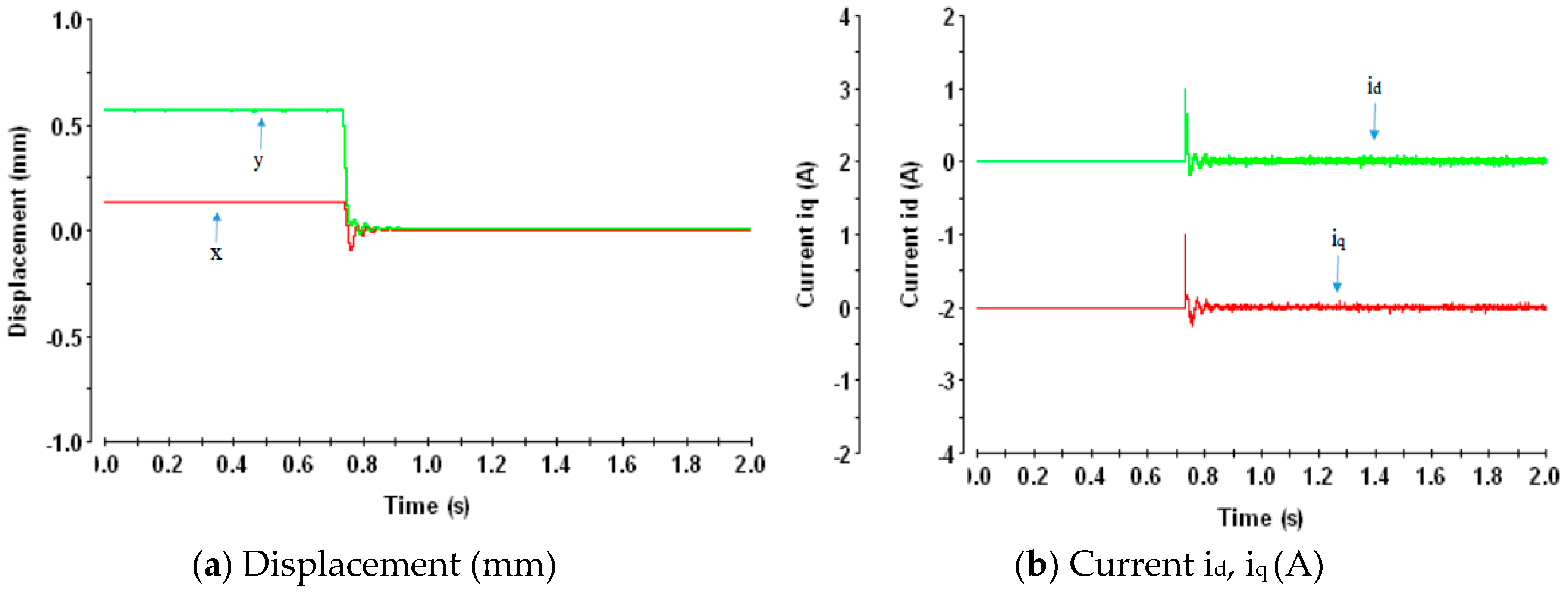
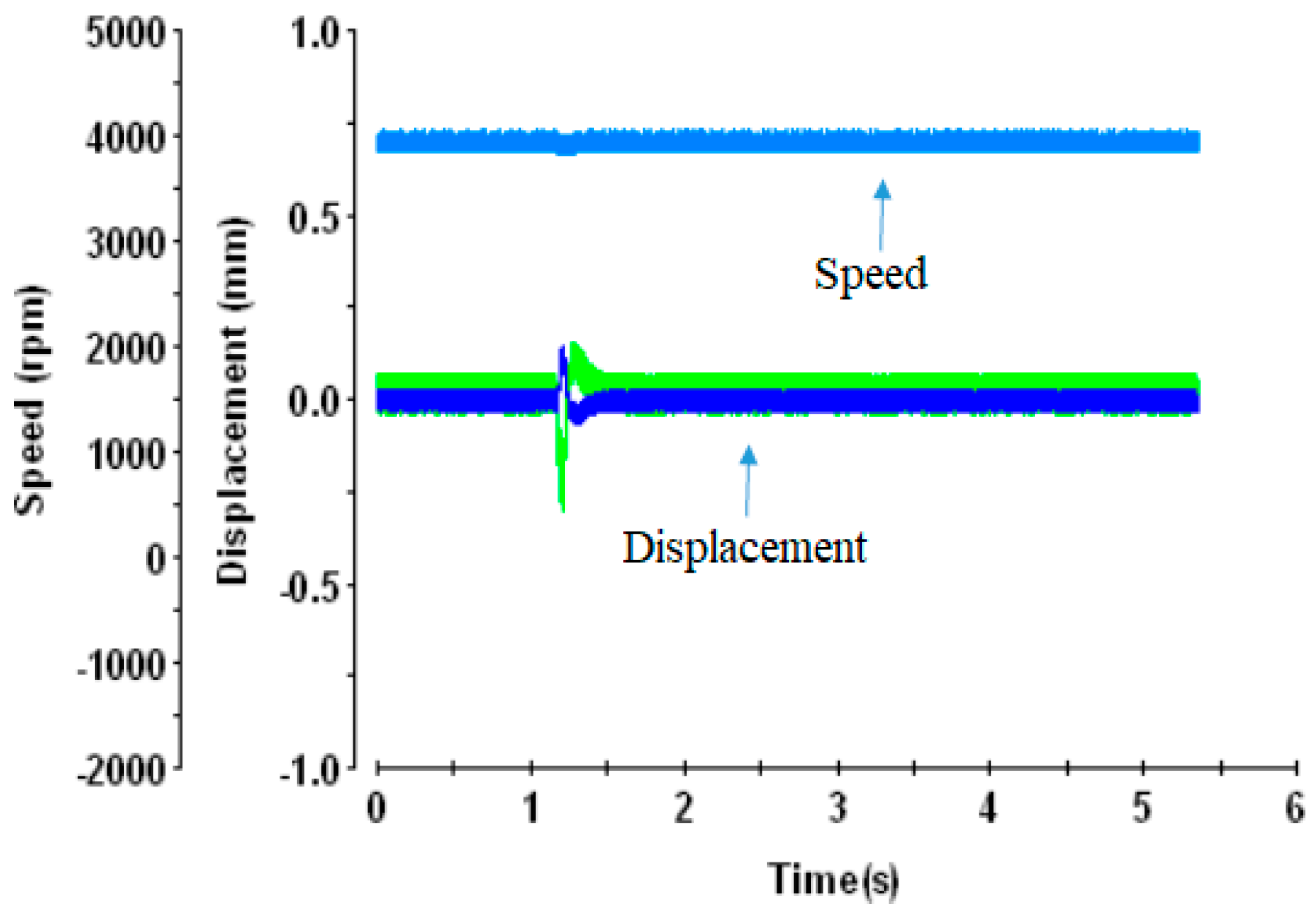
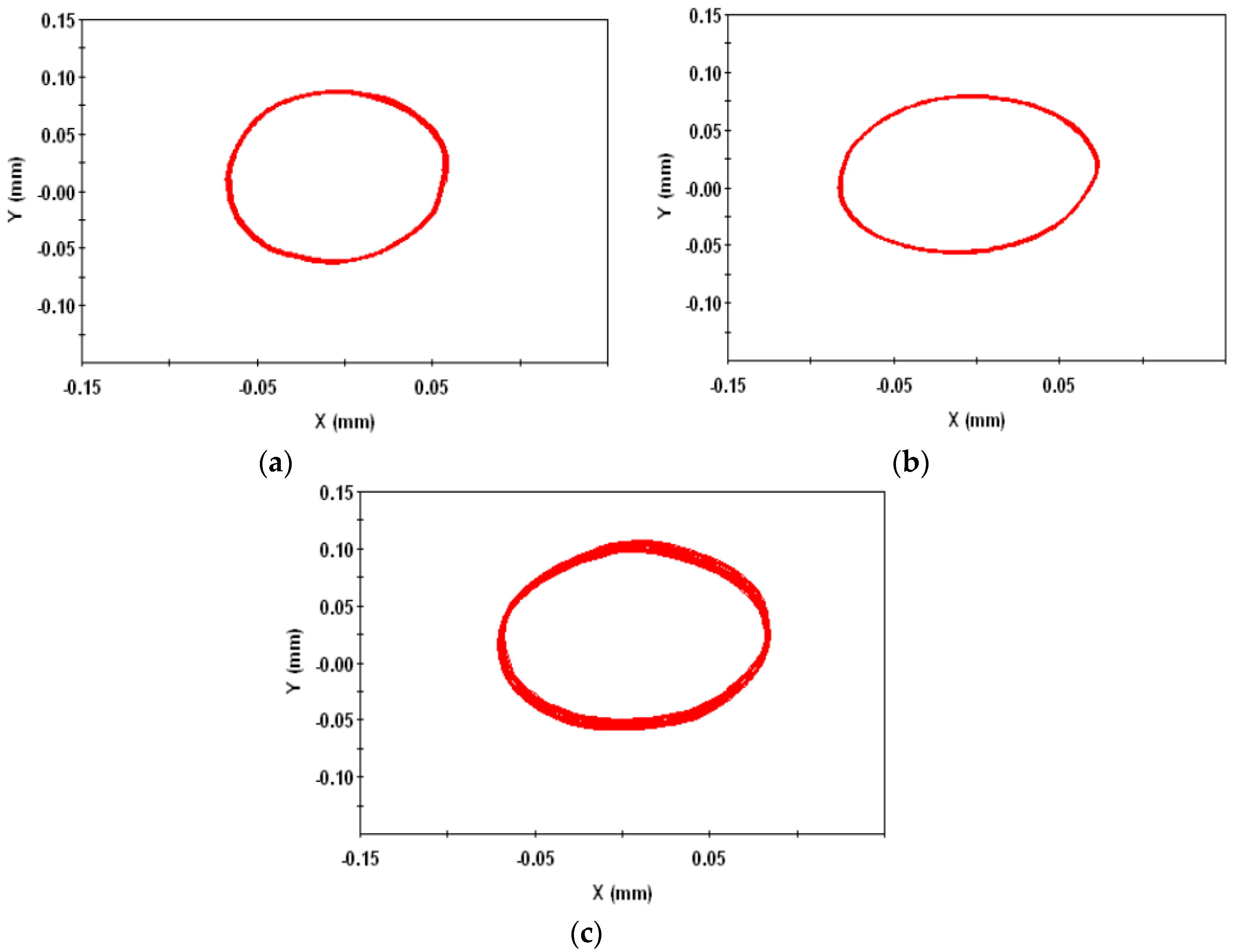
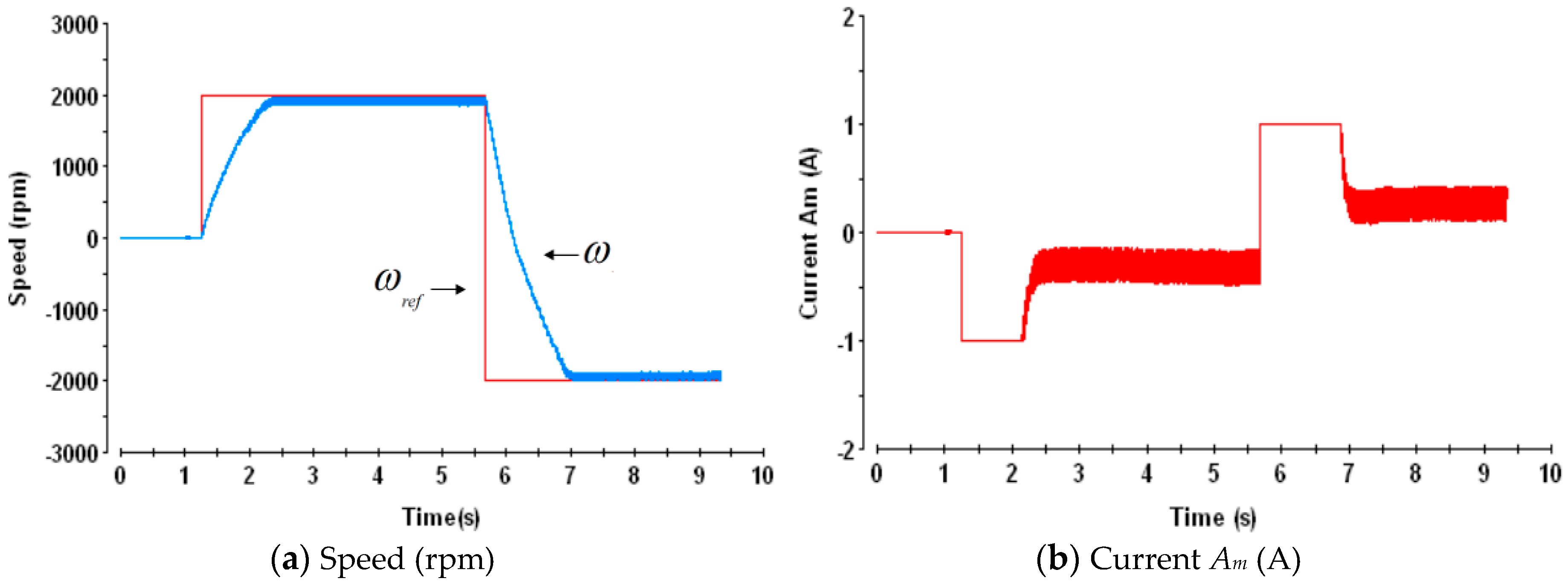
3.3. Experimental Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbol | Unit | Description |
| Rad | The angular position of the rotor | |
| Rad | The angular around origin coordinate | |
| Rad | The angular position of the +a-phase winding | |
| Nm | The total torque of the motor | |
| N | The amplitude of bearing force of +a, +d, −a, −d phase | |
| N | The amplitude of torque force of +a, +d, −a, −d phase | |
| Fa, Fb, Fc | N | The total forces acting on the rotor by two symmetrical phases a and d, b and e, c and f, respective |
| ,, | A | The bearing currents of a-phase, b-phase and c-phase |
| , | A | The amplitude of direct axis bearing current and the quadrate axis bearing current |
| ,, | A | The torque currents of a-phase, b-phase and c-phase |
| A | The amplitude of the torque current | |
| Nm | The total torque generated by two symmetrical phases a and d, b and e, c and f, respective | |
| Rad | The phase of the torque current | |
| , | m | The parallel component and the serial component of the winding |
| , | current-torque coefficients | |
| , | current-force coefficients | |
| M | Kg | Weight of the rotor |
| R | m | The radius of the rotor |
| r | m | The radius of the winding |
| a | m/s2 | The acceleration of the rotor |
| Fx, Fy | N | Bearing forces on the x-axis and y-axis |
| Fl, Flx, Fly | N | Load Forces |
| Tl | Nm | Load Torque |
| , | PI controllers’ coefficients | |
| ,, | PID controllers’ coefficients | |
| Pole point of the position controller | ||
| Pole point of the speed controller |
References
- Okada, Y.; Dejima, K.; Ohishi, T. Analysis and comparison of PM synchronous motor and induction motor type magnetic bearing. IEEE Trans. Ind. Appl. 1995, 32, 1047–1053. [Google Scholar] [CrossRef]
- Ren, Z.; Stephens, L.S. Closed-loop performance of a six degree-of freedom precision magnetic actuator. IEEE/ASME Trans. Mechatron. 2005, 10, 666–674. [Google Scholar] [CrossRef]
- Schneider, T.; Binder, A. Design and evaluation of a 60.000 rpm permanent magnet bearingless high speed motor. In Proceedings of the 7th International Conference on Power Electronics and Drive Systems 2007, Bangkok, Thailand, 27–30 November 2007; pp. 1–8. [Google Scholar]
- Nguyen, Q.D.; Ueno, S. Analysis and Control of Non-Salient Permanent Magnet Axial-Gap Self-Bearing Motor. IEEE Trans. Ind. Electron. 2011, 58, 2644–2652. [Google Scholar] [CrossRef]
- Nguyen, Q.D.; Ueno, S. Modeling and Control of Salient-Pole Permanent Magnet Axial Gap Self-Bearing Motor. IEEE/ASME Trans. Mechatron. 2011, 16, 518–526. [Google Scholar] [CrossRef]
- Ueno, S.; Iseki, R.; Jiang, C. Stability of a tilt-controlling axial gap self-bearing motor with single-stator. Mech. Eng. J. 2017, 4, 1–12. [Google Scholar] [CrossRef]
- Qu, R.; Aydin, M.; Lipo, T.A. Performance comparison of dual-rotor radial-flux and axial-flux permanent-magnet BLDC machines. In Proceedings of the IEEE International Electric Machines and Drives Conference, Madison, WI, USA, 1–4 June 2003. [Google Scholar]
- Salazar, A.O. A review of developments in bearingless motors. In Proceedings of the 7th International Symposium on Magnetic Bearings, Zurich, Switzerland, 23–25 August 2000; pp. 335–340. [Google Scholar]
- Yajima, S.; Takemoto, M.; Tanaka, Y.; Chiba, A.; Fukao, T. Total Efficiency of a Deeply Buried Permanent Magnet Type Bearingless Motor Equipped with 2-pole Motor Windings and 4-pole Suspension Windings. In Proceedings of the IEEE Power Engineering Society 2007 General Meeting, Tampa, FL, USA, 24–28 June 2007. [Google Scholar]
- Grabner, H.; Amrhein, W.; Silber, S.; Gruber, W. Nonlinear feedback control of a bearingless brushless DC motor. IEEE/ASME Trans. Mechatron. 2010, 15, 40–47. [Google Scholar] [CrossRef]
- Steinert, D.; Nussbaumer, T.; Kolar, J.W. Slotless Bearingless Disk Drive for High-Speed and High-Purity Applications. IEEE Trans. Ind. Electron. 2014, 61, 5974–5986. [Google Scholar] [CrossRef]
- Steinert, D.; Nussbaumer, T.; Kolar, J.W. Evaluation of One- and Two-Pole-Pair Slotless Bearingless Motors with Toroidal Windings. IEEE Trans. Ind. Appl. 2016, 52, 172–180. [Google Scholar] [CrossRef]
- Karnavas, Y.L.; Chasiotis, I.D. PMDC coreless micro-motor parameters estimation through Grey Wolf Optimizer. In Proceedings of the XXII International Conference on Electrical Machines (ICEM) 2016, Lausanne, Switzerland, 4–7 September 2016; pp. 865–870. [Google Scholar]
- Stamenkovic, I.; Milivojevic, N.; Schofield, N.; Krishnamurthy, M.; Emadi, A. Design Analysis and Optimization of Ironless Stator Permanent Magnet Machines. IEEE Trans. Power Electron. 2013, 28, 2527–2538. [Google Scholar] [CrossRef]
- Ueno, S.; Uematsu, S.I.; Kato, T. Development of a Lorentz-Force-Type Slotless Self-Bearing Motor. J. Syst. Design Dyn. 2009, 3, 462–470. [Google Scholar] [CrossRef] [Green Version]
- Ueno, S.; Kato, T. A Novel Design of a Lorentz-Force-Type Small Self Bearing Motor. In Proceedings of the 8th International Conference on Power Electronics and Drive Systems, Taipei, Taiwan, 2–5 Novemer 2009; pp. 926–931. [Google Scholar]
- Kobayashi, S.; Ooshima, S.K.M.; Uddin, M.N. A Radial Position Control Method of Bearingless Motor Based on d-q Axis Current Control. IEEE Trans. Ind. Appl. 2013, 49, 1827–1835. [Google Scholar] [CrossRef]
- Ooshima, M.; Kobayashi, S.; Uddin, M.N. Magnetic levitation tests of a bearingless motor based on d-q axis current control. In Proceedings of the 2012 IEEE Industry Applications Society Annual Meeting, Las Vegas, NV, USA, 7–11 October 2012. [Google Scholar]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, H.P.; Nguyen, X.B.; Bui, T.T.; Ueno, S.; Nguyen, Q.D. Analysis and Control of Slotless Self-Bearing Motor. Actuators 2019, 8, 57. https://doi.org/10.3390/act8030057
Nguyen HP, Nguyen XB, Bui TT, Ueno S, Nguyen QD. Analysis and Control of Slotless Self-Bearing Motor. Actuators. 2019; 8(3):57. https://doi.org/10.3390/act8030057
Chicago/Turabian StyleNguyen, Huy Phuong, Xuan Bien Nguyen, Trung Tuyen Bui, Satoshi Ueno, and Quang Dich Nguyen. 2019. "Analysis and Control of Slotless Self-Bearing Motor" Actuators 8, no. 3: 57. https://doi.org/10.3390/act8030057
APA StyleNguyen, H. P., Nguyen, X. B., Bui, T. T., Ueno, S., & Nguyen, Q. D. (2019). Analysis and Control of Slotless Self-Bearing Motor. Actuators, 8(3), 57. https://doi.org/10.3390/act8030057





