Sensorless Driving/Braking Control for Electric Vehicles
Abstract
1. Introduction
- (i)
- For motor driver design, the FOC algorithm was used on the AN1078 microchip, by Microchip Technology Co., Arizona [4], which can perform satisfactorily even when no position sensors are attached to the motor shaft. Low-inductance shunt resistors were used in three-phase inverters to measure the motor current.
- (ii)
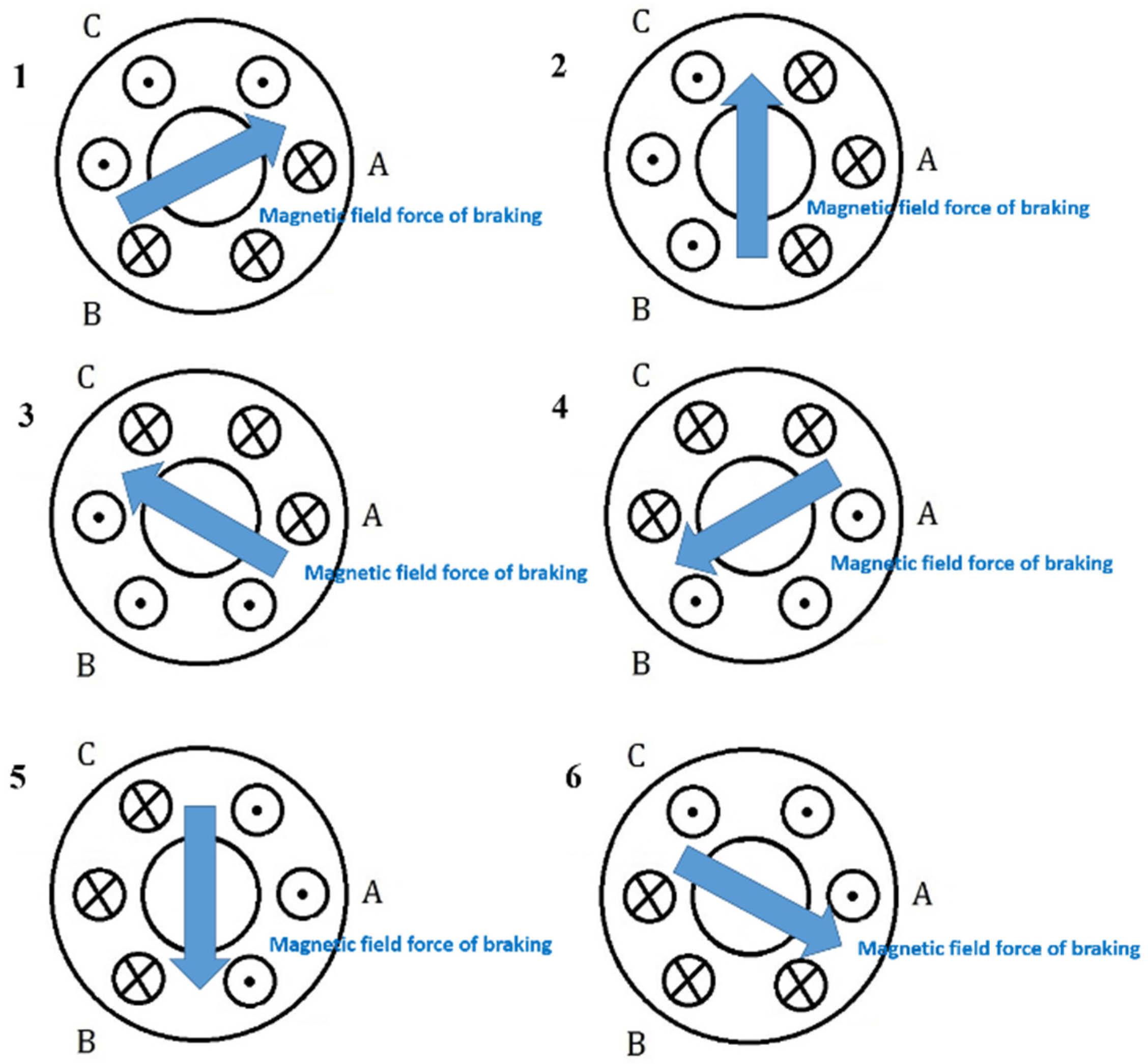
- Braking techniques—such as short-circuit [6], regenerative [7,8,9], kinetic [10], super-capacitor [11], and slip control-based braking [12]—regenerative braking are currently used. However, the braking effect decreases considerably when the battery is fully charged. In addition, the low conversion efficiency generally results in unsatisfactory braking performance. Therefore, an electromagnetic braking system was proposed in this research. Back electromotive force (back EMF) generated by the motor was used in the proposed braking system. The braking effect can be enhanced by intermittently reversing the direction of the magnetic field force from driving to braking using a permanent magnet synchronous motor (PMSM) stator coil. To achieve this enhanced braking, the relationship between the rotor angle and brake signal was determined according to a specific function. Combining this function with the aforementioned FOC-based driving mechanism, we can adjust the braking effect according to the parameters of a proportional integral controller. An ultracapacitor was added in the braking loop to boost instantaneous braking energy.
- (iii)
- For effective ABS realization, we first estimated the slip ratio, because determining the precise speed of electric bikes during movement in sensorless motors is difficult. According to studies [13,14,15], the sliding mode and current controls can be used to maintain the slip ratio within the optimal range for ensuring adhesion to the road. Underwater robots have been used in applications such as ocean development, ocean investigations, military operations, and marine environment protection. High-performance autonomous underwater vehicles are required for various applications, such as military defense and marine protection, especially for propulsion and maneuverability.
2. Model
2.1. Principle of FOC
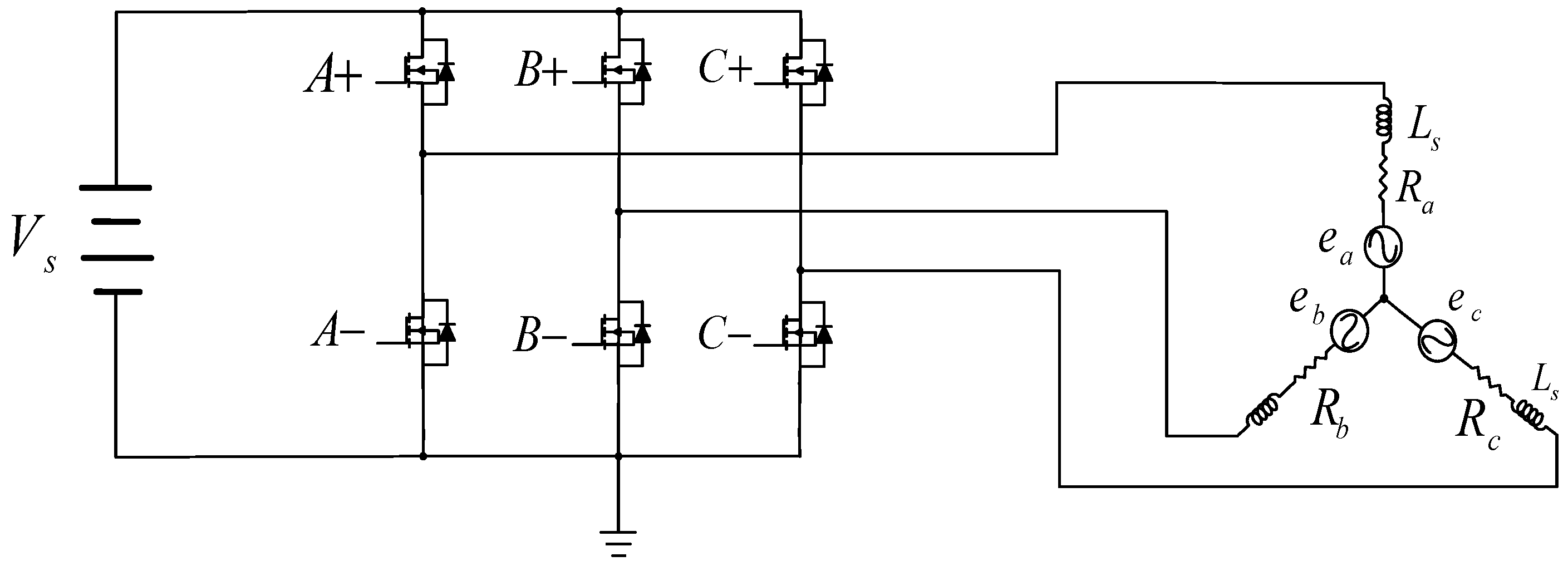
2.2. Sensorless Driver Design
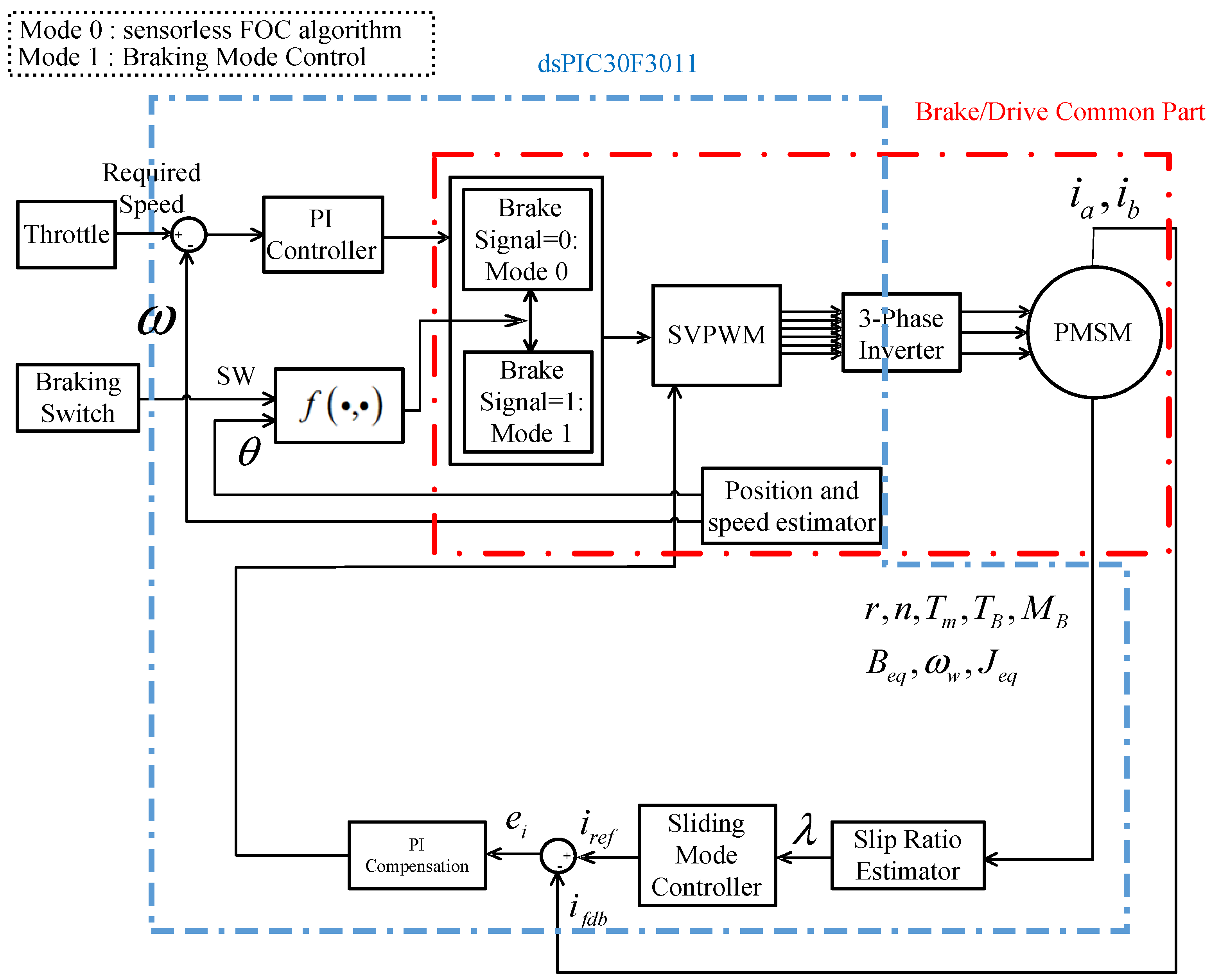
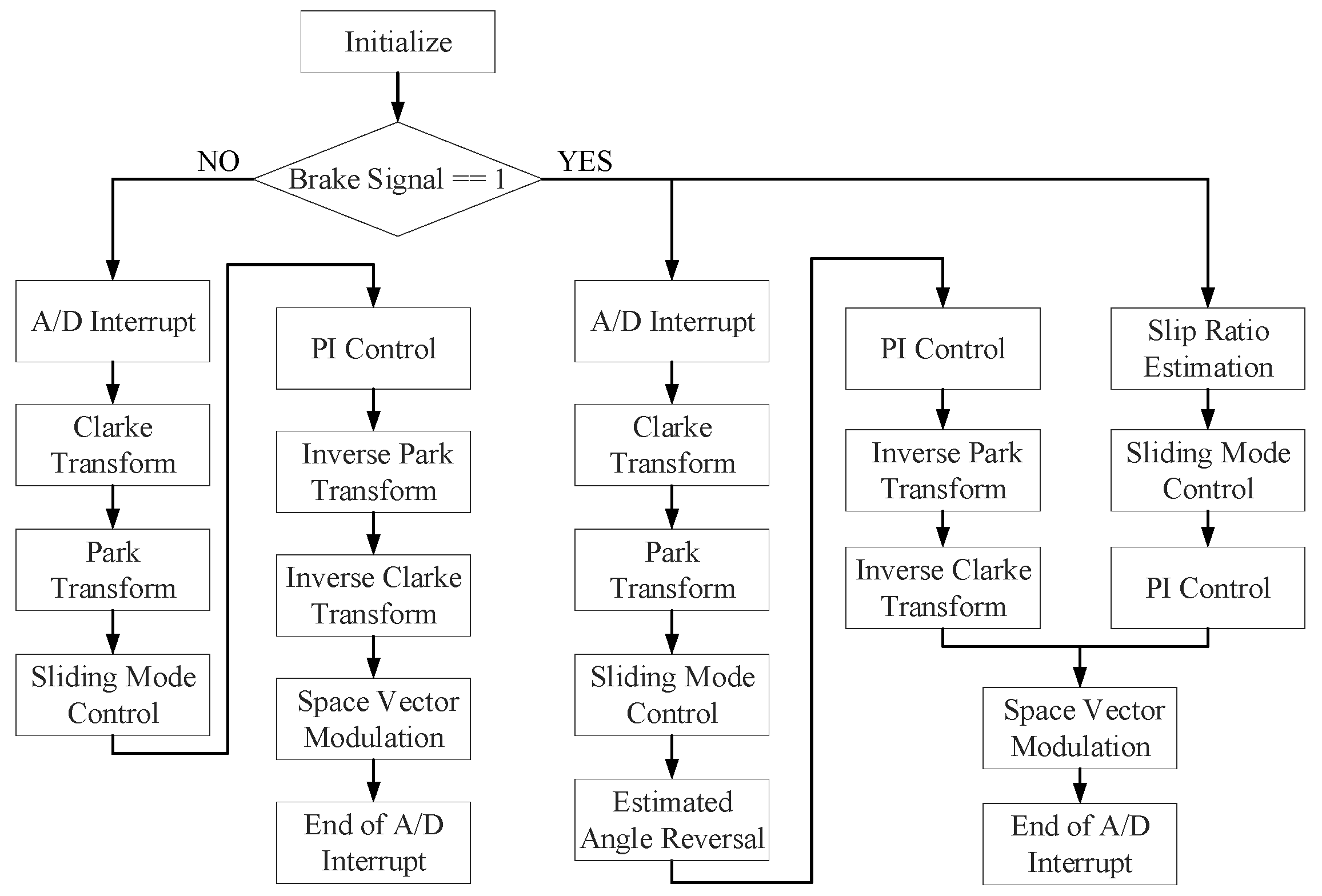
3. Integrated Driving/Braking Control
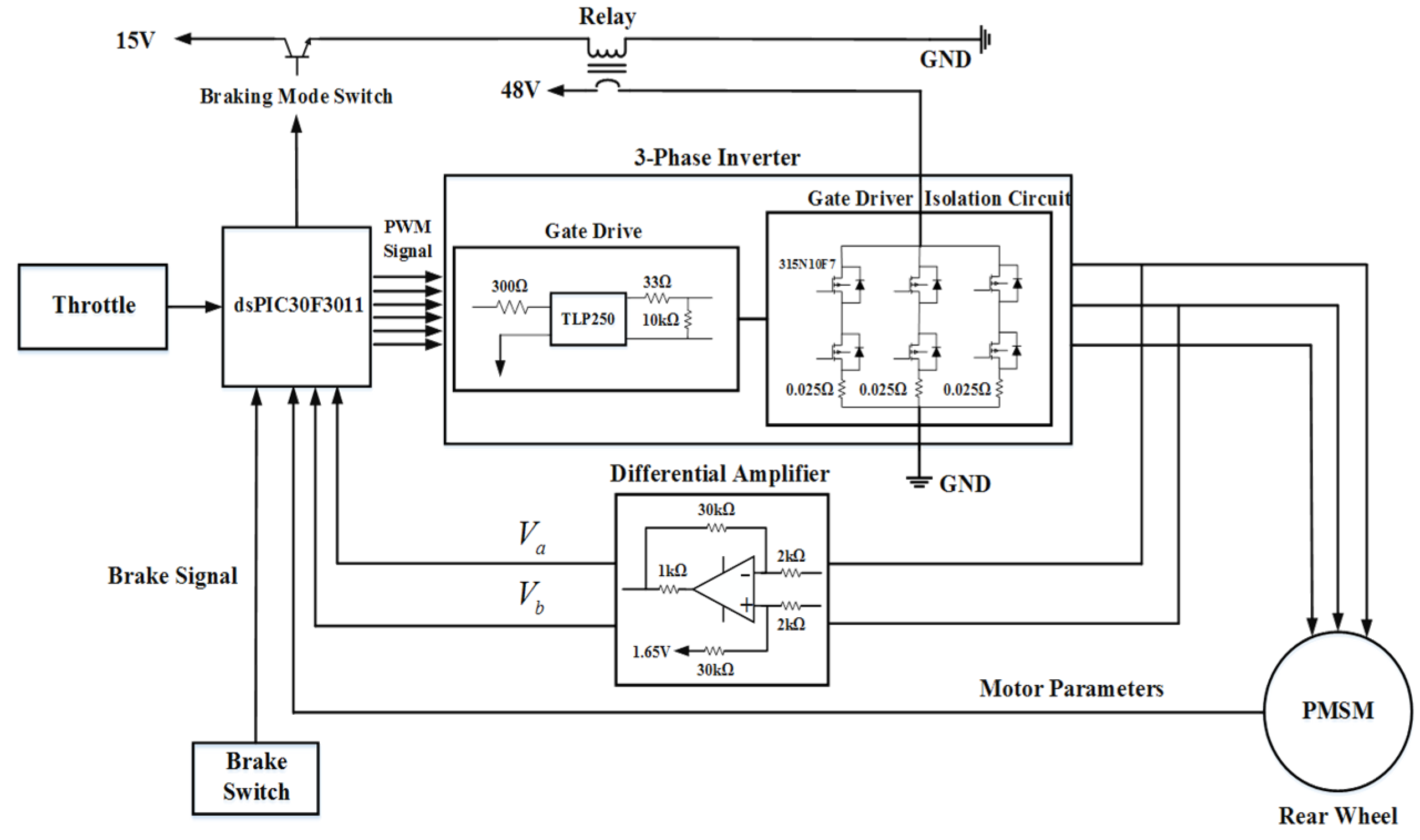
3.1. Structure of the Driver
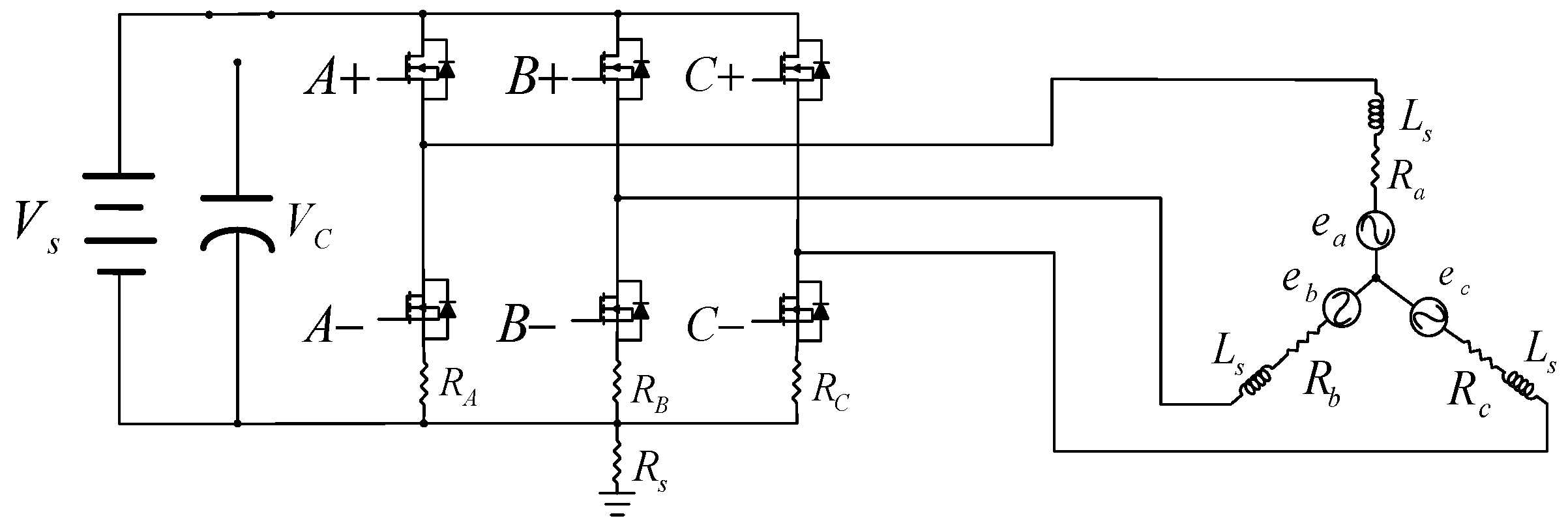
3.2. FOC-Based Braking Control Design
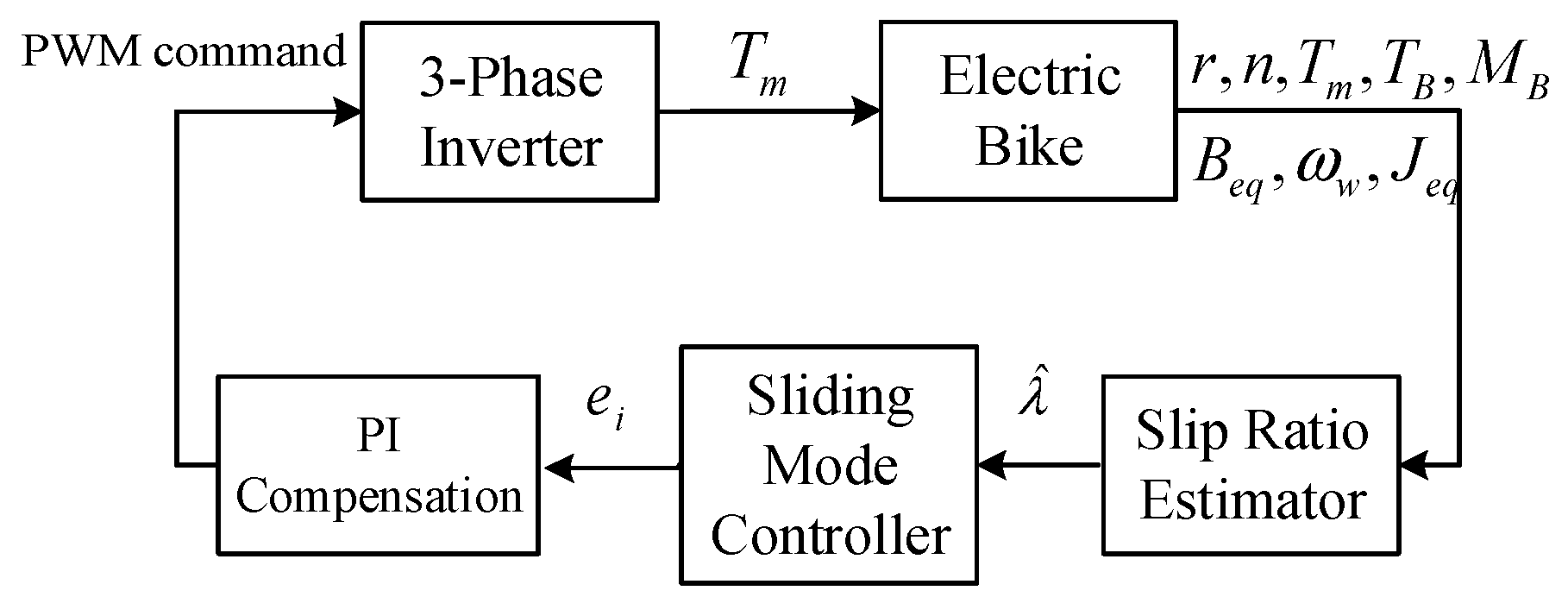
3.3. Design of Anti-Lock Braking System
3.4. Design of Slip Ratio Estimator
3.5. Design of Slip Ratio Control
4. Experimental Implementation
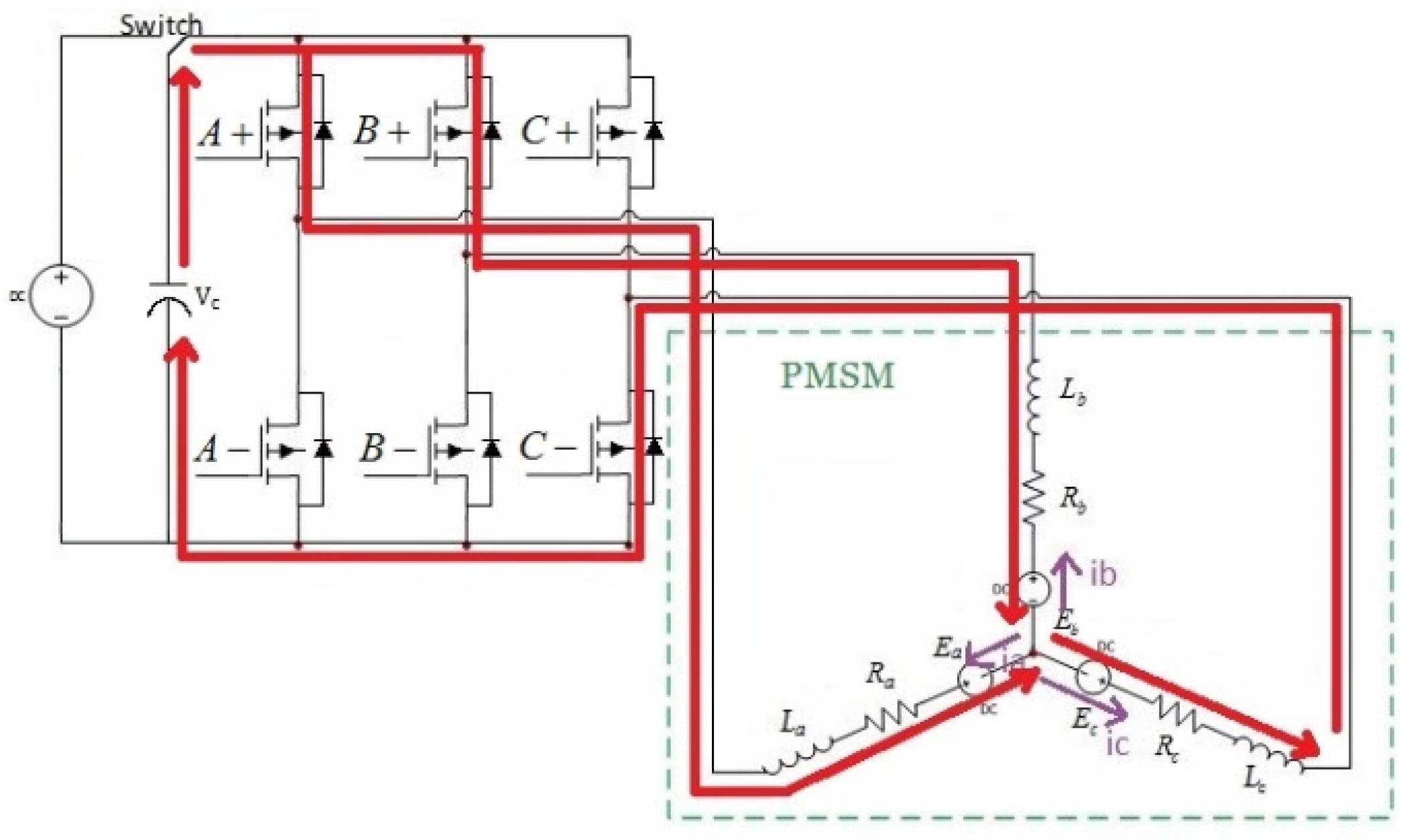
4.1. Hardware Realization
4.2. Software Design
5. Experimental Results
5.1. Driver Implementation
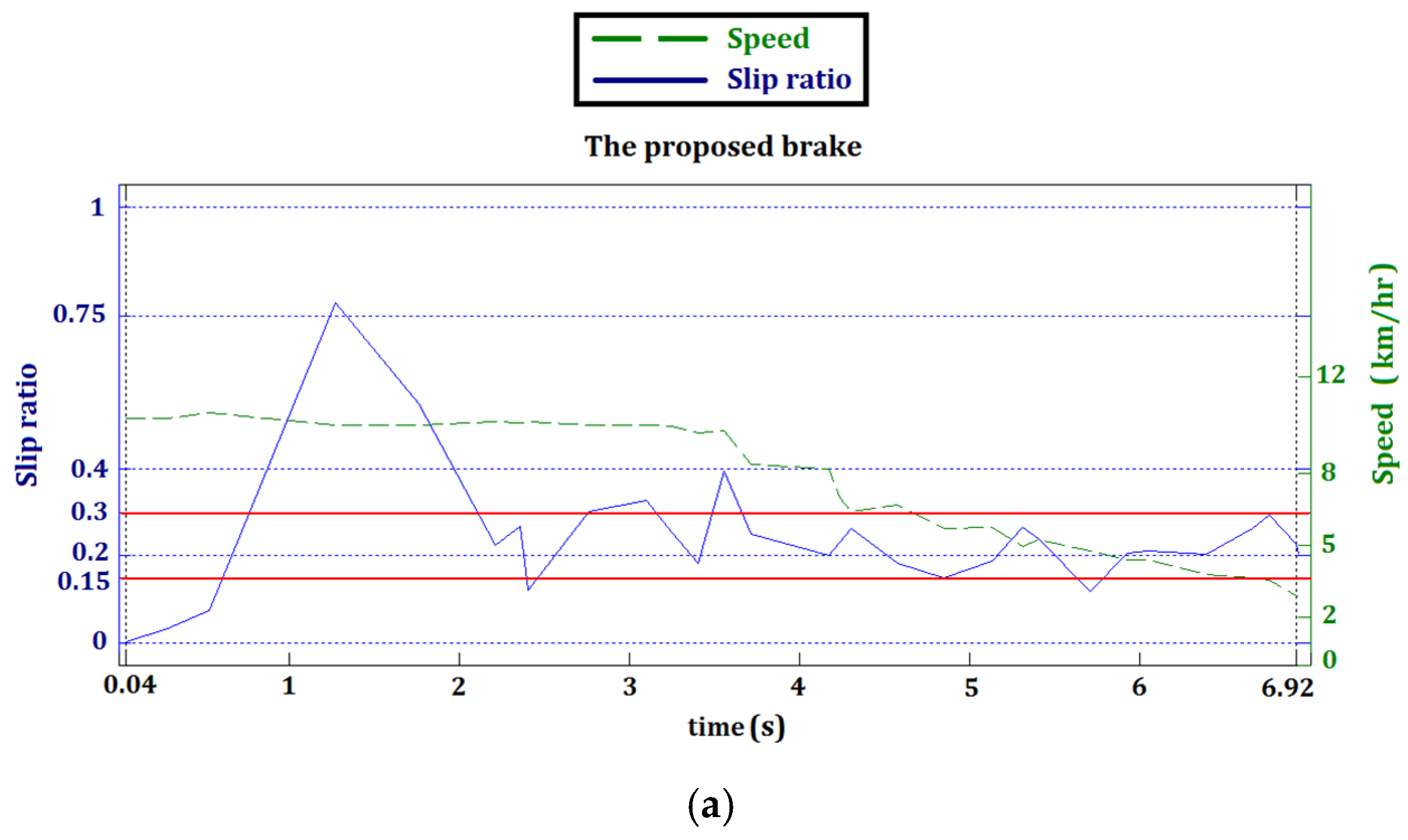
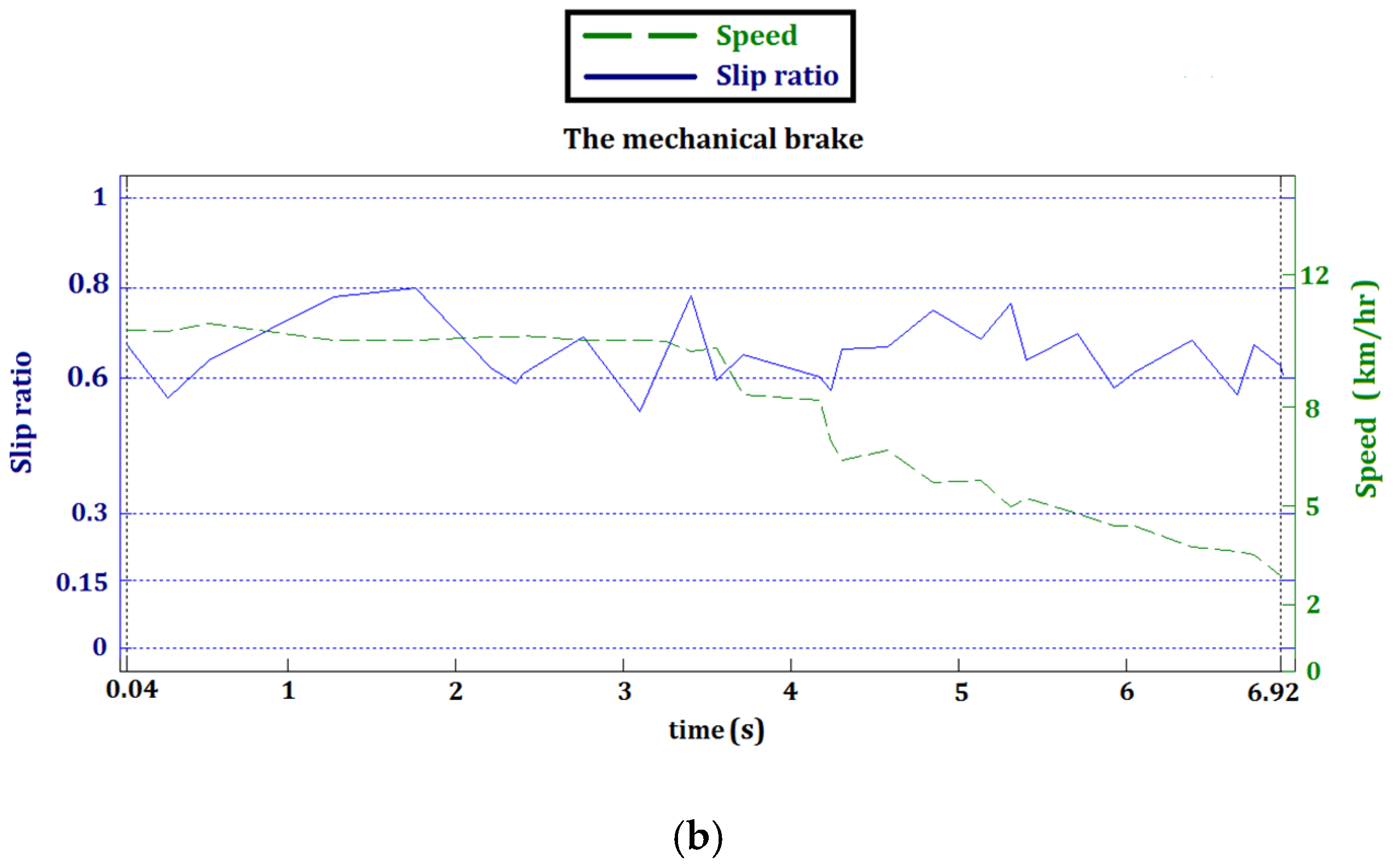
5.2. Braking System Realization
6. Discussions
7. Conclusions
8. Patent
Author Contributions
Funding
Conflicts of Interest
References
- Sahu, B.; Mohanty, K.B.; Pati, S. A comparative study on fuzzy and PI speed controllers for field-oriented induction motor drive. In Proceedings of the International Conference on Industrial Electronics, Control and Robotics, Wellington, New Zealand, 25–27 May 2009; pp. 2203–2212. [Google Scholar]
- Sharma, P.K.; Sindekar, A.S. Performance analysis and comparison of BLDC motor drive using PI and FOC. In Proceedings of the International Conference on Global Trends in Signal Processing, Information Computing and Communication, Jalgaon, India, 22–24 December 2016; pp. 485–492. [Google Scholar]
- Luo, J.; Namburu, M.; Pattipati, K.R.; Qiao, L.; Chigusa, S. Integrated model-based and data-driven diagnosis of automotive antilock braking systems. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2010, 40, 321–336. [Google Scholar] [CrossRef]
- Zambada, J.; Deb, D. Sensorless field oriented control of a PMSM. AN1078 Microchip Technol. Inc. 2010, 1–28. [Google Scholar]
- Jing, H.; Liu, Z.; Chen, H. A switched control strategy for antilock braking system with on/off valves. IEEE Trans. Veh. Technol. 2011, 60, 1470–1484. [Google Scholar] [CrossRef]
- Chen, Y.; Lv, X.; Shen, Y. Analysis of three-phase short circuit for dual-redundancy PMSM with low thermal coupling and non-electromagnetic coupling between windings. In Proceedings of the International Conference on Electrical Machines and Systems, Pattaya, Thailand, 25–28 October 2015; pp. 1434–1438. [Google Scholar]
- Yang, M.J.; Jhou, H.L.; Ma, B.Y.; Shyu, K.K. A cost-effective method of electric brake with energy regeneration for electric vehicles. IEEE Trans. Ind. Electron. 2009, 56, 2203–2212. [Google Scholar] [CrossRef]
- Naseri, F.; Farjah, E.; Ghanbari, T. An efficient regenerative braking system based on battery/supercapacitor for electric, hybrid, and plug-in hybrid electric vehicles with BLDC motor. IEEE Trans. Veh. Technol. 2017, 66, 3724–3738. [Google Scholar] [CrossRef]
- Li, Y.; Lv, C.; Zhang, J.; Zhang, Y.; Ma, W. High-precision modulation of a safety-critical cyber-physical system: Control synthesis and experimental validation. IEEE/ASME Trans. Mechatron. 2018, 23, 2599–2608. [Google Scholar] [CrossRef]
- Li, W.; Wang, X.; Leng, X.; Wang, M. Modeling and simulation of automobile braking system based on kinetic energy conversion. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008; pp. 1–3. [Google Scholar]
- Chen, X.; Yang, J.; Yu, F. Model and simulation of a super-capacitor braking energy recovery system for urban railway vehicles. In Proceedings of the WASE International Conference on Information Engineering, Beidaihe, China, 16–17 August 2010; pp. 295–300. [Google Scholar]
- Ataei, M.; Khajepour, A.; Jeon, S. Reconfigurable integrated stability control for four-and three-wheeled urban vehicles with flexible combinations of actuation systems. IEEE/ASME Trans. Mechatron. 2018, 23, 2031–2041. [Google Scholar] [CrossRef]
- Lin, W.C.; Lin, C.L.; Hsu, P.M.; Wu, M.T. Realization of anti-lock braking strategy for electric scooters. IEEE Trans. Ind. Electron. 2014, 61, 2826–2833. [Google Scholar] [CrossRef]
- Lin, C.L.; Yang, M.Y. Design of anti-lock braking system for electric vehicles via short-circuit braking. In Proceedings of the IEEE International Conference on Mechanic Automation and Control Engineering, Inner Mongolia, China, 15–17 July 2011; pp. 1176–1179. [Google Scholar]
- Lin, C.L.; Lin, W.C. ABS control design for two-wheel drive electric vehicles. In Proceedings of the IEEE International Conference on Mechanic Automation and Control Engineering, Inner Mongolia, China, 15–17 July 2011; pp. 1011–1014. [Google Scholar]
- Abassi, M.; Khlaief, A.; Saadaoui, O.; Chaari, A.; Boussak, M. Performance analysis of FOC and DTC for PMSM drives using SVPWM technique. In Proceedings of the IEEE International Conference on Sciences and Techniques of Automatic Control & Computer Engineering, Monastir, Tunisia, 21–23 December 2015; pp. 228–233. [Google Scholar]
- Kumar, P.; Dhundhara, S.; Makin, R. Performance analysis of PMSM drive based on FOC technique with and without MRAS method. In Proceedings of the International Conference on Recent Advances and Innovations in Engineering, Jaipur, India, 23–25 December 2016; pp. 1–6. [Google Scholar]
- Texas Instruments Incorporated. Field Orientated Control of 3-Phase AC-Motor; Literature Number: BPRA073.1998; Texas Instruments Incorporated: Dallas, TX, USA, 2017. [Google Scholar]
- DeCarlo, R.A.; Zak, S.H.; Matthews, G.P. Variable structure control of nonlinear multivariable systems: A tutorial. Proc. IEEE 1988, 76, 212–232. [Google Scholar] [CrossRef]
- Suzuki, T.; Fujimoto, H. Slip ratio estimation and regenerative brake control without detection of vehicle velocity and acceleration for electric vehicle at urgent brake-turning. In Proceedings of the IEEE International Workshop on Advanced Motion Control, Nagaoka, Niigata, Japan, 21–24 March 2010; pp. 273–278. [Google Scholar]
- Chen, S.Y.; Chiang, H.H.; Liu, T.S.; Chang, C.H. Precision motion control of permanent magnet linear synchronous motors using adaptive fuzzy fractional-order sliding-mode control. IEEE/ASME Trans. Mechatron. 2019, 24, 741–752. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Kiencke, U.; Nielsen, L. Automotive Control Systems; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Lin, C.L.; Hsieh, M.C.; Chen, T.C. Integrated driving and braking control unit for electric bike. SAE Int. J. Veh. Dyn. Stab. NVH 2018, 2, 223–242. [Google Scholar] [CrossRef]
- Lahue, K.C. Automotive Brakes and Antilock Braking Systems; West Publishing Co.: Eagan, MN, USA, 1995. [Google Scholar]
- Tacx i-Genius T2000 Virtual Reality Trainer–Multiplayer. Available online: https://www.evanscycles.com/tacx-i-genius-t2000-virtual-reality-trainer-multiplayer-EV152529 (accessed on 21 March 2020).

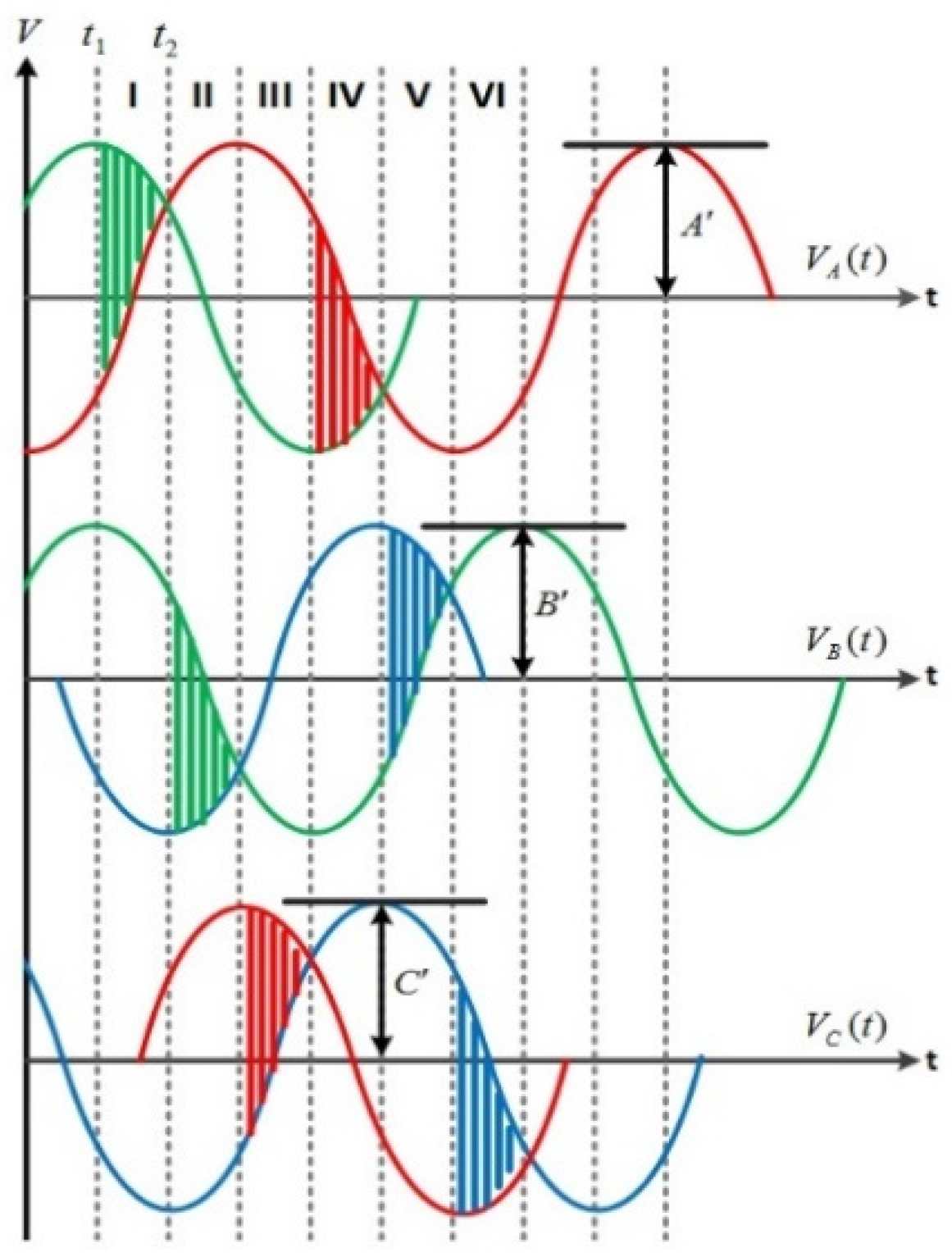



| Region of Vref | The Order of Vector Combination of Vref |
|---|---|
| S1(0° ≤ θ ≤ 60°) | V0 → V1 → V2 → V7 → V7 → V2 → V1 → V0 |
| S2(60° ≤ θ ≤ 120°) | V0 → V3 → V2 → V7 → V7 → V2 → V3 → V0 |
| S3(120° ≤ θ ≤ 180°) | V0 → V3 → V4 → V7 → V7 → V4 → V3 → V0 |
| S4(180° ≤ θ ≤ 240°) | V0 → V5 → V4 → V7 → V7 → V4 → V5 → V0 |
| S5(240° ≤ θ ≤ 300°) | V0 → V5 → V6 → V7 → V7 → V6 → V5 → V0 |
| S6(300° ≤ θ ≤ 360°) | V0 → V1 → V6 → V7 → V7 → V6 → V1 → V0 |
| Voltage Vector | Control Logic of Driving | Voltage Vector | Control Logic of Braking | ||||
|---|---|---|---|---|---|---|---|
| Phase A | Phase B | Phase C | Phase A | Phase B | Phase C | ||
| V0 | 0 | 0 | 0 | V7 | 1 | 1 | 1 |
| V1 | 1 | 0 | 0 | V6 | 1 | 0 | 1 |
| V2 | 1 | 1 | 0 | V5 | 0 | 0 | 1 |
| V3 | 0 | 1 | 0 | V4 | 0 | 1 | 1 |
| V4 | 0 | 1 | 1 | V3 | 0 | 1 | 0 |
| V5 | 0 | 0 | 1 | V2 | 1 | 1 | 0 |
| V6 | 1 | 0 | 1 | V1 | 1 | 0 | 0 |
| V7 | 1 | 1 | 1 | V0 | 0 | 0 | 0 |
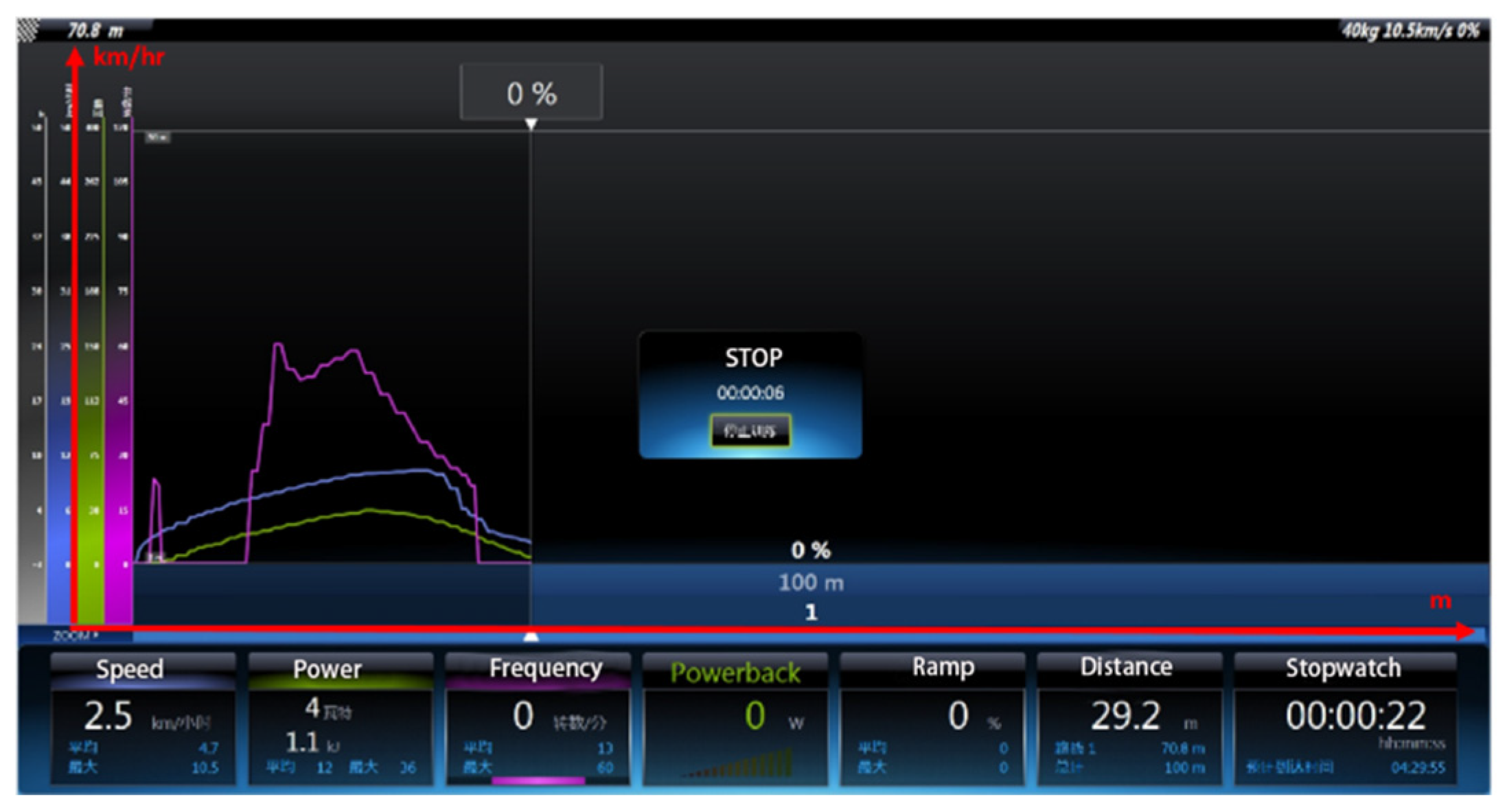
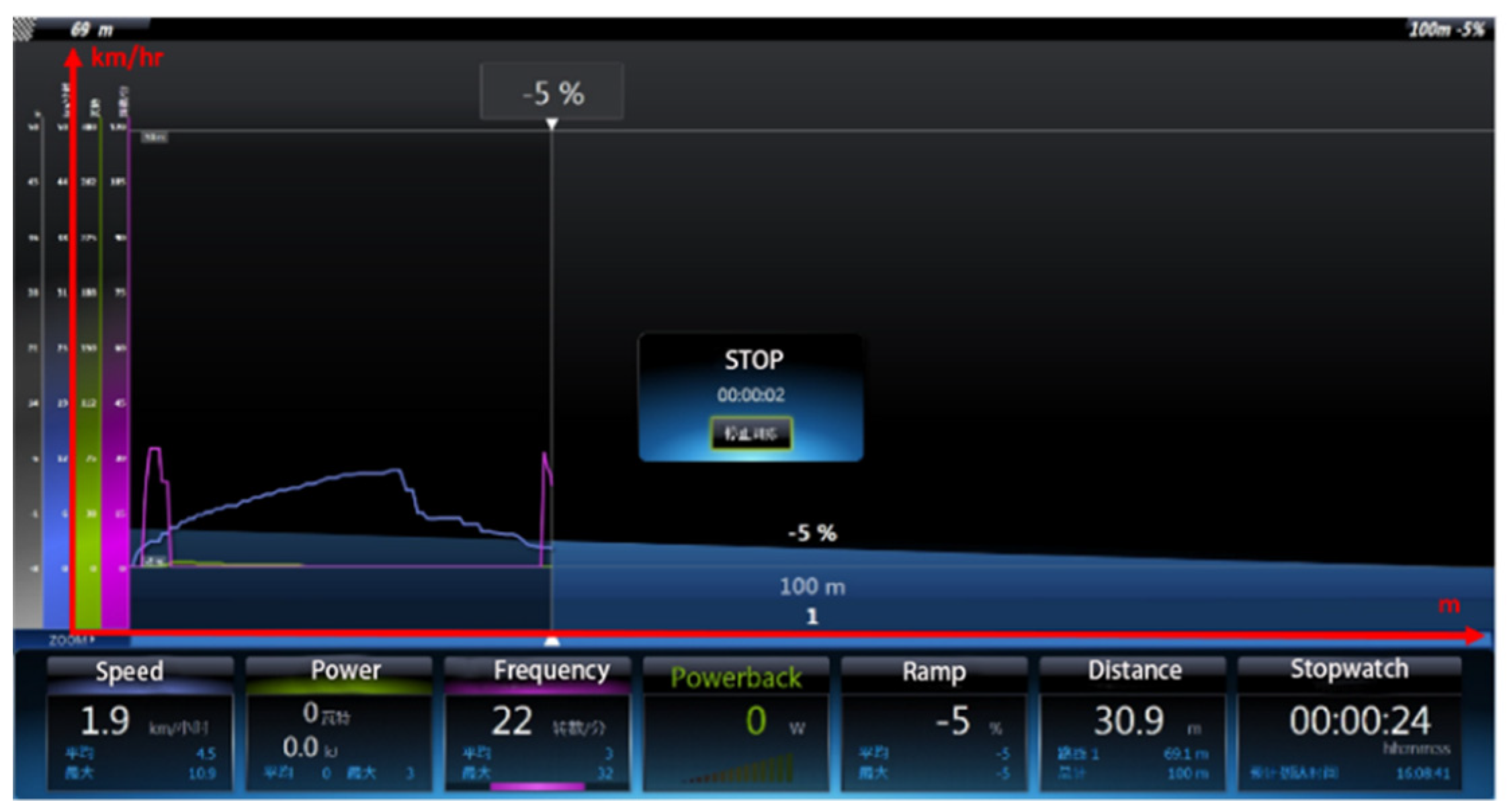
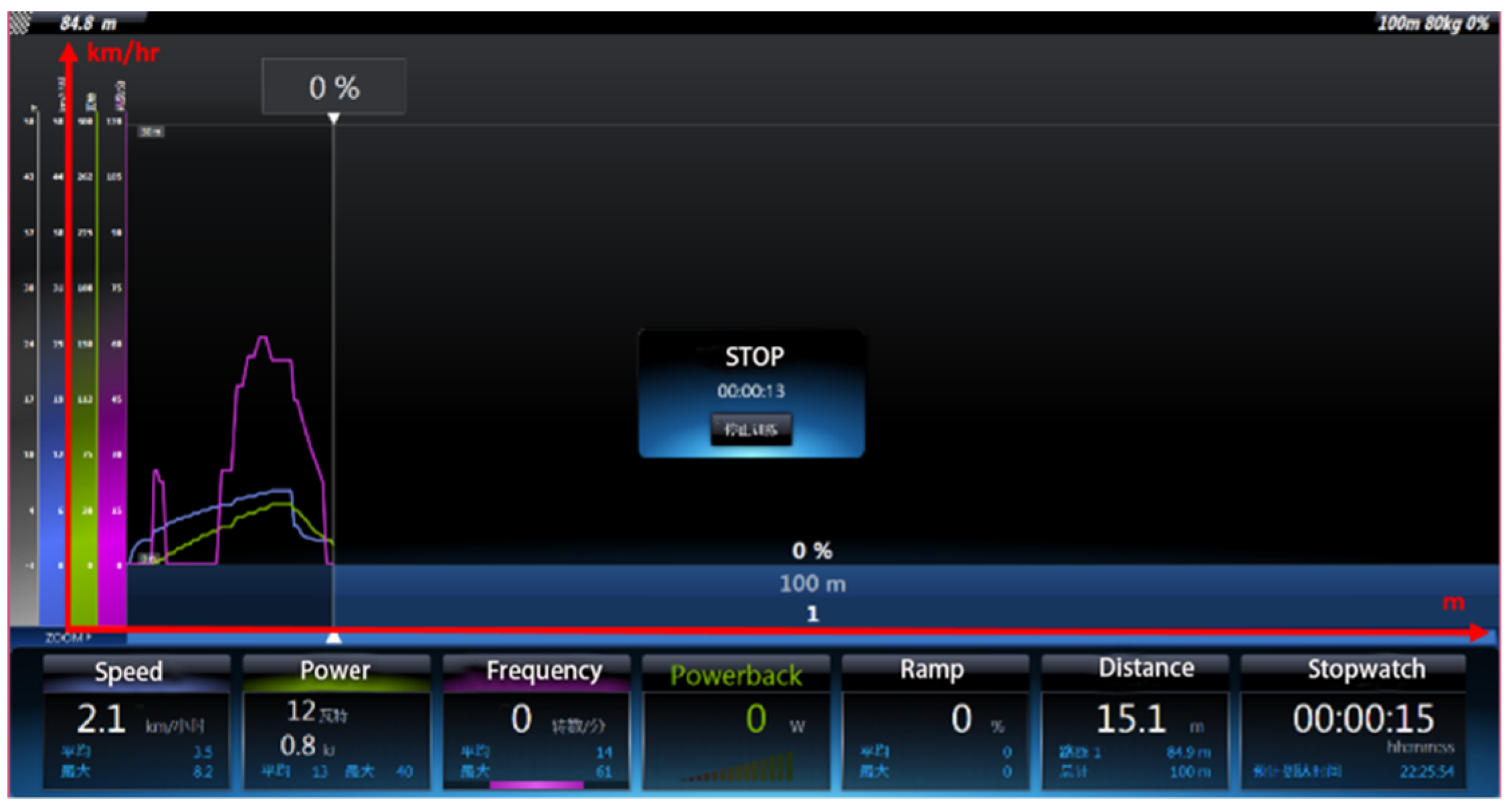
| Road Condition | Braking Speed (km/hr) | Cyclist Weight (kg) | Brake Method | Stopping Distance (m) |
|---|---|---|---|---|
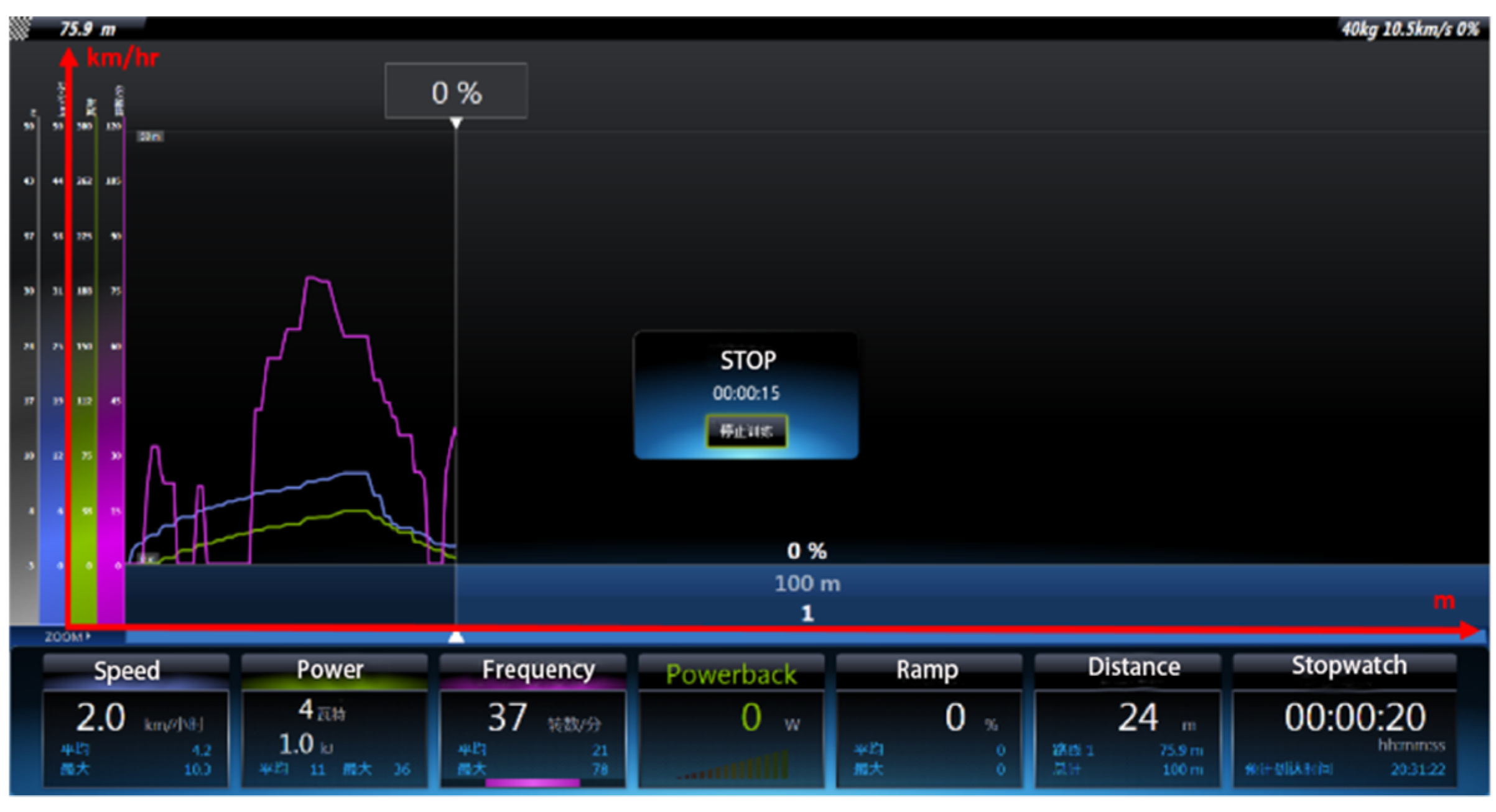
| flat | 10.5 | 40 | lower-arm three-phase short-circuit brake | 29.2 |
| electromagnetic brake | 24 | |||
| 60 | lower-arm three-phase short-circuit brake | 32.1 | ||
| electromagnetic brake | 26.3 | |||
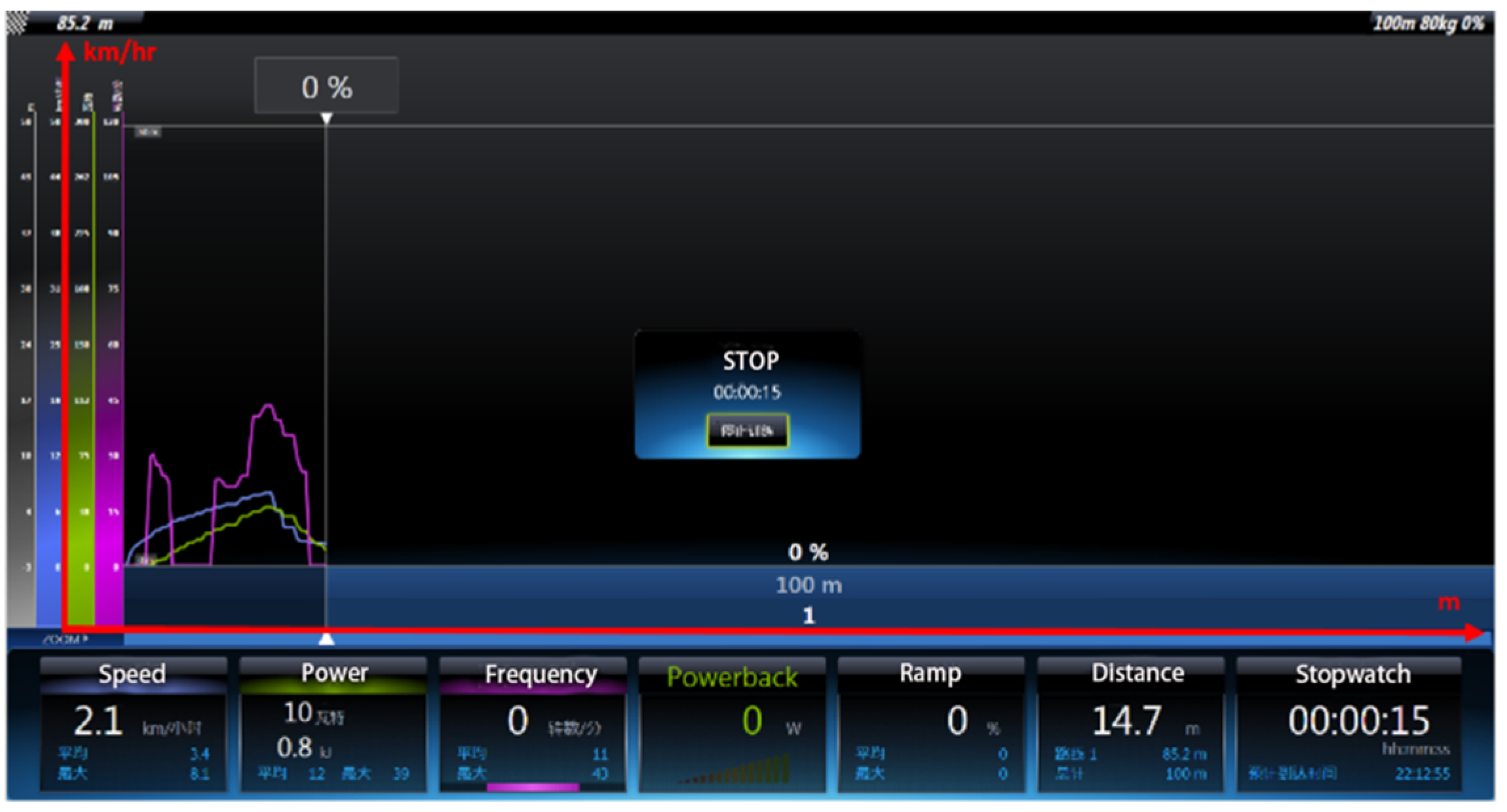
| 8.2 | 80 | lower-arm three-phase short-circuit brake | 15.1 | |
| 8.1 | electromagnetic brake | 14.7 | ||
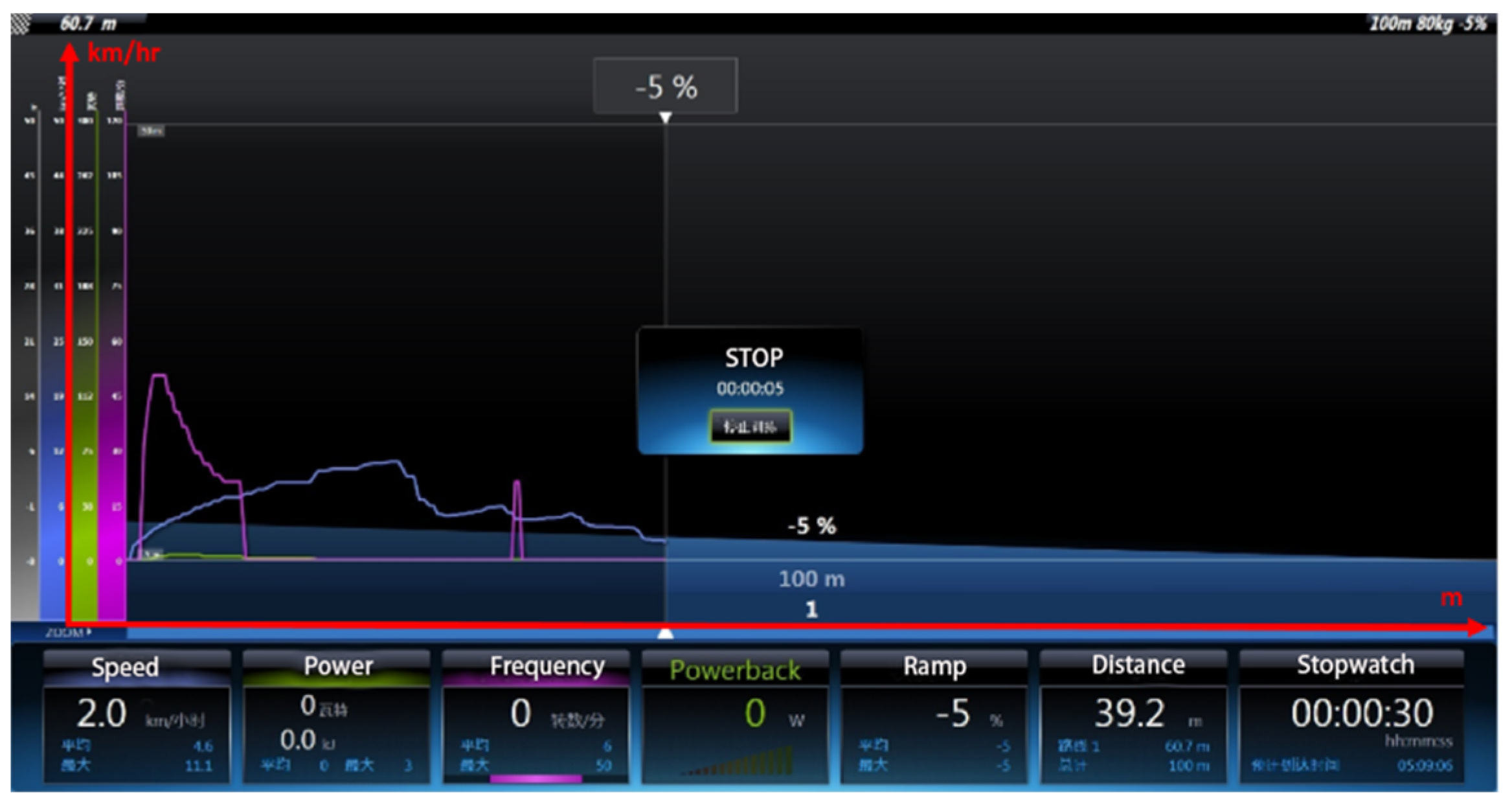
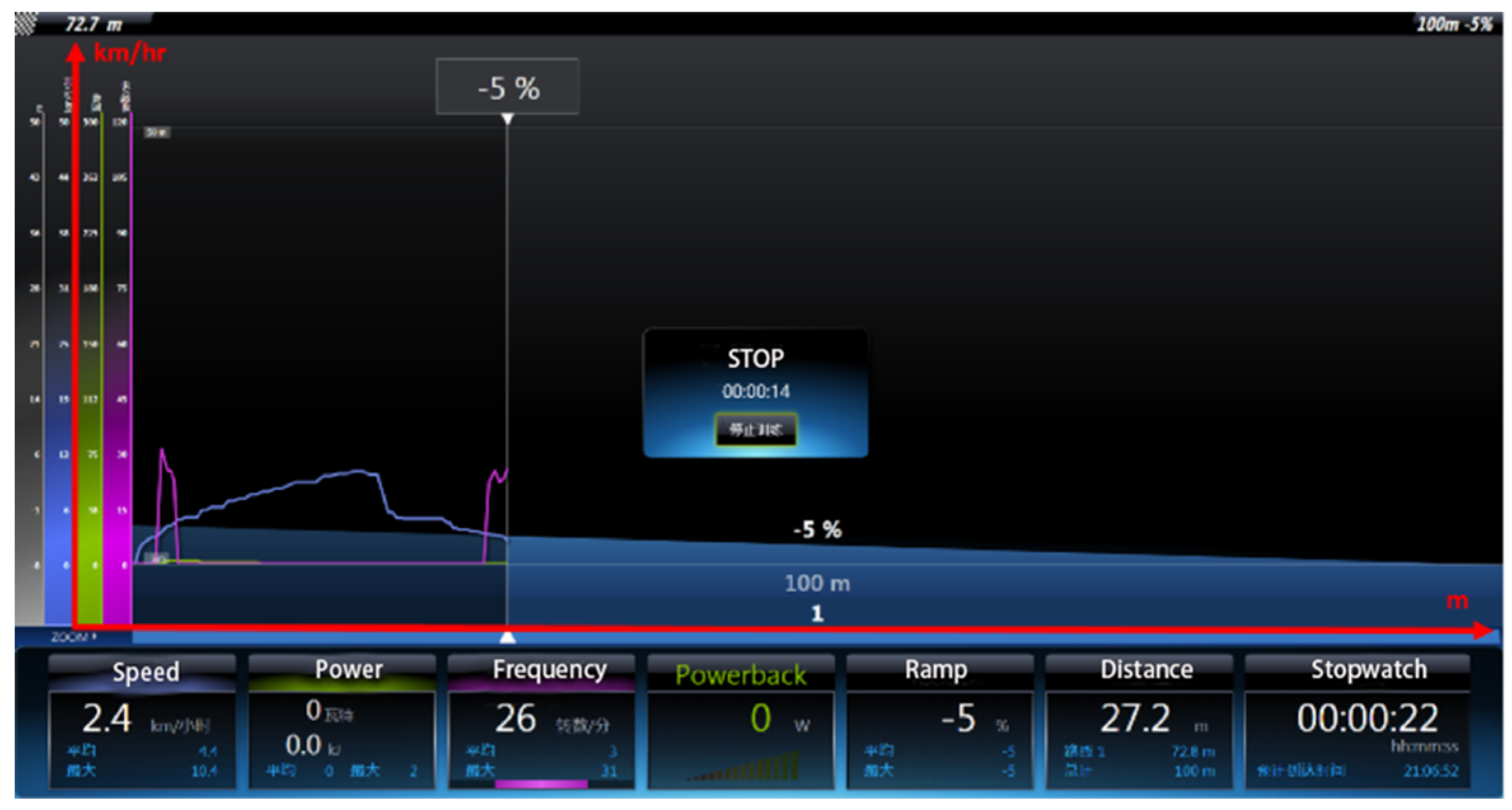
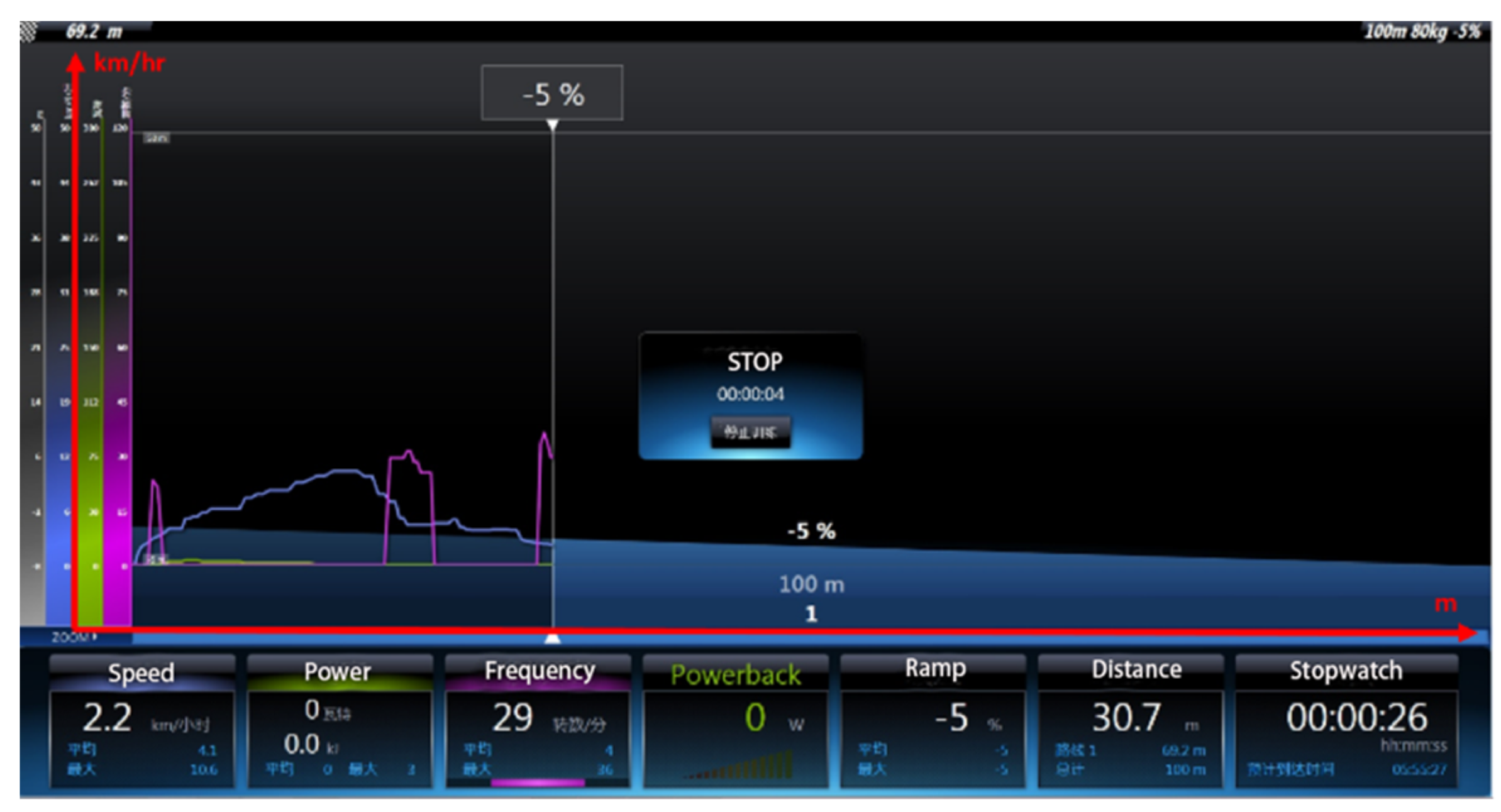
| downhill slope −5% * | 10.5 | 40 | lower-arm three-phase short-circuit brake | 30.9 |
| electromagnetic brake | 27.2 | |||
| 60 | lower-arm three-phase short-circuit brake | 32.5 | ||
| electromagnetic brake | 26.4 | |||
| 80 | lower-arm three-phase short-circuit brake | 39.2 | ||
| electromagnetic brake | 30.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, E.-P.; Cheng, J.; Tu, J.-H.; Lin, C.-L. Sensorless Driving/Braking Control for Electric Vehicles. Actuators 2020, 9, 22. https://doi.org/10.3390/act9010022
Chen E-P, Cheng J, Tu J-H, Lin C-L. Sensorless Driving/Braking Control for Electric Vehicles. Actuators. 2020; 9(1):22. https://doi.org/10.3390/act9010022
Chicago/Turabian StyleChen, En-Ping, Jiangfeng Cheng, Jia-Hung Tu, and Chun-Liang Lin. 2020. "Sensorless Driving/Braking Control for Electric Vehicles" Actuators 9, no. 1: 22. https://doi.org/10.3390/act9010022
APA StyleChen, E.-P., Cheng, J., Tu, J.-H., & Lin, C.-L. (2020). Sensorless Driving/Braking Control for Electric Vehicles. Actuators, 9(1), 22. https://doi.org/10.3390/act9010022




