Effect of Electromagnetic Damping on System Performance of Voice-Coil Actuator Applied to Balancing-Type Scale
Abstract
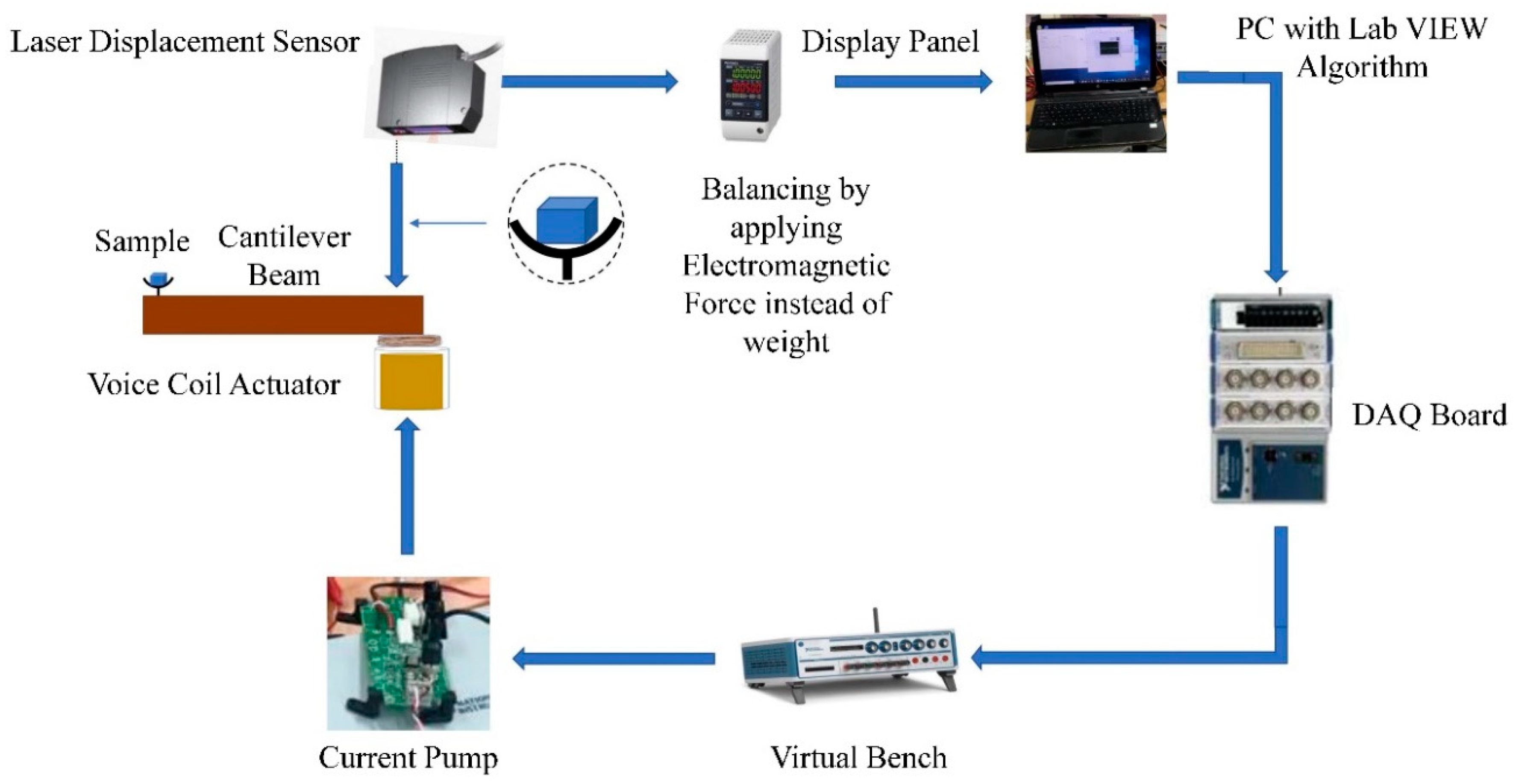
:1. Introduction
1.1. Background
1.2. Objective
2. Theoretical Analysis
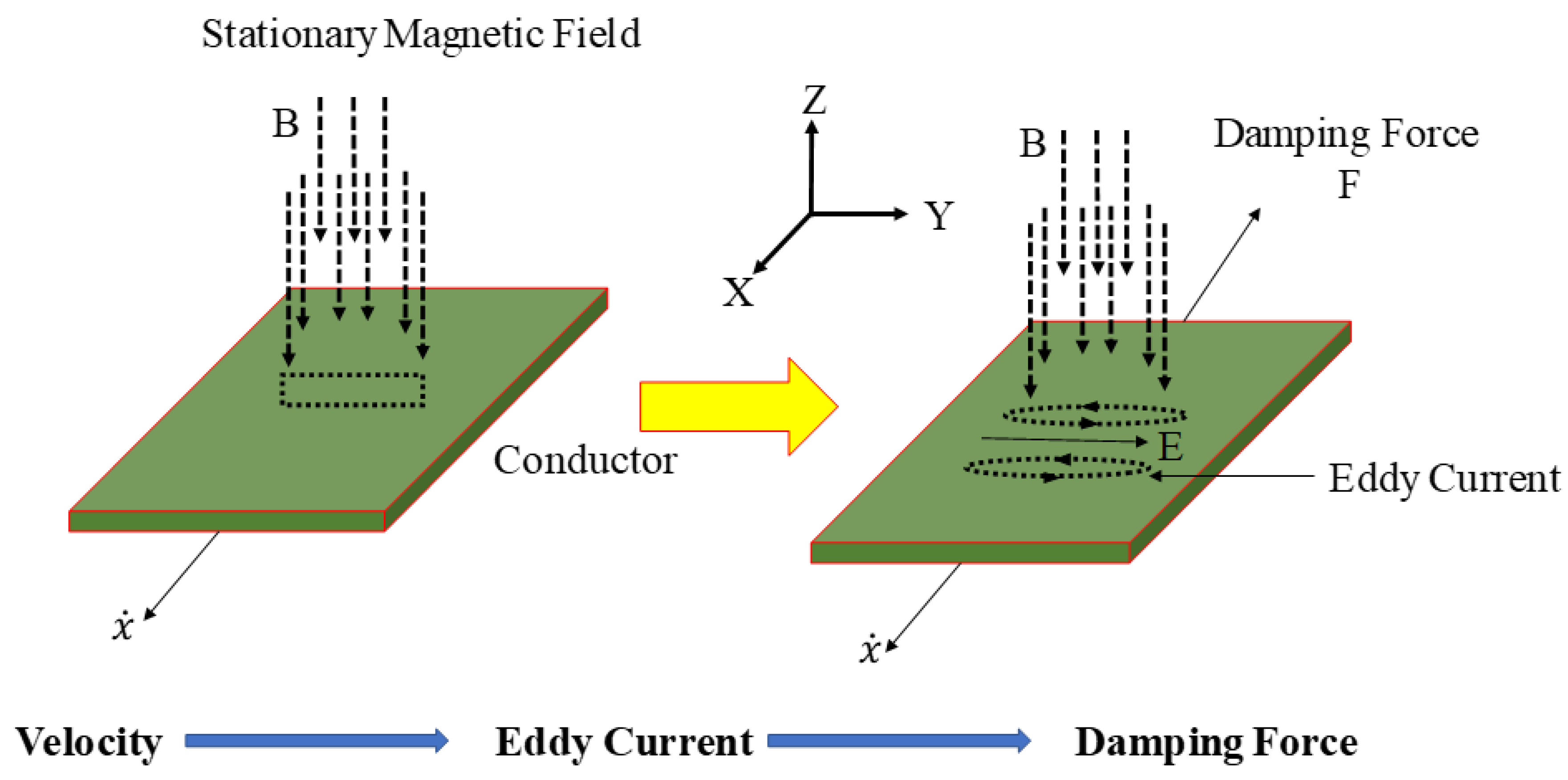
2.1. Electromagnetic Damping Principle
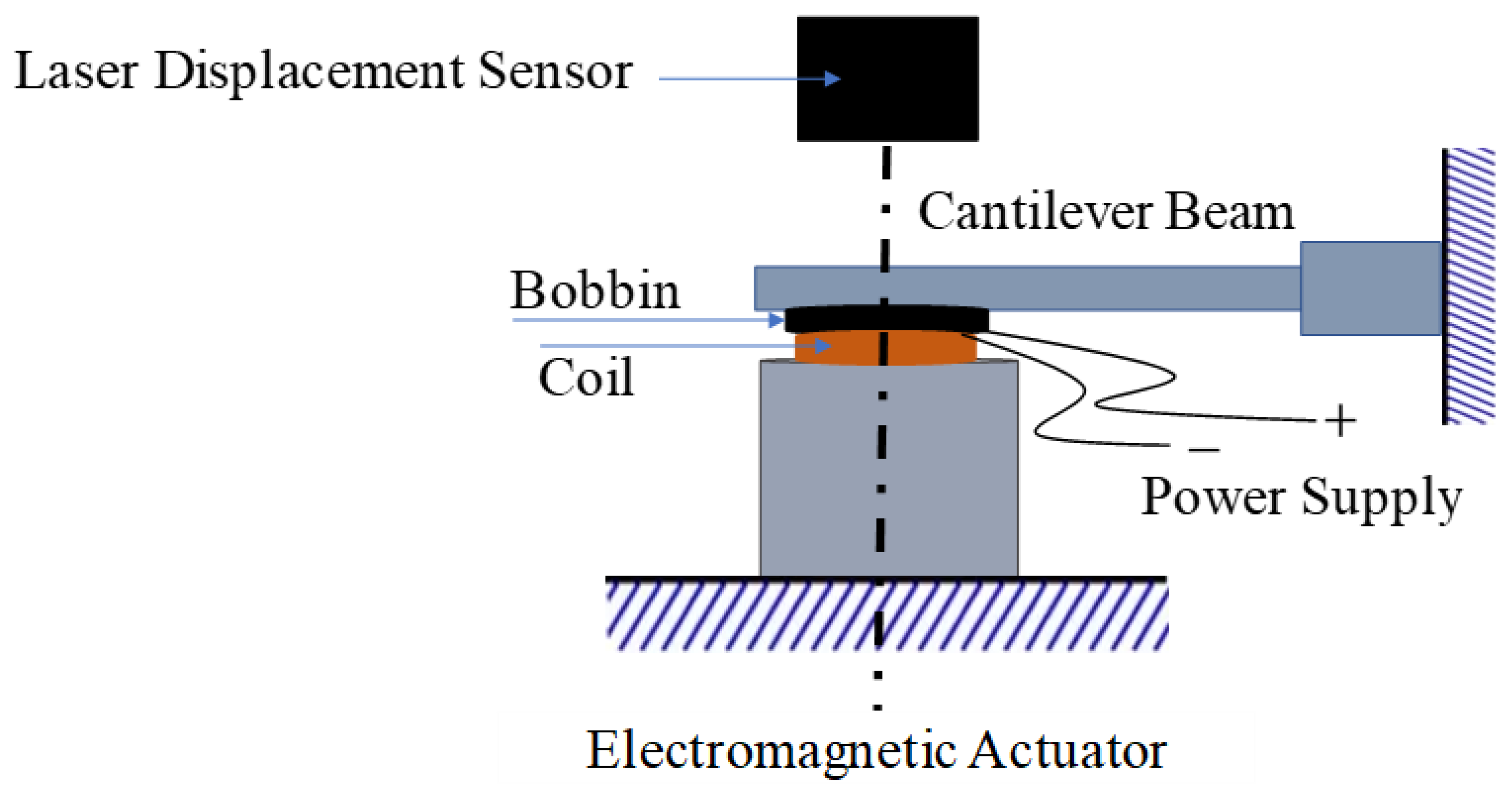
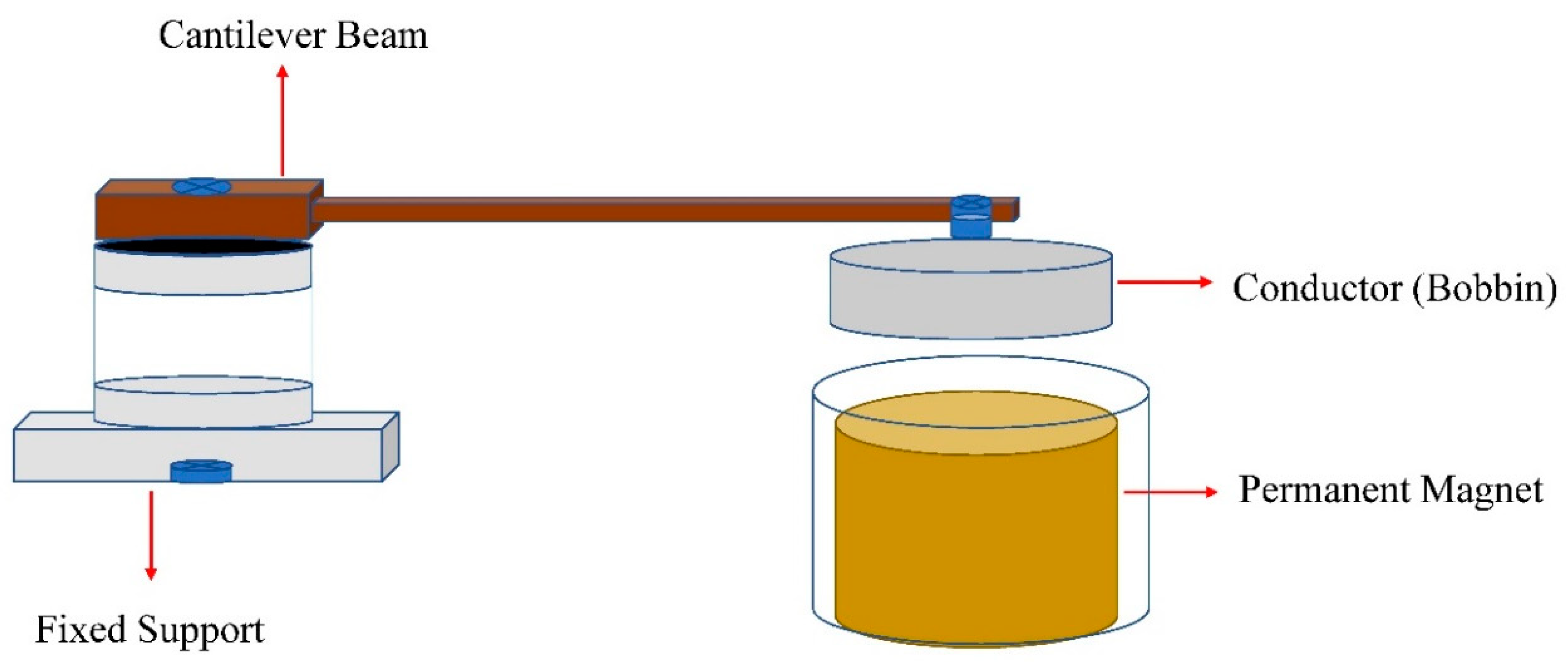
2.2. Use of Electromagnetic Damping in Voice Coil Actuator
3. System Modelling for System Identification
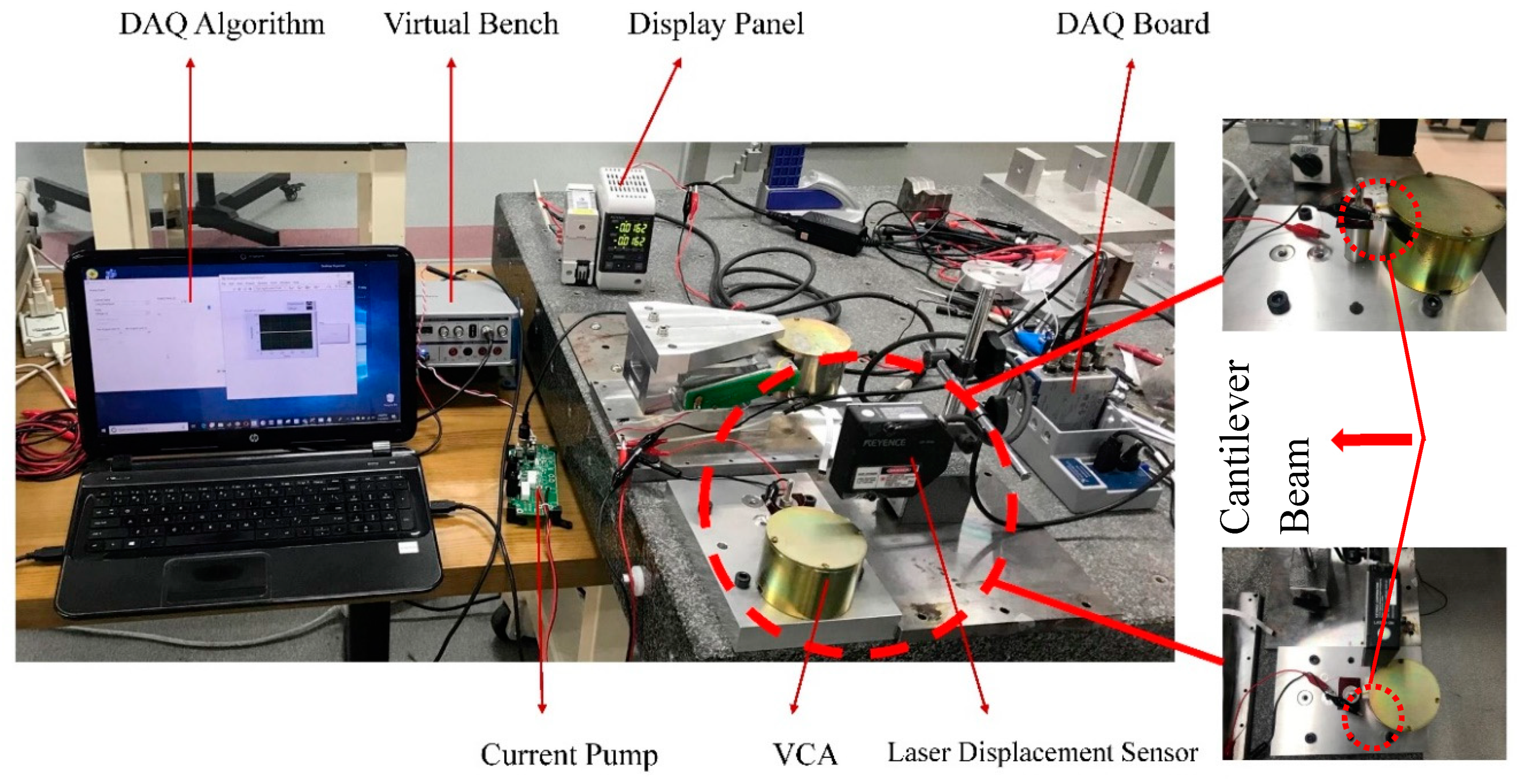
3.1. System Modelling
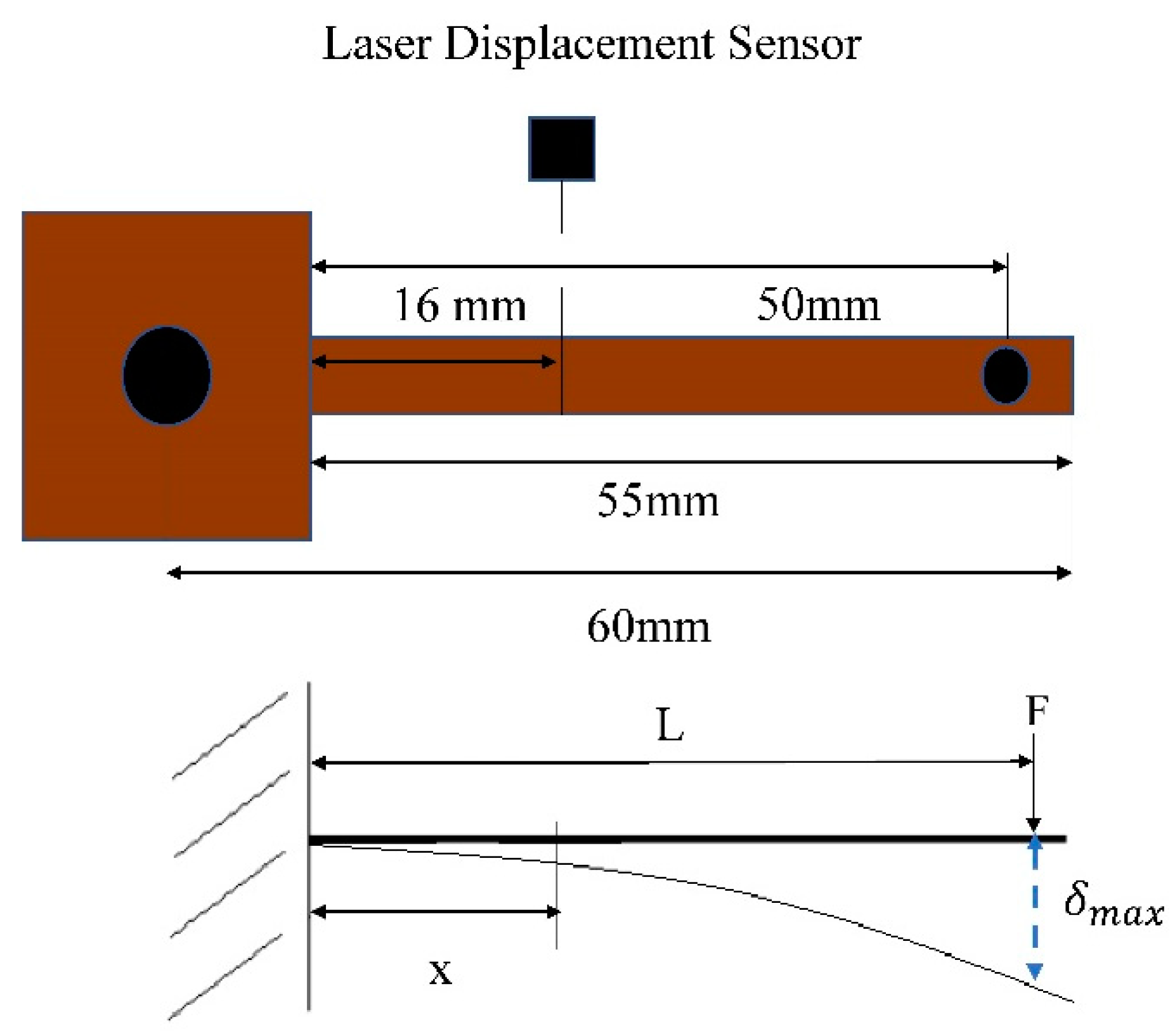
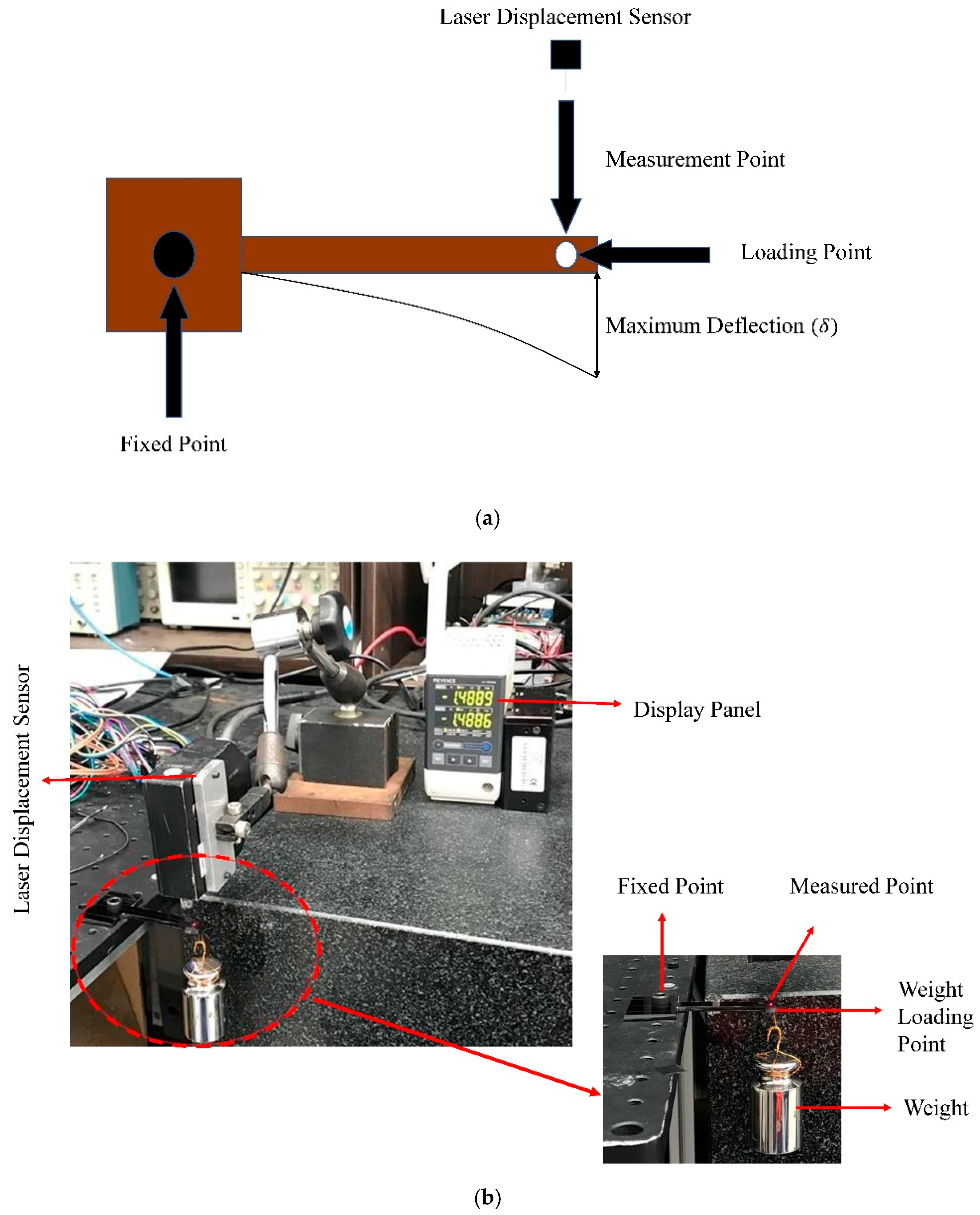
3.2. Modeling of Cantilever Beam
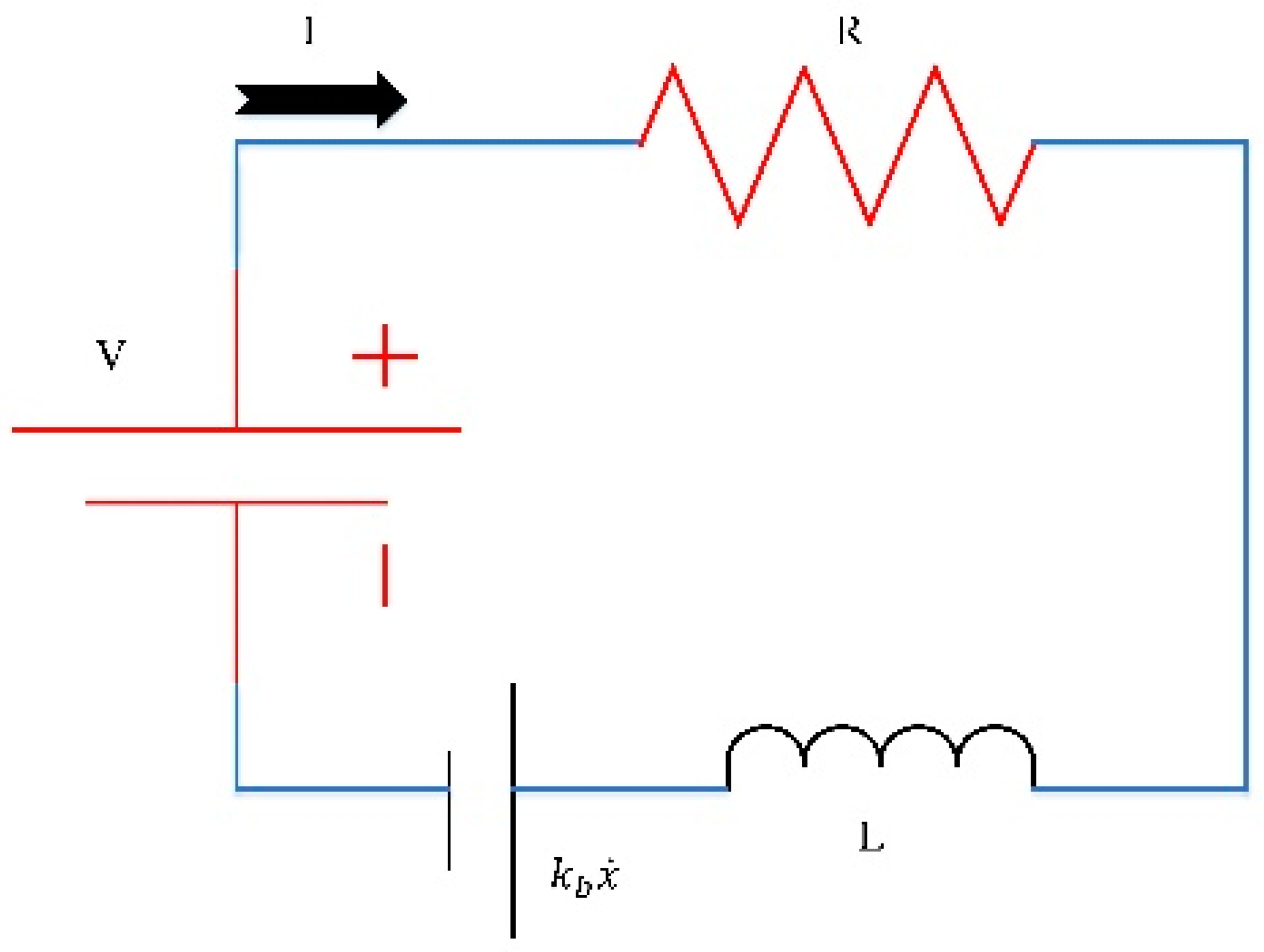
3.3. Electrical Modelling of Voice-Coil Actuator (VCA)
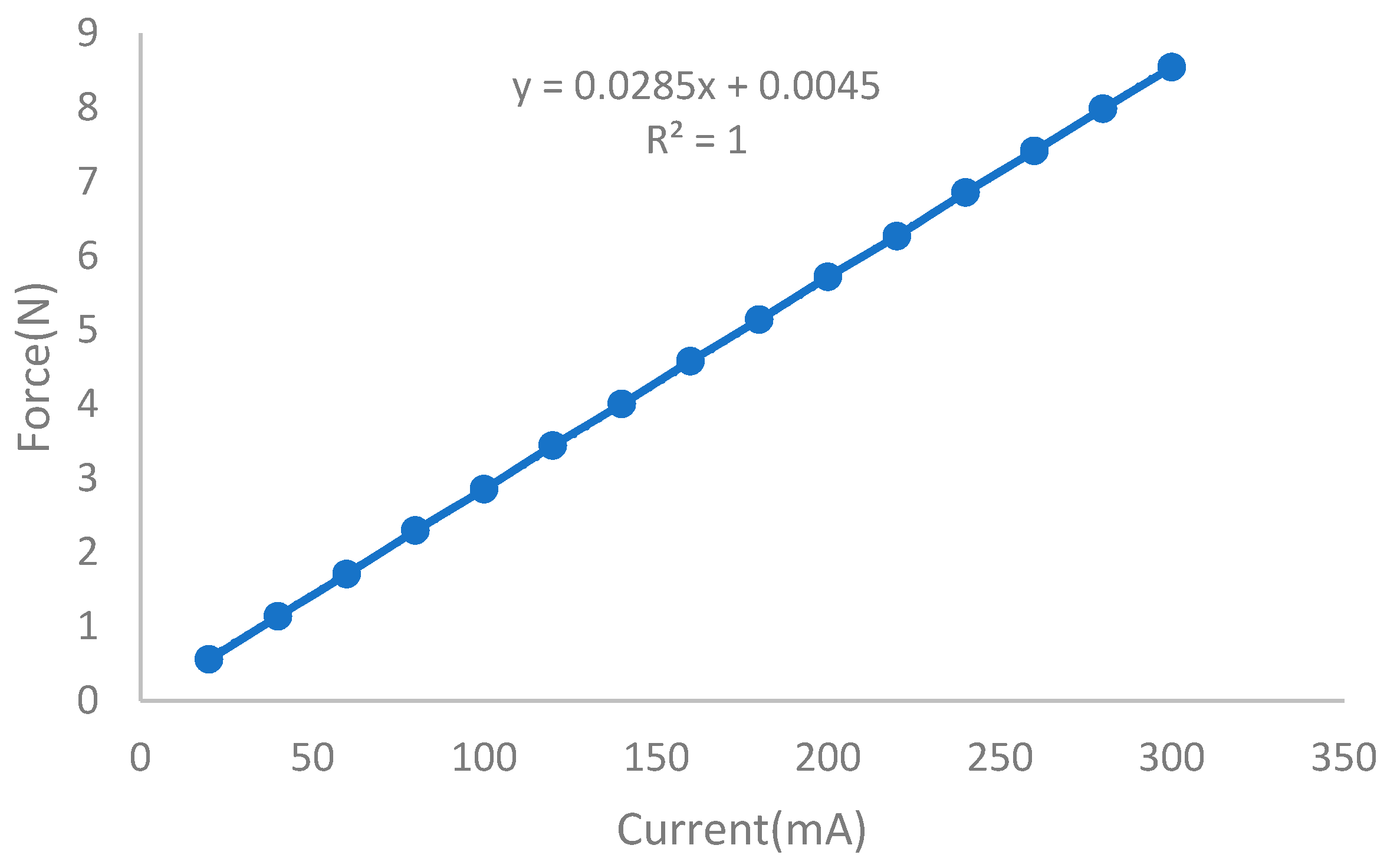
3.4. Force–Current Relationship of VCA
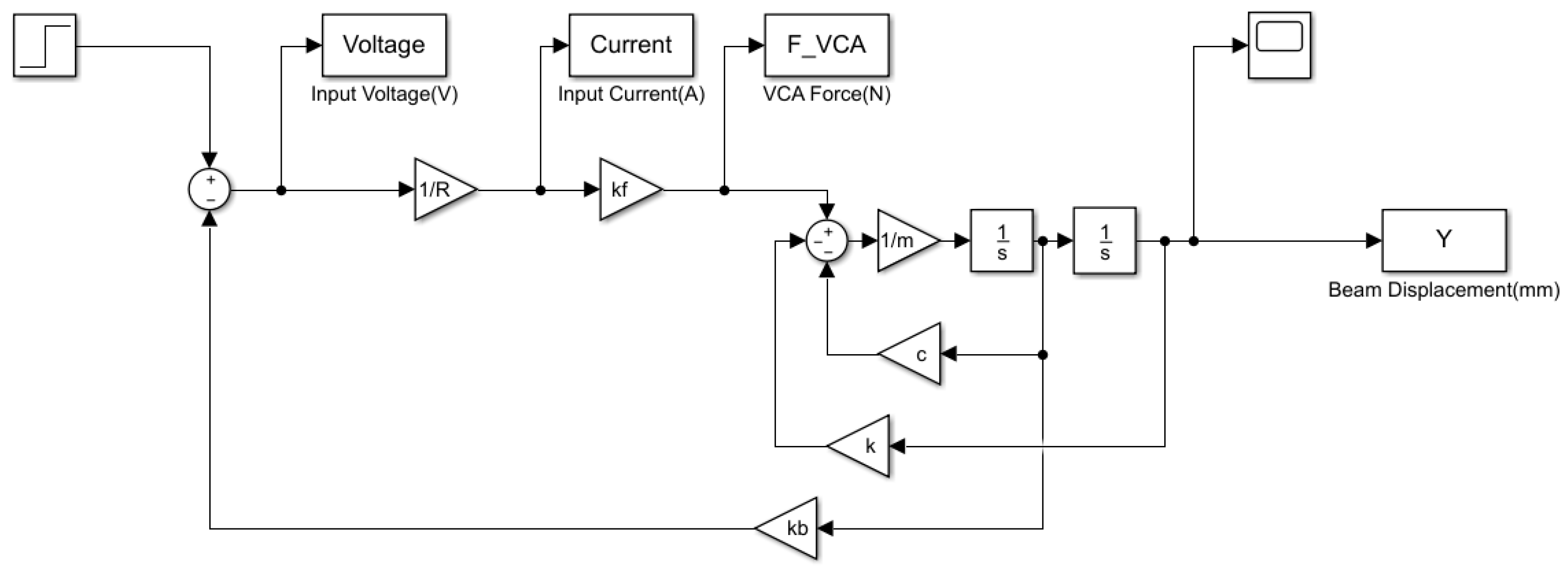
3.5. Simulink Model
4. System Identification
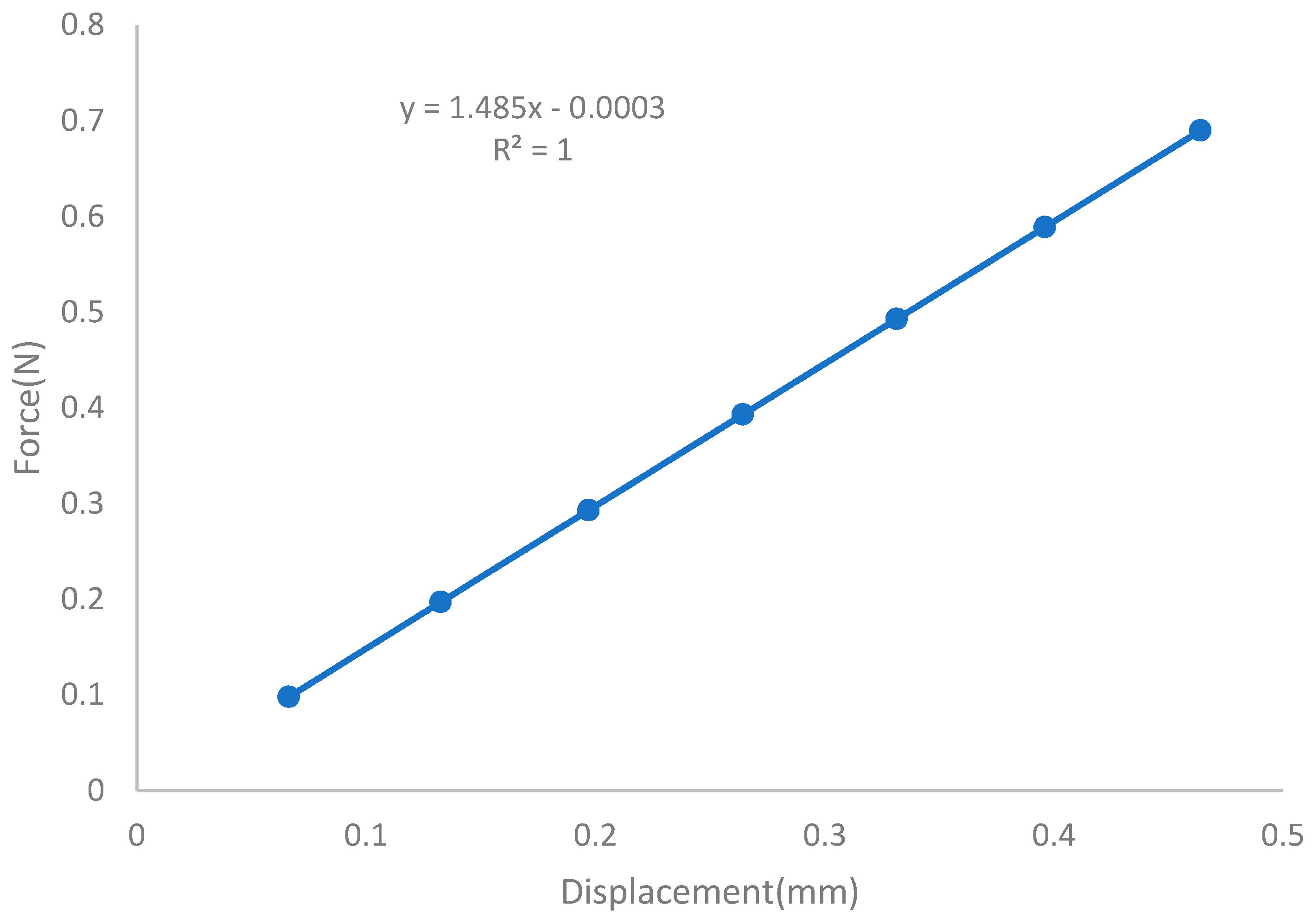
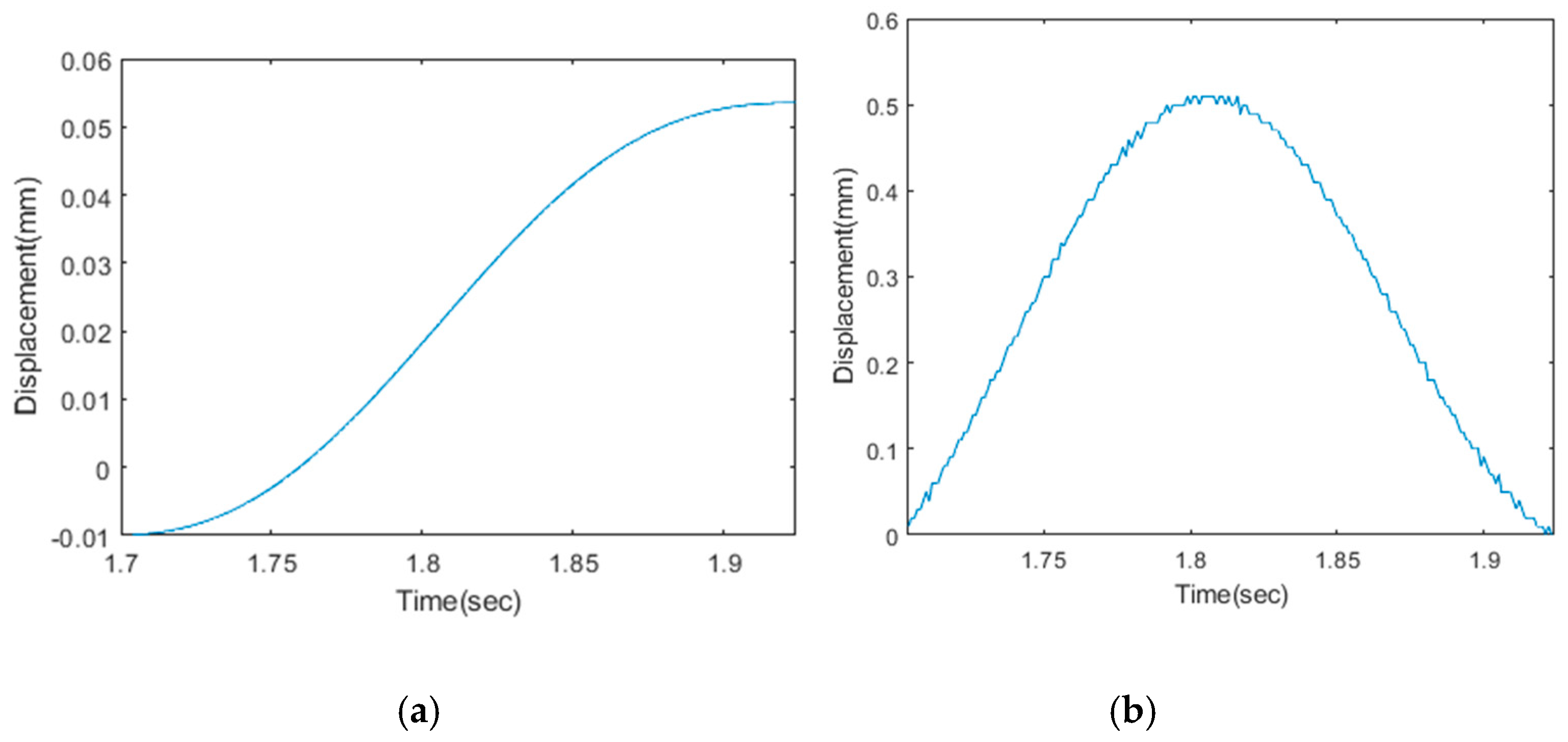
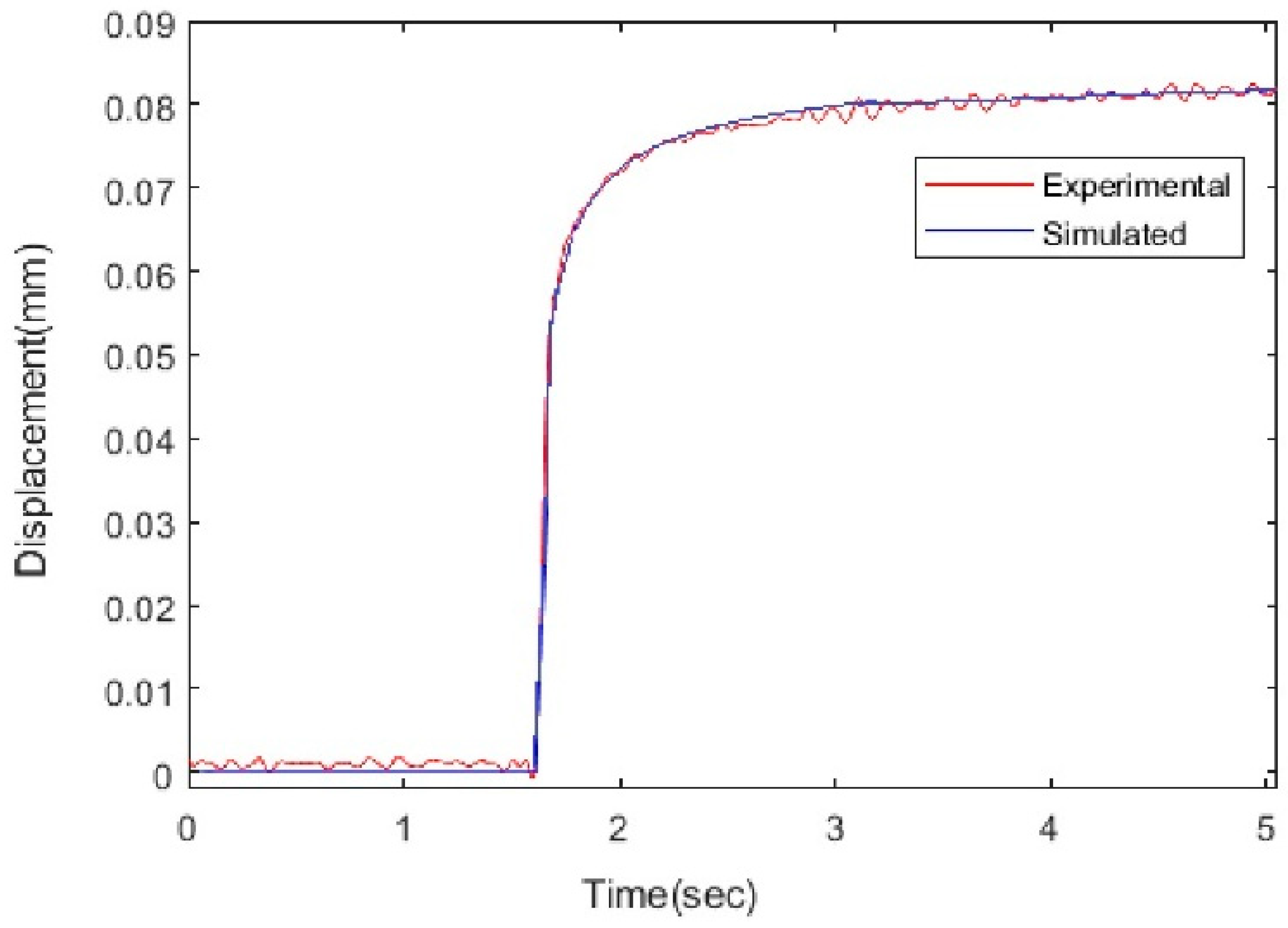
4.1. Spring Constant with VCA
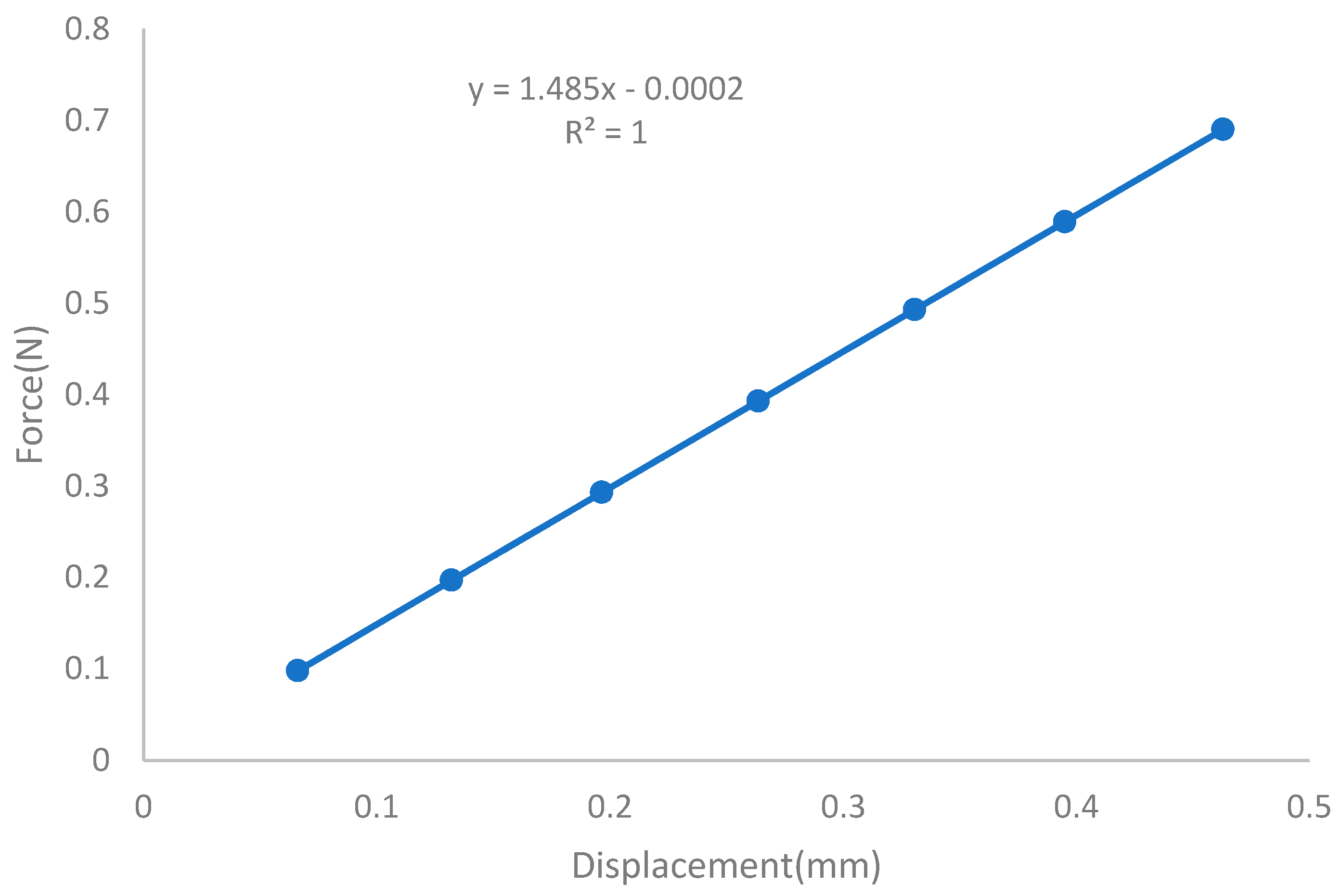
4.2. Spring Constant without VCA
4.3. Equivalent Mass
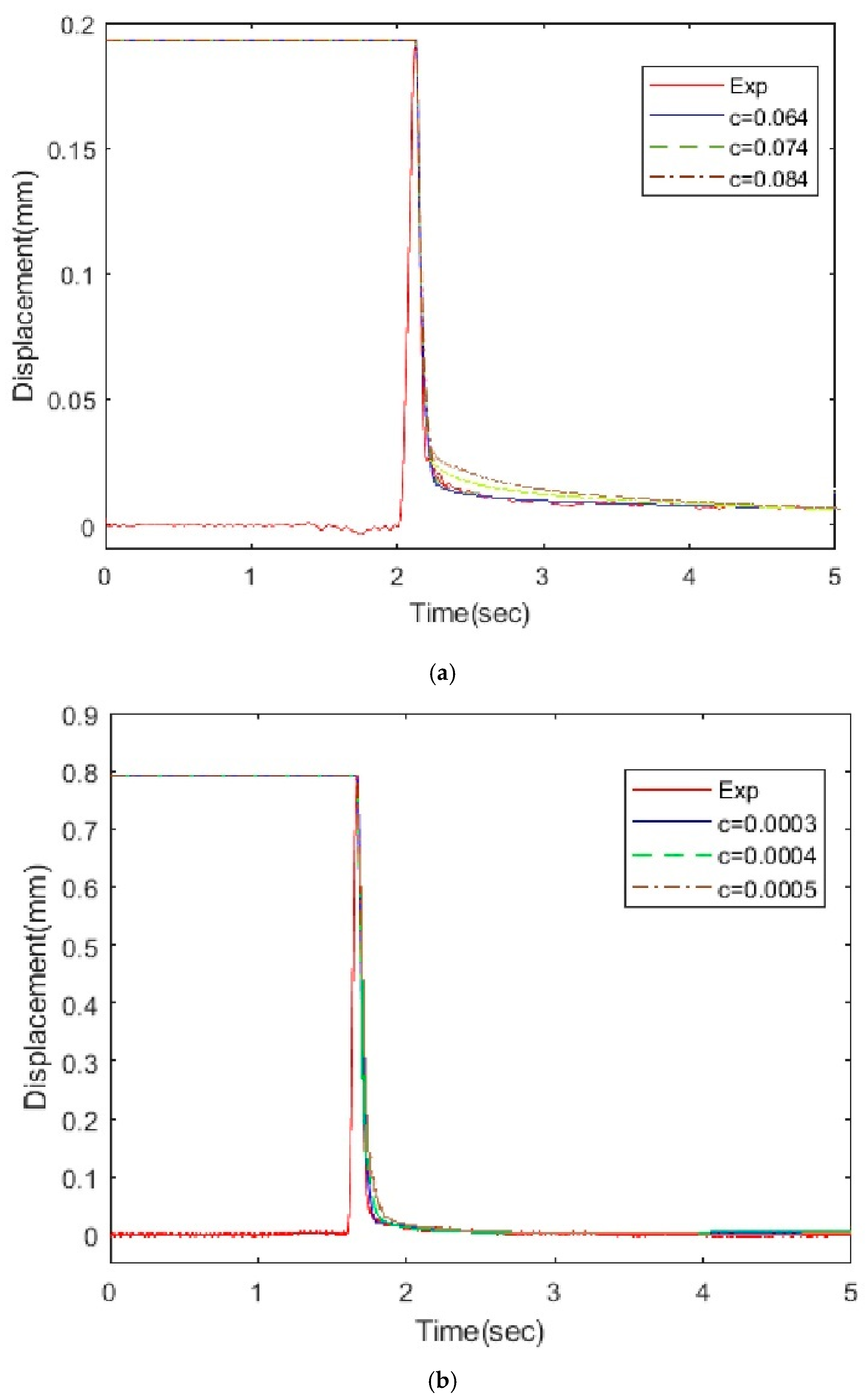
4.4. Damping Coefficient
5. Factors that Affect Performance of Voice-Coil Actuator
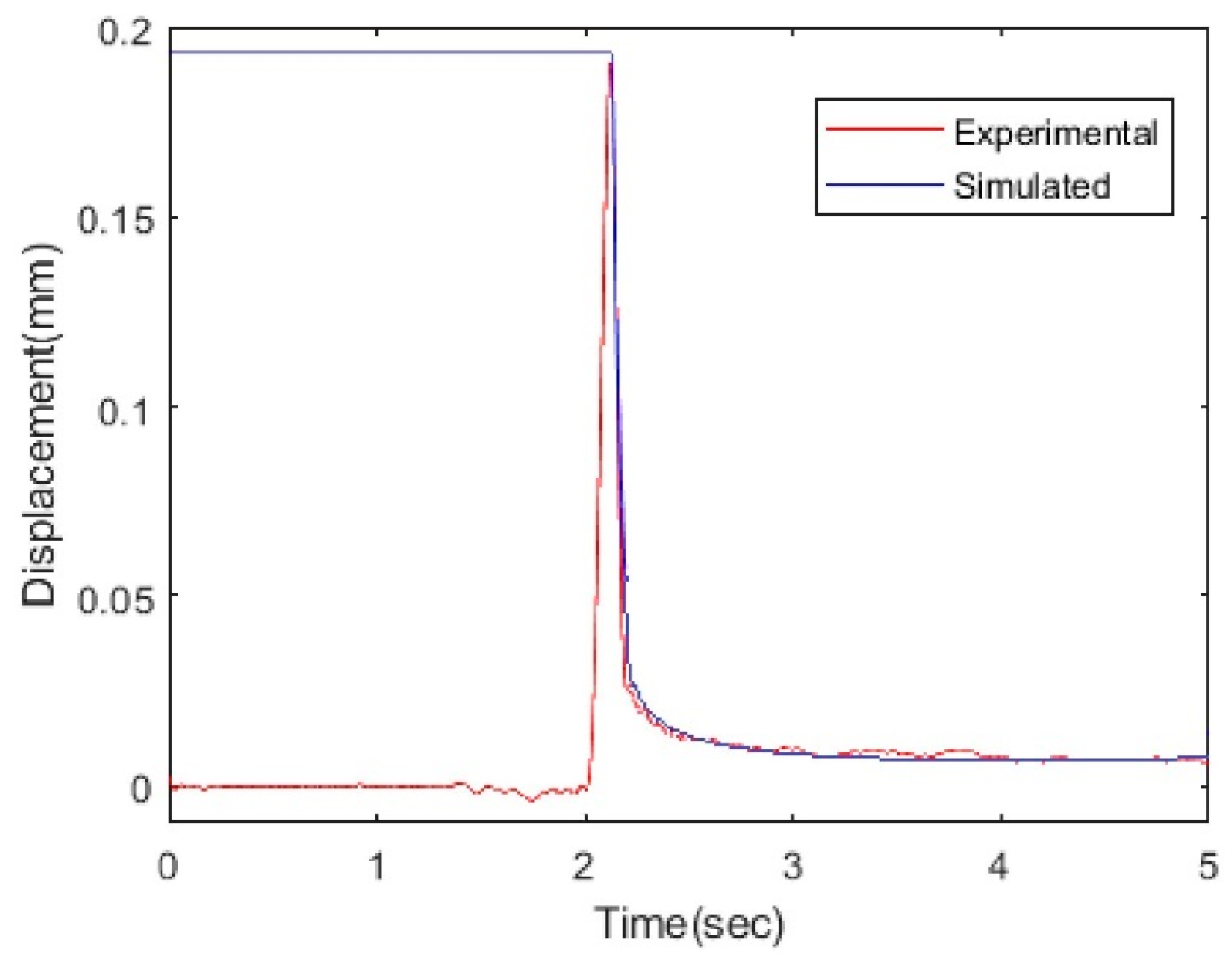
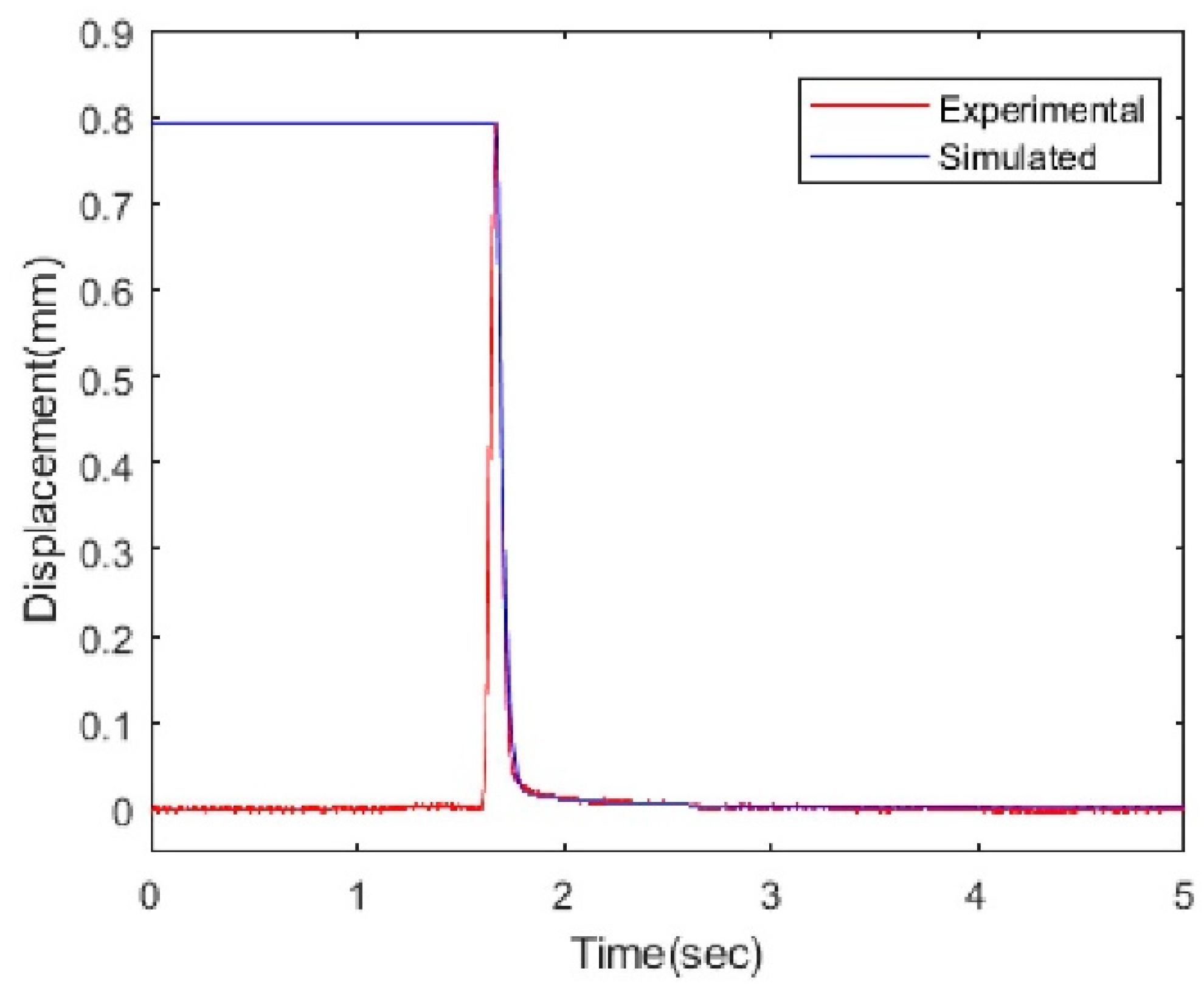
5.1. Effect of Electromagnetic Damping
5.2. Effect of Material Conductivity
5.2.1. Electromagnetic Force with VCA for Both Materials
5.2.2. Electromagnetic Force without VCA for Both Materials
6. Conclusions
- The cantilever beam with an attached bobbin acts as a conducting coil floating in a permanent magnet as the current is applied and the beam is returned to balance form by the EMFC, and not by applying any weight to balance the beam.
- From theory and simulations, the system identification was confirmed, experimentally determining which had the best agreement in each case, that is, with and without the VCA.
- The preliminary electromagnetic damping test was performed using step input current to record the step response with and without the VCA and by using different selected materials for the bobbin, namely, aluminum (conductor) and plastic (non-conductor). The electromagnetic damping force was more in the conductive case and less in the non-conductive case. Therefore, the non-conductive material was found to be the best choice to satisfy the fast time-response requirements; it also overcomes the electromagnetic damping by increasing the system performance.
- The conductivity of the material plays an important role that is directly related to the magnetic flux of the material; therefore, we selected a large-diameter coil because small-diameter coils were damaged as we applied more current.
- After conducting all the experiments, we concluded that a non-conductive material is best for our system and it will be applied to a balancing-type scale to improve the performance of the VCA.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Website Access Products. How do Balances and Scales Work? Available online: https://www.adamequipment.com/aeblog/how-do-balances-and-scales-work (accessed on 31 January 2020).
- Amthor, A.; Weiß, H.; Kaiser, I.; Rogge, N. Analysis, physically motivated modeling and system identification of electromagnetic force compensated balances (EMFC). Tech. Mess. 2015, 82, 393–401. [Google Scholar]
- Yamakawa, Y.; Yamazaki, T. Mathematical model of check-weigher with electromagnetic force balance system. Acta Imeko 2014, 3, 9. [Google Scholar] [CrossRef]
- Yamakawa, Y.; Yamazaki, T. Simplified Dynamic Model for High-Speed Checkweigher. Int. J. Mod. Phys. Conf. Ser. 2013, 24, 1360036. [Google Scholar] [CrossRef]
- Hwang, J.D.; Kwak, Y.K.; Jung, H.; Kim, S.H.; Ahn, J.H. Minimization of modeling error of the linear motion system with voice coil actuator. Int. J. Control Autom. Syst. 2008, 6, 54–61. [Google Scholar]
- Singh, R.; Sharma, M.; Singh, V.P. An experimental study of vibration control of cantilever beam using eddy current damper. Int. J. Appl. Eng. Res. 2012, 7, 1491–1496. [Google Scholar]
- Bae, J.S.; Hwang, J.H.; Park, J.S.; Kwag, D.G. Modeling and experiments on eddy current damping caused by a permanent magnet in a conductive tube. J. Mech. Sci. Technol. 2009, 23, 3024–3035. [Google Scholar] [CrossRef]
- Cheng, T.-H.; Oh, I.-K. Vibration suppression of beam by using magnet-coil. Model. Signal Process. Control Smart Struct. 2008, 6926, 692618. [Google Scholar]
- Bae, J.S.; Kwak, M.K.; Inman, D.J. Vibration suppression of a cantilever beam using eddy current damper. J. Sound Vib. 2005, 284, 805–824. [Google Scholar] [CrossRef]
- Matsuzaki, Y.; Ikeda, T.; Nae, A.; Sasaki, T. Electromagnetic forces for a new vibration control system: Experimental verification. Smart Mater. Struct. 2000, 9, 127–131. [Google Scholar] [CrossRef]
- Sodano, H.A.; Bae, J.S.; Inman, D.J.; Keith Belvin, W. Concept and model of eddy current damper for vibration suppression of a beam. J. Sound Vib. 2005, 288, 1177–1196. [Google Scholar] [CrossRef]
- Sodano, H.A.; Inman, D.J. Non-contact vibration control system employing an active eddy current damper. J. Sound Vib. 2007, 305, 596–613. [Google Scholar] [CrossRef]




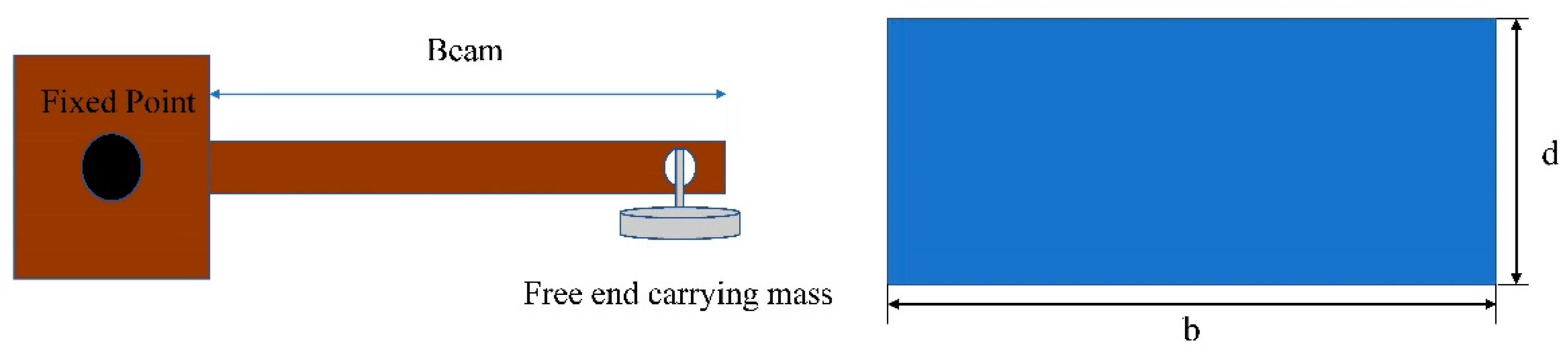


| Property | Value |
|---|---|
| Young Modulus of Cantilever Beam | |
| Density of Cantilever Beam | |
| Thickness of Beam | |
| Length of Beam | |
| Width of Beam | |
| Depth of Beam | |
| Number of coil turns | |
| Thickness of Copper Coil | |
| The conductivity of Copper Coil |
| Components | Specification | Values |
|---|---|---|
| Model | 0.0652 | |
| (Aluminum) (Plastic) | 0.3 | |
| 0.025 | ||
| 1.485 | ||
| VCA | 28.9 | |
| 24.535 | ||
| 28.46 | ||
| 100 |
| Current(mA) | Force(N) |
|---|---|
| 20 | 0.55917 |
| 40 | 1.13796 |
| 60 | 1.70694 |
| 80 | 2.29554 |
| 100 | 2.85471 |
| 120 | 3.44331 |
| 140 | 4.00248 |
| 160 | 5.58127 |
| 180 | 5.14044 |
| 200 | 5.71923 |
| 220 | 6.26859 |
| 240 | 6.85719 |
| 260 | 7.41636 |
| 280 | 7.98534 |
| 300 | 8.54451 |
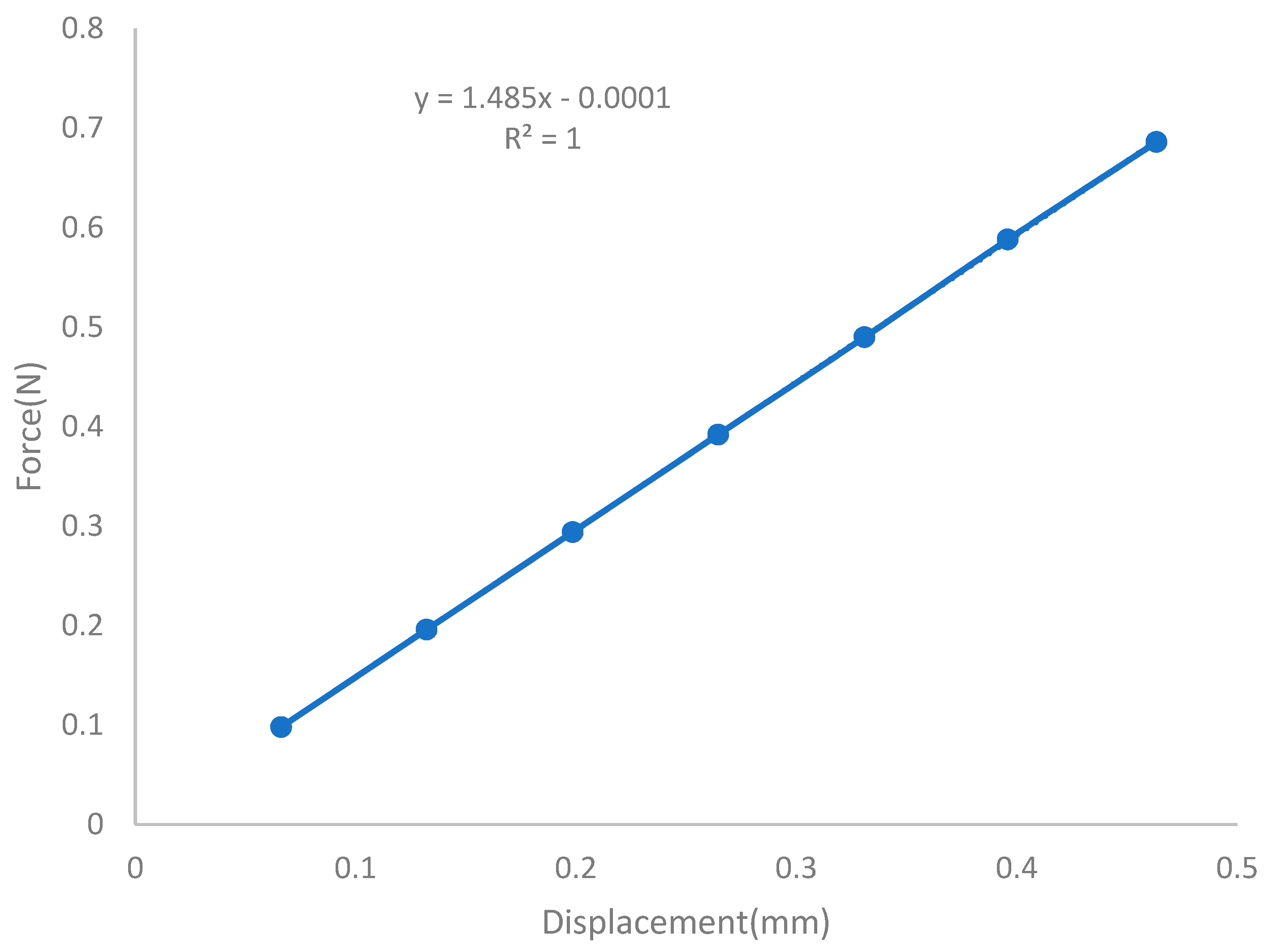
| Voltage | Current | Force | Laser Point Deflection Measured Values | Laser Point Deflection Theoretical Values | Loading Point Deflection Measured Values | Loading Point Deflection Theoretical Values |
|---|---|---|---|---|---|---|
| 0.1 | 0.0034 | 0.098 | 0.0091 | 0.0090 | 0.0663 | 0.0661 |
| 0.2 | 0.0069 | 0.197 | 0.0183 | 0.01813 | 0.1325 | 0.1321 |
| 0.3 | 0.0103 | 0.293 | 0.0272 | 0.02697 | 0.1970 | 0.1965 |
| 0.4 | 0.0138 | 0.393 | 0.0367 | 0.03618 | 0.2643 | 0.2636 |
| 0.5 | 0.0173 | 0.493 | 0.0462 | 0.04538 | 0.3315 | 0.3307 |
| 0.6 | 0.0207 | 0.589 | 0.0551 | 0.05422 | 0.3961 | 0.3951 |
| 0.7 | 0.0242 | 0.690 | 0.0642 | 0.06352 | 0.4640 | 0.4629 |
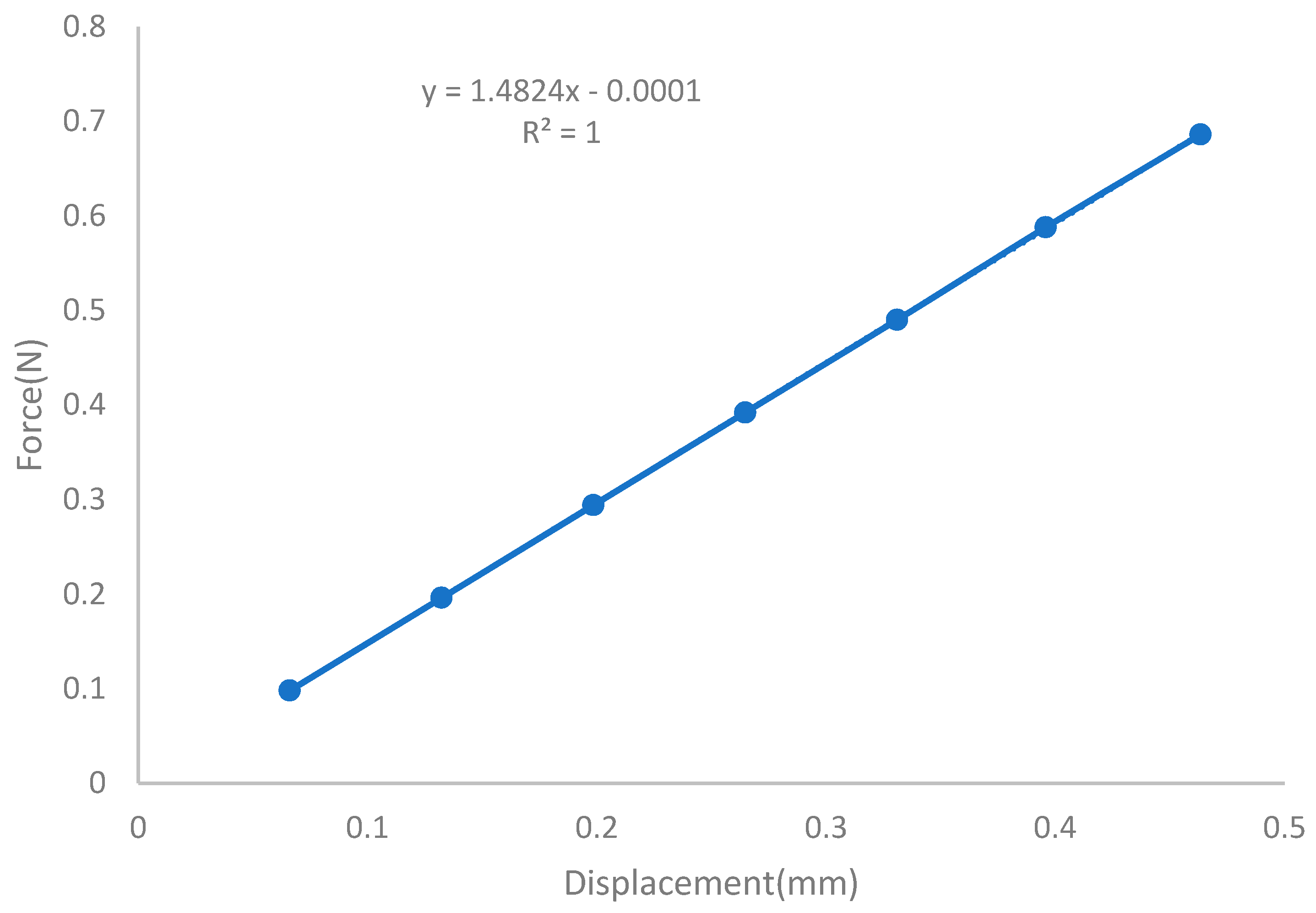
| Weight | Force | Experimental Deflection | Theoretical Deflection |
|---|---|---|---|
| 0.01 | 0.098 | 0.0662 | 0.0661 |
| 0.02 | 0.196 | 0.1322 | 0.1323 |
| 0.03 | 0.294 | 0.1985 | 0.1985 |
| 0.04 | 0.392 | 0.2645 | 0.2647 |
| 0.05 | 0.490 | 0.3309 | 0.3309 |
| 0.06 | 0.588 | 0.3958 | 0.3958 |
| 0.07 | 0.686 | 0.4633 | 0.4633 |
| Properties | Values |
|---|---|
| Conductivity of Copper Coil | |
| Magnetic Flux Density | |
| Length of Coil | |
| Number of Turns | |
| Thickness of Wire | |
| Permeability | |
| Electrical Conductivity of Aluminum | |
| Electrical Conductivity of Plastic | |
| Relative Velocity | |
| Electromagnetic Force (aluminum) | |
| Electromagnetic Force (Plastic) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdullah; Ahn, J.-H.; Kim, H.-Y. Effect of Electromagnetic Damping on System Performance of Voice-Coil Actuator Applied to Balancing-Type Scale. Actuators 2020, 9, 8. https://doi.org/10.3390/act9010008
Abdullah, Ahn J-H, Kim H-Y. Effect of Electromagnetic Damping on System Performance of Voice-Coil Actuator Applied to Balancing-Type Scale. Actuators. 2020; 9(1):8. https://doi.org/10.3390/act9010008
Chicago/Turabian StyleAbdullah, Jung-Hwan Ahn, and Hwa-Young Kim. 2020. "Effect of Electromagnetic Damping on System Performance of Voice-Coil Actuator Applied to Balancing-Type Scale" Actuators 9, no. 1: 8. https://doi.org/10.3390/act9010008
APA StyleAbdullah, Ahn, J.-H., & Kim, H.-Y. (2020). Effect of Electromagnetic Damping on System Performance of Voice-Coil Actuator Applied to Balancing-Type Scale. Actuators, 9(1), 8. https://doi.org/10.3390/act9010008





