1. Introduction
The micropositioning stage plays an important role in today’s engineering applications. Differently from conventional stages based on rigid-body joints, the flexure-based compliant mechanisms deliver strokes by elastic deformations of the material. The micropositioning stage based on flexure hinges can provide an output movement with desirable properties of no wear, no friction, no backlash, vacuum compatibility, repeatable motion, and low cost [
1,
2,
3,
4,
5,
6]. Thus, it has been widely used in scanning probe microscopy, precision alignment, cell microinjection, etc.
In practical applications, a micropositioning stage with two degrees-of-freedom (2-DOF) of translational motion, high precision, and a large range of motion has a growing demand in various fields in recent years. According to previous research, there are two kinds of kinematic structures which can provide multi-dimensional motion, i.e., the serial-kinematic structure [
7,
8,
9,
10] and the parallel-kinematic structure [
11,
12,
13,
14]. In earlier works, the serial-kinematic structure was widely adopted. The reason lies in that the serial-kinematic category has a simple structure with an easy control strategy, as the 2-DOF movements can be handled separately. As the demand of accuracy becomes higher, parallel-kinematic structure has attracted more attention from researchers, as it provides lower inertia, smaller cumulative error, and higher resonant frequency [
15,
16]. With the moving platform directly connected by multiple limbs, the parallel-kinematic structure can achieve identical dynamic behavior in the two directions. Concerning the actuation aspect, the voice coil motor (VCM) is widely used for driving micropositioning stages, because it can provide large linear stroke, large acceleration, and infinitesimal resolution compared with the piezoelectric actuator (PZT) [
15,
16,
17,
18]. Therefore, the VCM is capable of delivering a centimeter-level stroke along with a high resolution.
One of the desired performances for a flexure-based xy micropositioning stage is compact physical size with a large motion stroke. The main challenge is that those two criteria are contradictory. A large motion stroke requires a narrower and longer leaf flexure, which goes against with the criterion of compact physical design. Moreover, an excessively slender leaf flexure results in low resonant frequency, and the minimal parameters of leaf flexure are limited by manufacturing. There were several strategies presented to overcome this issue in previous work. Based on multistage compound parallelogram flexures (MCPFs), Xu [
11] presented an xy micropositioning stage with a two-layered structure, which is more compact than the designs with one layer. However, if too many MCPFs are used in the design, the space of one layer may not be taken advantage of fully. Wu and Xu [
17] proposed a more compact xy micropositioning stage, which is composed of bridge-type amplifiers and right-circular flexure hinges. It combines the compactness and advantages of parallel-kinematic structure well, but the motion stroke is limited by its piezoelectric actuator. Liu et al. [
15] placed the MCPFs on the z-axis rather than on the xy plane, making it more compact on the xy plane with less extra structures. However, as the special structure limits the selection of VCMs, a complex driving program and analytical modeling need to be solved to adapt the special structure. Moreover, the majority of the available xy micropositioning stages are designed with solid output platforms [
19,
20]. However, such designs cannot be conveniently used under an inverted microscope or an upright microscope (common setup in biological micromanipulation) with a bottom light source.
To this end, a novel xy micropositioning stage is presented in this paper, which offers a large, hollow output platform. It has a parallel-kinematic structure and is actuated by two VCMs. The novel design takes full advantage of the space on the xy plane and z-axis, and it has a simple structure actuated by VCMs for achieving a large motion stroke. The stroke structure and motion-decoupling structure are the same to facilitate straightforward analytical modeling, and a symmetrical structure is adopted owing to its motion stability. It is notable that the proposed design adopts four identical layers of flexure structures, which facilitates the fabrication process and improves the compactness of the xy stage in plane. The reported structure provides a larger platform than previous designs, along with larger strokes in x and y-axes. The whole structure is compact enough for use with a small microscope [
5]. The xy stage is designed with one of the most fundamental structures as the basic structure along with novel assembly method to achieve the desired function.
The mechanism design and analytical modeling are presented in
Section 2 and
Section 3, respectively. The simulation study is described in
Section 4; the simulation evaluation revealed the promising performance of the designed xy stage and also verified the analytical model. The difference between those results was analyzed in detail. Moreover, a comparison study with the previous designs was carried out and is described in
Section 5. Finally,
Section 6 concludes this paper.
2. Mechanism Design
Mechanism design of the proposed xy stage is presented in this section. The designed xy stage is constructed by four basic structures, two groups of fixtures, a platform, and a base. In this work, the stage mechanical design and decoupling mechanical design have the same structure (i.e., basic structure), which offers convenience for manufacturing. The symmetrical structure also provides benefits on stable and compact design. The details of the structure are presented in the following.
2.1. Basic Structure and Fixture
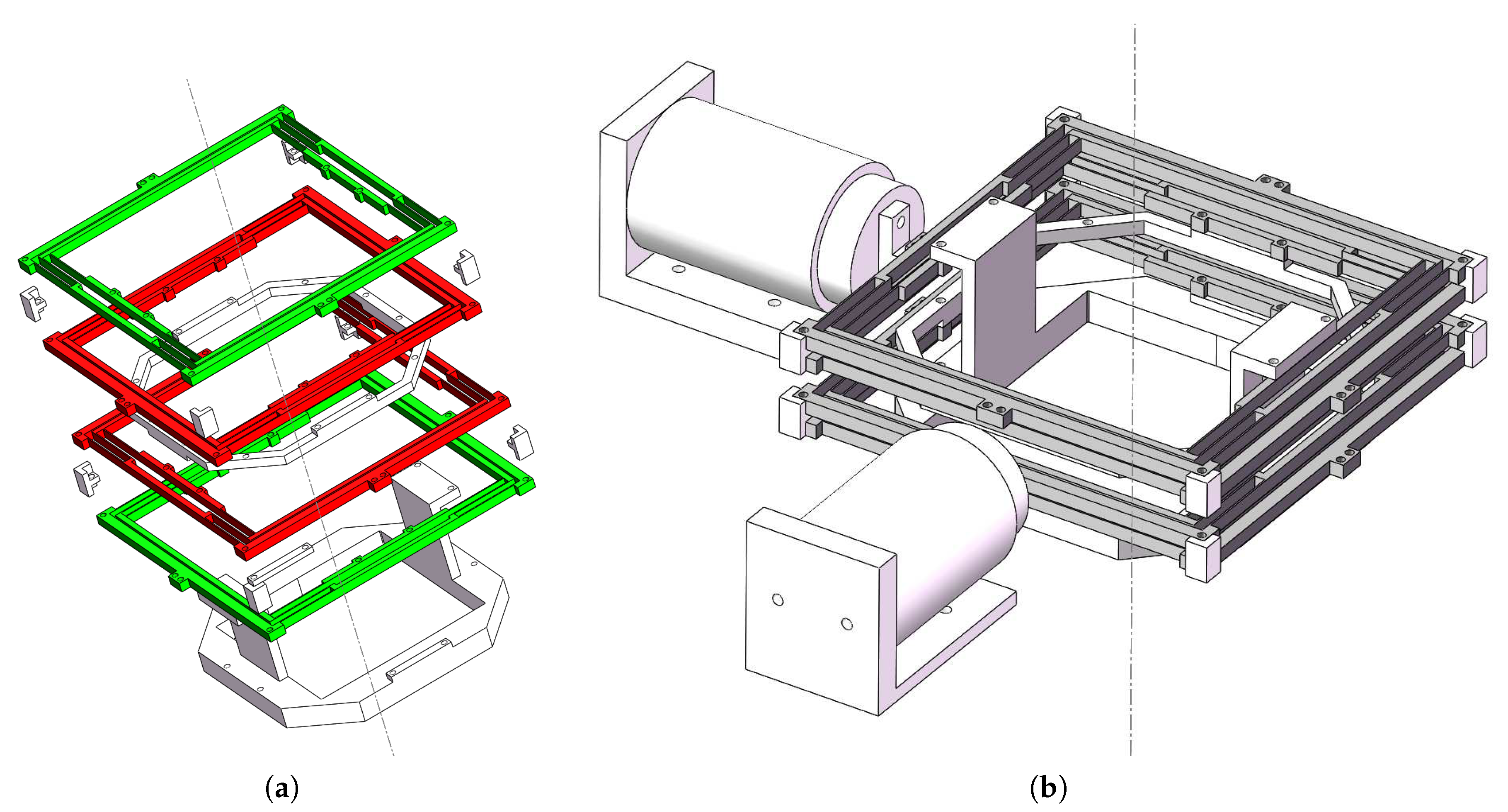
The basic structure is shown in
Figure 1a. This structure provides a large stroke by employing multistage compound parallelogram flexures (MCPF) [
11]. As an improved design of the compound parallelogram flexures (CPFs), the MCPF has a large range of motion, according to previous research. MCPF meets the requirement of compactness and adapts to practical manufacturing. The range of motion of the MCPF depends on the ranges of motion of the basic modules (CPF) and the number
N of basic modules, as shown in
Figure 1b.
The basic structure in
Figure 1a has two MCPFs with 1.5 basic modules. Differently from the intuitive structure of MCPF, those two MCPFs were designed to tackle the following three issues.
(a) To make a large output platform, the MCPFs are extended horizontally. In this way, the size of the platform can reach up to 100 × 100 mm2.
(b) The module number N of the MCPF is not an integer. This design involves half of CPF, which can reverse the direction of output motion. In this design, reversing the output motion direction improves the compactness effectively. Here, 1.5 basic modules provide enough motion, as the range of motion also depends on CPF. The ranges of motion of CPFs can be improved by using narrower and longer leaf flexures, as there is still enough space for them. The parameters of this part will be presented in the simulation study later. All of the motions are realized by leaf flexures of basic structures and all basic structures are of the same design.
(c) These two MCPFs are connected with each other by leaf flexures of secondary modules, which are designed to overcome the undesirable bending flexures. Once fixing the output end of the basic structure, it provides a force along the y-axis. The secondary module of leaf flexures on the top bends inward, and the secondary module leaf flexures on the bottom will bend outward. It is easy to find that the directions of bending tendency of the two MCPFs are always contrary. Hence, the connection can overcome the undesirable bent flexures and ensure a translational displacement.
When a torque is exerted to the basic structure, it also causes undesirable bent flexures. To tackle this issue, fixtures and a novel assembly method are used. As per previous research on xy stages, the structures can eliminate the torque by introducing a square-shaped frame. In this design, the square frame is combined with two basic structures and fixtures. The fixture is shown in
Figure 2a. The special structure of the fixtures locks the two basic structures, which has favorable effect on eliminating the torque. In this design, there are four layers of basic structures. Using the beams of MCPFs to constitute frames for leaf flexures reduces the weight of the whole design dramatically, as compared with that using frames directly. In this way, the assembled stroke structure for one axis is shown in
Figure 2b.
2.2. Platform and Base
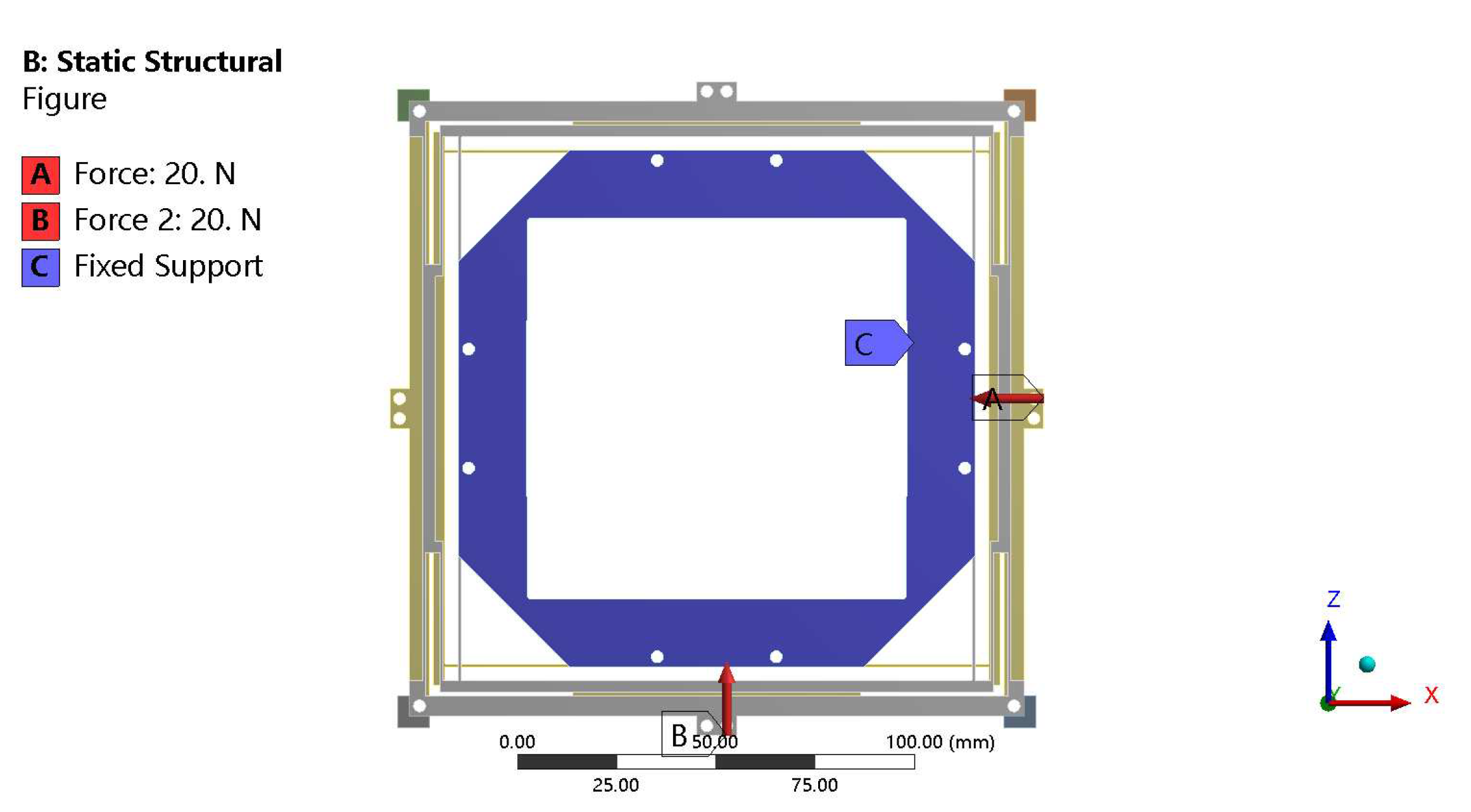
The output platform is designed as a large hollow stage, which adapts for experimental use under a microscope, including cell microinjection and material micromanipulation. The platform is the output end of this design. It has 12 fixing points; four points are used for the experimental stage, four for the x-axis stroke structure, and four for the y-axis stroke structure, as shown in
Figure 3. The gaskets over fixing points of the platform bond the x and y-axis stroke structures directly. The motions of these two stroke structures are transmitted to the output platform, and the pure motions on x-axis and y-axis are compounded by the platform.
The base design is shown in
Figure 4. There are four fixing points to mount the design on the experimental bench. Like the platform, the base has gaskets to bond with x and y-axis stroke structures.
2.3. Stage Assembly
The assembled stage is shown in
Figure 5. The base is the frame for the whole design, which provides support to other structures. The stroke structure at the bottom is responsible for the motion on the x-axis, while the stroke structure at the top is for the motion on the y-axis. The platform is fixed between the two stroke structures. To present the operating principle of the stage, the four layers of basic structures are numbered from bottom to top as 1st, 2nd, 3rd, and 4th layer, respectively. From the rule of these serial layers, the 1st and 2nd layers constitute the x-axis stroke structure, while the 3rd and 4th layers constitute the y-axis stroke structure. The 1st and 4th layers are connected with the base directly, so are called stroke mechanical designs. These two layers provide the strokes relative to the static base. Then, the strokes are transmitted to the decoupling mechanical designs, i.e., the 2nd and 3rd layers, by the group of fixtures. The decoupling mechanical designs are connected to the platform, and the final motion output is given by the platform. As shown in
Figure 2b, when defining the red layer as the decoupling mechanical design and the green layer as the stroke mechanical design, the operating principle is clear to observe. The fixed points connect the static base, the input point connects the VCM, and the output points connect the platform; refer to
Figure 5a.
As shown in
Figure 5b, the linear strokes are provided by two VCMs connecting to the decoupling mechanical design, whose directions are orthometric to the motion direction of the MCPFs on the 2nd and 3rd layers. As presented earlier, the beams of the two layers can be treated as a square frame. The linear stroke on the decoupling mechanical design will be received by the stroke mechanical design. In this way, the VCMs do not suffer from transverse displacement.
The mechanical design and operating principles have been presented in this section, and analytical modeling is introduced in the following section.
3. Analytical Modeling
In this section, analytical modeling of the xy micropositioning stage is presented. According to the description in mechanism design, there is only one structure, i.e., the basic structure, which is used to realize the function of the stage. As the basic structure is constituted by MCPFs and MCPFs generate large elastic deformation through the leaf flexures, the modeling is most relevant to the leaf flexure [
11].
In previous research, the force–displacement relationship of MCPF has been given; it must be presented in this section for the mechanism design. After considering the boundary conditions of the deformation, the stiffness of MCPF can be determined as
where
l and
b denote the length and width of the leaf flexure, while
h and
E are the thickness and Young’s modulus of the material, respectively.
As the total deformation of output platform on each axis is uniformly distributed on each flexure hinge of the MCPF, the deformation of each hinge is relatively small. Therefore, the nonlinear stiffness of MCPF under large deformation is ignored in this paper. Actually, if each flexure hinge undergoes large deformation, the equation of equivalent stiffness Equation (
1) does not hold, as the stiffness is nonlinear. The nonlinear stiffness modeling is beyond the scope of this work.
From Equation (
1), the maximum translation of one-sided design is calculated further as
where
is the yield stress of the material. From Equation (
2),
is positively related to
l and
N, and negatively related to
h. That means that a larger length and smaller width of the leaf flexure provide larger stroke. In practical applications, the parameters
l and
h are limited by the manufacturing tolerance, while
N is limited by the compactness requirement. As
N increases, the size and weight of the stage will increase dramatically, because the beam of the additional CPF becomes longer.
also depends on the space between different modules in one MCPF, which is not expressed in Equation (
2) directly.
In this design, the module number of MCPF was chosen as
for illustration. Thus, the sum of two-sided maximum translation is
Considering safety and a practical situation, the assigned maximum translation should be less than . After confirming the range of the assigned translation, the maximum driving force to generate the motion can be calculated accordingly.
The stiffness of the basic structure should be determined. As the structure is constituted by two MCPFs, the stiffness of the basic structure is
. According to the section of mechanism design, on one axis (x or y-axis), there is one stroke mechanical design for this axis and decoupling mechanical design for the other axis. The conditions are enough to determine the stiffness of the stage on one axis as follows.
The maximum driving force occurs on one-sided maximum translation, which is half of
. Considering Equation (
2),
is calculated by
In this design, to provide enough driving force, the VCMs are selected to provide larger maximum force than .
For the three most important parameters in this study, which are the maximum translation on one side (x), safety factor (s), and resonant frequency (f), the equations are derived in the following.
Considering Equations (
1) and (
4), the equation of maximum translation on one side should be presented as
For the safety factor, considering Equations (
1) and (
2),
satisfies the equation
which proves that
in this structure. The equation of
s is as follows.
Define
and
as the deformations on two axes, respectively. Considering the motion decoupling of mechanical design, the mechanical system can be simplified as a two-dimensional mass-spring system. Thus, the free motion equation (in the absence of external forces) is shown as follows:
where
K can be calculated by Equation (
4), and
m is the equivalent mass of the moving block for the stage. Then, the resonant frequency has the relationship with the parameters given below.
Equations (
6), (
8), and (
10) will be used to calculate the analytical results of the design for comparison study with the simulation results in the next section.
6. Conclusions
An xy flexure micropositioning stage with a large hollow platform has been presented in this work, which has a parallel-kinematic structure and is actuated by two VCMs. The proposed stage has four layers of structure, which greatly reduces the dimensions on the xy plane. By separating the stroke mechanical design and decoupling mechanical design, it provides convenience for further experimental study and potential commercial use. The simulation result showed that the hollow of the platform reaches up to 95 × 95 mm
2 and the range of motion reaches up to 7.0873 × 7.0873 mm
2. The large hollow platform, large range of motion, and compact structure of the design ensure that it can be used directly in practical applications with a microscope. Moreover, the novel structure, which takes full advantage of MCPF beams, is able to reduce the weight, increase the frequency, and save space for the design effectively. Considering
Table 3, the range of motion can be further improved, as the maximum actuation force is obviously smaller than in previous designs. This design has advantages on integrated performance of compactness, decoupling, range of motion, safety factor, and natural frequency as compared with previous designs. In the future work, an experimental study of the xy stage will be produced. This design which has better performance and is better at adapting to practical manufacturing will be confirmed by optimization, and the parameters of the design will be verified by experiments in practice.