Optimal Force Allocation and Position Control of Hybrid Pneumatic–Electric Linear Actuators
Abstract
:1. Introduction
2. Plant Dynamics
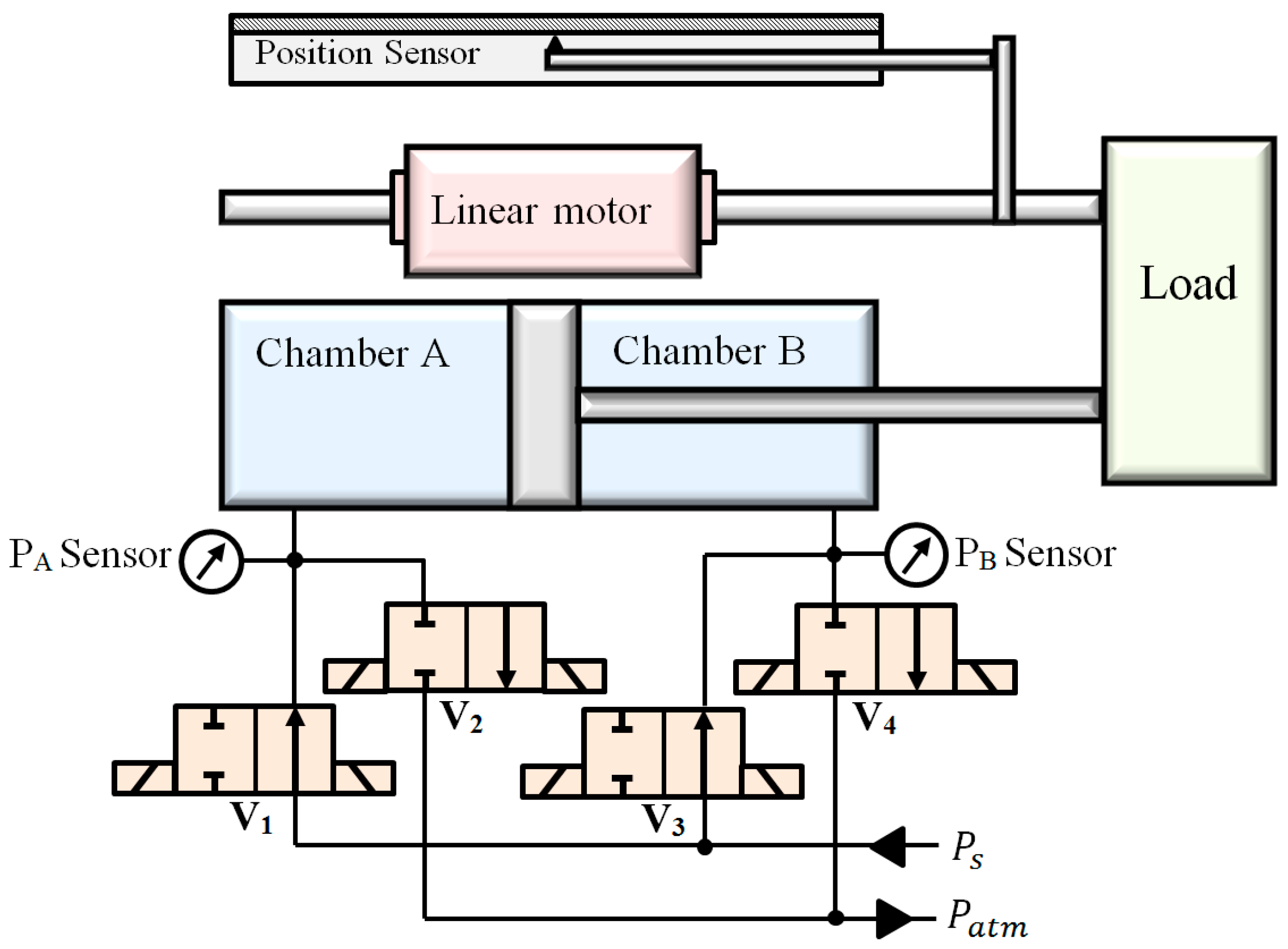
2.1. Plant Structure
2.2. Mathematical Model
3. Controller Design
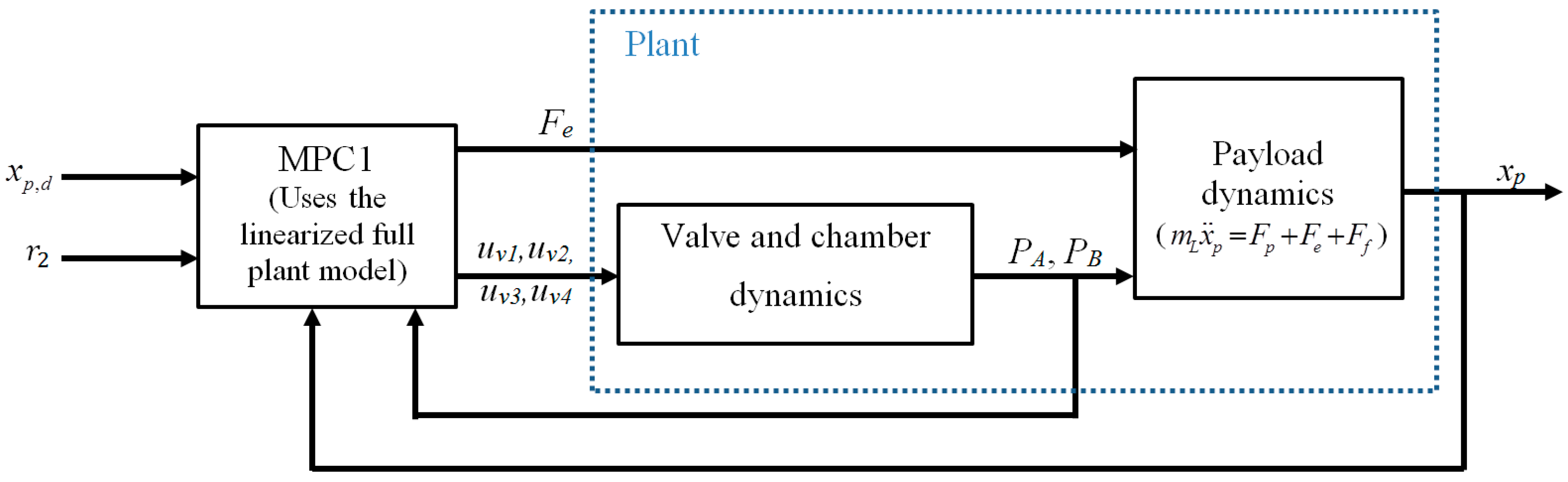
3.1. MPC1: Controller with Linearized Full Plant Model
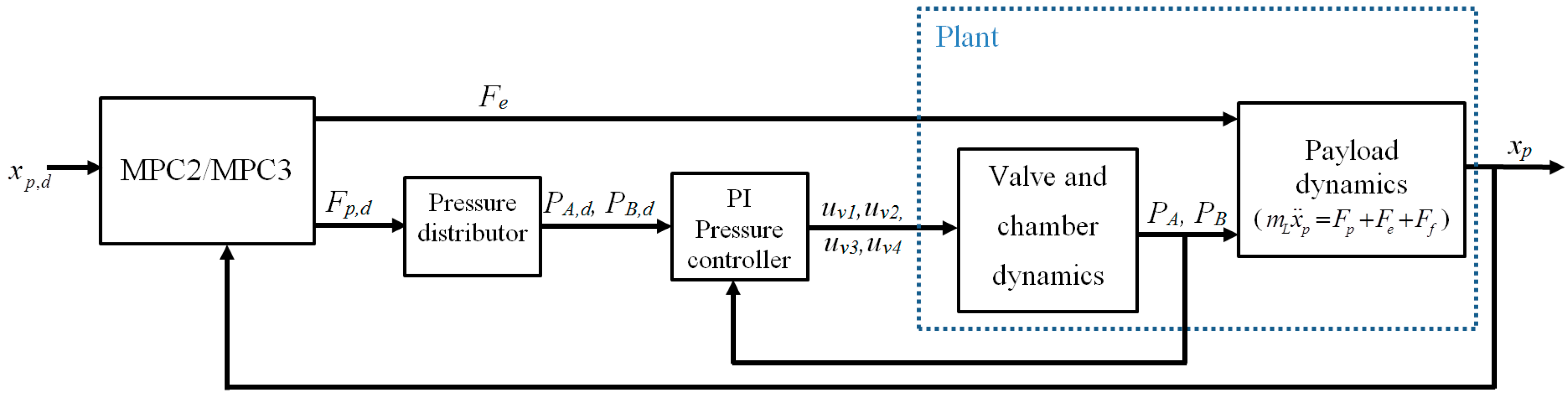
3.2. MPC2: Simplified Two-Loop Controller
3.3. MPC3: Modified Two-Loop Controller
3.4. Linear Two-Loop Controller
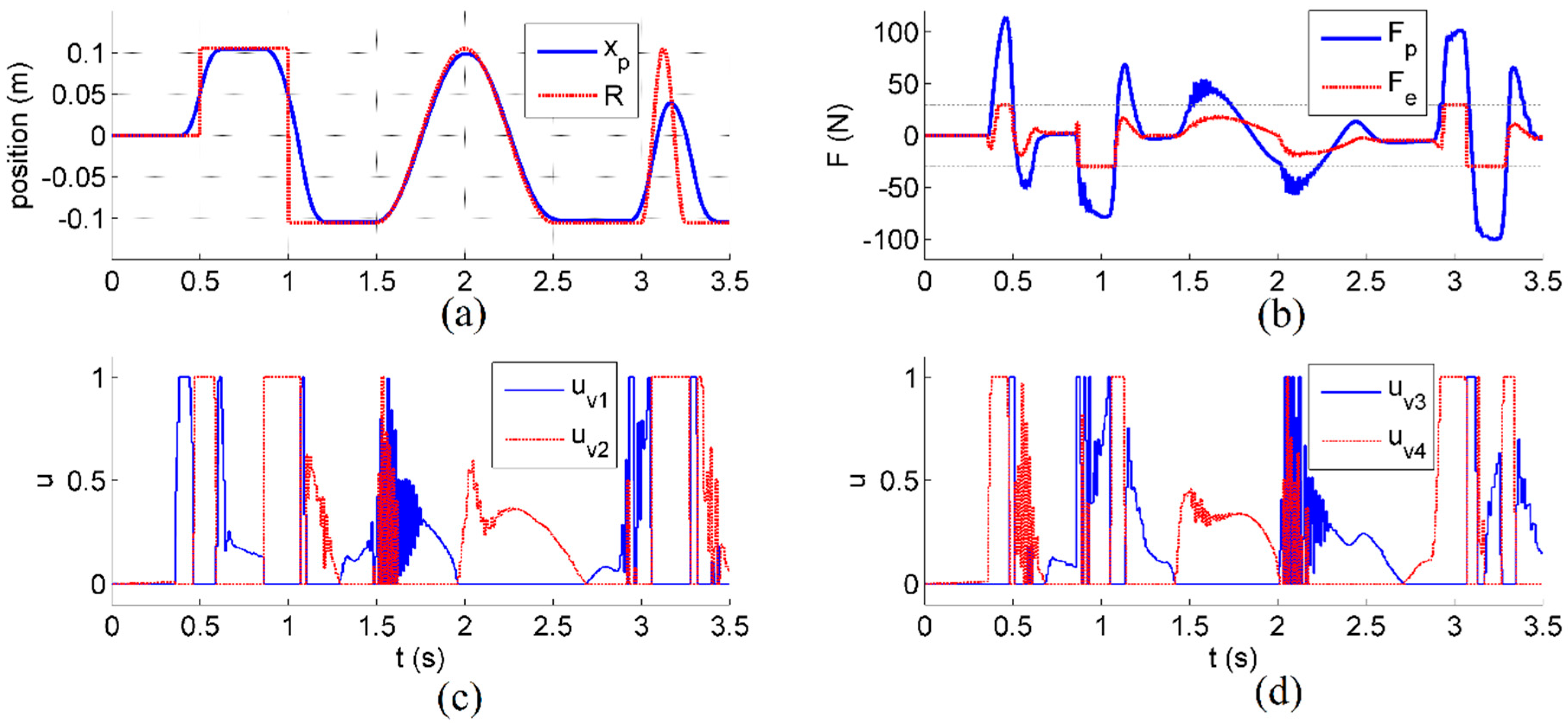
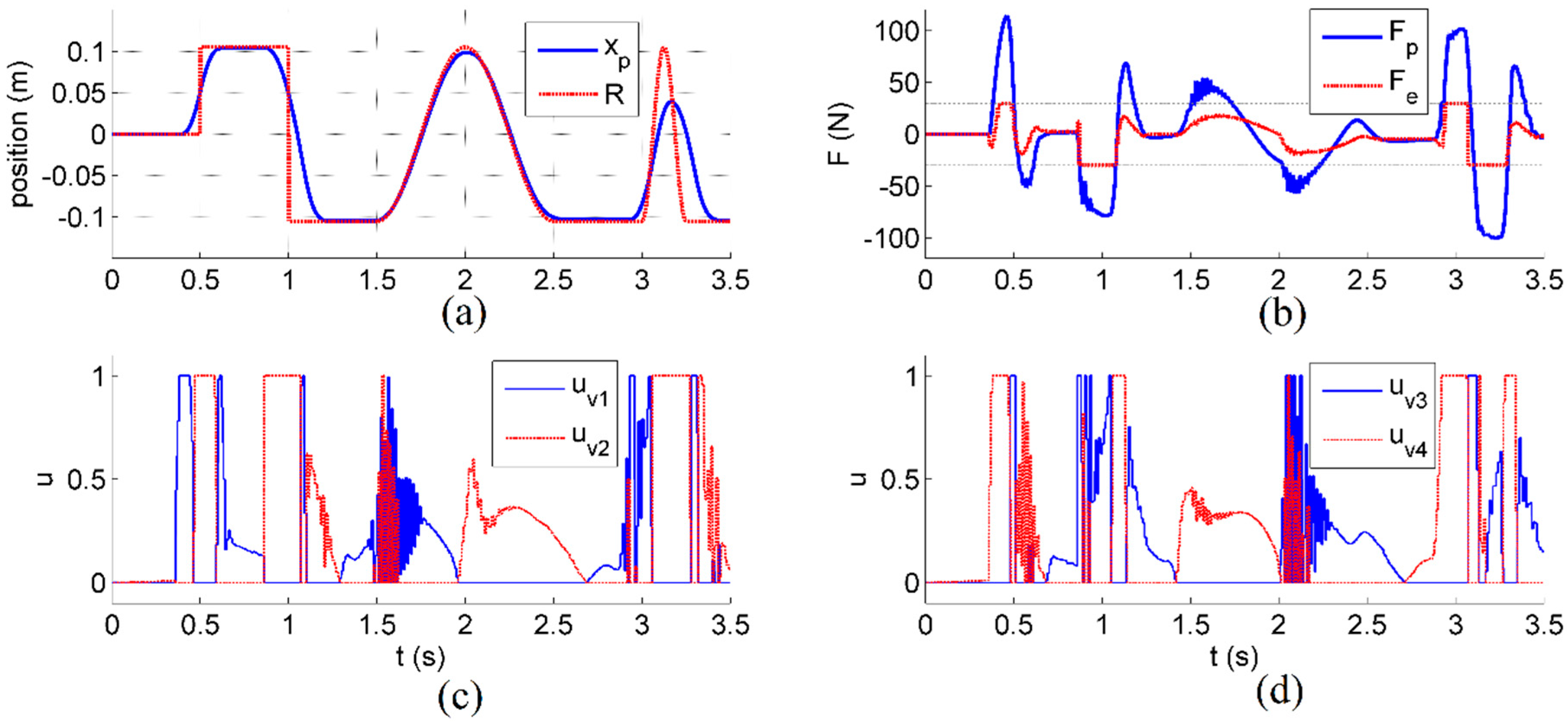
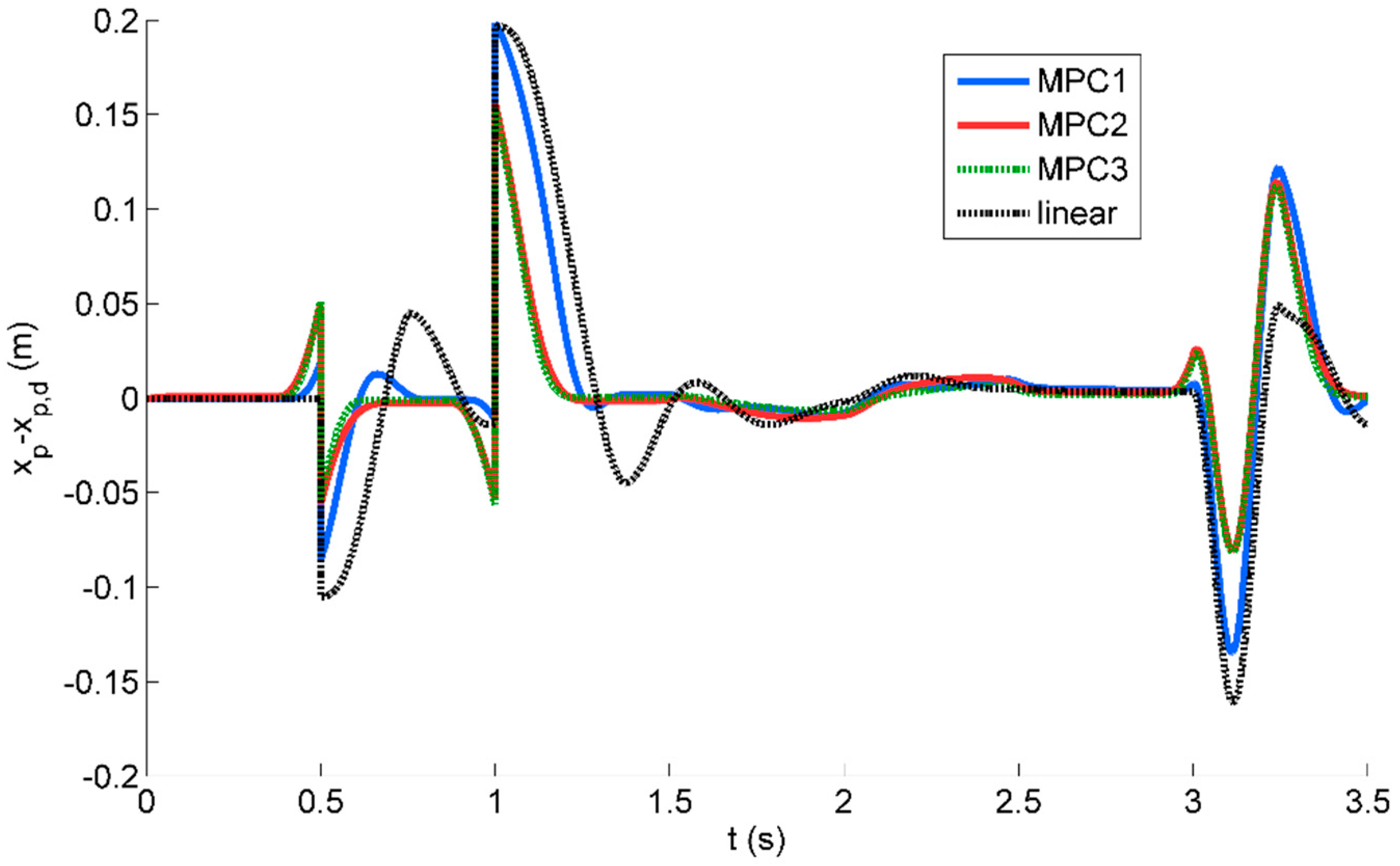
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Matrices for the State Space Models Used in MPC1, MPC2, and MPC3
References
- ISO/TS 15066:2016. Robots and Robotic Devices-Collaborative Robots; International Organization for Standardization: Geneva, Switzerland, 2016. [Google Scholar]
- Shin, D.; Sardellitti, I.; Khatib, O. A hybrid actuation approach for human-friendly robot design. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 1747–1752. [Google Scholar]
- Rouzbeh, B.; Bone, G.; Ashby, G.; Li, E. Design, Implementation and Control of an Improved Hybrid Pneumatic-Electric Actuator for Robot Arms. IEEE Access 2019, 7, 14699–14713. [Google Scholar] [CrossRef]
- Petrosky, L.J. Hybrid Electro-Pneumatic Robot Joint Actuator. U.S. Patent 478 225 828, 1 November 1988. [Google Scholar]
- Takemura, F.; Pandian, S.R.; Nagase, Y.; Mizutani, H.; Hayakawa, Y.; Kawamura, S. Control of a hybrid pneumatic/electric motor. In Proceedings of the 2000 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2000) (Cat No 00CH37113) IROS-00, Takamatsu, Japan, 31 October–5 November 2002; Volume 1, pp. 209–214. [Google Scholar]
- Teramae, T.; Noda, T.; Hyon, S.-H.; Morimoto, J.; Noda, T. Modeling and control of a Pneumatic-Electric hybrid system. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; Volume 4, pp. 4887–4892. [Google Scholar]
- Ishihara, K.; Morimoto, J. An optimal control strategy for hybrid actuator systems: Application to an artificial muscle with electric motor assist. Neural Netw. 2018, 99, 92–100. [Google Scholar] [CrossRef] [PubMed]
- Sharbafi, M.A.; Shin, H.; Zhao, G.; Hosoda, K.; Seyfarth, A. Electric-Pneumatic Actuator: A New Muscle for Locomotion. Actuators 2017, 6, 30. [Google Scholar] [CrossRef] [Green Version]
- Bone, G.; Chen, X. Position control of hybrid pneumatic-electric actuators. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 1793–1799. [Google Scholar]
- Bone, G.; Xue, M.; Flett, J. Position control of hybrid pneumatic–electric actuators using discrete-valued model-predictive control. Mechatronics 2015, 25, 1–10. [Google Scholar] [CrossRef]
- Nakata, Y.; Noda, T.; Morimoto, J.; Ishiguro, H. Development of a pneumatic-electromagnetic hybrid linear actuator with an integrated structure. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 6238–6243. [Google Scholar]
- Mori, S.; Tanaka, K.; Nishikawa, S.; Niiyama, R.; Kuniyoshi, Y. High-Speed Humanoid Robot Arm for Badminton Using Pneumatic-Electric Hybrid Actuators. IEEE Robot. Autom. Lett. 2019, 4, 3601–3608. [Google Scholar] [CrossRef]
- Johansen, T.A.; Fossen, T.I. Control allocation-A survey. Automatica 2013, 49, 1087–1103. [Google Scholar] [CrossRef] [Green Version]
- Härkegård, O. Dynamic Control Allocation Using Constrained Quadratic Programming. J. Guid. Control. Dyn. 2004, 27, 1028–1034. [Google Scholar] [CrossRef] [Green Version]
- Galeani, S.; Pettinari, S. On dynamic input allocation for fat plants subject to multi-sinusoidal exogenous inputs. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 2396–2403. [Google Scholar]
- Lofberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation (IEEE Cat No 04CH37508) CACSD-04, New Orleans, LA, USA, 2–4 September 2005; pp. 284–289. [Google Scholar]
- Mattingley, J.; Boyd, S. CVXGEN: A code generator for embedded convex optimization. Optim. Eng. 2011, 13, 1–27. [Google Scholar] [CrossRef]
- Hanger, M.; Johansen, T.A.; Mykland, G.K.; Skullestad, A. Dynamic model predictive control allocation using CVXGEN. In Proceedings of the 2011 9th IEEE International Conference on Control and Automation (ICCA), Santiago, Chile, 19–21 December 2011; pp. 417–422. [Google Scholar]
- Ning, S.; Bone, G. Development of a nonlinear dynamic model for a servo pneumatic positioning system. In Proceedings of the IEEE International Conference Mechatronics and Automation, Niagara Falls, ON, Canada, 29 July–1 August 2005; pp. 43–48. [Google Scholar]
- Taheri, B.; Case, D.; Richer, E. Force and Stiffness Backstepping-Sliding Mode Controller for Pneumatic Cylinders. IEEE/ASME Trans. Mechatronics 2014, 19, 1799–1809. [Google Scholar] [CrossRef]
- Richer, E.; Hurmuzlu, Y. A High Performance Pneumatic Force Actuator System: Part I—Nonlinear Mathematical Model. J. Dyn. Syst. Meas. Control. 1999, 122, 416–425. [Google Scholar] [CrossRef]


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 4.909 × 10−4 m2 | (MPC3) | 106 | |
| 4.123 × 10−4 m2 | 287 J/kg·K | ||
| 0.040418 | (MPC1) | diag([1, 1, 1, 1, 10−3]) | |
| 0.156174 | (MPC2) | diag([0.1, 0.5]) | |
| 0.5393 | (MPC3) | diag([0.1, 0.5]) | |
| 44.4 N·s/m | (MPC1) | 0 | |
| 13 N | (MPC2) | diag([0.1, 0]) | |
| 18 N | (MPC3) | diag([0.1, 0]) | |
| 1.4 | 293 K | ||
| 2000 N/m | Numerical integration timestep | 0.0005 s | |
| 30 N·s/m | (MPC2) | [−30, −60]T | |
| 500 N/m | (MPC2) | [30, 60]T | |
| 50 N·s/m | 5000 Pa·s | ||
| 5 × 10−5 Pa−1 | 70 | ||
| 5 × 10−4 Pa−1s−1 | 0.585 | ||
| 0.3 m | −7.51 | ||
| 0.03 m | 38.1 | ||
| 10 kg | −46.9 | ||
| 15 | 18.2 | ||
| 101,000 Pa | −21.3 | ||
| 0.528 | 3.42 | ||
| 404000 Pa | 5 × 10−5 | ||
| (MPC1) | diag([104, 10−3]) | 0 | |
| (MPC2) | 106 | 0.0015 s |
| Parameter | Value | |||
|---|---|---|---|---|
| MPC1 | MPC2 | MPC3 | Linear | |
| Sampling period (Ts) | 10 ms | 10 ms | 10 ms | 1 ms |
| Position tracking RMSE | 44.7 mm | 29.9 mm | 23.9 mm | 53.0 mm |
| Mean Absolute Fp | 29.73 N | 28.11 N | 28.81 N | 33.58 N |
| Mean Absolute Fe | 11.74 N | 7.78 N | 11.12 N | 12.24 N |
| Average calculation time per sample | 4.5 ms | 3.9 ms | 4.3 ms | 0.003 ms |
| Maximum calculation time per sample | 8.5 ms | 6.4 ms | 7.2 ms | 0.02 ms |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rouzbeh, B.; Bone, G.M. Optimal Force Allocation and Position Control of Hybrid Pneumatic–Electric Linear Actuators. Actuators 2020, 9, 86. https://doi.org/10.3390/act9030086
Rouzbeh B, Bone GM. Optimal Force Allocation and Position Control of Hybrid Pneumatic–Electric Linear Actuators. Actuators. 2020; 9(3):86. https://doi.org/10.3390/act9030086
Chicago/Turabian StyleRouzbeh, Behrad, and Gary M. Bone. 2020. "Optimal Force Allocation and Position Control of Hybrid Pneumatic–Electric Linear Actuators" Actuators 9, no. 3: 86. https://doi.org/10.3390/act9030086
APA StyleRouzbeh, B., & Bone, G. M. (2020). Optimal Force Allocation and Position Control of Hybrid Pneumatic–Electric Linear Actuators. Actuators, 9(3), 86. https://doi.org/10.3390/act9030086






