Position Control with ADRC for a Hydrostatic Double-Cylinder Actuator
Abstract
1. Introduction
2. System Principle and Mathematical Model
2.1. System Principle
2.2. System Mathematical Model
2.3. Controller Design
2.3.1. Tracking Differentiator (TD)
2.3.2. Extended State Observer (ESO)
2.3.3. Nonlinear State Error Feedback (NLSEF)
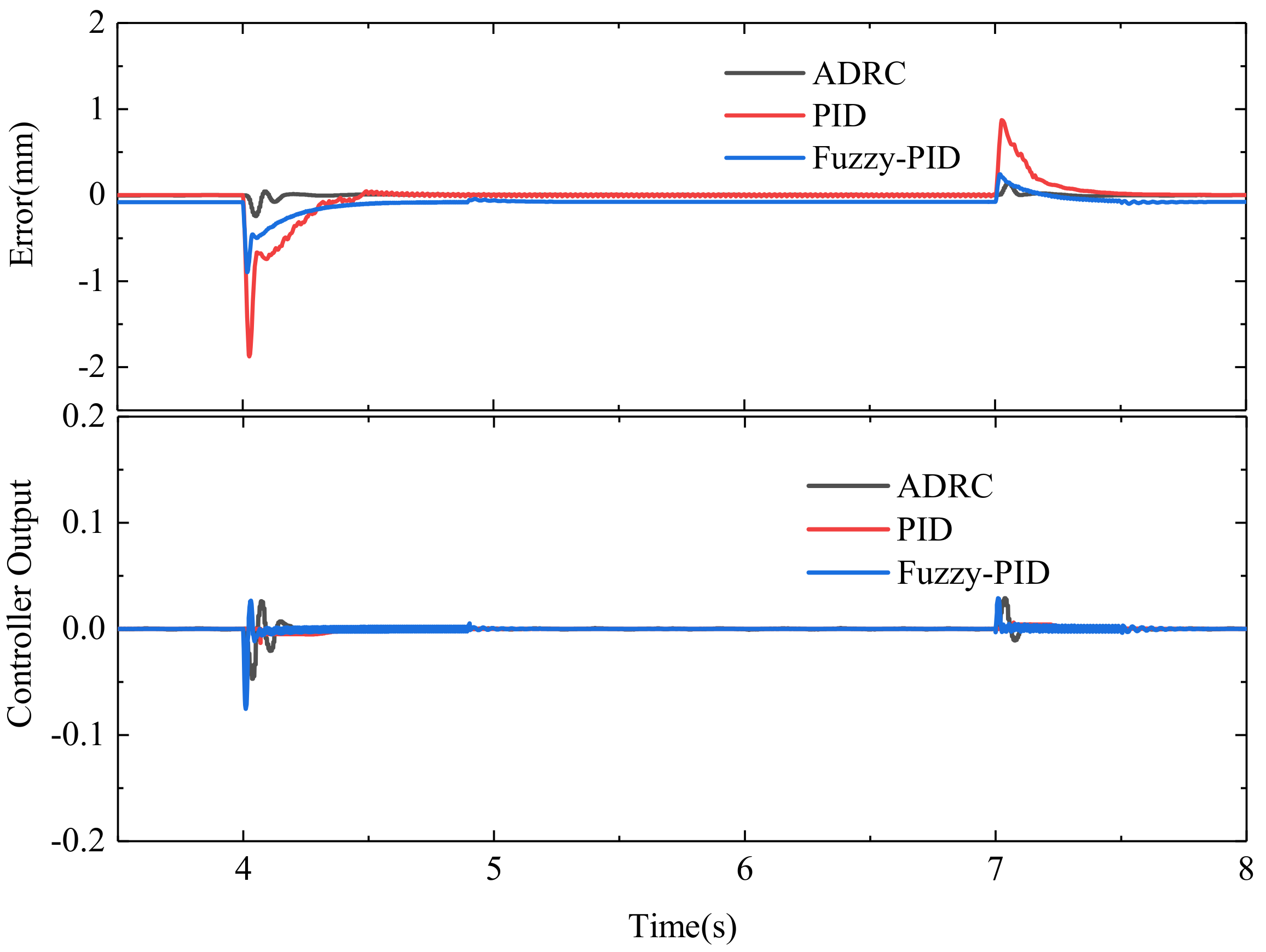
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chao, Q.; Zhang, J.; Xu, B.; Huang, H.; Pan, M. A Review of High-Speed Electro-Hydrostatic Actuator Pumps in Aerospace Applications: Challenges and Solutions. J. Mech. Des. 2019, 141, 050801-1. [Google Scholar] [CrossRef]
- Kim, J.-H.; Hong, Y.-S. Improvement of Backdrivability of a Force-Controlled EHA by Introducing Bypass Flow Control. Int. J. Precis. Eng. Manuf. 2020, 21, 819–830. [Google Scholar] [CrossRef]
- Fu, Y.; Han, X.; Sepehri, N.; Zhou, G.; Fu, J.; Yu, L.; Yang, R. Design and performance analysis of position-based impedance control for an electrohydrostatic actuation system. Chin. J. Aeronaut. 2018, 31, 584–596. [Google Scholar] [CrossRef]
- Ahn, K.K.; Nam, D.N.C.; Jin, M. Adaptive Backstepping Control of an Electrohydraulic Actuator. IEEE/ASME Trans. Mechatron. 2013, 19, 987–995. [Google Scholar] [CrossRef]
- Dong, L.; Yan, H.; Feng, L.; Tan, Q. Modelling and performance analysis of designed energy-efficient eha under gravity loads. Internat. J. Model. Identificat. Control 2018, 30, 253–260. [Google Scholar] [CrossRef]
- Minav, T.; Pietola, M.; Filatov, D.M.; Devyatkin, A.V.; Heikkinen, J. Fuzzy control of direct-driven hydraulic drive without conventional oil tank. In Proceedings of the 2017 XX IEEE International Conference on Soft Computing and Measurements (SCM), St. Petersburg, Russia, 24–26 May 2017; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2017; pp. 444–447. [Google Scholar]
- Minav, T.; Heikkinen, J.; Schimmel, T.; Pietola, M. Direct Driven Hydraulic Drive: Effect of Oil on Efficiency in Sub-Zero Conditions. Energies 2019, 12, 219. [Google Scholar] [CrossRef]
- Hyvärinen, J.; Karlsson, M.; Zhou, L. Study of concept for hydraulic hose dynamics investigations to enable understanding of the hose fluid–structure interaction behavior. Adv. Mech. Eng. 2020, 12, 1–18. [Google Scholar] [CrossRef]
- Farong, K.; Zhe, W.; Jiafeng, D.U.; Dong, L.I.; Jianan, X.U.; Linglan, H.E. Study on force tracking control of eha active suspensions. China Mech. Eng. 2017, 28, 2964–2970. [Google Scholar] [CrossRef]
- João, F.C.; João, B.P.; Fernando, G.A. Accurate motion control of a pneumatic linear peristaltic actuator. Actuators 2020, 9, 63. [Google Scholar] [CrossRef]
- Hao, W.; Kan, J. Application of self-tuning fuzzy proportional-integral-derivative control in hydraulic crane control system. Adv. Mech. Eng. 2016, 8, 1–10. [Google Scholar] [CrossRef]
- Truong, D.Q.; Ahn, K.K. Force control for hydraulic load simulator using self-tuning grey predictor—Fuzzy PID. Mechatronics 2009, 19, 233–246. [Google Scholar] [CrossRef]
- Ahn, K.K.; Truong, D.Q.; Thanh, T.Q.; Lee, B.R. Online self-tuning fuzzy proportional—Integral—Derivative control for hydraulic load simulator. Proc. Inst. Mech. Eng. Part I J. Syst. 2008, 222, 81–95. [Google Scholar] [CrossRef]
- Ye, Y.; Yin, C.-B.; Gong, Y.; Zhou, J.-J. Position control of nonlinear hydraulic system using an improved PSO based PID controller. Mech. Syst. Signal Process. 2017, 83, 241–259. [Google Scholar] [CrossRef]
- Esfandiari, M.; Sepehri, N.; Esfandiari, M. Controller Design and Stability Analysis of Output Pressure Regulation in Electrohydrostatic Actuators. J. Dyn. Syst. Meas. Control. 2018, 141, 041008. [Google Scholar] [CrossRef]
- Erik, E.; Georg, B.; Nathan, M. Analysis of the influence of suspension actuator limitations on ride comfort in passenger cars using model predictive control. Actuators 2020, 9, 77. [Google Scholar] [CrossRef]
- Yang, R.; Fu, Y.; Zhang, L.; Qi, H.; Han, X.; Fu, J. A Novel Sliding Mode Control Framework for Electrohydrostatic Position Actuation System. Math. Probl. Eng. 2018, 2018, 1–22. [Google Scholar] [CrossRef]
- Bone, G.M.; Xue, M.; Flett, J. Position control of hybrid pneumatic–electric actuators using discrete-valued model-predictive control. Mechatronics 2015, 25, 1–10. [Google Scholar] [CrossRef]
- Yang, G.; Yao, J. Output feedback control of electro-hydraulic servo actuators with matched and mismatched disturbances rejection. J. Frankl. Inst. 2019, 356, 9152–9179. [Google Scholar] [CrossRef]
- Castañeda, L.; Luviano-Juárez, A.; Ochoa-Ortega, G.; Chairez, I. Tracking control of uncertain time delay systems: An ADRC approach. Control. Eng. Pr. 2018, 78, 97–104. [Google Scholar] [CrossRef]
- Wu, Y.; Zheng, Q. ADRC or adaptive controller—A simulation study on artificial blood pump. Comput. Biol. Med. 2015, 66, 135–143. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Bai, W.; Yang, S.; Song, K.; Huang, Y.; Xie, H. ADRC with Adaptive Extended State Observer and its Application to Air–Fuel Ratio Control in Gasoline Engines. IEEE Trans. Ind. Electron. 2015, 62, 5847–5857. [Google Scholar] [CrossRef]
- Zhu, E.; Pang, J.; Sun, N.; Gao, H.; Sun, Q.; Chen, Z. Airship horizontal trajectory tracking control based on Active Disturbance Rejection Control (ADRC). Nonlinear Dyn. 2013, 75, 725–734. [Google Scholar] [CrossRef]
- Wu, Z.-H.; Guo, B.-Z. Approximate decoupling and output tracking for MIMO nonlinear systems with mismatched uncertainties via ADRC approach. J. Frankl. Inst. 2018, 355, 3873–3894. [Google Scholar] [CrossRef]
- Aboudrar, I.; el Hani, S.; Heyine, M.S.; Naseri, N. Dynamic Modeling and Robust Control by ADRC of Grid-Connected Hybrid PV-Wind Energy Conversion System. Math. Probl. Eng. 2019, 2019, 1–19. [Google Scholar] [CrossRef]
- Liu, C.; Luo, G.; Chen, Z.; Tu, W.; Qiu, C. A linear ADRC-based robust high-dynamic double-loop servo system for aircraft electro-mechanical actuators. Chin. J. Aeronaut. 2019, 32, 2174–2187. [Google Scholar] [CrossRef]
- Tian, Y.; Liu, B.; Gao, H.W.; Li, W.Q. Modeling and Simulation of Electro-Hydraulic Proportional Position Control System with the Flexible Hose. Adv. Mater. Res. 2012, 468, 2094–2099. [Google Scholar] [CrossRef]






















| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| m | 50 kg | r | 0.003 m | c1 | 140 |
| AP1 | 3.77 × 10−4 m2 | l | 10 m | γ1 | 0.5 |
| AP2 | 4.91 × 10−4 m2 | k11 | 6 × 105 | c2 | 120 |
| AA1 | 3.14 × 10−4 m2 | k12 | 5000 | γ2 | 0.1 |
| AA2 | 2.01 × 10−4 | k2 | 1 × 106 | cj | [−1.0 −0.5 0 0.5 1] |
| fs | 50 N | μvisc | 200 N·s/m | bj | 5 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| P | 7 | β02 | 100 | α2 | 0.4 |
| I | 0.01 | β03 | 30 | b0 | 0.02 |
| h | 0.002 | β1 | 50 | b | 5 |
| h0 | 0.002 | β2 | 0.1 | r | 0.005 |
| β01 | 50 | α1 | 0.5 | δ | 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Ji, H.; Chang, R. Position Control with ADRC for a Hydrostatic Double-Cylinder Actuator. Actuators 2020, 9, 112. https://doi.org/10.3390/act9040112
Wang B, Ji H, Chang R. Position Control with ADRC for a Hydrostatic Double-Cylinder Actuator. Actuators. 2020; 9(4):112. https://doi.org/10.3390/act9040112
Chicago/Turabian StyleWang, Bin, Hengyu Ji, and Rui Chang. 2020. "Position Control with ADRC for a Hydrostatic Double-Cylinder Actuator" Actuators 9, no. 4: 112. https://doi.org/10.3390/act9040112
APA StyleWang, B., Ji, H., & Chang, R. (2020). Position Control with ADRC for a Hydrostatic Double-Cylinder Actuator. Actuators, 9(4), 112. https://doi.org/10.3390/act9040112




