A Miniaturized Dual-Slider Linear Actuator Using Electrostatic Adhesion and Inertia Drive
Abstract
1. Introduction
2. Principle and Design of the Linear Actuator
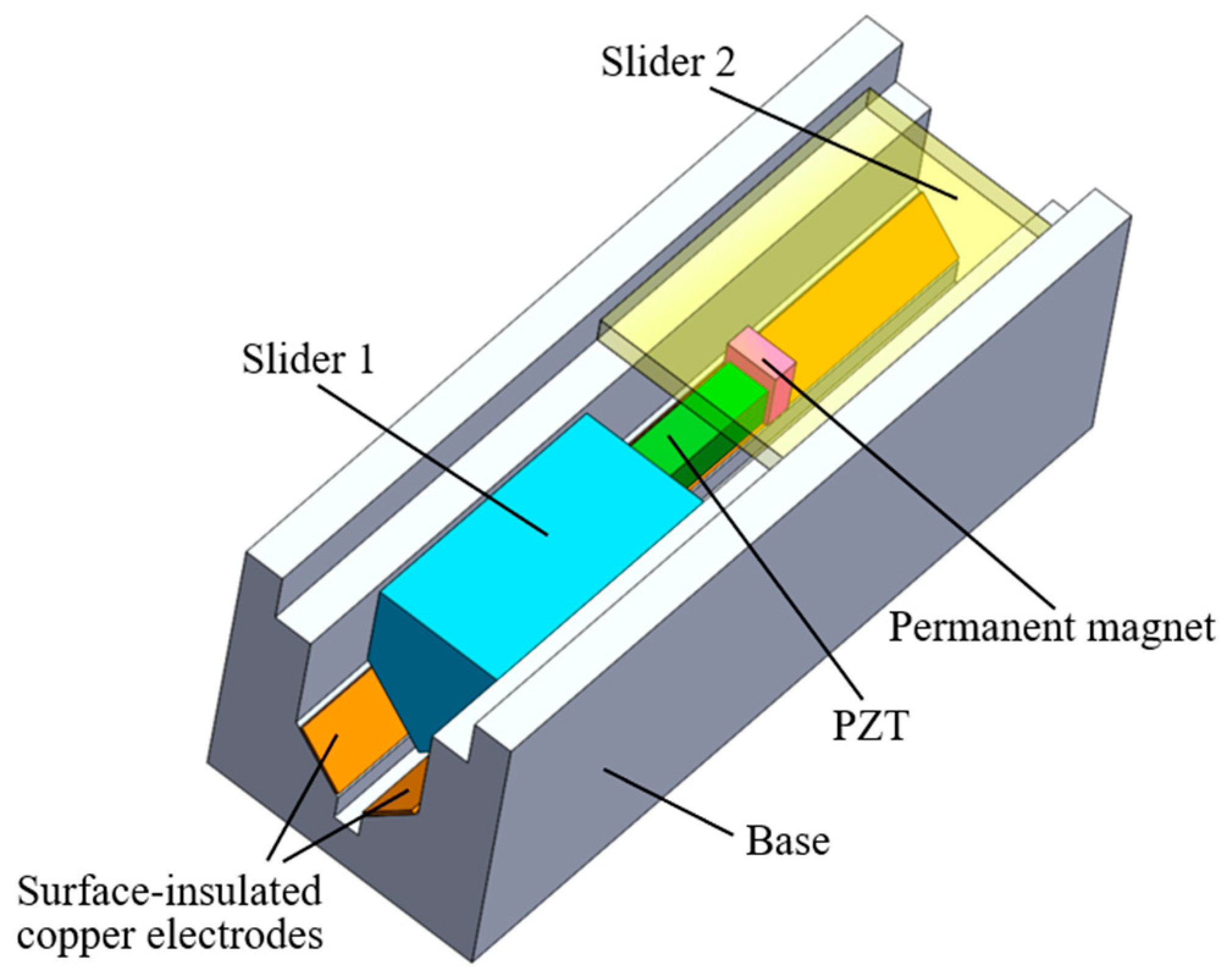
2.1. Design of the Dual-Slider Linear Actuator
2.2. Electrostatic Adhesion for IDM-SIDM Conversion
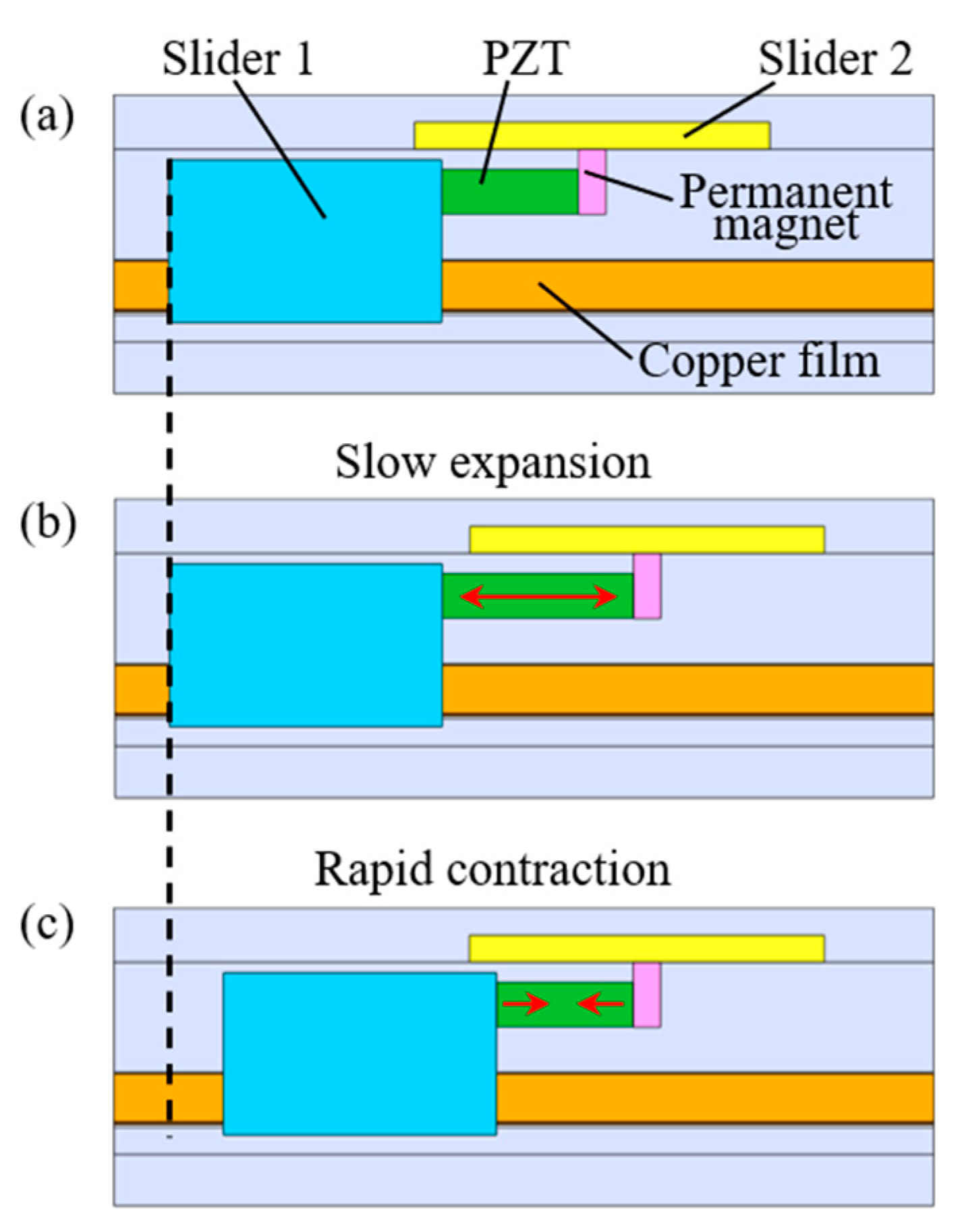
2.3. Inertia Drive for Dual-Slider Positioning
3. Experiments
3.1. Performance of the Electrostatic Adhesion
3.2. Dynamic Behavior of the PZT
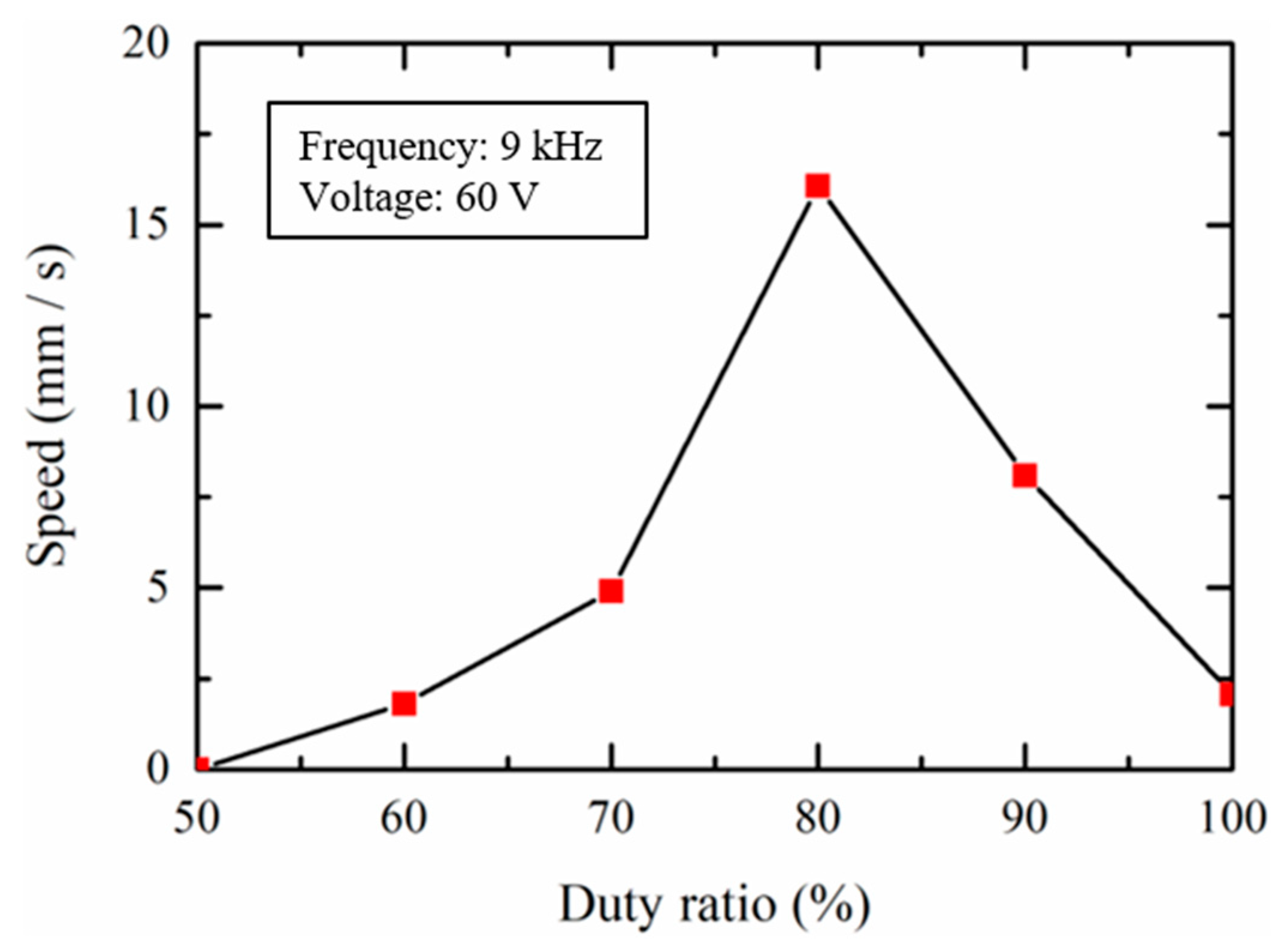
3.3. Driving Characteristics of the Slider 1
3.4. Driving Characteristics of the Slider 2
3.5. Other Performance of the Dual-Slider Positioning
3.5.1. Crosstalk of the Slider 2 in the IDM Mode
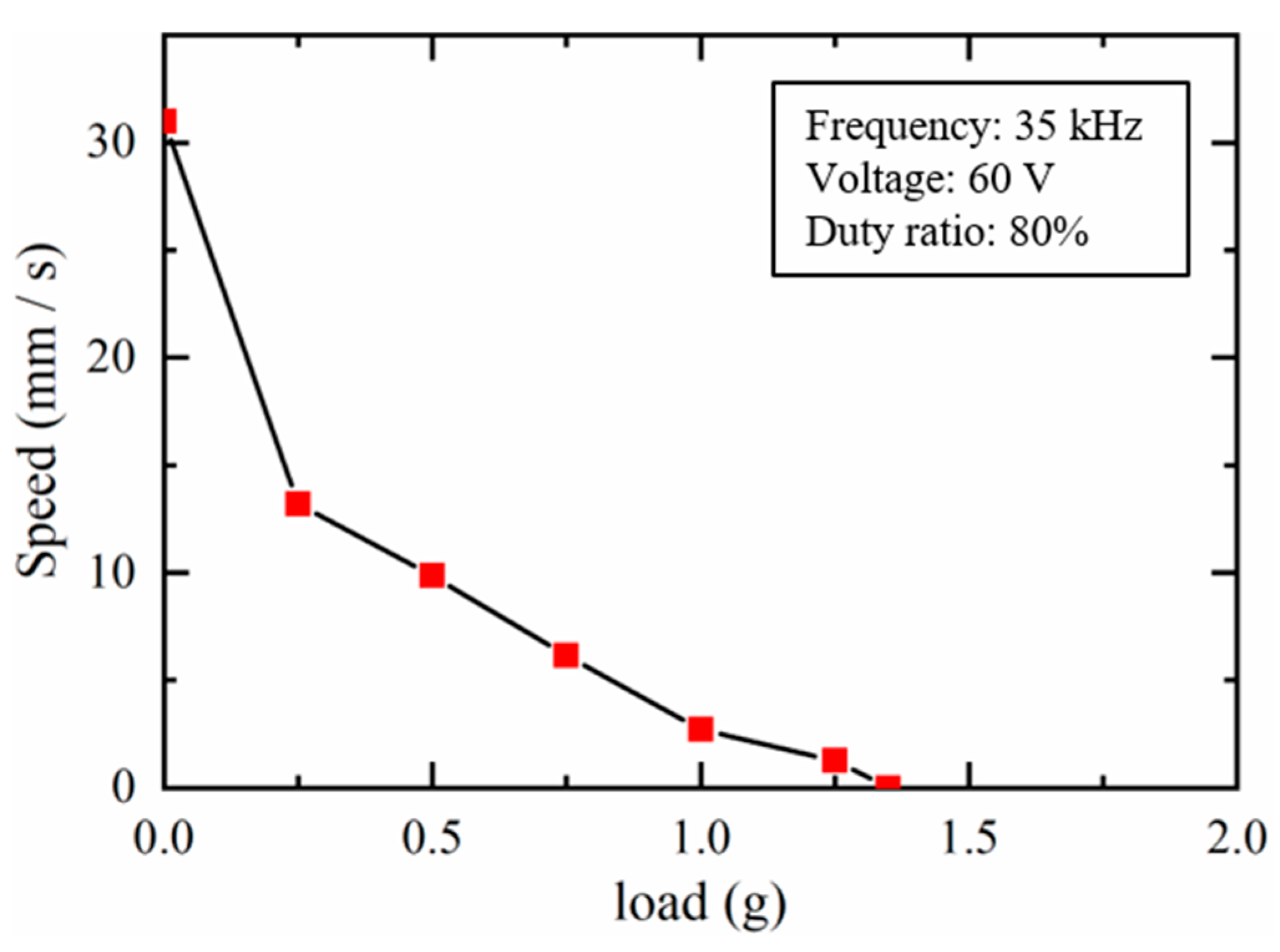
3.5.2. Load Capacity of the Dual Sliders
3.5.3. “Slip-Slip” Performance of the Dual Sliders
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, X.; Yamamoto, A. A multi-slider linear actuator using modulated electrostatic attraction and inertia effect. In Proceedings of the 2016 11th France-Japan & 9th Europe-Asia Congress on Mechatronics (MECATRONICS)/17th International Conference on Research and Education in Mechatronics (REM), Compiegne, France, 15–17 June 2016; pp. 296–297. [Google Scholar]
- Nguyen, T.A.; Konishi, S. Characterization of sliders for efficient force generation of electrostatically controlled linear actuator. J. Micromech. Microeng. 2014, 24, 055012. [Google Scholar] [CrossRef]
- Peng, Y.; Cao, J.; Guo, Z.; Yu, H. A linear actuator for precision positioning of dual objects. Smart Mater. Struct. 2015, 24, 125039. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, Y.; Zhang, M.; Yu, H.; Peng, Y. Modeling and experimental verification of a dual-slider piezo-actuated linear motor. Instrum. Exp. Tech. 2019, 62, 876–880. [Google Scholar] [CrossRef]
- Ozeki, Y.; Hata, T.; Shibatani, K.; Nagai, F.; Mori, N.; Nakabayashi, Y.; Mitsugi, N.; Nakano, S.; Bhatia, V.; Gregorski, S.J. Miniature multiple-axes adaptive optics unit employing SIDMs and its application to an efficient green laser module. Konica Minolta Technol. Rep. 2009, 6, 82–87. [Google Scholar]
- Matsusaka, K.; Ozawa, S.; Yoshida, R.; Yuasa, T.; Souma, Y. Ultracompact optical zoom lens for mobile phone. In Proceedings of the SPIE-IS&T Electronic Imaging, San Jose, CA, USA, 20 February 2007; p. 650203. [Google Scholar]
- Zhang, Y.; Lu, T.-F.; Al-Sarawi, S. Formulation of a simple distributed-parameter model of multilayer piezoelectric actuators. J. Intell. Mater. Syst. Struct. 2016, 27, 1485–1491. [Google Scholar] [CrossRef]
- Li, J.W.; Chen, X.B.; An, Q.; Tu, S.D.; Zhang, W.J. Friction models incorporating thermal effects in highly precision actuators. Rev. Sci. Instrum. 2009, 80, 045104. [Google Scholar] [CrossRef]
- Peng, J.Y.; Chen, X.B. Modeling of piezoelectric-driven stick–slip actuators. IEEE/ASME Trans. Mechatron. 2010, 16, 394–399. [Google Scholar] [CrossRef]
- Hunstig, M.; Hemsel, T.; Sextro, W. Modelling the friction contact in an inertia motor. J. Intell. Mater. Syst. Struct. 2013, 24, 1380–1391. [Google Scholar] [CrossRef]
- Xia, H.; Han, L.; Pan, C.; Jia, H.; Yu, L. Simulation of motion interactions of a 2-DOF linear piezoelectric impact drive mechanism with a single friction interface. Appl. Sci. 2018, 8, 1400. [Google Scholar] [CrossRef]
- Pan, P.; Zhu, J.; Gu, S.; Ru, C. Development of stick-slip nanopositioning stage capable of moving in vertical direction. Microsyst. Technol. 2020, 26, 2945–2954. [Google Scholar] [CrossRef]
- Li, J.; Huang, H.; Morita, T. Stepping piezoelectric actuators with large working stroke for nano-positioning systems: A review. Sens. Actuators Phys. 2019, 292, 39–51. [Google Scholar] [CrossRef]
- Peng, Y.; Peng, Y.; Gu, X.; Wang, J.; Yu, H. A review of long range piezoelectric motors using frequency leveraged method. Sens. Actuators Phys. 2015, 235, 240–255. [Google Scholar] [CrossRef]
- Spanner, K.; Koc, B. Piezoelectric motors, an overview. Actuators 2016, 5, 6. [Google Scholar] [CrossRef]
- Hunstig, M. Piezoelectric inertia motors—A critical review of history, concepts, design, applications, and perspectives. Actuators 2017, 6, 7. [Google Scholar] [CrossRef]
- Higuchi, T.; Yamagata, Y.; Furutani, K.; Kudoh, K. Precise positioning mechanism utilizing rapid deformations of piezoelectric elements. In Proceedings of the IEEE Proceedings on Micro Electro Mechanical Systems, An Investigation of Micro Structures, Sensors, Actuators, Machines and Robots, Napa Valley, CA, USA, 11–14 February 1990; pp. 222–226. [Google Scholar]
- Okamoto, Y.; Yoshida, R. Development of linear actuators using piezoelectric elements. Electron. Commun. Jpn. Part III Fundam. Electron. Sci. 1998, 81, 11–17. [Google Scholar] [CrossRef]
- Yoshida, R.; Okamoto, Y.; Okada, H. Development of smooth impact drive mechanism (2nd report)-optimization of waveform of driving voltage. J. Jpn. Soc. Prec. Eng. 2002, 68, 536–542. (In Japanese) [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Peng, Y.; Song, X.; Zhang, Y.; Zhang, M. Waveform optimization of a two-axis smooth impact drive mechanism actuator. J. Intell. Mater. Syst. Struct. 2020. [Google Scholar] [CrossRef]
- Ha, J.-L.; Fung, R.-F.; Yang, C.-S. Hysteresis identification and dynamic responses of the impact drive mechanism. J. Sound Vib. 2005, 283, 943–956. [Google Scholar] [CrossRef]
- Fung, R.-F.; Han, C.-F.; Ha, J.-L. Dynamic responses of the impact drive mechanism modeled by the distributed parameter system. Appl. Math. Model. 2008, 32, 1734–1743. [Google Scholar] [CrossRef]
- Shao, Y.; Shao, S.; Xu, M.; Song, S.; Tian, Z. An inertial piezoelectric actuator with miniaturized structure and improved load capacity. Smart Mater. Struct. 2019, 28, 055023. [Google Scholar] [CrossRef]
- Wang, H.; Yamamoto, A.; Higuchi, T. A crawler climbing robot integrating electroadhesion and electrostatic actuation. Int. J. Adv. Rob. Syst. 2014, 11, 191. [Google Scholar] [CrossRef]
- Wang, H.; Yamamoto, A. Analyses and solutions for the buckling of thin and flexible electrostatic inchworm climbing robots. IEEE Trans. Rob. 2017, 33, 889–900. [Google Scholar] [CrossRef]

















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Wang, H.; Zhang, Y.; Liu, W.; Liu, L.; Peng, Y. A Miniaturized Dual-Slider Linear Actuator Using Electrostatic Adhesion and Inertia Drive. Actuators 2020, 9, 114. https://doi.org/10.3390/act9040114
Song X, Wang H, Zhang Y, Liu W, Liu L, Peng Y. A Miniaturized Dual-Slider Linear Actuator Using Electrostatic Adhesion and Inertia Drive. Actuators. 2020; 9(4):114. https://doi.org/10.3390/act9040114
Chicago/Turabian StyleSong, Xian, Hongqiang Wang, Yangkun Zhang, Wenming Liu, Li Liu, and Yuxin Peng. 2020. "A Miniaturized Dual-Slider Linear Actuator Using Electrostatic Adhesion and Inertia Drive" Actuators 9, no. 4: 114. https://doi.org/10.3390/act9040114
APA StyleSong, X., Wang, H., Zhang, Y., Liu, W., Liu, L., & Peng, Y. (2020). A Miniaturized Dual-Slider Linear Actuator Using Electrostatic Adhesion and Inertia Drive. Actuators, 9(4), 114. https://doi.org/10.3390/act9040114






